1.
Introduction
Increased blood viscosity may damage blood vessels and increase the risk of heart attacks and vascular strokes, the leading causes of death globally. Scientists have commonly used drugs like aspirin to reduce blood viscosity. However, taking aspirin in high doses results in various side effects such as blood clots, stomach bleeding, ulcers, and even ringing in the ears. Magnetic field therapy may be a potent way to lower the risk of heart attacks. For decades, magnetic fields have been used in medical diagnostics, such as magnetic resonance imaging (MRI). In hospitals, high-strength magnets of 1.5 to 3 teslas have been used with no harmful effects on the body and improve nerve signals. However, more magnetic therapy research for a health and safety solution under various physiological and experimental conditions is required for correct treatment protocols to prevent heart attack and vascular stroke.
Blood is a predominantly shear-thinning fluid primarily related to the rheological properties of red blood cells (RBC) [1,2]. RBC aggregation is reversible and shear dependent. This aggregation is reformed at low shear rates and is dispersed at high shear. According to Baieth [3] and Connes et al. [4], increasing shear rates decreases blood viscosity exponentially. Blood is a non-Newtonian homogeneous fluid treated as an electrically conducting magnetic fluid. It exhibits magnetohydrodynamic (MHD) properties. A wide range of research was conducted practically and theoretically to study the influence of the magnetic field on blood viscosity and blood flow characteristics. Yamamoto et al. [5] experimented with investigating the impact of a magnetic field on the change of blood viscosity. It is found that a 1.5-tesla making a change in blood oxygenation causes an increment in blood viscosity and a shear rate of blood flow. The relative blood viscosity decreases as a function of the applied magnetic field. Some researchers [6,7] used rheometers with varying shear rates to measure blood viscosity in a static magnetic field. A change in blood viscosity alters blood vessels' velocity and flow rate. According to experimental results from Haik et al. [8], when exposed to a high magnetic field of 10 tesla, the blood flow rate can be reduced by 30% due to increased blood viscosity. Mathematical models have been developed for various situations under a transverse magnetic field [9,10,11,12,13,14]. They pointed out that increasing the intensity of the transverse magnetic field reduces blood flow rate. Moreover, Tzirakis et al. [15] presented a Symmetric Weighted Interior Penalty formulation to study the impact of the magnetoviscous effects on the generated viscosity of non-Newtonian biomagnetic fluid flow. Gayathri and Shailendhra [16] studied blood flow in human arteries under a magnetic field. The results indicated that there was no significant change in velocity and parameters such as relative residence time, wall shear stress (WSS), and oscillatory shear index were observed up to 3 teslas in small arteries.
Several studies on the influence of magnetic fields on temperature were conducted under various conditions. Misra et al. [17] examined the flow and heat transfer in a parallel plate channel with stretching walls of a viscoelastic electrically conducting fluid under a magnetic field effect. They showed that the magnetic field enhances the blood temperature. According to Dar [18], thermal radiation and an angled magnetic field affect the peristaltic transport of blood flow with variable viscosity. It shows that increasing the thermal radiation parameter and the magnetic strength decreases the axial speed, while increasing the heat source/sink parameter or the angle of inclination of the magnetic field increases the axial speed. Alimohamadi and Sadeghy [19] demonstrated that a bi-directional magnetic field can lower the wall shear stress and temperature of hot spots on porous plaque in stenotic arteries.
Additionally, much research focusing on the impact of temperature-dependent viscosity has been carried out. Nadeem and Akbar [20] reported that the viscosity variation depending on temperature for blood and oil is more prominent than other impacts. Also, Makinde and Onyejekwe [21] examined the MHD steady flow and heat transfer between two parallel plates of an electrically conducting fluid with temperature-dependent variable viscosity. They discovered that as viscosity increases, the heat transfer rate at the stationary wall decreases. Shit and Majee [22] studied unsteady blood flow and heat transfer characteristics with various viscosity values subjected to magnetic and vibration environments. The results show that an increase in the temperature-dependent viscosity increases the flow rate and temperature.
On the other hand, the magnetic field can improve blood circulation while relaxing blood vessels. In Tao-Huang experiment [23], velocity of blood is set to be in the same direction as the magnetic field lines inside a tool measuring blood viscosity. They reported that the exposed magnetic field of 1.3 teslas for at least 1 minute could dramatically reduce the blood viscosity by 20 to 30%. A similar study was carried out by Kadhim [24]. The viscosity of blood samples was determined under a 1.5-tesla MRI magnetic field using a U-tube viscometer and a mathematical formula. It is observed that the blood viscosity drops as the time of magnetic field exposure increases. This viscosity reduction is significant for 1 minute and 15-minute exposure samples. Furthermore, Keshtkar et al. [25] used the finite element method to simulate fluctuations of blood velocity in pulse electromagnetic fields. The results show that strong pulses of transient electromagnetic fields enhance fluid velocity with lower fluctuations at various temperatures. Javadzadegan et al. [26] reported the magnetic effects on blood viscosity and wall shear rate. An increase in high or ultra-high magnetic field strengths results in beneficial and adverse effects, such as lower viscosity in smaller areas of low wall shear stress and increased maximum wall shear stress.
This paper presents a MHD blood flow and heat transfer through a system of coronary arteries with LAD stenosis. The system of coronary arteries consists of the base of the aorta, the right coronary artery (RCA), and the left coronary artery (LCA), with two branches, including left circumflex (LCX) and left anterior descending (LAD) coronary arteries. According to the literature, this study hypothesizes that the exerted magnetic field parallel to the blood flow direction can reduce blood viscosity and enhance blood flow. The imposed magnetic field strength-dependent and temperature-dependent variables have been considered for a modified non-Newtonian blood viscosity. The work is structured as follows. The mathematical model of the study problem is presented in Section 2, and the numerical technique is illustrated in Section 3. Section 4 concerns a numerical example. The conclusion and discussion are summarized in Section 5.
2.
Mathematical model
To investigate the effect of the magnetic field on blood flow behavior through the coronary system. Blood is assumed to be an incompressible non-Newtonian fluid. The applied magnetic field has an impact on fluid viscosity after 60 seconds [23]. Based on a non-Newtonian model, blood viscosity (η) depends on shear rate, temperature, and magnet strength [27,28]. Here, the viscosity of the incompressible MHD non-Newtonian fluid is
As blood loses viscosity and decreases surface tension on the arterial wall when the blood temperature rises with high activation energy, we thus define the term H(t) by
where T is the blood temperature, α∈[0,0.4] is Arrhenius activation energy [29], Tα=37∘C denotes the tissue temperature and Ts=25∘C is the surrounding temperature. The modified Carreau-Yasuda viscosity model is used for blood viscosity. In Eq (2.1), ˆη is determined by
with shear rate given by
In Eq (2.1), B0 is the external magnetic field, (c1+c2|B0|)<1 and other model parameters are constants.
The pulsatile MHD flow and heat transfer of blood through the system of coronary arteries with stenosis are governed by a set of partial differential equations, including the continuity Eq (2.4), the momentum Eq (2.5), the energy Eq (2.6) and the Maxwell's equation for magnetic field (2.9):
where u=(u1,u2,u3)T is the velocity vector, p,T denote respectively pressure and temperature of blood, and ρ,cp,k denote the density, the heat capacity and thermal conductivity. F is the Lorentz force term, determined by
where J=σ(E+u×B) denotes the induced current density vector, E denotes the electric field, and B is the magnetic field that is assumed to be in the form of
with the induced magnetic field b which can be calculated based on Ohm's law and Maxwell's equation by
where μ and σ denote the media's magnetic permeability and electrical conductivity, respectively. The heat source term or the Joule heating rate, ST in Eq (2.6), and the magnetic source term Sb in Eq (2.9) are respectively determined by
To define the above unsteady state MHD problem completely, boundary and initial conditions are required. Here, we set the behavior of blood flow as the pulsatile conditions for pressure and flow rate in the terms of periodic functions P(t)=P(t+mTc) and Q(t)=Q(t+mTc) for m=1,2,3,…,M with cardiac period Tc=0.80 s. The waveforms of P(t) and Q(t) can be represented by the following Fourier series.
where ¯p represents the mean pressure, ¯Q is the mean flow rate, ω=2πTc is the angular frequency with the period Tc, and M denotes the number of harmonics considered.
At the aorta inlet (∂Ωin) with an inlet cross-sectional area of A,
● the velocity and temperature are defined by
● the magnetic flux is set to zero: ∫∂ΩinB⋅nds=0.
At the arterial wall (∂ΩΓ) with a unit outward normal vector n,
● the no-slip condition and the thermal convection condition are applied:
● the thin wall condition of induced magnetic field is applied:
where rp(xc) is mean radius of the arterial cross section c along the flow channel and h is the arterial wall thickness.
On the arterial outlets (∂Ωout) with a unit outward normal vector n,
● the pulsatile pressure is imposed to the outlet boundary (∂Ωout), i.e.,
● the temperature gradient is set to zero: ∂T∂n=0,
● the magnetic flux across the outlet cross section area is set to zero : ∫∂ΩoutB⋅nds=0.
For initial conditions, we set, for all x=(x,y,z)∈Ω,
Thus, the MHD blood flow and heat transfer in the coronary artery system with LAD stenosis is governed by the following initial boundary value problem (IBVP).
IBVP: Find vector functions u(t) and b(t), and scalar functions p(t) and T such that the field Eqs (2.4)–(2.6) and (2.9), and all boundary conditions are satisfied.
3.
Numerical approximation
3.1. Variational statement
The variational statement corresponding to the above initial boundary value problem is:
Find u,b∈[H1(Ω)]3 and p,T∈H1(Ω) such that all essential boundary conditions of b,u,p,T are satisfied and
where H1(Ω)={v|v,∂v∂x,∂v∂y,∂v∂z∈L2(Ω)} is a Sobolev space class and H1(Ω)=span{ϕi}∞i=1, with the norm ∥v∥2L2(Ω) and H1v={v∈H1|vis vanished on boundary}.
The notations a(u,v) and L(v) in Eq (3.1) represent respectively a bilinear form of u and v, and a linear form of v:
with
3.2. Galerkin Finite Volume Formulation
Based on standard Galerkin method, let Hh(Ω)=span{ϕn}Nn=1⊂H1(Ω) and Hh0=span{ϕn}Nn=1⊂H10, the problem (3.1) becomes
Find bh,uh∈[Hh(Ω)]3, and ph,Th∈Hh(Ω) such that all essential boundary conditions are satisfied and
with
The error distribution over Ω depends on the selection for the basis function ψn. To construct a control volume method, we choose nodal basis functions ψn=ϕn at coordinate xn of the element n:
Applying the gradient and divergence theorems with the approximate solutions yields, for i,j=1,2,3,
with
where |Ωn| is the volume of element Ωn.
Thus, the system of Eq (3.7) can be written in matrix form as
where U,B,T and P are global vectors with Un,Bn,Tn and Pn denoting the velocity, induced magnetic fields, temperature, and pressure at element n, and all coefficient matrices refer to global matrices. Matrices Db, Du and DT correspond to convection-diffusion terms. The matrix A corresponds to the pressure term. Matrices F,ST and Sb are the forcing terms.
4.
Numerical example
4.1. Computation domain and Model parameters
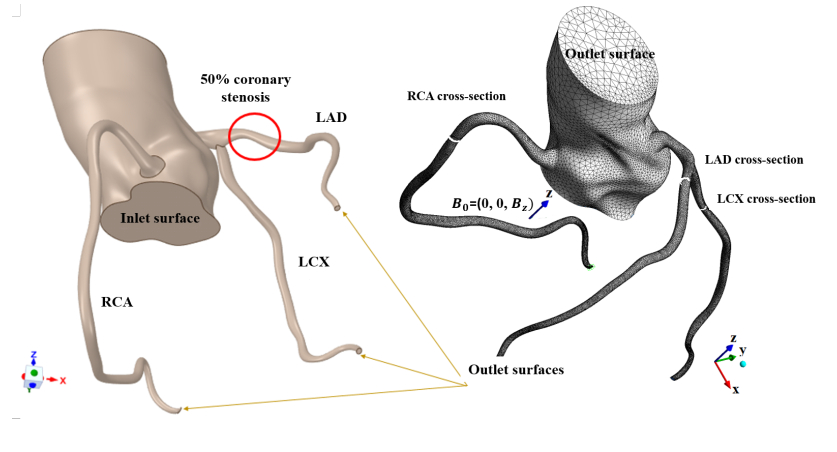
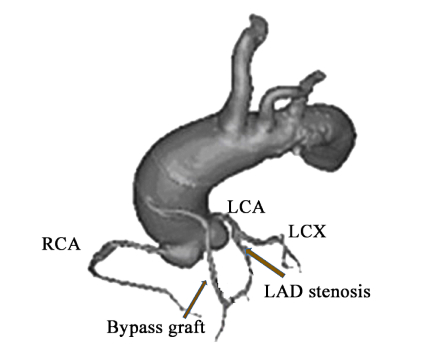
Based on the conventional angiogram of a coronary system having a LAD stenosis with bypass grafting as shown in Figure 1, our computational domain is the system of coronary arteries, including the regular RCA, the stenosed LAD, and the normal LCX, as shown in Figure 2. The ANSYS 2020 R1 software was used to conduct the simulation study. To speed up blood flow in the coronary arteries, we applied the external magnetic field in the same direction as inlet blood flow through the aorta, i.e.,
which creates the Lorentz force opposing pulsatile blood flow in the aorta but supports the flow rate of blood in the RCA, the LAD and the LCX.
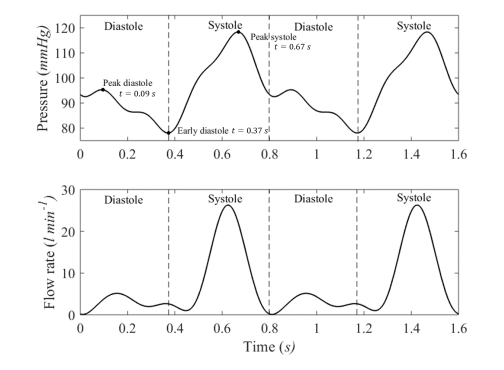
In the human cardiovascular system, heartbeat induces pulsatile pressure. During ventricular systole, with the ventricular wall contracted, the pressure within the ventricular wall exceeds that at the aortic root. When the ventricle relaxes during diastole, the aortic valve closes and the pressure within the wall falls below diastolic pressure. Consequently, blood is pumped from the aorta to the right and the left coronary arteries. Figure 3 shows the inflow periodic waveforms of blood pressure and flow rate with a cardiac cycle of 0.8s, which is typically within the valid range [30,31,32,33]. The general model parameters used in this numerical simulation are shown in Table 1 [33] and Table 2 [16,34,35,36]. Table 1 presents the values of αpm,βpm,αQm and βQm used in Eqs (2.11) and (2.12). Properties of blood and coronary artery are shown in Table 2.
4.2. Numerical results
Three values of the imposed magnetic field, |B0|=1,2 and 3 teslas, are chosen and applied parallel to the aorta. The impacts of the magnetic field on the magnitude of induced magnetic field (b), the magnitude of Lorentz force (F), blood shear rate (˙γ), the percentage of viscosity reduction, speed, and temperature distribution are presented in the following graphical and tabular forms. The results are considered at the 76th cardiac cycle after applying the external magnetic fields with the absence of temperature-dependent viscosity.
4.2.1. Induced magnetic field and Lorentz force
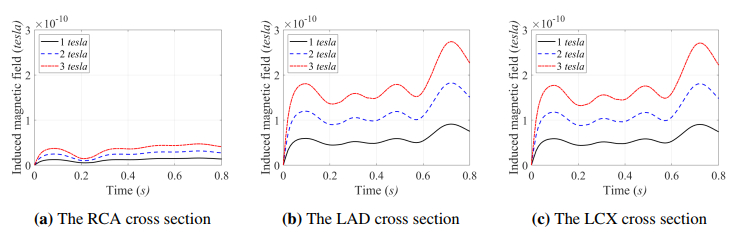
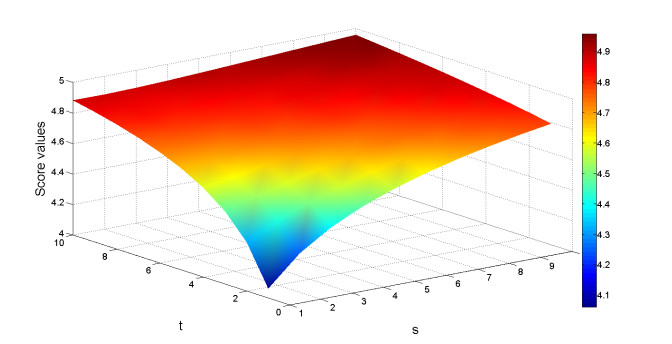
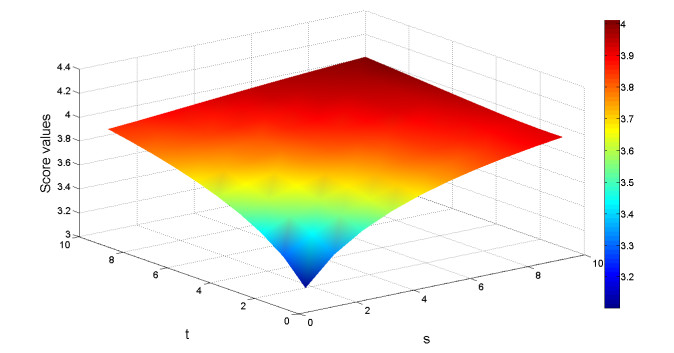
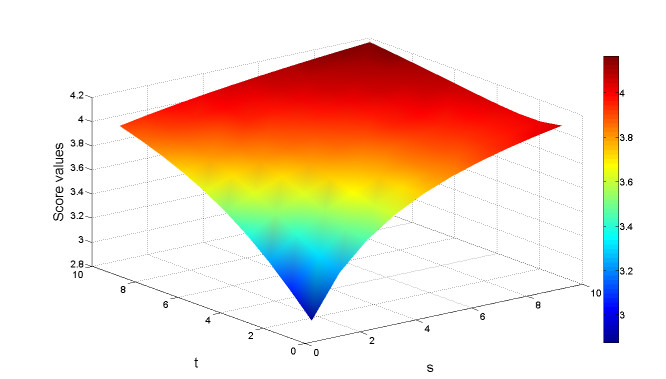
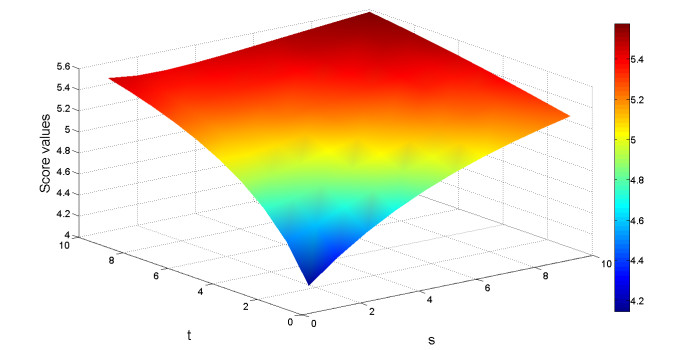
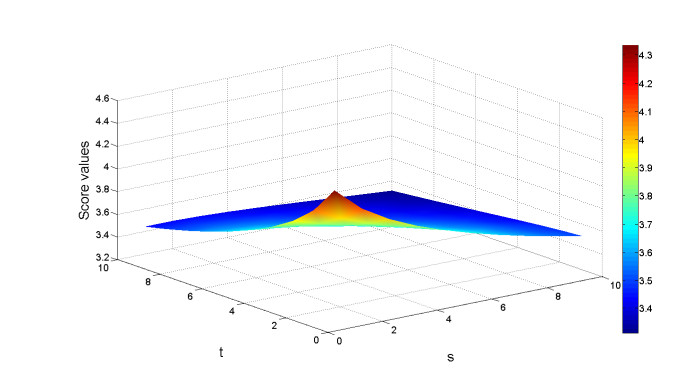
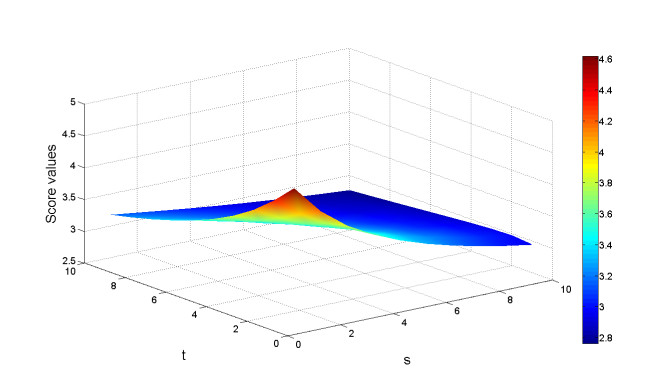
By increasing the magnetic intensity, B0, the magnitude of induced magnetic field, b, increases significantly for each artery cross section, as shown in Figure 4. The smallest magnitude of induced magnetic field occurs at the RCA cross section since this cross section is parallel to the inlet aorta, whereas the other cross sections are inclined towards it.
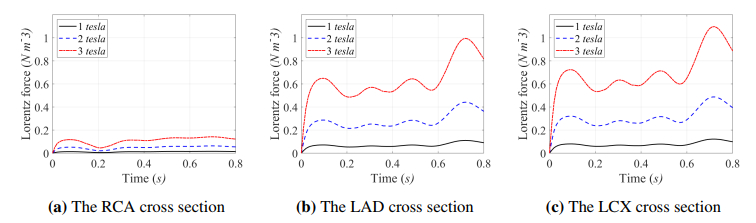
Applying a magnetic field to fluid results in the Lorentz force, which slows down the fluid in the aorta but speeds up the fluid in the RCA, the LAD and the LCX arteries. Figure 5 illustrates the magnitude of Lorentz force, F, obtained from the model with different |B0| values of 1, 2 and 3 teslas. It is noted that the force increases as the magnetic field increases.
4.2.2. Characteristics of blood flow and temperature
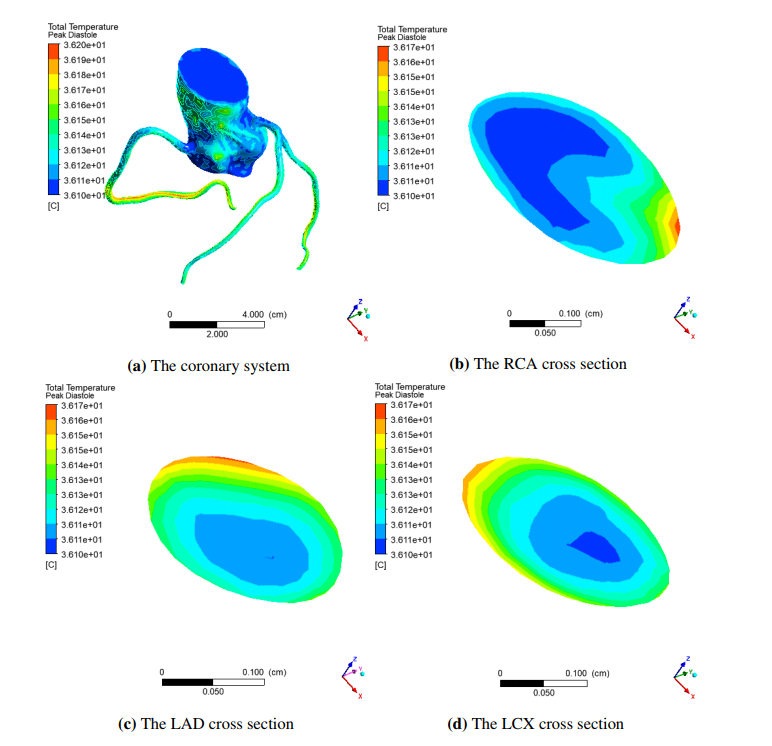
Since we focus on the coronary arteries, we thus consider the temperature distribution during diastole, which is the relaxation phase of the heart. To investigate the effect of magnetic field on temperature distribution using an initial blood temperature of 37∘C, temperature distribution on the RCA, the LAD and the LCX cross sections of the coronary system is examined. The results as shown in Figure 6 show the surface plots of temperature distributions obtained from the model with magnetic field strength of 1 tesla at the peak diastole. Temperatures vary between 36.1 and 36.2∘C on these three cross sections and the presence of a high temperature appears to be associated with arterial curvature.
Table 3 presents percentage of viscosity reduction obtained from the model with and without magnetic field. The percentage of viscosity reduction is determined from the results obtained from the unapplied and imposed magnetic fields. Three percentage values of viscosity reduction including average, minimum, and maximum viscosity for each cross section at different times are used to evaluate the magnetic effect. According to Table 3, the blood viscosity reduces as magnetic field strength increases. A high-intensity magnetic field produces a high percentage of viscosity reduction. For magnetic field intensities of 1, 2, and 3 tesla, the LAD cross section produces the average viscosity reduction in the ranges of [6.97%, 9.18%], [17.78%, 23.78%] and [22.22%, 29.75%], respectively. It is noted that percentage of viscosity reduction has a wide range of minimum values varying from about 6.91 to 74.18%, but a small range of maximum values varying from 23.15 to 31.62%. Our results align to the findings of the Tao-Huang experiment [23] and numerical studies [24,25,26].
Although each investigated cross section shaped like an ellipse with major and minor axes, we present model variables including the shear rate and the speed of blood only along the major axis.
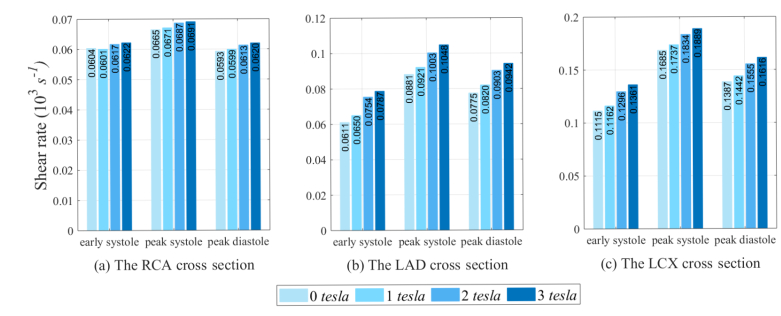
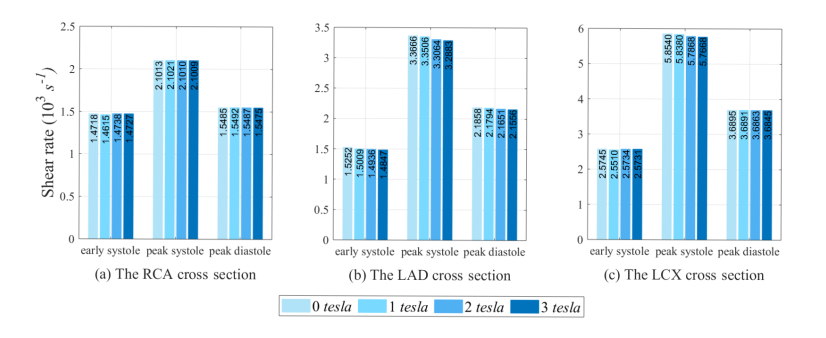
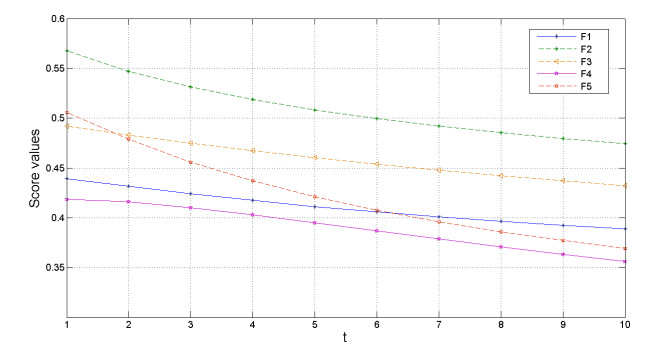
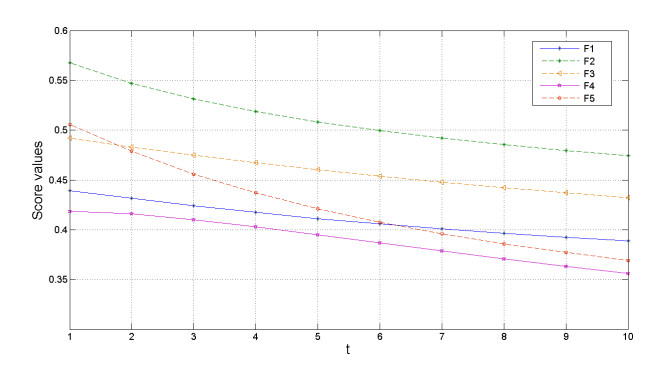
Figures 7 and 8 are bar plots of the minimum and maximum values of shear rate. The results indicate that the minimum shear rate increases as the magnetic field intensity increases. The minimum and maximum shear rates along the major axis of the LCX cross section for all choices of the magnetic strength are higher compared to other cross sections. For the model with a 3-tesla strength at the peak systole, the minimum shear rate along the major axis of the LCX artery is about 44.52 and 63.42% higher than those of the LAD artery and the RCA, respectively. This may relate to the greater curvature of the LCX artery with higher blood speed. However, there is no significant difference in maximum shear rate obtained from the model with different magnetic intensity as shown in Figure 8. Similarly, the maximum shear rate along the major axis of the LCX artery obtained from the model with a 3-tesla strength at the peak systole is about 42.98 and 63.57% higher than those of the LAD artery and the RCA.
For wall shear stress (WSS) investigation, the results are analysed along the total distance around the shape of each investigated cross section. The speed and flow rate are examined from the investigated cross sections. The comparison of the influence of magnetic fields on values of WSS, speed, and flow rate at the peak systole and the peak diastole on three cross sections with varying magnetic intensities ranging from 0 to 3 tesla is demonstrated in Table 4. The results reveal a decrease in maximum WSS as an increase in the magnetic field strength. The maximum values of WSS and speed at the peak systole are greater than those at the peak diastole. For the LAD artery, the WSS rises from 13.0838 to 13.4209 Pa at the peak systole and from 8.3849 to 8.4894 Pa at the peak diastole when magnetic intensity drops from 3 to 0 tesla.
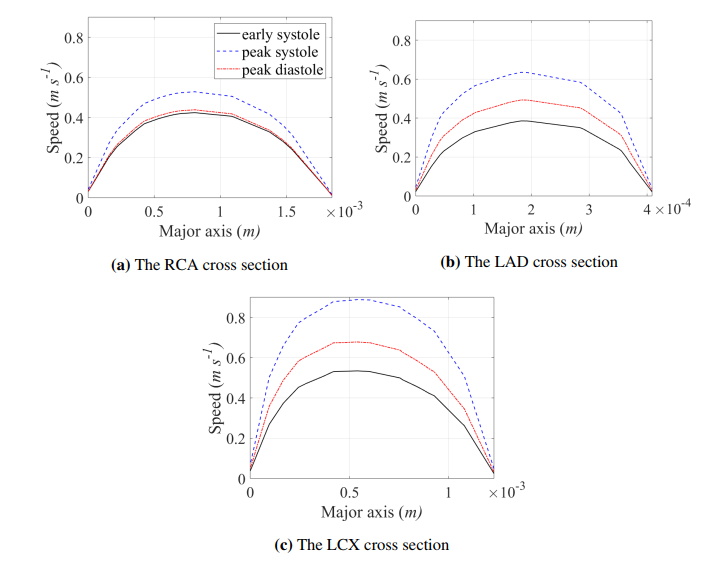
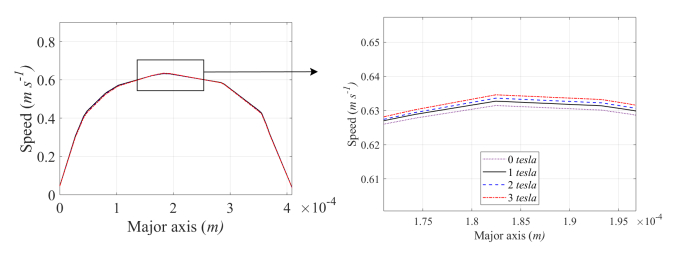
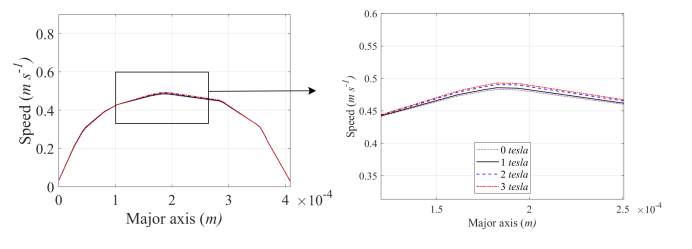
The blood speed in a full-wave cycle along the major axes of the RCA, the LCA, and the LCX cross sections obtained from the model with the magnetic intensity of a 3-tesla is investigated. The results show that the maximum speed along all investigated major axes is at the peak systole as shown in Figure 9. It is observed that the velocity profile of blood over the investigated cross section is parabolic. Blood speed along the LAD major axis reaches a maximum of 0.3976, 0.6461, and 0.5068 m⋅ s−1 during the early systole, the peak systole, and the peak diastole, respectively. Comparison of blood speed along major axes of LAD cross section for various values of magnetic field intensity at the peak systole and the peak diastole are made. The model with increasing amounts of magnetic field intensity improves blood flow with higher speed in the system of coronary artery. It is observed that higher magnetic strength produces greater blood speed as shown in Figures 10 and 11. As flow rate is directly proportional to the fluid speed. The flow rates across the investigated cross sections are also investigated. An increase in the magnetic field strength increases blood flow rate. It is more noticeable that maximum flow rates through LAD cross section increase about 0.83% at the peak systole and 2.78% at the peak diastole for the model with a 3-tesla magnetic intensity, compared to the one without a magnetic field.
In general, the blood flow rate is normally 10 ml⋅ min−1 with associated wall shear rates varying from 100 to 32,000 s−1 (equivalent to wall shear stress (WSS) between 0.35 and 112 Pa) depending on the presence of stenosis and the dimensions of flow channels [38]. The results here are acceptable as we obtain blood flow through the regular LCX artery with a normal flow rate while in the LAD artery with stenosis, a small flow rate of blood is obtained.
5.
Conclusions and discussion
Coronary artery disease (CAD), the most predominant form of heart disease, is one of the most common causes of death worldwide. Recent advances in treating patients with the CAD show promising effects in managing the CAD. These treatments combine different scientific disciplines of biotechnology and tissue engineering and have led to the development of novel therapeutic strategies. Magnetic therapy is one of the practical approaches widely used nowadays in medicine for preventing CAD, particularly myocardial infarction. Thus, it is essential to understand the impact on blood flow during acute exposure to a magnetic field. Recently, the effect of magnetic fields on blood flow has been a crucial topic for biomedical engineers.
The novelty of this paper is to introduce a new suggestion for variation imposed magnetic field effects on three-dimensional pulsatile MHD flow of blood in the three-dimensional system of coronary arteries with coronary stenosis. Blood is assumed to be incompressible non-Newtonian fluid through the system of coronary arteries, including the base of the aorta, the RCA, and two branches (LAD and LCX) of the LCA. Based on Carreau Model, blood viscosity depends on the blood temperature and Arrhenius activation energy. This study investigates the impact of magnetic field exposure on blood flow and temperature distribution in the system of the coronary arteries, with coronary stenosis appearing at the proximal LAD artery.
Findings from our study confirm that the magnetic field can control the heat and blood flow characteristics through the system of coronary arteries with coronary stenosis. The heat created from the magnetic field improves blood temperature. There is a change in the viscosity in the presence of a magnetic field. A stronger magnetic field reduces blood viscosity and enhances blood speed. However, other assumptions involved in the proposed three-dimensional pulsatile MHD flow model are also unrealistic to some extent. For example,
● Artery components of the RCA, the LAD, and the LCX arteries are not included in our computation domain.
● Although blood can flow through the inner layer of the arterial wall, in this study, the impact of the magnetic field on blood in this innermost layer is not considered.
● Blood is a biomagnetic fluid. It is necessary to select a magnetic field with an acceptable range of influence on the blood flow. However, this study only chose the magnetic field in a small range between 1 and 3 teslas.
These flaws restrict the implementation of the proposed model. However, the proposed model is still a powerful tool to estimate blood speed and temperature distribution in the system of coronary arteries with coronary stenosis. In future research, the arterial wall and branches of the RCA, the LAD, and the LCX arteries must be included in the computation domain. Blood flow through both the flow channel and the inner layer of the arterial wall must be investigated. In addition, the effect of the magnetic field intensity in small, medium, and high ranges on blood flow must be analysed numerically.
Acknowledgments
The first author would like to thank the Science Achievement Scholarship of Thailand (SAST) and the Faculty of Graduate Studies, Mahidol University, Thailand. The first author also thanks you to the School of Electrical Engineering, Computing and Mathematical Sciences, Curtin University, Australia, for all facilities supported during one year of student visit in 2020.
Data Availability
The data used to support the findings of this study are available from the corresponding authors upon request.
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: