A framework for long-lasting, slowly varying transient dynamics

1.   Introduction

Transient phenomena occur everywhere and are a growing subject of interest in modeling, especially in ecology ^[1,2]. A well-known example of transience is the "honeymoon period" of a disease, a period after the onset of mass vaccination wherein the number of infected individuals temporarily stays at a low level for a very long period of time ^[3]. This has been observed in both model simulations and real epidemiological systems ^[4,5]. Honeymoon periods may end with a resurgence of the disease that may be mistakenly attributed to a change in the system (e.g., pathogen evolution) when it is actually only the natural (and possibly volatile) end of a temporary but long-lasting respite from epidemics. Another type of transient phenomena is a temporary "population collapse" that occurs in many relatively simple models of interacting populations. In particular, fisheries exhibit these types of dynamics that can also last for decades despite the implementation of strict management practices ^[6,7]. A careful understanding of transient dynamics can have important ramifications in the control and prediction of the behaviour of complex systems for which asymptotic dynamics have already been established, including many examples arising from eco-epidemiological applications ^[8,9,10].

A series of pioneering papers by Hastings et al. ^[11,12], Morozov et al. ^[13,14] and Francis et al. ^[15] showed that transient behaviours can be organized into a classification system, related to the presence of invariant sets (such as saddle points and other saddle-type structures) or the disappearance of one as a parameter value is changed. In ^[13] long transience were characterized as either (1) having fast transitions between different dynamical regimes relative to other timescales of the dynamics, or (2) evolving "very slowly" for a long time compared to other relevant timescales. Motivated by the second characterization, we proposed definitions of mathematical quantities called "transient points" and "transient centers" in ^[16] to give technical and model-independent definitions of dynamics for which a certain observable of the system evolves "very slowly" for a "long time". In the case of the honeymoon period of the disease, we can set the observable to be the number of infectious individuals and show that this can be made to vary as slowly as desired for as long a period of time as desired if the trajectory goes through points in phase space with small enough initial numbers of infectious individuals ^[16]. These points cluster about states with zero infectious individuals and these states form an invariant set near which arbitrarily long and arbitrarily slow honeymoon periods can be generated. We note that only the observable is changing slowly at this point, the other states of the system (such as the number susceptible or recovered individuals), which are usually not observed in application, are typically not changing slowly during the honeymoon period ^[4].

In this paper we expand upon the previous work in ^[16] to formally define behaviours like honeymoon periods and temporary population collapses. We also look further into the properties of transient centers and their applications to ecological models. We emphasize here that we use the term "transient centers" for brevity, but what we mean are points that give rise to nearby trajectories where a fixed observable of the system can be made to vary arbitrarily slowly for a temporary period of time that can be made arbitrarily long. The concept of other types of transient dynamics including those characterized by rapid transitions between different regimes is beyond the scope of this study.

In Section 2 we establish our notation and give a quick overview of the results from ^[16], including our technical definitions of transience and transient centers. In Section 3 we present some extensions of our basic theory of transient centers, and in Section 4 we further extend this theory to apply to reachable transient centers. In Section 5 we derive sufficient and easily verifiable conditions to that which equilibria and associated trajectories are comprised of transient centers. In Section 6 we present applications of the new results to simple systems and in Section 7 we present applications to models from ecology and epidemiology. In Section 8 we review some of the implications of the new results and discuss future directions.

2.   Preliminaries

Let $f\in C(\mathbb{R}^n, \mathbb{R}^n)$. We consider the following autonomous ordinary differential equation system,

We use the notation $\phi^t \xi$ to denote the value at time $t$ of the solution to the initial value problem (2.1) with initialization given by $x(0) = \xi$. We also use the notation $|\cdot|$ to denote the $\ell_2$ norm. Throughout this manuscript, we make the following two assumptions,

(H1) For any $x(0) = \xi\in\mathbb{R}^n$, the system has a unique solution that is differentiable for all $t\in\mathbb{R}$.

(H2) For any $x(0) = \xi\in\mathbb{R}^n$, the system has a solution that is continuous in $\xi$ for all $t\in\mathbb{R}$.

We begin by reviewing some definitions and theorems from ^[16]. First, we define transient points as points whose forward trajectory exhibits long transient behaviour.

Definition 2.1 (Transient points, based on Definition 5.1 from ^[16]). Let $\xi\in\mathbb{R}^n$, $v\in C ^1(\mathbb{R}^n, \mathbb{R})$ and $s > 0$. Let $Dv(x) = \nabla v(x) \cdot f(x)$, this is the derivative of $v$ along the trajectories of solutions to (2.1). We define $T_{s}(\xi)$ to be,

Let $T > 0$. We say that $\xi$ is a $(v, s, T)-$transient point if $T < T_{s}(\xi) < \infty$.

Thus a $(v, s, T)$-transient point $\xi$ is a point such that if a trajectory is initialized at $\xi$, the value of the function $v$ along that solution changes slower than $s$ for longer than a given time scale $T$. While $v$ is changing slower than $s$ we say that the dynamics are "slow". The requirement that $T_s(\xi) < \infty$ guarantees that the value of $v$ does eventually stop being slow, distinguishing this slow transient dynamics from Lyapunov stable dynamics.

The value of $T_s(\xi)$ clearly depends on the choice of $v$ and the right-hand-side function $f$ in (2.1). When we need to specify $v$ and $f$ clearly we use the notation $T_s^{v, f}(x)$ instead of $T_s(x)$ to denote the expression in (2.2). Next, we define transient centers to be points whose neighborhoods contain transient points of arbitrary slowness $s$ over arbitrary time scales $T_D$.

Definition 2.2 (Transient centers, Definition 6.1 from ^[16]). Let $v\in C^1(\mathbb{R}^n, \mathbb{R})$. We call $\xi$ a $v$-transient center if there exists $S > 0$ such that for all $0 < s < S$ and all $T > 0$, in every neighborhood of $\xi$ there exists a $(v, s, T)$-transient point.

We also include the following theorem which provides necessary conditions for a point to be a transient center.

Theorem 2.3 (Theorem 6.2 from ^[16]). Let $v\in C^1(\mathbb{R}^n, \mathbb{R})$. If $\xi$ is a $v$-transient center then $Dv(\xi) = 0$.

Proof. If $|Dv(\xi)| = c\ne 0$ then from the continuity of $Dv$ we can find a neighbourhood with no $(v, s, T)$-transient points if $s = \frac{c}{2}$, which contradicts $\xi$ being a $v$-transient center. A similar proof is provided in ^[16].

We showed in ^[16] (and for completeness we will also prove here in Theorem 3.1 parts (a)–(b)) that not only is $Dv = 0$ at the transient center, but it remains zero throughout the entire forward trajectory of $\xi$. This led us to define $\Xi$, a collection of all points that satisfies the condition above in ^[16]. The set $\Xi$ is a set of candidates for transient centers.

Clearly this set $\Xi$ depends on the choice of $v$ and the right-hand-side function $f$ in (2.1). When it is important to denote what $v$ and $f$ are being used, we use the notation $\Xi^{v, f}$ instead of $\Xi$ to denote the set in (2.3). Clearly any equilibria of (2.1) is in $\Xi$. For any $\xi\in\Xi$, it is clear from the definition that along trajectories initialized near $\xi$ the value of $v$ can be made to vary slowly. However, for $\xi$ to be a transient center, we require trajectories to eventually exit the slow region.

3.   Basic properties of transient centers

In this section we strengthen some of the results we proved in ^[16] and derive additional results that demonstrate the basic properties of transient centers.

We begin with some of the basic properties of transient centers in Theorem 3.1. Some of these properties have already been presented in ^[16], but we include those parts here for completeness. The notation $D^m v(\phi^t \xi)$ refers to the $m$th derivative with respect to $t$ of $v$ along the trajectory $\phi^t \xi$. For any set $B\subset \mathbb{R}^n$ we use the notation $\phi^t B = \{\phi^t x: x\in B\}$.

Theorem 3.1. Let $v\in C^1(\mathbb{R}^n, \mathbb{R})$. If $\xi$ is a $v$-transient center then the following statements hold,

(a) $\phi^t\xi$ is a $v$-transient center for all $t\geq 0$.

(b) If $v\in C^{m}(\mathbb{R}^n, \mathbb{R})$ and $f\in C^{m-1}(\mathbb{R}^n, \mathbb{R}^n)$ then $D^k v(\phi^t\xi) = 0$ for $t\geq 0$, $k = 1, 2, \dotsc, m$ and $m\in\mathbb{Z}_{ > 0}$.

(c) If $Dv(\phi^{-t}\xi) = 0$ for all $t > 0$, $\phi^t\xi$ is a $v$-transient center for all $t\in\mathbb{R}$.

(d) $\xi$ is an $(\alpha v+\beta)$-transient center for all $\alpha\ne0$ and $\beta\in \mathbb{R}$.

(e) If $\xi$ is also a $u$-transient center and $|Du|\leq |Dw|\leq |Dv|$, where $u$ and $w\in C^1(\mathbb{R}^n, \mathbb{R})$, then $\xi$ is also $w$-transient center.

(f) Let $\xi\in\Xi$ and $\zeta\in\mathbb{R}^n$. Suppose that for any neighborhood $B$ of $\zeta$ there exist $\tau, t\in\mathbb{R}$ such that $\phi^\tau \xi \in \phi^t B$ then $\zeta$ is also a $v$-transient center.

Proof of (a). Let $S > 0$ be an $S$ that satisfies the requirements of $\xi$ being a transient center. Let $t > 0$ and $C$ be an arbitrary neighborhood of $\phi^t \xi$. By (H1)–(H2) we can find a neighborhood $B$ of $\xi$ such that $C\subset \phi^t B$. Let $s\in(0, S)$ and $T > 0$ be arbitrary. By choice of $S$, we can find a $(v, s, T+t)$-transient point $x$ in $B$. This maps to $\phi^t x\in C$ which is a $(v, s, T)$-transient point. This proves that $\phi^t\xi$ for arbitrary $t\geq 0$ is also a $v$-transient center with the same $S$. Another similar proof of this result is also presented in ^[16].

Proof of (b). For any fixed $m\in \mathbb{Z}_{ > 0}$ the base case $k = 1$ follows from part (a). The result follows from induction.

Proof of (c). Let $S > 0$ be an $S$ that satisfies the requirements of $\xi$ being a transient center. Consider $g(x, \tau) = |Dv(\phi^{-\tau}x)|$ for $x\in\mathbb{R}^n$ and $\tau > 0$. From $v\in C^1(\mathbb{R}^n, \mathbb{R})$, $f\in C(\mathbb{R}^n, \mathbb{R}^n)$, (H1)–(H2), $g(x, \tau)$ is continuous in both of its arguments. From parts (a)–(b) and the requirements of part (c), we must have $g(\xi, \tau) = 0$ for all $\tau$. Let $t > 0$, $s\in(0, S)$, $T > 0$ and $B$ be an arbitrary neighborhood of $\phi^{-t}\xi$. Let $R > 0$ be such that $B_R(\phi^{-t}\xi)\subset B$. Consider the collection of values $r_\tau$ for $\tau\in[0, t]$ defined as $r_\tau = \max\{r\in[0, R]: |Dv(\phi^{-\tau}x)| < s \; \forall x\in B_{r_\tau}\}$. By the continuity of $g$, $r_\tau > 0$ for all $\tau\in[0, t]$ and thus, by compactness, $r = \min_{\tau\in[0, t]} r_\tau > 0$. Since $\xi$ is a $v$-transient center, there exists $x\in B_r(\xi)$ that is a $(v, s, T)$-transient point. This maps to $\phi^{-t}x\in B$. By choice of $r$, $x$ must be a $(v, s, T+t)$-transient point, which means it is also a $(v, s, T)$-transient point. Thus $\phi^{-t}\xi$ must be a $v$-transient center for all $t > 0$. Putting this together with part (a) completes the proof of this part of the theorem.

Proof of (d). This easily follows from $T_s^{\alpha v+\beta, f}(\xi) = T_{s/|\alpha|}^{v, f}(\xi)$ if $\alpha\ne 0$.

Proof of (e). Let $u$, $v$ and $w\in C^1(\mathbb{R}^n, \mathbb{R})$. Suppose that $\xi$ is both a $u$- and $v$-transient center and $|Du|\leq |Dw|\leq |Dv(x)|$ for all $x\in\mathbb{R}^n$. Since $\xi$ is a $u$ and $v$-transient center, then there is an $S > 0$ such that for every $s\in(0, S)$ and $T > 0$, in every neighborhood of $\xi$ there is an $x$ such that $T < T_{s}^{u, f}(x) < \infty$ and $T < T_{s}^{v, f}(x) < \infty$. It follows that, $T < T_s^{v, f}(x)\leq T_{s}^{w, f}(x)\leq T_{s}^{u, f}(x) < \infty$. It follows that $\xi$ is also a $w$-transient center.

Proof of (f). By parts (a) and (c), since $\xi\in\Xi$ it follows that $\phi^{\tau-t}\xi$ is a $v$-transient center for any choice of $\tau$ and $t$. Let $S > 0$ be an $S$ that satisfies the requirements of $\phi^{\tau-t} \xi$ being a transient center. Let $B$ be a neighborhood of $\zeta$ and find $\tau, t$ such that $\phi^{\tau}\xi\in\phi^t B$. This means $\phi^{\tau-t}\xi\in B$ and we can find an $x\in B$ that is a $(v, s, T)$-transient point for any $s\in(0, S)$ and $T > 0$. Thus $\zeta$ is also a $v-$transient center.

Remark 3.2. Here are some remarks on the statements in Theorem 3.1.

(i) The condition that $Dv(\phi^t\xi) = 0$ for all $t < 0$ cannot be omitted in part (c). An example of why is presented in Example 6.4.

(ii) Theorem 6.11 from ^[16], which asserts that if there exists positive constants $a$ and $b$ such that $a|Dv|\leq |Du|\leq b|Dv|$ then a $v$-transient center $\xi$ is also a $u$-transient center, can also be proven from Theorem 3.1 parts (d) and (e).

(iii) Part (f) generalizes part (a) to include limit points. An example of when this applies is when the trajectory of $\xi$ will enter any neighborhood of $\zeta$ infinitely often forward or backward in time. This causes the transient center property of $\xi$ to translate to $\zeta$ as well. An application of this is given in Example 6.5.

In ^[16] we proved that if $\xi\in\Xi$ we do not need to find $(v, s, T)$-transient points for all $T > 0$ to show the transient center property. Instead it is enough to find points that eventually leave the slow region. For completeness we present this theorem here as Theorem 3.3 and give a stronger result in Theorem 3.4.

Theorem 3.3 (Theorem 6.8 from ^[16]). Let $v\in C^1(\mathbb{R}^n, \mathbb{R})$ and $\xi\in\Xi$. If there exists $S > 0$ such that for all $0 < s < S$, in any neighborhood of $\xi$ there is an $x$ such that $T_s(x) < \infty$ then $\xi$ is a $v$-transient center.

Proof. Let $S$ be as given in the conditions of the theorem. Let $s\in(0, S)$, $B$ be a neighborhood of $\xi$ and $T > 0$. Recall from Theorem 3.1 parts (a)–(b) we know that $Dv(\phi^t \xi) = 0$ for all $t\geq 0$. From $v\in C^1(\mathbb{R}^n, \mathbb{R})$, $f\in C(\mathbb{R}^n, \mathbb{R}^n)$ and (H1)–(H2), there exists $r > 0$ small enough such that $B_r(\xi)\subset B$ and $Dv(\phi^{T} z) < s$ for all $z\in B_r(\xi)$. Since $B_r(\xi)$ is a neighborhood of $\xi$ then by the requirements of the theorem there must be a point $x\in B_r(\xi)$ such that $T_s(\xi) < \infty$. By our choice of $r$ this must also satisfy $T_s(\xi) > T$. Thus $x\in B$ is a $(v, s, T)$-transient point. Since it is possible to find such a point for all neighborhoods $B$, $s\in(0, S)$ and $T > 0$, $\xi$ must be a $v$-transient center. A similar proof of this theorem is also presented in Theorem 6.8 in ^[16].

The next result changes the previous "if" statement to an "if and only if" statement with a simpler requirement that $T_s(x) < \infty$ for just one fixed slowness value $S^* > 0$ instead of requiring the property for all arbitrarily small slowness values $s\in(0, S)$.

Theorem 3.4. Let $v\in C^1(\mathbb{R}^n, \mathbb{R})$ and $\xi\in\Xi$. The point $\xi$ is a $v$-transient center if and only if there exists $S^* > 0$ such that in every neighborhood of $\xi$ there is an $x$ such that $T_{S^*}(x) < \infty$.

Proof. $\boxed{\rightarrow }$ Suppose that $\xi$ is a transient center. From the definition of a transient center, there exists an $S > 0$ such that for all given $s\in(0, S)$ and $T > 0$, in every neighborhood of $\xi$ there exists a $(v, s, T)$-transient point $x$. Set $S^*\in(0, s]$ and choose any $T > 0$. Recall that a $(v, s, T)$ transient point must have $T < T_{S^*}(x) < T_s(x) < \infty$. Thus in every neighborhood of $\xi$ we can always find an $x$ such that $T_{S^*}(x) < \infty$.

$\boxed{\leftarrow}$ Suppose that $\xi\in\Xi$ and there exists $S^* > 0$ such that in every neighborhood of $\xi$ there is an $x$ with $T_{S^*}(x) < \infty$. From the definition of $T_s(x)$ and the continuity of $Dv(\phi^t x)$, we must have $T_s(x) < T_{S^*}(x) < \infty$ for all $s\in(0, S^*)$. It follows from Theorem 3.3 that $\xi$ is a transient center.

The following corollary is a useful restatement of Theorem 3.4 that makes it clear what conditions are equivalent to a point $\xi\in\Xi$ not being a transient center.

Corollary 3.5. Let $v\in C^1(\mathbb{R}^n, \mathbb{R})$ and $\xi\in\Xi$. The point $\xi$ is not a transient center if and only if for all $s > 0$ and there exists a neighborhood $\mathcal{N}$ of $\xi$ such that $T_s(x) = \infty$ for all $x\in\mathcal{N}$.

4.   Reachable transient centers

In this section we further develop the ideas behind reachable transient points and reachable transient centers that we introduced in ^[16]. We begin by recalling the definitions of such points.

Definition 4.1. Consider the system (2.1) with $v\in C^1(\mathbb{R}^n, \mathbb{R})$. Let $T > 0$, $s > 0$ and $\xi$ be a $(v, s, T)$-transient point of this system. We call $\xi$ a reachable $(v, s, T)$-transient point if $\xi$ is also a $(v, s, T)$-transient point for the system with reversed time,

We denote the solution to (4.1) with initial condition $x(0) = \xi$ by $\hat \phi^t \xi$ and note that $\hat\phi^t\xi = \phi^{-t}\xi$.

Lemma 4.2 (Adapted from Theorem 8.2 from ^[16]). Let $\xi\in\mathbb{R}^n$, $\tau > 0$ and $\hat{\xi} = \phi^\tau\xi$. There exists a unique solution to (4.1) such that $\hat{\phi}^0\hat{\xi} = \hat{\xi}$ and for all $t\in[0, \tau]$ we have $\phi^{\tau-t}\xi = \hat{\phi}^t\hat{\xi}$.

Proof. Refer to the proof of Theorem 8.2 in ^[16].

In this section we also use the notation $\hat T_s(\xi)$ denote the hitting time (2.2) for the time-reversed system. In terms of our earlier notation where we specify $v$ and $f$, we have that $\hat T_s(\xi) = T^{v, -f}_s(\xi)$. From Lemma 4.2 it is clear that if $\xi$ is a reachable $(v, s, T_D)$-transient point of (2.1), there exists $\hat{\xi}$ with $|Dv(\hat{\xi})| = s$ such that,

Definition 4.3. Let $v\in C^1(\mathbb{R}^n, \mathbb{R})$. We call $\xi$ a reachable $v$-transient center if there exists $S > 0$ such that for all $0 < s < S$ and all $T > 0$, in every open neighborhood of $\xi$ there exists a reachable $(v, s, T)$-transient point.

Theorem 4.4. Let $v\in C^1(\mathbb{R}^n, \mathbb{R})$. Suppose that a point $\xi\in \mathbb{R}^n$ is a reachable $v$-transient center of (2.1). Then,

(a) $\xi$ is a $v$-transient center for both the forward equation (2.1) and the time-reversed equation (4.1).

(b) $\xi\in \Xi$.

Proof. Part (a) follows from the symmetry in Definitions 2.2, 4.1 and 4.3. Part (b) follows from part (a) and Theorem 3.1 part (a).

The converse of Theorem 4.4 part (a) does not hold. This is is easily illustrated by Example 4.5.

Example 4.5. Consider the system (2.1) in one-dimension with $f(x) = |x|$. The general solution to this system is,

Set $v(x) = x$ and $\xi = 0$. Then, $Dv(\phi^t x(0)) = |\phi^t x(0)|$. Let $s > 0$ and $T_D > 0$. We derive that,

Clearly, $x(0) = \epsilon se^{-T}$ for $\epsilon\in(0, 1)$ are the only $(v, s, T)$-transient points of (2.1).

Similarly we can solve for the same quantity for the time-reversed system (4.1),

It follows that $x(0) = -\epsilon se^{-T} < 0$ are the only $(v, s, T)$-transient points of (4.1) for any $\epsilon\in(0, 1)$.

The calculations above illustrate several things. First, the original (forward time) system (2.1) with $f(x) = |x|$ has $(v, s, T)$-transient point in every neighborhood of $\xi = 0$. Second, the reversed-time system (4.1) also has a $(v, s, T)$-transient point in every neighborhood of $\xi = 0$. Third, the two systems have different transient points and these transient points are not reachable. Thus, $\xi = 0$ is a $v$-transient center of both the forward time system and the reversed-time system, but it is not a reachable $v$-transient center.

We are able to obtain similar properties as in Theorem 3.1 for reachable transient centers.

Theorem 4.6. Let $v\in C^1(\mathbb{R}^n, \mathbb{R})$. If $\xi$ is a reachable $v$-transient center then the following statements hold,

(a) $\phi^t\xi$ is a reachable $v$-transient center for all $t\in\mathbb{R}$.

(b) If $v\in C^m(\mathbb{R}^n, \mathbb{R})$ and $f\in C^{m-1}(\mathbb{R}^n, \mathbb{R}^n)$ then $D^k v(\phi^t\xi) = 0$ for $t\in\mathbb{R}$, $k = 1, 2, \dots, m$ and $m\in\mathbb{Z}_{ > 0}$.

(c) $\xi$ is a reachable $v$-transient center for the reversed flow.

(d) $\xi$ is a reachable $(\alpha v+\beta)$-transient center for all $\alpha\ne0$ and $\beta\in\mathbb{R}$.

(e) If $\xi$ is also a reachable $u$-transient center and $|Du|\leq |Dw|\leq |Dv|$, where $u$ and $w\in C^1(\mathbb{R}^n, \mathbb{R})$, then $\xi$ is also a $w$-transient center.

(f) If $\zeta\in\mathbb{R}^n$ is such that for any open neighborhood $B$ of $\zeta$ there exist $\tau, t\in\mathbb{R}$ such that $\phi^\tau\xi\in \phi^t B$ then $\zeta$ is also a $v$-transient center.

Proof of (a). Let $S > 0$ be an $S$ that satisfies the requirements of $\xi$ being a reachable $v$-transient point.

Consider $g(x, \tau) = |Dv(\phi^{\tau}x)|$ for $x\in\mathbb{R}^n$ and $\tau\in\mathbb{R}$. From $v\in C^1(\mathbb{R}^n, \mathbb{R})$, $f\in C(\mathbb{R}^n, \mathbb{R}^n)$, (H1)–(H2), $g(x, \tau)$ is continuous in both of its arguments. From Theorem 4.4 part (b) we must have $g(\xi, \tau) = 0$ for all $\tau$. Let $t\in\mathbb{R}$, $s\in(0, S)$, $T > 0$ and $B$ an arbitrary neighborhood of $\phi^t \xi$. Let $I = [0, t]$ if $t\geq 0$ and $[t, 0]$ otherwise. Let $R > 0$ be such that $B_R(\phi^{t}\xi)\subset B$. Consider the collection of values $r_\tau$ for $\tau\in I$ defined as $r_\tau = \max\{r\in[0, R]: |Dv(\phi^{\tau}x)| < s \; \forall x\in B_{r_\tau}\}$. By the continuity of $g$, $r_\tau > 0$ for all $\tau\in[0, t]$ and thus, by compactness, $r = \min_{\tau\in I} r_\tau > 0$. Since $\xi$ is a reachable $v$-transient center, there exists $x\in B_r(\xi)$ that is a reachable $(v, s, T+|t|)$-transient point. This maps to $\phi^{t}x\in B$. By choice of $r$ we get that:

● If $t\geq 0$ then $\phi^t x$ must be a $(v, s, T)$-transient point for the forward system and a $(v, s, T+2|t|)$-transient point for the time-reversed system.

● If $t < 0$ then $\phi^t x$ must be a $(v, s, T+2|t|)$-transient point for the forward system and a $(v, s, T)$-transient point for the time-reversed system.

In either case, $\phi^t x$ is a reachable $(v, s, T)$-transient point. This proves that $\phi^t\xi$ is a reachable $v$-transient center.

Proof of (b). For any fixed $m\in \mathbb{Z}_{ > 0}$ the base case $k = 1$ follows from Theorem 4.4 part (c). The result follows from induction. The other cases follow using induction.

Proof of (c). This follows from the Definition 4.3.

Proof of (d). This result follows from observing that $T_s^{\alpha v+\beta, f}(\xi) = T_{s/|\alpha|}^{v, f}(\xi)$ and $T_s^{\alpha v+\beta, -f}(\xi) = T_{s/|\alpha|}^{v, -f}(\xi)$ if $\alpha\ne 0$.

Proof of (e). This is very similar to the proof of Theorem 3.1 part (e).

Proof of (f). This uses part (a) and is similar to the proof of Theorem 3.1 part (f).

Remark 4.7. The main differences between the results for reachable transience centers (Theorem 4.6) and the original results (Theorem 3.1) is that we do not require an extra condition for $t < 0$ for part (a), and $\xi\in \Xi$ in part (f) is already guaranteed by Theorem 4.4.

The next result shows that if $\xi\in\Xi$ then we can simplify the conditions to prove that $\xi$ is a reachable transient center. This follows the style of Theorem 3.4 for simple transient centers.

Theorem 4.8. Let $v\in C^1(\mathbb{R}^n, \mathbb{R})$ and $\xi\in\Xi$. The point $\xi$ is a reachable transient center if and only if there exists $S^* > 0$ such that in every neighborhood of $\xi$ there is an $x$ such that $T_{S^*}(x) < \infty$ and $\hat T_{S^*}(x) < \infty$

Proof. This proof is similar to the proof of Theorem 3.4.

5.   Equilibria and transient centers

We now move on to finding conditions for equilibria to be transient centers. Recall that an equilibrium $\xi$ of (2.1) is Lyapunov stable if for every $\epsilon > 0$ there exists $\delta > 0$ such that $|\xi-x| < \delta$ implies $|\xi-\phi^t x| < \epsilon$. Using Corollary 3.5, we easily prove that Lyapunov stable equilibria are in $\Xi$ but they cannot be transient centers. This means stable nodes, stable spirals and centers cannot be transient centers for any choice of $v$.

Theorem 5.1. Let $v\in C^1(\mathbb{R}^n, \mathbb{R})$.

(a) If $\xi$ is an equilibrium of (2.1) then $\xi\in\Xi$.

(b) If $\xi$ is a Lyapunov stable equilibrium of (2.1) then $\xi$ is not a $v$-transient center.

Proof of (a). Let $\xi$ be an equilibrium. Then $\phi^t\xi = \xi$, $f(\xi) = 0$ and $Dv(\phi^t\xi) = Dv(\xi) = \nabla v(\xi)\cdot f(\xi) = \nabla v(\xi)\cdot 0 = 0$ for all $t\in\mathbb{R}$. This shows that $\xi\in\Xi$.

Proof of (b). Let $\xi$ be a Lyapunov stable equilibrium. From part (a), $\xi\in\Xi$. Let $s > 0$ and $\mathcal{N}_1$ be any bounded neighborhood of $\xi$. Since $v$ is continuously differentiable, $|\nabla v(x)|$ is continuous in $x$ and we can find an $M > 0$ such that $|\nabla v(x)| < M$ for all $x\in\mathcal{N}_1$. Since $f$ is continuous and $f(\xi) = 0$ we can find a neighborhood $\mathcal{N}_2$ of $\xi$ such that $\mathcal{N}_2\subset \mathcal{N}_1$ and $|f(x)| < \frac{s}{M}$ for all $x\in\mathcal{N}_2$. Finally, since $\xi$ is Lyapunov stable, we can find a neighborhood $\mathcal{N}_3$ of $\xi$ such that $\mathcal{N}_3\subset\mathcal{N}_2$ and $\phi^t x \in \mathcal{N}_2$ for all $x\in\mathcal{N}_3$ and $t\geq 0$. Thus, for any $x\in\mathcal{N}_3$, $|Dv(\phi^t x)| = |\nabla v(\phi^t x)\cdot f(\phi^t x)|\leq |\nabla v(\phi^t x)|| f(\phi^t x)| < (M)\big(\frac{s}{M}\big) = s$ for all $x\in\mathcal{N}$. Since this is true for arbitrary $s > 0$, it follows from Corollary 3.5 that $\xi$ is not a transient center.

Next we recall the definitions of stable/unstable subspaces, sets and manifolds associated with (2.1) following ^[17]. Here we use the notation $\phi^{-t}$ to denote the flow in backward time, with $\phi^{-t}\hat \xi = \hat\phi^t\hat\xi$. We also use the notation $H_v(x)$ to represent the Hessian matrix of $v$ and $Jf(x)$ to represent the Jacobian of any function $f\in C^1(\mathbb{R}^n, \mathbb{R}^n)$ evaluated at $x\in\mathbb{R}^n$. A superscript $T$ denotes the transpose of matrix or vector.

Definition 5.2 (Stable/unstable subspaces, sets and manifolds ^[17]). Let $f\in C^1(\mathbb{R}^n, \mathbb{R}^n)$, $\xi$ be an equilibrium of (2.1) and $A = Jf(\xi)$. The subspace $E$ and $F$ defined below are respectively the stable and unstable spaces of the linearization of (2.1) system about $\xi$.

where $\lambda_i$ is an eigenvalue of $A$ with multiplicity $a_i$, for $i = 1, \dotsc, n$. We define the stable set $\mathcal{W}^E(\xi)$ and unstable set $\mathcal{W}^F(\xi)$ to be,

On a fixed neighborhood $U(\xi)$ of $\xi$, we can also define the stable manifold $M^E(\xi)$ and unstable manifold $M^F(\xi)$ to be,

where

If $\xi$ is a hyperbolic fixed point, Teschl ^[17] has shown that there is a neighborhood $U$ of $\xi$ such that,

where $G$ is the topological conjugacy obtained from Hartman-Grobman Theorem in ^[17] (also presented in the appendix for convenience as Lemma 8.2).

Theorem 5.3. Let $v\in C^2(\mathbb{R}^n, \mathbb{R})$ and $f\in C^1(\mathbb{R}^n, \mathbb{R}^n)$. Suppose that $0$ is a hyperbolic equilibrium of the system (2.1) and $A = Jf(0)$. Let $E$ and $F$ respectively be the stable and unstable eigenspaces associated with $0$. If $F = \{0\}$ then $0$ cannot be a $v$-transient center. If $E = \{0\}$ then $0$ cannot be a reachable $v$-transient center.

Proof. This follows from Theorems 5.1 and 4.4.

Now we consider unstable equilibria and when they are transient centers. We first look at unstable equilibria of linear systems.

Theorem 5.4. Let $f(x) = A(x-\xi)$ for some $A\in\mathbb{R}^{n\times n}$ with at least one positive and real eigenvalue. Let $F$ be the unstable eigenspace of $\xi$. If $\{\xi+z:z\in F\}\not\subset\{x:\nabla v(x)\cdot f(x) = 0\}$ then $\xi$ is a $v$-transient center.

Proof. For ease of notation we first set $\xi = 0$. Let $A$ and $F$ be as required in the theorem. We can find a point $x^*\in F$ such that $x^*\notin\{x:\nabla v(x)\cdot f(x) = 0\}$. Then $S^* = |\nabla v(x^*)\cdot f(x^*)| > 0$. Since $f(\xi) = 0$ clearly $x^*\ne 0$.

By considering the system in reversed time initialized at $x^*$ we derive the unique trajectory $e^{-At}x^*$ and we know that $e^{-At}x^* \in F$ for all $t$ (Lemma 8.1). Since this subspace is spanned by the generalized eigenvectors of $A$ corresponding to eigenvalues with positive real parts, we must have $e^{-At}x^* \to 0$ as $t\to \infty$. For every neighborhood of $\bf{0}$ there exists a $t > 0$ such that the point $e^{-At}x^*$ is in that neighborhood. Going back to the linear flow in forward time, this point has the property that $T_{S^*}(e^{-At}x^*) = t < \infty$. By Theorem 3.4, $0$ is a $v$-transient center.

The proof of the case for general $\xi\in\mathbb{R}^n$ follows easily using the translation $y = x-\xi$ and the system $\frac{dy}{dt} = Ay$.

This last theorem on unstable equilibria of linear systems being transient centers can be extended to hyperbolic unstable equilibria of nonlinear systems. Later we present and prove a more general theorem that works for nonlinear systems as Theorem 5.7 which includes a condition to show reachability. The ideas behind this theorem is very similar to the last proof but with more technical detail to deal with the nonlinearity. This requires Lemmas 5.5 and 5.6.

Lemma 5.5. Let $v\in C^2(\mathbb{R}^n, \mathbb{R})$ and $f\in C^1(\mathbb{R}^n, \mathbb{R}^n)$. The gradient of $Dv(\phi^t\xi)$ is given by,

Proof. This follows from using the product rule on $\nabla Dv|_{\phi^t\xi} = \nabla \big(\nabla v\cdot f\big)|_{\phi^t\xi}$.

Next we present a $\lambda$-lemma which we will use to prove our main results in this section. We recall first that $\lambda$-lemmas are used to describe the trajectories near a hyperbolic manifold. Here we only present a version for hyperbolic fixed points. For the case of general hyperbolic manifolds refer to ^[18] and ^[19].

Lemma 5.6 ($\lambda$-lemma). Let $f\in C^1(\mathbb{R}^n, \mathbb{R}^n)$. Suppose that $0$ is a hyperbolic equilibrium of the system (2.1) with associated nontrivial stable manifold $M^E$ and nontrivial unstable manifold $M^F$. Let $x^{**}\in M^E$ and $x^*\in M^F$. For any neighbourhoods $B_0$ of $0$, $B_1$ of $x^*$ and $B_2$ of $x^{**}$, there exists $x\in B_0$ and $t_1, t_2 > 0$ such that $\phi^{t_1}x\in B_1$ and $\phi^{-t_2}x\in B_2$.

Proof. Since $0$ is a hyperbolic fixed point then $\mathbb{R}^n = E\oplus F$. If $E$ or $F$ is $\{0\}$ the proof is trivial. So we consider the case when both are non-trivial. By the Hartman-Grobman Theorem (as stated in the appendix as Lemma 8.2) there exists a homeomorphism $G$ with open domain $U$ containing $0$ such that for all $x\in U$,

Let $r > 0$ be sufficiently small so that there exists $R > 0$ such that,

Since $x^{**}\in M^E$ and $x^{*}\in M^F$ we must have $\phi^t x^{**}\to 0$ and $\phi^{-t} x^{*}\to 0$ as $t\to \infty$. For simplicity, we first assume that $\phi^t x^{**}\in B_r(0)$ and $\phi^{-t}x^{*}\in B_r(0)$ for all $t > 0$. In this case we can just work with intersections of the given neighborhoods with $B_r(0)$ instead of the full neighborhoods. So without loss of generality we assume that $B_1, B_2, B\subset B_r(0)$.

Since both $E$ and $F$ have nonzero dimension, for any $x$ we can write $G(x) = G_F(x)\oplus G_E(x)$ where $G_F(x)\in F$ and $G_E(x)\in E$. Since $x^*\in M^F$, we know that $G(x^*)\in F$ so $G_F(x^*) = G(x^*)$.

We also set,

Since $0$ is a hyperbolic fixed point neither of these are zero and we can find positive constants $b^+_ <$, $b^-_ >$, and $|\ell| < \min\{|\lambda^+_ < |, |\lambda^-_ < |\}$ such that,

where $\|\cdot\|$ is the $\ell_2$ matrix norm.

For any $t_1, t_2 > 0$, we can define

Then for all $t\in [-t_2, t_1]$,

Thus for all $t\in [-t_2, t_1]$, $\phi^tx\in U$. Since $G\circ\phi^{-t_2} x = e^{-At_2} G(x) = e^{-A(t_1+t_2)}G(x^*)+G(x^{**})$ then,

Furthermore, since $G\circ \phi^{t_1} x = e^{At_1} G(x) = e^{At_1} (e^{-At_1}G(x^*)+G(\phi^{t_2}x^{**})) = G(x^*)+e^{A(t_1+t_2)}G(x^{**})$ then,

Finally,

Since $\ell -\lambda^+_ <$ and $\ell +\lambda^-_ >$ are both negative numbers, we can take $t_1, t_2$ large enough so that $G\circ \phi^{-t_2}x\in G(B_1)$, $G(x)\in G(B_0)$ and $G\circ \phi^{t_1}x\in G(B_2)$. Since $G$ is a homeomorphism, these choices of $t_1$, $t_2$ and the choice of $x$ as defined in (5.9) have the required properties of the theorem.

We now consider the general case (no longer assuming that $\phi^t x^{**}\in B_r(0)$ and $\phi^{-t}x^{*}\in B_r(0)$ for all $t > 0$). Since $x^{**}\in M^E$ and $x^{*}\in M^F$, there exists $s > 0$ such that $\phi^t x^{**}\in B_r(0)$ and $\phi^{-t}x^{*}\in B_r(0)$ for all $t > s$. Let $\hat x^{**} = \phi^s x^{**}$ and $\hat x^{*} = \phi^{-s} x^{**}$. The results above can be applied to $\hat x^{**}$ and $\hat x^{*}$. This means for every neighborhood $B$ of $0$, $\hat B_2$ of $\hat x^{**}$ and $\hat B_1$ of $\hat x^*$ we can derive $\hat t_1, \hat t_2 > 0$ and $x$ such that $x\in B$, $\phi^{\hat t_1} x\in \hat B_1$ and $\phi^{-\hat t_2} x\in \hat B_2$. Now, for any neighborhood $B_2$ of $x^{**}$ and $B_1$ of $x^*$, we can set $\hat B_2 = \phi^s B_2 = \{\phi^s y:y\in B_2\}$ and $\hat B_1 = \phi^s B_1 = \{\phi^s y:y\in B_1\}$ which are neighborhoods of $\hat x^{**}$ and $\hat x^{*}$ respectively. Applying the previous result and setting $t_1 = s+\hat t_1$, $t_2 = s+\hat t_2$ completes the proof of the theorem.

We are now in the position to provide conditions that guarantee that a hyperbolic equilibrium point is a reachable transient center. To prove this we use the $\lambda$-lemma and the idea that one way to reach the slow region is by staying close to the stable manifold.

Theorem 5.7. Let $v\in C^2(\mathbb{R}^n, \mathbb{R})$ and $f\in C^1(\mathbb{R}^n, \mathbb{R}^n)$. Suppose that $0$ is a hyperbolic equilibrium of the system (2.1) and $A = Jf(0)$. Let $E$ and $F$ respectively be the stable and unstable eigenspaces associated with $0$. If $A^T \nabla v(0) \not\perp F$ then $0$ is a $v$-transient center. If in addition, $A^T \nabla v(0) \not\perp E$, then $0$ is a reachable $v$-transient center.

Proof. Since $0$ is a hyperbolic fixed point then none of the eigenvalues of $A$ have zero real part. If we were only interested in transient centers without reachability, a proof of the first part of this theorem can be similar to the proof of Theorem 5.4 where we selected a point in the unstable subspace and mapped it backwards in time closer to the unstable equilibrium. In the nonlinear case we would instead choose a point in the unstable manifold and map it backwards in time towards the equilibrium.

We now give a proof of the theorem for the case when both $E$ and $F$ have nonzero dimension and the second part of the theorem, which is concerned with reachability, can apply. To prove both parts, we cannot just select a point on the unstable manifold since those are not reachable transient points. Instead we select a point that that has components in both the unstable and stable manifold.

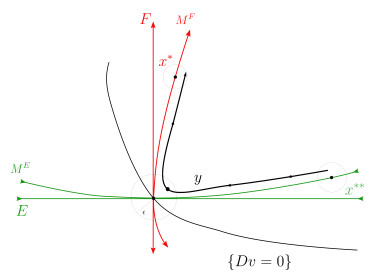
For any $v\in C^2(\mathbb{R}^n, \mathbb{R})$, it is clear that $0\in \Xi$. Since $0$ is an equilibrium we must have $\phi^t 0 = 0$ for all $t$. In addition, $f(\phi^t 0) = f(0) = 0$ and $Jf(\phi^t 0) = A$. Using Lemma 5.5 at $\xi = 0$ yields $\nabla(Dv)(0) = A^T\nabla v(0)$. Suppose $A^T \nabla v(0) \not\perp F$, since the level curve $Dv = 0$ is perpendicular to $\nabla(Dv)$ at $x = 0$, we thus know that $F$ is transversal to the level curve $Dv = 0$. By Theorem 9.6 in ^[17] we know there exists an invariant unstable manifold $M^F$ that is tangent to $F$ at $x = 0$. We apply the same argument on unstable manifold. Therefore for all small enough $r > 0$, there exists a $k > 0$ and $x^*\in M^F\cap B_r(0)$, $x^{**}\in M^E\cap B_r(0)$ such that $|Dv(x^*)| > k$ and $|Dv(x^{**})| > k$. An example illustration is provided in Figure 1.

By Lemma 5.6 we know that for any neighborhood $B_{r_2}(x^{**})$, $B_{r_0}(0)$ and $B_{r_1}(x^*)$, there exists $x\in B_{r_0}(0)$ and $t_1, t_2$ such that $\phi^{t_1}x\in B_{r_1}(x^*)$ and $\phi^{-t_2}x\in B_{r_2}(x^{**})$. By taking $r_1$ and $r_2$ to be small enough we know that $|D(\phi^{t_1}x)| > \frac{k}{2}$ and $|D(\phi^{t_2}x)| > \frac{k}{2}$. Thus $T_{\frac{k}{2}}(x) < \infty$ and $\hat{T}_{\frac{k}{2}}(x) < \infty$. Since $r_0$ is arbitrary, it follows from Theorem 4.8 that $0$ is a reachable $v-$transient center.

Recall that in Theorem 3.1 the transient center property can translate along the trajectory as well as to an $\omega$-limit point. The next theorem shows that such property can also translate from the limit point back to any trajectories that converges to it if $\eta$ is hyperbolic fixed point and the trajectory is in $\Xi$.

Theorem 5.8. Let $v\in C^2(\mathbb{R}^n, \mathbb{R})$ and $f\in C^1(\mathbb{R}^n, \mathbb{R}^n)$. Suppose that $0$ is a hyperbolic equilibrium of the system (2.1) and $A = Jf(0)$. Let $\xi\in\Xi$. If $A^T\nabla v(0)\not\perp F$ and $\phi^t\xi\to 0$ then $0$ and $\xi$ are both $v$-transient centers.

Proof. From the first part of Theorem 5.7, $0$ is a $v$-transient center. The proof that $\xi$ is also a $v$-transient center is similar to the proof of Theorem 5.7. Again let $U$ and $G$ be as given by the Hartman-Grobman theorem so that $U$ is neighborhood of $0$ such that for all $x\in U$, whenever $\phi^t x\in U$, we have (5.6) holds. We also again choose $r > 0$ and $R > 0$ sufficiently small so that (5.7) holds.

Let $x^{*}\in M^F$ be chosen so that for some $k > 0$, $|Dv(x^*)| > k$ (it is possible to do this following the same reasoning as in Theorem 5.7). Since $\phi^t\xi\to 0$, we know that $\xi\in M^E$. By Lemma 5.6, for any $r_1 > 0$, $r_2 > 0$, and $r > 0$, there exists $x\in B_r(0)$, $t_1 > 0$ and $t_2 > 0$ such that $\phi^{-t_2}x\in B_{r_2}(\xi)$ and $\phi^{t_1}x\in B_{r_1}(x^*)$. Thus by taking $r_1$ small enough we can get $\phi^{t_1}x$ close enough to $x^*$ so that $|D(\phi^{t_1}x)| > \frac{k}{2}$. Thus $T_{\frac{k}{2}}(x^{**})\leq t_1+t_2 < \infty$. Since $\xi\in\Xi$ and $r_2$ is arbitrary, by Theorem 3.4 it follows that $\xi$ is a $v-$transient center.

6.   Simple examples

In this section we present some simple applications to help demonstrate the results of the previous three sections. For brevity we use the notation $(a, b)$ for a vector, we mean a column vector $[a, b]^T$. Additionally, instead of using $x$ to denote a vector representing the state of the system as in previous sections, here we use $x$ to denote the first component of two-dimensional states denoted by $(x, y)$.

Example 6.1 (Application of Theorems 3.4, 4.8, 5.4, and 5.7). Consider the following system,

Let $v(x, y) = x$. We note that this simple, linear system was discussed in Example 6.13 from ^[16] where we proved that the origin is a $v$-transient center using a preliminary theorem on transient centers. Here we prove the same result using Theorem 5.4, and furthermore show that the origin is not reachable. In addition, we show that the origin is a reachable $v$-transient center if we change the choice of observable to $v(x, y) = y$.

We first set $v(x, y) = x$. The eigenvalues of $A$ are 1 and -1. This implies that $(0, 0)$ is an unstable hyperbolic equilibrium (specifically a saddle point). The eigenvector of $A$ corresponding to the positive eigenvalue $\lambda = 1$ is $(2, 1)$ so $F = {\rm{span}}\; ((2, 1))$. We also easily compute that $\{(x, y): \nabla v(x, y)\cdot f(x, y) = 0\} = \{(0, y):y\in\mathbb{R}\} = {\rm{span}}\; ((0, 1))$. Clearly, $F = {\rm{span}}\; ((2, 1)) \not\subset {\rm{span}}\; ((0, 1)) = \{(x, y): \nabla v(x, y)\cdot f(x, y) = 0\}$. By Theorem 5.4, the origin is a $v$-transient center.

To show that the origin is not a reachable $v$-transient center, we use the explicit solution of the linear system. Starting from an initial point $(x(0), y(0))$, the solution for all $t\in\mathbb{R}$ is given by,

Thus, $v(t) = x(0)e^t$. Let $S^* > 0$. For any open neighborhood of the origin we can find $(x(0), y(0))$ such that $T_{S^*}(x(0), y(0)) < \infty$. From the exact solution, such a point needs to satisfy $0 < |x(0)| < S^*$ and $T_{S^*}(x(0), y(0)) = \ln(\frac{S^*}{x(0)})$. However, any such point will also have $|v(t)| = |x(0)|e^t < S^*$ for all $t < 0$ implying that $\hat T_{S^*}(x(0), y(0)) = \infty$. By Theorem 3.4 the origin is a $v$-transient center and by Theorem 4.8 it is not a reachable $v$-transient center.

Now consider the case $v(x, y) = y$. We can use Theorem 5.7 to prove that $\xi$ is a reachable $v$-transient center. We already found $F = {\rm{span}}\; ((2, 1))$. It is also easy to show that $E = {\rm{span}}\; ((0, 1))$. Since

Clearly, $A^T \nabla v(\xi) \not\perp E$ and $A^T \nabla v(\xi) \not\perp F$. Thus $\xi$ is a reachable $v$-transient center. This result is maintained even if we add small nonlinear perturbations to the system.

Example 6.2 (Application of Theorems 3.1 and 5.1). Consider the system given by,

Let $v(x, y) = x$. This is Example 5.5 from ^[16] where we gave a direct proof that $\xi = (0, 0)$ is a $v$-transient center. Here we further show that all points in the candidate set $\Xi$ (given by (2.3)) are $v$-transient centers except for the equilibrium at $(1, 0)$.

From part (a) in Theorem 3.1, all points on the trajectory of $\xi = (0, 0)$ in forward and backward time, which is the invariant set $L = \{(0, y):y\in\mathbb{R}\}$, must be $v$-transient centers. Consider the set $\Xi$ corresponding to this system,

The point $(1, 0)$ is the only point in $\Xi$ that is not in the invariant set $L$. This point is the only equilibrium of the system. The Jacobian evaluated at $(1, 0)$ has eigenvalues $\pm i$, which means that $(1, 0)$ is a non-hyperbolic equilibrium. Observe that while trajectories have $xy\ne 0$ we can write $\frac{dy}{dx} = \frac{x-1}{-xy}$, which allows us to find a constant $C$ along such portions of the trajectory by solving this separable differential equation and deriving

We can now show that $(1, 0)$ is a Lyapunov stable equilibrium by considering the function,

Outside the invariant set $L$, this function is positive except it is zero at the point $(1, 0)$. Furthermore, along trajectories of (6.4) outside of $L$ we have $\frac{dV}{dt} = \big(\frac{1}{x}-1, -y\big)\cdot (-xy, x-1) = 0$. Thus $V$ is a Lyapunov function that shows the point $(1, 0)$ is Lyapunov stable. From Theorem 5.1, $(1, 0)$ cannot be a $v$-transient center for any choice of $v$. This gives an example of a point in $\Xi$ that is not a $v$-transient center.

Example 6.3 (Application of Theorems 5.3 and 5.7). Consider the system given by,

The origin is clearly an equilibrium of this system. The Jacobian of the right-hand-side function evaluated at $(0, 0)$ is given by,

The eigenvalues of the Jacobian evaluated at the origin are $1\pm \sqrt{3}i$. Thus the point $(0, 0)$ is an unstable hyperbolic fixed point of this system. The set $F$ from (5.1) is all of $\mathbb{R}^2$. Thus Theorem 5.7 guarantees that any choice of $v$ such that $A^T \nabla v(0, 0)\ne \bf(0, 0)$, the origin would be a $v$-transient center. Since $\det(A)\ne 0$ then any choice of $v$ such that $\nabla v(0, 0)\ne (0, 0)$, such as $v = x$ or $v = y$, is guaranteed to make the origin a $v$-transient center. We note that it is evident from the phase-plane diagram of this system that there are also non-constant choices of $v$ such that $\nabla v(0, 0)\ne (0, 0)$ that would make the origin a $v$-transient center.

We also note that for this system, $E = \{(0, 0)\}$. So for any choice of $v$, we have $A^T \nabla v(0, 0)\perp E$. and we cannot apply the second part of Theorem 5.7. From Theorem 5.3, the origin cannot be a reachable $v$-transient center for any choice of $v$.

Example 6.4 (Illustrating the necessity of the condition in Theorem 3.1 part (c)). Consider the following system,

Here we show that the condition that $Dv(\phi^t\xi) = 0$ for all $t < 0$ in Theorem 3.1 part (c) cannot be omitted.

We note that $v\in C^1(\mathbb{R}^2, \mathbb{R}^2)$ and,

Since $x(t) = x(0)+t$ and $y(t) = y(0)$ for all $t\in\mathbb{R}$ we find that $\Xi = \{(x, 0):x\geq 0\}$. Let $\epsilon\in(0, 1)$. Starting from initial point $(x, \epsilon)$ with $x\geq 0$ the forward trajectory is $(x +t, \epsilon)$, and $|Dv(x +t, \epsilon)| = \epsilon e^{x + t}$ for $t\geq 0$. Thus every point $(x, 0)$ for $x\geq 0$ is clearly a $v-$transient center. In particular that means $\phi^t (0, 0) = (t, 0)$ for all $t\geq 0$. However if we consider $t < 0$, $\phi^t (0, 0) = (t, 0)$ is not a reachable transient center since $Dv(t, 0) = t^2\neq 0$ for $t < 0$.

Example 6.5 (Application of Theorems 3.1 part (f), 3.4 and 5.1). Consider the following system,

Let $v = x$. We restrict our focus to the dynamics on the invariant subset $\{(x, y): x\geq 0, y\geq -1\}$.

We first prove that $(0, 0)$ is a $v$-transient center and use this to prove that $(0, -1)$ is also a $v$-transient center. Both are equilibria of (6.13) and are therefore, by Theorem 5.1, in $\Xi$. We note that $(0, 0)$ is a non-hyperbolic equilibrium of (6.13) so our results for hyperbolic equilibria do not apply.

Observe that in the set $K: = \{(x, y):0\leq x\leq 1, -1\leq y\leq 0\}$ we have $x'\geq 0$ and $y'\leq 0$. So for any small $\epsilon\in(0, 1)$ such that the initial point $(x(0), y(0)) = (\epsilon, -\epsilon)\in K$, the resulting forward trajectory cannot exit $K$ via the boundaries $x = 0$ and $y = 0$. In addition, $y' = (x-1)(y+1)\geq (\epsilon-1)(y+1)$ then by Gronwall's inequality, $y(t)\geq -1+ (1-\epsilon)e^{(\epsilon-1)t}$ which implies that the trajectory also cannot exit $K$ via the boundary $y = -1$. Finally, $y(t)\leq y(0) = -\epsilon$ for $t\geq 0$ so $x' = -xy \geq \epsilon x$, by Gronwall inequality we have $x(t)\geq e^{ \epsilon t}x(0) = \epsilon e^{\epsilon t}$. Thus this trajectory will exit $K$ in finite time $t^* > 0$ via the boundary $x = 1$. Let $(x(t^*), y(t^*)) = (1, y^*)$ be the point of exit where we must have $y^*\in(-1, -\epsilon)$.

Let $L(x, y) = (x-\ln(x))+(y+1-\ln(y+1))$. Then,

which means $L$ is invariant along trajectories of (6.13). Thus for small $\epsilon$,

This shows us that as $\epsilon\to 0^+$ we take $y^*\to -1$. Thus we can choose $\epsilon$ small enough so that,

Since this is true for all small enough $\epsilon > 0$ we conclude that $(0, 0)$ is a $v-$transient center by using $S = \frac{1}{2}$ in Theorem 3.4. Now since $\{(0, -1)\}$ is the omega limit set of $(0, 0)$, by Theorem 3.1 part (f), we can also conclude that $(0, -1)$ is a $v$-transient center.

7.   Application to models in ecology and epidemiology

Example 7.1. Consider the specific form of the predator-prey model studied in Hastings et al. ^[11],

Here $x$ denotes the prey population and $y$ denotes the predator population. We consider the dynamics in the invariant and biologically relevant set $\{(x, y):x\geq 0, y\geq 0\}$. All model parameters are assumed to be positive. The parameter $a$ is the prey reproduction rate, $K$ is the prey carrying capacity and $m$ is the predator death rate. The interaction between predator and prey is described using a type Ⅱ functional response with parameters $r$ and $b$. The parameter $\epsilon$ is called the slow-fast parameter since taking small values of $\epsilon$ allows the timescale of the dynamics of $y$ to be longer than $x$.

We previously showed numerically in ^[16] that if solutions are initialized close to the invariant set $\{x = 0\}$, we get trajectories that remain close to that set for a long time at the beginning of the trajectory (but when they move away they do not necessarily return to be close to $x = 0$ later on as happens in the case when $\epsilon$ is small). This showed that the parameter $\epsilon$ is not the direct cause of long transience about $x = 0$, rather that is caused by the invariant set itself. However, taking small values of $\epsilon$ does tend to push trajectories of this system close to the invariant set which makes the transient behaviour more "reachable".

Let $v = x$. We now formally prove that points in the invariant set $\{(0, y):y\geq 0\}$ are $v$-transient centers and therefore cause arbitrarily slow dynamics for arbitrarily long periods of times (for any fixed $\epsilon > 0$). We begin by noting that the origin is an equilibrium for the system with the Jacobian matrix evaluated at the origin given by,

Thus $E = {\mbox{span}}\{(0, 1)\}$ and $F = {\mbox{span}}\{(1, 0)\}$. Since $(0, 0)$ is a hyperbolic equilibrium, it follows from ^[17] that ${\mbox{dim}}(M^E) = {\mbox{dim}}(M^F) = 1$. Moreover, it is easy to check that $\mathcal{W}^E = \{(0, y):y\in\mathbb{R}\}$ is part of the stable set as defined in Definition 5.2.

The set $\{Dv = 0\} = \{(0, y):y\geq 0\}\cup\{(x, y):x\ne 0, y = \frac{a(x+h)}{r }(1-\frac{x}{K})\}$. Since $\{(0, y):y\geq 0\}$ is invariant, we have $\{(0, y):y\geq 0\}\subseteq \Xi$. Finally, since $\nabla v = (1, 0)$ we compute that,

From $(a, 0)\cdot (1, 0) = a\neq 0$ we know $A^T \nabla v(0, 0)\not\perp F$. By Theorem 5.8, $(0, 0)$ is a $v$-transient center and so are all points on $\{(0, y):y\geq 0\}$. This shows that this invariant set causes arbitrarily slow changes in the prey for arbitrarily long periods.

Since $A^T \nabla v(0, 0) \perp E$ we cannot use Theorem 5.7 to show that $(0, 0)$ is a reachable transient center and have this reachability property translate to all of $\{(0, y):y\geq 0\}$. However, we can prove this for the case when $m < br$. The proof is provided below and divided into three parts.

Theorem 7.2. Consider the system given in Example 7.1 with $v = x$. The set $\{(0, y):y\geq 0\}$ is comprised of reachable $v$-transient centers.

Let $m < br$. It follows that $0 < br < 2br-m$ and,

Set $\delta = \min\big\{\frac{hm}{2br-m}, \frac{K}{2}\big\}$, $\hat \eta = \frac{(\delta+h)(a+1)}{r}$, $\eta = \frac{ah(1-\frac{\delta}{K})}{2r}$ and $S^* = \frac{1}{2} \min \big\{\delta\big(1+\frac{a\delta}{K}\big), a\delta(1-\frac{\delta}{K})(1-\frac{h}{2(\delta+h)})\big\}$. We also use the notation $\mathbb{R}^2_+ = \{(x, y):x > 0, y > 0\}$ and define the following sets in $\mathbb{R}^2_+$:

Part 1. Proof that $T_{S^*}(x_0, y_0) < \infty$ for all $(x_0, y_0)\in L$. We already know that the trajectories of this system initiated in $L$ cannot exit $L$ via the $x = 0$ boundary or the $y = 0$ boundary. We will show that an initial point $(x_0, y_0)\in L$ with trajectory $\phi^t(x_0, y_0) = (x(t), y(t))$ exits $L$ for the first time via the $x = \delta$ boundary in finite time. Since $\frac{x}{x+h}$ is monotone increasing for $x > 0$ it follows from (7.3) and $m < br$ that on $L$,

It follows from this and (7.1) that $\frac{dy}{dt} = -\epsilon y \Big(m-\frac{br x}{ x+h}\Big) < -\frac{\epsilon ym}{2}$ while the trajectory is in $L$. By Gronwall's inequality, $y(t)\leq y_0 e^{-\frac{\epsilon m}{2}t}\in(0, \eta)$ and thus the trajectory cannot exit $L$ via the $y = \eta$ boundary either.

Next, we note that in $L$ we have,

Thus by Gronwall's inequality we must have $x(t)\geq x_0 e^{\frac{a}{4}t}$ for all $t\geq 0$ such that the trajectory remains in $L$. Thus, $\phi^t (x_0, y_0) = (x(t), y(t))$ will exit $L$ via the $x = \delta$ boundary in finite time. We denote this time by $t^*$ and so we can write $x(t^*) = \delta$ and $y(t^*)\in(0, \eta)$. Clearly $t^* < \frac{4}{a}\ln\big(\frac{\delta}{x_0}\big)$.

Finally, since $y(t^*) < \eta = \frac{ah(1-\frac{\delta}{K})}{2r}$, we obtain,

This proves that $T_{S^*}(x_0, y_0) < t^* < \infty$. This holds for all $(x_0, y_0)\in L$.

Part 2. Proof that $\hat T_S(\hat x_0, \hat y_0) < \infty$ for all $(\hat x_0, \hat y_0)\in \hat L$. Consider the time-reversed system (4.1) where $f$ is given in (7.1). We already know that the trajectories of this system initiated in $\hat L$ cannot exit $\hat L$ via the $\hat x = 0$ boundary. We will show that an initial point of the form $(\hat x_0, \hat y_0)\in \hat{L}$ with trajectory $\hat\phi^t(\hat x_0, \hat y_0) = (\hat x(t), \hat y(t))$ exits $\hat L$ for the first time via the $\hat x = \delta$ boundary in finite time. In this case since the bounds on $\hat x$ are the same as the bounds on $x$ in Part 1, we can apply (7.5) and derive that for as long as the trajectory remains in $\hat L$ we have $\frac{d\hat y}{dt} = \epsilon \hat y \Big(m-\frac{br\hat x}{\hat x+h}\Big)\notag > \frac{\epsilon \hat y m}{2}$. By Gronwall's inequality it follows that $\hat y(t)\geq \hat y_0 e^{\frac{\epsilon m}{2}t} > \hat \eta$ and the trajectory cannot leave $\hat L$ via the $\hat y = \hat\eta$ boundary.

Next we note that in $\hat L$ we have,

By Gronwall's inequality, we must have $\hat x(t) \geq \hat x_0 e^t$. Thus, for $(\hat x_0, \hat y_0)\in \hat{L}$ the trajectory $\hat \phi^t (\hat x_0, \hat y_0)$ will exit $\hat{L}$ via the $\hat x = \delta$ boundary in finite time. We denote this time by $\hat t^*$ so we can write $\hat x(\hat t^*) = \delta$ and $\hat y(t^*) > \hat\eta$. Clearly $\hat t^* < \ln\big(\frac{\delta}{\hat x_0}\big)$.

Finally, since $\hat y(t^*) > \hat \eta = \frac{(\delta+h)(a+1)}{r}$ then,

This implies that $\hat{T}_{S^*}(\hat x_0, \hat y_0) < t^* < \infty$. This argument holds for all $(\hat x_0, \hat y_0)\in \hat L$.

Part 3. Proof that $\{(y, 0):y\geq 0\}$ is comprised of reachable transient centers. We first note that $\eta = \frac{ah(1-\frac{\delta}{K})}{2r}\leq \frac{ah}{2r} < \frac{(\delta+h)(a+1)}{r} = \hat \eta$. Also, on the invariant set $x = 0$, we have $\frac{dy}{dt} = -\epsilon y \Big(m-\frac{br x}{ x+h}\Big) = -\epsilon m y$ so $\phi^t(0, y_0) = (0, y_0 e^{-\epsilon m t})$. Thus, $\phi^\tau\xi = \phi^{\tau}(0, 2\hat\eta) = (0, \frac{\eta}{2})$ if $\tau = \frac{1}{\epsilon m}\ln\big(\frac{4\hat \eta}{\eta}\big)$.

Let $\xi = (0, 2\hat \eta)$ which is clearly in $\Xi$. By continuity of the solutions with respect to initial conditions, we can guarantee that after time $\tau$ our solution is close to $(0, \frac{\eta}{2})$ by initializing close to $(0, 2\eta)$ at time $0$. In particular, we can find an $r > 0$ small enough such that for $\hat x_0\in(0, r)$ it follows that $\phi^\tau(\hat x_0, 2\eta)$ is close enough to $(0, \frac{\eta}{2})$ to guarantee that it is in $L$. Thus by our choice of $r$, $\hat x_0\in(0, r)$ implies $(\hat x_0, 2\eta)\in \hat L$ and $\phi^\tau(\hat x_0, 2\eta)\in L$. From parts 1–2, it follows that $T_{S^*}(\hat x_0, 2\eta)\leq \tau + T_{S^*}(\phi^\tau(\hat x_0, 2\eta)) < \infty$ and $\hat T_{S^*}(\hat x_0, 2\eta) < \infty$. Since we can find such a point $(\hat x_0, 2\eta)$ in every neighborhood of $(0, 2\eta)$, it follows from Theorem 4.8 that $(0, 2\eta)$ is a reachable $v$-transient center. Since the forward and reversed time trajectory of $(0, 2\eta)$ is $\{(0, y):y > 0\}$ and the forward trajectory has limit point $(0, 0)$, it follows from Theorem 4.6 that the entire set $\{(0, y):y\geq 0\}$ is comprised of reachable $v$-transient centers.

Example 7.3. Consider susceptible-infectious-recovered (SIR) model with vaccination. This has been studied in detail in the literature including ^[20] and their transient dynamics have been explored in ^[4,16].

We assume all parameters are positive and that the basic reproduction number $R_p = \frac{\beta(1-p)}{\gamma+\mu} > 1$ with $R_0 = \frac{\beta}{\gamma+\mu}$ being the basic reproduction number in the absence of vaccination. The dynamics are invariant and biologically feasible in the region where $S\geq 0$ and $I\geq 0$. This has a unique disease free equilibrium (DFE) at $(1-p, 0)$ and an endemic equilibrium at $\big(\frac{1}{R_0}, \frac{\mu}{\beta}(R_p-1)\big)$. For this system we set $v = I$, the fraction of infectious individuals.

The Jacobian at the DFE is

The eigenvalues $\lambda_1$ and $\lambda_2$ with corresponding eigenvectors $v_1$ and $v_2$ are given by,

Since $R_p > 1$, we have that $E = {\mbox{span}}(v_1)$, $F = {\mbox{span}}(v_2)$. For $v = I$, we have $Dv = \frac{dI}{dt} = (\beta S-\gamma-\mu)I$. Thus, $\{(S, I):S\geq 0, I = 0\}\subset \Xi$ and

Clearly $A^T\nabla v\not\perp F$ since $R_p > 1$. It is also easy to show that $DFE$ attracts every point from $\{(S, I):S\geq 0, I = 0\} = \Xi$. Thus, by Theorem 5.8 the set $\{(S, I):S\geq 0, I = 0\}$ is comprised of $v$-transient centers.

Since $A^T\nabla v\perp E$, we cannot use Theorem 5.7 to show reachability of $(0, 0)$ and thus we cannot easily say anything about the reachability of $\{(S, I):S\geq 0, I = 0\}$. In this case it may be possible to make arguments similar to what we did in Example 7.1 to show that under certain parameter conditions the set is comprised of reachable transient centers. In particular, if initial conditions are given by the prevaccine era endemic equilibrium (obtained by setting $p = 0$ in the expression for the endemic equilibrium), under certain parameter regimes we obtain numerical trajectories that get very close to $\{(S, I):S\geq 0, I = 0\}$ leading to prolonged honeymoon periods after the initiation of mass vaccination. Deriving these parameter regimes is a subject of future study but some numerical results are availabline in ^[4].

Example 7.4. We consider another type of SIR model. This extension of the SIR model allows for a changing total population size and is from Shan et al. ^[21].

We assume all parameters are positive and $\lim_{I\to 0}\mu(b, I) = \mu_1$ for all $b > 0$. The dynamics are invariant and biologically feasible in the region where $S\geq 0$, $I\geq 0$ and $R\geq 0$. There is a unique disease free equilibrium (DFE) at $\xi = (\frac{A}{\delta}, 0, 0)$. We further assume that the basic reproduction number of this system $R_0 = \frac{\beta}{d+\nu+\mu_1} > 1$. We again set the observable $v = I$ for this system.

The Jacobian at the DFE is,

The eigenvalues and corresponding eigenvectors are given by,

Since $R_0 > 1$, we have that $E = {\mbox{span}}(v_1, v_3)$ and $F = {\mbox{span}}(v_3)$. Thus, $\{(S, I, R):S\geq 0, I = 0, R\geq 0\}\subset \Xi$,

and $A^T\nabla v\not\perp F$. It is also easy to show that $DFE$ attracts every point from $\{(S, I, R):S\geq 0, I = 0, R\geq 0\} = \Xi$. Thus by Theorem 5.8 this set is comprised of $v$-transient centers.

8.   Summary and future work

We presented a more comprehensive quantification of long transient dynamics that was initially developed in ^[16]. Here we focus on transient centers, points in state space that give rise to long transience in its vicinity. One interesting aspect of transient centers is that it can easily translate from point to point. If an initial point is a transient center, this property translates along the trajectory forward in time. This property can also translate in reversed time along the trajectory if the initial point is in $\Xi$, a set of candidates for reachable transient centers. Moreover, if the trajectory converges to a limit point and it belongs to $\Xi$, the limit point will also be transient center.

We also further developed the concept of reachability, an important property that makes the transient dynamics generated by transient centers attainable from other points in state space. Many of our results for basic transient centers were extended to reachable transient centers. In addition, a new result (Theorem 5.7) provides easily verifiable conditions to show when a hyperbolic fixed point with some generic assumptions is a reachable transient center. We also presented applications of our results to both simple systems and more complex models from eco-epidemiology.

There are many directions we are interested in continuing on in our study of long transience and transient centers. In particular, we are interested in non-equilibrium transient centers. One possible direction is an extension of Theorem 5.7 to foliations with hyperbolic leaves. Another is an application to slow-fast systems with multiple turning points on the slow manifold.

Acknowledgments

The research of AL and FMGM is part of the Mathematics for Public Health program funded by the Natural Sciences and Engineering Research Council of Canada. Part of this work was conducted while FMGM was visiting the Mathematical Institute at the University of Oxford.

Conflict of interest

The authors declare there is no conflict of interest.

Appendix

In this Appendix we continue to assume that (H1) and (H2) hold. Recall that the solution to (2.1) with initial condition $x(0) = \xi$ evaluated at time $t$ is denoted by $\phi^t\xi$. The solution to (4.1) with initial condition $\hat x(0) = \xi$ evaluated at time $t$ is denoted by $\hat\phi^t\hat\xi$.

Lemma 8.1. Let $f(x) = Ax$ where $A\in\mathbb{R}^{n\times n}$.

(i) The solution to (2.1) with $x(0) = \zeta\in \mathbb{R}^n$ is $\phi^t \zeta = e^{At}\zeta$ for $t\in\mathbb{R}$.

(ii) The solution to (4.1) with $x(0) = \zeta\in\mathbb{R}^n$ is given by $\hat\phi^t \zeta = e^{-At}\zeta$ for $t\in \mathbb{R}$.

(iii) Suppose that $A$ has at least one real and positive eigenvalue. Let $F$ be the unstable eigenspace associated with $A$. If $\zeta\in F$ then $\hat\phi^{t} \zeta\in F$ for all $t\in\mathbb{R}$ and $|\hat\phi^{t} \zeta|\to 0$ as $t\to \infty$.

Proof. This follows from the basic theory of linear ordinary differential equations with constant coefficients ^[17,22].

Lemma 8.2 (Hartman-Grobman Theorem from ^[23]). Suppose that $\xi$ is a hyperbolic fixed point of the system (2.1). Let $\psi^t \zeta$ be the solution at time $t$ of the linearized system,

Then there exists an open set $U$ containing $\xi$ and homeomorphism $G$ with domain $U$ such that,

whenever $x$ is in $U$ and both sides of the equation are defined.

Proof. See proofs of the Hartman-Grobman Theorem [23,page 354].