Multi-leader-follower group consensus of stochastic time-delay multi-agent systems subject to Markov switching topology

1.   Introduction

In practical applications of a multi-agent system (MAS), there will be some agents that are the tracking targets of other agents. These agents are commonly called leaders and the other agents in the MAS are called followers accordingly. Leader-following consensus has attracted much interest due to its wide application in formation flight, sensor networks, and other engineering areas ^[1,2,3]. In the case of a single leader, the leader-following issue can be summarized as follows: how to construct an appropriate control protocol (or algorithm) that is able to make the followers' states in the system track the state of the leader. Tang et al. ^[4] designed a distributed coordination protocol on the basis of a sampled-data control scheme to solve the leader-following consensus problem. Wang and Ji ^[5] considered directed communication topology and gave leader-follower consensus conditions for general linear MASs. In Reference [6], Jiang et al. proposed a non-fragile sampled-data control protocol, under which the $\mathcal{H}_\infty$ leader-following consensus is reached in the presence of the Lipschitz nonlinearity. To address the leader-following consensus under cyber attacks, Liu et al. ^[7] proposed an event-triggered control consensus protocol.

As for the multiple leaders' case, the purpose of consensus control is often to make followers' states go into the region generated by the states of these leaders. This type of consensus is called multi-leader-follower (MLF) group consensus (or containment consensus). In the case when there are multiple leaders, Ji et al. ^[8] proposed hybrid stop-go schemes to ensure the MLF group consensus. In Reference [9], Ma et al. checked the MLF group consensus of MASs modeled by discrete-time equations and presented several distributed control protocol designs based on either state feedback or output feedback. In Reference [10], Wang et al. considered a class of high-order MASs and proposed a novel distributed observer-based MLF group consensus control protocol. For recent work on MLF group consensus, one can refer to References [11,12,13,14,15,16,17] and papers cited therein.

Although significant progress has been made in the area of MLF group consensus of MASs, there are two issues that need to be investigated further. On the one hand, the agents under consideration in most of the existing literature are assumed to have deterministic delay-free dynamic behaviors. As noted in References [18,19,20], however, sometimes it is necessary to use stochastic or functional differential equations to model the dynamics of agents in engineering applications. On the other hand, most studies are based on a fixed communication topology. In practice, however, the communication topology between agents may change greatly with time, and the next topology often only depends on the current topology (see e.g., References [21,22,23]). In view of this, compared with the fixed topology, the Markov switching topology seems to be a better candidate.

Motivated by the above observations, this paper focuses on the MLF group consensus issue for stochastic time-delay MASs subject to Markov switching topology. Unlike the existing literature on this issue, the system considered here is assumed to be perturbed by Brownian motion and the communication topology between agents is assumed to be dynamically changing but obey a continuous-time finite-state Markov chain. The purpose is to determine a distributed control protocol to make sure that the followers' states converge in mean square to a convex hull generated by the leaders' states. The major contributions of this work are two-fold: 1) By introducing a model transformation, the MLF group consensus is transformed into a mean-square stability issue of a new system; 2) By utilizing the Lyapunov stability theory, graph theory, as well as several inequality techniques, an easy-to-check sufficient condition is proposed, under which the required feedback gain can be easily acquired.

2.   Preliminaries

Notations: In this paper, $\mathbb{R}^{q}$ and $\mathbb{R}^{p\times q}$ denote the $q$-dimensional Euclidean space as well as the family of all $p\times q$ real matrices, respectively. The symbol $\left\Vert \cdot \right\Vert$ stands for the Euclidean norm and $\otimes \ $ represents the Kronecker product. For a matrix $M \in \mathbb{R}^{p\times p}$, let $\lambda _{M}(M)$ and $\lambda _{m}(M)$ denote the maximum and minimum eigenvalues of matrix $M$ respectively, and $\mathscr{S}({M})$ be the sum of $M$ itself and its transpose ^[24]. Set $T\subset \mathbb{R}^{q}$ is called convex if $(1-\sigma)\gamma +\sigma \rho$ $\in$ $T$ for any $\gamma, \rho \in T$ and $\sigma \in \lbrack 0, 1]$. For a set $O = \left\{ o_{1}, o_{2}, \, \cdots, \, o_{r}\right\}$, $o_{i}\in \mathbb{R}^{q}$, $i = 1, 2, \, \cdots, \, r$, denote its convex hull by ${co} \{O\} = \left\{ \Sigma _{i = 1}^{r}p_{i}o_{i}|p_{i}\geq 0, \Sigma _{i = 1}^{r}p_{i} = 1\right\}$. For a vector $v = [v_1, \cdots, \, v_m]^T$ (respectively, a matrix $U = (u_{ij})_{m\times n}$), denote its $1$ norm by $\left\Vert v\right\Vert _{1} = \sum_{i = 1}^{n}\left\vert v_{i}\right\vert$ (respectively, $\left\Vert U\right\Vert _{1} = \max_{1\leq j\leq n}\sum_{i = 1}^{n}\left\vert u_{ij}\right\vert)$ and $\infty$ norm by $\left\Vert v\right\Vert _{\infty } = \max_{1\leq i\leq n}\left\vert v_{i}\right\vert$ (respectively, $\left\Vert U \right\Vert _{\infty } = \left\Vert U^{T}\right\Vert _{1} = \max_{1\leq i\leq n}\sum_{j = 1}^{n}\left\vert u_{ij}\right\vert$). For column vectors $u_1, \, \cdots, \, u_m$, denote $[u_1^T, \, \cdots, \, u_m^T]^T$ as $col\{u_1, \, \cdots, \, u_m\}$.

Moreover, let $G = (V, E, A)$ be a directed graph representing the communication topology of the MAS, $V = \left\{ v_{1}, v_{2}, \, \cdots, \, v_{n+m}\right\}$ be the node set, $\ E = \left\{ e_{ji} :e_{ji} = (v_{j}, v_{i})\right\} \subseteq V\times V$ be the edge set, and $A = \left[ a_{ij}\right]$ be the adjacency matrix with $a_{ij} = 1$ for $e_{ji}\in$ $E$ and $a_{ij} = 0$ for $e_{ji}\notin$ $E$. For $e_{ji} \in E$, $v_{j}$ is viewed as a neighbor of $v_{i}$. A node is called a leader if it has no neighbors, and a follower if it has at least one neighbor. Define $\mathcal{L = }\left[ l_{ij}\right] \in \mathbb{R}^{(n+m)\times (n+m)}$ as the Laplacian matrix of $G$, where $l_{ij} = -$ $a_{ij}$ for $i\neq j$ and $l_{ii} = \Sigma _{j = 1, j\neq i}^{n}$ $a_{ij}$. Denote by $s$ the number of possible interaction topologies, and $s_{t}:[0, \infty ]\rightarrow S = \{1, \, \cdots, \, s\}$ a switching signal that governs the switches between the variable topologies. Then, the directed graph $G$ at time $t$ is defined as $G_{s_{t}} = (V_{s_{t}}, E_{s_{t}}, A_{s_{t}})$. Simultaneously, the adjacency matrix and the Laplacian matrix can be re-defined as $A_{s_{t}} = \left[ a_{ij}^{s_{t}}\right]$ and $\mathcal{L}^{s_{t}}\mathcal{ = }\left[ l_{ij}^{s_{t}}\right]$, respectively. Assume that there are $m$ leaders and $n$ followers. Then $\mathcal{L }^{s_{t}}$ can be partitioned as:

where

Consider a class of MAS driven by Brownian motion. The dynamic process of the $i$-th follower affected by random disturbance is described as follows:

in which $x_{i}(t)\in \mathbb{R}^{m_{1}}$ is the state of the $i$-th follower, $u_{i}(t)\in \mathbb{R}^{m_{2}}$ is the control input, $\eta (t)\in \mathbb{R}$ is the one-dimensional standard white noise, $\mathcal{A}\in \mathbb{R}^{m_{1}\times m_{1}}$, $\mathcal{A}_{\tau }\in \mathbb{R} ^{m_{1}\times m_{1}}$, $\mathcal{B}\in \mathbb{R}^{m_{1}\times m_{2}}$, and $\mathcal{C}\in \mathbb{R}^{m_{1}\times m_{1}}$ are constant matrices, $\tau$ stands for a constant time delay ^[25,26], and $N_{1} = \{1, 2, \, \cdots, \, n\}$ denotes the set of indices for the followers. One can rewrite system (2.2) as the following Itô stochastic differential equation:

in which $\omega(t)$ denotes a standard Brownian motion defined on a complete probability space $(\Omega, \mathscr{F}_t, \mathscr{P})$ ^[27]. The $i$-th leader's dynamic equation is as follows:

where $N_{2} = \{n+1, \, \cdots, \, n+m\}$ is the set of indices for the leaders, $x_{i}(t)\in \mathbb{R}^{m_{1}}$ denotes the leader's state, and $f_{i}(x_{i}(t), t)\in \mathbb{R}^{m_{2}}$ stands for a pre-designed control input. It is assumed that the following conditions are met:

where $\varepsilon$ $> 0$. System (2.4) can also be rewritten in the standard Itô differential form as:

It should be noted that the form of random disturbance considered in systems (2.3) and (2.6) is state-dependent, which means that the disturbance is not entirely normal exterior noise.

Suppose that $\left\{ s_{t}, t\geq 0\right\}$ is a continuous-time finite-time Markov chain that chooses values in $S = \{1, ..., s\}$ according to transition probability

where $\zeta > 0, \ \lim_{\zeta \rightarrow 0}(o(\zeta)/\zeta) = 0$, and $\pi _{ij}\geq 0$ (for $i\neq j$) is the transition rate from mode $i$ at time $t$ to mode $j$ at time $t+\zeta$ and $\pi _{ii} = -\Sigma _{j = 1, j\neq i}^{s}\pi _{ij}$ ^[28,29,30].

For the analysis and synthesis of stochastic MASs which are given in Eqs (2.3) and (2.6), we make the following assumptions for deriving our main results.

Assumption 1. For every follower $i\in N _{1}$, there is at least one leader $j \in N _{2}$ that has a directed path from $j$ to $i$.

Assumption 2. At any time $t$, the communication topology among followers is an undirected connected graph.

In the present work we proposed a distributed control protocol as follows:

where $\alpha$ and $\beta$ are positive scalars, and $\mathcal{K}_{s_{t}}\in \mathbb{R}^{m_{2}\times m_{1}}$ is the feedback gain. The specific form of $\xi _{i}(t)$ is as follows:

Remark 1 Assumptions 1 and 2 have been broadly adopted in the existing literature on the MLF group consensus issue (see, e.g., ^{[12,13,15,31]}). It follows from Assumption 1 that each follower is reachable from its leader. Assumption 2 further implies that the followers of a leader can communicate with each other.

Remark 2. During the last two decades, a number of results on the MLF group consensus of MASs have been reported (see, e.g., ^{[11,12,13,14,15,16,17]}). Unlike the existing literature, which always assumes that all agents have deterministic and delay-free dynamic behaviors, both the leaders and the followers considered in this paper are modeled by stochastic functional differential equations. It is also worth mentioning that most studies on this topic are based on a fixed communication topology, while in this paper, the communication topology is allowed to be changeable over time according to a Markov chain. Thus, the research object of this paper is more practical and general regardless of the dynamics of agents or topology structure.

At this point, the MLF group consensus issue discussed can be summarized as: designing a control protocol in the form of (2.7) so that the followers' states described by system (2.3) converge to a convex hull generated by the leaders' states of system (2.6) in mean square.

3.   Main results

To solve the MLF group consensus issue, the following three Lemmas are useful:

Lemma 1. ^[32] With Assumptions 1 and 2, one has that $\mathcal{L}_{1}^{s_{t}} > 0$, each entry of $-(\mathcal{L}_{1}^{s_{t}})^{-1}\mathcal{L}_{2}^{s_{t}}$ is nonnegative, and the sum of each row of $-(\mathcal{L}_{1}^{s_{t}})^{-1}\mathcal{L}_{2}^{s_{t}}$ equals to one, where $\mathcal{L}_{1}^{s_{t}}$ and $\mathcal{L}_{2}^{s_{t}}$ are defined in (2.1).

Lemma 2. ^[33] For any matrices $Z_{1}\in \mathbb{R}^{m\times n}, Z_{2}\in \mathbb{R}^{p\times q}, Z_{3}\in \mathbb{R}^{n\times r}$, and $Z_{4}\in \mathbb{R}^{q\times s}$, one has$(Z_{1}\otimes Z_{2})(Z_{3}\otimes Z_{4}) = (Z_{1}Z_{3})\otimes (Z_{2}Z_{4}).$

Lemma 3. ^[34] Given a symmetric matrix $Z = \left[\begin{array}{cc}Z_{11} & Z_{12} \\Z_{21} & Z_{22}\end{array}\right]$, $Z < 0$ is equivalent to $Z_{22} < 0 \, and \, \ Z_{11}-Z_{12}Z_{22}^{-1}Z_{12}^{T} < 0.$

For convenience, we define $x_{\phi}(t) = col\big{\{} x_{1}(t), \, \cdots, \, x_{n}(t)\big{\}}$, $u_{\phi}(t) = col\big{\{} u_{1}(t), \, \cdots, \, u_{n}(t)\big{\}}$, $x_{\psi}(t) = col\big{\{} x_{n+1}(t), \, \cdots, \, x_{n+m}(t)\big{\}}$, and $\xi (t) = col\big{\{} \xi _{1}(t), \, \cdots, \, \xi _{n}(t)\big{\}}$. Then (2.8) is able to be written as

Define

Then, by Lemmas 1 and 2, we obtain

It follows from (2.7) and (3.3) that

Substituting (3.4) into (2.3) results in

where $f(t) = col\big{\{} f_{n+1}(x_{n+1}(t), t), \, \cdots, \, f_{n+m}(x_{n+m}(t), t) \big{\}}$. From (3.3) and (3.5), we have

Then, using (3.3), (3.6), and Lemma 2, gives

The following theorem gives the criterion for the MLF group consensus issue.

Theorem 1. If system (3.7) is stable inmean square, then the followers' states in (2.3) converge toa convex hull generated bythe leaders' states in (2.6) in mean-square. More specifically,

where

Proof. In view of (3.3) and (3.7), the proof of this theorem can be easily completed and is thus omitted here.

Remark 3. Theorem 3.1 shows that, through the model transformation in (3.2), the MLF group consensus issue for system (3.1) can be transformed into a mean-square stability issue for system (3.7), which will be handled later by using the stochastic Lyapunov stability theory, graph theory, as well as several inequality techniques.

It is time to present our design method for the needed control protocol.

Theorem 2. Suppose that there exist two scalars $\alpha > 0$, $\beta > \varepsilon$, and matrices $P_{l} > 0$ and $Q > 0$\ such that

for any $i \in \{1, \, \cdots, \, n\}$ and $l \in \{1, \, \cdots, \, s\}$, where

with $\lambda _{i}^{l}$ being the $i$-th eigenvalue of $\mathcal{L}_{1}^{l}$, $j \neq l$, and $\pi_{lj}\neq 0$.Then, the MLF group consensus issue is solvable, and the required control protocol is given by (2.7) with $\alpha$, $\beta$, and

Proof: Define a Lyapunov functional as

Then, we can get

Utilizing the generalized Itô formula ^[35] to $e^{kt}V(t)(k > 0)$ yields

where $\mathfrak{L}$ is used to represent the weak infinitesimal operator. For $s_{t} = l$, we can write

Substituting (3.9) into (3.13) yields

According to the properties of $\infty$ norm and $1$-norm for real vectors, we can get

Using (2.5) and Lemma 1, it follows from (3.15) that

Using (3.14), (3.16), (3.17) and noting $\left\Vert \Psi \right\Vert _{\infty }\leq \left\Vert \Psi \right\Vert _{1}$, we have

Because $\mathcal{L}_{1}^{l}$ is symmetrical, there exists a unitary matrix $\mathfrak{U}\in \mathbb{R}^{n\times n}$ such that

Define

Then (3.18) reduces to

which can be rewritten as follows:

where

Using a congruent transformation to $\nabla$ by pre and post multiplying it with $\left[ \begin{array}{cc} P_{l} & 0 \\ 0 & Q \end{array} \right]$ and its transpose gives

where

By Lemma 3, (3.8) guarantees that $\left[ \begin{array}{cc} \Xi _{2} & \lambda _{i}^{l}\mathcal{A}_{\tau }Q \\ \ast & -Q \end{array} \right] < 0$, which together with (3.20) implies $\nabla < 0$. Thus, we have from (3.19) that

For convenience, we set $\tilde{\lambda}_l = \lambda _{M}(\nabla)\lambda _{M}({\mathfrak{UU}^{T}}\otimes I_{m_{1}})$ and write the above inequality as

Now, by (3.10)–(3.12), and (3.21), we have

where

Select a constant $k > 0$ small enough such that $D_{0l} < 0$ and define

Then, with the aid of (3.22), it is not hard to obtain

which means that system (3.7) is exponential stable in mean square and, thus, in view of Theorem 1, the MLF group consensus is reached. This completes the proof.

When there is no time delay, system (3.7) reduces to

In the case, the following corollary can be derived directly from Theorem 2. The proof is omitted for the sake of brevity.

Corollary 1. Given two positive constants $\beta$ and $\varepsilon$, with $\beta > \varepsilon$, suppose that there are matrices ${P_l} > 0$\and $Q > 0$\ such that

for any $i \in \{1, \, \cdots, \, n\}$ and $l \in \{1, \, \cdots, \, s\}$, where

with $\lambda _{i}^{l}$ being the $i$-th eigenvalue of $\mathcal{L}_{1}^{l}$, $j \neq l$, and $\pi_{lj}\neq 0$. Then, the MLF group consensus issue is solvable. And the required control protocol is given by (2.7) with $\alpha$, $\beta$, and $\mathcal{K}_{l} = -B^{T}P_{l}^{-1}\, (l = 1, \, \cdots, \, s)$.

Next, consider the situation that the MAS is subjected to a fixed topology. Then, (3.7) becomes

and one can write the following result:

Corollary 2. Given two positive scalars $\beta$ and $\varepsilon$ with $\beta > \varepsilon$, suppose that there are matrices $P$ $> 0$ and $Q > 0$, such that

holds, where

Then, the MLF group consensus issue is solvable. And the required control protocol is given by (2.7) with $\alpha$, $\beta$, and $\mathcal{K} = -B^{T}P^{-1}$.

4.   Numerical example

Consider a MAS consisting of seven dynamic multi-agents, where each agent corresponds to a mass-spring-damper system ^[36]. Let the 6-th and 7-th agents are leaders and the rest are followers. The parameter settings are as follows:

Note that, for $f_{6}(x_{6}(t), t)$ and $f_{7}(x_{7}(t), t)$, the parameter $\varepsilon$ can be chosen as $\varepsilon = 13$.

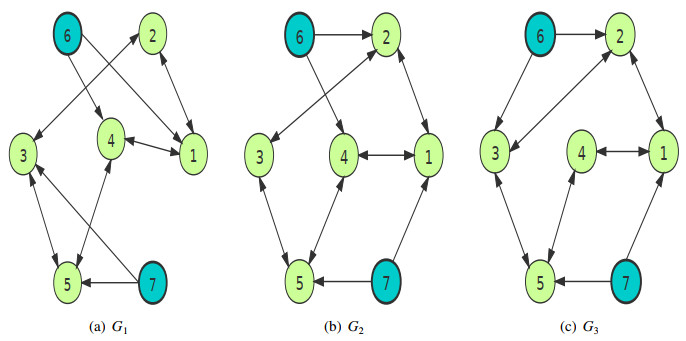
Figure 1 shows three possible communication topologies, where nodes 1–7 correspond to agents 1–7, respectively. Set $\beta = 15$ and the transition rate matrix between $G_{1}$, $G_{2}$, and $G_{3}$ as

Then, with the aid of Theorem 2, the feedback gain matrices can be gained as

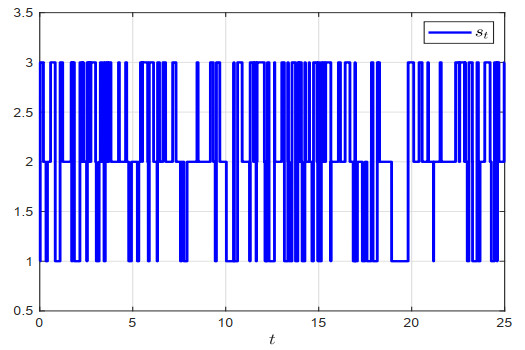
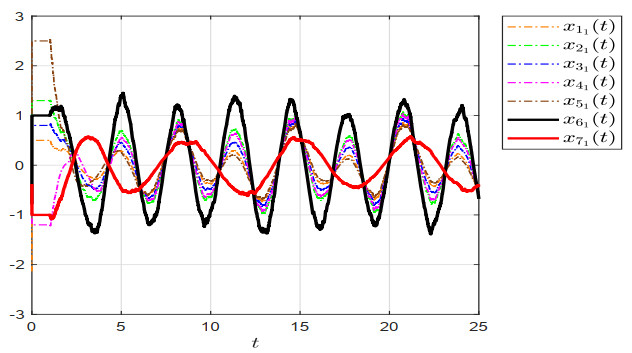
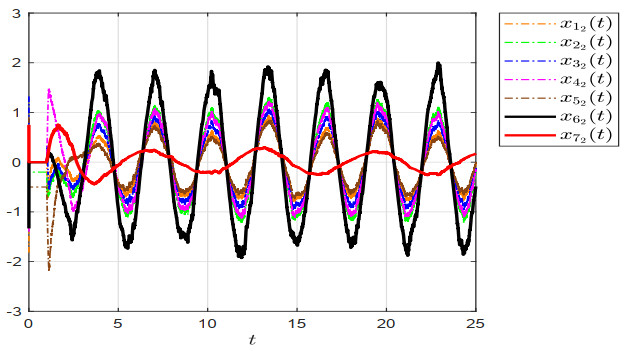
Figure 2 depicts the Markov switching signal, and the three modes correspond to the three communication topologies in Figure 1. Under the designed controller, Figures 3 and 4 show the evolutions of the system states trajectories. It can be observed that, after a period of time, the states of agents 1–5 (the followers) enter the region generated by the state trajectories of agents $6$ and $7$ (the leaders). Therefore, the simulation results confirm that the designed control protocol is effective.

5.   Conclusions

In this paper, the MLF group consensus issue of a class of stochastic time-delay agent systems with Markov switching topology has been studied. By using a model transformation, the group consensus problem has been transformed into the stability control problem of the system in (3.7). Then, it has been shown that the MLF group consensus can be guaranteed if the system in (3.7) is stable in mean-square (see Theorem 3.1). With the aid of Lyapunov stability theory, graph theory, as well as several inequality techniques, a sufficient condition for the solvability of the MLF group consensus issue has been proposed (see Theorem 3.2). It has been proved that the control protocol can ensure the followers' states converge to a convex hull generated by the leaders' states in mean square. Lastly, a numerical example with simulation has been provided to verify the effectiveness of the given MLF group control protocol.

Acknowledgments

This work was supported by the Natural Science Foundation of the Anhui Higher Education Institutions (Grant no. KJ2020A0248).

Conflict of interest

The authors declare there is no conflict of interest.