Analysis of design parameters of round-window stimulating type electromagnetic transducer by a nonlinear lumped parameter model of implanted human ear

1.   Introduction

The number of age-related and other hearing loss people reached 1.27 billion, and hearing loss is the fourth prevalence non-fatal disease worldwide ^[1]. According to the portion of the ear dysfunction, the hearing loss is classified into three main types: conductive hearing loss, sensorineural hearing loss and mixed hearing loss (a combination of both conductive loss and sensorineural loss). Because it can't be treated with drugs and surgery, sensorineural hearing loss is mainly alleviated by traditional hearing aids. Nevertheless, there are many defects of traditional hearing aids, such as low output gain, acoustic feedback and occlusion of ear canal ^[2]. To solve these traditional hearing aids' defects, many institutions have developed middle ear implants (MEIs) that can treat hearing loss by stimulating the patient's ossicular chain through the implanted transducer's mechanical vibration ^[3,4,5]. However, it is difficult to attach the transducer to the ossicular chain in patients with middle ear disease, such as chronic otitis media and middle ear malformation ^[6]. To resolve this problem, Colletti et al. ^[7] proposed and proved the feasibility of the hearing compensation method through round-window stimulation clinically, which provides a new treatment scheme for patients with the mixed hearing loss.

Although the feasibility of the round-window driving type transducer in the treatment of hearing loss has been proved clinically, its postoperative performance shows great individual differences among patients ^[8]. In order to improve the round-window stimulation's performance, many scholars have conducted experiments on the reasons for the large individual differences in postoperative performance. The experimental results of Arnold et al. ^[9] proved that implanting a subcutaneous connective tissue between the round-window membrane and the transducer can increase the acoustic energy transfer efficiency from the transducer to the cochlea. Meanwhile, placing the transducer vertically on the round-window membrane can effectively improve the hearing compensation performance. The support of the transducer has little effect on hearing compensation performance. However, the supporting material used in the experiment only is subcutaneous soft tissue with low stiffness, and comparative study of other supporting materials were not conducted. Schraven et al. ^[10] found that the hearing compensation performance is better when most of the round-window membrane contacts with the transducer. The results of Maier et al. ^[11] indicated that applying preload force within a safe range can effectively ameliorate the hearing compensation performance. The above studies provide significant references for the optimization of the round-window stimulating electromagnetic transducers' design parameters. However, due to the ultra-small structure and complex geometric shape of human ear ^[12], it is difficult to systematically study the effect of design parameters of the round-window stimulating electromagnetic transducer by experiment.

In view of the difficulties of experimental research, many scholars have carried out theoretical research by establishing human ear's finite element (FE) model or lumped parameter model ^[13,14]. Zhang et al. ^[12] established a FE model of human ear to study the influences of transducer's cross-sectional area and weight on the round-window stimulation. Liu et al. ^[15,16] studied the effect of coupling layer elastic modulus and transducer's cross section and mass on the round-window stimulation by FE analysis, and also investigated the effect of stimulation sites on the hearing compensation performance. Zhang et al. ^[17] numerically compared the acoustic transmission characteristics of cochlea under forward and round-window stimulation. Tian et al. ^[18] analyzed the effects of round-window driving type transducer's coupling conditions on the hearing compensation performance. Chen et al. ^[19] found the effects of round-window membrane's thickening, hardening and area shrinkage on round-window stimulation. The above researches of FE model lay a foundation for the optimization of the design parameters of round-window stimulation, but the internal structure of the electromagnetic transducer has not been taken account in the modeling process and the analysis of transducer driving characteristic is not allowed. At the same time, the lumped parameter model can provide the theoretical basis and analyze the parameters of the transducer theoretically ^[20]. Moreover, compared with the FE model, the benefit of lumped parameter model is lower computational cost, and the effects of the parameters of lumped parameter model can be more easily understood ^[21,22]. In view of the above advantages, many lumped parameter models of human ear were established ^[23,24,25]. Rusinek et al. ^[26] studied the incus-body driving type transducer by a lumped parameter model. Heckler et al. ^[27] analyzed the effects of preload force, support stiffness and intermediate layer damping on the round-window stimulation from the mechanical aspects, and achieved fruitful results. However, Heckler et al. ^[27] overlooked the nonlinear stiffness of annular ligament in the modeling process. And the driving force of transducer is simplified as an excitation force, which is not allowed to analyze the influence of the transducer's electromechanical coupling coefficient on the round-window stimulating electromagnetic transducer' performance.

To solve the above problems, we established a human ear-transducer coupling lumped parameter model, which considers the nonlinear stiffness of the annular ligament ^[28] and the internal structure of electromagnetic transducer. In the lumped parameter model, the masses that represent the human ear and the implanted transducer are coupled through spring and damper. Based on the nonlinear lumped parameter model, we investigated the effects of four design parameters of the round-window stimulating electromagnetic transducer, i.e., excitation voltage, electromechanical coupling coefficient, support stiffness and preload force.

The rest of this paper is organized as follows: we established the human ear-electromagnetic transducer coupling lumped parameter model, and confirmed the reliability of the model by comparing its predicted results with the experimental data of stapes velocity under forward and reverse stimulations in Section 2. In Section 3, the effects of excitation voltage, electromechanical coupling coefficient, support stiffness and preload force on the hearing compensation under round-window stimulation were systematically analyzed. Finally, Section 4 are the discussion of the results and conclusions.

2.   Human ear-electromagnetic transducer coupling lumped parameter model

2.1.   Modeling of human ear-electromagnetic transducer coupling lumped parameter model

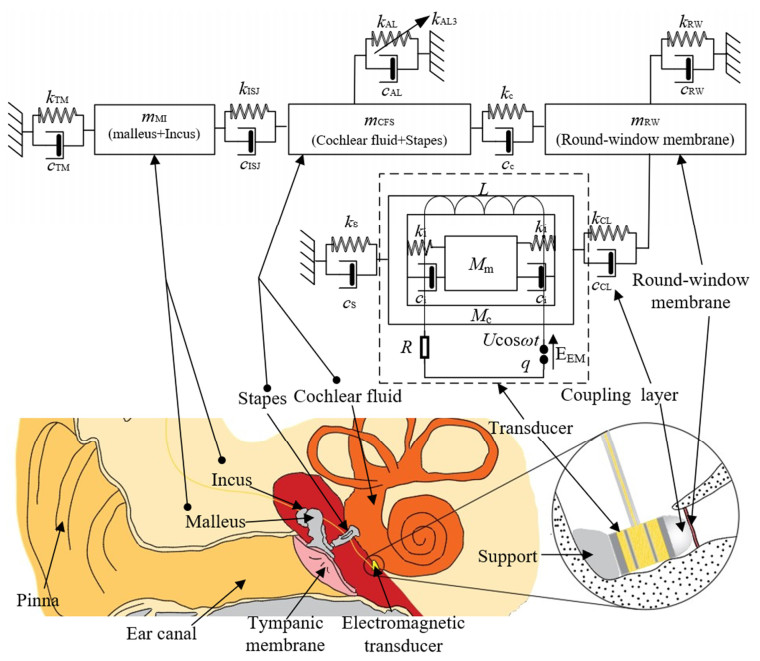
In order to analyze the effects of the design parameters of the MEI's electromagnetic transducer on its the round-window stimulation's performance, a six degrees of freedom human ear-transducer coupling lumped parameter model was built, as shown in Figure 1. Since the lumped parameter model is the simplification of the material object, several significant hypotheses were made. Firstly, the hydrodynamics of cochlea and the vibration of basilar membrane were omitted. Secondly, the response of human ear implanted with electromagnetic transducer was not affected by the sound frequency ^[26]. Therefore, in this model, the malleus, incus, stapes, cochlear fluid and round-window membrane were simplified as rigid bodies in translational motion. Since the response of malleus and incus to excitation is relatively consistent, malleus and incus were represented by a mass block ^[27,29]. Under the round-window stimulation, there is a hydraulic transmission between the cochlear fluid and the stapes, and the transmission ratio is the area ratio of the oval window to the round window ^[27]. Therefore, cochlear fluid and the stapes were simplified to a degree of freedom and represented by a mass block ^[27].

The lumped parameter model is usually composed of multiple mass blocks (m) connected with spring (k) and damper (c). As shown in Figure 1, the constructed human ear model has three mass blocks: malleus-incus complex (m_MI), cochlear fluid-stapes complex (m_CFS) and round-window membrane (m_RW). The malleus connects with the temporal bone through the tympanic membrane (TM); the malleus-incus complex and the cochlear fluid-stapes complex are connected by the incudo-stapedial joint (ISJ); the stapes connects with the temporal bone through the annular ligament (AL) and the cochlear fluid connects with the temporal bone through the round-window (RW) membrane. There is a hydraulic transmission between the stapes and the cochlear fluid; the transmission ratio (i_h) is the area ratio of the oval window (OW) to the round-window (RW) ^[27]. The electromagnetic transducer model is mainly composed of a metal case (M_c) and a magnet (M_m). A coil is wound around the metal case. The electromagnetic transducer is fixed in the round-window niche by a support (S). The transducer transmits the vibration to the cochlea through the round-window membrane. A coupling layer, which is usually a piece of fascia in clinic, is put between the transducer and the round-window membrane to improve the transmission of the transducer's vibration ^[30]. The electromagnetic transducer' magnet is driven by the ampere force and connected with the case through a spring (k_i) and a damper (c_i). The circuit that excites the magnet is composed of inductance (L), resistance (R) and voltage source (Ucosωt). E_EM is the electromotive force that generates ampere force to drive the electromagnetic transducer. Therefore, according to the lumped parameter model established in this paper, the governing differential equations of this model were as follows:

where: x is the mechanical coordinates of mass blocks and q represents the charge in the circuit. In order to simplify the equations and facilitate modeling, we used ${\tilde k}_{\rm{i}\rm{j}}$ and ${\tilde c}_{\rm{ij}}$ to describe the stiffness and damping that connect m_i and m_j. Besides, ${\tilde k}_{\rm{ii}}$ is sum of all the stiffnesses connected to m_i, and ${\tilde c}_{\rm{ii}}$ is sum of all the damping connected to m_i. The mass block represented by m_i can be known from Eq (4). Moreover, the parameters of the governing differential equations were defined as follows:

By introducing the dimensionless parameters, dimensionless coordinates (x₁~x₅), dimensionless time (τ) and dimensionless frequency (Ω), the differential equations of motion took the form:

where the dimensionless coordinates and parameters were defined as follows:

In this paper, the lumped parameter model was established in SIMULINK according to the above governing differential equations of the model, and the model-predicted results were solved in MATLAB through the ode15s solver.

In the numerical analysis, it was assumed that x₀ = 1 mm, q₀ = 1 mC and ω₀ = 400 rad/s were the reference values. Considering previous clinical report utilized the fascia to couple the transducer with the round-window membrane ^[31], we initially selected the fascia to simulate the coupling layer. Specifically, the elastic modulus (E), the thickness (t) and the area of the fascia is 1.778 MPa ^[32], 0.1 mm ^[33], 2 mm^{2 [33]}, respectively. Two layers of fascia was used as the coupling layer ^[35]; therefore, the coupling layer's stiffness was set to 17780 N/m. And four layers of fascia were assumed to simulate the support of transducer. Due to the small displacement of the electromagnetic transducer and the uniform distribution of the magnetic field, the electromechanical coupling coefficient (α₀) is a constant ^[24]. The parameters of the lumped parameter model listed in Table 1 are taken from ^[26,27].

2.2.   Verification of the human ear-electromagnetic transducer coupling lumped parameter model

In order to verify the reliability of the human ear model, the stapes velocity calculated by the model under sound pressure stimulation was compared with the experimental data, as shown in Figure 2. The experimental data of the stapes velocity was measured by Shin et al. ^[34] under the stimulation of a 94 dB sound pressure level (SPL) sound applied at the tympanic membrane. As shown in Figure 2, although the model-predicted stapes velocity deviates slightly from the experimental data in specific data, it was consistent with Shin et al.'s the experimental data in overall trend.

Considering that the model was used to study the performance of the round-window stimulating electromagnetic transducer, the stapes velocity calculated by the model under the round-window stimulation were also compared with the experimental data in Figure 3. The stapes velocity represented by the black line was quoted from ^[35]. In this experiment, the coupling layer was 2 pieces of fascia, the excitation site was the round-window membrane, the excitation voltage was 100-mV_p-p, and the transducer was electromagnetic transducer with support. The stapes velocity represented by the red line was quoted ^[34]. As shown in Figure 3, the model-predicted stapes velocities are between Nakajima et al.'s experimental data and Shin et al.'s experimental data. Meanwhile, the trend of the model-predicted curve is consistent with that of the experimental data.

Based on the above comparisons, it can be seen that our model-predicted results match well with the experimental data. Besides, the model can simulate the dynamic characteristics of human ear under the round-window stimulation. Therefore, it is feasible to study the influences of design parameters of the round-window stimulating electromagnetic transducer by the lumped parameter model.

3.   Results

3.1.   Effect of the electromagnetic transducer's excitation voltage

The working principle of the round-window stimulating electromagnetic transducer is that the excitation voltage (U) excites the electromagnetic transducer to produce mechanical vibration, and the electromagnetic transducer transmits the vibration to the cochlea through the round-window membrane. Therefore, excitation voltage is the energy source of electromagnetic transducer's vibration. In order to investigate the influence of excitation voltage on the hearing compensation performance, the influence of excitation voltage and frequency on stapes displacement was studied based on the dimensionless six degrees of freedom model. As shown in Figure 4, the resonance frequency of stapes displacement does not change with the change of dimensionless excitation voltage (u). The resonance frequency of dimensionless stapes displacement (x₂) under different dimensionless excitation voltages (u) is always 3.

3.2.   Effect of the electromagnetic transducer's electromechanical coupling coefficient

The electromechanical coupling coefficient (α₀) is another important parameter affecting the vibration amplitude of electromagnetic transducer. The electromechanical coupling coefficient (α₀) is essentially the product of magnetic flux density (B) and conductor length (l). The electromechanical coupling coefficient affects the ampere force ($α_0\dot{q}$) that excites the transducer magnet. The motion of the electromagnetic transducer's case and magnet causes the induced electromotive force ($α_0\left({\dot{x}}_c-{\dot{x}}_m\right)$) to be generated in the circuit. This indicated that the electromechanical coupling coefficient describes an interaction between the electromagnetic transducer's circuit and mechanical system. Therefore, the electromechanical coupling coefficient is an important design parameter of the round-window stimulating electromagnetic transducer.

Based on the human ear-electromagnetic transducer coupling model, we obtained the bifurcation diagram of dimensionless stapes velocity (v₂) versus the electromechanical coupling coefficient (α₀) for dimensionless excitation frequency (Ω) equal to 3, as shown in Figure 5. The black color points represent the classical Poincaré points, and the blue line denotes the maximal Lyapunov exponent (L_max) calculated by the Wolf algorithm ^[36]. And a system with one or more positive Lyapunov exponents is defined to be chaotic ^[36]. The dimensionless resonance frequency of stapes displacement was 3. The system exhibited unstable periodic solution at α₀ < 0.72 N/A and 1.94 N/A < α₀ < 2.1 N/A, and chaotic motion occurred at 0.72 N/A < α₀ < 1.94 N/A. Besides, the dimensionless stapes displacement amplitudes (max(x₂)) at α₀ = 0-5 N/A were analyzed in Figure 6. The stapes displacement amplitude appeared to increase first and then decrease with the increase of α₀ for Ω = 3, 10 and 20. Furthermore, the region where chaotic motion occurs is affected by frequency. The chaotic motion occurred at 0.72 N/A < α₀ < 2.44 N/A for Ω = 10, and the chaotic motion occurred at 0.72 N/A < α₀ < 3.04 N/A for Ω = 20. The phase diagrams with Poincaré points under different electromechanical coupling coefficients were shown in Figure 7. The system exhibited unstable periodic solution (Figure 7(a)) at α₀ = 2 N/A. The state of chaotic motion changed to periodic motion (Figure 7(b)–(d)) though in verse period-doubling bifurcation near α₀ = 2.1 N/A, which is consistent with Figure 5.

3.3.   Effect of the electromagnetic transducer's support stiffness

The effect of electromagnetic transducer's support stiffness (k_S) and dimensionless excitation frequency (Ω) on the performance of round-window stimulating electromagnetic transducer is shown in Figure 8. It indicates that the resonance frequency increases with the increasing of the transducer's support stiffness. The relationship between the resonance frequency and the stiffness of the support is shown by the red dashed line in Figure 8, where, the resonance frequency of stapes displacement is 0.8 for k_S = 0.01 N/m (the end of transducer was set to free ^[27]); the resonance frequency of stapes displacement is 1.8 for k_S = 1000 N/m (the supporting material was assumed as superior mallear ligament with the thickness in 1 mm ^[37]); the resonance frequency of stapes displacement is 3 for k_S = 3356 N/m (the supporting material was assumed as fascia with the thickness in 1 mm ^[32]); the resonance frequency of stapes displacement is 4.8 for k_S = 8890 N/m (the supporting material was assumed as fascia with the thickness in 0.4 mm ^[32]); and the resonance frequency of stapes displacement is 5 for k_S = 10000 N/m (the supporting material was assumed as superior incudal ligament with the thickness in 1 mm ^[38]).

In order to further study the effect of support stiffness on stapes displacement amplitude, we calculated the dimensionless stapes displacement amplitude (max(x₂)) under different dimensionless excitation frequencies (Ω) and support stiffnesses (k_S), the results are shown in Figure 9. In Figure 9, when Ω = 0.8, x₂ = 4.3×10⁻⁸ at k_S = 0.01 N/m, and x₂ = 1.8×10⁻⁸ at k_S = 10000 N/m, the stapes displacement amplitude decreases significantly; when Ω = 5, x₂ = 4×10^-8 at k_S = 0.01 N/m, and x₂ = 4.03×10⁻⁸ at k_S = 10000 N/m, the stapes displacement amplitude increases slightly; when Ω = 10, x₂ = 2.68×10⁻⁸ at k_S = 0.01 N/m, and x₂ = 2.78×10⁻⁸ at k_S = 10000 N/m, the stapes displacement amplitude increases slightly; when Ω = 10, x₂ = 9.03×10⁻⁹ at k_S = 0.01 N/m, and x₂ = 9.47×10⁻⁹ at k_S = 10000 N/m, the stapes displacement amplitude increases slightly. Therefore, the increasing of support stiffness has an obvious impact on stapes displacement in the low frequency region and minor impact on stapes displacement in mid-high frequency region.

3.4.   Effect of the electromagnetic transducer's preload force

A practically implantable transducer should produce a hearing compensation performance of at least 100 dB SPL ^[39]. Therefore, we set the transducer's excitation voltage to 0.7 mV since it can stimulate the stapes displacement equivalent to the one stimulated by a 100 dB SPL sound pressure applied at the eardrum^[40]. Based on the stimulation of excitation voltage, different static forces were applied to simulate the preload force acting on the transducer with different amplitudes. Therefore, based on the result of the lumped parameter model without preload force, the equivalent sound pressure levels under four different preloads were analyzed. The curve of equivalent sound pressure level can be calculated according to Eq (5) as:

where x_s is the stapes displacement under different preload forces, x_{s, 0} is the stapes displacement under the same stimulation without preload force, and L_eq is the equivalent sound pressure level.

The model-calculated equivalent sound pressure level under five different preload forces are shown in Figure 10. Due to the nonlinear structural characteristics of human ear, the curves of equivalent sound pressure level vary in a nonlinear way. When the excitation frequency is less than 1000 Hz, the equivalent sound pressure level decreases with the preload force increasing. When the excitation frequency is larger than 1000 Hz, the equivalent sound pressure level increases with the increase of the preload force. The equivalent sound pressure level is maximum when the excitation frequency equals to 1800 Hz.

4.   Discussion and conclusions

According to the verification of the model, the human ear-electromagnetic transducer coupling lumped parameter model can predict the human ear response under forward stimulation and round-window stimulation. Therefore, it is feasible to analyze the design parameters of the round-window stimulating electromagnetic transducer by the lumped parameter model. This paper mainly analyzed four important design parameters of the electromagnetic transducer, i.e., the excitation voltage, the electromechanical coupling coefficient, the supporting stiffness and the preload force.

To improve the coupling condition between the transducer and the round window membrane, a piece of fascia is always placed as a coupling layer between them in clinical practice ^[30,31]. However, literature reports on this coupling layer's influence on the transducer's performance has shown mixed results. Schraven et al.'s study shows that using the coupling layer significantly improves the transducer's energy transmission ^[41]; whereas, Marino et al. reported the opposite effect, i.e., placing the coupling layer deteriorate the transducer's efficiency ^[42]. To investigate the influence of this coupling layer, we carried out a comparative study in our model as shown in Figure 11. During this study, we changed the Young's modulus and thickness of the coupling layer, respectively. The Young's modulus of 1.778 MPa and 0.35 MPa were used to simulate the fascia and round window membrane, respectively. The 0.1 mm is the thickness of the fascia.

This result shows that the layer number of the fascia used as the coupling layer has slight influence on the transducer's performance. In contrast, decreasing the coupling layer's young's modulus significantly reduces the transducer stimulated stapes displacement. Thus, the coupling layer especially the one with small Young's modulus would deteriorate the transducer's performance. This result is consistent with Marino et al.'s report but contrary to Schraven et al.'s study. The discrepancy may attribute to the ignorance of the geometry of the round window membrane and the transducer in our model ^[43].

The first natural frequency calculated by the lumped model is 1100 Hz, which is consistent with the first natural frequency (1.26 ± 0.2 kHz) of the normal human ear measured by Homma et al. ^[44]. Through the calculation results of the lumped parameter model, it was found that the change of excitation voltage did not alter the system's natural frequency. Therefore, changing the excitation voltage is a good way to adjust the hearing compensation performance.

The electromechanical coupling coefficient connects the mechanical system and circuit system in the model, which may be the design parameter with significant impact on the hearing compensation performance. Due to the nonlinear characteristics of human ear, the maximal Lyapunov exponent was positive at α₀ < 2.1 N/A, which means that the system exhibited unstable periodic solution or chaotic motion. And the stapes displacement appeared to increase firstly and then decrease with the electromechanical coupling coefficient increasing. The reason is that the ampere force driving the transducer is the product of the electromechanical coupling coefficient and the current. Although the increase of electromechanical coupling coefficient not only increases the ampere force at first, but also enlarges the induced electromotive force. And the increase of the induced electromotive force leads to a decrease of current. The reduction of current reduces the ampere force exciting the electromagnetic transducer. Finally, the increase of electromechanical coupling coefficient results in the decrease of stapes displacement. Therefore, under the premise of no chaotic motion, in order to obtain a good hearing compensation performance, the appropriate value of the electromechanical coupling coefficient is within 2.1–5 N/A.

Clinically, a soft tissue, which is a piece of cartilage ^[45] or a piece of fascia ^[30], is placed behind the transducer to stabilize the transducer. These two types of soft tissues have different stiffness. Our result shows that the increase of the support's stiffness enlarged the resonance frequency of the stapes displacement and reduced the stapes displacement near the resonance frequency, deteriorating the transducer's hearing compensation performance at low frequency. Given the significance of the resonance frequency, the support stiffness should be as small as possible to optimize the electromagnetic transducer's hearing compensation. Therefore, in terms of the transducer's compensation performance, placing a fascia, which has a relatively small stiffness, behind the transducer is better than placing the cartilage.

Because the preload force is affected by the transducer excitation force ^[27], the mechanical properties of transducer and differences in human ear characteristics between different patients, the optimal value for the preload force is hard to determine. If the patients suffer from hearing loss in high frequency, increasing the preload force is a suitable treatment option. Besides, considering the safety and round-window membrane integrity ^[46], the preload force of 10 mN is a suitable choice.

Acknowledgments

This research was funded by National Natural Science Foundation of China (grant number 51775547), NSFC-ERC project (grant number 52111530235) and the Priority Academic Program Development of Jiangsu Higher Education Institutions.

Conflict of interest

The authors declare no conflict of interest.