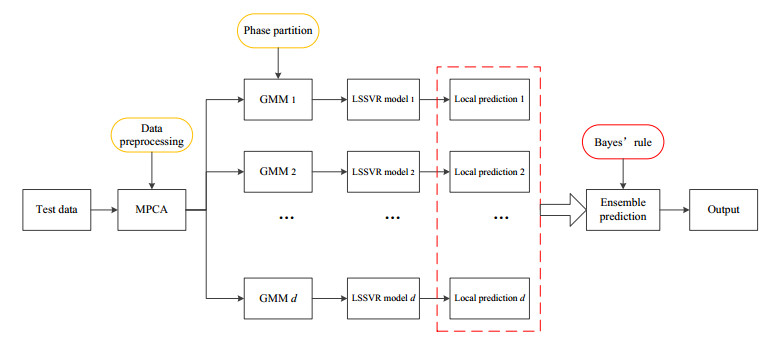
Traditional single model based soft sensors may have poor performance on quality prediction for batch processes because of the strong nonlinearity, multiple-phase, and time-varying characteristics. Therefore, a phase partition based ensemble learning framework upon least squares support vector regression (LSSVR) is proposed for soft sensor modeling. Firstly, multiway principal component analysis (MPCA) is employed to handle high-dimensional datasets and extract essential correlation information. Then, different operation phases of the process can be identified by the phase partition strategy based on Gaussian mixture model (GMM) method. Meanwhile, the optimal Gaussian component number is determined by Bayesian information criterion (BIC) technique. Further, multiple localized LSSVR models are constructed to characterize the various dynamic relationships between quality and process variables for local regions, while the grid search (GS) and ten-fold cross-validation methods are introduced to parameter optimization for each local model. Finally, the posterior probability for each test sample with respect to different phases can be estimated by Bayesian inference strategy, and local outputs are integrated to produce the final quality prediction results. Feasibility and superiority of the proposed soft sensor are validated through a case study for penicillin fermentation process. It can achieve satisfactory prediction accuracy and effectively tackle nonlinear and multi-phase modeling problems in chemical and biological processes.
1.
Introduction
In chemical processes, accurate real-time predictions of product quality are highly desirable, which is critical to realize successful process control, monitoring and optimization [1,2]. However, due to the costs of online analyzer and offline laboratory analysis, the process often encounters the great challenge of lacking reliable quality estimation. Soft sensing technique, which aims to construct theoretical or statistical models that can describe the functional relationship between process variables (easy-to-measure variables) and quality variables (difficult-to-measure variables), is proposed to address this issue and attracts much attention in both academia and industry. Generally, soft sensors can be classified into three groups: Model-driven, data-driven and mixed models [3,4,5,6]. Compared with model-driven method, data-driven one does not require in-depth mechanical knowledge of processes and only relies on recorded process datasets, which shows great flexibility and low complexity. Many dynamical models, such as nonlinear autoregressive with exogenous inputs (NARX) [7], and data-driven models, such as partial least squares (PLS), artificial neural networks (ANN), support vector machine (SVM), and Gaussian process regression (GPR) [8,9,10,11,12], have been successfully applied to online quality prediction.
Batch processes play an important role in the production of food, drugs, special chemicals and biological industrial products, which have high requirements for product quality and safe operation. In addition to the nonlinear and time-varying characteristics, other distinct characteristics, such as instability, finite duration, and batch-to-batch variations, are quite different from those of continuous processes [13,14]. It is difficult to construct accurate predictive models as the operating conditions vary. Furthermore, datasets obtained from batch processes are high-dimensional, including different batches, variables, and sampling time. Thus, they cannot be directly used for modeling and need to be preprocessed. Generally, multidimensional datasets contain abundant process information that can contribute to informative models, but it may also lead to information redundancy and complex model structure. Thus, dimension reduction and significant feature information extraction are crucial in satisfactory soft sensor development. Multiway principal component analysis (MPCA) [15,16,17] and multiway PLS (MPLS) [18,19] have been successfully applied in the fault diagnosis and soft sensing for batch processes. MPCA can be used to realize data analysis and preprocessing. Variable-wise unfolding method, which tends to keep the track of variables and retain the overall change information of process variables in batch and time, is introduced to obtain the two-dimensional datasets. Then, ordinary PCA is applied to dimensionality reduction and extract maximum amount of process information, making it more effective to soft sensor modeling.
Traditional nonlinear soft sensors can achieve a universal generalization performance in quality prediction of chemical processes. However, many of them rely on a single global model under the assumption that the operating phases and conditions are constant in the whole process. With operating conditions or product demands changing, processes exhibit apparent multiphase behaviors while different phases present various process characteristics, thereby resulting in the poor regression accuracy of global models.
Ensemble learning has been investigated and developed to be an effective tool to improve the generalization performance of soft sensors, especially for multiphase or multimode batch processes [20]. Under ensemble learning framework, the process dataset is partitioned into several local domains, then a series of local high-performance models are constructed and integrated to make a final quality prediction. Instead of global model construction, ensemble model based soft sensors can greatly enhance estimation accuracy and maintain satisfactory performance for a long time even though process characteristics change. The first step of ensemble learning method is to generate subsets from process data samples. Several popular data partition approaches include bagging [21], boosting [22], clustering [23] and the subspace method [24]. Clustering based methods, such as K-means, fuzzy C-means (FCM) [25], and Gaussian mixture model (GMM) [26], have been widely used and have shown their effectiveness in data clustering for multiphase processes. For example, Wang et al. used GMM to create local partitions and verified the feasibility and reliability of the proposed soft sensor [26]. However, this method only considers one batch of process data and does not take multiphase characteristics into account. In addition, the dataset length of each batch may not be equal because of the complex operating conditions in actual processes. Prediction combination is another important step of ensemble learning method. Traditional approaches for this purpose are averaging, voting, Bayesian inference, and learning method [2,20,26]. Bayesian fusion method has been proven to be a natural fit for ensemble model combination due to its strong statistical learning and analytical abilities from datasets [27,28]. It can remarkably and effectively utilize the limited process information.
Motivated to address the aforementioned issues, a novel ensemble learning based soft sensor, namely ensemble least squares support vector regression (LSSVR) [29,30] based on GMM method (GMM-LSSVR), is developed in this paper for the quality prediction of multiphase/multimode nonlinear batch processes. Firstly, MPCA is applied to data unfolding and information extraction for original 3-dimensional process datasets. In this method, the feature vectors corresponding to the large feature values are selected to form a subspace, where original datasets are mapped, then the preprocessed low-dimensional data matrix can be obtained for soft sensor modeling. Secondly, the Bayesian information criterion (BIC) [31] technique is introduced to determine the optimal number of Gaussian components for phase partition. And the newly obtained datasets are divided into several different subsets by GMM method to produce ensemble components. Thirdly, the grid search (GS) [32] method is used to generate all possible parameter pairs (σ, γ) due to its significant search effect and easy implementation. Meanwhile, ten-fold cross-validation [33] technique is employed to calculate the average relative error and evaluate the optimality of each pair. In such cases, an optimal parameter pair can be determined for each local LSSVR model, which greatly contributes to reliability enhancement. Finally, the Bayesian inference strategy is used to estimate the posterior probability of each test sample with respect to different operation dynamics and multiple models are combined with posterior probability based weightings for the final prediction.
The remainder of this paper is organized as follows. Section 2 briefly reviews LSSVR model, MPCA and GMM methods. Section 3 presents some details of the proposed novel soft sensor, including its modeling method, parameters determination, and combination strategy. Section 4 evaluates the effectiveness of the modeling method via simulation results in a batch process. Finally, Section 5 draws the conclusions of this paper.
2.
Preliminaries
2.1. Least squares support vector regression (LSSVR)
The LSSVR model is modified from support vector regression (SVR) [29]. Instead of inequality constraints applied, LSSVR uses equality constraints in the optimization problem in order to turn the convex quadratic optimization procedure into the solution of linear equations, which has shown its great ability in dealing with significant nonlinearity in batch processes. Thus, LSSVR is applied to construct local models upon the several partitioned regions in this paper.
Given {(xi,yi)}Ni=1, LSSVR algorithm aims to find the mapping between the input vector x∈Rd and the output vector y∈R. Suppose y=(y1,y2,⋯,yN)T∈RN, the output regression is regarded as an objective function minimization problem with constraints [29].
where Z=(φ(x1),φ(x2),⋯,φ(xN))∈Rnh×N, φ:Rd→Rnh represents a mapping from lower dimensional to higher dimensional Hilbert space with nh dimensions, ζζ=(ζ1,ζ2,⋯,ζN)T represents the matrix of slack variables, and γ represents the positive real regularized parameter.
By introducing Lagrange multipliers αα=(α1,α2,⋯,αN)T, the optimization problem of Lagrangian function can be formulated as
The following linear equations can be obtained by referring to the Karush-Kuhn-Tucker (KKT) condition for optimality.
Then, a linear system can be described by simplifying equations and eliminating ωω and ζζ as
where H=K+γ−1IN∈RN×N. In the positive definite matrix, K=ZTZ∈RN×N is a kernel matrix composed of kernel functions that satisfy Mercer's theorem.
In this work, the Gaussian kernel function is adopted to be the kernel function of LSSVR:k(xi,xj)=exp{−‖xi−xj‖22σ2}, where σ is hyperparameter of the kernel function. Suppose the solutions of (4) are αα∗=(α∗1,α∗2,⋯,α∗N)T and b∗, the output LSSVR can be described as
2.2. Multiway principal component analysis (MPCA)
In batch processes, the collected datasets are related to batches, variables and sampling time. Excessive data information may lead to information redundancy and deteriorate the estimation performance of soft sensor models. MPCA method has been proven to be effective in dimensionality reduction and widely used in data preprocessing of batch processes.
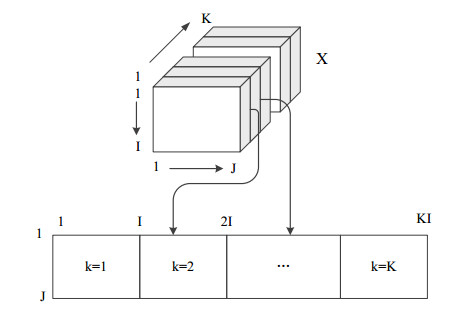
The dataset of a batch process can be given as a three-dimensional matrix X(I×J×K), where I is the process batch, J is the measurement variable, and K is the sampling time. In variable-wise method, MPCA promotes the variable-wise unfolding of data matrix X to obtain a two-dimensional matrix X(KI×J) with dimension KI×J on which ordinary PCA is performed [16]. The schematic diagram of this method is illustrated in Figure 1.
In this way, the original dataset can be rewritten into a new KI-dimensional variable space, then the new data matrix is preprocessed by
where xi,j,k denotes the measurement of jth variable of ith batch in kth sampling time. Each variable can obtain the mean and variance of the measurement values in all batches at all sampling time after standardization. As shown in Figure 1, the dataset unfolding method can better reflect the trajectory information and process characteristics of process variables.
For the standard dataset X(KI×J), PCA is performed as follows
where T(KI×Θ) represents the score matrix, P(J×Θ) represents the load matrix, and E(KI×Θ) represents the residual matrix. Θ is the number of selected principal components according to the cumulative contribution rate of all components.
2.3. Gaussian mixture model (GMM)
As an effective probabilistic approach for data clustering, GMM is widely used for process monitoring and soft sensor application. The main purpose of GMM method is to identify and localize phase of data samples in batch processes.
Consider a training dataset consisting of N data samples x∈Rn×m and y∈Rn×1, the probability density function of the dataset can be expressed as
where n denotes the number of data samples, n=1,2,⋯,N, m is the dimensionality of input vector, and Θ={μ1,…,μG,∑1,…,∑G} is the parameters of GMM with G-component Gaussian mixture distribution. The distribution parameters include mean vector μg, covariance matrix ∑g, and prior probability πg of the gth Gaussian component, while the mixing coefficients satisfy.
And p({\bf{x}}\mathit{\boldsymbol{|}}{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_g}) is probability density for Gaussian mixture distribution, which can be given by
Assume that data samples follow a mixture of a finite number of Gaussian distributions, it can be seen that each Gaussian component has three parameters ({\mu _g}, {{\rm{\Sigma }}_g}, {\pi _g}), which can be determined by maximizing the logarithmic likelihood function as
Then, expectation maximization (EM) algorithm, is introduced to estimate the optimal parameters by iterative calculation, which consist of E step and M step:
E step: Evaluate the posterior probability that ith training data samples, which belongs to the gth Gaussian component by using current parameter values.
M step: Obtain the corresponding likelihood function via the posterior probability calculated by E step. Re-estimate the parameters using the current value.
The parameter estimation process is not completed until the convergence is satisfied. For batch processes, the number of Gaussian components of GMM model corresponds to the number of stages of the process. Moreover, the mixing coefficient of each Gaussian component for a data sample is determined by the average posterior probability of the sample with respect to the corresponding component.
3.
Modeling method based on ensemble learning
3.1. Parameter determination
Parameter determination is an important step of model construction, and it can directly affect the generalization behavior of regression models. The multi-model parameter optimization method shows its strong superiority in tackling parametric uncertainty problems when industrial processes are complex and time-varying [34].
LSSVR models need to determine regularization coefficients and kernel parameters. The commonly used methods for parameter determination include GS and swarm intelligence optimization [36,37,38,39]. In this study, the parameters of the LSSVR model are determined by ten-fold cross-validation and GS methods. First, for the parameter pair (σ, γ) that needs to be determined, GS method is used to form the grid in the given parameter selection interval. Second, the average relative error (Eq. (17)) of the corresponding model is calculated by ten-fold cross-validation method at the grid point. Finally, the parameter pair with the minimum error value is selected as an optimal pair.
where N denotes the number of test samples, and {y_i} and {\widehat y_i} represent the actual and predicted values of ith test sample, respectively.
The steps of LSSVR parameter determination are presented as follows:
Step 1: Assign an initial value to σ and γ.
Step 2: Determine the search range of σ and γ.
Step 3: Determine the grid point position of the first cross-validation calculation according to the initial value.
Step 4: Select ten-fold cross-validation as the objective function of grid point calculation. Then calculate the errors of all grid points.
Step 5: Compare the error results and determine an optimal parameter pair.
3.2. Multiphase modeling strategy
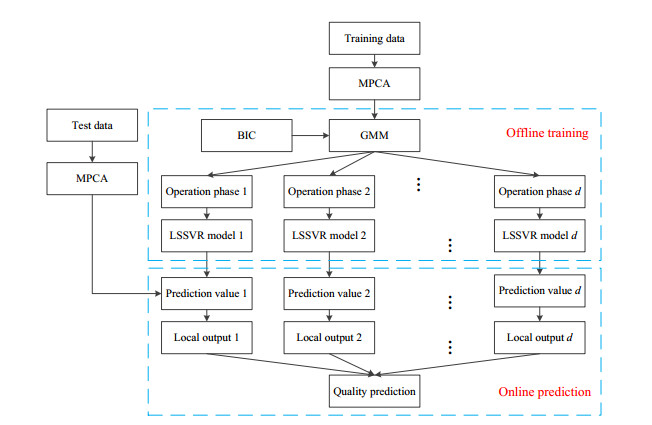
Some traditional soft sensors construct a global regression model for quality prediction; it ignores the multiphase and multistage characteristics of batch processes. Fortunately, ensemble learning based local modeling methods, which can better meet the requirements of prediction accuracy by combining multiple local models, have drawn increasing attention to improving the performance of soft sensors. Therefore, a novel soft sensor, referred to as ensemble LSSVR based on GMM (GMM-LSSVR), is proposed for quality prediction in multiphase batch processes. First, MPCA is employed to data preprocessing, including three-dimensional data unfolding and dimensionality reduction. And GMM method is applied to divide the preprocessed dataset into multiple local domains. Then, several local LSSVR models are constructed for all identified subsets. Meanwhile, optimal hyperparameters are determined by combining ten-fold cross-validation with GS method. Finally, according to the posterior probability of the new sample to each operation period (Eq (18)), the high-performance predictions of local LSSVR models are integrated to produce the overall prediction results by using the Bayesian inference and finite mixture mechanism, as shown in Eq (19).
where {x_q} denotes a new test sample, {S_g} = \left\{ {{{\bf{x}}^g}, {y^g}} \right\}, {\rm{ }}g = 1, 2, \cdots , G denotes G operation periods, y_q^g denotes the output value of {x_q} with respect to gth model.
When GMM method is applied, the BIC technique is introduced to determine the number of Gaussian components in an intuitive and persuasive way, which can be formulated as
where N is the number of training samples, d is the parameter number of Gaussian components, \log L({\bf{x}}\mathit{\boldsymbol{| \boldsymbol{\varTheta} }}) is the logarithmic likelihood function. It aims to balance model complexity and estimation accuracy. By calculating and comparing, the number of Gaussian components that corresponds to the minimum BIC value is selected as the optimal number for phase partition in the process.
Figure 2 illustrates the online prediction steps of test samples based on GMM-LSSVR method. The proposed soft sensor modeling strategy is shown in Figure 3.
4.
Case study
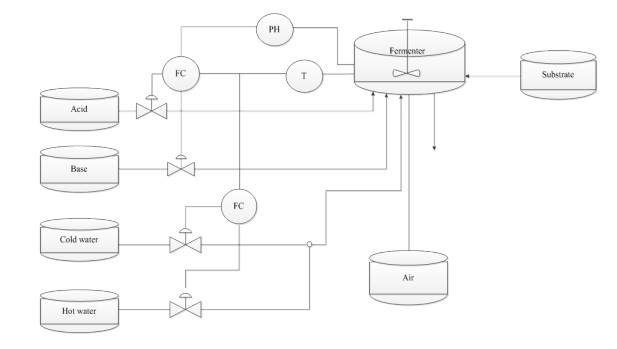
Penicillin fermentation process is a typical microbial fermentation reaction and is often used to be a benchmark process for monitoring, controlling, and quality prediction. This process is a complex multivariable coupled biochemical procedure and often contains significant nonlinearity and time-varying behavior, which can be generally divided into three stages: growth, penicillin synthesis and autolysis stages [20]. Figure 4 shows the flow diagram of penicillin fermentation process. During the whole cultivation process, bacterial growth and antibiotic synthesis process are completed under suitable fermentation conditions such as temperature, pH, and oxygen concentration and so on. Considering the costs of offline chemical analysis and hardware sensors, designing a high-performance soft sensor plays an important role in real-time estimation of penicillin concentration.
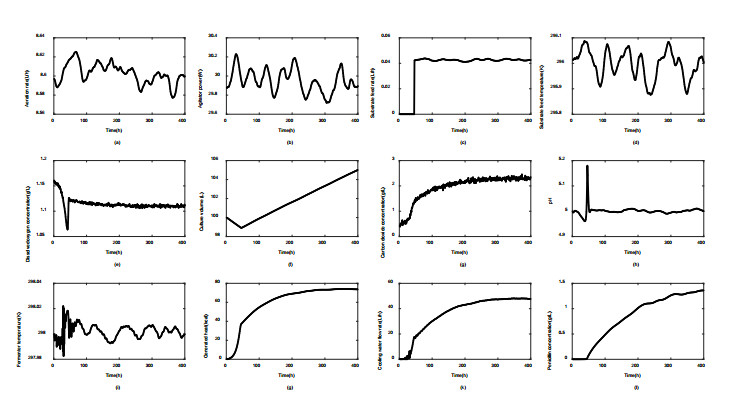
A simulation platform named PenSim has been widely used to simulate fed-batch penicillin fermentation process under different operating conditions [20]. In this study, all process data samples for experiments are collected via running the PenSim platform. There are total 16 process variables in the simulation plant, and 11 highly related variables are selected as input variables, which are listed in Table 1. The typical trend plots of input and quality variables are depicted in Figure 5. The entire duration of each batch is set as 400 hours, while the sampling interval is set as 1 hour. Under the normal operating condition, a total of 4 training batches (named as Batches 1 to 4) are obtained for soft sensor model construction, while the additional 2 test batches (named as Batches 5 and 6) are collected for model performance evaluation.
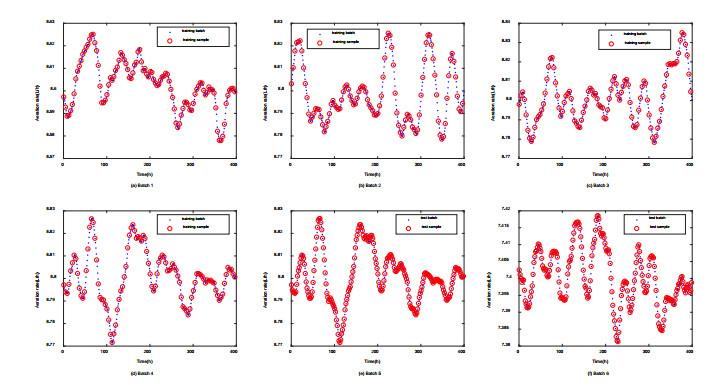
For model construction, 100 data samples are collected evenly from Batches 1 to 4, respectively. As a result, training dataset is composed of 400 samples, while additional 200 samples that collected evenly from Batch 5 compose the test dataset 1, and other 200 samples from Batch 6 compose the test dataset 2. Here, two test datasets are used for model evaluation: test dataset 1 in Batch 5 and test dataset 2 in Batch 6 with noisy condition. Suppose that the measure noise is the zero-mean Gaussian noise with variance of 0.01, the dataset 2 is used to study the behavior of the proposed soft sensor model under noisy measure environment. In order to show the sampling strategy more intuitively, for examples, we collect the aeration rate (one of the input variables) values every 4 hours in the training Batch 1. The sampling time plots of aeration rate are illustrated in Figure 6, where the red points represent the data samples selected for modeling. Figure 6a–d and e–f gives the sampling time of aeration rate in the training batches and test batches, respectively. The sampling time plots of other input variables are like that of aeration rate.
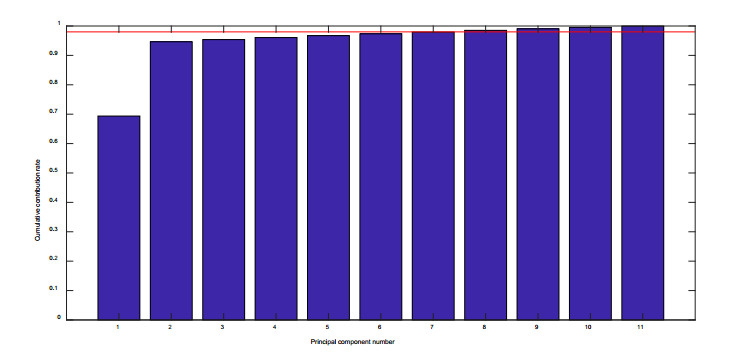
Then, MPCA is applied to data preprocessing. Firstly, two-dimensional modeling datasets can be obtained from original multidimensional datasets by variable-wise data unfolding method. Then, PCA, as a well-known technique in statistics and machine learning, is used to compress the input variables, and extract the most important information of the process. The relationship between principal components number and cumulative contribution rate for input dataset is illustrated in Figure 7. In this study, the principal component number can be set as 7 because the corresponding cumulative contribution rate achieves 0.98. As a result, the dimensionally reduced data is obtained and imported into soft sensor models for training.
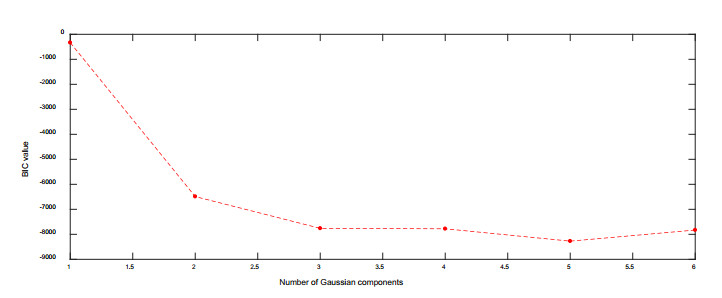
The BIC value is calculated according to the obtained data matrix to determine the optimal number of Gaussian components. The relationship between the number of Gaussian components and BIC values is shown in Figure 8. When the number of Gaussian components is small, BIC values decrease dramatically. As the number increases, which changes from 3 to 6, BIC values change smoothly. In order to simplify model structure as much as possible and prevent the model from overfitting, the optimal number of Gaussian components is set as 3.
Four soft sensor models have been constructed in the following study:
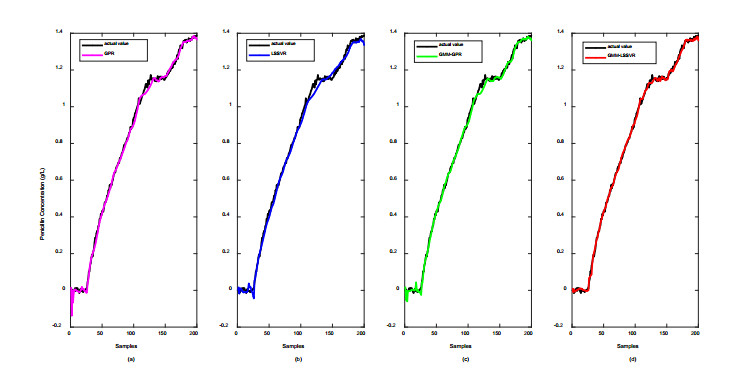
(ⅰ) GPR: A global GPR model constructed from the preprocessed dataset.
(ⅱ) LSSVR: A global LSSVR model constructed from the preprocessed dataset.
(ⅲ) GMM-GPR: An ensemble model based on several local GPR models constructed from local preprocessed datasets that are obtained by using GMM method.
(ⅳ) GMM-LSSVR: An ensemble model based on several local LSSVR models constructed from local preprocessed datasets that are obtained by using GMM method.
To verify the prediction capabilities of the soft sensors with penicillin concentration, three performance indices including root-mean-square error (RMSE), tracking precision (TP) and coefficient of determination (R2) are used, which are defined as follows:
where {\overline y _i} is the ith mean value, \sigma _{true}^2 is the variance of the true value of test samples, \sigma _{error}^2 is the variance of error between the true and predicted values of the test samples. The estimation accuracy of a soft sensor model can be reflected by the RMSE and TP indices, and R2 gives information about how much of the total variance in the output predictions can be explained by the model. In this study, the search ranges of γ and σ are set as {\rm{ \mathsf{ γ} }} \in \left\{ {{2^{ - 7}}, {2^{ - 5}}, \cdots , {2^{ - 15}}} \right\} and \sigma \in \left\{ {{2^{ - 12}}, {2^{ - 10}}, \cdots , {2^3}} \right\}, respectively.
Table 2 shows the quantitative comparison of the performance indicators for different four soft sensors. The comparison of global modeling and local learning methods shows that ensemble GPR model and ensemble LSSVR model perform better than global GPR and global LSSVR, respectively, because the RMSE value of the former is smaller than that of the latter. Clearly, GMM based multiple models can accurately and effectively describe the multiphase characteristics of batch process and enhance the ability of model interpretation. Therefore, for penicillin fermentation process, multi-model modeling has higher estimation accuracy and smaller prediction error. Similarly, by comparing GMM-GPR model with GMM-LSSVR model, it can be found that the ensemble LSSVR model based soft sensor has higher prediction accuracy and better tracking effect for penicillin concentration, whereas the ensemble GPR model based soft sensor has bigger RMSE values and smaller TP values. This result shows that, although the prediction performance of GMM- ensemble GPR model is improved compared with the global GPR model, poor predictions for test samples are still observed. As presented, the prediction performance of GMM-GPR model is far inferior to that of GMM-LSSVR model. Despite the presence of noise, as studied for dataset 2 in Batch 6 with noise, GMM-LSSVR based soft sensor still outperforms other different soft sensors. Three performance indicators can demonstrate the feasibility and superiority of the proposed method.
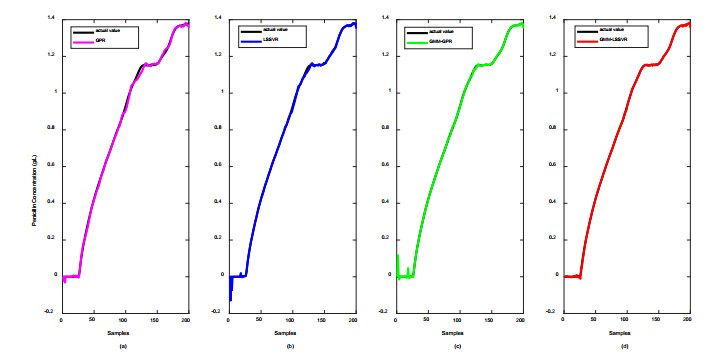
To present the regression performance of different soft sensors, the prediction results of penicillin concentration for global modeling and local learning methods is depicted in detail in Figures 9 and 10. As shown in Figure 9, the prediction curve of penicillin concentration by GMM-LSSVR model is more in line with the true value curve, thereby showing that the predicted value of penicillin concentration in this method is closer to the true value, and the prediction accuracy is also significantly higher than that of global LSSVR model. Furthermore, the prediction error of GMM-LSSVR model for test samples is reduced, and its generalization performance is better compared with that of GMM-GPR model. Similar analysis conclusions can be made according to the quality prediction results of Batch 6, which is given in Figure 10. This soft sensor modeling method can effectively improve the prediction capability and regression accuracy of global LSSVR model and can better complete the prediction of penicillin concentration.
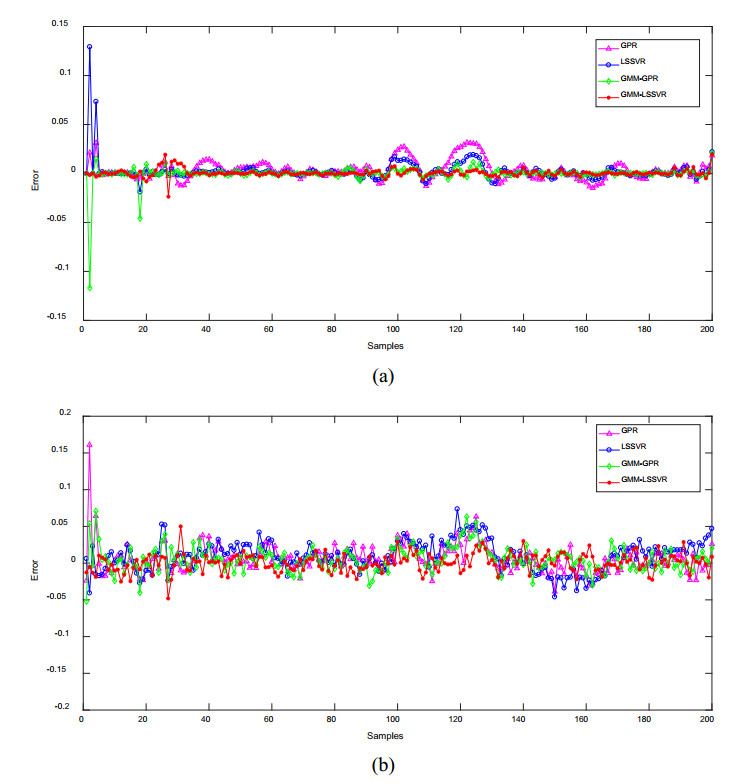
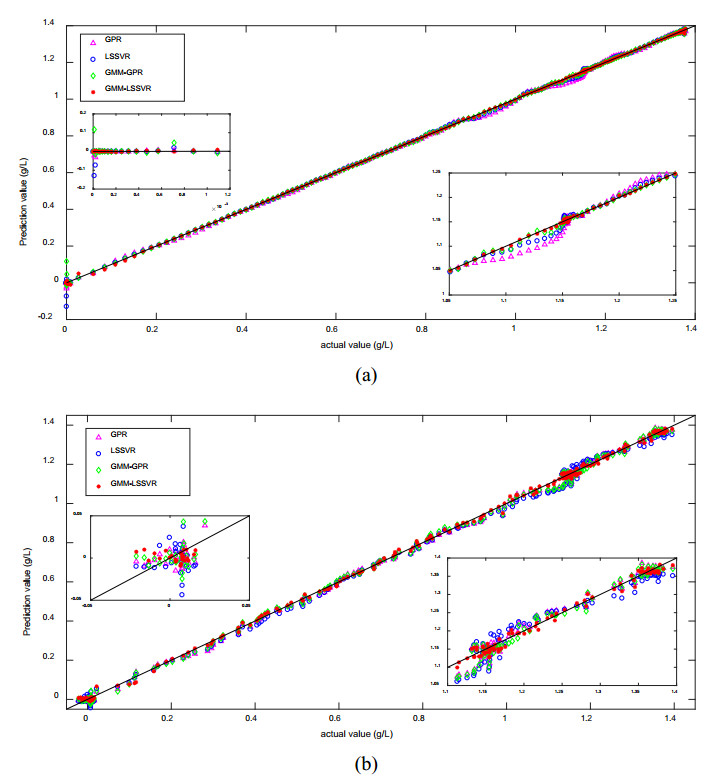
To further illustrate the effectiveness of the proposed method, Figure 11 shows the comparison of the prediction errors of penicillin concentration for four soft sensors. It can be clearly seen that whether there is noise or not, the prediction error of the GMM-LSSVR model fluctuates less near 0, showing that the prediction results of the model are more consistent with the real results, and the tracking ability is stronger. Compared with different modeling methods, the GMM-LSSVR based soft sensor provides an accurate prediction of the true value of penicillin concentration and has good regression performance. In addition, the scatter plots of prediction results for penicillin concentration is presented in Figure 12. Compared with other scatters, the red asterisk scatters that correspond to GMM-LSSVR are more compactly distributed in the diagonal line, which shows that the proposed method can further improve the tracking performance and regression accuracy of the soft sensor. It can deliver reliable and accurate estimation of quality variable despite the presence of noise.
5.
Conclusion
A smart soft sensor based on ensemble LSSVR models is proposed to deal with nonlinear, time-varying, and multiphase characteristics in batch processes. First, MPCA method is applied to be an effective tool for data unfolding and dimensionality reduction. Then, the new obtained dataset can be partitioned into several local regions, where local LSSVR models are constructed. Second, local LSSVR models are constructed for each operation period, respectively. Meanwhile, GS method and ten-fold cross-validation procedure are introduced to local model parameter determination. In this way, each local LSSVR model with a pair of optimal parameters can provide superior regression accuracy. Finally, an ensemble regression model is established by combining different local models by Bayesian fusion strategy and we can obtain the final prediction for test samples from ensemble LSSVR model online. Detailed analyses and comparative studies for penicillin fermentation process show that the proposed soft sensor is feasible and can deliver reliable and accurate quality prediction. In addition, we may be able to improve our future work for soft sensor development by applying cellular neural network approach.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant No.61773182), and the Subtopics of National Key Research and Development Program of China (Grant No.2018YFC1603705-03).
Conflict of interest
The authors declare no conflict of interest in this paper.









 DownLoad:
DownLoad: