Transmission dynamics and optimal control of stage-structured HLB model

1.   Introduction

Huanglongbing (HLB), more commonly known as citrus greening disease, is one of the most dangerous and devastating diseases of citrus worldwide ^[1,2]. Two decades ago, it invaded the Western Hemisphere, primarily Florida and Brazil, where it has spread rapidly and caused major damage to global citrus production. It is estimated that citrus acreage in Florida has decreased by 40% and production by 49% since their historical peaks, all of which occurred in the last 20 years ^[3]. Up to 2015, 20% of Brazil's commercial citrus species has been infected with HLB, and the disease caused great damage to citrus industry by shortening tree lifespan and poor yield and quality ^[4]. In S$\tilde{a}$o Paulo, 64.1% of the commercial citrus blocks and 6.9% of the citrus trees were affected by HLB in 2012 ^[5]. In addition, Ganzhou is the top citrus producing area in Jiangxi Province, China, with an annual production of approximately 1.2 million tons ^[6,7]. However, the producing-area has also suffered from the widespread out of HLB and the output has significantly decreased in recent years ^[8]. The citrus acreage in Ganzhou had decreased from 2.48 million acres in 2013 to 1.00 million acres in 2018.

HLB is caused by phloem-restricted bacteria of the Candidatus Liberibacter group, which can be transmitted by two species of citrus psyllids, the Asian citrus psyllid (ACP), Diaphorina citri Kuwayama, and the African citrus psyllid, Trioza erytrae ^[3]. ACP is divided into eggs, $1^{st}$ through $5^{th}$ nymphal instars and adults ^[9]. The five nymphal instars of ACP can be differentiated by their distinct morphological characteristics ^[10]. Adults and nymphs are capable of acquiring the HLB pathogen after feeding on an infected plant for 30 min or longer ^[11]. Although the nymphs hardly move, they soon become Las-carrying (Candidatus Liberibacter asiaticus) adults with the ability to fly and transmit Las to other citrus plants. Thus the control period of vector psyllid should include the nymphal stages ^[10]. The results from ^[10] reported that psyllids can carry Las in either adult or nymphal stages, expect in the $1^{st}$ and $2^{nd}$ instars, the $3^{rd}$ through $5^{th}$ instars have stronger transmission ability than adults.

Generally a healthy citrus tree is inoculated by infected nymphs and adults, there is an incubation period in which the tree exhibits no symptoms but may act as a source of the disease ^[2]. The survey results from ^[12,13] indicated that the incubation period from grafting to development of HLB symptoms is 3 to 12 months under greenhouse conditions. Since incubation period is long and diagnosis is difficult, citrus trees can not be easily found in time after infection. This issue reduces the effectiveness of control strategy in which infected trees are removed to eliminate sources of HLB ^[14].

Recently, mathematical modeling has become an important and useful tool in understanding the epidemiology of vector-transmitted plant pathogens ^{[15,16,17,18,19]}. For citrus HLB, a few mathematical models currently exist which analyze how HLB spreads within individual trees ^[20], within a citrus grove ^{[21,22,23,24,25]}, or from grove to grove ^[26]. In ^[21], the authors reviewed how mathematical models have yielded useful insights into controlling disease spread for vector-borne plant diseases, especially HLB. Note that, for citrus psyllid, different stages have different biological characters, such as reproductive potential, growth, temperature tolerance, transmission efficiency. Therefore, it is very necessary to consider the stage structure of psyllid in mathematical model, including eggs, the $1^{st}$ and $2^{nd}$ nymphal instars, the $3^{rd}$ through $5^{th}$ nymphal instars and adults. However, the stage structure of psyllid has not been discussed in the previous HLB models. Motivated by the preceding discussion, our first purpose of this paper is to formulate and investigate a HLB model, in which the incubation period of citrus tree and the stage structure of psyllid are taken into consideration.

There is no good source of genetic resistance to HLB in the genus citrus, and the disease cannot be cured once the trees are infected ^[2,27]. Current programs for HLB have focused on nutrient solution injection to reduce the infection of the bacteria, removal of infected trees to reduce sources of the disease and insecticide spraying control of the psyllid vector and planting with HLB-free nursery stock ^[2]. The second aim of this paper is to achieve awareness about the most desirable technique for minimizing the transmission of HLB by using the optimal control theory.

In this paper, different from the previous simple classification of psyllid into susceptible and infected populations, we consider that citrus psyllid in different stages have different abilities and ways to transmit HLB. Based on the above facts, in the next section, we establish a stage-structured HLB model, and obtain the basic reproductive number $R_0$ of the model. In Section 3, we obtain the equivalent threshold condition $T_0$ of the basic reproductive number $R_0$, and prove extinction of the disease when $R_0\leq1$ while persistence of the disease when $R_0 > 1$. In Section 4, we apply the optimal control technique to minimize the population of infected citrus trees, dead trees and total number of vector population. Different control strategies should be used for the elimination of infection in the population of citrus trees. In Section 5, we use numerical simulation to demonstrate and support the theoretical results. In the last section, we give a brief conclusion.

2.   A mathematical model and the basic reproductive number $R_0$

2.1.   Model formulation

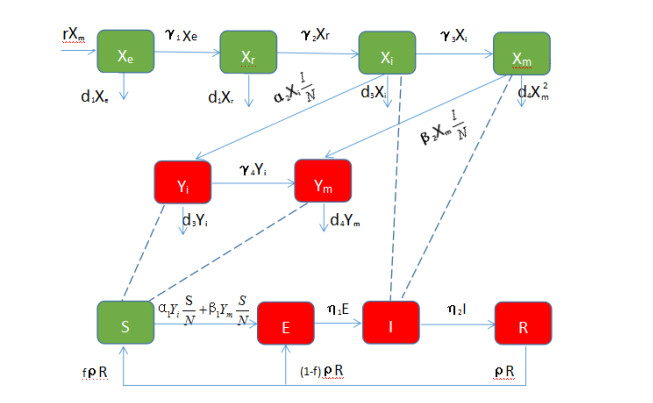
In this subsection, Citrus HLB model where transmission is via vector psyllids is formulated. The notation used in the mathematical model includes four states for citrus tree population. $S$ denotes susceptible trees (individuals who can be infected by disease) and $R$ represents dead trees. Due to the latency delay we split the infected trees into a latent stage, $E$ (individuals who infected and asymptomatic but no infectious) and an infectious stage, $I$ (individuals who have the ability to transmit the disease to others). Let $N(t)$ be the total numbers of citrus tree population at time $t$ in a grove, that is, $N(t) = S(t)+E(t)+I(t)+R(t)$. Based on the fact that $3^{rd}$ through $5^{th}$ nymphal instars can transmit HLB, the citrus psyllid population is divided into six state variables. We let $X_e$ represent eggs (produced by susceptible adults of psyllids), $X_r$ denote $1^{st}$ and $2^{nd}$ nymphal instars (individuals who do not have the ability to transmit the disease to other susceptible trees), $X_i$ and $Y_i$ denote $3^{rd}$ through $5^{th}$ susceptible and infected nymphal instars, respectively. $X_m$ and $Y_m$ denote susceptible and infected adults of psyllid, respectively. We assume that the grove is subject to roguing and replanting management strategy. Moreover, we ignore the natural mortality rate of the citrus tree. The model flow diagram is depicted in Figure 1. Considering HLB transmission between citrus trees and psyllids, we establish the following HLB model.

In model (1), dead trees are rogued at a rate $\rho$ and the corresponding spots are replanted with new trees. We assume that a proportion $f\in [0, 1]$ of the newly planted trees will be healthy and a proportion $1 - f$ will become infected to a latent stage immediately. We also assume $\eta_1, \gamma_1, \gamma_3$ and $\gamma_4$ are the conversion rates, $\eta_2$ is the disease-induced mortality rate of tree, $r$ denotes oviposition rates of susceptible adult psyllid, $d_1$ and $d_2$ represent the natural mortality rates of eggs and $1^{st}$ through$2^{nd}$ nymphal, respectively, $d_3$ is the natural mortality rate of $3^{rd}$ through $5^{th}$ nymphal, $d_4$ is the natural mortality rate of adult psyllid. Let $\alpha_1$ be the infection rate from $3^{rd}$ through $5^{th}$ infected nymphals to susceptible trees, $\alpha_2$ be the infection rate from infected trees to $3^{rd}$ through $5^{th}$ susceptible nymphals, $\beta_1$ be the infection rate from infected adult psyllid to susceptible trees, and $\beta_2$ be the infection rate from infected trees to susceptible adult psyllids.

Subject to the restriction $\frac{dN(t)}{dt} = \frac{dS(t)}{dt}+\frac{dE(t)}{dt}+\frac{dI(t)}{dt}+\frac{dR(t)}{dt}\equiv 0$, without loss of generality, let $N(t) = 1$, and now $S+E+I+R = 1$. Here $S$, $E$, $I$ and $R$ are defined separately as susceptibility rate, latent rate, infection rate and removal rate, respectively. Thus, system $(1)$ can be reduced to the form:

From biological considerations, we study $(2)$ in the closed set $\Gamma = \{(S, E, I, R, X_e, X_r, X_i, X_m, Y_i, Y_m)\in R^{10}\; |\; S, E, I, R\geq 0, S+E+I+R = 1, X_e, X_r, X_i, X_m, Y_i, Y_m\geq 0\}$, which is invariant set under nonnegative initial conditions. It is easy to proof the boundedness of the solutions of system (2). We omit it.

The system $(2)$ always exists a disease-free equilibrium (DFE) $P_0 = (S^0, 0, 0, 0, X^0_e, X^0_r, X^0_i, X^0_m, 0, 0)$, where

2.2.   The basic reproductive number $R_0$

The basic reproductive number $R_0$ of an infectious disease is a fundamental concept in the study of disease transmissions. It represents the average number of secondary cases produced, in a completely susceptible population, by a typical infective individual ^[28]. If $R_0 < 1$, then on average an infected individual produces less than one new infected individual over the course of its infectious period, and the infection cannot grow. Conversely, if $R_0 > 1$, then each infected individual produces, on average, more than one new infection, and the disease can invade the population ^[29]. Diekmann et al. ^[29] define $R_0$ as the spectral radius of the next generation matrix. That is, we rewrite the vector field of $(2)$ as

and $\mathscr{V}_i(x) = \mathscr{V^-}_i(x)-\mathscr{V^+}_i(x)$, where $x = (E, I, R, Y_i, Y_m, S, X_e, X_r, X_i, X_m),$

$F, V$ are defined as

where $\hat{P}_0 = \left(0, 0, 0, 0, 0, S^0, X_e^0, X_r^0, X_i^0, X_m^0\right)$. Thus

Obviously, $-V$ is cooperative. By simple computation, we get

The eigenvalues of $FV^{-1}$ are determined by

It is easy to obtain that the spectral radius of $FV^{-1}$ is:

where

3.   Main results

3.1.   An equivalent threshold quantity $T_0$

In order to give a more reasonable biological interpretation, we give an equivalent threshold quantity as

where $R_1$ and $R_2$ are defined in (4). The biological meaning of quantity $T_0$ can be explained as follows. Suppose that a single infected tree in stage $E$ is introduced into a completely susceptible grove. The average number of secondary infections resulting from the psyllid in stage $X_i$ (that is susceptible $3^{rd}$ through $5^{th}$ nymph) contact infected tree is,

Further, the average number of secondary infections resulting from the psyllid in stage $X_m$ (that is susceptible adult psyllid) contact infected tree is,

The citrus tree will necessarily be removed in the $R$ stage and will on average produce $1-f$ newly infected $E$ trees. Thus the expected number of secondary infections is exactly $T_0$. In the following, we will prove the equivalence of $T_0$ and $R_0$ for the local stability of the DFE $P_0$.

Theorem 3.1. (ⅰ) $R_0 < 1$ if and only if $T_0 < 1$.

(ⅱ) $T_0 < 1$ if and only if all eigenvalues of the Jacobian matrix of system (2) evaluated at DFE $P_0$ have negative real parts.

Proof. It follows from (3) that the basic reproductive number $R_0$ is the largest positive root of

Clearly, the leading coefficient of $\rho(\lambda)$ is positive, and thus $R_0 < 1$ if and only if

Therefore, $\rho(1) > 0$ is equivalent to $T_0 < 1$ and the first assertion holds.

Next, we want to prove the second assertion. Calculating the Jacobian matrix of system (2) at the DFE $P_0$:

Clearly, $J(P_0)$ can be seen as a block matrix of $2\times2$ and each block is a $5\times5$ matrix. The eigenvalues are determined by the following characteristic equation of $J(P_0):$

Any root $\lambda$ of $p(\lambda)$ with $Re(\lambda)\geq 0$ is also a root of $q(\lambda)$ defined by

Obviously, $q(\lambda)$ is monotone increasing in $\lambda$ when $\lambda > 0$. It follows from that, since the leading coefficient of $p(\lambda)$ is positive, we know that $p(\lambda)$ has no positive real roots if and only if $q(0) > 0,$ which is equivalent to

that is, $T_0 < 1$. Next, we need to prove all complex eigenvalues of $J(P_0)$ have negative real parts. Suppose the contrary. Then we define $G(\lambda) = 1-q(\lambda)$ and suppose $p(\lambda) = 0$ with $Re(\lambda)\geq0$ and $Im(\lambda)\neq0.$ Then $G(\lambda) = 1$ where

We claim $|G(\lambda)| < G(Re(\lambda))$. From (5), we have

where $\Upsilon = (Re(\lambda)+\eta_1)(Re(\lambda)+\eta_2)$, and the second inequality is strict since $Im(\lambda)\neq0$. Then we get $T_0\! < \!1\Leftrightarrow q(0)\! > \!0 \Leftrightarrow G(0)\! < \!1,$ which implies $G(Re(\lambda)) < 1$ since $G$ is decreasing in $\lambda$. Thus $|G(\lambda)| < G(Re(\lambda)) < 1$. This contradicts $G(\lambda) = 1$.

3.2.   Extinction of the disease when $R_0 < 1$

Theorem 3.2. If $R_0 < 1$, then the DFE $P_0$ of system (2) is globally attractive.

Proof. Note that $R_0 < 1$ implies that $f > 0$. Suppose $\limsup_{t \rightarrow \infty} E(t) = m > 0.$ Then for every $\varepsilon > 0$ there exists $\tau _1 > 0$, such that

It follows from the third equation of system (2) and (6) that

for all $t\geq \tau_1$. Then there exists $\tau_2 > \tau_1$ such that

for all $t\geq \tau_2$. It follows from the fourth equation of system (2) and (7) that

for all $t\geq \tau_2$. Thus there exists $\tau_3 > \tau_2$ such that

Further, from system (2), we have

Considering the auxiliary system of (9):

Clearly, (10) is a quasi-monotone system, and the unique positive equilibrium $(X^0_e, X^0_r, X^0_i, X^0_m)$ of system (10) is globally asymptotically stable if $R_0 < 1$. By comparison theorem in differential equations, we obtain that there exists $\tau_4 > \tau_3$ such that

for all $t\geq \tau_4$. Substituting (7) and (11) into the ninth equation of system (2), we have that

for all $t\geq \tau_4$. Then there exists $\tau_5 > \tau_4$ such that

for all $t \geq \tau_5$. Substituting (7), (11) and (12) into the last equation of system (2), we get that

for all $t\geq \tau_5$. Thus there exists $\tau_6 > \tau_5$ such that

for all $t\geq \tau_6$. Now, substituting (8), (12) and (13) into the second equation of system (2), we get that for $t\geq \tau_6$

Then there exists $\tau_7 > \tau_6$ such that

for all $t\geq \tau_7$. Letting $\varepsilon\rightarrow 0$, the inequality (14) becomes

It follows from Theorem 3.1 that, $R_0 < 1$ implies $T_0 < 1$. Thus $\limsup_{t\rightarrow \infty}E(t) < m,$ a contradiction. So $m = 0$. Following (7), (8), (12)-(14) and the nonnegativity of the solutions, we have $\lim_{t\rightarrow \infty}E(t) = \lim_{t\rightarrow \infty}I(t) = \lim_{t\rightarrow \infty}R(t) = \lim_{t\rightarrow \infty}Y_i(t) = \lim_{t\rightarrow \infty}Y_m(t) = 0$. By the theory of asymptotically autonomous semiflows (see ^[30]), we have

Therefore all nonnegative solutions converge to the DFE $P_0$.

3.3.   Persistence of the disease when $R_0 > 1$

It follows from Theorem 3.1 that DFE is locally asymptotically stable as $R_0 < 1$, while DFE is unstable as $R_0 > 1$. Theorem 3.2 in subsection 3.2 illustrates the global stable result of DEF for the case $R_0 < 1.$

Theorem 3.3. If $R_0 > 1$, then the disease is uniformly persistent for system (2). That is, there is a positive constant $\varepsilon_0 > 0$, such that

Proof. Denote $\widetilde {K} = \{(S, E, I, R, X_e, X_r, X_i, X_m, Y_i, Y_m)\in R^{10}_+\}$, $K_0 = \{(S, E, I, R, X_e, X_r, X_i, X_m, Y_i, Y_m)\in \widetilde {K}:S\geq 0, E > 0, I > 0, R > 0, X_e\geq 0, X_r\geq 0, X_i\geq 0, X_m\geq 0, Y_i > 0, Y_m > 0\}$, and $\partial K_0 = \widetilde{K}\backslash K_0$. Let $u(t, t_0, x_0)$ be the unique solution of system (2) with the initial value $x_0 = (S_0, E_0, I_0, R_0, X_{e0}, X_{r0}, X_{i0}, X_{m0}, Y_{i0}, Y_{m0})$ at time $t_0$.

Define poincaré map $P:\widetilde{K}\rightarrow \widetilde{K}$ associated with system (2) as follows:

Set

We claim that

Obviously, $\{(S, 0, 0, 0, X_e, X_r, X_i, X_m, 0, 0)\; |\; S\geq 0, X_e\geq 0, X_r \geq 0, X_i\geq 0, X_m\geq 0\}\subseteq M_\partial$. Next, We want to show

If (16) does not hold, then there exists a point $(S_0, E_0, I_0, R_0, X_{e0}, X_{r0}, X_{i0}, X_{m0}, Y_{i0}, Y_{m0})\in M_\partial \backslash \{(S, 0, 0, 0, X_e, X_r, X_i, X_m, 0, 0)\; |\; S\geq 0, X_e\geq 0, X_r \geq 0, X_i\geq 0, X_m\geq 0\}$. Next, for the five initial values $E_0, I_0, R_0, Y_{i0},$ and $Y_{m0}$, we divided into four cases to discuss.

Case (i) One initial value is equal to zero, and the others are lager than zero. Without loss of generality, we choose $E_0 = 0, I_0 > 0, R_0 > 0, Y_{i0} > 0$ and $Y_{m0} > 0.$ It is obvious that $S(t) > 0, Y_i(t) > 0, Y_m(t) > 0$ and $R(t) > 0$ for any $t > t_0.$ Then from the second equation of system (2), we get $\frac{dE(t)}{dt}|_{t = t_0} = \alpha_1 Y_i(t_0)S(t_0)+\beta_1Y_m(t_0)S(t_0)+(1-f)\rho R(t_0) > 0.$ Thus, $(S, E, I, R, X_e, X_r, X_i, X_m, Y_i, Y_m)\notin \partial K_0$ for $0 < t-t_0\ll 1$. This is a contradiction. The other subcases can be similarly proved.

Case (ii) Two initial values are equal to zero, and the others are larger than zero. Let $E_0 = I_0 = 0, R_0 > 0, Y_{i0} > 0$ and $Y_{m0} > 0.$ It is obvious that $S(t) > 0, Y_i(t) > 0, Y_m(t) > 0,$ and $R(t) > 0$ for any $t > t_0$. From the second equation of system (2), we get $\frac{dE(t)}{dt}|_{t = t_0} = \alpha_1 Y_i(t_0)S(t_0)+\beta_1Y_m(t_0)S(t_0)+(1-f)\rho R(t_0) > 0$. So $E(t) > 0$ for $0 < t-t_0\ll 1$. This implies that $I(t) > 0$ for $0 < t-t_0\ll 1$. Therefore, we have $(S, E, I, R, X_e, X_r, X_i, X_m, Y_i, Y_m)\notin \partial K_0$ for $0 < t-t_0\ll 1$. This is a contradiction. Similarly, we can prove the other subcases.

Case (iii) Three initial values are equal to zero, and the others are larger than zero. Set $E_0 = I_0 = R_0 = 0, Y_{i0} > 0$ and $Y_{m0} > 0.$ Clearly, $S(t) > 0, Y_i(t) > 0$ and $Y_m(t) > 0$, for any $t > t_0$. It follows from the second equation of system (2) that $\frac{dE(t)}{dt}|_{t = t_0} = \alpha_1Y_i(t_0)S(t_0)+\beta_1Y_m(t_0)S(t_0) > 0$. So $E(t) > 0$ for $0 < t -t_0\ll 1$. It follows from the third and fourth equations of system (2) that $I(t) > 0$ and $R(t) > 0$ for $0 < t -t_0\ll 1$. Therefore, $(S, E, I, R, X_e, X_r, X_i, X_m, Y_i, Y_m)\notin \partial K_0$ for $0 < t-t_0\ll 1$. This is a contradiction. Similarly, we can prove the other subcases.

Case (iv) Four initial values are equal to zero, and the other is larger than zero. Set $E_0 = I_0 = R_0 = Y_{i0} = 0$ and $Y_{m0} > 0$. It is easy to see that $S(t) > 0$ and $Y_m(t) > 0$ for all $t > t_0$. From the second equation of system (2), we can get $\frac{dE(t)}{dt}|_{t = t_0} = \alpha_1Y_i(t_0)S(t_0) > 0$, for $0 < t-t_0\ll 1$. So $E(t) > 0$ for $0 < t -t_0\ll 1$. It follows from the third, fourth and ninth equations of system (2) that $I(t) > 0$, $R(t) > 0$ and $Y_i(t) > 0$ for $0 < t -t_0\ll 1$. Thus, $(S, E, I, R, X_e, X_r, X_i, X_m, Y_i, Y_m)\notin \partial K_0$ for $0 < t-t_0\ll 1$. This is a contradiction. Similarly, we can prove the other subcases.

Thus

In the following, we proceed by contradiction to prove that there exists $\xi > 0$ such that

where $P_0 = (S^0, 0, 0, 0, X^0_e, X^0_r, X^0_i, X^0_m, 0, 0).$

It follows from Theorem 2 in ^[31] that $R_0 > 1 \Longleftrightarrow \rho(FV^{-1}) > 1 \Longleftrightarrow \rho(\exp{(F-V)}) > 1$. Therefore, if $R_0 > 1$, we can choose $\varepsilon_1 > 0$ sufficiently small such that

where

If (17) does not hold, then for any $\zeta > 0$, we have

Without loss of generality, suppose that

By the continuity of the solution with respect to initial values, we have that there exists sufficiently small $\varepsilon_1 > 0$ such that

For any $t\geq t_0$, there exists an integer $l\in \mathbb{Z_+}$ such that $t-t_0 = l+\hat{t}$, where $\hat{t}\in [0, 1)$. It follows from (19) that

Therefore, we have

From system (2) and inequality (20), we get

Obviously, system (21) is a quasi-monotonic system. Consider the following comparison system:

where $\hat{Z}(t) = (\hat{E}(t), \hat{I}(t), \hat{R}(t), \hat{Y_i}(t), \hat{Y_m}(t))^T$ and

By ^[32], we know that there exists a positive vector $v$ such that $\hat{Z}(t) = v\exp(\eta t)$ is a solution of system (22), where $\eta = \ln \rho(\exp{(F-V-M_{\varepsilon_1})})$. From (18), we can get $\eta > 0$ and thus $\hat{Z}(t)\rightarrow\infty$ as $t\rightarrow \infty$, that is, $\hat{E}(t)\rightarrow\infty$, $\hat{I}(t)\rightarrow\infty$, $\hat{R}(t)\rightarrow\infty$, $\hat{Y_i}(t)\rightarrow\infty$ and $\hat{Y_m}(t)\rightarrow\infty$ as $t\rightarrow \infty$. According to the comparison theorem in differential equations, we can easily obtain that

This contradicts with the boundedness of the solutions. Thus, we have proved that (17) holds and $P$ is weakly uniformly persistent with respect to $(K_0, \partial K_0)$.

Obviously, the poincaré map $P$ has a global attractor $P_0$. $P_0$ is an isolated invariant set in $\widetilde{K}$ and $W^S(P_0)\bigcap K_0 = \emptyset$, and it is acyclic in $M_\partial$. Every solution in $M_\partial$ converges to $P_0$. According to Zhao ^[33], we derive that $P$ is uniformly persistent with respect to $(K_0, \partial K_0)$. This implies that the solution of system (2) is uniformly persistent with respect to $(K_0, \partial K_0)$, that is, (15) holds.

4.   Optimal control problem

Optimal control theory has been used to explore optimal control strategies for various infectious diseases ^[34,35,36]. The purpose of this section is to seek an optimal integrated strategy to prevent the spread of citrus HLB. In the following, we begin with the presentation of the optimal control problem for the transmission dynamics of HLB in order to derive nutrient solution injection, removal of infected trees and insecticide spraying strategies with minimal implementation cost. We will show that it is possible to implement control techniques while minimizing the cost of implementation of such measures.

In the host citrus trees population, the associated force of infections are reduced by factors of $(1-u_1)$, where $u_1$ measures the precaution effort of nutrient solution injection. The control variable $u_2$ represents the removing of infected trees. The control variable $u_3$ shows the eradication effort of insecticide spraying. It follows that the reproduction rate of psyllid population (including egg, nymph, adult stages) is reduced by a factor of $(1-u_3)$. Based on the assumptions and extensions mentioned above, system (2) with control strategy can be improved as following forms:

subject to nonnegative initial conditions, here $r_0$ is a conversion rate.

For the optimal control problem of (23), we consider the control variables $u(t) = (u_1, u_2, u_3)\in U$ relative to the state variables $S, \; E, \; I, \; R, \; X_e, \; X_r, \; X_i, \; X_m, \; Y_i, \; Y_m$ where control variables are bounded and measured with

where $T$ represents the control period. Let $V$ be the total number of psyllid population, that is, $V = X_e+X_r+X_i+X_m+Y_i+Y_m$. For the control problem, we now define the objective functional as

subject to the control system (23). The objective is to minimize the cost functional (25). That is, the goal is minimizing the number of infected trees, dead trees and psyllid populations and the cost of implementing the control, by using possible minimal control variables $u_i(t)\ (i = 1, \; 2, \; 3)$. We choose to model the control efforts via a linear combination of quadratic terms, $u_i^2(t)\; (i = 1, 2, 3)$. Further, the constants $A_1, A_2, A_3$ and $B_1, B_2, B_3$ represent a measure of the relative cost of the interventions over the interval $[0, T]$. In order to find an optimal control, $u^*_1, \; u^*_2, \; u^*_3$ such that

where $U$ is defined in (24) and subject to control system (23) with nonnegative initial conditions. Next, we use Pontryagin's Maximum Principle to solve this optimal control problem.

4.1.   Existence of the control problem

Following the idea of ^[37], we prove firstly the existence of the optimal control problem.

Theorem 4.1. For the objective functional $J(u_1, u_2, u_3) = \int^{T}_{0}(A_1I+A_2R+A_3V+\dfrac{B_1}{2}u^2_1+\dfrac{B_2}{2}u^2_2+\dfrac{B_3}{2}u^2_3)dt$, associated with model (23) defined in $U$, then there exists an optimal control $u^* = (u^*_1, u^*_2, u^*_3)$, such that $J(u^*_1, u^*_2, u^*_3) = \min \limits_{U} J(u_1, u_2, u_3)$.

Proof. By Theorem Ⅲ.4.1 from ^[37], we only need to check the following assumptions:

$(H_1)$ The set of controls and corresponding state variables is nonempty.

$(H_2)$ The control set $U$ is convex and closed.

$(H_3)$ Right hand side of each equation in control problem (23) is continuous, bound above by a sum of the bounded control and state, and can be written as a linear function of $U$ with coefficients depending on time and the state.

$(H_4)$ There exist constants $C_1, C_2 > 0$ and $\beta > 1$ such that the integrand of the objective functional $L(y, u, t)$ is concave and satisfies

Obviously, the state variables and the set of control are bounded and nonempty which confirm $(H_1)$. Note that the solutions are bounded, so the admissible control set is bounded and convex, which confirms $(H_2)$. The system is bilinear in control variables, so it confirms $(H_3)$ (since the solutions are bounded). The hypothesis $(H_4)$ can be verified as

where $C_1, C_2 > 0, A_1, A_2, A_3, B_1, B_2, B_3 > 0, B_4 > 0$ and $\beta > 0$. In view of the result given by Lukes ^[38], we have that there exists an optimal control strategy $(u_1^*, u_2^*, u_3^*)$ minimizing $J(u_1, u_2, u_3)$.

Next we explore the minimal value of $J(u_1, u_2, u_3)$. To accomplish this, we define the Lagrangian $L$ and Hamiltonian $H$ for the optimal control problem (23) as

and

where $X = (S, E, I, R, X_e, X_r, X_i, X_m, Y_i, Y_m),$ $U = (u_1, u_2, u_3)$ and $\lambda = (\lambda_1, \lambda_2, \lambda_3, ..., \lambda_{10})$.

4.2.   Optimal control solution

In this subsection, by using Pontryagin's Maximum Principle ^[39], we will obtain the optimal solution of the control system (23).

Let $u^*_1, u^*_2$ and $u^*_3$ represent the optimal solution of the control problem (26), then there exists a nontrivial vector function $\lambda(t) = (\lambda_1(t), \lambda_2(t), \lambda_3(t), ..., \lambda_{10}(t))$ satisfying three equalities:

(ⅰ) the state equation

(ⅱ) the optimality condition

(ⅲ) the adjoint equation

Now, we apply the necessary conditions to the Hamiltonian $H$ given by (27). Following the results in ^[39], we can obtain the following conclusions.

Theorem 4.2. Let $\hat {y}^* = (\hat {S}^*, \hat {E}^*, \hat {I}^*, \hat {R}^*, \hat {X}^*_e, \hat {X}^*_r, \hat {X}^*_i, \hat {X}^*_m, \hat {Y}^*_i, \hat {Y}^*_m)$ be an optimal solution associated with the optimal control strategy $u^*(t) = (u^*_1(t), u^*_2(t), u^*_3(t))$ for the optimal control problem (26), then there exists adjoint variables $\lambda_i, (i = 1, 2, ..., 10)$ satisfying

with transversality conditions

Further, the control $u^*_1, u^*_2, u^*_3$ are given by

Proof. To determine the adjoint equations and the transversality conditions we use the Hamiltonian (27). The adjoint system results from Pontryagin's Maximun Principle ^[39].

with $\lambda_i(T) = 0\ (i = 1, 2, \cdots, 10)$.

To obtain the characterization of the optimal control given by (28), solving the equations

on the interior of the control set and applying the property of the control space $U$, we can derive (28) holds.

5.   Numerical simulations

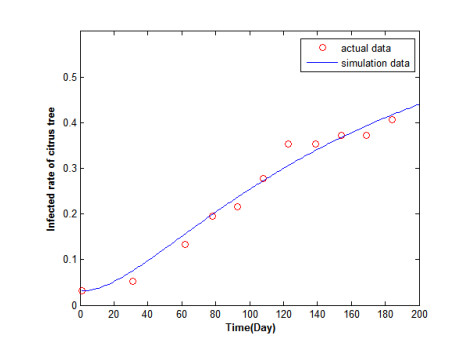
In this section, we use firstly the model (2) to simulate the data on the number of infected citrus trees of Yuan Orchard from June, 2015 to December, 2015. Yuan Orchard is located in Ganzhou, China, which is one of our monitoring sites for citrus HLB. The infected rates of trees $I(t)$ are given in Table 1. Numerical simulation of $I(t)$ is shown in Figure 2. In order to carry out the numerical simulations, we need to estimate the model parameters. We get these parameter values in three ways: some parameter values ($\eta_1, \eta_2$, $r, \gamma_1, \gamma_2, \gamma_3$, $d_1, d_2, d_3, d_4, r_0$) are obtained from the literature; some parameter values ($\rho, f$) are estimated; and other parameter values ($\alpha_1, \alpha_2, \beta_1, \beta_2$) are fitted by the MATLAB tool fminsearch, which is fitted by calculating the minimum sum of square ($MSS$) (see ^[40]):

By using the parameter values in Table 1, we can obtain $\alpha_1 = 0.00494\; \text{month}^{-1}, \alpha_2 = 0.00043\; \text{month}^{-1}, \beta_1 = 0.0097\; \text{month}^{-1}$ and $\beta_2 = 0.002258\; \text{month}^{-1}$ by fitting in simulations. All parameter values of the model are given in Table 2.

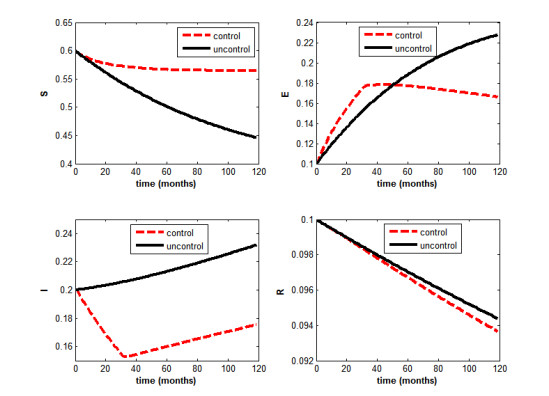
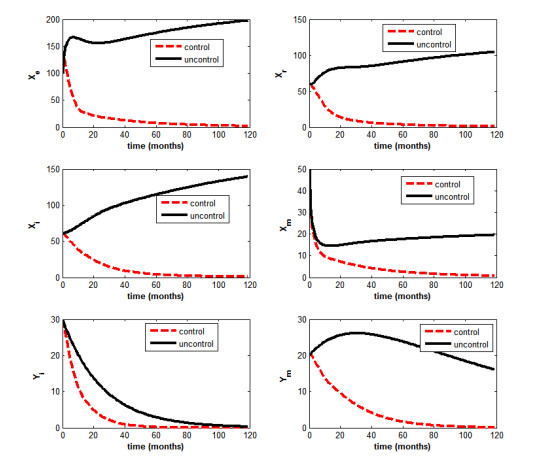
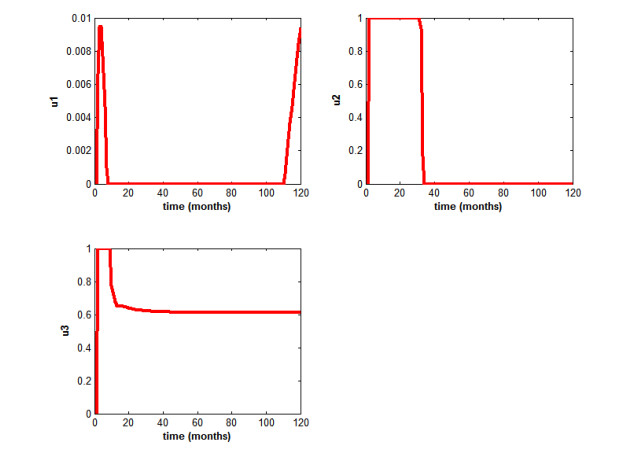
Next, we numerically examine the effect of the optimal control strategy on the spread of citrus HLB in a population of trees and psyllids. In this simulation without control population is labeled with bold line and the control by a dashed line. The weight constant values in the objective functional are $A_1 = 800; A_2 = 2000; A_3 = 2; B_1 = 200; B_2 = 1; B_3 = 50$. The control $u_1$, $u_2$ and $u_3$ are all used to optimize the objective function $J$. Figures 3 and 4 showed that the control strategy resulted in a decrease in the number of infected citrus trees $I$, dead citrus trees $R$, psyllids at each stage, $X_e, X_r, X_i, X_m, Y_i$ and $Y_m$ while an increase is observed in the number of susceptible citrus trees $S$. In Fig. 5, we can observe that the optimal control profile for $u_1$, $u_2$ and $u_3$. Note that parameter values used in the numerical simulations are given in Table 1, and the initial conditions are taken as $S(0) = 0.6, E(0) = 0.1, I(0) = 0.2, R(0) = 0.1$, $X_e(0) = 100, X_r(0) = 60, X_i(0) = 60, X_m(0) = 50, Y_i(0) = 30, Y_m(0) = 20$.

6.   Conclusion

In this paper, based on the mechanism and characteristics of citrus HLB transmission, we proposed a vector-borne plant disease model with stage structure in psyllids and studied the effect of intervention strategy in controlling the spread of HLB. We calculated the basic reproduction ratio $R_0$ for the epidemic model, and showed that the disease would die out when $R_0 < 1$, and the disease would be endemic when $R_0 > 1$.

Moreover, by using the optimal control theory, we analyzed the intervention strategy, nutrient solution injection, removal of infected trees and insecticide spraying, to determine the optimal integrated strategy. Using the Pontryagin's Maximum Principle, we investigated the existence of the optimal control problem. In addition, we minimized the number of infected citrus trees, dead citrus trees and the total number of psyllid population, by using three control variables. Numerical simulations illustrated the effectiveness of the proposed control problem.

Acknowledgments

The research has been supported by the Natural Science Foundation of China (11561004) and the Key Science and Technology Program of Jiangxi Province (20143ACF60012).

Conflict of interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.