Global dynamics for a multi-group alcoholism model with public health education and alcoholism age

1.   Introduction

A small intake of alcohol may be beneficial to health, but alcoholism, also known as alcohol dependence or alcohol abuse, is among the main healthy risky behavior due to the high relevance of negative health and social effect. Alcohol consumption has been identified as a major contributor to the global burden of chronic disease, injury and economic cost ^[1,2,3]. The World Health Organization reports the harmful use of alcohol causes approximately 3.3 million deaths every year (or 5.9% of all the global deaths), and 5.1% of the global burden of disease is attributable to alcohol consumption ^[4]. Furthermore, alcoholism is reported to be among the major concerns to public health in many countries, like UK ^[5,6]. Recently, the study of alcoholism model has become an important aspect of social epidemic. A great number of literatures can be found where healthy risky behavior, including drinking, smoking, drug use and obesity, are viewed as a treatable contagious disease, see ^[7,8,9,10] and the reference contained therein. In particular, several alcohol models described by ordinary differential equations or delay differential equations have been investigated extensively (see ^{[11,12,13,14,15,16,17,18,19,20,21,22]}). In ^[11], the authors modelled alcoholism as a contagious disease and studied how "infected" drinking buddies spread problem drinking. Manthey et al. ^[12] studied campus drinking and suggested that the basic reproductive numbers are not sufficient to predict whether drinking behavior will persist on campus and that the pattern of recruiting new members play a significant role in the reduction of campus alcohol problems. The impact of environmental factors and peer influences on the distribution of heavy drinking was studied in ^[13,16]. In addition, the two-stage models: one stage where people who admit to having a alcohol problem and other stage where people who do not admit to having a alcohol problem have been developed in ^[17,18]. Bhunu ^[19] studied the co-interaction of alcoholism and smoking in a community. Walters et al. ^[20] also discussed alcohol problems, and their results showed that an increase in the recovery rate decreased the proportion of binge drinkers in the population. Xiang et al. ^[21] considered the effect of constant immigration on drinking behavior. Wang et al. ^[22] presented a deterministic mathematical model for the spread of alcoholism with two control strategies to gain insights into this increasingly concerned about health and social phenomenon. The optimal control strategies are derived by proposing an objective functional and using Pontryagin's Maximum Principle. Zhu et al. ^[23] formulated a alcohol model with the impact of tax and investigated their dynamical behaviors. Other related drinking epidemic or population models, we refer to see ^{[24,25,26,27,28,29,30,31,32,33]}.

Public health education (e.g. Radio, Newspapers, Billboards, TV, and Internet, etc.) has been used to control the alcohol problems, which can not only influence the individuals' behavior but also increase the governmental health care involvement to control the spread of heavy drinking. These behavioral responses can change the transmission patterns and decline to drink. In recent years, many mathematical models ^{[34,35,36,37]} have been used for studying the impact of awareness programs by media on drinking problem. In ^[35], the authors studied drinking dynamics and focused on awareness programs and treatment in the modelling process. They extended the model in ^[34] via including a treatment class and established some sufficient conditions for the stability of the alcohol-free and alcohol-present equilibria. Xiang et al. ^[36] also studied a drinking model with public health education campaigns. Their results showed that awareness programs is an effective measure in reducing alcohol problems. These studies suggested that public health education and media had huge impact in controlling the spread of alcoholism. Recently, Ma et al. ^[37] proposed an alcohol consumption model with awareness programs and time delay described by including media function $S\frac{M}{k_{0}+M}$, where $M$ was the cumulative density of awareness programs driven by media. The results showed that the time delay in alcohol consumption habit which developed in susceptible population might result in a Hopf bifurcation.

Actually, it has been found that heterogeneity (e.g., age, sex, space and so on) exists in many aspects of social epidemic transmission processes. Since multi-group models play important roles in considering the heterogeneity of host population, the study of the multi-group models can contribute to clarify the transmission pattern of infectious diseases in more realistic situations. There are lots of studies of the global stability of multi-group epidemic models, in which a general approach is used (see ^{[38,39,40,41,42,43,44,45,46]}). This graph-theoretic approach is sufficiently general to be applicable to a variety of coupled systems. On the other hand, since the pioneering work of Hoppensteadt established an age-dependent epidemic model in 1974 ^[47], the effects of the age factor on the multi-group epidemic models have already been studied by many researchers (see ^{[48,49,50,51]}). Dynamical behaviors of these multi-group epidemic models with age structure have been studied, respectively. However, to our knowledge, there are few studies on the alcoholism model in heterogeneous populations. In particular, we should notice that the impact of the age of alcoholism on other people is different. Thus, the study of the multi-group alcoholism model with public health education and age of alcoholism can contribute to the control of alcohol problems in more realistic situations.

In this paper, motivated by the above works, we formulate a novel and more reasonable multi-group alcoholism model with public health education and alcoholism age to describe alcoholism spread in a heterogeneous host population. Inspired by the method developed in ^[38,39,40], we construct Lyapunov functionals and obtain the global stability of the alcohol-free equilibrium and alcohol-present equilibrium. Our results demonstrate that, for age structured multi-group alcoholism model, this graph-theoretic approach can be successfully applied by choosing an appropriate weighted matrix as well. At the same time, our main results indicate that public health education is beneficial for alcoholism control, and alcoholism age structure does not alter the dynamical behaviors.

This paper is organized as follows. In next section, we formulate a more reasonable multi-group alcoholism model with public health education and alcoholism age. Some preliminary setting for the multi-group and age-dependent alcoholism model are presented in Section 3. In Section 4, we state our main results of this paper. We prove the global asymptotic stability of the alcohol-free equilibrium $P_{0}$ for $R_{0}\leq1$ by using the theory of non-negative matrices and the classical method of Lyapunov functional. By applications of the graph-theoretic approach to the method of Lyapunov functionals, we prove the existence, uniqueness and global asymptotic stability of the alcohol-present equilibrium $P^{*}$ for $R_{0}>1$. In Section 5, the effects of the public health education and alcoholism age are given. A brief discussion is also given in last section.

2.   Model formulation

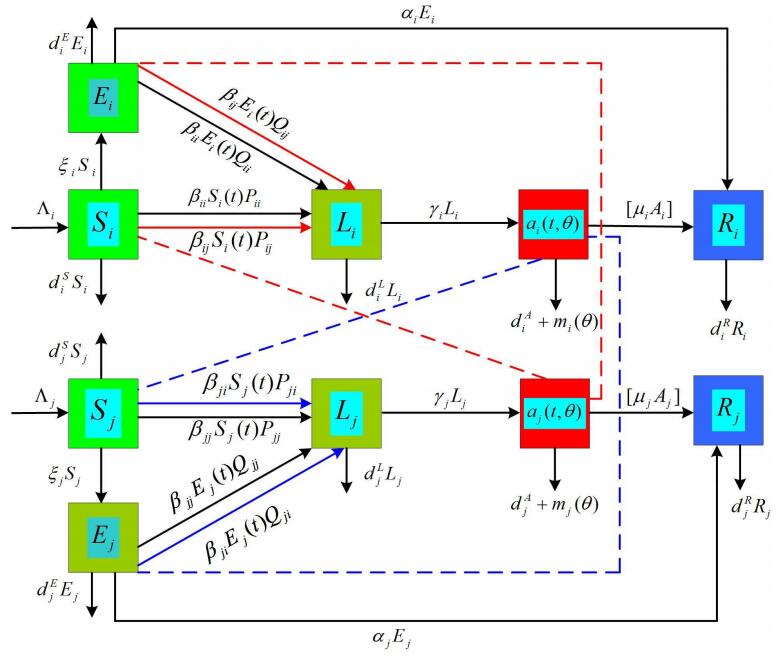
Let $n\in\mathbb{N}$ be the number of groups, the heterogeneous host population is divided into $n$ homogeneous groups. For $i$-th ($1\leq i\leq n$) group, it is further classified as five compartments: the uneducated susceptible individuals $S_{i}(t)$ who do not drink or drink only moderately and do not accepted the public health education, but may one day develop light drinkers, the educated susceptible individuals $E_{i}(t)$ who do not drink or consume alcohol in moderation and accepted the public health education, but may one day also develop light drinkers, the light drinkers $L_{i}(t)$ who often consume alcohol but they don't influence other people, the alcoholics $A_{i}(t)$ who have drinking problems or addictions (i.e. heavy drinkers) and they will influence susceptible individuals, and the recovered drinkers $R_{i}(t)$ who are the recovered drinkers and permanently quit drinking. In $i$-th ($1\leq i\leq n$) group, we assume that the susceptible individuals, the light drinkers and the recovered drinkers are homogeneous at time $t$. The alcoholics individuals is structured by the age of alcoholism $\theta$, and $a_{i}(t, \theta)$ be the alcoholism age density of the individuals in the alcoholism individuals with alcoholism age $\theta$ at time $t$. Suppose that $a_{i}(t, \theta) = 0$ for all sufficiently large $\theta>\theta^{+}$, where $\theta^{+}$ is the maximum ages of alcoholism which is finite. Then $A_{i}(t) = \int_{0}^{\infty}a_{i}(t, \theta)d\theta$ is the number of heavy drinkers at time $t$. Furthermore, we make the following assumptions:

(H1) In group $i$, at any moment in time, new recruits enter the uneducated susceptible population at a rate $\Lambda_{i}>0$.

(H2) In group $i$, via public health education, the uneducated susceptible individuals in $S_{i}$ class turn into the educated susceptible individuals $E_{i}$ class at a constant rate $\xi_{i}>0$.

(H3) In group $i$, the coefficient of alcoholism transmission for susceptible individuals ($S_{i}$ or $E_{i}$) turn into light drinkers ($L_{i}$) is $\beta_{ij}\geq 0$ for some reasons (e.g. through peer pressure), in which a susceptible individual contact with heavy drinkers $A_{j}$ come from the $j$-th group.

(H4) Some educated individuals who never have a drink due to the effect of the public health educational campaigns, and the proportion $\alpha_{i}>0$ is that fraction of $E_{i}$ who move into the $R_{i}$ class.

(H5) The heavy drinkers in $A_{i}$ class can recover (due to counselling, health reasons, treatment, prohibition, or tax hiked on alcohol beverages, etc.) and will permanently quit drinking. The proportion $\mu_{i}>0$ is that fraction of $A_{i}$ who move into the $R_{i}$ class.

(H6) The $n$-square contact matrix $B^{(n)} = (\beta_{ij})_{n\times n}$ is irreducible ^[41], where $\beta_{ij} \geq 0$.

Remark 1: Assumption (H6) implies that every pair of groups is joined by an infectious path so that the presence of a heavy drinking individual in the first group can cause "infection" in the second group.

The other parameters description of the model are presented in Table 1.

Here, all the parameters are positive. Furthermore, the following assumptions are made.

(H7) We assume that $p_{ij}(\theta), q_{ij}(\theta), m_{i}(\theta)\in L_{+}^{1}(0, +\infty)$ are nonnegative and essential bounded, and they are all non-decreasing functions of the age of alcoholism $\theta$. If $\theta\geq \theta_{0}$, then $p_{ij}(\theta)\equiv p_{max}$, $q_{ij}(\theta)\equiv q_{max}$, and $m_{i}(\theta)\equiv m_{max}$, where $0<\theta_{0}\leq \theta^{+}$.

Because the effect of public health education, here the infectivity $q_{ij}(\theta)$ is reduced relatively for educated individuals, i.e., $q_{ij}(\theta) \leq p_{ij}(\theta)$ (the smaller, the better). For simplicity, we set $P_{ij} = \int_{0}^{\infty}p_{ij}(\theta)a_{j}(t, \theta)d\theta$, $Q_{ij} = \int_{0}^{\infty}q_{ij}(\theta)a_{j}(t, \theta)d\theta$, and $[\mu_{i}A_{i}]$ stands for $\int_{0}^{\infty}\mu_{i}a_{i}(t, \theta)d\theta.$ Under assumptions (H1)-(H6), the alcoholism transmission diagram is depicted in Figure 1.

The transfer diagram leads to the following multi-group age structured SELAR alcoholism model with public health education:

The initial conditions and boundary conditions of model (2.1) are respectively given by:

where $L_{+}^{1}(0, +\infty)$ is the space of functions that are nonnegative and Lebesgue integrable.

Remark 2: Neglecting the heterogeneity and alcoholism age, Xiang et al. ^[36] constructed a SEARQ drinking model with public health educational campaigns, its threshold stability was achieved.

3.   Preliminaries

In this section, some primary results are presented for establishing our main conclusions.

3.1.   Volterra formulation

Note that the variables $R_{i}(t)$ does not appear in the first four equations of (2.1), it suffices to study the dynamical behaviors of the following reduced sub-system (3.1):

Let

then $\Gamma_{0i}(\theta)$ is the probability of an alcoholism individual in the $i$-th group surviving to alcoholism-age $\theta$. Using the approach introduced by Webb ^[53], integrating along the characteristic lines and incorporating the boundary conditions, we can obtain that

Substituting (3.3) into the equations for $S_{i}'(t), E_{i}'(t)$ and $L_{i}'(t)$ of system (3.1), we have

where

It is easy to check that $\lim_{t\longrightarrow \infty} F_{1}(t) = 0, \lim_{t\longrightarrow \infty} F_{2}(t) = 0$. Furthermore, set

Obviously, $h_{i}(\theta)\geq g_{i}(\theta), i = 1, 2, \cdots, n$. Then, by application of the results in ^[54], any equilibrium of system (3.4) (if it exists), must be a solution of the following limiting system associated with (3.4):

The behavior of system (3.1) is equivalent to the system (3.5). Once the solution of system (3.5) is determined, we can obtain $a_{i}(t, \theta)$ from (3.3). So that the stability of the equilibrium of system (2.1) is the same as that of system (3.5). In this paper, we focus on the system (3.5).

3.2.   State space

For system (3.5), we need the appropriate fading memory space of continuous functions as follows (see Atkinson et al. ^[52]):

which is a Banach space endowed with the norm $\parallel\phi\parallel_{\lambda_{i}}: = sup_{s\leq0}\mid\phi(s)\mid e^{\lambda_{i}s}<+\infty$, where $\mathbb{R}_{+} = [0, +\infty]$, $\lambda_{i}$ is a positive constant. Let $\phi_{it}(s)\in C_{\lambda_{i}}$ be such that $\phi_{it}(s) = \phi_{i}(t+s), s\in(-\infty, 0].$ Thus, we consider the system (3.5) in the phase space

For system (3.5), the existence and uniqueness of the solution with the initial and boundary conditions (2.2) can be checked by the standard approaches in ^[53]. Furthermore, we clams that any solution of system (3.5) with nonnegative initial conditions remains nonnegative.

We define a continuous solution semi-flow $\Phi: \mathbb{R}_{+} \times X\longrightarrow X$ associated with (3.5):

Let

where $\eta_{i} = \min\{d_{i}^{S}, d_{i}^{E}, d_{i}^{L}, d_{i}^{A}, d_{i}^{R}\}$. And denote the interior of $\Omega$ as:

Lemma 3.1. For system (3.5), $\Omega$ is positively invariant for $\Phi$, i.e., $\Phi(t, x_{0})\in \Omega, \forall x_{0} \in \Omega, t \geq0$.

Proof. First, we prove that all solutions of system (3.5) with the initial and boundary conditions (2.2) remains nonnegative. By continuity of the solutions of system (3.5) and $S_{i}(0) = \phi_{1}^{i}\geq0$, we claim $S_{i}(t)\geq0$ for all $t\geq0, i = 1, 2, \cdots, n.$ In fact, we assume that there exists a $i_{1}\in\{1, 2, , \cdots, n\}$ such that $S_{i_{1}}(t)$ lost its positivity for the first time at $t_{1}>0$, i.e., $S_{i_{1}}(t_{1}) = 0$. However, from the first equation of (3.5), we can see $\frac{ {\rm d} S_{i_{1}}(t_{1})}{ {\rm d} t} = \Lambda_{i_{1}} > 0$ which is a contradiction to the fact that $S_{i_{1}}(t)>S_{i_{1}}(t_{1}) = 0$ for any $0\leq t<t_{1}$.

Similarly, we shall show that $E_{i}(t)\geq0$ for all $t \geq0, i = 1, 2, \cdots, n.$ Otherwise, we assume that there exists a $i_{2}\in\{1, 2, , \cdots, n\}$ and the first time $t_{2}>0$ such that $E_{i_{2}}(t_{2}) = 0$. However, from the second equation of (3.5) one obtains $\frac{{\rm d}E_{i_{2}}(t_{2})}{{\rm d}t} = \xi_{i_{2}}S_{i_{2}}(t_{2}) > 0$ which follows from the nonnegativity of $S_{i}(t)$ for all $t\geq0, i = 1, 2, \cdots, n.$ Thus, $E_{i}(t)\geq0$ for all $t\geq0, i = 1, 2, \cdots, n.$

Furthermore, we conclude that there is a $i_{3}\in\{1, 2, , \cdots, n\}$ and the first time $t_{3}>0$ such that $L_{i_{3}}(t_{3}) = 0$. Note that $0<t_{3}-\theta<t_{3}$, thus, $L_{i_{3}}(t_{3}-\theta)>0$. Using the similar arguments and the third equation of (3.5), we gets $\frac{{\rm d}L_{i_{3}}(t_{3})}{{\rm d}t} > 0.$ This is a contradiction which implies the nonnegativity of $L_{i}(t)$ for all $t\geq0, i = 1, 2, \cdots, n.$

Second, we prove that all solutions of system (3.5) with the initial and boundary conditions (2.2) remains bounded. The total population size is $N(t) = \sum_{i = 1}^{n}N_{i}(t)$. In the $i$-th group, $N_{i}(t) = S_{i}(t)+E_{i}(t)+L_{i}(t)+\int_{0}^{\infty}a_{i}(t, \theta)d\theta+R_{i}(t).$ Let $\eta_{i} = \min\{d_{i}^{S}, d_{i}^{E}, d_{i}^{L}, d_{i}^{A}, d_{i}^{R}\}$, then

this suggesting

Then, we have

Therefore, we can obtain that $\Omega$ is positively invariant for $\Phi$, i.e., $\Phi(t, x_{0})\in \Omega, \forall x_{0} \in \Omega, t \geq0$. This proof is completed.

Our results in this paper will be stated for system (3.5) in $\Omega$, and can be translated straightforwardly to system (3.1). Moreover, all positive semi-orbits in $\Omega$ have compact closure in $X$ (see ^[52]), and thus have non-empty $\omega$-limit sets. We have the following result.

Lemma 3.2. All positive semi-orbits in $\Omega$ have non-empty $\omega$-limit sets.

Lemma 3.3. System (3.5) is point dissipative, that is, there exists constants $M_{i}>0$ such that for each solution of (3.5) there is a $T_{i}>0$ such that $\parallel S_{it}\parallel_{\lambda_{i}}\leq M_{i}, \parallel E_{it}\parallel_{\lambda_{i}}\leq M_{i}$ and $\parallel L_{it}\parallel_{\lambda_{i}}\leq M_{i}$ for all $t\geq T_{i}, i = 1, 2, \cdots, n$.

Proof. Let $W_{i} = \max_{t\in[0, T_{i}]}S_{i}(t)>0$, then, for any $t\geq T_{i}$ and any $\varepsilon_{i}>0$, we get

where the last estimation was obtained by three separations to $u\leq 0, 0\leq u\leq T_{i}$ and $T_{i}\leq u\leq t.$ Hence, we can choose $M^{S}_{i}>0$ such that $\parallel S_{it}\parallel_{\lambda_{i}}\leq M^{S}_{i}$. Similary, we can also prove that $\parallel E_{it}\parallel_{\lambda_{i}}\leq M^{E}_{i}$ and $\parallel L_{it}\parallel_{\lambda_{i}}\leq M^{L}_{i}$. Set $M_{i} = \max\{M^{S}_{i}, M^{E}_{i}, M^{L}_{i}\}>0$, this proof is completed for all $t\geq T_{i}, i = 1, 2, \cdots, n$.

3.3.   Equilibria

System (3.5) always has a alcohol-free equilibrium $P_{0} = (S_{1}^{0}, E_{1}^{0}, 0, ..., S_{n}^{0}, E_{n}^{0}, 0)\in\mathbb{R}_{+}^{3n}$, where

Let

The alcohol-present equilibrium of system (3.5) is given by

then it is determined by the following system of equations

The basic reproduction number $R_{0}$ (see ^[38,55,56]) is defined as the spectral radius of a matrix $M_{0}$, that is,

It acts as a threshold as is shown in the following result. We shall establish that the dynamical behaviors of system (3.5) are completely determined by values of $R_{0}$.

4.   Main results

In this section we state and prove our main results concerning the global dynamics of system (3.5).

4.1.   Global stability of $P_{0}$

Theorem 4.1. Assume that the matrix $B^{(n)} = (\beta_{ij})_{n\times n}$ is irreducible.

(1) If $R_{0}\leq1$, then the unique alcohol-free equilibrium $P_{0}$ of system (3.5) is globally asymptotically stable in $\Omega$;

(2) If $R_{0}>1$, then $P_{0}$ is unstable and system (3.5) is uniformly persistent, i.e., there exists a positive constant $c> 0$ such that $\limsup_{t\longrightarrow \infty}S_{i}(t)\geq c, \limsup_{t\longrightarrow \infty}E_{i}(t)\geq c, \limsup_{t\longrightarrow \infty} L_{i}(t)\geq c, i = 1, 2, \ldots, n$. Furthermore, system (3.5) has at least one alcohol-present equilibrium $P^{*}$ in $\Omega^{o}$.

Proof. (1) Let $S = (S_{1}, S_{2}, ..., S_{n})^{T}, E = (E_{1}, E_{2}, ..., E_{n})^{T},$ we define a matrix-valued function

It is easy to see that $M(S^{0}, E^{0}) = M_{0}$, where $S^{0} = (S_{1}^{0}, S_{2}^{0}, ..., S_{n}^{0})^{T},$ $E^{0} = (E_{1}^{0}, E_{2}^{0}, ..., E_{n}^{0})^{T}$. We also have

First, we will prove the uniqueness of alcohol-free equilibrium in $\Omega$. If $R_{0}\leq1$, $(S, E)\neq (S^{0}, E^{0})$, then we obtain

Since $B^{(n)} = (\beta_{ij})_{n\times n}$ is irreducible, we know nonnegative matrix $M(S, E)$ and $M_{0}$ are also irreducible. Using the Perron-Frobenius theorem (see Theorem 2.1.4 or Corollary 2.1.5 in ^[58]), we get

Therefore, $\rho(M(S, E)) < 1$ holds when $R_{0} = \rho(M_{0})\leq 1$ and $(S, E)\neq (S^{0}, E^{0})$. This implies that the vector equation $M(S, E)L = L$ has only the trivial solution $L = 0$, where $L = (L_{1}, L_{2}, ..., L_{n})^{T}$. Thus $P_{0}$ is the unique equilibrium of system (3.5) in $\Omega$ if $R_{0}\leq1$.

Next, we claim that the alcohol-free equilibrium $P_{0}$ is globally asymptotically stable in $\Omega$. Since $M_{0}$ is irreducible, there exists a positive left eigenvector $\omega$ of $M_{0}$ corresponding to $\rho(M_{0})$, i.e.,

where $\omega = (\omega_{1}, \omega_{2}, ..., \omega_{n})$ and $\omega_{i} > 0, i = 1, 2, ..., n$. We introduce the Volterra-type function $\varphi(x) = x-1-\ln x, x>0,$ which is positive definite and attains its global minimum $\varphi(1) = 0$ at $x = 1$. Note that $\omega$ is a strictly positive left eigenvector. We define a Lyapunov functional $L_{afe}(t):(S_{i}, E_{i}, L_{i})\rightarrow\mathbb{R}$ as

which is nonnegative and continuously differentiable. Here

where $c_{i} = \frac{\omega_{i}}{d_{i}^{L}+\gamma_{i}}$, $m_{j}(\theta) = \int_{\theta}^{\infty}h_{j}(s)ds$ and $n_{j}(\theta) = \int_{\theta}^{\infty}g_{j}(s)ds$. Obviously, $m_{j}(0) = \int_{0}^{\infty}h_{j}(s)ds = B_{j}, \frac{d m_{j}(\theta)}{d\theta} = -h_{j}(\theta)$, and $n_{j}(0) = \int_{0}^{\infty}g_{j}(s)ds = C_{j}, \frac{d n_{j}(\theta)}{d\theta} = -g_{j}(\theta)$.

It follows from Lemmas 3.1 and 3.3 that $L_{afe}(t)$ is nonnegative and bounded for big enough positive $t>0$. It is clear that $L_{afe}(t)$ with the equality holds if and only if $S_{i} = S_{i}^{0}, E_{i} = E_{i}^{0}, L_{i} = 0$. First, calculating the time derivative of $H_{1}(t)$ along with the solutions of system (3.5), using the equation $\Lambda_{i} = (d_{i}^{S}+\xi_{i})S_{i}^{0}$, we have

Second, calculating the time derivative of $H_{2}(t)$ along with the solutions of system (3.5). Let $t-\theta = s$, then $-\infty<s<t$, we obtain

Similar to $H^{'}_{2}(t)$, we get derivative of $H_{3}(t)$ along with the solutions of system (3.5). Let $t-\theta = s$, then $-\infty<s<t$, we obtain

Using (4.1)-(4.3), we have

If $R_{0} = \rho(M_{0}) < 1$, then (4.4) implies $L = 0$, and $\frac{d L_{afe}(t)}{dt} = 0$ if and only if $L = 0$.

If $R_{0} = \rho(M_{0}) = 1$, from (4.4), we see $\frac{d L_{afe}(t)}{dt} = 0$ implies $(\omega_{1}, \omega_{2}, \ldots, \omega_{n})\cdot(M_{0}L-L) = 0,$ that is

where $I_{n}$ denote the $n$-dimensional identity matrix. Hence, if $(S, E)\neq(S^{0}, E^{0})$, then we have

so the solution of (4.5) is only the trivial value $L = 0$. Summarizing the above statements, we see that $\frac{d L_{afe}(t)}{dt} = 0$ implies that either $L = 0$ or $R_{0} = 1$ and $(S, E) = (S^{0}, E^{0})$. It can be verified that the largest compact invariant subset of $\left\{(S_{1}, E_{1}, L_{1}, ... , S_{n}, E_{n}, L_{n})\in\Omega: \frac{d L_{afe}(t)}{dt} = 0\right\}$ is the singleton $\left\{P_{0}\right\}$. Therefore, by Lemma 3.2 and the Lyapunov-LaSalle invariance principle (see Theorem 3.4.7 in ^[59]), we can see that $P_{0}$ is globally attractive in $\Omega$ if $R_{0}\leq1$. The local asymptotical stability of the disease-free equilibrium $P_{0}$ comes from the relationship between the eigenvalues of the linearized matrix and $R_{0}$, which can be proved using the same proof as one for Corollary 5.3.1 in ^[60] (The detailed process is omitted here). Then, together with the local asymptotical stability of $P_{0}$, we know that the alcohol-free equilibrium $P_{0}$ is globally asymptotically stable in $\Omega$ when $R_{0}\leq1$.

(2) Suppose that $R_{0} = \rho(M_{0})>1$, and $L\neq0$. By continuity and (4.4), we have

which implies that $\frac{d L_{afe}(t)}{dt}>0$ in a sufficiently small neighborhood of the alcohol-free equilibrium $P_{0}$ in $\Omega^{0}$. This implies that the alcohol-free equilibrium $P_{0}$ is unstable when $R_{0}>1$.

Next, with a uniform persistence result in ^[61] and a similar argument as in the proof of Proposition 3.3 of ^[62], we can show that the instability of $P_{0}$ implies that system (3.5) is uniformly persistent when $R_{0}>1$, i.e., there exists a positive constant $c> 0$ such that

provided $\left(S_{1}(0), E_{1}(0), L_{1}(0), ..., S_{n}(0), E_{n}(0), L_{n}(0)\right)\in \Omega^{0}$.

Furthermore, using the uniform persistence of system (3.5), together with the uniform boundedness of solutions, we shall establish the existence of the alcohol-present equilibrium $P^{*}$ (see Theorem 2.8.6 in ^[63] or Theorem D.3 in ^[64]). This completes the proof of theorem 4.1.

4.2.   Global stability of $P^{*}$

In following section, we devote to the alcohol-present equilibrium of system (3.5) is globally asymptotically stable. In order to prove our results, we will construct the proper Lyapunov functional and apply subtle grouping technique in estimating the derivatives of Lyapunov functional guided by graph theory, which was recently developed by Guo et al. in ^[38,39] and Li et al. ^[40]. Here, we quote some results from graph theory which will be used in the proof of our main results. We refer the reader to ^[38,39,40] and the references cited therein for more details of these concepts and results.

Given a non-negative matrix $A = (a_{ij})_{n\times n}$, the $directed ~ graph$ $G(A)$ associated with $A$ has vertices {1, 2, ..., n} with a directed arc $(i, j)$ from $i$ to $j$ if and only if $a_{ij}\neq0$. It is $strongly ~ connected$ if any two distinct vertices are joined by an oriented path. Matrix $A$ is irreducible if and only if $G(A)$ is strongly connected.

A tree is a connected graph with no cycles. A subtree $T$ of a graph $G$ is said to be $spanning$ if $T$ contains all the vertices of $G$. A $directed tree$ is a tree in which each edge has been replaced by an arc directed one way or the other. A directed tree is said to be $rooted$ at a vertex, called the root, if every arc is oriented in the direction towards to the root. An $oriented cycle$ in a directed graph is a simple closed oriented path. A $unicyclic graph$ is a directed graph consisting of a collection of disjoint rooted directed trees whose root are on an oriented cycle.

For a given nonnegative matrix $(\bar{\beta}_{ij})_{n\times n}$, $\bar{\beta}_{ij}\geq0, 1\leq i, j\leq n$. Let

be the Laplacian matrix of the directed graph $(\bar{\beta}_{ij})_{n\times n}$, and $C_{ij}$ denote the cofactor of the $(i, j)$ entry of $\bar{B}$. For the linear system

the following results hold (see Lemma 2.1 in ^[38] and Theorem 2.2 in ^[40]).

Lemma 4.1 (^[38]) Assume that $(\bar{\beta}_{ij})_{n\times n}$ is irreducible and $n\geq2$. Then following results hold:

(1) The solution space of system (4.7) has dimension 1;

(2) A basis of the solution space is given by

where $C_{ii}$ denotes the cofactor of the $k$-th diagonal entry of $\bar{B}$, $1\leq i\leq n$;

(3) For all $1\leq i\leq n,$

where $\mathbb{T}_{i}$ is the set of all directed spanning subtrees of $G(\bar{B})$ that are rooted at the $i-th$ vertex, $w(T)$ is the weight of a directed tree $T$, and $E(T)$ denotes the set of directed arcs in a directed tree $T$;

(4) For all $1\leq i\leq n$,

Lemma 4.2. (^[40]) Assume that $v_{i}$ is the same meaning in Lemma 4.1, and $n\geq2$, then

where $F_{ij}(x_{i}, y_{j}), 1\leq i, j\leq n$ is an arbitrary function, $\mathbb{T}$ is the set of all spanning unicyclic graphs of $G(\bar{B})$, $w(T)$ is the weight of a directed tree $T$, $CT$ denotes the oriented cycle in a unicyclic graph $T$, and $E(CT)$ denotes the set of directed arcs in $CT$.

Let $P^{*} = (S_{1}^{*}, E_{1}^{*}, L_{1}^{*}, ..., S_{n}^{*}, E_{n}^{*}, L_{n}^{*})$ be the alcohol-present equilibrium of system (3.5), then $S_{i}^{*}, E_{i}^{*}, L_{i}^{*} ( i = 1, 2, ..., n)$ are determined by the following equations

In the following section, we prove that the alcohol-present equilibrium $P^{*}$ is globally asymptotically stable when $R_{0}>1$. In particular, this proof implies that the endemic equilibrium is unique in the region $\Omega^{0}$ when it exists. Therefore, we have the following main result on the uniqueness and global stability of the positive equilibrium $P^{*}$ when $R_{0}>1$.

Theorem 4.2. Assume that $B^{(n)} = (\beta_{ij})_{n\times n}$ is irreducible. If $R_{0}>1$, then the alcohol-present equilibrium $P^{*}$ of system (3.5) is globally asymptotically stable in $\Omega^{0}$ and thus is the unique positive equilibrium.

Proof. Case Ⅰ: $n = 1$

The multi-group system (3.5) reduces to a single-group system as follows

where $h(\theta) = \gamma p(\theta)\Gamma_{0}(\theta), \int_{0}^{\infty}h(\theta)d\theta = B$ and $g(\theta) = \gamma q(\theta)\Gamma_{0}(\theta), \int_{0}^{\infty}g(\theta)d\theta = C$. The alcohol-present equilibrium $P^{*}$ of system (4.9) satisfies the following equations

Let $(S(t), E(t), L(t))$ be any solution of system (4.9) with non-negative initial data, we construct a Lyapunov functional $V_{ape}(t):(S, E, L)\rightarrow\mathbb{R}$ as follows

which is nonnegative and continuously differentiable. Here we define

where $\varphi(x) = x-1-\ln x$, $m(\theta) = \int_{\theta}^{\infty}h(s)ds, m(0) = B, \frac{d m(\theta)}{d\theta} = -h(\theta),$ and $n(\theta) = \int_{\theta}^{\infty}g(s)ds, n(0) = C, \frac{d n(\theta)}{d\theta} = -g(\theta).$ It is clear that $V_{ape}(t)$ is bounded for all $t\geq0$, and $V_{ape}(t)\geq 0$ with the equality holds if and only if $S(t) = S^{*}, E(t) = E^{*}, L(t) = L(t-\theta) = L^{*}$.

Using the equations in (4.9) and $\Lambda = (d^{S}+\xi)S^{*}+\beta S^{*}L^{*}B$, and differentiating $V_{1}(t)$ along system (4.8), we have

Further, let $s = t-\theta$ and base on fact that $\frac{d m(\theta)}{d\theta} = -h(\theta)$, we obtain

Similarly, base on fact that $\frac{d n(\theta)}{d\theta} = -g(\theta)$, we have

Combining (4.10)-(4.13), we get

From (4.14), we conclude that $\frac{d V_{ape}(t)}{dt}\leq 0$ and with the equality holds if and only if $S(t) = S^{*}, E(t) = E^{*}, L(t) = L(t-\theta) = L^{*}$ for all $t\geq0$. Thus, the largest invariant set $\{\frac{d V_{ape}(t)}{dt} = 0\} = \{P^{*}\}$. Therefore, using the LaSalle's Invariance Principle, we get the alcohol-present equilibrium $P^{*}$ is globally attractive in $\Omega^{0}$ if $R_{0}>1$ for $n = 1$.

Case Ⅱ: $n\geq2$

In the following, we are going to consider the case $n\geq2$. Let

and matrix $\bar{B}$ as given in (4.6). Since $B^{(n)} = (\beta_{ij})_{n\times n}$ is irreducible, we know the matrix $\bar{B}$ is also irreducible. Let $v = \{v_{1}, \ldots, v_{n}\}, v_{ i}> 0$ be a basis for the solution space of linear system (4.7), i.e., $\bar{B}v = 0$ as described in Lemma 4.1.

Let $(S_{i}(t), E_{i}(t), L_{i}(t)) ( 1\leq i\leq n)$ be any solution of system (3.5) with non-negative initial data. For such $v = \{v_{1}, \ldots, v_{n}\}$, we define a Volterra-type Lyapunov functional $U_{ape}(t):(S_{i}, E_{i}, L_{i})\rightarrow\mathbb{R}$ as follows

which is nonnegative and continuously differentiable, where

where $m_{j}(\theta) = \int_{\theta}^{\infty}h_{j}(s)ds, m_{j}(0) = B_{j}, \frac{d m_{j}(\theta)}{d\theta} = -h_{j}(\theta),$ and $n_{j}(\theta) = \int_{\theta}^{\infty}g_{j}(s)ds, n_{j}(0) = C_{j}, \frac{d n_{j}(\theta)}{d\theta} = -g_{j}(\theta).$

By the definition of the fading memory space, Lemmas 3.2 and 3.3, we known that $U_{ape}(t)$ is well-defined, that is, $U_{ape}(t)$ is bounded for all $t\geq0$. It is clear that $U_{ape}(t)\geq0$ with the equality holds if and only if $S_{i}(t) = S_{i}^{*}, E_{i}(t) = E_{i}^{*}, L_{i}(t-\theta) = L_{i}(t) = L_{i}^{*}.$ Differentiating $U_{1}(t), U_{2}(t), U_{3}(t)$ along the solutions of system (3.5), and using the equilibrium equations (4.8), we get

Further, let $s = t-\theta$ and base on fact that $\frac{d m_{j}(\theta)}{d\theta} = -h_{j}(\theta)$, we obtain

Similarly, base on fact that $\frac{d n_{j}(\theta)}{d\theta} = -g_{j}(\theta)$, we have

Combining (4.15)-(4.17), we get

Using $\varphi(x) = x-1-\ln x$ and $\bar{\beta}_{ij} = \beta_{ij}L_{j}^{*}(S_{i}^{*}B_{j}+E_{i}^{*}C_{j})$, we rearrange the terms in (4.18) as follows

Now, we are going to show that $\frac{d U_{ape}(t)}{dt}\leq 0$. From the properties of function $\varphi(x)$, it is easy to see that we only need to consider the last two items in (4.19). In what follows, we first prove that the penultimate item

In fact, from (4.7) $\bar{B}v = 0$, we get

Note that $\bar{\beta}_{ij} = \beta_{ij}L_{j}^{*}(S_{i}^{*}B_{j}+E_{i}^{*}C_{j})$, we obtain

Using this equation, we can obtain

Therefore, we have

holds for all $L_{1}, L_{2}, \cdots, L_{n}>0$.

Next, we will show that the last item is also equal to zero. Let

Then, we will find that

holds for all $L_{1}, L_{2}, \cdots, L_{n}>0$.

In fact, by the Kirchhoff's Matrix-Tree Theorem in Lemmas 4.1 and 4.2 (see ^[38]-^[40]), we known that $v_{i} = C_{ii}$ is a sum of weights of all directed spanning subtrees $T$ of $G$ that are rooted at vertex $i$. So, each term $v_{i}\bar{\beta}_{ij}$ is the weight $w(Q)$ of a unicyclic subetaaph $Q$ of $G$, obtained from such a tree $T$ by adding a directed arc $(i, j)$ from the root $i$ to vertex $j$. Thus, the meaning of double sum in (4.22) can be considered as a sum over all unicyclic subetaaphs $Q$ containing vertices $\{1, 2, \ldots, n\}$, that is

For each unicyclic subetaaph $Q$, we can see that

which implies that

For example, we set $n = 2$, the unique cycle $CQ$ has two vertices with the cycle $1\rightarrow 2 \rightarrow 1$, and $E(CQ) = \{(1, 2), (2, 1)\}$. Then we can get $v_{1} = \bar{\beta}_{21}$, $v_{2} = \bar{\beta}_{12}$, and

So, we have $W_{n}\equiv 0$ holds for all $L_{1}, L_{2}, \cdots, L_{n}>0$.

Therefore, combining with (4.19)-(4.20), (4.22) and using properties of $\varphi(x)$, we have $\frac{d U_{ape}(t)}{dt}\leq 0$ for all $(S_{1}, E_{1}, A_{1}, \ldots, S_{n}, E_{n}, A_{n})\in\Omega^{0}$, and with the equality holds if and only if $S_{i}(t) = S_{i}^{*}, E_{i}(t) = E_{i}^{*}, L_{i}(t) = L_{i}(t-\theta) = L_{i}^{*}$ for all $t\geq0$, $\theta\in [0, \theta^{+}]$, $i = 1, \ldots, n$. We conclude that the largest invariant set $\{\frac{d U_{ape}(t)}{dt} = 0\} = \{P^{*}\}$. The $\omega$-limit set of $\Omega^{0}$ consist of just the alcohol-present equilibrium $P^{*}$. Therefore, using the LaSalle's Invariance Principle, we see that the alcohol-present equilibrium $P^{*}$ is globally attractive in $\Omega^{0}$ if $R_{0}>1$ for $n\geq 2$.

As for the local asymptotical stability of the alcohol-present equilibrium $P^{*}$, which can be proved by the way of Corollary 5.3.1 in ^[60]. Therefore, using an argument similar to that in the proof of Theorem 4.1 (1), the alcohol-present equilibrium $P^{*}$ is globally asymptotically stable in $\Omega^{0}$ if $R_{0}>1$, which consequently implies that the alcohol-present equilibrium $P^{*}$ is unique. The proof of Theorem 4.2 is completed.

5.   Education and alcoholism age effects

In this section, we will discuss the effects of the public health education and alcoholism age on the alcohol control. It follows from Theorems 4.1 and 4.2 that the global dynamics of system (3.5) are completely determined by the basic reproduction number

where $S_{i}^{0} = \frac{\Lambda_{i}}{d_{i}^{S}+\xi_{i}}$, $E_{i}^{0} = \frac{\xi_{i}\Lambda_{i}}{(d_{i}^{S}+\xi_{i})(d_{i}^{E}+\alpha_{i})}$, and $B_{j} = \int_{0}^{\infty}h_{j}(\theta)d\theta$, $C_{j} = \int_{0}^{\infty}g_{j}(\theta)d\theta$.

For convenience, we assume that the natural death rate of susceptible population (including uneducated and educated susceptible population) is the same, that is, $d_{i}^{S} = d_{i}^{E}$. To investigate the effect of the public health education, we consider the special case with $\xi_{i} = 0$, which is the rate of the susceptible population who accepted the public health education entering into the educated class. Then for $\xi_{i} = 0$, we have $\hat{E_{i}^{0}} = 0$ and $\hat{S_{i}^{0}} = \frac{\Lambda_{i}}{d_{i}^{S}}$. Note that $\frac{\Lambda_{i}}{d_{i}^{S}}-\frac{\Lambda_{i}}{d_{i}^{S}+\xi_{i}} = \frac{\xi_{i}\Lambda_{i}}{d_{i}^{S}(d_{i}^{S}+\xi_{i})}>\frac{\xi_{i}\Lambda_{i}}{(d_{i}^{S}+\xi_{i})(d_{i}^{E}+\alpha_{i})}$ and $B_{j}\geq C_{j}$, we can obtain that

This implies that public health education leads to the basic reproduction number decline. On the other hand, the reproduction number $R_{0}$ is an increasing function of transmission coefficient $\beta_{ij}$. By increasing public health educational campaigns at all social levels, the value of $\xi_{i}$ will be increase. Hence, the awareness about drinking will alert the susceptible individuals so that they isolate themselves and decline to drink or drink moderately. This leads to a decrease in the value of $\beta_{ij}$. In this case, the value of the reproduction number $R_{0}$ will be decrease. Considering both the cost and the practical purposes, efforts to increase public health education are more effective in controlling the spread of alcohol problems than efforts to increase the number of individuals who have access to treatment. Therefore, public health education is one of the effective measures to control the spread of alcohol problems and it is beneficial for alcoholism control in the whole society.

However, $R_{0}$ is a decreasing function of $\gamma_{i}$ which is the rate of the light drinkers enter into the alcoholism compartment. From the assumption (H7), alcoholism age $\theta$ will cause the value of the reproduction number $R_{0}$ increase, which is bad for alcoholism control. It suggests that the longer the light drinkers stay in their compartment, the better alcohol problems will be controlled.

6.   Discussion

The goal of this paper is to analysis threshold dynamics of a multi-group alcoholism epidemic model with public health education and alcoholism age in heterogeneous populations. Our results expands the previous related works which have been obtained in single-group models without alcoholism age. Mathematical analysis shown that the global asymptotic behavior of multi-group alcoholism model is completely determined by the size of the basic reproduction number $R_{0}$. By using the theory of non-negative matrices and the classical method of Lyapunov functional, Theorem 4.1 implies that the alcohol problems dies out in the sense that alcoholism fractions go to zero from all the groups if $R_{0}\leq1$. By applications of the graph-theoretic approach to the method of Lyapunov functionals, we proved the existence, uniqueness and global asymptotic stability of the alcohol-present equilibrium $P^{*}$ for $R_{0}>1$, see Theorem 4.2. Our results implies that the alcoholism will persist in all the groups of the population and will eventually settle at a constant level in each group.

Our main results indicate that the dynamics of alcoholism model (2.1) is similar to that for the models without considering multi-group and alcoholism age. That is, heterogeneity of populations does not alter the dynamical behaviors as shown in ^[36]. However, our model is more realistic than the corresponding models already established. Because by decomposing the heterogeneous population into several subetaoups, the effects of both the intra-group and inter-group are considered. Moreover, inclusion of alcoholism population with alcoholism age leads to the basic reproduction number $R_{0}$ is increase. So the heterogeneity of populations plays an important role on $R_{0}$, it affects the global dynamics of the model. Strengthening public health education and controlling the age of drinking have a positive role in alcoholism control. In addition, there is an innovation in the method of study in this paper. Our findings in this paper may be valuable for the health workers who are performing alcoholism control. These results are provided with intention to inform and assist policy-makers in targeting education and treatment resources for maximum effectiveness.

Of course, other factors, such as time lag for alcoholism or nonlinear transmission rate, taking into account the model which will make the model more realistic. In addition, relapse is very common when it comes to drinking. Research on these issues remains to be completed in the future.

Acknowledgments

This research is supported by the NNSF of China (11461041 and 11661050), the NSF of Gansu Province (148RJZA024 and 061706), and the Development Program for HongLiu Outstanding Young Teachers in Lanzhou University of Technology. We are grateful to the anonymous referees and the editors for their valuable comments and suggestions which improved the quality of the paper.

Conflict of interest

The authors declare that there is no conflict of interests regarding the publication of this paper.