Global stability of multi-group SIR epidemic model with group mixing and human movement

1.   Introduction

Since Kermack and Mckendrick ^[1] formulated the compartmental ODE model to study epidemiology, extensively mathematical models have been used to explore the transmission dynamics of infectious diseases. Most of these mathematical models are assumed that the host population is homogeneously mixed. In reality, the host population is often heterogenous and it can be divided into several groups with different transmission patterns ^[2]. For example, it seems more reasonable to make a division into two groups for measles and mumps due to the different contact patterns between children and adults. The sexually transmitted diseases (such as, HIV/AIDS and gonorrhea) can be divided into serval groups according to the number of sexual partners. Therefore, multi-group epidemic models are emerged to investigate how the population heterogeneity affect the spread of disease.

Note that the study of the mathematical properties of multi-group epidemic model can obtain suitable measures for the control of infectious diseases. Recently, numerous literatures (see for example, ^{[3,4,5,6,7,9,8,10,11,12,13,2]} and the references therein) are dedicated to study such models on the theoretical and analytical properties including the existence, uniqueness of solutions and global stability of each equilibrium of the model. Particularly, Guo et al. ^[3,4] proposed a graph theory to Lyapunov functional technique, which simplified the proof on the global stability for the positive equilibrium of multi-group model. Hereafter, the graph-theoretical approach was widely used in studying the global dynamics of various multi-group models (see for example, ^[6,10,12] and references therein).

Nowadays, with the recent development of worldwide transportation, infected individuals can easily travel from one place to another which is thought to be one of the main reasons of the global pandemic of diseases. For instance, SARS first appeared in Guangdong Province of China in November, 2002. This destructive disease soon spread to other areas of China and, in the days that followed, to other parts of the world ^[13]. Ebola appeared in Guinea in March, 2014. It then spread to other countries including the United States, Spain and the United Kingdom ^[15]. Thus, it is necessary to incorporate human movement into epidemic model to clarifying how it affects the pattern of disease prevalence.

Recently, several researchers focus on the dynamics of multi-group models that incorporate the movement of human movement. In ^[16], Arino et al. explored the dynamics of a multi-group epidemic model with individuals movement. Liu and Takeuchi obtained the local stability of a two-species epidemic model with transport-related infection ^[17]. Wang and Yang studied the global dynamics of a two-patch SIS model with infection during transport ^[14]. In ^[18], Sun and Wu gained the stability of multi-group models with cross-dispersal. However, fewer studies obtained the global dynamics of general multi-group model with human movement.

Motivated by these facts, in this paper we aim to study the global dynamics of a general multi-group SIR model that incorporate explicit human movement between groups. The whole population is divided into $n$ distinct groups ($n\ge1$). The $i$-th ($1\le i\le n$) group is further partitioned into three compartments: the susceptible, infectious and removed, the number of individuals at time $t$ are denoted by $S_i(t), I_i(t)$ and $R_i(t)$, respectively. Like in ^[16], the diseases is assumed to be horizontally transmitted between humans according to standard incidence (see, for example, ^[19]) with $\beta_{ij}$ the rate of disease transfer from infective individual in group $j$ to susceptible individual in group $i$. The rate of human movement, from group $i$ to group $j$, is given by $m_{ij}$ with $m_{ij}\ge0$ and is assumed to be the same for each type of individual. Therefore, the multi-group SIR epidemic model with human movement can be described by the following system of $3n$ ordinary differential equations

where the prime ($'$) denotes the differentiation with respect to time $t$ and the sub-population number $N_i = S_i+I_i+R_i$. In patch $i$, $\mu_i$ is both the birth and death rate; $p_i$ is the proportion of immune at birth; $\gamma_i$ is the recovery rate. Here, parameters $\mu_i, \gamma_i$ are positive constants and $p_i, \beta_{ij}, m_{ij}$ are non-negative constants.

In this model, we consider disease transmission can occur not only in the same groups ($\beta_{ij} > 0$ for $i = j$) but also in different groups ($\beta_{ij} > 0$ for some $i\neq j$). This kind of system is called epidemic model with hybrid of multi-group ^[3] or epidemic model with group mixing ^[12]. To our knowledge, Kuniya and his cooperators studied several multi-group epidemic models with group mixing and population movement (see, for example ^[5,20,21]). In this paper, we will use the graph-theoretical approach ^[3,4] to present the global dynamics of multi-group SIR model (1.1) with both group mixing and human movement.

The organization of this paper is as follows. In the next section, we quote some results from graph theory which are very useful in the proof of our main results. In Section 3, we study the existence of equilibria and derive the expression of control reproduction number. We investigate the global stability of each equilibrium in Sections 4 and 5. Two numerical examples are performed to verify our theoretical results in Section 6. A brief conclusion is given in the final section.

2.   Preliminaries

Let $A = (a_{ij})_{n\times n}$ and $C = (c_{ij})_{n\times n}$ be nonnegative matrices, namely, all of their elements are nonnegative. We write $A\ge C$ if $a_{ij}\ge c_{ij}$ for all $i$ and $j$, $A > C$ if $A\ge C$ and $A\neq C$, and $A\gg C$ if $a_{ij} > c_{ij}$ for all $i$ and $j$. The matrix $A$ which satisfies $A\gg0$ is called positive matrix.

Definition 1. (^[22], p.27) An $n\times n$ matrix $A$ is cogredient to a matrix $P$ if for some permutation matrix $Q$, $QAQ^{T} = P$ (superscript $T$ represents transpose). $A$ is reducible if it is cogredient to

where $A_1$ and $A_3$ are square matrices, or if $n = 1$ and $A = 0$. Otherwise, $A$ is irreducible.

Denote $G(A)$ as the associated directed graph of $n\times n$ matrix $A$, which is a set of $n$ vertices and a set of directed arcs joining two vertices. Irreducibility of matrices can be easily tested using the associated directed graphs.

Definition 2. (^[22], p.30) A directed graph $G(A)$ is strongly connected if for any ordered pair $(Q_i, Q_j)$ of vertices of $G(A)$, there exists a sequence of edges (a path) which leads from $Q_i$ to $Q_j$.

Theorem 1. (^[22], p.30) Matrix $A$ is irreducible if and only if $G(A)$ is strongly connected.

The matrix $A$ has nonpositive off-diagonal and nonnegative diagonal entries, we have the following results on $A$.

Definition 3. (^[22], p.133) Any matrix $A$ of the form

for which $s\ge \rho(B)$ (the spectral radius of $B$), is called an M-matrix. Here, $I$ is identity matrix.

Lemma 1. (^[22], p.134) If all off-diagonal entries of matrix $A$ are nonpositive, then the followings are equivalent.

$(ⅰ)$ $A$ is a nonsingular M-matrix;

$(ⅱ)$ $A$ is semipositive; that is, there exists $x\gg0$ with $Ax\gg0$;

$(ⅲ)$ $A$ is inverse-positive; that is, $A^{-1}$ exists and $A^{-1}\ge0$;

$(ⅳ)$ $A$ does not reverse the sign of any vector; that is, if $x\neq0$ and $y = Ax$, then $x_iy_i > 0$ for some subscript $i$.

Consider a linear system

where $A = (a_{ij})_{n\times n}$ with $a_{ii} = -\sum_{j\neq i}^na_{ji}$ and $a_{ij}\le0$ for all $i\neq j$. Then the following lemma holds.

Lemma 2. (^[3], Lemma 2.1) Assume that the matrix $A$ in linear system (2.1) is irreducible and $n\ge2$. Then the solution space of system (2.1) has dimension 1, and a basis of the solution space can be given by

where $A_{ii} > 0$ denotes the cofactor of the $i$-th diagonal entry of $A$, $1\le i\le n$.

3.   Equilibria and control reproduction number

Denote contact matrix $B = (\beta_{ij})_{n\times n}$ and the movement matrix $M = (m_{ij})_{n\times n}$. Unless otherwise indicated, in this paper, matrices $B$ and $M$ are always assumed to be irreducible. In fact, contact matrix $B$ is irreducible which means that an infected individual in the first group can cause infection to a susceptible individual in the second group through an infection path. While, movement matrix $M$ is irreducible which means that each patch are strongly connected with respect to human movement.

For ease of notations, let ${\rm diag}(a_i)$ denote a diagonal matrix whose diagonal entries starting in the upper left corner are $a_1, a_2, \cdots, a_n$ and off-diagonal elements are all zero, and define $n\times n$ matrices

Obviously, matrix $G_0$ is also irreducible due to the assumption that movement matrix $M$ is irreducible. Since all off-diagonal entries of matrix $G_{\mu}$ are negative and the sum of the entries in each column is positive, it follows from the equivalent conditions of Lemma 1 that matrix $G_{\mu}$ is a nonsingular irreducible M-matrix and is inverse-positive, i.e., $G_{\mu}^{-1}$ exists and $G_{\mu}^{-1}\ge0$.

Notice that the total population number $N(t) = \sum_{i = 1}^nN_i(t) = \sum_{i = 1}^n(S_i(t)+I_i(t)+R_i(t))$ satisfies the equation $N'(t) = \sum_{i = 1}^nN_i'(t) = 0$, which implies that $N(t)$ is always constant, denoted by $N_c$. Therefore, the feasible region

is positively invariant with respect to system (1.1).

In absence of infectious disease, we have the following results on the existence and uniqueness of the disease-free equilibrium for system (1.1).

Theorem 2. $\rm (ⅰ)$ There exits a unique disease-free equilibrium $E^0 = (S_1^0, 0, R_1^0, \cdots, S_n^0, 0, R_n^0)\in\mathbb{R}_+^{3n}$ for system (1.1).

$\rm (ⅱ)$ There exists only one equilibrium whose coordinates include zero, i.e., the disease-free equilibrium $E^0$.

Proof. First we prove (ⅰ). In absence of infectious diseases, the disease-free equilibrium of system (1.1) must satisfy the following linear system

The algebraic equations (3.1) can be easily expressed by the following form of matrix system

where # = $(\#_1, \#_2, \cdots, \#_n)^{T}$ and $\#$ represents $S, I, R$ and $N$. It follows from $\sum_{i = 1}^nN_i = N_c$ and Lemma 2 that linear system $G_0{{\bf{N}}} = 0$ has a unique positive solution ${{\bf{N}}} = {{\bf{N}}}^0$ with

where $\nu_i > 0$ is the cofactor of the $i$-$th$ diagonal entry of $G_0$. Substituting ${\mathit{\bf{N}}}^0$ into the first two equation of (3.2), it is easy to derive that the first equation of (3.2) has a unique solution ${\mathit{\bf{S}}} = {\mathit{\bf{S}}}^0$ and the second equation has a unique solution ${\mathit{\bf{R}}} = {\mathit{\bf{R}}}^0$, where

and

Next we prove (ii). Using Lemma 2 and $G_0$ is irreducible, it follows from the third equation of (3.2) that $N_i > 0$ at any equilibrium. Furthermore, it is impossible to have $S_i = 0$ at any equilibrium, since at $S_i = 0$ the first equation of (3.1) becomes $(1-p_i)\mu_iN_i+\sum_{j = 1}^n m_{ji}S_j > 0$. This is a contradiction. In the following, we only need to show that $I_i = 0$ for some $i$ implies that $I_j = 0$ for all $j$. If $I_i = 0$, it follows from the second equation of (1.1) that

Since $S_i > 0, I_i\ge0$ for all $i$, then equation (3.4) implies that

For the first equation of (3.5), if $m_{ji} > 0$, then $I_i = 0$ means $I_j = 0$ for any $1\le i, j\le n$, i.e.,

Following the Definition 2 and Theorem 1, the movement matrix $M$ is irreducible which ensures that there exists a sequence of ordered pairs $\{(i, \tau_1), (\tau_1, \tau_2), \cdots, (\tau_q, j)\}$ such that $m_{i\tau_1} > 0, m_{\tau_1\tau_2} > 0, \cdots, m_{\tau_qj} > 0$, $\tau_k = 1, 2, \cdots, n, \ k = 1, 2, \cdots, q$ and $q\ge0$. Applying (3.6) to each pair in such a sequence and using $I_i = 0$, we derive $I_{\tau_1} = 0, \ I_{\tau_2} = 0, \cdots, \ I_{j} = 0.$ Hence $I_j = 0$ for all $j$ provided that $M$ is irreducible. Similarly, if $B$ is irreducible, it follows from the second equation of (3.5) that $I_j = 0$ for all $j$. Therefore, the disease-free equilibrium $E^0$ is the only one equilibrium whose coordinates include zero.

We should remark that the system may be decoupled into several small systems and may have multiple boundary equilibria when the movement matrix $M$ is reducible (see, for example, ^[26] and references therein).

Using the techniques of van den Driessche and Watmough ^[25], the control reproduction number can be expressed as

where matrices $F = (\beta_{ij}S_i^0/N_j^0)_{n\times n}$ and $V = {\rm diag}(\mu_i+\gamma_i)+G_0$ respectively represent the new infection terms and the remaining transfer terms for entire population, and $\rho$ denotes the spectral radius.

4.   Global dynamics when $\mathfrak{R}_v < 1$

Notice that

The proof of Theorem 2 implies that system (4.1) has a unique positive equilibrium ${\mathit{\bf{N}}}^0$ and one can easily testify ${\mathit{\bf{N}}}^0$ is globally asymptotically stable in $\Gamma_1$ i, e., $\lim_{t\to\infty}N_i(t) = N_i^0$. Using the results from Castillo-Chavez and Tieme ^[24] and Mischaikow et al. ^[28], we can obtain the analytical results by considering the following limit system of system (1.1) in which the sub-population is assumed to be constant $N_i^0$

System (1.1) and (4.2) have the same set of equilibria and the same existence conditions as given in the previous section.

For the eventual boundedness of solutions $S_i, I_i, R_i$, $i = 1, 2, \cdots, n$ of system (4.2), we have the following lemma.

Lemma 3. For any solutions in $\Gamma_1$ of system (4.2), it holds that

in particular,

Proof. The first equation of (4.2) implies that

Using the right hand side of (4.3), let us define an auxiliary linear system

A simple calculation shows that the positive equilibrium $(\bar{S}_1^0, \bar{S}_2^0, \cdots, \bar{S}_n^0) = (S_1^0, S_2^0, \cdots, S_n^0)$ is the unique equilibrium of (4.4).

Let $g(x) = x-1-\ln x, \ x > 0$. One can easily verify that $g(x)\ge0$ with $g(x) = 0$ if and only if $x = 1$ and $(x-1)(1-y) = g(x)+g(y)-g(xy)$ for any $x, y\in\mathbb{R}_+$. Define

Differentiating $V_i^{\bar{S}}$ along system (4.4) and using $S_i^0$ is the positive equilibrium of system (4.4), simple calculation implies that

Let $V_{\bar{S}} = \sum_{i = 1}^nV_i^{\bar{S}}$. By using $\sum_{i = 1}^n\sum_{j = 1}^nm_{ji}S_j^0g\Big(\frac{\bar{S}_j}{S_j^0}\Big) = \sum_{i = 1}^n\sum_{j = 1}^nm_{ij}S_i^0g\Big(\frac{\bar{S}_i}{S_i^0}\Big)$, we have

which suggests that $V_{\bar{S}}'\big|_{ (4.4)}\le0$ with $V_{\bar{S}}'\big|_{ (4.4)} = 0$ if and only if $\bar{S}_i = S_i^0$. Using the LaSalle's Invariance Principle ^[29], the unique positive equilibrium $(\bar{S}_1, \bar{S}_2, \cdots, \bar{S}_n) = (S_1^0, S_2^0, \cdots, S_n^0)$ is globally asymptotically stable for system (4.4), i.e., $\lim_{t\to\infty}\bar{S}_i(t) = S_i^0$ for all $i$. Following the standard comparison theorem ^[11], we have $\limsup_{t\to+\infty}S_i(t)\le S_i^0, \ \ i = 1, 2, \cdots, n$.

If $S_i = S_i^0$ for some $i$ and $S_j\le S_j^0$ for all $j\neq i$, it follows from Lemma 3 and the first equation of system (4.2) that

This indicates that the subset of $\Gamma_1$

is the positively invariant with respect to system (4.2). Therefore, we can study system (4.2) in the feasible region $\Gamma$.

Theorem 3. $\rm (ⅰ)$ If $\mathfrak{R}_v < 1$, then the unique disease-free equilibrium $E_0$ of system (4.2) is globally asymptotically stable in $\Gamma$.

$\rm (ⅱ)$ If $\mathfrak{R}_v > 1$, then the disease-free equilibrium $E_0$ is unstable and system (4.2) is uniformly persistent in $\mathring{\Gamma}$ (the interior of $\Gamma$).

Proof. From Theorem 2 in van den Driessche and Watmough ^[25], the disease-free equilibrium $E_0$ of system (4.2) is locally asymptotically stable if $\mathfrak{R}_v < 1$, and unstable if $\mathfrak{R}_v > 1$.

Let ${\bf{I}} = (I_1, I_2, \cdots, I_n)^{T}$. Using the second equation of (4.2), it follows that

Let ${\mathit{\bf{u}}} > 0$ be the left eigenvector of the nonnegative matrix $FV^{-1}$ with respect to the eigenvalue $\rho(FV^{-1}) = \mathfrak{R}_v$, that is, ${\mathit{\bf{u}}}^{T}FV^{-1} = \mathfrak{R}_v{\mathit{\bf{u}}}^{T}$. Construct a Lyapunov function

Differentiating (4.5) along the system (4.2) yields

If $\mathfrak{R}_v < 1$, then $dV/dt\le0$ with $dV/dt = 0$ if and only if $I_i = 0$ for some $i$. Similar to the proof of Theorem 2, it follows that the only invariant set where $V' = 0$ is the singleton $\{E_0\}$. Therefore, by LaSalle's Invariance Principle ^[29], $E_0$ is globally asymptotically stable in $\Gamma$.

If $\mathfrak{R}_v > 1$, by continuity and $(\mathfrak{R}_v-1){\mathit{\bf{u}}}^{T}VI > 0$ for $I > 0$, we have $V' > 0$ in a neighborhood of $E_0$ in $\mathring{\Gamma}$. In this case, the solutions in $\mathring{\Gamma}$ sufficiently close to $E_0$ move away from $E_0$, that is, $E_0$ is unstable if $\mathfrak{R}_v > 1$. Using the uniform persistence result from ^[27] and the similar argument as in the proof of Proposition 3.3 of ^[30], we can show that the instability of $E_0$ implies the uniform persistence of (4.2).

5.   Global dynamics when $\mathfrak{R}_v > 1$

If $\mathfrak{R}_v > 1$, by Theorem 2.8.6 in ^[23] or Theorem D.3 in ^[11], the uniform persistence of (4.2) and the positive invariance of the compact set $\Gamma$ imply that system (4.2) admits at lest one equilibrium in $\mathring{\Gamma}$. Let $E^* = (S_1^*, I_1^*, R_1^*, \cdots, S_n^*, I_n^*, R_n^*)$ be an endemic equilibrium for system (4.2), then we have

Define

and

Let

where $B^*_{ii}$ is the cofactor of the $i$-$th$ diagonal entry of $B^*$ and $B^*_{ii} > 0$, $1\le i\le n$. Then, we have the following Lemma.

Lemma 4. The positive vector $\mathit{\boldsymbol{\omega}}$ is a basis of the solution space of linear system $B^*x = 0$. Furthermore, positive vector $\mathit{\boldsymbol{\omega}}$ satisfies

Proof. Matrices $B$ and $M$ are irreducible which imply that matrix $B^*$ is also irreducible. Then it follows from Lemma 2 that positive vector $\mathit{\boldsymbol{\omega}} = (\omega_1, \omega_2, \cdots, \omega_n)$ is a basis of the solution space of linear system $B^*\mathit{\boldsymbol{\omega}} = 0.$ This indicates that

Thus, one can derive from the expressions of $\bar{\beta}_{ij}$ given in (5.2) and the second equation of (5.1) that

Therefore, we have

Theorem 4. If $\mathfrak{R}_v > 1$, then the endemic equilibrium $E^*$ of system (4.2) is unique and it is globally asymptotically stable in $\mathring{\Gamma}$ under the condition $\sum_{j = 1}^n\omega_j\beta_{ji}\frac{S_j^*}{N_i^0} > \omega_i\gamma_i$.

Proof. We prove that $E^*$ is globally asymptotically stable in $\mathring{\Gamma}$, which implies that the endemic equilibrium is unique. Since $S_i+I_i+R_i = N_i^0$ and the variable $R_i$ does not appear in the first two equations in (4.2), then we can work on the following equivalent system

Let $g(x) = x-1-\ln x$ and

Note that $(x-1)(1-y) = g(x)+g(y)-g(xy)$ for any $x, y\in \mathbb{R}_+$, then using the equilibrium equations (5.1) and differentiating $V_i^S$ and $V_i^I$ along system (5.5), we have

and

Define a Lyapunov function as follows

Then combining equations (5.6) and (5.7) together, we have

In fact

where $\mathit{\boldsymbol{\omega}} = (\omega_1.\cdots, \omega_n)$, $\mathit{\boldsymbol{c_1}} = (S_1^*g(\frac{S_1}{S_1^*}), \cdots, S_n^*g(\frac{S_n}{S_n^*}))^T$, $\mathit{\boldsymbol{c_2}} = (I_1^*g(\frac{I_1}{I_1^*}), \cdots, I_n^*g(\frac{I_n}{I_n^*}))^T$, $M = (m_{ij})_{n\times n}$ and $Q = (\beta_{ij}\frac{S_i^*}{N_j^0}+m_{ji})_{n\times n}$. Therefore, from $\sum_{j = 1}^n\omega_j(\beta_{ji}\frac{S_j^*}{N_i^0}+m_{ij}) = \omega_i(\mu_i+\gamma_i+\sum_{j = 1}^nm_{ij})$ and the condition $\sum_{j = 1}^n\omega_j\beta_{ji}\frac{S_j^*}{N_i^0} > \omega_i\gamma_i$, we have

It is easily to verify that $V' = 0$ if and only if $S_i = S_i^*$ and

This equation is equivalent to $I_i = \alpha I_i^*$, where $\alpha$ is an arbitrary constant. Substituting $S_i = S_i^*, I_i = \alpha I_i^*$ into the first equation of (5.5), we have

Since the left-hand side of (5.10) is monotonically decreasing with respect to $\alpha$, it follows from the equation (5.1) that (5.10) holds if and only if $\alpha = 1$. That is, the only compact invariant subset of $V' = 0$ is the only singleton point $\{\tilde{E}^*\}$, here $\tilde{E}^* = (S_1^*, I_1^*, S_2^*, I_2^*, \cdots, S_n^*, I_n^*)$. Using the LaSalle's Invariance Principle ^[29] and the similar argument to the proof of Theorem 3, we can show that $\tilde{E}^*$ is unique and globally asymptotically stable for system (5.5). That is, the endemic equilibrium $E^*$ is unique and globally asymptotically stable for system (4.2) in $\mathring{\Gamma}$ if $\mathfrak{R}_v > 1$ and $\sum_{j = 1}^n\omega_j\beta_{ji}\frac{S_j^*}{N_i^0} > \omega_i\gamma_i$.

6.   Numerical simulations

In this section, we mainly perform some numerical simulations to verify the validity of the theoretical results carried out in the previous sections. In this paper, the simulations are performed by using Mathematica 10 software.

6.1.   Two-group system

We first consider the two-group case ($n = 2$), which is thought to be suitable for infectious diseases transmitted between two cities or communities. In this paper, we consider the unit of time as a year to model the long-term spread of disease. For the two-group system, we fix

If we denote $l_{ij}$ as the annual migration proportion from group $i$ to $j$, then migration rate $m_{ij}$ determined by $m_{ij} = -\ln(1-l_{ij})$. Here we take migration proportion $l_{12} = 0.1$ and $l_{21} = 0.11$, which means that 10% population migrate from group 1 to group 2 during one year and 11% population migrate from group 2 to group 1 during one year. We do not give the value of $l_{ii}$ (which determined the values of $m_{ii}$) due to the fact that the theoretical results are independent of migration rate $m_{ii}$ for all $i$. Under these settings, we only need to change the transmission rate $\beta_{ij}$ to explore the global stability of each equilibrium.

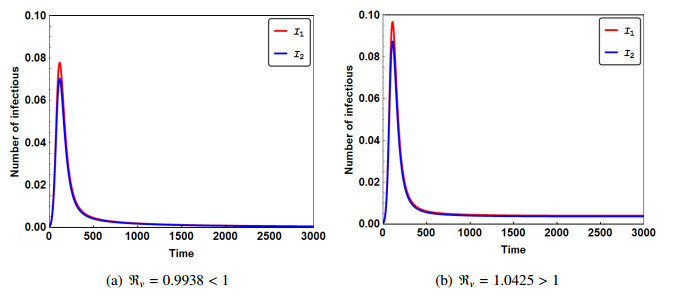
If $\beta = \left(\begin{array}{cc} 0.1144 & 0.0286 \\ 0.0429 & 0.1001 \end{array}\right)$, we have $\mathfrak{R}_v = 0.9938 < 1$. Following Theorem 3, we know that the disease-free equilibrium $E^0 = (0.2108, 0, 0.7396, 0.2918, 0, 0.6578)$ is the unique equilibrium of the system (1.1) and it is globally asymptotically stable in $\Gamma$. In fact, Figure 1(a) provides the simulations of this case and it reveals that each infected population converges to zero.

If $\beta = \left(\begin{array}{cc} 0.12 & 0.03 \\ 0.045 & 0.105 \end{array}\right)$, we have $\mathfrak{R}_v = 1.0425 > 1$. For this case, we have $\min\{\beta_{ii}S_i^*/N_i^*-\gamma_i\} = 0.0009 > 0$. Then, it follows from Theorem 4 that the positive equilibrium $E^* = (0.2978, 0.0039, 0.7485, 0.2801, 0.0036, 0.6659)$ is the unique endemic equilibrium and it is globally asymptotically stable in $\mathring{\Gamma}$. In fact, Figure 1(b) gives the simulation results for this case and it shows that each infected population converges to some positive steady states.

6.2.   A geographical spread of disease

We next consider the 50-group case ($n = 50$), which can be considered as the system of geographical spread of disease. Referring to the pervious example, we fix

We employ the following form of the movement matrix $M = (m_{ij})_{50\times50}$

where $\bar{m}_i = -\ln(1 - l_i), \ i = 1, 2$ with $l_1 = 0.15, \ l_2 = 0.1$. It is easy to see that the movement matrix $M$ is irreducible. Using the diffusive-like form of contact matrix $B = (\beta_{ij})_{50\times50}$ considered in ^[6], the contact matrix $B$ in this paper can be expressed as:

where $\alpha, \beta_x$ are positive constants. Obviously, contact matrix $B$ is irreducible. For simplicity, we fix $\alpha = 0.01$ and only change $\beta_x$ to observe the dynamical behavior of each equilibrium.

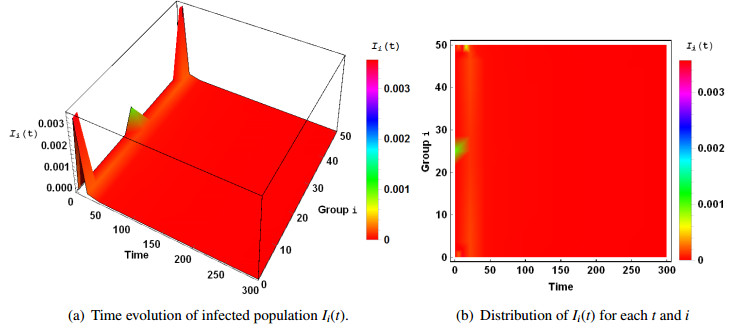
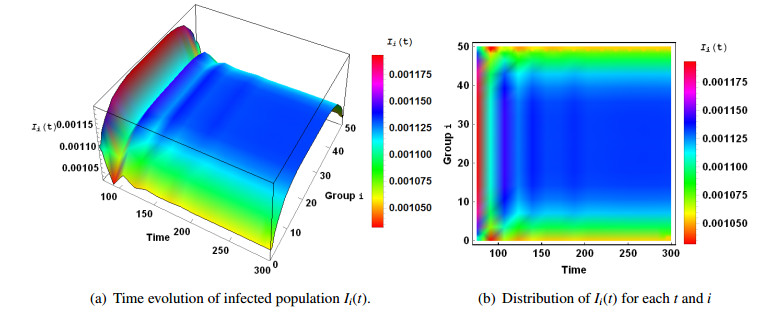
The simulations of system (1.1) with $n = 50$ can be seen in Figure 2 and Figure 3. In both figures, the discrete groups are connected smoothly by the Mathematica commands "Plot3D" and "DensityPlot".

If $\beta_x = 0.62$, in this case, we have $\mathfrak{R}_v = 0.9985 < 1$. Figure 2 gives the simulations of this case. It shows that each infected population converges to zero, i.e., the disease-free equilibrium is globally asymptotically stable if $\mathfrak{R}_v < 1$. This verifies the conclusion of Theorem 3.

If $\beta_x = 0.66$, in this case, we have $\mathfrak{R}_v = 1.0609 > 1$. Simulation results for this case are presented in Figure 3. It suggests that each infected population trends to some positive steady states, i.e., the endemic equilibrium is globally asymptotically stable when $\mathfrak{R}_v > 1$. This simulation confirms the theoretical results of Theorem 4.

In particular, by virtue of the form of contact matrix $B$ and movement matrix $M$, we can observe that two infection groups can cause infection to all groups. Meanwhile, the wave-like spreading pattern which connect the disease-free equilibrium $E^0$ and the endemic equilibrium $E^*$.

7.   Conclusion

In this paper, we investigate the complete global dynamics of a multi-group SIR model that incorporate group mixing and human movement. The results shows that model (1.1) exists a unique disease-free equilibrium, which is the only one equilibrium whose coordinates include zero. Meanwhile, model (1.1) has a unique endemic equilibrium if the control reproduction number $\mathfrak{R}_v > 1$. Due to the complexity of model (1.1), we simplify this model to the equivalent system (4.2). By using the graph-theoretical approach ^[3], we obtain that the disease-free equilibrium is global asymptotically stable if $\mathfrak{R}_v < 1$, and the endemic equilibrium is global asymptotically stable if $\mathfrak{R}_v > 1$ and $\sum_{j = 1}^n\omega_j\beta_{ji}\frac{S_j^*}{N_i^0} > \omega_i\gamma_i$.

Acknowledgments

This work was supported in part by the Natural Science Foundation of Ningxia University (No. ZR18011), the National Natural Science Foundation of China (Nos. 11671206 and 61662060). The author would like to thank Prof. Zhipeng Qiu at Nanjing University of Science and Technology for his valuable suggestions.

9.   Conflict of interest

The author declare there is no conflict of interest in this paper.