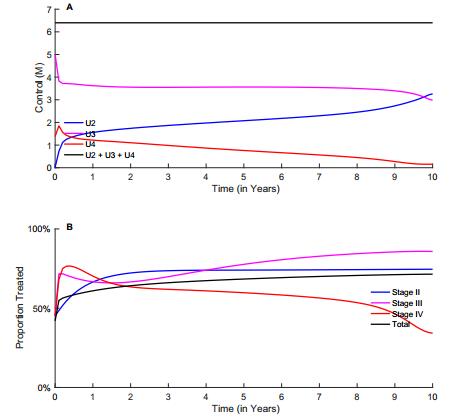
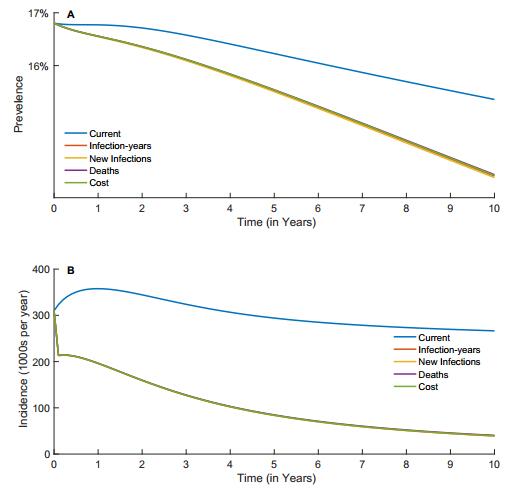
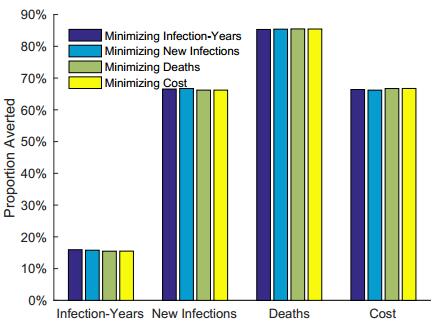
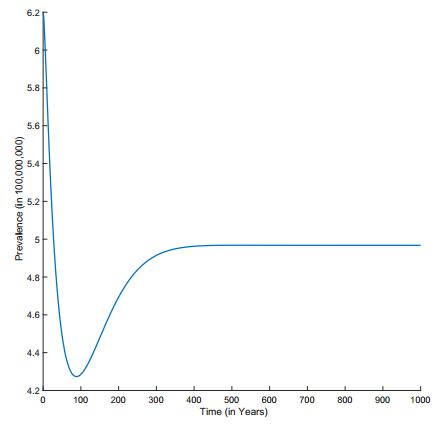
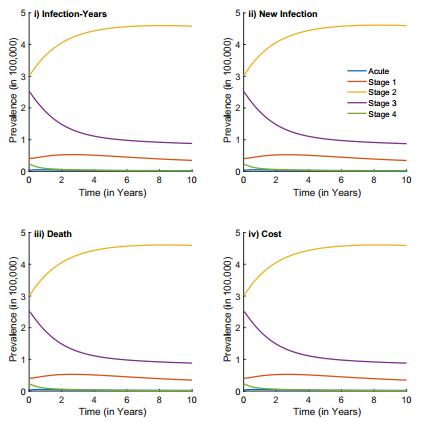
Apart from the traditional role of preventing progression from HIV to AIDS, antiretroviral drug therapy (ART) has been shown to have the additional benefit of substantially reducing infectiousness in infected people, making ART potentially an important strategy in the fight against HIV. We developed a mathematical model based on the WHO's 5-stage classification of HIV/AIDS disease progression. Our model stratifies the population by disease stage, diagnosis and treatment. We used optimal control methods and data from South Africa to determine the best time-dependent treatment allocation required to minimize new infections, infection-years, deaths and cost. Our results indicated that the treatment strategy to minimize infection-years and new infections is to place emphasis on early treatment (i.e., treatment in Stage Ⅱ & Ⅲ), while to minimize cost and death, the emphasis should be on late treatment (i.e., Stage Ⅲ & Ⅳ). Applying the optimal treatment strategy also leads to a substantial reduction in disease incidence and prevalence. The results of this study will hopefully provide some guidance for policymakers in determining how to best allocate antiretroviral drugs in order to maximize the benefits of treatment.
1.
Introduction
Transcription is not only a central process in life but also a pivotal step in gene expression since it determines when and how the genetic information stored in DNA is transcribed into messenger RNA (mRNA) molecules that are further translated into proteins that virtually participate in all cell functions. Transcription occurs often in a bursting fashion [1,2,3,4,5], leading to substantial variations in mRNA and further protein abundances. Single molecule measurement technologies have provided evidence for transcriptional bursting, i.e., production of mRNAs in bursts [6,7,8,9]. This noise has been identified as an important source of cell-to-cell variability [3,10,11,12,13,14,15,16]. Owing to its importance, stochastic transcription has received extensive attention in recent years. However, quantitative experiments of stochastic transcription call for a modeling effect that addresses transcriptional mechanisms in a systematic rather than case-by-case fashion.
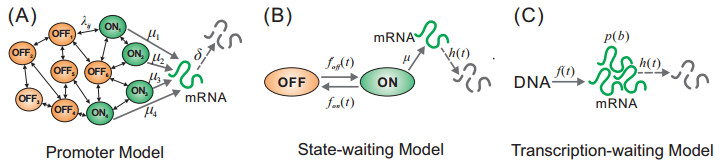
Transcription is the most complex step in gene expression, involving ordered assembly of pre-initiation complexes, recruitment of various polymerases, chromatin remodeling, binding and unbinding of transcription factors (TFs) to DNA regulatory sites, etc. [17,18,19]. These factors or processes either result in non-exponential distributions of ON and OFF times (i.e., the times that the gene dwells at active and inactive states) [11,16,20], or create complex promoter structures [18,21,22,23,24,25]. The former case occurs mainly because, e.g., some of the chromatin states are transcriptionally permissive, and together make up the ON-phase of the gene and allow for (repeated) multistep assembly of the preinitiation complex and promoter escape. This will motivate us to introduce a so-called queuing model of stochastic transcription, where the distributions of the ON and OFF times may be arbitrary. The latter case may occur in prokaryotic and eukaryotic cells. For example, the PRM promoter of phage lambda in E. coli is regulated by two different TFs binding to two sets of three operators that can be brought together by looping out the intervening DNA and as a result, the number of regulatory states of the PRM promoter may be up to 128 [26]. In contrast, eukaryotic promoters may be more complex since they would involve, e.g., nucleosomes competing with or being removed by TFs [27], and epigenetic regulations via histone modifications [19,28,29]. In a word, complex promoters with more than two activity states are not the exception but the rule as combinatorial control of gene regulation by multiple TFs is widespread [9,25,30,31]. This will motivate us to introduce another model of stochastic transcription (called the promoter model), where the promoter may contain many active and inactive states and there are random transitions among them. For both generalized models, an unsolved issue is how the upstream promoter dynamics affects the downstream expression dynamics, and in particular, how mRNA distribution is derived.
On the other hand, a different mRNA distribution describes a different pattern of cell-to-cell variability at the transcription level, or represents a different cellular phenotype. As a matter of fact, bimodality of gene expression, as a mechanism driving to phenotypic diversity, can enhance the survival of cells in a fluctuating environment [32]. Unimodality also has similar biological function, e.g., the unimodal expression of Tat (a vital gene in HIV-1 viral) can drive phenotypic diversity of clonal populations through inducing phenotypic bifurcation [33,34]. In simplified cases or under strong assumptions, previous studies showed that distributions of gene product (mRNA or protein) may follow simple distributions such as Poisson distribution [4,35], Gamma distribution [36,37] and Beta distribution [9,38,39]. These simple distributions provide explicit and intuitive relationships between cellular phenotypes and expression patterns. In general, however, the mRNA numbers follows more complex distributions expressed by confluent hypergeometric functions, as shown in previous studies [24,39]. This raises another question: How are unimodal or bimodal mRNA expressions robustly shaped? From the viewpoint of synthetic biology, studying this question is significant since it can help biologists design robust experiments and interpret their experimental results. We point out: (1) with the emergence of single cell measurement techniques, there have been increasingly rich data on distributions of gene systems [40,41]. These distributions, which are in general stationary, are still biologically reasonable if a set of reactions proceeds much faster than environmental changes; (2) the stationary distribution and the corresponding statistics are important quantities characterizing the steady-state behavior of many biochemical systems. Therefore, we will focus on the steady-state distribution and moments of mRNA.
This article is organized as follows. In section 2, we analyze a promoter model with arbitrarily complex promoter structure at the stochastic transcription level. By analysis, we find that there are conjugate relationships between mRNA distributions, which well reveal the essential principle of stochastic transcription in complex cases of TF regulation. In section 3, we analyze a queuing model of stochastic transcription, where waiting-time distributions are general (e.g., non-exponential). For this model, we derive an analytical formula for calculating raw moments, and give a strategy for reconstructing the mRNA distribution from raw moments. In section 4, by mathematical analysis combined with numerical simulation, we give robust regions for unimodal and bimodal expressions in two specific models of stochastic transcription. Finally, we conclude this paper and give some discussions.
2.
Analysis of a gene model with arbitrary promoter structure
2.1. Model description and stationary mRNA distribution
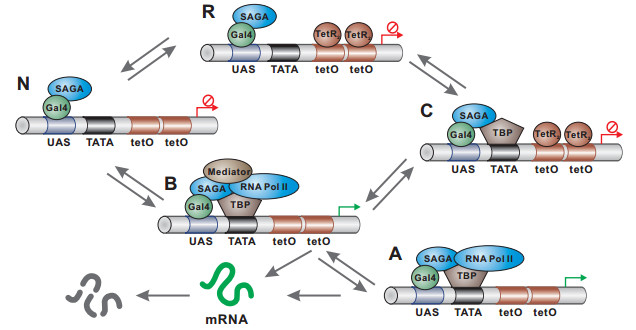
As pointed out in the introduction, a gene promoter (i.e., a regulatory sequence) may contain many activity states (referring to Figure 1, which shows a biologically feasible example [21]), and there are random transitions between these states. We assume that the promoter has N activity states in total. For analysis simplicity, we further assume that there is transcription only at ON state whereas there is no transcription at OFF state, and there are transitions among these states with constant transition rates. To incorporate effects of TF regulation, we assume that the TFs act directly on transition rates [21], so that these rates may change in some finite ranges. In addition, we assume that all the produced mRNAs degrade in a linear manner. Here we do not consider protein levels since mRNA levels can well explain stationary protein levels in many situations [42].
Denote by m the number of mRNA molecules, and let P(m;t) represent the distribution that mRNA has m molecules at the kth state of promoter and denote by P=(P1,⋯,PN)T the column vector consisting of these factorial distributions. Denote by λjj the transition rate from state-i to state-j (λjj=0 means that no transition occurs). Let the N×N matrix W=(λjj) describe transitions between promoter states (called transition matrix), the diagonal matrix Λ=diag(μ1,⋯,μN) describe exits of transcription (called transcription matrix) with μi representing the transcription rate of mRNA in state-i (μi=0 means that no transcription takes place), and the diagonal matrix δ=diag(δ1,⋯,δN) describe the degradation of mRNA. The chemical master equation describing mRNA dynamics takes the form
where E and E−1 are step operators and I is the identity operator. Clearly, the first term in Eq (2.1) describes promoter dynamics with transition matrix W being actually an M-matrix (i.e., the sum of every column or row elements is equal to zero), the second term describes the exits of transcription with transcription matrix Λ, and the third term describes the degradation dynamics of mRNA with degradation matrix δ (throughout this paper, we will assume that all the degradation rates are the same. Without loss of generality, we further assume that the common degradation rate is 1. This is equivalent to the normalization of all other parameters by this common rate). We point out that model (2.1) includes many previously-studied gene models as its particular case.
In order to solve (2.1), we simply introduce the convergent moment (CM) approach that we developed previously [43]. CMs of a distribution in the one-dimension bk=∑n≥k(nk)P(n),k= 0,1,2,⋯, all cases are defined as
with b0=1 that corresponds to the conservative condition of probability. It is easy to verify that the CMs defined in such a way are actually coefficients in the Taylor series of the probability-generating function, denoted by g(z), corresponding to the probability p(n), that is, bk=(1╱k!)∂kg(z)╱∂zk∣z=1. Importantly, if all the CMs are finite and given, we can have the following formula for reconstructing the distribution
where symbol (nk) represents the common binomial coefficients.
Now, we return to (2.1). Denote by bk the kth order CM of the total distribution P=∑Ni=1Pi and by b(i)k the kth order CM of the factorial distribution Pi. Next, we can derive the following CM equation from (2.1)
where W and Λ have been rescaled by δ, and bk=(b(1)k,⋯,b(N)k)T is a column vector consisting of factorial CMs. See Appendix A for the derivation of (2.4). Finding steady-state mRNA distribution is common interest. According to (2.3), the key is to find stationary CMs bk. For this, we have
Proposition 1 Steady-state CMs bk are given by
where uN=(1,1,⋯,1) is an N-dimensional row vector, 0,−α1,−α2,⋯,−αN−1 are nonzero characteristic values of M-matrix W; (iI−W)∗ is the adjacency matrix of matrix (iI−W); and b0=(b(1)0,⋯,b(N)0)T is given by
in which −β(j)1,−β(j)2,⋯,−β(j)N−1 are the characteristic values of Wj, the minor matrix of W after crossing out the jth row and jth column of the entry λjj of W.
Proof Here, we only provide main steps of the proof. See Appendix B for more details.
First, note that at steady state, (2.4) becomes the following iterative form
Using the fact that W is an M-matrix, i.e., the sum of every row elements is equal to zero, it is not difficult to verify (2.5).
Second, note that the Laplace's formula for M-matrix W gives
the null space of W is one-dimensional, and (2.7) holds for k=0 (implying Wb0=0). Therefore, we can set the formal expression of b0 as b0=c(det(W1),⋯,det(WN))T, where c is a constant, given by
Third, if we denote by
the characteristic polynomial of matrix W, it is not difficult to show
where "tr" represents the matrix trace.
Finally, using (2.10) and considering the components of vector b, we have
thus proving Proposition 1.
After having obtained all the stationary CMs, we can reconstruct the stationary mRNA distribution using (2.3). From (2.7) and using the fact that W is an M-matrix, we can show
Thus, it is particularly interesting that if all the states of the promoter are ON with the same transcription rate μ, i.e., if Λ=μIN, the mRNA number obeys to the following Poisson distribution
This indicates that the mRNA distribution is completely determined by a single parameter (transcription rate), independent of promoter structure. This property has the following implication: if transcription rates are not exactly the same, the corresponding mRNA distribution is definitely not a simple Poissonian one. In this case, deriving its analytical expression is challenging.
2.2. Conjugation
In order to address the above challenge, here we introduce the conception of conjugation. By conjugation we mean that for two gene models with the same transition pattern between promoter states (i.e., both have the same transition rate matrix W), denoted by Model A and Model B, if their transcription matrices take the specific forms: ΛA=diag((μ+ε)Ik,μIN−K) for Model A and ΛB=diag(μIK(μ+ε)IN−k) for Model B, where ε is a real number and may be equal to −μ, and K is a positive integer of less than N, next we call Model A conjugate to Model B or vice versa. Such conjugation is existent in natural or synthetic biological systems, e.g., for the example illustrated in Figure 1(A) (denoted by Model A), if states C, R, and N are active while states B and A are inactive, the resulting model becomes a conjugate model of Model A. The conjugation is useful in revealing relationships between complex mRNA distributions. In the following, for a system of gene expression with promoter states, let P(m;t)=(P1(m;t),⋯,PN(m;t))T and G(z;t)=(G1(z;t),⋯,GN(z;t))T be the column vectors consisting of factorial probabilities Pi(m;t) with 1≤i≤N and the corresponding factorial probability-generating functions Gi(z;t) with Gi(z;t)=∑m≥0Pi(m;t)zm and 1≤i≤N, respectively; let P(m;t)=∑Ni=1Pi(m;t) and G(z;t)=∑Ni=1Gi(z;t) represent the total probability and the corresponding total probability-generating function, respectively.
2.3. Distribution properties
The above CM approach can in principle give the exact mRNA distributions in gene models with arbitrary promoter structure, which however may be complex in form [25]. For example, for the common ON-OFF model of stochastic transcription, we know that the mRNA distribution is expressed by a complex confluent hypergeometric function [24]. To see that these reconstructed distributions belong to which types, we check the corresponding Fano factors defined as the ratio of variance over mean. This is because if the Fano factor is less than 1, the distribution is sub-Poissonian, if it is equal to 1, the distribution is Poissonian, and if it is greater than 1, the distribution is sup-Poissonian [45]. For clarity, we consider a specific case, that is, the promoter has one ON state and N−1 OFF states, which altogether form a loop (i.e., the so-called DNA loop [46]). In this case, we can show
where ⟨m⟩ represents the mean number of mRNA molecules and can be expressed as ⟨m⟩=μ⟨τon⟩/(⟨τon⟩+⟨τoff⟩) with μ being the transcription rate, and ⟨τon⟩ and ⟨τoff⟩ representing the mean times dwelling at ON and OFF states, respectively. We can prove that β(N)i≤αi for any i=1,2,⋯,N−1. Therefore, the term in the big bracket of (2.15) is larger than or equal to zero, implying that for stochastic gene transcription, the mRNA distribution is either sup-Poissonian or Poissonian, independent of promoter topology. Regarding conjugation between two systems of gene expression with the same number of promoter states, we have the following theorem.
Theorem 1 For two conjugate stochastic transcription Models A and B, if we let two pairs PA(m;μ), GA(z), and PB(m;μ), GB(z) represent the distributions and probability-generating functions
where s=z−1.
Proof Consider the following two models of stochastic transcription
Model A:
Model B:
Introduce probability-generating functions: GA(z;t)=∑m≥0P(m;t)zm, GB(z;t)=∑m≥0Q(m;t)zm. Then
Assume δ=δI with δ being a positive constant, and set s=z−1. Next, we have
where τ=δt, ˜W and ˜ΛA have been scaled by δ. Similarly, we can obtain
where ˜ΛB has been scaled by δ. Multiplying e−εs on both sides of (2.17) and noting that s is unrelated to τ yield
In other words, under the transformation GA=eεsFA, (2.17) is transformed into
which is similar to (2.18) in form, where ˜ΛA−εI=−˜ΛB is a constant matrix. Thus, according to the transformation GA=eμsFA and noting that −s∂/∂s=−(−s)∂/∂(−s), we know that the first equality in (2.16) holds. Furthermore, through the relationship P(m;t)=(1/m!)(∂mG/∂zm)|z=0, where P=∑Ni=1Pi and G=∑Ni=1Gi are respectively the total probability distribution and the total probability-generating function, it is not difficult to verify that the second equality in (2.16) also holds. To that end, the proof of Theorem 1 is completed.
From (2.16), we see that PA(m;μ) is actually a binomial convolution of PB(m;μ) and a Poisson distribution. We point out that by making use of the conjugation idea, one can find analytical distributions in complex gene models, e.g., the gene model with one OFF state and two ON states is difficult to solve but the gene model with two OFF state and one ON states is easy to solve. Using the conjugation idea, we can transform the question of solving the former into that of solving the later. To show this point clearly, here we consider a more general case. Assume that for some multi-state model of stochastic transcription, the steady-state equations for probability-generating functions are
where s=z−1, and parameter ε may take any value in the interval [−μ,μ]. This equation group seems difficult to solve since the corresponding gene model contains multiple nontrivial transcription exits. However, the following equation group
which corresponds to the gene model with one ON state and N−1 OFF states and hence is easy to solve [24]. Moreover, using the above CM approach, we can obtain the solution for the total generating function Fs=∑Ni=1Fi(s)
where nFn(a1,⋯,anb1,⋯,bn|;σ) is a confluent hypergeometric function [44]. Note that (2.20) and (2.21) are conjugate under the transformation Gi=eμsFi. Thus, we obtain the analytical expression for the total generating function Gs=∑Ni=1Gi(s)
Furthermore, using the relationship P(m)=Gm(0)/m!, we obtain analytical steady-state mRNA distribution in the underlying model of stochastic transcription, which is given by
Before concluding this section, we discuss the relationship between this hypergeometric type distribution and Poissonian distribution. In fact, if there is only one ON state without OFF state, the distribution is Poissonian. Also, if there is only one OFF state without ON state, the distribution is degenerative. Consider a promoter structure with K ON states and L OFF states. For slow promoter switch rates, one observes the characteristic distribution that results from the mixture of K Poissonian distributions and L degenerate distributions approximately. For fast promoter switch rates, the characteristic distribution is a Poissonian distributions with mean synthetic rate approximately. For moderate promoter switch rates, the characteristic distribution is very complicated hypergeometric type.
3.
Analysis of a gene model with any waiting-time distributions
3.1. Calculation of raw moments
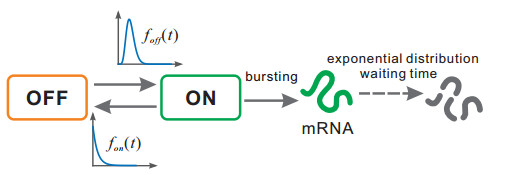
The extensively used two-state model of gene expression [37,47,48,49,50] assumes that gene promoter has two states: one active (ON) state and one inactive (OFF) state and two transition rates between these states are constants (implying that times that the gene dwells at ON and OFF states, i.e., ON and OFF times, follow exponential distributions). However, transcription depends on the chromatin template that accumulates over time until the promoter becomes active [24]. This implies that OFF times do not follow a simple exponential distribution but may be general [51]. Similarly, ON times may also follow a non-exponential distribution [20]. Some recent experimental papers [52,53] also showed non-exponential promoter switching times. In addition, the mRNA degradation may undergo a multistep process, implying that the distribution of mRNA's half lifetimes may be non-exponential. For such a gene model that one can find its prototypes in the real biological systems [16], there are few studies. Here, we apply standard results from the queuing theory [50,51,54,55] to analyze a state-waiting model of stochastic transcription with general waiting-time distributions fon(t), foff(t), and h(t), referring to Figure 2. A similar model was previously studied in [56]. Importantly, we derive explicit formulae for calculating the moment-generating function corresponding to the mRNA distribution, which can in turn be used for quantitative analysis of mRNA noise and even for reconstruction of the mRNA distribution. We point out that the gene model considered here can be viewed as an extension of the gene model considered above. In fact, for the later, we can show [25]
where W=(W00,W10W01,W11) is a block matrix, uK=(1,1,⋯,1) and uL=(1,1,⋯,1) are two row vectors. Here, W11 and W00 describe transitions among the ON states and among the OFF states respectively, whereas W10 and W01 describes how the ON states transition to the OFF states and vice versa respectively. Note that two functions fon(t) and foff(t) are in general the sums of exponential functions of t, implying that ON- or OFF-times follows a non-exponential distribution.
Assume that the synthesis rate of mRNA, μ, is a constant. Denote by P(m;t) the mRNA distribution at time t and by W(z;t) the corresponding moment-generating function with the initial condition denoted by Winit(z)=W(z;0). Unlike the case of common gene models where waiting-time distributions are exponential, we in general cannot establish the master equation for P(m;t) in the case of general waiting-time distributions fon(t), foff(t), and h(t), since the corresponding processes are non-Markovian. Therefore, we will turn to consider moments of P(m;t), and apply queuing theory to establish integral equations for moment-generating functions.
First, we establish the following proposition.
Proposition 2 Let h(t) be the survival probability density function and H(t)=∫∞th(τ)dτ be the survival function of mRNA. We have
Proof In order to prove (3.2), we need to make assumptions: (Ⅰ) there are N mRNAs produced at time t=0. In general, N itself is a random variable, and every mRNA Xi (1≤i≤N) at time t is also a stochastic variable, taking the value of either 1 (representing survival) or 0 (representing death); (Ⅱ) every Xi is independent of random variable N (this assumption seems reasonable from the viewpoint of biology); (Ⅲ) all the stochastic variables Xi (1≤i≤N) are independent of one another, each following a Bernoulli distribution with the moment-generating function given by M(z)=1+H(t)(ez−1) [20,50,54].
Note that the total molecule number of mRNA at time t, given by S=X1+⋯+XN, is a random variable. By the definition of moment-generating function, we know W(z;t)=⟨ezS⟩S. Also note that the mean ⟨ezS⟩S can be expressed as ⟨ezS⟩S=⟨⟨ez(X1+⋯+XN)|N⟩X⟩N. The above assumption (Ⅲ) implies ⟨⟨ez(X1+⋯+XN)|N⟩X⟩N=⟨⟨ezX1|N⟩X⋯⟨ezXN|N⟩X⟩N. Again by the definition of moment-generating function, we have ⟨ezXi|N⟩Xi=M(z) with 1≤i≤N and the above assumption (Ⅱ) yields ⟨ezXi|N⟩Xi=⟨(M(z))N⟩N=⟨eNlog(M(z))⟩N. According to the meaning of Winit(z), we know Winit(log(M(z))=⟨eNlog(M(z))⟩N. Substituting the known expression M(z)=1+S(t)(ez−1) into Winit(log(M(z)), we immediately obtain (3.2) and Proposition 2 is thus proved.
Next, we follow the standard derivation of the moment-generating function in queuing theory to derive an integral equation for Winit(z) [20,54], which is a key for calculating raw moments. For this, we give the following proposition.
Proposition 3 The initial moment function Winit(z) satisfies the following integral equation
where ρt=μ∫t0H(τ)dτ.
Proof Let time t=0 be the beginning of an OFF-state and W(z;t) be the moment-generating function of mRNA molecules at time t (0≤t≤ton+toff) as motioned above. The completion of one cycle (OFF- and ON state) define the boundary condition:
This equation in principle determines Winit(z) due to Winit(z)=W(z;0) if W(z;t) is known. However, the expression of W(z;t) seems difficult to derive. Here, we introduce another strategy to calculate Winit(z), which is based on specification of moment-generating functions during an OFF duration and an ON duration.
Given the distribution of mRNA life times, h(t), the probability that one mRNA molecule is still present after time Δt is a Bernoulli random variable with the moment-generating function given by 1+H(Δt)(ez−1) [50,51,54]. Starting with the moment-generating function W(z;0)=Winit(z) and considering only degradation of mRNAs, the compound moment-generating function at time Δt is given by
Therefore, at the end of an OFF-state (denoted by toff the corresponding time), the moment-generating function W(z;toff) should be equal to the integral of the initial moment-generating function Winit(log(1+H(s+t)(ez−1))) multiplied by the OFF-time distribution foff(t) over the infinite interval (0,∞), that is,
To that end, we have given the expression for the moment-generating function during an OFF duration.
Next, we derive the moment-generating function during an ON duration. During this period, degradation of the mRNA molecules that are present at the beginning of bursts continues as described through the function 1+H(t)(ez−1) with the moment-generating function given by, W(z;toff+μ)=Winit(log(1+H(μ+toff)(ez−1))), where μ represents a moment of the ON duration. Besides, mRNAs are also created and degraded according to a birth-death process with an exponential waiting time. This process can be described by a Poissonian distribution with the average ρμ=μ∫μ0H(τ)dτ (remark: if the mRNA synthesis rate is a constant μ and the survival probability density function of mRNA is h(t), this mRNA distribution is Poissonian [67]). Correspondingly, according to the definition, we know that the moment-generating function is given by Weffect(z;toff+μ)=eρμ(ez−1). The combination of the above two aspects produces an effective burst size. Note that during an ON duration, the probability distribution of the mRNA number should be the convolution of the distribution of the number of those molecules that are still present from previous bursts and the effective burst-size distribution, that is,
Then, W(z;toff+ton) is given by integrating W(z;toff+μ) over the infinite interval of μ∈(0,∞), i.e.,
which is just (3.3). Note that (3.8) can be rewritten as
which is actually (3.4). To that end, we have actually proven Proposition 3.
In general, solving the integral equation (3.3) is difficult since two functions fon(t) and foff(t) are arbitrary. However, we can use (3.3) to calculate moments of the mRNA distribution at time t=0. For example, by differentiating both sides of (3.3) at z=0, it is not difficult for us to derive the expression of the first-order initial raw moment
According to the definition of moment-generating function, we know that Winit(0)=1. Similarly, we can derive the expression of the second-order initial raw moment
Other higher-order initial raw moments can also be derived similarly. Detailed expressions are omitted due to complexity.
Now, we give explicit formulae for calculating raw moments of any order. Let F(s) and G(s) be the cumulative functions of the duration distributions at OFF and ON states, respectively. Next, we have Foff(t)=∫t0foff(s)ds and Fon(t)=∫t0fon(s)ds. According to definitions, the mean OFF and ON times are calculated according to
respectively. Note that the derivatives of W(z;toff+μ) at z=0 give the raw moments of the mRNA distribution at time t=toff+μ during an ON duration, denoted by ⟨mk⟩μ, whereas the derivatives of W(z;toff) at z=0 give the raw moments of the mRNA distribution at the end time t=toff of an OFF duration, denoted by ⟨mk⟩s. Then, the total moments of the mRNA copy number distribution should be the sum of the two parts obtained by averaging over all times according to their probabilities, that is,
where k=1,2,⋯,. In (3.13), we emphasize that ⟨mk⟩s is obtained by calculating the k-order derivative of function Winit(log(1+H(s)(ez−1))) at z=0 whereas ⟨mk⟩μ by calculating the k-order derivative of function ∫∞s=0Winit(log(1+H(s+μ)(ez−1)))eρμ(ez−1)foff(s)ds at z=0. We point out that although we have derived general formula for calculating raw moments, e.g., (3.13), the actual calculation would be complex even if waiting times follow exponential distributions, referring to Appendix C.
3.2. Reconstructing the mRNA distribution from its raw moments
As shown above, we can calculate raw moments of any orders. In spite of this, the common interest is in finding the corresponding distribution. Here, we consider the question of how the mRNA distribution is reconstructed from the raw moments obtained above. For the above model with general waiting-time distributions, it is easy to show that CMs of the steady-state mRNA distribution bk defined by (2.2) are linear combinations of raw moments that however have been given using the above method, e.g.,
More generally, we can give explicit relationships between convergent moments and common moments. For example, central moments (denoted by μk) can be expressed as
where R(k,i,j)=(−1)i(ki)S(k−i,j) and S(n,k) is the Stirling number of the second kind [65]. According to (3.15), we can in turn use central moments to express CMs (details are omitted here). In a word, all the CMs can be given if all the raw moments are given using the above method (but the related calculations would be complex. See the following content). Thus, according to (2.3), we can in principle reconstruct the mRNA distribution although waiting-time distributions may be general.
3.3. Compared with some known results: effect of non-Markovianity
As applications of the above general expressions, here we first give explicit formulae for the mRNA mean and the mRNA noise, which actually establish a relationship between the above two models through initial two moments. Here, we assume h(t)=δe−δt and δ represents the mean degradation rate of mRNA. Firstly, consider the mRNA mean. Calculations (see Appendix C) yield
This formula is well known for the common ON-OFF model [24]; [57] but here derived in a more general case (i.e., ON and OFF waiting times follow general distributions. In other words, the formula for the mRNA mean in the case of non-exponential waiting-time distributions is the same as in the case of exponential waiting-time distributions). Secondly, consider the mRNA noise. If the mRNA noise is defined as the ratio of the variance over the square of the mean, by complex calculations (see an example in Appendix C), we can derive
where Loff(s) and Lon(s) are the Laplace transforms of functions foff(t) and fon(t), respectively. In (3.18), the first term represents the factorial noise due to the birth and death of mRNA whereas the second term represents the factorial noise due to switching between two promoter states. In particular, if two transition rates between ON and OFF states are constants, implying that ON and OFF waiting-time distributions are exponential, (3.17) is reduced to the following known form [24,58]
Therefore, (3.16) and (3.17) are the extensions of the mRNA mean and the mRNA noise in the common two-state model of stochastic transcription. In addition, if we consider a model of stochastic transcription where the promoter is assumed to have one ON state and multiple OFF states, which altogether form a loop, (3.16) and (3.18) still hold although the OFF times follow an non-exponential distribution (implying non-Markovianity) [24].
Next, we show that in the limit of fast switching, the mRNA distribution can become Poissonian irrespective of the distribution of mRNA life times, . In fact, in the limit of fast switching, the second term on the right-hand-side of (3.17), which describes the promoter noise, approximates zero. Thus, the resulting mRNA noise can be approximated as η2m≈1⟨m⟩, implying that the mRNA number approximately follows a Poissonian distribution independent of the distribution of mRNA life times. Interestingly, the author [55] recently gave intuitive interpretations for Poisson steady-state distribution of the mRNA number.
In order to show effects of non-Markovianity on the mRNA mean and the mRNA noise, we consider that ON- and OFF-times follow Erland distributions:
where kon and koff describe the shapes of the distributions and take integers; θon and θoff are two parameters and take positive real numbers. Note that if kon=1 (or koff=1), the only one ON (or OFF) state is considered, corresponding to the case of exponential distribution (Markovian). By simple calculations, we can show
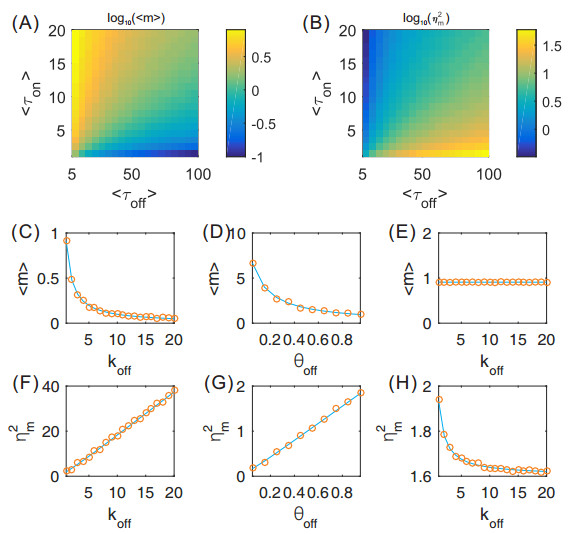
The numerical results are shown in Figure 3, which shows effects of non-Markovianity on the mRNA mean and the mRNA noise. Specifically, for the same mean ON and OFF times, a larger mRNA mean corresponds to a smaller mRNA noise (Figure 3(A, B)); the mRNA mean is a monotonically decreasing function of koff=1 (in a nonlinear manner. See Figure 3(C, D)) whereas the mRNA noise intensity is a monotonically increasing function of koff=1 (in an approximately linear manner. See Figure 3(F, G)). Figure 3(E, H) shows that if the mean mRNA is fixed, the mRNA noise is a monotonically decreasing function of koff=1, implying that non-Markovianity can reduce the mRNA noise.
Finally, we point out that at first glance, there is a big difference between the two models, but there is a close relationship between them. First, if the only first two moments are considered, the model analyzed in section 3 above (i.e., the queuing model) can be viewed as an extension of the model analyzed in section 2 above (i.e., the promoter model). In fact, (3.1) implies that the distributions of ON- and OFF-times in the promoter model are the algebraic sum of exponential functions but those of ON- and OFF-times in the queuing model may be more general distributions. Second, the mRNA mean is given by the same formula (3.16) for both models, and the formula for the mRNA noise in the queuing model, given by (3.17), is an extension of that for the mRNA noise in the promoter model, given by (3.18). Third, for both models, we can reconstruct the mRNA distribution from the respective CMs that are given by (2.5) for the promoter model or by the method given in the above subsection 3.2 for the queuing model. In addition, we can show that in the limit of fast switching, the mRNA distribution becomes Poissonian for both models. In fact, for the promoter model, this point is easily verified as for the common ON-OFF model. For the queuing model, the second term on the right-hand-side of (3.14) will disappear in the limit of fast switching. Some related discussions were done in [55].
4.
Parametric regions for robust unimodality and bimodality
As a mechanism contributing to phenotypic diversity, bimodality of gene expression can enhance the survival of cells in a fluctuating environment. However, an unsolved question is how unimodality or bimodality appears or disappears. Here we address this question.
Although we have given analytical expressions of mRNA distributions in the previous sections, they are in general complex in form. On the other hand, a proper cellular phenotype characterized by the shape of some distribution is important for the cell to enhance the survival of cells in a fluctuating environment [33]. Thus, we naturally consider a question of how unimodal and bimodal expressions are robustly formed or how reaction rate parameters impact unimodal and bimodal regions. This nontrivial issue seems to have not been studied previously. Here we will address the issue by theoretical analysis combined with numerical simulation. The aim of this section is twofold: the one is to better help the reader understand the given-above complex distributions, and the other is to lay a theoretical foundation for finding parametric regions for unimodality and bimodality. We point out that biologically, if a unimodal distribution is wide enough, it can work as well as bimodal distribution in driving phenotypic heterogeneity [59].
For clarity, we will consider two cases separately. The following analysis is tedious, and the theoretical results are established based on properties of complex confluent hypergeometric functions.
4.1. Case of two-state gene model
Here, we consider and analyze a representative model of stochastic transcription. Assume that the gene promoter has one ON state and one OFF state (implying N=2 in the above general model). For convenience, denote by λ the transition rate from ON to OFF state whereas by γ the transition rate from OFF to ON state and by μ the transcription rate of mRNA, and set the mRNA degradation rate as δ=1 (this is equivalent to the normalization of three parameters μ, λ and γ by δ). According to the above analysis, the corresponding mRNA distribution can be expressed as
Note that μ>1 always holds since μ represents the transcription rate normalized by the degradation rate. We distinguish two cases to give theoretical results on unimodal and bimodal mRNA distributions: (A) P(1)>P(0); (B) P(1)<P(0).
Theorem 2 P(1)>P(0). For any μ>1,λ>0 and γ>0, there is an integer m0>0 such that P(m+1)−P(m)>0 for 0≤m≤m0 whereas P(m+1)−P(m)≤0 for m>m0. In this case, P(m) is unimodal.
Proof Using the integral expression of hypergeometric function
we can rewrite Eq (4.1) as
Thus,
implying that P(m+1)−P(m)<0 for any m>˜m=μ−1>0. On the other hand, we have P(1)−P(0)>0. Therefore, if we set m0=min{m|P(m+1)−P(m)<0,m>˜m}, then we know that P(m+1)−P(m)≥0 for 0≤m≤m0 whereas P(m+1)−P(m)<0 for m>m0. This finished the proof of theorem 2.
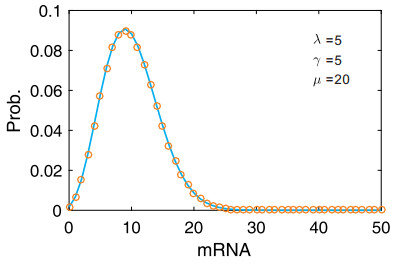
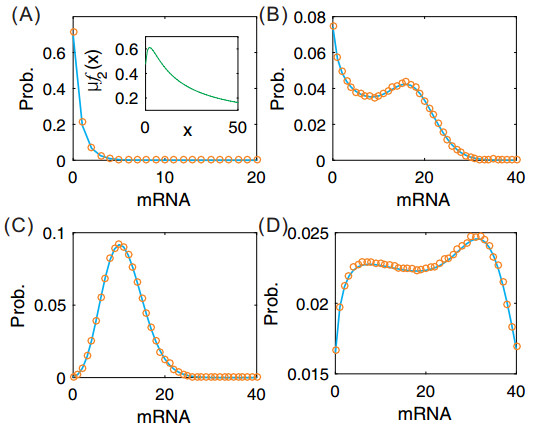
The reader can refer to the numerical result in Figure 4, where a representative mode of mRNA distribution is shown. This figure verifies that our theoretical prediction is in accordance with the numerical result.
Theorem 3 For the case of P(1)<P(0), we have: (1) If λ≥1 and μλ≤λ+γ, or if λ<1 and μ≤min(γ+1−λ+2√(1−λ)γ,1+γ/λ), P(m) is unimodal; (2) If μ≥λ+γ+2 and 2(γ+1−2λ)μ≤(λ+γ−1)2−1, P(m) is bimodal.
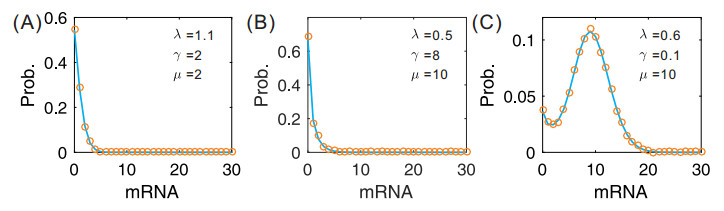
The proof of this theorem is put on Appendix E. Here we show numerical results, referring to Figure 5.
4.2. Case of multiple-state gene model
Here, we only analyze a simple case: the promoter has one active state and two inactive states. Denote by λ2 and λ′2 the transition rates between two OFF states, by λ1 and γ1 the transition rates from one OFF state to ON state and from ON state to the OFF state respectively, and by λ2 and γ2 the transition rates from the other OFF state to ON state and from ON state to the OFF state, respectively. According to the previous analysis, we know that the mRNA number follows a hypergeometric following distribution given by
where
Note that all the parameters have been normalized by the degradation rate δ, and αi and βi, i=1,2, may be complex. In the following, we only consider they are real.
In order to find parametric regions for unimodality and bimodality, we introduce the following lemma.
Lemma 1 If b≥a and c≥d, then we have the Kummer-type transform of the form
Note that for any m, we have
where two confluent functions are given according to Eq (4.6). Using Lemma 2, it is not difficult to prove the following two lemmas.
Lemma 2 For any nonnegative integer m, then we have the inequality
Lemma 3 For any m, we have the following estimation
where ξ2=(1−μ4(m+α2))(1−μ4(m+β2)).
Similar to the case of the common two-state model, we may distinguish two cases to find parametric regions for unimodality and bimodality in a gene model with one active state and two inactive states. That is, we consider two cases separately: P(1)>P(0) and P(1)<P(0). The key equation to be solved is that under what conditions of reaction rates, the difference P(m+1)−P(m) is positive or negative. When one wants to estimate the sign of this difference, the above three lemmas are useful.
By analysis, one is able to know that P(m) is unimodal under some conditions of reaction rates whereas it is bimodal under other conditions of reaction rates. For example, we can rigorously prove the following result: For P(1)<P(0), if μβ1β2<α1α2 and μf2(˜x)≤1 are simultaneously satisfied, where f2(x)=[(β1+x)(β2+x)]/[(x+1)(α1+x)(α2+x)] and ˜x is the extreme point of f2(x), P(m) is unimodal. In fact, first note that μβ1β2<α1α2 can guarantee P(1)<P(0) due to Eq (4.8). Second, for function f2(x), we know by calculation that there is a ˜x such that f2(x) reaches its maximum at x=˜x, referring to the inset of Figure 6(A). Apparently, if μf2(˜x)≤1, P(m+1)<P(m) for all m, indicating that P(m) monotonically decreases with regard to m. Therefore, P(m) is unimodal. The numerical simulation has verified the correctness of our analysis, referring to Figure 6(A).
5.
Conclusion and discussion
Transcription is a core process in life, but how upstream promoter kinetics affects downstream transcription dynamics remains to be not fully understood. Here, we have analyzed two representative yet general models of stochastic transcription. For the queuing model of transcription with general waiting-time distributions, we have derived a general formula for calculating raw moments of any order. In turn we have proposed an efficient method–the CM method, to reconstruct the mRNA distribution, where CMs are actually linear combinations of raw moments but the former has better properties than the latter, e.g., CMs converge to zero as their orders tend to infinity. For the multistate model of transcription with arbitrarily complex promoter structure, we have derived exact steady-state mRNA distributions, which are expressed by generalized confluent hypergeometric functions. Moreover, we have found that there are conjugate relationships among these complex distributions. For both models, we have shown that the mRNA distribution is in general sup-Poissonian. In addition, we have analyzed robust regions for unimodality and bimodality for two specific yet representative models. By combining numerical simulation, we have found parametric regions for how unimodal and bimodal expressions are robustly shaped. Importantly, our analysis methods and results can save time for investigate gene expression behavior than numerical simulations. Our analysis lays a foundation for quantitative analysis of stochastic gene transcription whereas our results would be helpful for designing biologically robust gene regulatory circuits.
Although our analyzed models of stochastic transcription are general, i.e., they include many previously-studied models as their particular cases, we still neglect some other processes underlying transcription, such as alternative splicing [35], DNA methylation [18], RNA nuclear retention [61], cell division [62], negative feedback [19,32] and spatial heterogeneity [63,64]. These processes or factors can also impact the transcription level or transcription efficiency, but how this impact is mathematically analyzed and how exact analytical results are derived would need to develop new mathematical models and new analytical methods. In particular, when extracellular dynamic and stochastic regulatory signals are considered, the theoretical or numerical analysis would be challenging since the corresponding chemical master equation will become a non-Markovian system in this case. In addition, we have given conservative parametric regions for robust unimodal and bimodal expressions by analyzing complex mRNA distributions in two simple models of stochastic transcription, but a gene model with multiple active states may exhibit various modes of distribution, including unimodality, bimodality and multimodality [25]. Theoretically proving this point or giving exact parametric regions for multimodality seems difficult.
We point out that our first model of stochastic transcription belongs to the so-called GIX/G/∞ system in queueing theory [50,54]. Using this theory, one can also derive formulae for calculating raw moments in a gene model of stochastic transcription where the mRNA lifetime follows a general distribution rather than an exponential distribution considered here, besides that ON and OFF times follow general distributions. In addition, we point out that it looks like a big difference between the two gene models studied above, but we can establish the relationship between them by calculating the mRNA noise. This is because that (3.16) always holds for both models. These models are all convergent, referring to some discussions in [66], and the corresponding mRNA distributions exhibit discontinuities [68], which can easily be verified from the expressions of the distributions reconstructed from our CMs.
Until now, the study of stochastic transcription focuses on the following two classes of models: (1) The first class is the so-called promoter models where the promoter has arbitrary activity states (either ON or OFF) and there are random transitions among these states, e.g., the model studied in this paper or referring to Figure 7(A); (2) The second class is the so-called queuing models, where the waiting times, e.g., from OFF to ON states, from ON to OFF states, from DNA to mRNA, or for a multistep process of mRNA degradation, follow a distribution. Note that this class of models can further be classified as more specified models by considering combinations of the mentioned cases, e.g., the state-waiting model in Figure 7(B) and the transcription-waiting model in Figure 7(C). These two classes of models were partially studied [25,56,66,68]) and some interesting results were also obtained [25,52,53,56,66,68]. In principle, our queuing model studied in this paper includes the queuing models in the existing literature as its special cases, and our results obtained in the paper can partially reproduce some previous results, at least those for the first two moments obtained under the same assumed conditions. Although we have established partial connections between the two classes of models, deeper connections are worth further study.
Finally, it is worth mentioning that the CM method that we simply introduced here would have broad applications in modeling, analysis and simulation of biochemical reaction networks including complex gene regulatory networks. In fact, apart from two remarkable advantages mentioned in this paper, i.e., CMs tend to zero as their orders go to infinity; CMs can be used to reconstruct the corresponding distribution, there are other advantages, e.g., according to the definition of CMs, we can derive the time evolution equations for CMs based on the chemical master equation, which are a linear equation group with constant coefficients. Thus, one can use CM equations to study how upstream promoter dynamics affect downstream expression dynamics, and may reveal dynamical mechanisms behind it, which would be difficult by directly analyzing the chemical master equation.
Acknowledgments
This work was partially supported by Grant Nos. 91530320, 91230204, 2014CB964703, 11475273, and 11631005.
Conflict of interest
The authors declare there is no conflict of interest.
Appendix
A. Derivation of (2.4) in the main text
Let b(i)k be the convergent moments corresponding to the factorial distribution Pi. According to the CM definition, we have
Note that (1) in the main text is expressed in the component as
Also note that for any fixed i:1≤i≤N, we have
Therefore, the summing over all the possible m being greater than or equal to k in (A1) yields
Assume that all the degradation rates are equal and denote by δ the common degradation rate. Using δ to normalize all the parameters and setting τ=δt, we can obtain
where bk=(b(1)k(t),b(2)k(t),⋯,b(N)k(t))T is a column vector. (A2) is just (4) in the main text.
B. Details for the proof of proposition 1 in the main text
At steady state, it follows from (4) in the main text or (A2) that
Note that the W matrix describing the promoter structure is an M-matrix (i.e., the sum of elements in every row is equal to zero, implying that the determinant of W is equal to zero, or det(W)=0). Therefore, (kI−W) is a reversible matrix with the inverse given by (kI−W)−1=1det(kI−W)(kI−W)∗ in which (iI−W)∗ and det(iI−W) are the adjacency matrix and the determinant of matrix (iI−W), respectively. Left multiplying (kI−W)−1 on both sides of (B1) yields
from which we have
If we denote by uN=(1,1,⋯,1) a N-dimensional row vector, uNbk=∑Ni=1b(i)k=bk holds. Left multiplying uN on both sides of (B3) yields
where b0=(b(1)0,b(2)0,⋯,b(N)0)T is a column vector.
Next, we derive the expressions of b(i)0(1≤i≤N). The results are
where −α1,−α2,⋯,−αN−1 are nonzero characteristic values of matrix W whereas −β(j)1,−β(j)2,⋯,−β(j)N−1 are those of Wj, the minor matrix of W after crossing out the jth row and jth column of the entry λij of W. In fact, det(W)=0 implies WW∗=det(W)I=0. As a direct consequence of Laplace's formula for the determinant of matrix W, we have
where
since −β(j)1,−β(j)2,⋯,−β(j)N−1 are the characteristic values of matrix Wj. Note that the null space of W is one-dimensional due to rank(W)=N−1, and that (B1) still holds for k=0 (i.e., Wb0=0). Therefore, from the combination of (B6) and Wb0=0, we can express b0 as
where c is a constant. Also note that b(i)0(t)=∑m≥0Pi(m;t) according to the CM definition and ∑Ni=1∑m≥0Pi(m;t)≡1 for any t≥0 due to the conservative condition of the total probability. Therefore, we have the constraint condition uNb0=1, which in combination with (B8) gives
If we denote by fw(x)=det(xIN−W)=x(x+α1)⋯(x+αN−1) the characteristic polynomial of matrix W, it is easy to show that
On the other hand, Jacobi's formula gives
where "tr" represents the matrix trace. The combination of (B10) and (B11) gives the equality
Thus, we have the relationship
due to (B7).In addition, note that c=(−1)N−1∏N−1i=1αi due to c=1∑Nk=1det(Wk), and b(k)0=c⋅det(Wk) due to b0=c(det(W1)⋮det(WN)), as well as det(Wk)=(−1)N−1∏N−1i=1β(k)i due to the fact that −β(k)i(1≤i≤N)are the characteristics of matrix Wk. Therefore, we have
To that end, the proof of Proposition 1 in the main text is finished.
C. Derivation of (3.16) and (3.17) in the main text
For clarity, here we consider only the case of constant degradation rate (δ). First, we derive the analytical expression for the mRNA mean. According to (33), (34) and ρu=μδ(1−e−δu)as well as definitions in the main text, we can respectively show
Substituting these expressions into (36) in the main text yields
where
Therefore, we have
This gives the analytical expression for the mean mRNA in the case that the on-state and off-state lifetimes follow general distributions, i.e., (3.16) in the main text.
Next, we derive the analytical expression for the mRNA noise intensity. The key is to give the second-order moment (m2). Note that
Simple calculation yields
Using (C1) and according to the noise definition, we can obtain the analytical expression for the mRNA noise intensity
D. Queuing model simulation algorithm
In the queuing model of stochastic transcription, we assume that the synthesis rate and degradation rate of mRNA are μ and δ respectively. And the times that the gene dwells at ON and OFF states are assumed to follow general distributions fon(t) and foff(t) respectively. Let g(t) be gene state and m(t) be the mRNA number in the cell at time t. If the gene dwells at ON state, g(t)=1, ortherwise g(t)=0. We propose the following stochastic simulation algorithm to obtain exact numerical realizations of the mRNA synthesis and degradation process m(t).
0. Initialize the time t=t0 and the system's state m(t)=m0.
1.if g(t)=1
generate a waiting time τon according to probability fon(t)
set τendon=t+τon
repeat
update the mRNA's state m(t) and based on Gillespie simulation algorithm[60] for reactions
∅→mRNA and mRNA→∅ whose reaction propensity functions are given by a1(m(t))=μ
and a2(m(t))=δm(t) respectively
until t≥τ end on
set g(t)=0
else
generate a waiting time τ off according to probability foff(t)
set τ eff off =t+τ off
repeat
update the mRNA's state m(t) and based on Gillespie simulation algorithm[60] for reaction
mRNA→∅ whose reaction propensity function is given by a2(m(t))=δm(t)
until t≥τ end off
set g(t)=1
end
2. Record trajectories (t,g(t),m(t)) as desired. Return to Step 1, or else end the simulation.
3. After discarding the early part of the trajectories (the burn-in phase), the remaining realizations are used to estimate the steady-state probability distribution and the related statistics.
E. Proof of Theorem 3 in the main text
Note that for any m, we have
and
For clarity, we distinguish the following three cases.
First, if μλ≤λ+γ,μ(λ+m)≤(m+1)(λ+γ+m) holds for m=0, implying that P(1)<P(0) is guaranteed.
Second, note that if λ≥1, the function f1(x)=μ(λ+x)(x+1)(λ+γ+x) has no extreme value with regard to, implying that it is monotonically decreasing. Therefore, the inequality u(λ+m)≤(m+1)(λ+γ+m) holds for all in this case. Thus, if λ≥1 and μλ≤λ+γ, P(m) is unimodal.
Third, if λ<1, the function f1(x) reaches its maximum at the unique point ˜x=−λ+√γ(1−λ). Furthermore, If u(λ+˜x)≤(˜x+1)(λ+γ+˜x), f1(˜x)≤1, implying that P(m+1)<P(m) holds for all. Therefore, P(m) is also unimodal in this case. However, μ(λ+˜x)≤(˜x+1)(λ+γ+˜x) is equivalent to (μ+λ−γ−1)√(1−λ)γ≤2(1−λ)γ, which is further equivalent to μ≤γ+1−λ+2√(1−λ)γ. Thus, we know that if two inequalities λ<1 and μ≤min(γ+1−λ+2√(1−λ)γ,1+γ/λ) are simultaneously satisfied, P(m) is unimodal, referring to Figure 4(A) and (B) in the main text.
Now, we turn to considering bimodality. It is not difficult to establish the inequality
for any m, where ξ1=1−μ(√λ+m+√λ+m+1)2. According to the expression of P(m)=Γ(λ+m)e−μμmm!Γ(λ+γ+m)Γ(λ+γ)Γ(λ)1F1(γ,λ+γ+m;μ), we have P(m+1)P(m)>ξ2(λ+m)μ(m+1)(λ+γ+m), where ξ2=1−μ4(λ+m). Thus, in order to ensure that P(m) is bimodal, we only need to find a m1>1 such that (1−μ4(λ+m1))(λ+m1)μ(m1+1)(λ+γ+m1)>1. However, this inequality can be rewritten as
Therefore, if μ≥λ+γ+2 and (μ−λ−γ−1)2≥μ2−4λμ+4(λ+γ) (the latter is equivalent to 2(γ+1−2λ)μ≤(λ+γ−1)2)) are simultaneously satisfied, we know that there is at least one such that









 DownLoad:
DownLoad: