1.
Introduction
Energy supplier selection (ESS) is necessary for contemporary energy management and acquisition. The selection of an energy supplier may have significant ramifications, impacting both the financial aspects of energy consumption and the preservation of the environment. ESS ensures energy distribution aligns with environmentally conscious and environmentally friendly standards. Choosing the right energy supplier can maximize energy availability, minimize harmful emissions, and support a green and sustainable way to generate energy. During a time dominated by growing environmental concerns and the shift toward renewable energy alternatives, the precise and intelligent selection of energy distributors remains crucial for companies and people-oriented to healthier and more environmentally conscious energy choices. In actual situations, determining an object's connection entails a complicated and unexpected procedure. Zadeh [1] proposed the fuzzy sets (FS), a tool for merging contradictory and uncertain data. Turksen [2] extended the interval-valued fuzzy sets (IVFS), where membership values are in intervals than single numbers. The technique performs an adequate task of capturing the unpredictable nature of complicated systems. IVFS is essential in fuzzy influencing, enabling precise decision-making in complex and uncertain situations. Even so, when assessing decision-making that involves non-membership degrees (NMD), conventional FS and IVFS have certain limitations. Atanassov [3] developed the theory of intuitionistic fuzzy sets (IFS) with a complex structure to tackle these deficiencies. Atanassov [4] upgraded this technique by integrating interval-valued intuitionistic fuzzy sets (IVIFS) into IFS.
Yager [5] introduced the Pythagorean fuzzy set (PFS) as a potential elimination of the shortcomings that exist in fuzzy set (FS) models arising from inaccurate and unreliable facts by enhancing the fundamental criterion T+J≤1 and reformulated it as T2+J2≤1. Peng and Yang [6] expanded the PFS to encompass interval-valued Pythagorean fuzzy sets (IVPFS). This integration provided insight into the Pythagorean fuzzy sets (PFS) foundation. Yager [7] presented the concept of q-rung orthopair fuzzy sets (q-ROFS) and examined fundamental operations and properties of the framework by amending the condition T2+J2≤1 to Tq+Jq≤1, where q>2. Joshi et al. [8] put forward the interval-valued q-rung orthopair fuzzy sets (IVq-ROFS) by revising the specifications from (Tu)2+(Ju)2≤1 to (Tu)q+(Ju)q≤1, where q>2. While substantial advancements are anticipated, parametric chemistry remains challenged by issues related to irregularities and reliability. The complex interaction between variability and obscurity in parametric chemistry sometimes involves inconsistencies, deception, or impartiality, requiring the development of novel mathematical concepts and methodologies. The soft set (SS), designed by Molodtsov [9], facilitates the management of perplexing or ambiguous matters. Khizar et al. [10,11] introduced the type 2 soft sets with fundamental operations and bipolar soft sets in the union of two isomorphic hemi-rings. Jiang et al. [12] introduced a modification known as interval-valued IFSS (IVIFSS) to address inconsistencies and confusion in decision-making (DM) problems by offering essential protocols. As mentioned, the approach considers choice and non-preference information, leading to a more comprehensive assessment of alternatives. The Pythagorean fuzzy soft set (PFSS) is designed to address the ongoing examination of intellectual items. Peng et al. [13] created PFSS by combining PFS and SS, which have advantageous characteristics. Zulqarnain et al. [14] developed aggregation operations for interval-valued Pythagorean fuzzy soft sets (IVPFSS) and proposed a multi-attribute group decision-making (MAGDM) method.
Hussain et al. [15] developed weighted average aggregation operators in q-ROFSS, which is a prominent execution of PFSS. Yang et al. [16] developed the q-ROFSS methodology to IVq-ROFSS by including basic calculations and creating AOs and interaction AOs that utilize specific mathematical methods. Soft set (SS) structures are beneficial in decision-making (DM) problems due to their essential nature and reliance on a single parameter for evaluation. However, there are instances where it may be required to divide parameters into more specialized subcategories. One can incorporate many sub-parameters into the DM method by utilizing hypersoft sets (HSS) [17]. While SS frameworks may suit specific situations, they cannot discern between separate elements. To obtain precise outcomes, it is crucial to regard parameters as sub-parameters in various decision-making scenarios. Different strategies can be applied to handle difficult situations, each with its decision-making methods. Debnath [18] introduced fundamental procedures for the interval-valued intuitionistic fuzzy hypersoft set (IVIFHSS) to address MCDM challenges. Zulqarnain et al. [19] transformed the notion of intuitionistic fuzzy hypersoft sets (IFHSS) to Pythagorean fuzzy hypersoft sets (PFHSS). They also applied a multi-criteria decision-making (MCDM) approach to strengthen the aggregation operators (AOs) in the interval-valued Pythagorean fuzzy hypersoft set (IVPFHSS) [20]. Khan et al. [21] developed algebraic operational rules for q-ROFHSS, extending the existing operational laws. Zulqarnain et al. [22] enhanced Einstein's operational rules for q-ROFHSS by merging Einstein AOs with DM methods.
The need to address scenarios in which decision-makers fail and alternatively provide multiple values for every factor prompted the alteration of q-ROFHSS to its interval form. Zulqarnain et al. [22] produced q-ROFHSS and exploited their Einstein AOs to tackle this problem. A new multiple attribute decision-making (MADM) method emerged utilizing these operators to evaluate the Bitcoin trade. The IVq-ROFHSS method delivers a more precise representation of unpredictability and imprecision in decision-making procedures and a comprehensive grasp of their operational principles. The integration of IVq-ROFHSS will enhance the reliability and pragmatism of decision-making by adeptly addressing inconsistencies and imprecisions encountered in real-world scenarios.
Multiple necessary investigation inquiries will be evaluated to accomplish the specified objectives: What is the methodology for formulating the operational laws for Einstein aggregation in IVq-ROFHSS? Can Einstein aggregation operators effectively employ IVq-ROFHSS datasets to establish a reliable multi-attribute group decision-making (MAGDM) technique? How does the proposed technique compare with conventional approaches for accuracy, sensitivity, and practicality for various decision-making categories? To what extent does the execution of the suggested methodology improve experts' capacity to assess and rank alternatives, especially regarding the lack of clarity and fluctuation ingrained in IVq-ROFHSS data?
1.1. Motivation
A precise application of interval-valued q-rung orthopair fuzzy hypersoft sets is essential for decision-making under insufficient knowledge and inconsistency. The IVq-ROFHSS amalgamates the attributes of HSS and interval-valued q-rung orthopair fuzzy sets (IVq-ROFS), providing a robust framework for addressing ambiguity, inconsistencies, and inadequate data. IVq-ROFHSS has achieved notable advancements in tackling decision-making difficulties in ambiguous circumstances. While AOs are crucial in addressing DM problems, there is a scarcity of research that examines HSS and IVq-ROFS. The lack of study in the field suggests that the existing IVIFHSS [18] may encounter difficulties when the condition MDu+NMDu>1. IVPFHSS [20] can face challenges when evaluating a mixture of IVq-ROFHSNs or deliberately including them in situations where (MDu)2+(NMDu)2>1.
Although the Einstein AOs created for q-ROFHSS can solve this problem [22], they are not adequately equipped to handle the complexities of managing multi-sub-parametric values inside different intervals. The fact that Einstein AOs cannot be compatible with aggregation schemes relying on operational principles is highly significant. Furthermore, the model's generated findings are constrained, and the underlying prejudice in presenting the various choices has not been corrected. Considering the constraints above, the specified limitations motivate developing a more robust approach that efficiently handles alternatives specified within interval expressions in parametric formulations.
1.2. The contribution of the study
We present a novel technique to address the difficulties in extracting data from the IVq-ROFSS, IVIFHSS, and IVPFHSS structures. This project aims to efficiently collect uncertain data by implementing Einstein aggregation operators in the IVq-ROFHSS framework. Incorporating these evaluation objectives into optimal methods enhances the decision-making capabilities of MAGDM processes concerning these factors. This method is a comprehensive statistical analysis that demonstrates its effectiveness. Moreover, the subsequent text clarifies the objectives that this research endeavors to accomplish.
(1) We present Einstein operations for interval-valued q-rung orthopair fuzzy hypersoft set, which allow for formulating and verifying Einstein AOs specifically designed for IVq-ROFHSS. These AOs are usually known as IVq-ROFHSEWA and IVq-ROFHSEWG. We delve into the essential characteristics of these groundbreaking operators, including idempotency, boundedness, monotonicity, homogeneity, and shift-invariance. It is important to note that substantial research suggests that Einstein AOs are specifically designed to reduce ambiguity in the formal abilities that impact the decision-making process.
(2) The IVq-ROFHSS Einstein AOs are used to construct a new MAGDM technique. There are essentially two stages to the systematic approach, and they are as follows:
Integrating and merging separate pieces of data using IVq-ROFHSS Einstein AOs is the beginning step. The next step is determining the most cost-effective option by scoring the IVq-ROFHSS structure. This method incorporates accepted decision-making principles and offers workable options for complex decision-making difficulties.
(3) This systematic strategy will be applied to select the most advantageous provider in sustainable energy management.
(4) A thorough examination of crucial decision-making strategies and approaches will demonstrate the validity and utility of this MAGDM method.
This study is segmented into seven distinct sections. In the first section, we illustrate the significance of incorporating unpredictability and partial information into decision-making processes and emphasizes the constraints of commonly utilized Einstein AOs in resolving decision-making challenges. In Section 2, we summarize the essential ideas and concepts that drive the organizational formation follow-up study. This summary serves as a basis for comprehending the complexities of decision-making issues and the necessity for a more dependable and precise approach. Additionally, we present the interval-valued q-rung orthopair fuzzy hypersoft set along with its corresponding scoring function in the same section. In Section 3, we outline the operational principles proposed by Einstein and introduces the IVq-ROFHSEWA operator and its fundamental characteristics. In Section 4, we also present the IVq-ROFHSEWG operator along with its respective features. In Section 5, we introduce a novel MAGDM approach that relies on Einstein's AOs. In Section 6, we present a quantitative study that shows how the suggested approach can be used to identify the most suitable provider for sustainable energy management. In Section 7, we conduct a comparison analysis to assess the feasibility of the proposed model by comparing it to existing approaches in terms of accuracy and reliability. We further elucidate the benefits of the proposed approach in this section.
1.3. Literature review
In this section, we comprehensively assess the pertinent works on supplier selection and Einstein AOs in various fuzzy architectures. We investigate the underlying causes and achievements associated with its topic.
1.3.1. Fuzzy MAGDM techniques in sustainable supplier selection
As mentioned, the MAGDM technique is a highly effective approach for handling the complexities and uncertainties involved in supplier selection. Several academic studies have developed multiple models that use fuzzy MAGDM methodologies to address the issues of selecting suppliers in different industries. Samantra et al. [23] employed the VIKOR technique with fuzzy logic to address the MAGDM problem of supplier selection. The researchers tackled exciting aspects of their study. Zhang et al. [24,25] extended the Takagi‐Sugeno and discrete switched models for supply chain networks in a fuzzy control system. Yu et al. [26] presented a new method for group decision-making to identify sustainable suppliers by incorporating the extended TOPSIS technique into an IVPFS. The aim was to capture the viewpoints of various decision-makers and integrate incomplete information. Zhang et al. [27,28] presented a robust strategy and fuzzy emergency model for supply chain systems subject to disruptions.
Gurmani et al. [29] developed a MAGDM method incorporating an interaction and feedback mechanism within a T-spherical fuzzy framework. The researchers implemented partitioned Bonferroni mean operators to blend expert evaluations in selecting emergency healthcare providers. Wang [30] presented a method for collective decision-making in the selection of sustainable vendors. The concept employs an improved additive ratio assessment method within the linguistic T-spherical fuzzy framework. Wu et al. [31] utilized a linguistic MAGDM approach to identify dependable vendors by integrating the DEMATEL and VIKOR methodologies. Diao and Zhang [32] proposed the decision tree technique to enhance the information gain rate. In their study, Wang et al. [33] examined the use of Hamy mean operators with IVq-ROFS. They developed a MAGDM model to demonstrate the supplier selection process in sustainable supply chain management (SCM). Ali et al. [34] extended the Aczel-Alsina AOs for intuitionistic fuzzy soft sets. In the PFSS context, Zulqarnain et al. [35,36] developed the technique for order of preference by similarity to the ideal solution (TOPSIS) technique and algebraic AOs and Einstein AOs. They aimed to ascertain the best supplier for green SCM. Zhang and Zhang [37] developed the fuzzy robust control to mitigate the bullwhip effect in the uncertain closed‐loop supply chain. Hussain et al. [38] devised the TOPSIS technique within an intricate fuzzy rough framework to identify the provider in sustainable energy management.
Despite numerous research studies addressing supplier selection, sustainable energy management has not proposed a MAGDM technique to identify the best sustainable supplier by negotiating the IVq-ROFHSS structures. This technique establishes a trustworthy evaluation of sustainable supplier selection using the weights of the qualities mentioned earlier.
1.3.2. Einstein aggregation operators for different MAGDM problems
Multiple attempts of AOs were created and utilized to accurately assess different situations, resulting in significant interest and importance in this area of research. Wang and Liu [39,40] proposed using Einstein AOs in IFS to address complex MAGDM issues. Liu et al. [41] examined the efficacy of Einstein averaging aggregation operators in dealing with problems in MAGDM using IVIFS. Furthermore, Wang and Liu [42] extended the use of Einstein geometric AOs to include IVIFS and devised a decision-making approach to address issues related to MAGDM. Garg [43] introduced Einstein AOs for PFS. Asif et al. [44] developed the Hamacher aggregation operators in the PFS structure and used their presented operators in MADM problems. Rehman et al. [45,46] expanded a decision-making methodology to address MAGDM challenges and introduced Einstein AOs for IVPFS. Deveci et al. [47] have introduced a decision-making method that utilizes Einstein averaging AOs within a q-ROFS structure. Xu [48] extended the Einstein operations in the IVq-ROFS and developed an MCDM technique for bike-sharing recycling suppliers. This method is employed to assess safe tactics for using electric scooters. Zulqarnain et al. [49] explained Einstein's operational rules for PFSS and proposed using Einstein AOs to tackle complex real-world problems. Zulqarnain et al. [50,51] introduced the Einstein AOs for q-ROFSS and their decision-making approaches. They also developed the Einstein aggregation operators for IVq-ROFSS [52].
Sunthrayuth et al. [53] extended the MCDM model using the Einstein weighted average operator in the PFHSS structure. Zulqarnain et al. [54] proposed the Einstein-weighted geometric operator in the PFHSS framework and established a decision-making model for the material selection. Sajid et al. [55] developed several basic operations for intuitionistic fuzzy hypersoft sets. Huang et al. [56] adopted the multi-attribute grey target decision technique, merging a veto function with a hesitation zone, which is shown and utilized in a supplier selection problem for official cars, providing a pragmatic and efficient decision-making methodology. Saqlain [57] evaluated the complicated nature of decision-making in sustainable hydrogen production facilities with unpredictability, employing Intuitionistic Hypersoft Sets. Hamid and Abid [58] constructed a decision support system integrating the FHSS with machine learning methods to optimize the mobile phone selection procedure.
After thoroughly analyzing the relevant works, there is a lack of research on implementing Einstein operations to generate creative operators using IVq-ROFHSS. Therefore, it is imperative to examine the execution of Einstein's operations using IVq-ROFHSS data. The operational principles outlined and elucidated for IVq-ROFHSS provide a more precise evaluation of apprehension and inconsistency in the decision-making process. Given the prevalence of interval data in various industries such as economics, banking, hospitals, and engineering, it is essential to have the ability to utilize IVq-ROFHSS for analytical purposes.
2.
Preliminaries
In this section, we review essential concepts such as SS, HSS, PFHSS, IVPFHSS, and q-ROFHSS. Furthermore, we present the interval-valued q-rung orthopair fuzzy hypersoft set with its score function and comparison laws.
Definition 2.1. [9] Let U and E be the universe of discourse and attributes, respectively. Let P(U) be the power set of U and A⊆E. A pair (F,A) is called a soft set over U; its mapping is expressed as follows:
Also, it can be defined as follows:
Definition 2.2. [10] Let U and E be a universe of discourse and set of attributes, respectively and F(U) be a power set of U. Let A ⊆ E, then (F,A) is a fuzzy soft set over U; its mapping can be stated as follows:
Definition 2.3. [17] Let U be a universe of discourse and P(U) be a power set of U and k = {k1, k2, k3, ..., kn}, (n ≥ 1) and Ki represented the set of attributes and their corresponding sub-attributes, such as Ki ∩ Kj = φ, where i ≠ j for each n ≥ 1 and i, j ϵ {1, 2, 3 … n}. Assume K1 × K2 × K3× … × Kn = ⃛A = {d1h×d2k×⋯×dnl} is a collection of sub-attributes, where 1 ≤ h ≤ α, 1 ≤ k ≤ β, and 1 ≤ l ≤ γ, and α, β, γ ∈ N. Then the pair (F, K1 × K2 × K3× … × Kn = (F, ⃛A) is known as a hypersoft set and is defined as follows:
It is also defined as
Definition 2.4. [21] Let U be a universe of discourse and P(U) be a power set of U and k = {k1, k2, k3, ..., kn}, (n ≥ 1) and Ki represented the set of attributes and their corresponding sub-attributes, such as Ki ∩ Kj = φ, where i ≠ j for each n ≥ 1 and i, j ϵ {1, 2, 3 … n}. Assume K1 × K2 × K3× … × Kn = ⃛A = {d1h×d2k×⋯×dnl} is a collection of sub-attributes, where 1 ≤ h ≤ α, 1 ≤ k ≤ β, and 1 ≤ l ≤ γ, and α, β, γ ∈ N. and q−ROFSU be a collection of all q-rung orthopair fuzzy subsets over U. Then, the pair (F, K1 × K2 × K3× … × Kn = (F, ⃛A) is known as q-ROFHSS and is defined as follows:
It is also defined as
(F, ⃛A)={(ˇd,F⃛A(ˇd)):ˇd∈⃛A,F⃛A(ˇd)∈PFSU∈[0,1]}, where F⃛A(ˇd) = {⟨δ,TF(ˇd)(δ),JF(ˇd)(δ)⟩:δ∈U}, where TF(ˇd)(δ) and JF(ˇd)(δ) signifies the MD and NMD values of the attributes:
A q-rung fuzzy hypersoft number (q-ROFHSN) can be stated as F = {(TF(ˇd)(δ),JF(ˇd)(δ))}, where 0 ≤(TF(ˇd)(δ))q + (JF(ˇd)(δ))q≤ 1.
Definition 2.5. [20] Let U be a universe of discourse and P(U) be a power set of U and k = {k1, k2, k3, ..., kn}, (n ≥ 1) and Ki represented the set of attributes and their corresponding sub-attributes, such as Ki ∩ Kj = φ, where i ≠ j for each n ≥ 1 and i, j ϵ {1, 2, 3 … n}. Assume K1 × K2 × K3× … × Kn = ⃛A = {d1h×d2k×⋯×dnl} is a collection of sub-attributes, where 1 ≤ h ≤ α, 1 ≤ k ≤ β, and 1 ≤ l ≤ γ, and α, β, γ ∈ N. and IVPFSU be a collection of all interval-valued Pythagorean fuzzy subsets over U. Then the pair (F, K1 × K2 × K3× … × Kn = (F, ⃛A) is known as an interval-valued Pythagorean fuzzy hypersoft set and is defined as follows:
It is also defined as (F, ⃛A) = {(ˇd,F⃛A(ˇd)):ˇd∈⃛A,F⃛A(ˇd)∈IVPFSU∈[0,1]}, where F⃛A(ˇd) = {⟨δ,TF(ˇd)(δ),JF(ˇd)(δ)⟩:δ∈U}, where TF(ˇd)(δ)=[Tlˇdij,Tuˇdij] and JF(ˇd)(δ)=[Jlˇdij,Juˇdij] signifies the MD and NMD intervals of the sub-attributes and satisfies the following conditions Tlˇdij,Tuˇdij, Jlˇdij,Juˇdij ∈[0,1], and 0 ≤ (Tuˇdij)2+(Juˇdij)2≤1.
If the inequality (Tuˇdij)q+(Juˇdij)q>1, for q>2, holds for a specific decision, then the IVIFHSS [18] and IVPFHSS [20] are insufficient for accurately representing this information. There are certain circumstances where the IVq-ROF and HSS combination is known as IVq-ROFHSS. With a more extensive structure than IVq-ROFSS, this hybrid structure is a modified form of IVIFHSS and IVPFHSS. Optimizing the precision and predictability of challenging data collections, the IVq-ROFHSS method permits detailed analysis of fuzziness and resistivity. Due to its proven capacity to enhance the precision and uniformity of our strategy's outcomes, the IVq-ROFHSS is a precious tool for mathematical analysis and decision-making.
Definition 2.6. Let U be a universe of discourse and P(U) be a power set of U and k = {k1, k2, k3, ..., kn}, (n ≥ 1) and Ki represented the set of attributes and their corresponding sub-attributes, such as Ki ∩ Kj = φ, where i ≠ j for each n ≥ 1 and i, j ϵ {1, 2, 3 … n}. Assume K1 × K2 × K3× … × Kn = ⃛A = {d1h×d2k×⋯×dnl} is a collection of sub-attributes, where 1 ≤ h ≤ α, 1 ≤ k ≤ β, and 1 ≤ l ≤ γ, and α, β, γ ∈ N. and IVq−ROFSU be a collection of all interval-valued q-rung orthopair fuzzy subsets over U. Then the pair (F, K1 × K2 × K3× … × Kn = (F, ⃛A) is known as an interval-valued q-rung orthopair fuzzy hypersoft set and is defined as follows:
It is also defined as (F, ⃛A) = {(ˇd,F⃛A(ˇd)):ˇd∈⃛A,F⃛A(ˇd)∈IVq−ROFSU∈[0,1]}, where F⃛A(ˇd) = {⟨δ,TF(ˇd)(δ),JF(ˇd)(δ)⟩:δ∈U}, where TF(ˇd)(δ)=[Tlˇdij,Tuˇdij] and JF(ˇd)(δ)=[Jlˇdij,Juˇdij] signifies the MD and NMD intervals of the sub-attributes and satisfies the following conditionsTlˇdij,Tuˇdij, Jlˇdij,Juˇdij ∈[0,1], and 0 ≤ (Tuˇdij)q+(Juˇdij)q≤1.
Remark 2.1.
1) If (Tuˇdij)q+(Juˇdij)q≤ 1 and (Tuˇdij)2+(Juˇdij)2≤ 1 both are held. Then, IVq-ROFHSS reduce to IVPFHSS [20].
2) If (Tuˇdij)q+(Juˇdij)q≤ 1 and Tuˇdij+Juˇdij≤ 1 both are held. Then, IVq-ROFHSS reduce to IVIFHSS [18].
The earlier score function is ineffective in determining the optimum selection when the MD and NMD ranges are identical. Thus, we establish a more rigorous score mechanism for IVq-ROFHSNs to tackle such problems.
Definition 2.7. Let Tˇdk=([Tlˇdk,Tuˇdk],[Jlˇdk,Juˇdk]) be an IVq-ROFHSN. Then, its score can be defined as:
where [πlˇdk,πuˇdk]q, S(Tˇdk)∈[−1,1] shows hesitancy and q>2. For readers' appropriateness, the IVq-ROFHSN can be presented as T(ˇdk)={([Tlˇdk,Tuˇdk],[Jlˇdk,Juˇdk])}.
Let Tˇd11 = (Tˇd11,Jˇd11) and Tˇd12 = (Tˇd12,Jˇd12) be two IVq-ROFHSNs. Then
If S(Tˇd11)>S(Tˇd12), then Tˇd11≽Tˇd12.
If S(Tˇd11)<S(Tˇd12), then Tˇd11≼Tˇd12.
If S(Tˇd11)=S(Tˇd12), then
If ℶJˇd11>ℶJˇd12, then Tˇd11<Tˇd12;
If ℶqJˇd11 = ℶqJˇd12, then Tˇd11=Tˇd12.
So, to equate two IVq-ROFHSNs Jˇdij and TˇdijThe subsequent comparison rules are demarcated.
1) If S(Jˇdij) > S(Tˇdij), then Jˇdij > Tˇdij.
2) If S(Jˇdij) = S(Tˇdij), then
o If H(Jˇdij) > H(Tˇdij), then Jˇdij > Tˇdij;
o If H(Jˇdij) = H(Tˇdij), then Jˇdij = Tˇdij.
The Einstein operational laws for IVq-ROFHSS are proposed in the subsequent section, drawing motivation from the Einstein operations of q-ROFHSS presented by Zulqarnain et al. [22].
3.
Einstein weighted average operators for interval-valued q-rung orthopair fuzzy hypersoft numbers
The following section requires the aggregation operators for the initial data collection stage. We are developing Einstein operational rules that aggregate and analyze IVq-ROFHSS data. The IVq-ROFHSWA operator is introduced and examined in this scenario.
3.1. Einstein operational laws for IVq-ROFHSNs
Definition 3.1. Let Tˇdk=([Tlˇdk,Tuˇdk],[Jlˇdk,Juˇdk]), Tˇd11=([Tlˇd11,Tuˇd11],[Jlˇd11,Juˇd11]), and Tˇdk=([Tlˇd12,Tuˇd12],[Jlˇd12,Juˇd12]) be three interval-valued q-rung orthopair fuzzy hypersoft numbers, and β>0. Then, the Einstein operational laws for IVq-ROFHSNs are defined as:
1) Tˇd11⊕εTˇd12=([q√(Tlˇd11)q+(Tlˇd12)qq√1+(Tlˇd11)q(Tlˇd12)q,q√(Tuˇd11)q+(Tuˇd12)qq√1+(Tuˇd11)q(Tuˇd12)q],[q√2(Jlˇd11)q(Jlˇd12)qq√1+(1−(Jlˇd11)q)(1−(Jlˇd12)q),q√2(Juˇd11)q(Juˇd12)qq√1+(1−(Juˇd11)q)(1−(Juˇd12)q)])
2) Tˇd11⊗εTˇd12=([q√2(Tlˇd11)q(Tlˇd12)qq√1+(1−(Tlˇd11)q)(1−(Tlˇd12)q),q√2(Tuˇd11)q(Tuˇd12)qq√1+(1−(Tuˇd11)q)(1−(Tuˇd12)q)],[q√(Jlˇd11)q+(Jlˇd12)qq√1+(Jlˇd11)q(Jlˇd12)q,q√(Juˇd11)q+(Juˇd12)qq√1+(Juˇd11)q(Juˇd12)q])
3) βTˇdk=([q√(1+(Tlˇdk)q)β−(1−(Tlˇdk)q)βq√(1+(Tlˇdk)q)β−(1−(Tlˇdk)q)β,q√(1+(Tuˇdk)q)β−(1−(Tuˇdk)q)βq√(1+(Tuˇdk)q)β−(1−(Tuˇdk)q)β],[q√2((Jlˇdk)q)βq√(2−(Jlˇdk)q)β+((Jlˇdk)q)β,q√2((Juˇdk)q)βq√(2−(Juˇdk)q)β+((Juˇdk)q)β])
4) Tβˇdk=([q√2((Tlˇdk)q)βq√(2−(Tlˇdk)q)β+((Tlˇdk)q)β,q√2((Tuˇdk)q)βq√(2−(Tuˇdk)q)β+((Tuˇdk)q)β],[q√(1+(Jlˇdk)q)β−(1−(Jlˇdk)q)βq√(1+(Jlˇdk)q)β−(1−(Jlˇdk)q)β,q√(1+(Juˇdk)q)β−(1−(Juˇdk)q)βq√(1+(Juˇdk)q)β−(1−(Juˇdk)q)β]).
We aim to use Einstein AOs designed explicitly for the IVq-ROFHSS context; nevertheless, this goal is contingent upon the previously mentioned Einstein operational laws. These operators systematically handle imprecise and unclear data within the framework of IVq-ROFHSS, strengthening the reliability of decision-making procedures. A rigorous evaluation of the proposed Einstein AOs will be carried out to ensure that these operators can address the unique challenges posed by the IVq-ROFHSS structure.
Definition 3.2. Let Tˇdij=([Tlˇdij,Tuˇdij],[Jlˇdij,Juˇdij]) be a collection of interval-valued q-rung orthopair fuzzy hypersoft numbers. Then, the interval-valued q-rung orthopair fuzzy hypersoft Einstein weighted average operator is defined as:
IVq-ROFHSEWA: Δn→Δ
where i=1,2,…….n and j=1,2,…….m. Also, Ωi and γj be the weights of experts and multi sub-attributes such as Ωi > 0, ∑ni=1Ωi = 1, γj > 0, ∑mj=1γj = 1.
Theorem 3.3. Tˇdij=([Tlˇdij,Tuˇdij],[Jlˇdij,Juˇdij]) be a collection of interval-valued q-rung orthopair fuzzy hypersoft numbers. Then, the obtained aggregation value is also an IVq-ROFHSN and
where i=1,2,…….n and j=1,2,…….m. Also, Ωi and γj be the weights of experts and multi sub-attributes such as Ωi > 0, ∑ni=1Ωi = 1, γj > 0, ∑mj=1γj = 1.
Proof. The above-stated theorem will be proved using mathematical induction.
For n=1, we get Ωi=1. Then,
For m=1, we get γj = 1. Then,
Equation (3.1) is satisfied for n=1 and m=1.
For n=2 and m=1
Let L1=((1+(Tlˇd11)q)Ω1)γ1; M1=((1−(Tlˇd11)q)Ω1)γ1; N1=((1+(Tuˇd11)q)Ω1)γ1; O1=((1−(Tuˇd11)q)Ω1)γ1; L2=((1+(Tlˇd21)q)Ω1)γ1; M2=((1−(Tlˇd21)q)Ω1)γ1; N2=((1+(Tuˇd21)q)Ω1)γ1; O2=((1−(Tuˇd21)q)Ω1)γ1; ~L1=(((Jlˇd11)q)Ω1)γ1; ~M1=((2−(Jlˇd11)q)Ω1)γ1; ~N1=(((Juˇd11)q)Ω1)γ1; ~O1=((2−(Juˇd11)q)Ω1)γ1; ~L2=(((Jlˇd21)q)Ω1)γ1; ~M2=((2−(Jlˇd21)q)Ω1)γ1; ~N2=(((Juˇd21)q)Ω1)γ1; ~O2=((2−(Juˇd21)q)Ω1)γ1. Then, γ1(Ω1Tˇd11)=([q√L1−M1q√L1+M1,q√N1−O1q√N1+O1],[q√2~L1q√~M1+~L1,q√2~N1q√~O1+~N1]) and γ1(Ω2Tˇd21)=([q√L2−M2q√L2+M2,q√N2−O2q√N2+O2],[q√2~L2q√~M2+~L2,q√2~N2q√~O2+~N2]). So,
This shows that Eq (3.1) is held for n=2 and m=1. Let Eq (3.1) is true for n=β1 and m=β2. Then,
For n = {\beta }_{1}+1 and m = {\beta }_{2}+1 .
Let {L}_{1} = \prod _{j = 1}^{{\beta }_{2}}{\left(\prod _{i = 1}^{{\beta }_{1}}{\left(1+{\left({\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}\right)}^{q}\right)}^{{\Omega }_{i}}\right)}^{{\gamma }_{j}} ; {M}_{1} = \prod _{j = 1}^{{\beta }_{2}}{\left(\prod _{i = 1}^{{\beta }_{1}}{\left(1-{\left({\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}\right)}^{q}\right)}^{{\Omega }_{i}}\right)}^{{\gamma }_{j}} ; {N}_{1} = \prod _{j = 1}^{{\beta }_{2}}{\left(\prod _{i = 1}^{{\beta }_{1}}{\left(1+{\left({\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right)}^{q}\right)}^{{\Omega }_{i}}\right)}^{{\gamma }_{j}} ; {O}_{1} = \prod _{j = 1}^{{\beta }_{2}}{\left(\prod _{i = 1}^{{\beta }_{1}}{\left(1-{\left({\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right)}^{q}\right)}^{{\Omega }_{i}}\right)}^{{\gamma }_{j}} ; {L}_{2} = {\left({\left(1+{\left({\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}\right)}^{q}\right)}^{{\Omega }_{\left({\beta }_{1}+1\right)}}\right)}^{{\gamma }_{\left({\beta }_{2}+1\right)}} ; {M}_{2} = {\left({\left(1-{\left({\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}\right)}^{q}\right)}^{{\Omega }_{\left({\beta }_{1}+1\right)}}\right)}^{{\gamma }_{\left({\beta }_{2}+1\right)}} ; {N}_{2} = {\left({\left(1+{\left({\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right)}^{q}\right)}^{{\Omega }_{\left({\beta }_{1}+1\right)}}\right)}^{{\gamma }_{\left({\beta }_{2}+1\right)}} ; {O}_{2} = {\left({\left(1-{\left({\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right)}^{q}\right)}^{{\Omega }_{\left({\beta }_{1}+1\right)}}\right)}^{{\gamma }_{\left({\beta }_{2}+1\right)}} ; \widetilde {{L}_{1}} = \prod _{j = 1}^{{\beta }_{2}}{\left(\prod _{i = 1}^{{\beta }_{1}}{\left({\left({\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}\right)}^{q}\right)}^{{\Omega }_{i}}\right)}^{{\gamma }_{j}} ; \widetilde {{M}_{1}} = \prod _{j = 1}^{{\beta }_{2}}{\left(\prod _{i = 1}^{{\beta }_{1}}{\left(2-{\left({\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}\right)}^{q}\right)}^{{\Omega }_{i}}\right)}^{{\gamma }_{j}} ; \widetilde {{N}_{1}} = \prod _{j = 1}^{{\beta }_{2}}{\left(\prod _{i = 1}^{{\beta }_{1}}{\left({\left({\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right)}^{q}\right)}^{{\Omega }_{i}}\right)}^{{\gamma }_{j}} ; \widetilde {{O}_{1}} = \prod _{j = 1}^{{\beta }_{2}}{\left(\prod _{i = 1}^{{\beta }_{1}}{\left(2-{\left({\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right)}^{q}\right)}^{{\Omega }_{i}}\right)}^{{\gamma }_{j}} ; \widetilde {{L}_{2}} = {\left({\left({\left({\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}\right)}^{q}\right)}^{{\mathrm{\Omega }}_{\left({\beta }_{1}+1\right)}}\right)}^{{\gamma }_{\left({\beta }_{2}+1\right)}} ; \widetilde {{M}_{2}} = {\left({\left(2-{\left({\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}\right)}^{q}\right)}^{{\mathrm{\Omega }}_{\left({\beta }_{1}+1\right)}}\right)}^{{\gamma }_{\left({\beta }_{2}+1\right)}} ; \widetilde {{N}_{2}} = {\left({\left({\left({\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right)}^{q}\right)}^{{\mathrm{\Omega }}_{\left({\beta }_{1}+1\right)}}\right)}^{{\gamma }_{\left({\beta }_{2}+1\right)}} ; \widetilde {{O}_{2}} = {\left({\left(2-{\left({\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right)}^{q}\right)}^{{\mathrm{\Omega }}_{\left({\beta }_{1}+1\right)}}\right)}^{{\gamma }_{\left({\beta }_{2}+1\right)}} .
Equation (3.1) is satisfied for n = {\beta }_{1}+1 and m = {\beta }_{2}+1 . Thus, we can say that Eq (3.1) holds \forall n, m > 0 .
In Theorem 3.1, we claimed that the obtained result using IVq-ROFHSEWA operators is also an IVq-ROFHSN, which can be proved as follows:
We know {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}} = \left(\left[{\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right], \left[{\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]\right) be the IVq-ROFHSN, and 0\le {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}, {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\le 1 and {\left({\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right)}^{q}+{\left({\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right)}^{q}\le 1 , for q\ge 3 .
Since 0\le {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}\le 1 , 0\le {\left({\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}\right)}^{q}\le 1 , 1\le 2-{\left({\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}\right)}^{q}\le 2 , so, 0\le {\left({\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}\right)}^{q}\le 2-{\left({\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}\right)}^{q}\le 2 . Hence,
Similarly,
Since {\left({\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right)}^{q}+{\left({\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right)}^{q}\le 1 , so, \prod _{j = 1}^{m}{\left(\prod _{i = 1}^{n}{\left({\left({\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right)}^{q}\right)}^{{\Omega }_{i}}\right)}^{{\gamma }_{j}}\le \prod _{j = 1}^{m}{\left(\prod _{i = 1}^{n}{\left(1-{\left({\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right)}^{q}\right)}^{{\Omega }_{i}}\right)}^{{\gamma }_{j}} , \prod _{j = 1}^{m}{\left(\prod _{i = 1}^{n}{\left(1+{\left({\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right)}^{q}\right)}^{{\Omega }_{i}}\right)}^{{\gamma }_{j}}\le \prod _{j = 1}^{m}{\left(\prod _{i = 1}^{n}{\left({2-\left({\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right)}^{q}\right)}^{{\Omega }_{i}}\right)}^{{\gamma }_{j}} . Then
Thus, it is proved that the obtained value is also an IVq-ROFHSN.
Theorem 3.4. Let {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}} = \left(\left[{\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right], \left[{\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]\right) be a collection of IVq-ROFSHNs. Then,
Where, {\Omega }_{i} and {\gamma }_{j} be the experts and parameters weights, such as {\Omega }_{i}, {\gamma }_{j}\in \left[0, 1\right] , and \sum _{i = 1}^{n}{\Omega }_{i} = 1 ; \sum _{j = 1}^{m}{\gamma }_{j} = 1 \left(i = 1, 2, 3, \dots, m; j = 1, 2, 3, \dots, n\right) .
Proof. As we know
Similarly,
So,
Assume
Similarly,
Thus,
Let IVq-ROFHSWA\left({\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{11}}, {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{12}}, \dots, {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{nm}}\right) = {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}} = \left(\left[{\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right], \left[{\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]\right) and IVq-ROFHSEWA\left({\mathfrak{T}}_{\widehat{{\stackrel{ˇ}{d}}_{11}}}, {\mathfrak{T}}_{\widehat{{\stackrel{ˇ}{d}}_{12}}}, \dots, {\mathfrak{T}}_{\widehat{{\stackrel{ˇ}{d}}_{nm}}}\right) = {\mathfrak{T}}_{\widehat{{\stackrel{ˇ}{d}}_{ij}}} = \left(\left[{\mathcal{T}}_{\widehat{{\stackrel{ˇ}{d}}_{ij}}}^{l}, {\mathcal{T}}_{\widehat{{\stackrel{ˇ}{d}}_{ij}}}^{\mathcal{u}}\right], \left[{\mathcal{J}}_{\widehat{{\stackrel{ˇ}{d}}_{ij}}}^{l}, {\mathcal{J}}_{\widehat{{\stackrel{ˇ}{d}}_{ij}}}^{\mathcal{u}}\right]\right) . Using the above inequalities (3.2) and (3.3), which can be expressed as {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}\ge {\mathcal{T}}_{\widehat{{\stackrel{ˇ}{d}}_{ij}}}^{l} and {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\ge {\mathcal{T}}_{\widehat{{\stackrel{ˇ}{d}}_{ij}}}^{\mathcal{u}} \Rightarrow \left[{\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]\ge \left[{\mathcal{T}}_{\widehat{{\stackrel{ˇ}{d}}_{ij}}}^{l}, {\mathcal{T}}_{\widehat{{\stackrel{ˇ}{d}}_{ij}}}^{\mathcal{u}}\right] . Also {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}\le {\mathcal{J}}_{\widehat{{\stackrel{ˇ}{d}}_{ij}}}^{l} and {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\le {\mathcal{J}}_{\widehat{{\stackrel{ˇ}{d}}_{ij}}}^{\mathcal{u}} \Rightarrow \left[{\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]\le \left[{\mathcal{J}}_{\widehat{{\stackrel{ˇ}{d}}_{ij}}}^{l}, {\mathcal{J}}_{\widehat{{\stackrel{ˇ}{d}}_{ij}}}^{\mathcal{u}}\right] . So, S\left({\mathcal{F}}_{{\mathcal{ϛ}}_{ij}}\right) = {\left[{\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]}^{q}-{\left[{\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]}^{q}+\left(\frac{{\mathrm{e}}^{{\left[{\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]}^{q}-{\left[{\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]}^{q}}}{{\mathrm{e}}^{{\left[{\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]}^{q}-{\left[{\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]}^{q}}+1}-\frac{1}{2}\right){\left[{\rm{ \mathsf{ π} }}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\rm{ \mathsf{ π} }}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]}^{q}\le {\left[{\mathcal{T}}_{\widehat{{\stackrel{ˇ}{d}}_{ij}}}^{l}, {\mathcal{T}}_{\widehat{{\stackrel{ˇ}{d}}_{ij}}}^{\mathcal{u}}\right]}^{q}-{\left[{\mathcal{J}}_{\widetilde {{\mathcal{ϛ}}_{ij}}}^{\mathcal{l}}, {\mathcal{J}}_{\widetilde {{\mathcal{ϛ}}_{ij}}}^{ひ}\right]}^{q}+\left(\frac{{\mathrm{e}}^{{\left[{\mathcal{T}}_{\widehat{{\stackrel{ˇ}{d}}_{ij}}}^{l}, {\mathcal{T}}_{\widehat{{\stackrel{ˇ}{d}}_{ij}}}^{\mathcal{u}}\right]}^{q}-{\left[{\mathcal{J}}_{\widehat{{\stackrel{ˇ}{d}}_{ij}}}^{l}, {\mathcal{J}}_{\widehat{{\stackrel{ˇ}{d}}_{ij}}}^{\mathcal{u}}\right]}^{q}}}{{\mathrm{e}}^{{\left[{\mathcal{T}}_{\widehat{{\stackrel{ˇ}{d}}_{ij}}}^{l}, {\mathcal{T}}_{\widehat{{\stackrel{ˇ}{d}}_{ij}}}^{\mathcal{u}}\right]}^{q}-{\left[{\mathcal{J}}_{\widehat{{\stackrel{ˇ}{d}}_{ij}}}^{l}, {\mathcal{J}}_{\widehat{{\stackrel{ˇ}{d}}_{ij}}}^{\mathcal{u}}\right]}^{q}}+1}-\frac{1}{2}\right){\left[{\rm{ \mathsf{ π} }}_{\widehat{{\stackrel{ˇ}{d}}_{ij}}}^{l}, {\rm{ \mathsf{ π} }}_{\widehat{{\stackrel{ˇ}{d}}_{ij}}}^{\mathcal{u}}\right]}^{q} .
If S\left({\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}}\right) > S\left({\mathfrak{T}}_{\widehat{{\stackrel{ˇ}{d}}_{ij}}}\right) , then
If S\left({\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}}\right) = S\left(\left({\mathfrak{T}}_{\widehat{{\stackrel{ˇ}{d}}_{ij}}}\right), \right) , then
Using inequalities (3.4) and (3.5), we get
Theorem 3.5. Let {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}} = {\mathfrak{T}}_{\stackrel{ˇ}{d}} = \left(\left[{\mathcal{T}}_{\stackrel{ˇ}{d}}^{l}, {\mathcal{T}}_{\stackrel{ˇ}{d}}^{\mathcal{u}}\right], \left[{\mathcal{J}}_{\stackrel{ˇ}{d}}^{l}, {\mathcal{J}}_{\stackrel{ˇ}{d}}^{\mathcal{u}}\right]\right) be a collection of interval-valued q-rung orthopair fuzzy hypersoft numbers. Where {\mathcal{\Omega }}_{i} and {\mathrm{\gamma }}_{j} be the weights of experts and multi sub-attributes such as {\mathrm{\Omega }}_{i} > 0, \sum _{i = 1}^{n}{\mathrm{\Omega }}_{i} = 1, {\mathrm{\gamma }}_{j} > 0, \sum _{j = 1}^{m}{\mathrm{\gamma }}_{j} = 1 \forall i = \mathrm{1, 2}, \dots \dots.n and j = \mathrm{1, 2}, \dots \dots.m . Then,
Proof. As {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}} = {\mathfrak{T}}_{\stackrel{ˇ}{d}} = \left(\left[{\mathcal{T}}_{\stackrel{ˇ}{d}}^{l}, {\mathcal{T}}_{\stackrel{ˇ}{d}}^{\mathcal{u}}\right], \left[{\mathcal{J}}_{\stackrel{ˇ}{d}}^{l}, {\mathcal{J}}_{\stackrel{ˇ}{d}}^{\mathcal{u}}\right]\right) for any i = \mathrm{1, 2}, \dots \dots.n and j = \mathrm{1, 2}, \dots \dots.m . Then,
We know \sum _{i = 1}^{n}{\Omega }_{i} = 1 and \sum _{j = 1}^{m}{\gamma }_{j} = 1 . So,
Theorem 3.6. let {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{-} = \left(\left[min\left({\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}\right), min\left({\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right)\right], \left[max\left({\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}\right), max\left({\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right)\right]\right) and {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{+} = \left(\left[max\left({\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}\right), max\left({\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right)\right], \left[min\left({\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}\right), min\left({\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right)\right]\right) . Then
Proof. Let f\left(t\right) = \frac{1-t}{1+t} such as t\in \left[0, 1\right] . Then, {f}^{ˊ}\left(t\right) = -\frac{2}{{\left(1+t\right)}^{2}}\Rightarrow f\left(t\right)\ge {f}^{ˊ}\left(t\right) which shows that f\left(t\right) is decreasing. Let min\left({\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}\right) = {\mathcal{T}}_{{min}_{{\stackrel{ˇ}{d}}_{ij}}}^{l} , max\left({\mathcal{T}}_{{\mathcal{ϛ}}_{ij}}^{\mathcal{l}}\right) = {\mathcal{T}}_{{max}_{{\stackrel{ˇ}{d}}_{ij}}}^{l} , thus, {\left({\mathcal{T}}_{{min}_{{\stackrel{ˇ}{d}}_{ij}}}^{l}\right)}^{q}\le {\left({\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}\right)}^{q}\le {\left({\mathcal{T}}_{{max}_{{\stackrel{ˇ}{d}}_{ij}}}^{l}\right)}^{q} , then f\left({\left({\mathcal{T}}_{{max}_{{\stackrel{ˇ}{d}}_{ij}}}^{l}\right)}^{q}\right)\le f\left({\left({\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}\right)}^{q}\right)\le f\left({\left({\mathcal{T}}_{{min}_{{\stackrel{ˇ}{d}}_{ij}}}^{l}\right)}^{q}\right)
Similarly,
Let g\left(u\right) = \frac{2-u}{u} such as u\in \left[0, 1\right] . Then, {g}^{ˊ}\left(u\right) = -\frac{2}{{u}^{2}}\Rightarrow g\left(u\right)\ge {g}^{ˊ}\left(u\right) which shows that g\left(u\right) is decreasing. Let min\left({\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}\right) = {\mathcal{J}}_{{min}_{{\stackrel{ˇ}{d}}_{ij}}}^{l} , max\left({\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}\right) = {\mathcal{J}}_{{max}_{{\stackrel{ˇ}{d}}_{ij}}}^{l} , thus, {\left({\mathcal{J}}_{{min}_{{\stackrel{ˇ}{d}}_{ij}}}^{l}\right)}^{q}\le {\left({\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}\right)}^{q}\le {\left({\mathcal{J}}_{{max}_{{\stackrel{ˇ}{d}}_{ij}}}^{l}\right)}^{q} , then g\left({\left({\mathcal{J}}_{{max}_{{\stackrel{ˇ}{d}}_{ij}}}^{l}\right)}^{q}\right)\le g\left({\left({\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}\right)}^{q}\right)\le g\left({\left({\mathcal{J}}_{{min}_{{\stackrel{ˇ}{d}}_{ij}}}^{l}\right)}^{q}\right) , \frac{2-{\left({\mathcal{J}}_{{max}_{{\stackrel{ˇ}{d}}_{ij}}}^{l}\right)}^{q}}{{\left({\mathcal{J}}_{{max}_{{\stackrel{ˇ}{d}}_{ij}}}^{l}\right)}^{q}}\le \frac{2-{\left({\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}\right)}^{q}}{{\left({\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}\right)}^{q}}\le \frac{2-{\left({\mathcal{J}}_{{min}_{{\stackrel{ˇ}{d}}_{ij}}}^{l}\right)}^{q}}{{\left({\mathcal{J}}_{{min}_{{\stackrel{ˇ}{d}}_{ij}}}^{l}\right)}^{q}} . Thus,
Similarly,
Let IVq-ROFHSEWA\left({\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{11}}, {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{12}}, \dots, {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{nm}}\right) = {\mathfrak{T}}_{\stackrel{ˇ}{d}} = \left(\left[{\mathcal{T}}_{\stackrel{ˇ}{d}}^{l}, {\mathcal{T}}_{\stackrel{ˇ}{d}}^{\mathcal{u}}\right], \left[{\mathcal{J}}_{\stackrel{ˇ}{d}}^{l}, {\mathcal{J}}_{\stackrel{ˇ}{d}}^{\mathcal{u}}\right]\right) . Then, from inequalities (3.6) to (3.9), we get {\mathcal{T}}_{{min}_{{\stackrel{ˇ}{d}}_{ij}}}^{l}\le {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}\le {\mathcal{T}}_{{max}_{{\stackrel{ˇ}{d}}_{ij}}}^{l} , {\mathcal{T}}_{{min}_{{\stackrel{ˇ}{d}}_{ij}}}^{\mathcal{u}}\le {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\le {\mathcal{T}}_{{max}_{{\stackrel{ˇ}{d}}_{ij}}}^{\mathcal{u}} , {\mathcal{J}}_{{min}_{{\stackrel{ˇ}{d}}_{ij}}}^{l}\le {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}\le {\mathcal{J}}_{{max}_{{\stackrel{ˇ}{d}}_{ij}}}^{l} , {\mathcal{J}}_{{min}_{{\stackrel{ˇ}{d}}_{ij}}}^{\mathcal{u}}\le {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\le {\mathcal{J}}_{{max}_{{\stackrel{ˇ}{d}}_{ij}}}^{\mathcal{u}} . Thus,
If S\left({\mathfrak{T}}_{\stackrel{ˇ}{d}}\right) < S\left({\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{+}\right)\;\mathrm{a}\mathrm{n}\mathrm{d}\;S\left({\mathfrak{T}}_{\stackrel{ˇ}{d}}\right) > S\left({\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{-}\right) , then
If S\left({\mathfrak{T}}_{\stackrel{ˇ}{d}}\right) = S\left({\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{+}\right), then S\left({\mathfrak{T}}_{\stackrel{ˇ}{d}}\right) = {\left(\left[{\mathcal{T}}_{\stackrel{ˇ}{d}}^{l}, {\mathcal{T}}_{\stackrel{ˇ}{d}}^{\mathcal{u}}\right]\right)}^{q}-{\left(\left[{\mathcal{J}}_{\stackrel{ˇ}{d}}^{l}, {\mathcal{J}}_{\stackrel{ˇ}{d}}^{\mathcal{u}}\right]\right)}^{q}+\left(\frac{{e}^{{\left(\left[{\mathcal{T}}_{\stackrel{ˇ}{d}}^{l}, {\mathcal{T}}_{\stackrel{ˇ}{d}}^{\mathcal{u}}\right]\right)}^{q}-{\left(\left[{\mathcal{J}}_{\stackrel{ˇ}{d}}^{l}, {\mathcal{J}}_{\stackrel{ˇ}{d}}^{\mathcal{u}}\right]\right)}^{q}}}{{e}^{{\left(\left[{\mathcal{T}}_{\stackrel{ˇ}{d}}^{l}, {\mathcal{T}}_{\stackrel{ˇ}{d}}^{\mathcal{u}}\right]\right)}^{q}-{\left(\left[{\mathcal{J}}_{\stackrel{ˇ}{d}}^{l}, {\mathcal{J}}_{\stackrel{ˇ}{d}}^{\mathcal{u}}\right]\right)}^{q}}+1}-\frac{1}{2}\right){\left(\left[{\pi }_{\stackrel{ˇ}{d}}^{l}, {\pi }_{\stackrel{ˇ}{d}}^{\mathcal{u}}\right]\right)}^{q} = {\left(\genfrac{}{}{0pt}{}{max}{j}\genfrac{}{}{0pt}{}{max}{i}\left[{\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]\right)}^{q}-{\left(\genfrac{}{}{0pt}{}{min}{j}\genfrac{}{}{0pt}{}{min}{i}\left[{\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]\right)}^{q}+\left(\frac{{e}^{{\left(\genfrac{}{}{0pt}{}{max}{j}\genfrac{}{}{0pt}{}{max}{i}\left[{\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]\right)}^{q}-{\left(\genfrac{}{}{0pt}{}{min}{j}\genfrac{}{}{0pt}{}{min}{i}\left[{\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]\right)}^{q}}}{{e}^{{\left(\genfrac{}{}{0pt}{}{max}{j}\genfrac{}{}{0pt}{}{max}{i}\left[{\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]\right)}^{q}-{\left(\genfrac{}{}{0pt}{}{min}{j}\genfrac{}{}{0pt}{}{min}{i}\left[{\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]\right)}^{q}}+1}-\frac{1}{2}\right){\left(\left[{\pi }_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\pi }_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]\right)}^{q} , we have \left[{\mathcal{T}}_{\stackrel{ˇ}{d}}^{l}, {\mathcal{T}}_{\stackrel{ˇ}{d}}^{\mathcal{u}}\right] = \genfrac{}{}{0pt}{}{max}{j}\genfrac{}{}{0pt}{}{max}{i}\left\{\left[{\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]\right\} , and \left[{\mathcal{J}}_{\stackrel{ˇ}{d}}^{l}, {\mathcal{J}}_{\stackrel{ˇ}{d}}^{\mathcal{u}}\right] = \genfrac{}{}{0pt}{}{min}{j}\genfrac{}{}{0pt}{}{min}{i}\left\{\left[{\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]\right\} . Hence, {\left(\left[{\pi }_{\stackrel{ˇ}{d}}^{l}, {\pi }_{\stackrel{ˇ}{d}}^{\mathcal{u}}\right]\right)}^{q} = {\left(\left[{\pi }_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\pi }_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]\right)}^{q} . Then
If S\left({\mathfrak{T}}_{\stackrel{ˇ}{d}}\right) = S\left({\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{-}\right), then {\left(\left[{\mathcal{T}}_{\stackrel{ˇ}{d}}^{l}, {\mathcal{T}}_{\stackrel{ˇ}{d}}^{\mathcal{u}}\right]\right)}^{q}-{\left(\left[{\mathcal{J}}_{\stackrel{ˇ}{d}}^{l}, {\mathcal{J}}_{\stackrel{ˇ}{d}}^{\mathcal{u}}\right]\right)}^{q}+\left(\frac{{e}^{{\left(\left[{\mathcal{T}}_{\stackrel{ˇ}{d}}^{l}, {\mathcal{T}}_{\stackrel{ˇ}{d}}^{\mathcal{u}}\right]\right)}^{q}-{\left(\left[{\mathcal{J}}_{\stackrel{ˇ}{d}}^{l}, {\mathcal{J}}_{\stackrel{ˇ}{d}}^{\mathcal{u}}\right]\right)}^{q}}}{{e}^{{\left(\left[{\mathcal{T}}_{\stackrel{ˇ}{d}}^{l}, {\mathcal{T}}_{\stackrel{ˇ}{d}}^{\mathcal{u}}\right]\right)}^{q}-{\left(\left[{\mathcal{J}}_{\stackrel{ˇ}{d}}^{l}, {\mathcal{J}}_{\stackrel{ˇ}{d}}^{\mathcal{u}}\right]\right)}^{q}}+1}-\frac{1}{2}\right){\left(\left[{\pi }_{\stackrel{ˇ}{d}}^{l}, {\pi }_{\stackrel{ˇ}{d}}^{\mathcal{u}}\right]\right)}^{q} = {\left(\genfrac{}{}{0pt}{}{min}{j}\genfrac{}{}{0pt}{}{min}{i}\left[{\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]\right)}^{q}-{\left(\genfrac{}{}{0pt}{}{max}{j}\genfrac{}{}{0pt}{}{max}{i}\left[{\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]\right)}^{q}+\left(\frac{{e}^{{\left(\genfrac{}{}{0pt}{}{min}{j}\genfrac{}{}{0pt}{}{min}{i}\left[{\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]\right)}^{q}-{\left(\genfrac{}{}{0pt}{}{max}{j}\genfrac{}{}{0pt}{}{max}{i}\left[{\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]\right)}^{q}}}{{e}^{{\left(\genfrac{}{}{0pt}{}{min}{j}\genfrac{}{}{0pt}{}{min}{i}\left[{\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]\right)}^{q}-{\left(\genfrac{}{}{0pt}{}{max}{j}\genfrac{}{}{0pt}{}{max}{i}\left[{\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]\right)}^{q}}+1}-\frac{1}{2}\right){\left(\left[{\pi }_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\pi }_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]\right)}^{q} . Then \left[{\mathcal{T}}_{\stackrel{ˇ}{d}}^{l}, {\mathcal{T}}_{\stackrel{ˇ}{d}}^{\mathcal{u}}\right] = \genfrac{}{}{0pt}{}{min}{j}\genfrac{}{}{0pt}{}{min}{i}\left\{\left[{\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]\right\} , and \left[{\mathcal{J}}_{\stackrel{ˇ}{d}}^{l}, {\mathcal{J}}_{\stackrel{ˇ}{d}}^{\mathcal{u}}\right] = \genfrac{}{}{0pt}{}{max}{j}\genfrac{}{}{0pt}{}{max}{i}\left\{\left[{\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]\right\} . Hence, {\left(\left[{\pi }_{\stackrel{ˇ}{d}}^{l}, {\pi }_{\stackrel{ˇ}{d}}^{\mathcal{u}}\right]\right)}^{q} = {\left(\left[{\pi }_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\pi }_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]\right)}^{q} . Then
From inequalities (3.10) to (3.12), it is proved that
Theorem 3.7. Let {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}} = \left(\left[{\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right], \left[{\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]\right) and {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{*} = \left(\left[{\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l*}, {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}\mathcal{*}}\right], \left[{\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l*}, {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}\mathcal{*}}\right]\right) be the collections of two distinct IVq-ROFHSNs, such as if {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}}\le {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{*} \forall i, j . Then
Proof. Let u = f\left(t\right) = \sqrt[q]{\frac{1-{t}^{2}}{1+{t}^{2}}} , where t\in \left[0, 1\right] , then \frac{d}{d\left(t\right)}\left(f\left(t\right)\right) = -\frac{1}{q}{\left(\frac{1-{t}^{q}}{1+{t}^{q}}\right)}^{\frac{1}{q}-1}\left\{\frac{q{t}^{2q-1}+q{t}^{2q-1}}{{\left(1+{t}^{q}\right)}^{2}}\right\} < \; 0 . This shows that f\left(t\right) is decreasing on \left[0, \; 1\right] . If {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}}\le {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{*} , then f\left({\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}}\right)\le f\left({\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{*}\right) .
Where, {\Omega }_{i} > 0 , {\sum }_{i = 1}^{n}{\Omega }_{i} = 1 and {\gamma }_{j} > 0, {\sum }_{j = 1}^{m}{\gamma }_{j} = 1 . So,
Similarly,
Thus,
Let y = g\left(v\right) = \sqrt[q]{\frac{2-{v}^{q}}{{v}^{q}}} , v\in \left[0, 1\right] , then \frac{d}{dv}\left(g\left(v\right)\right) = -\frac{1}{q}{\left(\frac{2-{v}^{q}}{{v}^{q}}\right)}^{\frac{1}{q}-1}\left(\frac{2}{{\left({v}^{q}\right)}^{2}}\right) < 0 . This shows that g\left(v\right) is decreasing on \left[0, \; 1\right] . If {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}}\le {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{*} , then g\left({\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}}\right)\le g\left({\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{*}\right) .
As {\Omega }_{i} > 0 , {\sum }_{i = 1}^{n}{\Omega }_{i} = 1 and {\gamma }_{j} > 0, {\sum }_{j = 1}^{m}{\gamma }_{j} = 1 . So,
As {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l*}\le {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}
Using inequalities (3.13) and (3.14).
Similarly,
So,
Hence,
Theorem 3.8. Let {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}} = \left(\left[{\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right], \left[{\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]\right) be a collection of IVq-ROFHSNs and \beta > 0 . Then
Proof. We know that {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}} represents the collection of IVq-ROFHSNs and \beta > 0 . then
So,
Theorem 3.9. Let {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}} = \left(\left[{\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right], \left[{\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]\right) be a collection of IVq-ROFHSVs and {\mathfrak{T}}_{\stackrel{ˇ}{d}} = \left(\left[{\mathcal{T}}_{\stackrel{ˇ}{d}}^{l}, {\mathcal{T}}_{\stackrel{ˇ}{d}}^{\mathcal{u}}\right], \left[{\mathcal{J}}_{\stackrel{ˇ}{d}}^{l}, {\mathcal{J}}_{\stackrel{ˇ}{d}}^{\mathcal{u}}\right]\right) be an IVq-ROFHSV. Then
Proof. We know that {\mathfrak{T}}_{\stackrel{ˇ}{d}} and {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}} be two distinct IVq-ROFHSNs. Then,
From Eq (3.1),
4.
Einstein weighted average operators for interval-valued q-rung orthopair fuzzy hypersoft numbers
Considering Einstein's operational laws defined in Definition 3.1, the IVq-ROFHSEWG operator is proposed and evaluated.
Definition 4.1. Let {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}} = \left(\left[{\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right], \left[{\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]\right) be a collection of interval-valued q-rung orthopair fuzzy hypersoft numbers. Then, the IVq-ROFHSEWG operator is defined as
where i = \mathrm{1, 2}, \dots \dots.n and j = \mathrm{1, 2}, \dots \dots.m . Also, {\mathrm{\Omega }}_{i} and {\mathrm{\gamma }}_{j} be the weights of experts and multi sub-attributes such as {\mathrm{\Omega }}_{i} > 0, \sum _{i = 1}^{n}{\mathrm{\Omega }}_{i} = 1, {\mathrm{\gamma }}_{j} > 0, \sum _{j = 1}^{m}{\mathrm{\gamma }}_{j} = 1.
Theorem 4.2. Let {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}} = \left(\left[{\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right], \left[{\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]\right) be a collection of IVq-ROFHSNs. Then, the obtained aggregation value is also an IVq-ROFHSN and
where i = \mathrm{1, 2}, \dots \dots.n and j = \mathrm{1, 2}, \dots \dots.m . Also, {\mathrm{\Omega }}_{i} and {\mathrm{\gamma }}_{j} be the weights of experts and multi sub-attributes such as {\mathrm{\Omega }}_{i} > 0, \sum _{i = 1}^{n}{\mathrm{\Omega }}_{i} = 1, {\mathrm{\gamma }}_{j} > 0, \sum _{j = 1}^{m}{\mathrm{\gamma }}_{j} = 1.
Proof. Like Theorem 3.3.
Theorem 4.3. Let {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}} = \left(\left[{\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right], \left[{\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]\right) be a collection of IVq-ROFSHNs. Then
Where, {\Omega }_{i} and {\gamma }_{j} be the experts and parameters weights, such as {\Omega }_{i}, {\gamma }_{j}\in \left[0, 1\right] , and \sum _{i = 1}^{n}{\Omega }_{i} = 1 ; \sum _{j = 1}^{m}{\gamma }_{j} = 1 \left(i = 1, 2, 3, \dots, m; j = 1, 2, 3, \dots, n\right) .
Proof. Like Theorem 3.4.
Theorem 4.4. Let {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}} = {\mathfrak{T}}_{\stackrel{ˇ}{d}} = \left(\left[{\mathcal{T}}_{\stackrel{ˇ}{d}}^{l}, {\mathcal{T}}_{\stackrel{ˇ}{d}}^{\mathcal{u}}\right], \left[{\mathcal{J}}_{\stackrel{ˇ}{d}}^{l}, {\mathcal{J}}_{\stackrel{ˇ}{d}}^{\mathcal{u}}\right]\right) be a collection of interval-valued q-rung orthopair fuzzy hypersoft numbers. Where {\mathcal{\Omega }}_{i} and {\mathrm{\gamma }}_{j} be the weights of experts and multi sub-attributes such as {\mathrm{\Omega }}_{i} > 0, \sum _{i = 1}^{n}{\mathrm{\Omega }}_{i} = 1, {\mathrm{\gamma }}_{j} > 0, \sum _{j = 1}^{m}{\mathrm{\gamma }}_{j} = 1 \forall i = \mathrm{1, 2}, \dots \dots.n and j = \mathrm{1, 2}, \dots \dots.m . Then,
Proof. Like Theorem 3.5.
Theorem 4.5. Let {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{-} = \left(\left[min\left({\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}\right), min\left({\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right)\right], \left[max\left({\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}\right), max\left({\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right)\right]\right) and {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{+} = \left(\left[max\left({\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}\right), max\left({\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right)\right], \left[min\left({\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}\right), min\left({\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right)\right]\right) . Then
Proof. Like Theorem 3.6.
Theorem 4.6. Let {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}} = \left(\left[{\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right], \left[{\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]\right) and {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{*} = \left(\left[{\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l*}, {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}\mathcal{*}}\right], \left[{\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l*}, {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}\mathcal{*}}\right]\right) be the collections of two distinct IVq-ROFHSNs, such as if {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}}\le {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{*} \forall i, j . Then
Proof. Like Theorem 3.7.
Theorem 4.7. Let {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}} = \left(\left[{\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right], \left[{\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]\right) be a collection of IVq-ROFHSNs and \beta > 0 . Then
Proof. Like Theorem 3.8.
Theorem 4.8. Let {\mathfrak{T}}_{{\stackrel{ˇ}{d}}_{ij}} = \left(\left[{\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right], \left[{\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right]\right) be a collection of IVq-ROFHSVs and {\mathfrak{T}}_{\stackrel{ˇ}{d}} = \left(\left[{\mathcal{T}}_{\stackrel{ˇ}{d}}^{l}, {\mathcal{T}}_{\stackrel{ˇ}{d}}^{\mathcal{u}}\right], \left[{\mathcal{J}}_{\stackrel{ˇ}{d}}^{l}, {\mathcal{J}}_{\stackrel{ˇ}{d}}^{\mathcal{u}}\right]\right) be an IVq-ROFHSV. Then,
Proof. Similar to Theorem 3.9.
5.
Proposed multi-attribute group decision-making technique based on Einstein aggregation operators in IVq-ROFHSS structure
Let \mathfrak{H} = \left\{{\mathfrak{H}}^{1}, {\mathfrak{H}}^{2}, {\mathfrak{H}}^{\bf{3}}, \; \dots, {\mathfrak{H}}^{n}\right\} and \mathrm{\aleph } = \left\{{\mathrm{\aleph }}^{1}, {\mathrm{\aleph }}^{2}, {\mathrm{\aleph }}^{\bf{3}}, \dots, {\mathrm{\aleph }}^{s}\right\} be a collection of n experts and s alternatives. The weights of experts can be represented by \mathrm{\Omega } = {\left({\mathrm{\Omega }}_{1}, {\mathrm{\Omega }}_{2}, \dots, {\mathrm{\Omega }}_{n}\right)}^{T} such as {\mathrm{\Omega }}_{i} > 0 , \sum _{i = 1}^{n}{\mathrm{\Omega }}_{i} = 1 . Let \mathrm{Ϛ} = \left\{{d}_{1}, {d}_{2}, {d}_{3}, \; \dots, {d}_{m}\right\} be a collection of attributes with their corresponding sub-attributes, such as {\mathfrak{L}}^{{{'}}} = \left\{\left({d}_{1\rho }\times {d}_{2\rho }\times \dots \times {d}_{m\rho }\right)\mathrm{f}\mathrm{o}\mathrm{r}\; \mathrm{a}\mathrm{l}\mathrm{l}\rho \in \left\{1, 2, \dots, t\right\}\right\} . The weights of sub-attributes can be represented by \mathrm{\gamma } = {\left({\mathrm{\gamma }}_{1\rho }, {\mathrm{\gamma }}_{2\rho }, {\mathrm{\gamma }}_{3\rho }, \dots, {\mathrm{\gamma }}_{m\rho }\right)}^{T} such as {\mathrm{\gamma }}_{\rho } > 0 , \sum _{\rho = 1}^{t}{\mathrm{\gamma }}_{\rho } = 1 . For the reader's convenience, we can express the collection of sub-attributes, such as {\mathfrak{L}}^{{{'}}} = \left\{{\stackrel{ˇ}{d}}_{\partial }:\partial \in \left\{1, 2, \dots, m\right\}\right\} . The team of experts \left\{{\mathfrak{H}}^{i}:i = \; 1, \; 2, \dots, n\right\} provides their preferences for each alternative \left\{{\mathrm{\aleph }}^{\left(z\right)}:z = 1, \; 2, \; \dots, s\right\} in IVq-ROFHSNs: {\left({\mathrm{\aleph }}_{{\stackrel{ˇ}{d}}_{ik}}^{\left(z\right)}\right)}_{n\times m} = {\left({\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}, {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}\right)}_{n\times m} , where {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}} = \left[{\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right] and {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}} = \left[{\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\right] such as 0\le {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}, {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{l}, {\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\le 1 and {\mathcal{T}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}+{\mathcal{J}}_{{\stackrel{ˇ}{d}}_{ij}}^{\mathcal{u}}\le 1 , \forall i, j and q > 2 .
The MAGDM model can be described in the following way. Our approach is consistent with several studies' endeavors to address this issue. The data obtained from many sources, including our team of scientists, is combined using an aggregation method that can be applied across several channels. Figure 1 provides a summary of the diagram, which demonstrates the process that is under discussion. Analyzing this data aims to identify the most optimal alternatives to carry out the following actions:
Step 1. Construct the decision matrices with the corresponding sub-attributes for each alternative \left\{{\mathrm{\aleph }}_{z}:z = \; 1, \; 2, \; \dots, s\right\} in IVq-ROFHSNs.
Step 2. To analyze the matrix {\left[{\mathcal{\aleph }}_{{\stackrel{ˇ}{d}}_{ij}}^{\left(z\right)}\right]}_{n\times \mathrm{m}} , the parameters are divided into two categories: costs and benefits. When the parameters are the same, there is no need for the normalization procedure. Normalization is necessary to classify judgments that have several characteristic characteristics. The following is a description of the normalization techniques in order:
Step 3. Determine the cumulative values for each possibility using Eqs (3.1) or (4.1).
Step 4. Determine the score values for every alternative using Eq (2.1).
Step 5. The other options are arranged based on their scores to determine the most favorable alternative(s), with the greatest attainable value representing the preferred choice.
Step 6. Rank the alternatives.
6.
Application of the proposed MAGDM technique in energy
Energy suppliers are essential for managing energy by facilitating effective distribution and consumption. Energy intermediaries play a crucial role in connecting energy suppliers and customers, guaranteeing the reliable and cost-effective delivery of energy from different sources, including fossil fuels, nuclear power, and renewable resources. Energy providers play a crucial role in distributing energy and defining the energy market by providing various pricing plans, promoting competition, and encouraging innovation in energy solutions. Energy suppliers provide consumers with competitive rate structures and flexible contract terms, enabling them to make well-informed choices that align with their financial and operational requirements. By promoting the implementation of renewable energy sources and executing initiatives that minimize carbon footprints, energy suppliers are at the core of environmentally friendly activities. These inventions make demand-management tactics more efficient while also increasing energy efficiency. Their participation is necessary to create an energy system that is balanced, feasible, and efficient.
6.1. Criteria description
6.1.1. Reliability and service quality
An energy supplier's predictability and customer service are essential factors that significantly affect the consistency and stability of energy delivery to customers. A reliable renewable energy source that secures an adequate electrical supply, minimizing the frequency and duration of blackouts through sturdy structures and scheduled upkeep. The availability of the power supply is crucial for commercial and residential users since failures can lead to significant problems, operational failures, and monetary loss. Superb service level encompasses efficient and flexible client assistance that is easy to find to resolve queries and rectify complications, boosting client retention and credibility. Moreover, it is essential to obtain superior technical support to swiftly handle technological problems and ensure disruptions are effectively and quickly addressed. This assistance includes frequent revisions and transparent engagement during service disruptions or maintenance activities to ensure consumers are well-informed and prepared. Suppliers exhibiting remarkable reliability and service excellence often allocate substantial resources to advanced technologies such as smart grids and real-time monitoring systems. These technologies enhance the stability and efficiency of energy delivery. These attributes are crucial for forging a strong and dependable customer relationship, fostering enduring loyalty, and maintaining a competitive edge in the energy sector.
6.1.2. Sustainability and environmental impact
Modern energy providers are progressively concentrating on sustainability and reducing their environmental footprint, along with the global movement towards adopting more eco-friendly and liable energy techniques. Sustainable energy providers emphasize the integration of renewable energy sources, including solar, wind, and hydroelectric electricity, into their portfolios. This reduces reliance on fossil fuels and mitigates greenhouse gas emissions. This action contributes to alleviating climate change, promotes energy diversification, and strengthens security. Furthermore, numerous suppliers implement comprehensive strategies to reduce carbon emissions, including investments in energy-efficient technology and participation in carbon offset schemes. Environmental certifications, such as Green-e, bolster the credibility of their commitment to sustainable practices, providing consumers with confidence in their environmentally responsible choices. Sustainable energy providers often engage in community and environmental activities, including reforestation projects, habitat restoration, and educational campaigns to promote environmental awareness. These suppliers enhance the conservation of assets and safeguard ecosystems by emphasizing sustainability, thus securing a healthier earth for future generations. Their efforts also attract several ecologically conscious consumers seeking to align their energy consumption with their ecological values. Eventually, prioritizing sustainability and the environmental effects positions these suppliers as leaders in the energy sector and fosters a more resilient and sustainable energy system.
6.1.3. Contract terms and flexibility
Careful consideration of the agreement terms and mobility is required when selecting an energy provider; these factors directly affect the energy service's adaptability and convenience. Individuals can choose contract lengths that work for them from shorter contracts, which offer customers greater leeway to switch providers to longer ones that usually provide cost savings and rate stability. Familiarity with the renewal regulations is critical. If the renewal terms are fair and transparent, customers are protected from being forced into less favorable terms when the initial contract expires. Also, it is easy to change energy needs or preferences because you can change or improve plans without paying a hefty penalty. Importantly, exit provisions outline the steps to end the contract early without spending a fortune. Businesses with fluctuating energy needs or people planning to find this flexibility particularly useful. Flexible payment options, such as prepayment plans, budget billing, or monthly billing cycles, allow customers to manage their money better, boosting customer satisfaction. Energy providers can foster deeper, longer-lasting relationships by emphasizing transparent and adaptable contract conditions. With this strategy, they can win customers' trust while catering to their unique requirements.
6.1.4. Pricing and cost structures
Pricing and cost structures influence energy supplier selection since they influence affordable and predictable energy usage. Energy providers often provide customers with a choice between different rate plans. One option is a fixed rate, which offers protection and stability from fluctuations in the market. The other is a variable rate, which can be more advantageous when prices are low. In addition to the base rate per kilowatt-hour, there may be additional charges for service fees, maintenance costs, and penalties for early termination. It's important to understand the whole price structure. Consumers can better manage their budgets and avoid unexpected expenses when these prices are communicated clearly and openly. In addition, some providers may provide time-of-use or tiered pricing, which lets customers save money by adjusting their energy usage during off-peak times. Also, you can save money in the long run by taking advantage of sales and incentives, including rebates for energy-efficient equipment or discounted rates for longer commitments. By offering flexible price plans and clear, up-front pricing structures, energy providers empower customers to make educated selections that match their budgetary needs and consumption habits. A comprehensive pricing strategy is essential in the cutthroat energy market since it fosters customer confidence and satisfaction.
6.1.5. Reputation and track record
An energy provider's reliability, trustworthiness, and overall efficacy can be inferred from their track record and reputation, which are, therefore, essential factors to consider when making an evaluation. Over time, a solid reputation is built by reliably meeting or exceeding customer expectations, maintaining a steady flow of energy, and cultivating positive client relationships. You may learn a lot about a supplier's strengths and potential weaknesses by reading reviews and testimonials from current and previous customers. In addition, a supplier's track record of reliably meeting customer demands and complying with ever-changing regulations often indicates their skill in this area. Consideration of regulatory compliance is vital because suppliers who have faithfully adhered to industry standards and laws are more likely to maintain operational integrity and ethical practices. Recognized for their commitment to innovation and excellence, suppliers are given credibility boosts through awards, certificates, and other industry accolades. Suppose customers choose an energy provider with a solid reputation and a track record of success. In that case, they can rest assured that their energy will be reliably supplied and they will receive excellent service. Increased happiness and loyalty from customers is the inevitable outcome.
6.2. Numerical example
Let \mathfrak{H} = { {ESC}_{1} , {ESC}_{2} , {ESC}_{3} , {ESC}_{4} , {ESC}_{5} } be a collection of five energy supplier companies. Let \mathrm{\aleph } = \left\{{\mathrm{\aleph }}^{1}, {\mathrm{\aleph }}^{2}, {\mathrm{\aleph }}^{{3}}, {\mathrm{\aleph }}^{{4}}, {\mathrm{\aleph }}^{{5}}\right\} be a team of five experts with the same weights {\left(0.2, \; 0.2, \; 0.2, \; 0.2, \; 0.2\right)}^{T} . Experts define the crucial factors to find the most appropriate energy supplier, such as \mathrm{Ϛ} = { {d}_{1} = reliability and service quality, {d}_{2} = sustainability and environmental impact, {d}_{3} = contract terms and flexibility, {d}_{4} = pricing and cost structures, {d}_{5} = reputation and track record}. The sub-factors for these parameters are { {d}_{1} : reliability and service quality = { {d}_{11} = service availability, {d}_{12} = technical support }}, { {d}_{2} : sustainability and environmental impact = { {d}_{21} = carbon footprint, {d}_{22} = certifications and compliance}}, { {d}_{3} : contract terms and flexibility = { {d}_{31} = contract length, {d}_{32} = exit clauses}}, { {d}_{4} : pricing and cost structures = { {d}_{41} = incentives and discounts}}, and { {d}_{5} : reputation and track record = { {d}_{51} = customer reviews and testimonials}}. Let {\mathfrak{L}}^{{{'}}} = {d}_{1}\times {d}_{2}\times {d}_{3}\times {d}_{4}\times {d}_{5} represents the multi- sub-factors such as {\mathfrak{L}}^{{{'}}} = {d}_{1}\times {d}_{2}\times {d}_{3}\times {d}_{4}\times {d}_{5} = \left\{{d}_{11}, {d}_{12}\right\}\times \left\{{d}_{21}, {d}_{22}\right\}\times \left\{{d}_{31}, {d}_{32}\right\}\times \left\{{d}_{41}\right\}\times \left\{{d}_{51}\right\} = { \left({d}_{11}, {d}_{21}, {d}_{31}, {d}_{41}, {d}_{51}\right) , \left({d}_{11}, {d}_{22}, {d}_{31}, {d}_{41}, {d}_{51}\right) , \left({d}_{11}, {d}_{21}, {d}_{32}, {d}_{41}, {d}_{51}\right) , \left({d}_{11}, {d}_{22}, {d}_{32}, {d}_{41}, {d}_{51}\right) , \left({d}_{12}, {d}_{21}, {d}_{31}, {d}_{41}, {d}_{51}\right) , \left({d}_{12}, {d}_{22}, {d}_{31}, {d}_{41}, {d}_{51}\right) , \left({d}_{12}, {d}_{21}, {d}_{32}, {d}_{41}, {d}_{51}\right) , \left({d}_{12}, {d}_{22}, {d}_{32}, {d}_{41}, {d}_{51}\right) } = \left\{{\stackrel{ˇ}{d}}_{1}, {\stackrel{ˇ}{d}}_{2}, {\stackrel{ˇ}{d}}_{3}, {\stackrel{ˇ}{d}}_{4}, {\stackrel{ˇ}{d}}_{5}, {\stackrel{ˇ}{d}}_{6}, {\stackrel{ˇ}{d}}_{7}, {\stackrel{ˇ}{d}}_{8}\right\} with weights {\left(0.12, 0.18, \mathrm{0.1, 0.15}, 0.05, 0.22, 0.08, 0.1\right)}^{T} . After completing each component of the evaluation of these eight criteria, the stakeholders will select one of the five options per their views on IVq-ROFHSNs; a visual illustration of the employed method is given in Figure 2.
Implementing this technique makes it possible to deliver the solution that is ideally suitable under the specifications that have been stated. By evaluating these elements comprehensively, analysts may be able to provide the energy suppliers with the best and most ideal solution. IVq-ROFHSNs are used to transmit the expert opinions for each option presented in Table 1, which are then incorporated into the MAGDM approach. The Einstein AOs included in Sections 3 and 4 are used in this technique to determine which energy supplier is the most pragmatic in energy management.
6.2.1. Selection of energy supplier using the IVq-ROFHSEWA operator
Step 1. Decision matrices with the corresponding sub-attributes for each alternative in the form of IVq-ROFHSNs is given in Table 1.
Step 2. Pricing and cost structures {d}_{4} be the cost type parameter with sub-criteria {d}_{41} . The multi-sub characteristics and sub-criteria are \left\{{\stackrel{ˇ}{d}}_{1}, {\stackrel{ˇ}{d}}_{2}, {\stackrel{ˇ}{d}}_{3}, {\stackrel{ˇ}{d}}_{4}, {\stackrel{ˇ}{d}}_{5}, {\stackrel{ˇ}{d}}_{6}, {\stackrel{ˇ}{d}}_{7}, {\stackrel{ˇ}{d}}_{8}\right\} , as we are aware of. Since {d}_{41} appears in all multi-sub attributes, showing that each characteristic includes cost type sub-criteria. Consequently, normalize the decision matrix by following the normalization rule. Table 2 displays the normalization choice matrix.
Step 3. Determine the cumulative values for each possibility using Eq (3.1) for q = 3 . Which generates {\mathrm{\beth }}_{{1}} = ([0.35069, 0.65458], [0.29671, 0.63358]), {\mathrm{\beth }}_{{2}} = ([0.38897, 0.66723], [0.30126, 0.64717]), {\mathrm{\beth }}_{{3}} = ([0.37182, 0.62027], [0.30101, 0.63605]), {\mathrm{\beth }}_{{4}} = ([0.34067, 0.64117], [0.25761, 0.61134]), and {\mathrm{\beth }}_{{5}} = ([0.34911, 0.64584], [0.30784, 0.67697]).
Step 4. Determine the score values for every alternative using Eq (2.1), such as \mathcal{S}\left({\mathcal{\beth }}_{{1}}\right) = 0.50939, \mathcal{S}\left({\mathcal{\beth }}_{{2}}\right) = 0.51361, \mathcal{S}\left({\mathcal{\beth }}_{{3}}\right) = 0.50384, \mathcal{S}\left({\mathcal{\beth }}_{{4}}\right) = 0.51654, and \mathcal{S}\left({\mathcal{\beth }}_{{5}}\right) = 0.49191.
Step 5. The other options are arranged based on their scores to determine the most favorable alternative, such as \mathcal{S}\left({\mathcal{\beth }}_{{4}}\right) > \mathcal{S}\left({\mathcal{\beth }}_{{2}}\right) > \mathcal{S}\left({\mathcal{\beth }}_{{1}}\right) > \mathcal{S}\left({\mathcal{\beth }}_{{3}}\right) > \mathcal{S}\left({\mathcal{\beth }}_{{5}}\right) . Therefore, {\mathfrak{H}}^{{4}} is the best energy supplier, and the alternatives ranking prescribed by the IVq-ROFHSEWA operator can be described as: {\mathfrak{H}}^{{4}} > {\mathfrak{H}}^{{2}} > {\mathfrak{H}}^{{1}} > {\mathfrak{H}}^{{3}} > {\mathfrak{H}}^{{5}} .
6.2.2. Selection of energy supplier using the IVq-ROFHSEWG operator
The computations in Steps 1 and 2 resemble those in the investigation outlined in Section 6.3.2.
Step 3. Determine the cumulative values for each possibility using Eq. (4.1) for q = 3 . This produces {\mathrm{\beth }}_{{1}} = ([0.29138, 0.62165], [0.37765, 0.67284]), {\mathrm{\beth }}_{{2}} = ([0.32475, 0.62146], [0.36534, 0.69495]), {\mathrm{\beth }}_{{3}} = ([0.28198, 0.57671], [0.36014, 0.68786]), {\mathrm{\beth }}_{{4}} = ([0.25109, 0.61962], [0.33903, 0.64671]), and {\mathrm{\beth }}_{{5}} = ([0.28602, 0.60792], [0.38589, 0.71652]).
Step 4. Determine the score values for every alternative using Eq (2.1), such as \mathcal{S}\left({\mathcal{\beth }}_{{1}}\right) = 0.47539, \mathcal{S}\left({\mathcal{\beth }}_{{2}}\right) = 0.47286, \mathcal{S}\left({\mathcal{\beth }}_{{3}}\right) = 0.45717, \mathcal{S}\left({\mathcal{\beth }}_{{4}}\right) = 0.48557, and \mathcal{S}\left({\mathcal{\beth }}_{{5}}\right) = 0.45385.
Step 5. The other options are arranged based on their scores to determine the most favorable alternative, such as \mathcal{S}\left({\mathcal{\beth }}_{{4}}\right) > \mathcal{S}\left({\mathcal{\beth }}_{{1}}\right) > \mathcal{S}\left({\mathcal{\beth }}_{{2}}\right) > \mathcal{S}\left({\mathcal{\beth }}_{{3}}\right) > \mathcal{S}\left({\mathcal{\beth }}_{{5}}\right) .
Therefore, {\mathfrak{H}}^{{4}} is the best energy supplier, and the alternatives ranking prescribed by the IVq-ROFHSEWA operator is as follows: {\mathfrak{H}}^{{4}} > {\mathfrak{H}}^{{1}} > {\mathfrak{H}}^{{2}} > {\mathfrak{H}}^{{3}} > {\mathfrak{H}}^{{5}} .
7.
Sensitivity and comparative analysis
In the following section, we investigate the sensitivity of our technique and compare our evaluations with those of past research.
7.1. Impact of the IVq-ROFHSEWA operator's " q " deviation on alternate classifications
Both alternatives {\mathfrak{H}}_{{4}} and {\mathfrak{H}}_{{5}} adhere to the corporation's laws and regulations, with {\mathfrak{H}}_{{4}} being the one of preference and {\mathfrak{H}}_{{4}} be a most beneficial supplier in energy management. When 3\le q\le 12 , as indicated in Table 3, the ranking of alternatives remains unchanged and resilient. Specifically, {\mathfrak{H}}_{{4}} regularly outperforms {\mathfrak{H}}_{{2}} , {\mathfrak{H}}_{{1}} , {\mathfrak{H}}_{{3}} , and {\mathfrak{H}}_{{5}} . The score values decrease as the numerical value of " q " increases, illustrating the influence of the parameter " q " on evaluation calculations. When the expression {\left({MD}^{\mathcal{u}}\right)}^{q}+{\left({NMD}^{\mathcal{u}}\right)}^{q} > 1 , if q\ge 3 , both IVIFHSS [18] and IVPFHSS [20] are unable to refute this corroborating evidence. The versatility of the information extraction technique is contingent upon the specific value of the parameter " q ". The research illustrates the benefits of organizing a parameter in a way that enables specialists to analyze it effectively. It provides guidance on how to determine parameter values based on individual preferences.
The technique offered improves the integration of dependable evidence, clarifying ambiguous or untrustworthy material and enhancing its quality. Table 5 outlines the conversion of various hybrid structures of FS into the specific example of IVq-ROFHSS. All these alterations take place when components adhere. Professionals can perform a more comprehensive behavior evaluation using parameter " q ". Experts strongly recommended choosing the value of " q " to identify and assess a continuous pattern or trend. Through this investigation and assessment process, it has been determined that the results generated by the proposed methodology are superior to those gained by alternative methods. The influence of the " q " value on the obtained results is in Figure 3, displayed below.
The presented strategy enhances the incorporation of reliable evidence, explaining unclear or unreliable data, making it better. As described in Table 5, different hybrid structures of FS are converted into the case of IVq-ROFHSS. All these modifications occur while particular components conform. Experts can execute a more detailed behavior assessment using the parameter " q ". It is strongly advised that experts select the value of " q " to recognize and evaluate an ongoing pattern or trend. Through this process of inquiry and evaluation, it is identified that the outcomes produced by the approach that has been offered are more effective than those achieved by different methods. The impact of the " q " value on the results obtained is illustrated clearly in Figure 3, which can be seen below.
7.2. Impact of the IVq-ROFHSEWG operator's "q" deviation on alternate classifications
To determine how much the parameter " q " affects the final evaluation outcome, we compared several values for q . The data analysis revealed two distinct ranking patterns: {\mathfrak{H}}^{{4}} > {\mathfrak{H}}^{{1}} > {\mathfrak{H}}^{{2}} > {\mathfrak{H}}^{{3}} > {\mathfrak{H}}^{{5}} (q = 3-6) and {\mathfrak{H}}^{{4}} > {\mathfrak{H}}^{{2}} > {\mathfrak{H}}^{{1}} > {\mathfrak{H}}^{{3}} > {\mathfrak{H}}^{{5}} (q = 7-12) see Table 4. This adjustment did not affect the ranking of the most advantageous and least advantageous selections, which is an important and noteworthy point to consider. Furthermore, the gradual decrease in score values for the alternatives, along with an increase in q , indicates a clear dependence of score values on the parameter's value. During the preceding analysis, it became evident that altering the variable " q " could impact the arrangement of options in terms of their structure. Experts can independently assign a value to " q " to determine the most beneficial supplier. The study's findings emphasize the importance of expert discourse on the significance of the " q " parameter, even when the alternative rank remains consistent.
Altering the parameter q is crucial for exerting an impact on the reasoning behind available alternative options. When conventional methods such as IVIFHSS and IVPFHSS are insufficient for handling the observed data, IVq-ROFHSS successfully addresses this limitation. Therefore, experts can assess the reliability of the information by establishing a suitable value for q . Professionals must meticulously evaluate suitable parameter values while creating reliable, top-notch alternatives. The IVq-ROFHSEWG operator preserves the logical sequence of options when q\ge 7 . Thus, in this scenario, experts have the option to select a value of q\ge 7 . Figure 4 illustrates the influence of q on the arrangement of choices.
7.3. Comparison with different fuzzy structures
We describe the approach to dealing with the challenges of creating a sustainable supplier in energy management. We offer a systematic approach to tackling MAGDM difficulties with the IVq-ROFHSS methodology. When it comes to handling MAGDM difficulties, the suggested approach provides better accuracy and adherence than the currently used ones. The framework's versatility and comprehensiveness support predictable, stable, and customizable results. To cover various points of view, the proposed method can be modified to support several models with dynamic sequencing capabilities. We conducted thorough analytical analyses and assessments to show that our suggested strategy yields result similar to hybrid approaches. The proposed approach is adaptable and capable of converting various structures, including FS, IFS, PFS, and q-ROFS, into unique IVq-ROFHSS situations by adjusting specific configurations. This attribute allows for the intentional selection and future execution of object-specific particulars, making it ideal for incorporating unclear and conflicting information in decision-making processes. Based on thorough investigation and evaluation, the researchers have determined that their findings regarding the suggested technique have greater applicability compared to any other current organization. They recognize that the anticipated development of the data management system encompasses a broad spectrum of possibilities aimed at mitigating data-related problems in comparison to existing data management systems. In general, the proposed design is deemed efficient, versatile, and beneficial, surpassing current hybrid designs incorporating FS, IFS, PFS, and q-ROFS. Incorporating appropriate associations helps to resolve the integration issues that arise from upgrading IVq-ROFSS to IVq-ROFHSS. Applying periodic and vague assumptions to the existing framework is an unexpected yet favorable enhancement. This enhancement facilitates the methodical and suitable choice of well-being attributes. The DM technique in FS situations involves the combination of hypothetical and unpleasant aspects to surprise raise the relevance and complexity of the framework. Table 5 provides a comprehensive comparison of the features of the proposed and existing techniques. The proposed approach effectively addresses the challenges of establishing a sustainable energy provider and showcases flexibility and adaptability, making it a suitable tool for various decision-making objectives.
The implementation of a new MAGDM technique is driven by the necessity to address the limitations of existing fuzzy frameworks. This proposed methodology is notable for its utilization of IVq-ROFHSS, which enables a comprehensive assessment of the MD and NMD sub-attributes. The current hybrid models, such as IVFS, IVIFS, IVPFS, IVFSS, IVIFSS, IVIFHSS, IVPFSS, and IVPFHSS, could not adequately provide a comprehensive understanding of the technique's condition. The MAGDM methodology for IVq-ROFHSS is a dependable, accurate, versatile, and customizable method, suitable for many scenarios with varying levels of disparity, incongruities, and alteration. The research findings indicate that forthcoming technologies yield superior and more comprehensive results compared to present methods, as shown in Table 5. The proposed hybrid configuration of FS shows significant potential in various domains, including organizational studies, medical research, and decision-making processes including the management of inaccurate and unclear information. The proposed technique of DM under IVq-ROFHSS offers a more effective and successful method for addressing MAGDM difficulties.
7.4. Comparison with different fuzzy operators
Experiments and studies provide evidence of the efficacy of the established MAGDM approach. The investigations demonstrate that the results from this approach align with those achieved through traditional methods. The proposed framework enables incorporating specific information regarding alternative parameters into different decision-making procedures and addressing deficiencies in the available data. This enhances credibility and is founded on examining factual details on objects, making it a valuable instrument for evaluating ambiguous and perplexing data in management. The technique ensures data integrity by considering the interactions among the scores assigned to multiple components. This unique methodology surpasses previous methods by emphasizing perceptual understanding and coherence through clarifications, hence avoiding decisions influenced by erroneous preconceived notions. The proposed MAGDM technique thoroughly evaluates all options before choosing a supplier selection strategy in energy management. The model effectively handles these challenges and is thoroughly compared to current methodologies. The impacts of employing this approach in selecting a sustainable energy supplier are displayed in Table 6, demonstrating its effectiveness and reliability. When data is irrelevant or does not apply, it is represented as "n/a".
Table 6 demonstrates an evaluation matrix for analyzing multiple operators and their results. After assessing the data, it is apparent that the {\mathfrak{H}}^{{4}} alternate is the best alternative for sustainable energy suppliers. Table 6 indicates deficiencies in previous studies, as stated in the literature [41,42,45,46,48], particularly concerning parametric modelling. Operators in the literature [49,50] manage the parametric values of alternatives, but these studies cannot manage the expert's opinion in intervals form. The techniques described in [52] competently regulate the parametrized values linked to alternatives within the identified issue.
Managing sub-attributes of alternatives is an obstacle for present methods. The PFHSEWA [53] and PFHSEWG [54] operators have specific expertise to assess the information. However, these aggregation operators cannot deal with the situation when {\left(MD\right)}^{{2}}+{\left(NMD\right)}^{{2}} > 1 . On the other hand, the q-ROFHSEWA [22] and q-ROFHSEWG [22] operators competently deal with the issues mentioned above. Plans have solved this problem by incorporating interval forms and sub-attributes, as demonstrated in structures such as IVIFHSS [46] and IVPFHSS [48]. However, these efforts may not always be appropriate for any particular case. Whereas confident current aggregate operators can manage specific problems, there are situations where they are insufficient. The strategy suggested in this paper effectively tackles those issues, providing a more comprehensive and efficient solution for evaluating options. A comparative study assesses the proposed MAGDM model's effectiveness compared to other existing operators. The order of the five finest alternatives shows that the novel approach is in line with the conventional strategy, demonstrating the reliability and productivity of the proposed technique, which may provide precise and trustworthy results in many situations.
7.5. Limitations and future implications of the proposed structure
Interval-valued q-rung orthopair fuzzy hypersoft sets have some of the shortcomings:
(i) The mathematical structure may be challenging to recognize, especially for individuals unfamiliar with multifaceted fuzzy set ideas, thus impeding implementation.
(ii) The algorithm's performance is substantially reliant upon the reliability and specificity of its input data; inferior data may result in improper decisions.
(iii) The IVq-ROFHSS analyses are computationally challenging, making them insufficient for immediate decision-making scenarios or operations involving extensive databases.
(iv) However, intended to deal with incertitude, IVq-ROFHSS can fail to generally apply to all decision problems, particularly ones preferring an extra simplistic or direct technique.
(v) Selecting suitable parameters for IVq-ROFHSS may be unreliable, resulting in multiple outcomes due to various interpretations.
(vi) The conceptual basis of IVq-ROFHSS can be simpler than those of other fuzzy set ideas, impeding its acceptability into the broader research community.
(vii) Whereas IVq-ROFHSS attempts to boost decision-making, its effectiveness relative to conventional fuzzy methods or different MCDM strategies remains adequately confirmed, necessary for more empirical studies.
Managing such drawbacks in future studies may enhance the usefulness and stability of IVq-ROFHSS in real-world decision scenarios. This research connects to the investigation of Sarwar and Li [59], as it evaluates the implementation of fuzzy theory in decision-making, especially as it relates to IVq-ROFHSS. Our plan of using Einstein aggregation operators to boost MAGDM resembles the strategies that Xia et al. [60] and Gao et al. [61] used to build controllers and stabilizing strategies using Takagi-Sugeno fuzzy structures. Integrating fuzzy logic into our selection algorithms is essential for adequately handling convoluted cases, and we resolve problems identical to those encountered by Ge and Zhang [62], who developed dynamic inventory controllers in unreliable circumstances. Since we focus on combining fuzzy logic and sophisticated control techniques to manage both uncertainty and complexity in decision-making infrastructure, it is influenced by the work of Zhang et al. [63], Sun et al. [64], and Duan et al. [65].
8.
Conclusions
The effectiveness of MAGDM appears to be hindered by the interplay of multiple opposing facets that constitute a crucial component of complex problem domains. The conceptual framework of MAGDM must effectively incorporate all potential improvements that appropriately represent aspects from the engineering, business, and health sectors. Our main purpose of this study is to construct effective decision-making methods within the broader context of IVq-ROFHSNs. We present the concept of Interval-valued q-rung orthopair fuzzy hypersoft sets, which incorporate Einstein's operational laws. Based on these operational laws, we also suggest aggregation operators, namely IVq-ROFHSEWA and IVq-ROFHSEWG operators. These operators possess basic characteristics. To showcase the benefits of this analytical methodology, we carried out an empirical inquiry to ascertain the most viable sustainable energy provider in energy management. The comparison analysis emphasizes the method's effectiveness and longevity, demonstrating its ability to withstand challenges and assist decision-makers in the DM procedure.
Further study will prioritize the examination of Einstein-ordered AOs, the analysis of similarity and distance metrics, and their associated attributes. To further study the practical use of IVq-ROFHSNs in material selection, pattern identification, information fusion, medical diagnostics, and autonomous agriculture, we will investigate the integration of several MAGDM approaches. In addition, several ordered, algebraic, and topological structures for IVq-ROFHSNs will be proposed, focusing on their application in different DM techniques.
Author contributions
Muhammad Saqlain: Conceptualization, methodology, writing—original draft; Xiao Long Xin: Writing—original draft, supervision, and conceptualization; Rana Muhammad Zulqarnain: Writing—original draft, writing the review, and editing; Imran Siddique: Data validation, software, writing the original draft, and writing the review; Sameh Askar: Writing—original draft, funding acquisition, and project administration; Ahmad M. Alshamrani: Writing the review, language editing, and funding acquisition. All authors have read and agreed to the published version of the manuscript.
Acknowledgments
The authors present their appreciation to King Saud University for funding the publication of this research through the Researchers Supporting Program (RSPD2024R533), King Saud University, Riyadh, Saudi Arabia.
Conflict of interest
The authors declare no competing interests.
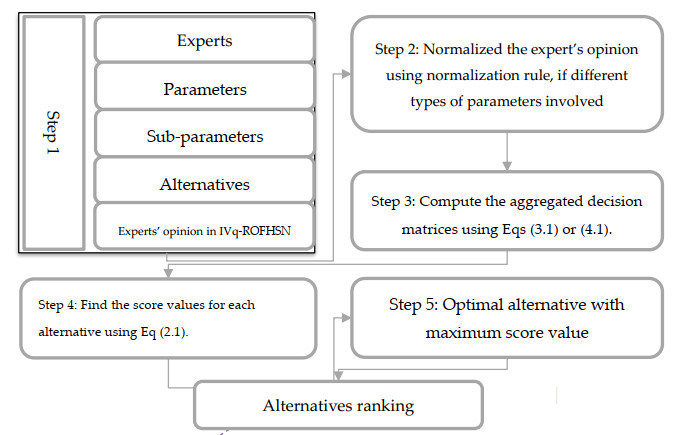









 DownLoad:
DownLoad: