An intelligent water drop algorithm with deep learning driven vehicle detection and classification

1.   Introduction

Because of improved living conditions and technological innovations in the healthcare sector, the world's aging population continues to increase at an unprecedented rate, which has far-reaching implications for society. Population aging presents economic, cultural and social challenges to individuals, families, societies and the global community. In the past few decades, there has been growing recognition that the health status, mortality risks, productivity and other socioeconomic characteristics of aging people have changed significantly in various parts of the world. Thus, there is a growing demand for old-age security and facilities, residential care homes and community elderly care for the aging population ^[1]. In this regard, government and non-government health and welfare organizations have been encouraged by the World Health Organization to implement strategies to create living homes that are more age friendly ^[2].

The emergence of gerontechnology (GT) can help ease aging-based health, family, and social burdens ^[1]. The aim of GTs is to improve the living environment and the access to important services and infrastructure of older persons, reimburse for their loss of individuality and, in due course, allow them to live at home as long as possible ^[3,4]. The term "gerontechnology" combines two words: "gerontology" which means the scientific study of aging, and "technology, " which means the research and development of various products and techniques. In the literature, several authors have focused on the application of GTs in different areas ^[5,6,7].

As the selection of GTs involves numerous criteria and uncertainties, it can be considered an uncertain multi-criteria decision-making (MCDM) problem. To deal with uncertainty, researchers have focused on the theory of fuzzy set (FS) ^{[8,9,10,11,12,13,14]}. As an advancement of the FS, the idea of an intuitionistic fuzzy set (IFS) ^[15] was later introduced. It can better describe the vagueness of data compared with FS theory. In an IFS, an object is described by its membership degree (MD), non-membership degree (ND) and hesitancy degree (HD) to illustrate the uncertain data more systematically. Yuan and Luo ^[16] suggested an MCDM tool by combining intuitionistic fuzzy (IF) entropy and evidential reasoning with experimental analyses. Yan et al. ^[17] proposed a hybridized MCDM framework for urban rail transit system selection under an IF environment. A multi-objective tool using the Markowitz and data envelopment analysis (DEA) cross-efficiency methods has been developed to evaluate portfolios under the IFS context ^[18]. Tripathi et al. ^[19] provided a distance measure for IFSs and applied it to introduce a modified IF complex proportional assessment (COPRAS) method. In recent years, many theories and applications related to IFSs have been presented ^{[20,21,22,23,24,25,26,27,28,29]}.

The divergence measure (DM) is an important and useful way to estimate the discrimination between two objects. In the context of the IFS, Vlachos and Sergiadis ^[30] first introduced the notion of DM, with applications in image segmentation and pattern recognition. Montes et al. ^[31] presented an axiomatic definition of the IF-DM with its properties. In recent years, several IF-DMs have been proposed, each with their unique advantages and disadvantages. For instance, Joshi and Kumar ^[32] proposed a Jensen-Shannon DM based on Jensen inequality and Shannon entropy under an IF environment. Verma ^[33] studied order-$\alpha$ DM for IFSs and applied it to the development of an algorithm for the intuitionistic fuzzy MCDM method. A new generalized parametric DM for IFSs, which is also used for medical diagnosis, was likewise developed ^[34]. Tripathi et al. ^[35] introduced a new IF-DM with excellent properties. They also used their measure to introduce a combined compromise solution (CoCoSo) method under the IFS context.

In realistic MCDM situations, choosing the most appropriate option from a set of options is a highly important task. In the literature, several MCDM approaches, such as the technique for order of priority by similarity to ideal solution (TOPSIS), COPRAS, additive ratio assessment (ARAS), weighted aggregated sum product assessment (WASPAS), CoCoSo and multi-attribute multi-objective optimization by ratio analysis (MULTIMOORA), have been introduced to address practical decision-making problems under diverse environments. Despite improvements that have been made to enhance the effectiveness of utility degree-based tools, such as TOPSIS, COPRAS, Viekriterijumsko Kompromisno Rangiranje, WASPAS, ARAS, and CoCoSo, in diverse MCDM circumstances, their problem-solving methods are subject to several limitations, and the ranking process is very complicated and challenging in some cases. To avoid the drawbacks of existing methods, Stanujkic et al. ^[36] proposed the idea of a simple weighted integrated sum product (WISP) as a more effective and useful MCDM method. The WISP incorporates the idea of the ARAS, WASPAS, CoCoSo and MULTIMOORA approaches and uses simpler normalization processes and four utility functions to obtain the overall utility degree (OUD) of options. After the pioneering work of Stanujkic et al. ^[36], Karabaševic et al. ^[37] gave the WISP tool using triangular fuzzy numbers and proved its usability through numerical examples. In the context of the IFS, a modified WISP method was developed by Zavadskas et al. ^[38] using square root and sum normalization procedures. Stanujkic et al. ^[39] generalized the WISP method from a single-valued neutrosophic perspective. They implemented their method in a tourist destination for nature & rural tourism under a single-valued neutrosophic environment. Recently, a q-rung orthopair fuzzy extension of the WISP method was proposed by Deveci et al. ^[40]. They applied their method to rank sustainable urban transportation in metaverse with uncertainty.

1.1.   Challenges identified from studies

From existing studies, we recognize the following gaps:

(1) The DM and score function are essential tools for IFSs. Various DMs and score functions have been presented by researchers in the literature. However, there is a need to develop an improved IF-DM and score function from an IF perspective.

(2) To avoid the redundant influence of subjective DEs' significance on the decision results, there is a need to derive the weights of the DEs' opinions.

(3) In the context of intuitionistic fuzzy MCDM methods, most previous studies have discussed extant objective weighting methods or subjective weighting methods. To avoid the shortcomings of objective or subjective weighting models, there is a need to develop an integrated weighting model for determining criteria weights. However, extant subjective weighting tools rarely consider the relative closeness coefficient (RCC) degree as a weighting tool from an IF perspective.

(4) Zavadskas et al. ^[38] presented the standard WISP method from an IF perspective. However, this method has some drawbacks: (ⅰ) it considers only a single normalization procedure, (ⅱ) it is unable to determine the objective and subjective weighting of the attribute, and (ⅲ) multiple preferences of decision experts (DEs) are missing.

(5) In the literature, only Halicka and Kacprzak ^[4] implemented the classical TOPSIS method in the evaluation of a set of GTs over a finite number of criteria. However, this method has limitations in solving the multiple criteria GT assessment problem under an IF environment.

1.2.   Research contributions

The notable research contributions of this study are as follows:

● To order intuitionistic fuzzy numbers (IFNs), this study proposes a new IF score function.

● To measure the discrimination degree for IFNs, a new DM and its properties are presented.

● This study proposes, for the first time, the score function and rank sum (RS) model-based weighting approach to derive DEs' weights in an IFS environment.

● To consider the RCC of each criterion, an IF-DM-based model is developed and further used to compute the criteria weights.

● This study also proposes the double normalization (DN)-based WISP method with a combination of the score function, the DM and the RCC, which can better describe the uncertainty of practical decision-making problems. This study implements the proposed IF-RCC-DN-WISP method in a case study of a GT assessment problem under an IFS context.

1.3.   Organization of the paper

The rest of this paper is organized as follows. Section 2 discusses the fundamental ideas of IFSs. Section 3 presents the new IF-DM and IF-score functions. Section 4 introduces an integrated IF-RCC-DN-WISP framework with the proposed DM, score function and RCC. Section 5 uses the developed method in a case study of different GTs for aging persons and people with disability. This section also presents a comparative analysis. Finally, Section 6 provides the conclusions and recommendations for further research.

2.   Preliminaries

This section describes certain elementary concepts related to the IFS.

Definition 2.1. ^[15] An IFS $A$ on a fixed set $X = \left\{ {{x_1}, \, \, {x_2}, \, \, ..., \, \, {x_n}} \right\}$ is given as

where ${\mu _A}:X \to [0, \, \, 1]$ shows the MD, and ${\nu _A}:X \to [0, \, \, 1]$ denotes the ND of an element ${x_i}$ to A in $X,$ with the condition $0 \leqslant {\mu _A}\left( {{x_i}} \right) + {\nu _A}\left( {{x_i}} \right) \leqslant 1.$ For ${x_i} \in X$ to A, the degree of indeterminacy is defined as ${\pi _A}\left( {{x_i}} \right) = 1 - {\mu _A}\left( {{x_i}} \right) - {\nu _A}\left( {{x_i}} \right)$ and $0 \leqslant {\pi _A}\left( {{x_i}} \right) \leqslant 1.$ Furthermore, Xu ^[41] defined the term $\left( {{\mu _A}({x_i}), \, \, {\nu _A}({x_i})} \right)$ called IFN as $\omega \, = \, \left( {{\mu _\omega }, \, {\nu _\omega }} \right)$, which fulfills ${\mu _\omega }, \, {\nu _\omega }\, \in \, \left[ {0, \, 1} \right]$ and $0\, \leqslant \, {\mu _\omega } + {\nu _\omega } \leqslant \, 1.$ The symbol IFS (X) shows all the IFSs on X.

Definition 2.2. ^[41,42] Consider an IFN $\omega \, = \, \left( {{\mu _\omega }, \, {\nu _\omega }} \right),$ and then

are said to be the score and accuracy degrees, respectively.

Definition 2.3. ^[41] Let ${\omega _j} = \left( {{\mu _{{\omega _j}}}, \, {\nu _{{\omega _j}}}} \right), j = 1, 2, ..., n$ be the IFNs. The weighted averaging and geometric operators in the IFNs are then presented as

where ${w_j} = {\left( {{w_1}, {w_2}, ..., {w_n}} \right)^T}$ is a weight value of ${\omega _j}, \, \, j = 1, 2, ..., n,$ with $\sum\nolimits_{j = 1}^n {{w_j} = 1} ,$$\, {w_j} \in \left[ {0, \, \, 1} \right].$

Definition 2.4. ^[31] Let ${A_1}, \, {A_2}, \, {A_3}\, \in \, IFSs\left( X \right).$ An IF-DM is a real-valued mapping $D:IFS\left(X\right)\times IFS\left(X\right)\to \mathbb{R}$ that satisfies the properties as

$({\rm{D1}})\; D\left( {{A_1}, \, {A_2}} \right)\, = \, D\left( {{A_2}, \, {A_1}} \right), \, \, \forall \, {A_1}, \, {A_2}\, \in \, IFSs\left( X \right),$

$({\rm{D2}})\; D\left( {{A_1}, \, {A_2}} \right)\, = \, 0\, \Leftrightarrow \, {A_1}\, = \, {A_2},$

(D3) $D\left( {{A_1}\, \cap {A_3}, \, {A_2}\, \cap {A_3}} \right)\, \leqslant \, D\left( {{A_1}, \, {A_2}} \right), \, \, \forall \, {A_3}\, \in \, IFS\left( X \right),$ and

$({\rm{D4}})\; D\left( {{A_1}\, \cup {A_3}, \, {A_2}\, \cup {A_3}} \right)\, \leqslant \, D\left( {{A_1}, \, {A_2}} \right), \, \, \forall \, {A_3}\, \in \, IFS\left( X \right).$

3.   Proposed DM and score function for IFSs

In this part of the study, we discuss the new DM and score function based on the exponential function for IFSs.

3.1.   New DM for IFSs

Definition 3.1. For any ${A_1}, \, {A_2} \in \, IFSs\left( X \right),$ the DM between ${A_1}$ and ${A_2}$ for IFSs is given by

Theorem 3.1. The measure $D\left( {{A_1}, \, {A_2}} \right)$ is a valid IF-DM.

Proof. (D1). It is obvious from (1) that $D\left( {{A_1}, \, {A_2}} \right)\, = \, D\left( {{A_2}, \, {A_1}} \right).$

(D2). If $D\left( {{A_1}, \, {A_2}} \right)\, = \, 0.$ From Eq (1), we then have

As both terms are nonnegative for all input values, we have

This implies that

It is possible that if ${\mu _{{A_1}}}\, = \, {\mu _{{A_2}}}$ and ${\nu _{{A_1}}}\, = \, {\nu _{{A_2}}},$ ${A_1}\, = \, {A_2}.$ Similarly, we can prove that if ${A_1}\, = \, {A_2},$ then $D\left( {{A_1}, \, {A_2}} \right)\, = \, 0.$

(D3).

From $\min \left\{ {{\mu _{{A_1}}}({x_i}), \, {\mu _{{A_3}}}({x_i})} \right\},$$\min \left\{ {{\mu _{{A_2}}}({x_i}), \, {\mu _{{A_3}}}({x_i})} \right\},$$\max \left\{ {{\nu _{{A_1}}}({x_i}), \, {\nu _{{A_3}}}({x_i})} \right\},$ and $\max \left\{ {{\nu _{{A_2}}}({x_i}), \, {\nu _{{A_3}}}({x_i})} \right\},$ we have

From (7) and (8), Eq (6) becomes

(D4). Similar to (D3)

Therefore, the proof is completed.

3.2.   New score function for IFSs

Definition 3.2. For any $\omega = \, \left( {{\mu _\omega }, \, {\nu _\omega }} \right),$ the score function of IFN $\omega$ is given by

Theorem 3.2. The score function ${\text{S}}$ of an IFN $\omega = \, \left( {{\mu _\omega }, \, {\nu _\omega }} \right)$ increases monotonically over ${\mu _\omega }$ and decreases monotonically over ${\nu _\omega }.$

Proof. The first partial derivative of Eq (9) over ${\mu _\omega }$ is given as

Likewise, the first partial derivative of Eq (9) over ${\nu _\omega }$ is presented as

Therefore, the theorem is proven.

Theorem 3.3. The score function ${\text{S}}$ of an IFN $\omega = \left( {{\mu _\omega }, \, {\nu _\omega }} \right)$ fulfills the given axioms:

(P1) ${\text{S}}\left( {(0, \, 1)} \right) = \, 0$ and ${\text{S}}\left( {(1, \, 0)} \right) = \, 1.$

$({\rm{P2}})\; 0 \leqslant {\text{S}}\left( \omega \right) \leqslant \, 1.$

Proof. (P1) For an IFN $\omega \, = \, \left( {0, \, 1} \right),$ based on Eq. (9), we get ${\text{S}}\left( {(0, \, 1)} \right) = \, 0$. For an IFN $\omega = \, \left( {1, \, 0} \right),$ based on Eq (9), we get ${\text{S}}\left( {(1, \, 0)} \right) = \, 1.$ Thus, we obtain ${\text{S}}\left( {(0, \, 1)} \right) = \, 0$ and ${\text{S}}\left( {(1, \, 0)} \right) = \, 1.$

(P2) According to (P1), we get $0 \leqslant {\text{S}}\left( \omega \right) \leqslant \, 1.$

Theorem 3.4. Let ${\omega _1} = \, \left( {{\mu _1}, \, {\nu _1}} \right)$ and ${\omega _2} = \, \left( {{\mu _2}, \, {\nu _2}} \right)$ be two IFNs. If ${\omega _1} \subseteq {\omega _2},$ that is, ${\mu _1}\, > \, {\mu _2}$ and ${\nu _1}\, < \, {\nu _2},$ then ${\text{S}}\left( {{\omega _1}} \right) \leqslant {\text{S}}\left( {{\omega _2}} \right).$

Proof. From Theorem 3.2, we know that ${\text{S}}\left( . \right)$ increases monotonically over ${\mu _\omega }$ and decreases monotonically over ${\nu _\omega }.$ Therefore, if ${\mu _1}\, > \, {\mu _2}$ and ${\nu _1}\, < \, {\nu _2},$ then ${\text{S}}\left( {{\omega _1}} \right) \leqslant {\text{S}}\left( {{\omega _2}} \right).$

Definition 3.3. Let ${\omega _1}, {\omega _2} \in IFNs.$ The comparative scheme based on the proposed score function is discussed to order any two IFNs ${\omega _1}$ and ${\omega _2}$ as follows.

● If $\bar {\text{S}}\left( {{\omega _1}} \right)\, > \, \bar {\text{S}}\left( {{\omega _2}} \right),$ then ${\omega _1}\, {\text{ f }} \, {\omega _2},$

● If $\bar {\text{S}}\left( {{\omega _1}} \right)\, < \bar {\text{S}}\left( {{\omega _2}} \right),$ then ${\omega _1}\, {\text{ p }} \, {\omega _2},$

● If $\bar {\text{S}}\left( {{\omega _1}} \right)\, = \bar {\text{S}}\left( {{\omega _2}} \right),$ then

■ If ${\text{S}}\left( {{\omega _1}} \right)\, > \, {\text{S}}\left( {{\omega _2}} \right),$ then ${\omega _1} {\text{ f }} \, {\omega _2},$

■ If ${\text{S}}\left( {{\omega _1}} \right)\, < {\text{S}}\left( {{\omega _2}} \right),$ then ${\omega _1} {\text{ p }} \, {\omega _2},$

■ If ${\text{S}}\left( {{\omega _1}} \right)\, = {\text{S}}\left( {{\omega _2}} \right),$ then ${\omega _1} = {\omega _2},$

o If $h\left( {{\omega _1}} \right)\, > \, h\left( {{\omega _2}} \right),$ then ${\omega _1} {\text{ f }} \, {\omega _2},$

o If $h\left( {{\omega _1}} \right)\, < \, h\left( {{\omega _2}} \right),$ then ${\omega _1} {\text{ p }} \, {\omega _2},$

o If $h\left( {{\omega _1}} \right)\, = \, h\left( {{\omega _2}} \right),$ then ${\omega _1} = {\omega _2}.$

4.   An integrated IF-RCC-DN-WISP method for MCDM problems

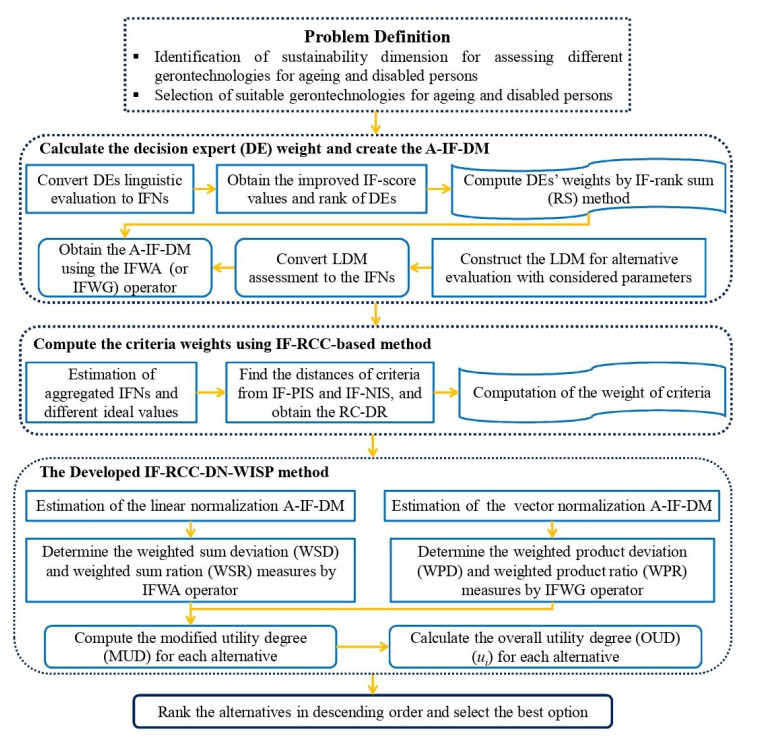
By uniting the notions of weighted sum measure (WSM) and weighted product measure (WPM), the conventional WISP model uses a normalization process and the four utility functions to find the overall utility value of an option. In this study, we propose an RCC and DN procedure-based intuitionistic fuzzy WISP approach called the IF-RCC-DN-WISP framework. In this method, we present a new score function and RS model-based procedure to derive the DEs' weights. The detailed procedure is as follows (see Figure 1).

Step 1: Form a linguistic decision matrix (LDM).

A group of DEs $\, \left\{ {{g_1}, \, {g_2}, \, ..., \, {g_l}} \right\}$ is formed to choose an appropriate option from a set of options $\left\{ {{T_1}, \, {T_2}, \, ..., \, {T_m}} \right\}$ over a criterion set $r = \, \left\{ {{r_1}, \, {r_2}, \, ..., \, {r_n}} \right\}.$ Assume that $M\, = \, {\left( {\chi _{ij}^{(k)}} \right)_{m \times n}} = {\left( {\mu _{ij}^{(k)}, \nu _{ij}^{(k)}} \right)_{m \times n}},$ $i\, = 1, \, 2, \, ..., m,$ $j\, = 1, \, 2, ..., n$ are the LDM presented by the DEs, where $\chi _{ij}^{(k)}$ describes the linguistic value (LV) rating of an option ${T_i}$ over criterion ${r_j}$ for ${k^{th}}$ expert.

Step 2: Compute the DEs' weights.

First, consider the significance of the DEs' opinions as linguistic variables. In accordance with the linguistic rating, the formula for the weight value is

Here, ${\varpi _k}\, \geqslant \, 0$ and $\sum\limits_{k\, = 1}^{\text{l}} {{\varpi _k}\, = \, 1} .$ The term l denotes the number of DEs, and r_k denotes the rank of the DE, k = 1, 2, 3, ..., l ^[43].

Step 3: Make an aggregated intuitionistic fuzzy decision matrix (A-IF-DM).

To combine the LDM, we apply Eq (3) (or Eq (4)) to the IF-DM $M\, = \, {\left( {\chi _{ij}^{(k)}} \right)_{m \times n}}$ and obtain the A-IF-DM $Z = {\left( {{z_{ij}}} \right)_{m\, \times \, n}},$ where

Step 4: Calculate the criteria weight using the IF-RCC-based method.

To find the criteria weights, the IF-RCC-based procedure is applied. Let $w = {\left( {{w_1}, {w_2}, ..., {w_n}} \right)^T}$ be the criteria weight with $\sum\limits_{j = 1}^n {{w_j}} \, = 1$ and $\, {w_j} \in \left[ {0, \, \, 1} \right]$. The process for determining the attribute weight by the IF-RCC-based model is discussed as follows:

Step 4a: Estimate the aggregated IFNs by combining the LDM assessment degrees provided by the DEs using the intuitionistic fuzzy weighted aggregation (IFWA) operator and obtained using $G = {\left( {{z_j}} \right)_{1 \times \, n}}.$

Step 4b: Discuss the IF ideal values.

An IFN has a positive ideal solution (PIS) and a negative ideal solution (NIS), which consider the ratings ${\phi ^ + }$ = (1, 0, 0) and ${\phi ^ - }$ = (0, 1, 0), respectively; it is noted that there are no significant differences in their results.

Step 4c: Derive the distances of the criteria from the IF-PIS and IF-NIS.

To compute the distances, the proposed IF-DM is applied. The measures $p_j^ +$ and $p_j^ -$ are applied in Eq (5) to elucidate the distances from $G = {\left( {{z_j}} \right)_{1 \times \, n}},$ and the IF-PIS and IF-NIS, respectively.

Step 4c: Compute the relative closeness-decision rating (RC-DR).

The RC-DR states the kind of optimization (benefit or cost) of each attribute.

Step 4d: Obtain the criteria weight $\left( {{w_j}} \right)$ as follows:

Step 5: Determine the normalized A-IF-DM using linear and vector normalization procedures.

Step 5a: The linear normalization process is given by

such that $\bar \mu _{ij}^{\left( 1 \right)} = \frac{{{\mu _{ij}}}}{{{{\max }_i}\;{\text{S}}\left( {{z_{ij}}} \right)}}, \, \, \bar \nu _{ij}^{\left( 1 \right)} = \frac{{{\nu _{ij}}}}{{{{\max }_i}\;{\text{S}}\left( {{z_{ij}}} \right)}}$, and ${\text{S}}\left( . \right)$ are the proposed score functions of the IFNs.

Step 5b: The vector normalization process is used to normalize the A-IF-DM $\not{\text{c}} = {\left( {{z_{ij}}} \right)_{m\, \times \, n}}$ into

such that

Step 6: Compute the measures of the weighted sum deviation (WSD) and weighted sum ratio (WSR) using a linear normalization procedure.

To obtain the deviation's measure, we first define the combined assessment degree using the IFWA operator for the benefit and cost criteria as

In accordance with the score values of the combined assessment degree, the measures of the WSD and WSR are defined as

Step 7: Compute the measures of the weighted product deviation (WPD) and weighted product ratio (WPR) using the vector normalization procedure.

We use vector normalization with the intuitionistic fuzzy weighted geometric (IFWG) operator for the benefit and cost criteria as

In accordance with the score values of the combined assessment degree, the measures of the WPD and WPR are defined as

Step 8: Compute the modified utility degree (MUD) of each option.

The degree of measures given in Eqs (21), (22), (25) and (26), can be zero, positive, or negative. Consequently, they should be mapped into interval [0, 1] using Eqs (27) and (30). Thus, the MUDs of each option are presented as follows:

Step 9: Determine the OUD of each option.

Step 10: Rank the alternatives as per the OUDs.

5.   Case study: Gerontechnology selection (GTS) for aging persons and people with disability

Gerontechnology combines gerontology and technology to satisfy the requirements of an aging society ^{[44,45,46,47]}. Gerontechnologies help enhance the quality of life of aging persons and provide them with access to goods, facilities and infrastructure ^[45].

In the study, we consider five GTs as GT groups or classes: housing and safety (T₁), mobility (T₂), interpersonal communication (T₃), care (T₄) and health (T₅). On the basis of a survey and discussions with experts, we use the following criteria: innovation (r₁), demand for gerontechnology (r₂), socio-ethical (r₃), usability (r₄), functionality (r₅), ease of use (r₆) and risk of use (r₇) ^[48]. The above-mentioned GTs are considered alternatives for this case study. In the evaluation process of the GTS, each DE uses their knowledge of the criteria considered.

To choose the best GT groups/classes, a group of four DEs (g₁, g₂, g₃ and g₄) is created. These DEs are from various disciplines and comprise researchers in GT groups/classes, stockholders, professors and managers. The respondent in each GT group/class evaluates the aforementioned criteria using an 11-stage scale, where "AB" means absolutely bad and "AG" means absolutely good.

The procedure for the execution of the IF-RCC-DN-WISP approach in the present case study is presented in the following:

Steps 1–3: Table 1 is taken from ^[49,50,51] to show the LVs with the IFNs and determine the DEs' weights and the above-mentioned criteria for prioritizing the GTs for aging persons and people with disability. From Table 1 and Eq (10), the DEs' weights are computed and displayed in Table 2. Table 3 shows the LDM by the DEs. From Eq (11) and Tables 2 and 3, the A-IF-DM is constructed and is presented in Table 4 as follows:

and so on.

Step 4: The distances of the A-IF-DM from the IF-PIS and IF-NIS are first computed using Eqs (12) and (13). The IF-RCC $r{c_j}$ is then estimated using Eq (14) and is mentioned in Table 5. Finally, the criterion weights are computed using Eq (15) and are depicted as

The values of the criteria weights are shown in Figure 2.

Here, Figure 2 presents the criteria weights with respect to the outcomes. Demand for gerontechnology (r₂), with a weight value of 0.1493, is the most important parameter for prioritizing GTs for aging persons and people with disability. Socio-ethical (r₃), with a weight of 0.1481, is the second most significant criterion. Ease of use (r₆) ranks third, with a weight value of 0.1476. Functionality (r₅) is fourth, with a weight value of 0.1440, followed by innovation (r₁), with a weight of 0.1392. Other criteria are considered crucial to the assessment of GTs for aging persons and people with disability.

Based on Eqs (16)–(18) and Table 4, the linear and vector normalization values are determined to prioritize the GTs for aging persons and people with disability, as specified in Tables 6 and 7.

Table 8 denotes the weighted IF values of the benefit and cost criteria for each option using Eqs (19) and (20) with the IFWA operator. The measures of WSD $s_i^d$ and WSR $s_i^r$ and their ranks are obtained using Eqs (21) and (22). Similarly, Table 9 displays the weighted IF values of the benefit and cost criteria for each GT option using Eqs (23) and (24) with the IFWG operator. The measures of WPD $p_i^d$ and WPR $p_i^r$ and their ranks are obtained using Eqs (25) and (26). With Eqs (27)–(30), we estimate the MUDs for prioritizing the GTs for aging persons and people with disability, which are shown in Table 10. The OUD measures for GTs are calculated using Eq (31). From Table 10, mobility (T₂) is the most appropriate GT for aging persons and people with disability.

5.1.   Comparative investigation with existing models

To demonstrate the effectiveness of the IF-RCC-DN-WISP framework, we relate the outcomes of the developed model with those of several extant models, such as IF-COPRAS ^[52], IF-WASPAS ^[53] and IF-CoCoSo ^[19]. The purpose of choosing the IF-COPRAS model is that it uses the vector normalization process. The purpose of choosing the WASPAS and CoCoSo models is that both approaches use the linear max normalization process and the integration of the WSM and WPM. Furthermore, both combine the WSM and WPM, and they use the linear max-min normalization process in which the cost and benefit criteria are treated differently.

5.1.1.   IF-COPRAS model

This method involves the following steps:

Steps 1–3: Follow the proposed model.

Step 4: Assume the criteria weight as per Gitinavard and Shirazi's ^[52] model.

Step 5: Obtain the sum of the ratings of the benefit-type and cost-type criteria as

where l is the number of benefit criteria, and n is the total number of criteria.

Step 6: Determine the relative degree (RD) of each option using

Step 7: Estimate the utility degree (UD) of each option using

The implementation results are presented in Table 11. Option mobility (T₂) is determined as the suitable GT for aging persons and people with disability, obtaining the highest RD (0.866).

5.1.2.   IF-WASPAS model

Steps 1–3: Follow the proposed model.

Step 4: Determine the criteria weight using Mishra et al.'s ^[53] model.

Step 5: Determine the WSM and WPM using Eqs (36) and (37), respectively,

Step 6: Determine the measure of UD using

Step 7: Prioritize the options as per the UD $\left( {{Q_i}} \right).$

Using Eqs (36)–(38), the WASPAS measures of GTs are presented in Table 12.

Therefore, the ranking of the options is ${T_2} {\text{ f }} {T_5} {\text{ f }} {T_4} {\text{ f }} {T_1} {\text{ f }} {T_3}$, and mobility (T₂) is a suitable choice with the maximum UD for aging persons and people with disability.

5.1.3.   IF-CoCoSo model

Steps 1–3: Similar to developed model

Steps 4 and 5: Follows Tripathi et al.'s ^[19] model

Step 6: Estimate the balanced compromise scores of options as

Step 7: The overall compromise solution (OCS) of options is computed as

Step 8: Rank the options with the OCS $\left( {{Q_i}} \right)$ in decreasing order.

The overall results are depicted in Table 13. From Table 13, mobility $\left( {{T_2}} \right)$ is the best alternative among the other GTs for aging persons and people with disability.

The results of the comparison are shown in Table 14 and Figure 3. From Table 14, it can be observed that the optimal GT is T₂ (mobility) for aging persons and people with disability using almost all MCDM tools. The advantages of the developed IF-RCC-DN-WISP model are as follows:

● The proposed method uses linear and vector normalization procedures, the IF-COPRAS method uses only the vector normalization procedure, and the IF-WASPAS and IF-CoCoSo methods use only the linear normalization procedure. Thus, the proposed method avoids information loss and provides more accurate decision results using different criteria.

● IF-WASPAS, IF-CoCoSo and the proposed method associate the WSM with the WPM to improve the accuracy of the results. In addition, the developed method uses the IFWA and IFWG operators, four utility measures and DN procedures, thus providing better results than the extant methods.

● The systematic assessment of DEs' weights using the proposed score function and RS model reduces imprecision and biases in the MCDM procedure.

● The developed method determines the criteria weights using the IF-RCC-based tool. By contrast, in IF-WASPAS ^[53], the criteria weight is obtained with a similarity measure-based tool. In IF-COPRAS, the criteria weight is chosen randomly.

From Figure 4, we can see that the developed IF-RCC-DN-WISP framework approach is highly consistent with existing models. The Spearman rank correlation (SRC) and WS-coefficients ^{[50,54,55,56]} of the preference orders of diverse existing models with the developed IF-RCC-DN-WISP methodology are presented in Table 14 and Figure 4. The SRC and WS coefficients show that the framework is a suitable system for associating the relationship of rankings, which implies its high uniformity for prioritizing GTs for aging persons and people with disability. Therefore, the developed method shows a good relationship with prioritization outcomes. It obtains results that are solid and highly consistent with those of existing methods.

6.   Conclusions

The evaluation of the GTS problem for aging persons and people with disability is assumed to be a difficult MCDM problem because of various criteria that need to be considered. The aim of this study was to introduce an MCDM model for prioritizing GTs for aging persons and people with disability from an IFS perspective. In this regard, a hybrid intuitionistic fuzzy MCDM framework called IF-RCC-DN-WISP was introduced with the integration of DN procedures, the IF-DM, the IF-score function and the RCC-based weight-determining model. A new DM and score function were therefore introduced in the IFS context. In this framework, new formulas were developed to assess the DEs and criteria weights. To demonstrate the implementation and potential of the approach, a case study of GTS was presented in an IF environment. The outcomes showed that the demand for gerontechnology, with a weight value of 0.1493, was the most important parameter for prioritizing GTs for aging persons and people with disability. Socio-ethical, with a weight value of 0.1481, was the second most significant criterion, followed by ease of use, with a weight value of 0.1476; functionality, with a weight value of 0.1440; and innovation, with a weight value of 0.1392. Other criteria were considered crucial for the assessment of GTs for aging persons and people with disability. It was also concluded that mobility is the most appropriate GT for aging persons and people with disability. A comparison with extant models showed the strength and stability of the obtained results. The findings proved that the developed method obtains solid and significant results that are highly consistent with those obtained by existing models.

In the future, it would be interesting to use the WISP model in other decision-making scenarios. The proposed WISP method can also be extended using diverse uncertain settings, such as Pythagorean fuzzy sets (PFSs), interval-valued Fermatean fuzzy sets, bipolar fuzzy sets, rough sets, linear Diophantine sets and T-spherical fuzzy sets, to name a few.

Acknowledgements

The authors express their appreciation to the King Salman Center for Disability Research for funding this work through Research Group No. KSRG-2022-009.

Conflicts of interest

The authors declare no conflicts of interest.