1.
Introduction
Let S be a subgroup of a group G. It is well-known that the operation (aS)(bS):=(ab)S is well-defined on the collection of (left) cosets of S if and only if S is normal in G. In this statement, the term "well-defined" means singlevalued. It was in 1934 that the French mathematician F. Marty considered the operation ⊡ defined on the set of left cosets of an arbitrary subgroup S in G as
In this way he obtained a structure with a multivalued operation, which becomes singlevalued in the case that S is normal in G. Marty isolated the fundamental axioms governing such structures in [33] and called them hypergroups. The properties of hypergroups were studied further by Marty in [34,35]. Independently of Marty's work, hypergroups appeared under the name "multigroups" in [12].
An interesting feature of Marty's axioms is that the axioms of group theory follow from them in the singlevalued case (cf. [36], Section 4]). Conversely, any group satisfies Marty's axioms. In this sense, hypergroups generalise groups by allowing the operation to be multivalued.
Another path to follow in generalising first-order algebraic structures to the multivalued case may be informally described as a syntactic replacement of the symbol for equality "=" with the set-membership relation "∈" to obtain, from known axioms and theorems, meaningful expressions in the multivalued case.
Let us be more precise by considering the particular example of group theory. If H is a set equipped with a multivalued operation ⊡, then one can postulate that for some element e∈H the following statements hold:
or
Clearly, the two properties above are in analogy with the existence of a neutral element and inverses usually postulated in group theory.
From this point of view, it is interesting to note that there are hypergroups (in the sense of Marty mentioned above) where both the latter or the former property fail, and others in which (1.1) or both properties hold (some of these examples will appear in Section 3 below). This and similar phenomena produce a quite rich hierarchy of hypergroups, especially if compared with that of groups. The number of isomorphism classes of finite structures also greatly increase: there are 8 isomorphism classes of hypergroups with two elements, while there exist 3999 non-isomorphic hypergroups with three elements (cf. [41]).
Observe further that a multivalued operation ⊡ on a set H induces two other multivalued operations* on H:
*These were originally denoted by x/y and y∖x in the literature, where the multivalued operation is usually denoted as a standard product. However, we adopt the convention to employ the "box-type" notation for multivalued operations, while reserving the usual binary operator symbols for standard operations.
Notice that if the operation ⋅ of a group G is viewed as the multivalued operation x⊡y:={x⋅y} (x,y∈G), then the above operations are clearly given by 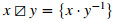 and
and 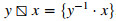 , where x−1 and y−1 denote the unique inverses of x and y, respectively. Nevertheless, in the general multivalued case,
, where x−1 and y−1 denote the unique inverses of x and y, respectively. Nevertheless, in the general multivalued case,  and
and  are not necessarily related to the inverses, in the sense of (1.2) above, of single elements (if they exist).
are not necessarily related to the inverses, in the sense of (1.2) above, of single elements (if they exist).
One of the first areas in which hypergroups found applications is geometry, notably initiated by the observations of Prenowitz (whose work culminated with the book [42]).
In the work of Prenowitz, the transposition axiom, governing the interplay between a multivalued operation ⊡ and the operations (1.3), becomes fundamental. The important notion of join space, namely a commutative hypergroup satisfying the transposition axiom, was introduced by Prenowitz, while transposition hypergroups were later considered by Jantosciak in [18], where the commutativity assumption is dropped and the transposition axiom generalised accordingly. If a transposition hypergroup has a neutral element e, in the sense of (1.1) above, then the validity of (1.2) follows (a proof of this fact can be found in [36], but the result is known since much before the publication of that article) and this type of hypergroups were called polygroups by Comer in [7].
As observed also in a more recent article [8] (see also [9,44]), commutative polygroups provide algebraic models for (axiomatic) projective geometries. On the other hand, as the work of Prenowitz shows, for more general incidence geometries the existence of a neutral element and inverses would often be too restrictive as, e.g., the join space of Euclidean geometry (cf. [42, Section 2.1]) does not have a neutral element.
Applications of commutative polygroups however are not limited to geometry. The name "canonical hypergroups" was previously coined by J. Mittas† to refer to commutative polygroups while he was studying the additive reducts of Krasner hyperfields. The latter structures were introduced by M. Krasner as a tool to approximate local fields of positive characteristic (and their absolute Galois group) by those of characteristic 0 (see [25,28,30,38]).
†Since the word "canonical" has a different meaning in category theory, in this paper we shall adopt Comer's terminology.
The author first met commutative polygroups during his PhD studies, mainly motivated by an interest in the model theory of valued fields, where the above mentioned Krasner's approximation techniques turn out to play a significant role. In fact, the theory of commutative polygroups provides a convenient algebraic framework for describing Flenner's leading term structures (also known as RV-structures, [15,45]). In fact, while in Flenner's original description RV-structures come equipped with a ternary relation, if one interprets it as a (binary) multivalued operation, then one obtains a Krasner hyperfield. The analogies with the singlevalued case (i.e., of fields) often provide smoother exposition of the theory and simplifications in the proofs of known theorems (perhaps most notably regarding quantifier elimination for Henselian valued fields of mixed characteristic). For more details, the reader may consult the author's doctoral dissertation [29] and references therein.
From a first-order perspective, a (binary) multivalued operation can only be described in the form of a ternary relation (which explains Flenner's approach to RV-structures), but this description does not fully reflect the input-output nature of operations to which algebraists are usually accustomed.
The possibility of modifying the notion of first-order signatures by allowing "multivalued function symbols" has been explored in a recently appeared preprint [10] and, although onerous to settle, seems to produce some interesting results regarding the first-order theory of Krasner hyperfields. It is worth noting that this mentioned generalisation of the notion of first-order signatures is an instance of a more general category-theoretic and signature-independent approach to model theory (cf. [11]).
From this point of view, it seemed to us inevitable for category theory to play a more direct role in the foundations of the theory of Krasner hyperfields and more generally of algebraic structures with multivalued operations. In fact, relations are often described as arrows in category theory, thus offering the possibility of restoring the directional nature of multivalued operations.
In the present paper, a characterisation theorem for commutative polygroups in purely category-theoretic terms over the category Set is derived (Theorem 4.8).
Our result is based solely on the fact that Set is a regular category and employs the construction of monoid objects in the category Rel formed by sets and relations, with respect to the monoidal structure given by cartesian products (as e.g., in [21]). In particular, the statement of our theorem yields definitions of commutative polygroups objects in any regular category and, in particular, in any topos (cf. [22, § A1,A2,A3]). In this regard, we mention [13], where the understanding of commutative polygroups from a topos theoretic perspective is also motivated.
Let us now list several authors, not mentioned above, which have considered commutative polygroups in their work.
(ⅰ) T. Nakano in [40] considered commutative polygroups in relation to modular lattices.
(ⅱ) M. Baker and N. Bowler in [3] (see also [6,14]) considered commutative polygroups in relation to matroid theory.
(ⅲ) O. Viro in [46] considered commutative polygroups in relation to tropical geometry and, more recently, J. Jun (see e.g., [23,24]) and P. Jell et al. in [20] have resumed Viro's work.
Furthermore, a very interesting preprint suggesting applications of commutative polygroups to the study of complexity of linear programming has recently appeared (cf. [37]).
The work related to matroid theory also inspired Nakamura and Reyes to investigate in [39] the most known categories formed by polygroups in great detail. On the one hand, their findings show that, while polygroups generalise groups, their categories are not as well-behaved. For example, they lack some binary coproducts and equalizers. Furthermore, in the commutative case, a monoidal structure generalising the bilinear tensor product of abelian groups is missing, obstructing a generalisation of the fact that rings are monoid objects in the category of abelian groups to their multivalued cousins multirings and hyperrings. On the other hand, it is observed in [39] that these and other flaws of the categories of polygroups can be overcome by considering categories of some slightly more general structures, which they called mosaics.
We observe that our characterisation theorem for commutative polygroups is readily extended to commutative mosaics. Thus, we take the opportunity to also consider the category of monoid objects over the category of commutative mosaics (in Set) with respect to the closed symmetric monoidal structure defined in [39] (where this same category of monoid objects have also been mentioned). In particular, for commutative monoids, we focus on the full subcategory formed by simple objects which, in turn, we observe to contain the category Kra of Krasner hyperfields (as a full subcategory).
Inevitably, the results of this part are based on some theorems in [39] which, at the moment we are writing, is not yet published. Since we believe all the necessary proofs in the preprint version [39] to be correct, while we give all the credit to the authors of [39] for those theorems, and we shall not repeat their proofs, instead referring to the just mentioned preprint version of the article (which we are confident will be eventually published).
Finally, at the end of the paper, we formulate a number of results relating the category Kra with other classical mathematical structures already present in the literature, in the form of existence theorems of faithully full functors into certain slice or coslice categories of Kra. We list below the classical categories that we take into consideration in this context.
● The category of formally real fields and order-preserving homomorphims of fields (Proposition 5.1).
● The category of valued fields and value-preserving homomorphisms (Proposition 5.2).
● The category of lattice-ordered abelian groups and order-preserving homomorphisms of groups (Proposition 5.5).
● The category of two-sided incidence groups and incidence-preserving group homomorphisms (Proposition 5.7).
Before ending this introductory section, let us briefly recap the organisation of the manuscript. In Section 2, we overview some of the main properties of the catregory Rel formed by sets and relations, which then generalise to the more general setting of regular categories, as we briefly explain later in the same section. Some basic theory of monoid objects in general monoidal categories will also be recalled. Section 3 combines some known facts in a new way and is devoted to the general theory of structures with a multivalued operation, with a particular focus on polygroups. Section 4 is devoted to the study of monoid objects in Rel and contains our characterisation result for commutative polygroups. Lastly, Section 5 focuses on the category Kra and its slice and coslice categories as explained above.
2.
Category theoretic preliminaries and terminology
Many references for category theory may be cited which cover the necessary background. Among these, besides the classic [31], we found [2,22,27] especially useful.
We shall assume little familiarity with the basic concepts of category, functor, natural transformation, and monoidal categories, which we will not explicitly define. As for basic notations, for a category C, we write A∈Ob(C) to mean that A is an object in C and, for any ordered pair (A,B) of objects in C, we denote the set of arrows f:A⟶B in C by C(A,B). For the composition of arrows the symbol ∘ will be employed, while the identity C-arrow of A∈Ob(C) will be written as 1A:A⟶A. The component at an object A of a natural transformation η will be denoted by ηA.
2.1. The category of sets and relations
Let A,B and C be sets and consider two binary relations R⊆A×B and S⊆B×C. The formula
defines a relation between A and C, called the composition of R and S. With this composition, sets and binary relations form a category Rel, where identities are given by the graphs of the corresponding identity functions in Set.
It is well-known that the category-theoretic product of two sets in Rel coincides with their coproduct in Rel, i.e., the disjoint union. In addition, the empty set ∅ is both initial and terminal in Rel.
On the other hand, it is well-known that the cartesian product × (i.e., the category-theoretic product in Set) together with any fixed singleton set {⋆} (i.e., a terminal object in Set) yield a symmetric monoidal structure on the category Rel.
The opposite relation of R is defined as follows:
To any relation R⊆A×B it bijectively corresponds the multivalued function fR:A⟶℘(B) mapping a∈A to the set of all b∈B such that (a,b)∈R. We leave the straightforward proof of the following statement to the reader.
Lemma 2.1. Let R⊆A×B be a relation from A to B and f:A⟶℘(B) the corresponding multivalued function. Then the following equivalences hold:
(i) R∘R†⊆1B if and only if f is singlevalued, i.e., f(a) is a singleton for all a∈A.
(ii) 1A⊆R†∘R if and only if f is everywhere defined, i.e., f(a)≠∅ for all a∈A.
As we already mentioned in the introduction, multivalued operations ⊡:H×H⟶℘(H) correspond bijectively to relations o⊡⊆(H×H)×H, that is, arrows H×H⟶H in the symmetric monoidal category (Rel,×,{⋆}).
2.2. Monoid objects in monoidal categories
Fix a monoidal category (C,⊗,I), where ⊗ and I denote the monoidal product bifunctor and unit, respectively. Let further α, μ and ν denote the associator, the left unitor and the right unitor, respectively and take an object M in C. We call any C-arrow M⊗M⟶M a categorial‡ operation on M in C.
‡Our choice for terminology here follows a remark made in the second page of the Preface in [17].
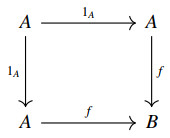
We say that a categorial operation o:M⊗M⟶M on M is associative if and only if the following diagram is commutative in C.
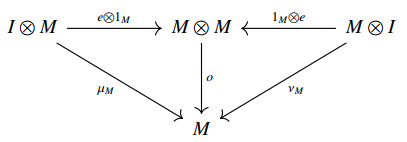
A monoid object in C is an object M together with a categorial operation o:M⊗M⟶M which is associative as well as a C-arrow e:I⟶M such that the following diagram is commutative in C.
The C-arrow e is said to be neutral for the operation o on M.
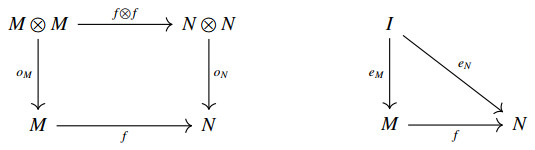
The category Mnd(C) is defined as having monoid objects M,N… in C as objects and, as arrows, all the C-arrows f:M⟶N in C making commutative the following diagrams in C.
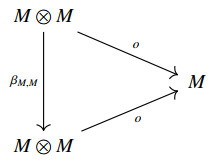
If C is symmetric monoidal, then for A,B∈Ob(C) we denote by βA,B:A⊗B⟶B⊗A the braiding isomorphism whose inverse is βB,A.
A categorial operation o:M⊗M⟶M on an object M in the symmetric monoidal category C is commutative if and only if the following diagram commutes in C:
A commutative monoid object in C is a monoid object (M,o,e) in C such that o is commutative. We denote by CMnd(C) the full subcategory of Mnd(C) formed by commutative monoid objects in C.
Example 2.2. Mnd(Set,×,⊤) (resp. CMnd(Set,×,⊤)), where × denotes the cartesian product and ⊤ any fixed singleton set, is the familiar category formed by monoids (resp. commutative monoids) and their homomorphisms.
2.3. Group objects in cartesian categories
Let us fix a category C. Recall the following:
● an object ⊤ in C is terminal if it satisfies the universal property of terminal objects:
for all objects X in C, there is a unique arrow !X:X⟶⊤.
● An object ⊥ in C is initial if it satisfies the universal property of initial objects:
for all objects X in C, there is a unique arrow !X:⊥⟶X.
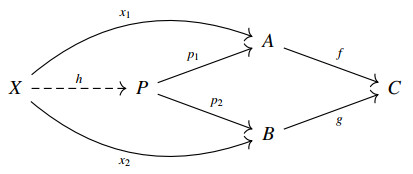
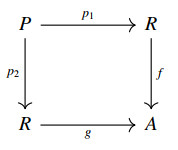
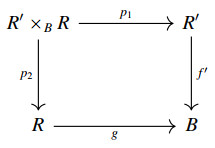
● A pullback in C of a pair of arrows f:A⟶C and g:B⟶C with the same target in C is an object P:=A×CB together with two arrows p1:P⟶A and p2:P⟶B in C (called projections) satisfying the universal property of pullbacks:
f∘p1=g∘p2 and for all objects X and arrows x1:X⟶A, x2:X⟶B in C such that f∘x1=g∘x2, there is a unique arrow h:X⟶P making the following diagram commutative:
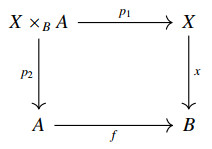
Example 2.3. Consider the category Set of sets and functions. Then any singleton set {⋆} is terminal, while ∅ is the unique initial object in Set. The pullback of f:A⟶C and g:B⟶C in Set is explicitly given by the following set:
together with the projections p1:(a,b)↦a and p2:(a,b)↦b.
Following [22], we shall call C locally cartesian whenever it has pullbacks of all pairs of arrows having the same target object in C.
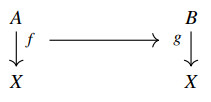
If X is an object in C, then the slice category C/X has C-arrows f:A⟶X, with A∈Ob(C), as objects, while a C-arrow a:A⟶B is an arrow
in C/X if and only if the following triangular diagram is commutative in C:
The coslice category X∖C can be defined as (Cop/X)op. It has C-arrows X⟶A, with A∈Ob(C) as objects, while each triangular and commutative diagram in C
defines an arrow a:f⟶g in X∖C.
Note that, for any C-arrow f:A⟶X, there is a unique C/X-arrow a:f⟶1X since the condition 1X∘a=f forces a to be equal to f in C. This means that 1X is a terminal object in the slice category C/X. Dually, 1X is initial in the coslice category X∖C.
A locally cartesian category with a terminal object is called cartesian (or finitely complete, see e.g., [22, Lemma 1.2.1]).
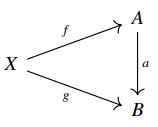
If C is a cartesian category with ⊤ being a fixed terminal object, then for two arrows f1:X⟶A and f2:X⟶B in C, the pairing (f,g):X⟶A×B:=A×⊤B is defined as the unique arrow X⟶A×B induced from f1 and f2 by the universal property of pullbacks and terminal objects (more precisely, by the universal property of products). It is standard practice to denote the pairing (1A,1A):A⟶A×A by Δ (or ΔA) and call arrows of this form diagonal arrows.
Example 2.4. For sets A, B and X, the pairing (f,g):X⟶A×B of two functions f:X⟶A and g:X⟶B in Set is given by the assignment x↦(f(x),g(x)), for x∈A.
Remark 2.5. In general monoidal categories, the existence of pairing arrows is not guaranteed. An example showing this is the category Ab formed by abelian groups and homomorphisms, where the monoidal structure is given by the tensor product of abelian groups.
Assume that a category C has binary products × and a terminal object ⊤ (this clearly holds if C is cartesian, but this assumption is not necessary). Then, (C,×,⊤) is a symmetric monoidal category. We will sometimes refer to this structure as the cartesian monoidal structure on C.
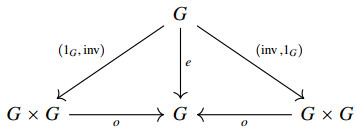
A (commutative) monoid object (G,o,e) in (C,×,⊤) is called an (abelian) group object in C if there exists a C-arrow inv:G⟶G, called group-inversion, making the following diagram commutative in C:
where, as it is common practice, the arrow e:⊤⟶G is identified with the arrow e∘!X:G⟶G.
The full subcategory of Mnd(C,×,⊤) formed by group objects in C (resp. abelian group objects in C) is denoted by Grp(C) (resp. Ab(C)).
Example 2.6. Grp(Set) and Ab(Set) are the categories formed by groups and abelian groups and group-homomorphisms, respectively.
2.4. Regular categories and relations
We fix again a category C. Recall the following:
∙ An arrow f:A⟶B in C is monic if the implication
holds, for any pair of parallel C-arrows gk:A′⟶A (k=1,2).
If C is locally cartesian, then a C-arrow f:A⟶B is monic if and only if the following diagram satisfies the universal property of pullbacks in C:
By a subobject of A∈Ob(C) we mean the C/A-isomorphism class of an object in C/A which is monic as an arrow in C. We write Sub(A) for the full subcategory of C/A whose objects are the subobjects of A.
By definition of C/A, for subobjects X,Y of A, if there is a C-arrow j′:X⟶Y such that i=j∘j′, where i:X⟶A and j:Y⟶A are the monic C-arrows given by definition of Sub(A), then it follows that j′ is monic and unique in C. This shows that Sub(A) is a partial order for any object in any category C. We shall call inclusion and denote by ⊑ (or ⊑A) the order relation of Sub(A). If C is locally cartesian, then Sub(A) is cartesian because the terminal object of C/A, 1A:A⟶A is trivially monic and thus yields a terminal object in Sub(A), for any A∈Ob(C). In this case, we shall call intersections, denoted by ⊓, the products in the cartesian category Sub(A). Note that
Example 2.7. All of the above in the category Set yield to the corresponding well-known notions, usually denoted by the rounded symbols ∩ and ⊆.
Definition 2.8. A relation from A to B in a category C with binary products is defined as a subobject of the product A×B in C.
Among relations between sets, equivalence relations often play a fundamental role. The notion of equivalence can be internalised in a wide class of categories, leading to the concept of congruence.
Definition 2.9. Let f:R⟶A and g:R⟶A be a parallel pair of arrows in a locally cartesian category C, such that (f,g):R⟶A×A is monic in C (this happens e.g., if f or g is a monic C-arrow itself). We say that (f,g) is a congruence on A in C if the following three conditions hold:
(R) There exists a C-arrow r:A⟶R such that f∘r=g∘r=1A.
(S) There exists a C-arrow s:R⟶R such that f∘s=g and g∘s=f.
(T) There exists a C-arrow t:R×AR⟶R in C such that f∘t=f∘p1 and g∘t=g∘p2, where (R×AR,p1,p2) is the pullback in C defined by the following diagram:
Observe that if f:A⟶B is an arrow in a locally cartesian category C, then the projections (p1,p2) of the pullback A×BA of f and itself is always a congruence on A in C. This congruence is called the kernel pair of f. In particular, for an object A in a cartesian category C, the following two congruences always exist:
(TC) the trivial congruence on A is obtained as the kernel pair of the terminal arrow !A, or, equivalently, as the terminal object in Sub(A×A), i.e., 1A×A.
(DC) the discrete congruence is obtained as the kernel pair of the identity arrow 1A, that is, ΔA.
Recall that a coequalizer in C of a pair of parallel arrows f,g:A⟶B in C is an object Q together with an arrow q:B⟶Q satisfying the universal property of coequalizers:
q∘f=q∘g, and for all objects X and arrows x:B⟶X in C such that x∘f=x∘g, there is a unique arrow h:Q⟶X such that h∘q=x.
Definition 2.10. Let (f,g):R⟶A×A be a congruence on an object A in a locally cartesian category C. An object Q in C is a quotient (object) of A in C, associated to the congruence (f,g) if there is a C-arrow q:A⟶Q which is a coequalizer of f and g in C.
If C is cartesian, with terminal object ⊤, then an object S in C is called simple (in C) if it admits precisely two quotients (up to isomorphisms) in C, namely ⊤ and S (corresponding to the trivial and the discrete congruence, respectively).
Example 2.11. A congruence (f,g) on a set A in Set is the same as an equivalence relation R⊆A×A, where f=p1∘i and g=p2∘i with i:R⟶A×A being the canonical inclusion map and p1,p2:A×A⟶A the product projections. The usual quotient map q:A⟶A/R yields a bijection (i.e., a Set-isomorphism):
Thus, the equivalence relation R is the kernel pair (q,q). Clearly, the only simple objects in Set are singletons.
Example 2.12. Simple objects in the category CRng formed by commutative rings and their homomorphisms are fields. This well-known fact follows from the (also well-known) bijective correspondence between congruences in CRng on a commutative ring A and the ideals of A.
Back to arbitrary relations, the following notion is needed.
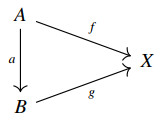
Definition 2.13. A category C has images if to each arrow f:A⟶B in C there corresponds a uniquely determined subobject m:Imf⟶B of the target B of f, which is moreover characterized as the least (with respect to ⊑B) subobject of B such that there is a C-arrow x:A⟶Imf through which f factors (i.e., f=m∘x).
If a category C has images, then an arrow f:A⟶B in C is called a cover if Imf and B are isomorphic in C. That is, covers are stable under pullbacks.
We can now define regular categories.
Definition 2.14. A cartesian category C is regular if it has images and, moreover, for each pullback square
if f is a cover, then p1 is also a cover.
Fact 2.15. ([22, Proposition 1.3.4]) For an arrow f:A⟶B in a regular category C, the following are equivalent:
(i) f:A⟶B is a cover.
(ii) f:A⟶B is the coequalizer of two parallel C-arrows gk:A′⟶A (k=1,2).
Definition 2.16 ([22]). Let C be a cartesian category with images. If f:R⟶A and g:R⟶B are C-arrows and their pairing (f,g):R⟶A×B is monic in C, then we say that the corresponding relation between A and B is tabulated by f and g or that (f,g) is a tabulation of R.
We give a proof of the following well-known fact for the sake of completeness.
Lemma 2.17. If C is a locally cartesian category with images, then for all relations r:R⟶A×B there are C-arrows f:R⟶A and g:R⟶B which tabulate r.
Proof. First set T:=Imr and consider the corresponding factorization of r:
Since r and i are monic by assumption, so must be r′. Now, set
where p1 and p2 are the product projections of A×B. The universal property of products guarantees that p1 and p2 are monic, thus so are f′ and g′, as well as f:=f′∘r′:R⟶A and g:=g′∘r′:R⟶B. It follows that the pairing (f,g):R⟶A×B is a relation from A to B and it follows that it defines the same subobject of A×B as r does, i.e., r is tabulated by f and g. □
Definition 2.18. Let C be a cartesian category with images and take two relations r:R⟶A×B and r′:R′⟶B×C. Further, let (f,g) and (f′,g′) tabulate r and r′, respectively. If
is a pullback square, then the relation between A and C tabulated by f∘p2 and g′∘p1 is called the composition of the relation r′ with the relation r and is denoted by r′∘r (or R′∘R).
Fact 2.19 ([22, Lemma 3.1.1 and subsequent remarks]). Let C be a cartesian category with images. The above defined composition is associative if and only if C is regular. Moreover, for all relations R from A to B, the discrete congruences ΔA=(1A,1A) and ΔB=(1B,1B) satisfy R∘ΔA=R and ΔB∘R=R.
Definition 2.20. If C is a regular category, then we denote by Rel(C) the category formed by the objects in C, having relations as arrows with composition and identities defined in Fact 2.19 above.
Example 2.21. Clearly, Set is a regular category. In addition, the category Rel considered in the Subection 2.1 is Rel(Set).
To a relation R from A to B in a regular category C there corresponds a relation R†:=βA,B∘R from B to A, where βA,B denotes the braiding isomorphism of the cartesian (symmetric) monoidal structure of C. Following up on Lemma 2.1, we give the following definition.
Definition 2.22. Let C be a regular category. For a Rel(C)-arrow R:A⟶B we say that
(1) R is singlevalued if R∘R†⊑1B,
(2) R is everywhere defined if 1A⊑R†∘R,
(3) R is a map if it is both singlevalued and everywhere defined.
In [22, Proposition 3.1.3] it is shown that, in a regular category C, each map R:A⟶B in Rel(C) is tabulated by 1A and some C-arrow f:A⟶B (the Rel(C)-arrow (1A,f) is called the graph of f). We shall often identify the maps in Rel(C) with the C-arrows of which they are graph (this identification produces no harm by [22, Theorem 3.2.10]).
In addition, as a consequence of the just mentioned observations, one obtains that R:A⟶B is an isomorphism in Rel(C) if and only if R†∘R=1A and R∘R†=1B and, therefore, R†=R−1. In particular, all Rel(C)-isomorphisms are maps.
Finally, we remark that, as in the case of Set, binary products and terminal objects in C define a symmetric monoidal structure on Rel(C). On the other hand, as we have seen for the case of Set, this monoidal structure on Rel(C) does not have to coincide with the cartesian monoidal structure of Rel(C).
3.
Structures with multivalued operations
Let H be a set and ℘(H) its power set. A multivalued operation ⊡ on H is a function which associates to every pair (x,y)∈H×H an element of ℘(H), denoted by x⊡y. If ⊡ is a multivalued operation on H, then for x,y∈H and X,Y⊆H we set
X⊡y:=X⊡{y}, and x⊡Y:={x}⊡Y.
To any multivalued operation ⊡ on H there correspond three multivalued operations:
∙ the multivalued operation twin§ of ⊡, defined for x,y∈H by the formula
§The term dual is also adopted in the literature.
∙ the multivalued operation left reciprocal of ⊡, defined for x,y∈H by the formula
and
∙ the multivalued operation right reciprocal of ⊡, defined for x,y∈H by the formula
3.1. Mosaics and polygroups
Definition 3.1. We shall call magma any set equipped with a multivalued operation. A magma (M,⊡) is called commutative if ⊡ and ⊡t coincide.
Definition 3.2. Let (M,⊡),(M′,⊡′) be magmata. A function f:M⟶M′ is called a homomorphism (of magmata) if it satisfies:
(Hom) f(x⊡y)⊆f(x)⊡′f(y), for all x,y∈M.
A homomorphism f:M⟶M′ is called strong if it satisfies the following property stronger than (Hom):
(sHom) f(x⊡y)=f(x)⊡′f(y), for all x,y∈M.
An isomorphism (of magmata) M≃M′ is a bijective homomorphism f:M⟶M′ whose inverse f−1 is a homomorphism M′⟶M.
Remark 3.3. It is not difficult to verify that isomorphisms are precisely bijective strong homomorphisms. On the other hand, examples of bijective homomorphisms which are not strong and strong homomorphisms which are not bijective are straightforward to construct as well (see e.g., Example 3.18).
Definition 3.4. An element e in a magma (M,⊡) is called neutral if e⊡x=x⊡e={x} holds, for all x∈M. A magma (M,⊡) with a neutral element e∈M for ⊡ is called unital magma.
Remark 3.5. If a neutral element e exists in a magma (M,⊡), then it is unique. To see this, the standard argument applies.
Definition 3.6. A homomorphism f:M⟶M′ between two unital magmata M and M′ with neutral elements e and e′, respectively, is called unitary if f(e)=e′. We denote the category formed by unital magmata and unitary (strong) homomorphisms by uMag (uMagstr).
Definition 3.7. Let (M,⊡) be a magma and ρ:M⟶M an endofunction. We say that (M,⊡) is ρ-reversible if the following property holds:
(RE) z∈x⊡y implies both x∈z⊡ρ(y) and y∈ρ(x)⊡z, for all x,y,z∈M.
Definition 3.8 ([39, Definition 2.3]). A (commutative) unital magma (M,⊡) with a neutral element e which is moreover ρ-reversible with respect to some endofunction ρ:M⟶M is called a (commutative) mosaic. By a (strong) homomorphism of mosaics we mean a unitary (strong) homomorphism of the underlying unital magmata. We introduce the following notation:
∙ Msc denotes the category formed by mosaics and their homomorphisms.
∙ CMsc denotes the category formed by commutative mosaics and their homomorphisms.
∙ Mscstr denotes the category formed by mosaics and their strong homomorphisms.
∙ CMscstr denotes the category formed by commutative mosaics and their strong homomorphisms.
The following is also observed in [39, page 7]. We make a slightly more precise statement and write a short proof for completeness.
Lemma 3.9 ([39]). Let (M,⊡,e,ρ) be a mosaic. Then ρ is a unitary isomorphism of magmata
satisfying the following property:
(RINV) e∈(x⊡ρ(x))∩(ρ(x)⊡x), for all x∈M.
In addition, the equivalences
hold, for all x,y,z∈M.
Proof. Indeed, x∈(x⊡e)∩(e⊡x) and ρ-reversibility imply e∈(ρ(x)⊡x)∩(x⊡ρ(x)). Conversely, if e∈(y⊡x)∩(x⊡y) for some y∈M, then by ρ-reversibility we may deduce that y∈e⊡ρ(x)={ρ(x)} and hence y=ρ(x). It follows that ρ(e)=e and that ρ is an involution. In addition, the validity of the following equivalences is readily verified, for all x,y,z∈M:
This shows that ρ is a strong homomorphism of magmata (M,⊡)⟶(M,⊡t) and thus an isomorphism. The rest of the assertions follow as well. □
Definition 3.10. For an element x in a unital magma (M,⊡,e), we call any y∈M such that e∈(x⊡y)∩(y⊡x) an inverse of x. If in (M,⊡,e) all elements have a unique inverse, then we denote by x−1 the inverse of any x∈M and call (M,⊡,e) an invertible magma.
The following is an immediate consequence of Lemma 3.9.
Corollary 3.11. Any mosaic (M,⊡,e,ρ) is an invertible magma, where x−1=ρ(x), for all x∈M.
Lemma 3.12. Let (M,⊡,e) and (M′,⊡′,e′) be invertible magmata and f:M⟶M′ a unitary homomorphism. Then f(x−1)=f(x)−1, for all x∈M.
Proof. The standard argument as, e.g., in [26, Remark 2.6], applies. □
Definition 3.13 ([7]). A (commutative) polygroup (P,⊡,e) is an invertible (commutative) magma which is reversible with respect to the endofunction x↦x−1 and where ⊡ is associative, that is, the following property is valid:
(ASC) (x⊡y)⊡z=x⊡(y⊡z), for all x,y,z∈P (where the equality is as subsets of P).
Remark 3.14. It follows from Corollary 3.11 above that polygroups are precisely associative mosaics.
Definition 3.15. By a (strong) homomorphism of polygroups we mean a (strong) homomorphism of the underlying mosaics.
We now observe that in invertible unital magmata, reversibility can be viewed as an associativity "localised at the neutral element". In this sense, mosaics can be viewed as "locally associative invertible magmata" (see also [43, Remark 3.15]).
Lemma 3.16. Let (M,⊡,e) be an invertible unital magma. The following statements are equivalent:
(i) (M,⊡,e) is ρ-reversible, with ρ(x):=x−1 for all x∈M.
(ii) For all x,y,z∈M, the following equivalence holds:
Proof. From e∈(x⊡y)⊡z we deduce that z−1∈x⊡y. If (i) is valid, then we obtain that x−1∈y⊡z and e∈x⊡(y⊡z) follows. The converse implication is derived similarly.
Assuming (ii), for all x,y,z∈M we obtain that
where we used Lemma 3.9. It follows that (M,⊡,e) is ρ-reversible with ρ(x)=x−1 for all x∈M. □
Corollary 3.17. Let (P,⊡,e) be a unital magma satisfying (ASC) and ρ:M⟶M an endofunction. The following statements are equivalent:
(i) (P,⊡,e) is ρ-reversible, i.e., (P,⊡,e,ρ) is a polygroup.
(ii) (M,⊡,e) is an invertible unital magma and ρ(x)=x−1, for all x∈M.
We list below some well-known examples of polygroups and mosaics. We choose the most common names for them as they already appear in the literature (cf. e.g. [3,6,23,30])
Example 3.18. (1) Any group (G,⋅,e) is a polygroup with respect to the multivalued operation defined by x⊡y:={x⋅y}, for all x,y∈G.
(2) Let K denote a set with two elements: 0 and 1. Set 0⊞x=x⊡0:={x} for all x∈K and 1⊡1:=K. Then (K,⊞,0) is a polygroup called the Krasner polygroup. We observe that the identity map {0,1}⟶{0,1} can be viewed as a bijective homomorphism Z/2Z⟶K which is not strong.
(3) Let S denote a set with three elements: 0, 1, and −1. Set 0⊞x=x⊞0:={x} for all x∈S, 1⊞1:={1}, −1⊞−1:={−1} and 1⊞−1=−1⊞1=S. Then (S,⊞,0) is a polygroup, called the sign polygroup.
(4) Let P denote the set of complex numbers with modulus 1 with the addition of the number 0. Set 0⊞z=z⊞0:={z} for all z∈P, z⊞−z=−z⊞z={−z,0,z} for all z∈P∖{0} and
for all z1,z2∈P∖{0}. Then (P,⊞,0) is a polygroup, called the phase polygroup. We observe that the map S⟶P given by the assignments 0↦0 and ±1↦±1 is a strong homomorphism which is not bijective.
(5) Let Γ be a totally ordered set and set T(Γ):=Γ∪{∞}, where ∞ is a symbol for an element not in Γ to which we extend the order so that ∞>γ, for all γ∈Γ. Set γ⊞∞=∞⊞γ:=}γ}, for all γ∈T(Γ) and for γ,δ∈Γ
Then (T(Γ),⊞,∞) is a polygroup, called the (generalized) tropical polygroup.
(6) Let F denote a set with three elements 0, 1, and −1. Set 0⊞x=x⊞0={x} for all x∈F and x⊞x=∅ for all x∈F∖{0} and 1⊞−1={0}. Then F is a commutative mosaic, which is not a (commutative) polygroup.
In the following proposition we collect a number of well-known properties of polygroups. In particular, we note that properties (i) and (ii) below show that all polygroups are hypergroups as defined by Marty (mentioned in the Introduction). Property (iii) offers yet another interpretation of the reversibility axiom, in the case of polygroups.
Proposition 3.19 (see e.g. [18,36]). Let (P,⊡) be a polygroup. Then the following statements hold:
(i) x⊡P=P⊡x=P, for all x∈P.
(ii) x⊡y≠∅, for all x,y∈P.
(iii)  and
and 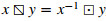 , for all x,y∈P.
, for all x,y∈P.
Proof. (i) The inclusion x⊡P⊆P is immediate. Conversely, note that, since e∈x⊡x−1, for any a∈P we have that
The equality P⊡x=P is deduced similarly.
(ii) By contradiction, if x⊡y=∅, then using (i),
(iii) By definition, 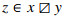 means x∈z⊡y, which is equivalent to z∈x⊡y−1 by reversibility. The equality
means x∈z⊡y, which is equivalent to z∈x⊡y−1 by reversibility. The equality 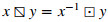 is derived similarly.
is derived similarly.
□
3.2. Partial multirings and hyperfields
The following facts have all been noted in [39] (article [5] also contains some closely related observations).
Fact 3.20 ([39, Theorem 1.1,Corollary 4.2]).
(i) The forgetful functor U∙:uMag⟶Set∙ creates all limits and all coproducts in uMag. In particular, uMag is complete and cocomplete¶.
¶Here, Set∙ denotes the familiar category of pointed sets, and U∙ maps a unital magma with neutral element e to the underlying set, pointed on e.
(ii) The categories Msc, CMsc, Mscstr, and CMscstr are closed under limits and colimits in uMag. In particular, they are complete and cocomplete.
(iii) Both the categories CMsc and CMscstr are regular.
(iv) The category formed by commutative polygroups and their (resp. strong) homomorphisms is closed under products and coequalizers in CMsc (resp. CMscstr).
(v) The category formed by commutative polygroups and their (strong) homomorphisms does not have all binary coproducts.
(vi) The category formed by commutative polygroups and their (strong) homomorphisms does not have all equalizers.
All of the above is relevant for the study of structures, called multirings (cf. e.g. [16,32]), which generalise rings by letting the additive abelian groups be commutative polygroups. In our setting, it is convenient to consider a slight generalisation of these structures.
Definition 3.21 ([25,32]). A (commutative) partial multiring with unity is a structure (A,⊞,⋅,0,1) which satisfies the following axioms:
(PM1) (A,⊞,0) is a commutative mosaic (with the additive notation, we will denote the inverse of x∈A with respect to ⊞ as x−).
(PM2) (A,⋅,1) is a (commutative) monoid.
(PM3) a0=0a=0, for all a∈A, and both of the following inclusions
hold, for all a,x,y∈A.
A commutative partial multiring with unity (H,⊞,⋅,0,1) is called a partial hyperfield if (H∖{0},⋅,1) is an abelian group.
In the following, we shall refer to partial multirings with unity simply as partial multirings. We note that multirings are precisely partial multirings with associative additive mosaic (i.e., with an additive commutative polygroup) and such that 0≠1, while partial hyperfields with associative additive mosaic are Krasner hyperfields (mentioned in the Introduction, see [25]).
Remark 3.22. Terminologies such as "additive hyperrings with unity and inclusive distributivity" can be found in the literature to refer to multirings. Usually, these more precise terminologies are employed when several types of structures with two multivalued operations are considered at the same time (cf. [19] and references therein). We shall not elaborate more on this aspect.
Examples of hyperfields and multirings may be found e.g. in [4,14,30,32]. The polygroups K, S, and P from Example 3.18 are all hyperfields with respect to the multiplication induced by that of complex numbers. In an analogous manner, the commutative mosaic F from Example 3.18(6) becomes a partial hyperfield.
Example 3.23. A singleton set O:={a} is a partial multiring with respect to the multivalued operation a⊞a:={a} and the multiplication a⋅a:=a. In this case, of course, we have that a is the neutral element in both the additive and the multiplicative structure at the same time. On the other hand, notice that O is not a partial hyperfield.
Definition 3.24. A (strong) homomorphism of partial multirings (A,⊞,⋅,0,1)⟶(A′,⊞′,⋅′,0′,1′) is defined to be a function f:A⟶A′ that is both a (strong) homomorphism of the additive mosaics and a homomorphism of the multiplicative monoids. We denote by pMrg (pMrgstr) the category of partial multirings and their (strong) homomorphisms.
Remark 3.25. pMrg and pMrgstr are cartesian categories. Indeed, given partial multirings (A,⊞,⋅,0,1), (A′,⊞′,⋅′,0′,1′), and B, the pullback of two (strong) homomorphisms f:A⟶B and g:A′⟶B is given by the commutative mosaic (A×BA′,⊞pb,(0,0′)), where
endowed with the component-wise multiplication induced by ⋅ and ⋅′. Note further that the canonical projection maps are, by definition, strong homomorphisms. On the other hand, the partial multiring O from Example 3.23 is obviously a terminal object in both pMrg and pMrgstr.
Definition 3.26. Let (A,⊞,⋅,0,1) be a partial multiring. A subset I of A is called a left (resp. right) ideal if it satisfies:
(ID1) a⊞b⊆I, for all a,b∈I.
(ID2) If a∈I and x∈A, then ax∈I (resp. xa∈I).
If I⊆A is both a left and a right ideal of A, then it is called an ideal.
The following results are proved in [23] for a restricted class of multirings (called Krasner hyperrings). We observe that all the proofs can easily be adapted to the case of partial multirings (the reader may directly verify this claim by looking at the proofs in [23, Section 3]). For simplicity, we shall often identify any congruence (f,g):R⟶A×A on a partial multiring A, with the object R. This shall produce no harm since Sub(A×A) is a poset-category.
Proposition 3.27 ([23]). Let A be a partial multiring and I an ideal of A. Then the relation
is a congruence on A in both pMrg and pMrgstr.
Conversely, if R is a congruence on a partial multiring A and we denote by IR the R-equivalence class of 0∈A, then IR is an ideal of A and ≡I and R coincide as relations on A.
Proof. See [23, Section 3]. □
Proposition 3.28 ([23]). Let A be a partial multiring. The kernel of a homomorphism f out of A:
is an ideal of A. Conversely, any ideal I of A is the kernel of a strong homomorphism out of A whose target is given by the set of ≡I-classes A/I:=A/≡I equipped with the partial multiring structure (A/I,⊞I,⋅I,[0]I,[1]I) defined on two ≡I-classes [x]I,[y]I∈A/I (where x,y∈A) by the following formulae:
Proof. See [23, Section 3]. □
We note now that if a congruence (f,g):R⟶A×A on a partial multiring A in pMrg is such that both f and g are strong homomorphisms, then it follows from Definition 2.9 that (f,g) is a congruence on A in pMrgstr as well. Thus, the above propositions have the following consequence.
Corollary 3.29. Let A be a partial multiring. Any congruence R on A in pMrg is the kernel pair of the strong homomorphism q:A⟶A/IR given by the canonical map x↦[x]IR. In particular, R is a congruence on A in pMrgstr as well. Moreover, A/IR is a quotient object of A in both pMrg and pMrgstr, associated to the congruence R.
Next, we observe the following analogue of a basic result in commutative ring theory.
Lemma 3.30 (cf. [26, Corollary 2.13]). A commutative partial multiring A is a partial hyperfield if and only if the only ideals of A are {0} and A.
Proof. It suffices to note that
is an ideal in any commutative partial multiring A, for all x∈A. Indeed, (ID2) holds by definition, while (ID1) is readily deduced from the distributivity assumption (PM3). The assertion follows by further noticing that (as in the classical case of rings and fields) the following equivalences hold for all x∈A:
□
In [39], the following fact is proved. We refer to [39] for any notion which we have not explicitly defined.
Fact 3.31 ([39, Theorems 4.9,4.11,and 4.16]). The category CMsc admits a closed symmetric monoidal structure given by a bifunctor ⊠ and the commutative mosaic F (cf. Example 3.18(6)). For all commutative mosaics M,M′, the object M⊠M′ represents the functor of bimorphisms.
In addition, there exists a fully faithful functor F from the category of multirings into the category Mnd(CMsc,⊠,F) whose essential image is formed by those monoid objects in CMsc which are associative mosaics.
Remark 3.32. It is clearly and extensively explained in [39] why it is necessary to consider the monoidal structure on CMsc (rather than directly on the polygroup's categories).
Let us observe:
Proposition 3.33. Mnd(CMsc,⊠,F)=pMrgstr and Mnd(CMscstr,⊠,F)=pMrgstr.
Proof. The statement follows by noticing first that axiom (PM3) is equivalent to the following statement:
(PM3′) For every a∈A, the assignments x↦ax and x↦xa define homomorphisms of mosaics:
Then statement (PM3') is equivalent to the product operation being a homomorphism of mosaics A×A⟶A, where A×A denotes the product mosaic (cf. Remark 3.25). On the other hand, since F is freely generated by 1, there is a unique arrow e:F⟶A in CMsc which is induced by the image e(1) of 1∈F in A. In addition, the commutativity of the diagram (2.2), in this case, is clearly equivalent to e(1) being the neutral element for the multiplication.
The assertion that the arrows in these categories coincide follows after noticing that the commutativity of the diagrams (2.3) for an arrow f:A⟶A′ in CMsc is equivalent to f being a homomorphism of monoids (cf. [39, Theorem 4.16]). □
We deduce the final result of this section from the previous proposition by Corollary 3.29 and Lemma 3.30.
Corollary 3.34. Partial hyperfields are precisely the simple objects in Mnd(CMsc,⊠,F).
Remark 3.35. It is evident that for a partial hyperfield (H,⊞,⋅,0,1), the assignment x↦a−1x yields the inverse of each homomorphism x↦ax. In particular, these homomorphisms are automatically strong in this case (for Krasner hyperfields, this fact was already noted e.g. in [32] and [16]).
4.
Monoid objects in Rel
To any multivalued operation ⊡ on a set M we have associated a relation o⊡⊆(M×M)×M which we interpret as a categorial operation on M in Rel. We note in addition that o⊡ is everywhere defined if and only if x⊡y≠∅, for all x,y∈M.
Notation. In the following, Reled denotes the category of sets and everywhere defined relations. By extension, for any regular category C, the category Reled(C) is defined by requiring its arrows to be everywhere defined relations in C.
Remark 4.1. It is not difficult to verify that the monoidal structure of (Rel(C),×,{⋆}) induces a monoidal structure on Reled(C), for any regular category C.
Proposition 4.2. Let (P,⊡,e,ρ) be a (commutative) polygroup and let o⊡⊆(P×P)×P denote the categorial operation in Rel associated to ⊡. Then (P,o⊡,{e}) is a (commutative) monoid object in the monoidal category (Reled,×,{⋆}).
In addition, if (P,⊡,e,ρ) is commutative, then ρ is an automorphism in Mnd(Reled,×,{⋆}).
Proof. An Reled-arrow {⋆}⟶H is the same thing as a non-empty subset of H and the Reled-arrow corresponding to {e} clearly makes the diagram (2.2) commutative in Reled. On the other hand, it is immediate to verify that the diagrams (2.1) and (2.4) for o⊡ commute in Reled if and only if ⊡ is associative and commutative, respectively.
The last assertion follows from Lemma 3.9, and Corollary 3.11 which imply that ρ=ρ−1 (being necessarily the inverse function in P) and the commutativity of the diagrams (2.3) for ρ:P⟶P is equivalent to ρ being a unitary strong homomorphism of magmata. □
It had already been pointed out in [21] that, while an arrow e:{⋆}⟶H in Set is, in fact, an element of H, such an arrow in Rel may be identified with a subset
Example 4.3 (Example 4 in [21]). Let C be a category with more than one object and such that the collections of arrows are sets. Then (M,∘,1) is a monoid object in (Rel,×,{⋆}), where
∘ denotes the composition of arrows in C, and
Note that to any C-arrow f:A⟶B in M there corresponds (functionally) a left neutral element, i.e., 1A, and a right neutral element, i.e., 1B.
In this section, we shall prove (see Proposition 4.5 below) that neutral but non-singleton subsets do not occur if one restricts to Reled.
For a monoid object (M,o,E) in (Rel,×,{⋆}), the commutativity of the left part of diagram (2.2) for o⊆(H×H)×H can be spelled out as follows:
(LU) For all x∈H, there is eℓx∈E such that (eℓx,x;x)∈o and, at the same time, for all e∈E and y∈H if (e,x;y)∈o, then y=x,
which (following [21]) we call the left unit axiom.
On the other hand, the right part of diagram (2.2) for o⊆(H×H)×H is equivalent to the following property:
(RU) For all x∈H, there is erx∈E such that (x,erx;x)∈o and, at the same time, for all e∈E and y∈H if (x,e;y)∈o, then y=x,
which we call the right unit axiom.
In a later analysis, one can prove (see [21, Proposition 1]) that both of the assignments x↦eℓx and x↦erx are necessarily functional (i.e., everywhere defined and singlevalued) and thus the final observation in Example 4.3 above reflects a fact which holds in full generality.
Let us now isolate for later reference the following consequence of (LU) and (RU).
Lemma 4.4. Let (H,o,E) be a monoid object in (Rel,×,{⋆}) and ⊡ the multivalued operation associated to o. Then for any e∈E and all x∈H we have that |x⊡e|,|e⊡x|≤1.
Proof. Indeed, y∈e⊡x (resp. y∈x⊡e) means that (e,x;y)∈o (resp. (x,e;y)∈o) and thus y=x follows by the left (resp. right) unit axiom. □
We now prove, as promised, that if (H,o,E) is a monoid object in (Reled,×,{⋆}), then the set E is a singleton.
Proposition 4.5. Let (H,o,E) be a monoid object in (Reled,×,{⋆}). Then the assignments x↦eℓx and x↦erx yield the same constant function. In particular, E is a singleton.
Proof. We denote by ⊡ the multivalued operation corresponding to the relation o⊆(H×H)×H. From Lemma 2.1 (2) and Lemma 4.4 we deduce that |x⊡e|=|e⊡x|=1 for all x∈H and all e∈E. Fix e1,e2∈E and x∈H. Since e1⊡e2={u} for some u∈H, using the associativity of ⊡, we obtain that
and it follows from [21, Proposition 1] that u=eℓx. Similarly, we have that
and it follows as above that u=erx∈E. Thus, eℓx=u=erx, for all x∈H, that is, the assignments x↦eℓx and x↦erx yield the same function x↦ex.
Now, if x,y∈H and ex,ey∈E are the (left and right) neutral elements corresponding to x and y, respectively, then again ex⊡ey={u} for some u∈H and, using the assumption on o and the associativity of ⊡ as before, we obtain that
Hence, u=ey follows again from [21, Proposition 1]. Similarly, we have that
so that u=ex follows as above. We have thus proved that ex=ey, that is, the assignment x↦ex yields a constant function. □
Corollary 4.6. A singleton set with the structure of the trivial monoid is both terminal and initial in the category Mnd(Reled,×,{⋆}).
For the sake of completeness, let us remark that the restriction to Reled is sufficient to deduce that the neutral set is a singleton, but it is not necessary as the following example shows.
Example 4.7. Let M:={e,x} be a set with two elements. Define on M a multivalued operation ⊡ by setting e⊡e={e}, x⊡e=e⊡x={x}, and x⊡x=∅. Further, let o be the categorial operation corresponding to ⊡. It is straightforward to verify that (X,o⊡,{e}) is a monoid object in Rel. In addition, note that, while e is neutral in M for ⊡, we have that (M,⊡,e) is not invertible, since e−1=e, while e∉∅=x⊡x and thus x has no inverse in M.
4.1. Commutative polygroup objects
We have seen in Proposition 4.2 that if (P,⊡,e) is a polygroup, then (P,o⊡,{e}) is a monoid object in Reled. The converse of this statement however clearly does not hold. Indeed, any monoid object M in Set is a monoid object in Rel as well ([21, Example 2]). On the other hand, clearly such M is reversible if and only if it is a group (cf. Lemma 3.9).
The next theorem characterises the monoid objects in Reled which do correspond to polygroups.
We fix a terminal object ⊤ in Set, i.e., a singleton, for the rest of the section.
Theorem 4.8. Let P be a set, o⊆(P×P)×P a categorial operation on P in Reled with associated multivalued operation ⊡, E a subset of P≃⊤×P, and ρ:P⟶P an arrow in Set. The following statements are equivalent:
(i) E is a map in Reled, i.e., E={e} (for some e∈E) and, moreover, (P,⊡,e,ρ) is a commutative polygroup.
(ii) (P,o,E) is a commutative monoid object in Reled and the graph (1P,ρ) of ρ is an isomorphism in Mnd(Reled,×,⊤) satisfying, in addition, the following property:
(INV) E⊆o∘(1P,ρ) and for any monic Rel-arrow J:P⟶P, tabulated by the Set-arrows j:P⟶P and j′:P⟶P, we have that
Proof. We begin by showing that (ii) implies (i). As in Lemma 4.5, the requirement that (P,o,E) is a monoid object in Reled implies that E={e}. It follows that E is a map in Reled and that (P,⊡,e) is a unital magma. Associativity and commutativity for ⊡ are equivalent to associativity and commutativity for o⊡, respectively (as we mentioned in the proof of Proposition 4.2). Thus, (P,⊡,e,ρ) is a commutative polygroup by Corollary 3.17 which shows that (P,⊡,e) is ρ-reversible. Indeed, property (ii) in Corollary 3.17 clearly follows from property (INV) and the other assumptions on the endofunction ρ.
For the converse implication, assume (i). We may employ Proposition 4.2 to deduce that (P,o,E:={e}) is a commutative monoid object in Reled and, in particular, that E is a map in Reled. Now, Lemma 3.9 together with the fact that ⊡ and ⊡t coincide by assumption show that ρ-reversibility for (P,⊡,e,ρ) implies that (the graph of) ρ is an automorphism of P in Mnd(Reled,×,⊤) satisfying, moreover, property (INV). □
Definition 4.9 (Commutative polygroup objects in regular categories). Let C be a regular category and equip Rel(C) with the symmetric monoidal structure induced by products × and a (fixed) terminal object ⊤ in C. An object P together with Reled(C)-arrows o:P×P⟶P and E:⊤⟶P, as well as a C-arrow ρ:P⟶P is called a commutative polygroup object over C if and only if it satisfies statement (ii) of Theorem 4.8, where Set, Reled, and ⊆ are replaced by C, Reled(C), and ⊑, respectively.
Remark 4.10. Let C be a regular category. Since maps in Rel(C) are comparable by ⊑ if and only if they are equal, it follows from property (INV) that for a fixed commutative polygroup object (P,o,E,ρ) the C-arrow ρ is uniquely determined by the rest of the structure. Indeed, if (P,o,E,ρ) and (P,o,E,ρ′) are both polygroup objects over C, then property (INV) applied to both (P,o,E,ρ) and (P,o,E,ρ′) implies, e.g., that (1P,ρ′)⊑(1P,ρ), and thus ρ=ρ′.
Remark 4.11. With some extra effort, non-commutative polygroup objects may also be defined over regular categories following an analogous path. However, this would certainly require a convenient way to handle twin multivalued operations (cf. Lemma 3.9).
Remark 4.12. Commutative polygroup objects have been defined via a detour from a regular category C through its category of relations Rel(C). Since C and Rel(C) have the same collection of objects, the arrows of a category of commutative polygroup objects can be defined according to whether one wants these to be arrows or relations in C.
For the case of the category formed by commutative polygroups and their homomorphisms considered in Section 3, the former choice is made (i.e., any arrow is a Set-arrow), as opposed to a Rel-arrow.
On the other hand, we note that categories formed by commutative polygroups and multivalued homomorphisms (equivalently, Rel-arrows) have also been considered in the literature, see e.g. [5, Definition 2.14 and 2.17]. In the just mentioned reference, a great variety of distinct possibilities for the defining properties of such morphisms can be found for both of the above described choices and each yielding to a distinct category having commutative polygroups as objects.
5.
The category of Krasner hyperfields and other categories
For the results in this section, we shall denote by Kra (Krastr) the category formed by Krasner hyperfields and (strong) multiring-homomorphisms between them. By the results at the end of Section 3, Kra (Krastr) is the full subcategory of simple objects in Mnd(CMsc,⊠,F) (Mnd(CMscstr,⊠,F)) whose additive mosaics are associative.
There are a number of theorems in the literature which relate Krasner hyperfields to classical objects. We state below some of these results in the form of existence theorems of certain fully faithful functors‖ into certain slice (or coslice) categories of Kra and Krastr by certain well-known Krasner hyperfields. Most proofs can be recovered from the literature and we give the appropriate citations below while limiting ourself to necessary verifications only. Our hope is that more statements of this form will be discovered to hold where slice or coslice categories of Kra, Krastr, Mnd(CMsc,⊠,F), or Mnd(CMscstr,⊠,F) are taken over other hyperfields, partial hyperfields, or partial multirings.
‖We recall that a fully faithful functor is a functor whose arrow assignments are all bijections.
For the definitions of real hyperfields and their positive cones as well as valued hyperfields and their value groups, mentioned below, we refer to, e.g., [26].
Proposition 5.1 ([26]). There is a fully faithful functor F from the category of formally real fields into the slice category Kra/S. The latter slice category is the category of real hyperfields and homomorphisms f:H1⟶H2 such that f(H+1)⊆H+2, where H+k denotes the positive cone of Hk for k=1,2. The essential image of the functor F is formed by real hyperfields with singlevalued addition.
Proof. See [26, Remark 3.2]. □
Proposition 5.2 ([28]). Let Γ be an ordered abelian group. There is a fully faithful functor from the category of valued fields (K,v) with value group vK being an ordered subgroup of Γ into the slice category Kra/T(Γ). The latter slice category is the category of valued hyperfields and homomorphisms f:(H1,v1)⟶(H2,v2) such that v1∘f=v2. The essential image of the functor F is formed by valued hyperfields with singlevalued addition.
In addition, the system (RVγ(K))vK∋γ≥0 of Flenner's leading term structures associated to any valued field (K,v) naturally forms a diagram in Kra/T(Γ), and (K,v) is a cone over this diagram in Kra/T(Γ), while the completion of (K,v) by Cauchy sequences is its limit cone.
Proof. See [28,30]. Flenner's leading term structures were originally defined in [15]. □
Before stating the next result, let us briefly introduce some necessary concepts.
Definition 5.3. A lattice-ordered abelian group (or commutative l-group) is a lattice (L,∧,∨) where a commutative group operation ⋅ is defined on L such that for all x,y,a∈L the following equalities hold:
A homomorphism of l-groups is a group homomorphism f:L⟶L′ which is a lattice homomorphism as well, i.e., for all x,y∈L, the following equalities hold:
Remark 5.4 ([1, Proposition 1.1.6]). The underlying lattice of an l-group is distributive, thus, in particular, it is a modular lattice. For the notions of distributive and modular lattices we refer to e.g., [1].
Proposition 5.5 ([40]). There is a fully faithful functor F from the category formed by commutative l-groups with a top element and their homomorphisms into the coslice category K∖Kra. The essential image is made by those objects K⟶H in K∖Kra where
defines a lattice order ≤ on H such that for all x,y∈H the following equality holds:
Proof. In [40, Theorem 1], Nakano observed that the multivalued operation ⊞ defined by (5.3) on a lattice (L,∧,∨) is associative if and only if L is modular. Furthermore, by definition, we have that
In particular, it follows that 0∈L is neutral for ⊞ if and only if 0≥x for all x∈L, i.e., 0 is a top element for L and each x∈L is its own unique inverse in the (evidently commutative) mosaic (L,⊞,0). Thus, Nakano's result and Remark 5.4 above yield that if L is the underlying lattice of a commutative l-group, then (L,⊞,0) is a commutative polygroup.
Furthermore, property (5.1) of commutative l-groups implies that, for any l-group L, the group operation ⋅ is distributive on the multivalued operation ⊞, i.e., for all x,y,a∈L, the following equality holds:
We deduce, moreover, that if 0 is a top element in a commutative l-group L and a∈L, then a⋅0 must be a top element as well. Thus, a⋅0=0⋅a=0 follows from the uniqueness of the top element in L.
We have proved that (L,⊞,⋅,0,1) is a Krasner hyperfield. Since 0 is a top element in L we immediately obtain that
Hence, the obvious map K⟶L is a homomorphism of hyperfields, defining the object assignment of the functor F.
Now, we claim that if f:L⟶L′ is a homomorphism of l-groups, then the same map is a homomorphism of the corresponding hyperfield. Indeed, if z∈x⊞y holds in the hyperfield (L,⊞,⋅,0,1) defined above, then we deduce
that is, f(z)∈f(x)⊞f(y). It follows that F is fully faithful.
The validity of the rest of the assertions is now immediate to verify. □
For the next result we need to introduce some terminology as well.
Definition 5.6. By a projective geometry we mean a set P with a family L of subsets of P satisfying the following three properties:
(Pr1) Two distinct points p,q∈P determine a unique line ℓ=ℓ(p,q) such that p,q∈ℓ.
(Pr2) If a line ℓ intersects two sides of a triangle, not on a vertex, then ℓ also intersects the third side of that triangle, that is, for all distinct p,q∈P, all s∈P∖ℓ(p,q), all q′∈ℓ(p,q)∖{p}, and all s′∈ℓ(p,s)∖{p}, the lines ℓ(q,s) and ℓ(q′,s′) are incident.
(Pr3) Any line in L contains at least three distinct points in P.
A map f:(P,L)→(P,L) between projective geometries is called incidence-preserving if for all p∈P and ℓ∈L the following equivalence holds:
A (two-sided) incidence group is defined as a projective geometry (P,L), equipped with a group operation ⋅, defined on P, and satisfying the following property:
(IG) For all p∈P the functions P⟶P induced by the assignments x↦p⋅x and x↦x⋅p are incidence-preserving.
By a homomorphism of incidence groups we shall mean an incidence-preserving group homomorphism.
Proposition 5.7 ([9]). There is a fully faithful functor F from the coslice category K∖Krastr into the category of incidence groups and their homomorphisms. The essential image is made by those incidence-groups whose lines contain at least four distinct points.
Proof. The object assignment of the functor is defined [9, Proposition 3.5] by mapping the target hyperfield of a strong homomorphism K⟶H to its multiplicative group P:=H∖{0} and setting the line determined by distinct p,q∈P to be (p⊞q)∪{p,q}. It is also proved there that in the projective geometries obtained in this way, lines contain at least four distinct points.
If f:H⟶H′ is a strong homomorphism of hyperfields, then we define F(f) to be its restriction to H∖{0}, which yields a group homomorphism F(f):P⟶P′. We claim that, as a map between projective geometries, F(f) is incidence-preserving. If p∈P and ℓ∈L, then, by assumption, there are distinct x,y∈P∖{p} such that ℓ=(x⊞y)∪{x,y}. Since f is a strong homomorphism we obtain that
Conversely, if p∉ℓ, then we deduce from the above equivalences that f(p)∉f(x)⊞f(y). In addition, if f(p)=f(x), then f(y)≠f(x) follows. In this case, since in P′ lines have at least four points, we may find distinct
In particular, it follows that z′1,z′2∈f(H). We further deduce that the line λ:=(z′1⊞z′2)∪{z′1,z′2} contains f(x)=f(p) and f(y). Since, at this point, p∉f−1(z′1)∩f−1(z′2) holds, we deduce from f(x)=f(p),f(y)∈z′1⊞z′2 that p,x,y∈z1⊞z2, for some zk∈f−1(z′k)≠∅ (k=1,2), which contradicts the initial assumption p∉ℓ=ℓ(x,y). Similarly, one shows that the assumption f(p)=f(y) yields to a contradiction. We conclude that F(f) is a homomorphism of incidence groups.
On the other hand, if f:H∖{0}⟶H∖{0} is a homomorphism of incidence groups, then its obvious extension f:H⟶H′ is a strong homomorphism of hyperfields and thus yields an arrow in K∖Krastr. In fact, from the arguments employed above, if follows that, if x,y∈H∖{0} are distinct, then the following equivalence
holds, for all z∈H. Since any hyperfield H corresponding to an object in K∖Krastr must satisfy x⊞0={x} and x⊞x={0,x} for all x∈H, it follows that the arrow-assignment of the functor F defined above is also invertible, completing the proof of the proposition. □
Remark 5.8. Since homomorphisms of hyperfields are defined to be homomorphisms of multirings, we also obtain fully faithful functors into the corresponding slice or coslice categories of Mnd(CMsc,⊠,F).
Remark 5.9. It is not clear whether slicing or coslicing by the phase hyperfield P is related to any known category. As we mentioned above, we leave the investigation of this and similar problems open for future research.
6.
Conclusions
Extending classical algebraic theories and results by allowing operations to be multivalued often poses nontrivial challenges. At the time in which this article is being written, among all multivalued algebraic structures, Krasner hyperfields seem to have attracted the attention of the mathematical community more than others and this fact motivated the focus on commutative polygroups (i.e., canonical hypergroups).
We should remark that the results on the category Mnd(CMsc,⊠,F) of partial multirings do not directly generalise to regular categories. For that, Theorem 4.8 should be extended to a characterisation of (commutative) mosaics over Set. We believe that such a result can be achieved, but we leave the investigation for future research.
We furthermore highlight that, in view of [22, Corollary 2.3.5], topoi are regular categories and thus we have a definition of commutative polygroup objects in any topos. This represents a step forward with respect to the program of investigating commutative polygroups from a topos theoretic perspective (as motivated in [13]).
Finally, the problems described in [5], where commutative polygroups appear as the additive structure of hypermodules, regarding the possibilities of generalising homological algebra to the multivalued case, may also be closely related to the results of this paper.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
My sincere gratitude is directed to N. Cangiotti and H. Bordbar for taking part to several discussions which helped to improve the paper significantly, as well as to I. Cristea for her tireless support. In addition, credit goes to the anonymous referees whose helpful comments added great value to the final version of this manuscript.
Conflict of interest
The authors declare no conflict of interest.









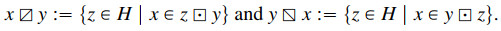
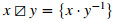 and
and 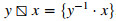 , where
, where  and
and  are not necessarily related to the inverses, in the sense of (1.2) above, of single elements (if they exist).
are not necessarily related to the inverses, in the sense of (1.2) above, of single elements (if they exist).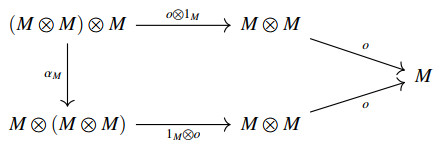
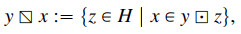
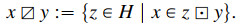
 and
and 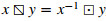 , for all
, for all 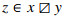 means
means 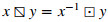 is derived similarly.
is derived similarly.



 DownLoad:
DownLoad: