Stochastic evolution game analysis of the strategic coalition of enterprise pollution control

1.   Introduction

After several decades of rapid technological advancement and economic growth, the world is now facing alarming levels of pollution and environmental degradation, including high emissions and severe global warming ^[1,2]. China, since its reform and opening-up, has experienced remarkable economic development and has become the second-largest economy in the world. However, the past extensive model of economic growth has resulted in ecological damage, environmental pollution, and other pressing issues. These problems not only hinder development but also negatively impact the environment. As Dongbin observed in ^[3], the contradiction between the economy and the natural environment has been growing alongside social and economic development. Therefore, it is crucial to address these environmental challenges urgently.

The current study focuses less on the analysis of behavior between firms and more on the evolutionary game analysis between the government and enterprises ^[4]. Consequently, this research endeavors to establish a dynamic evolutionary game model for strategic coalitions in enterprise pollution control. Drawing from existing research, the study utilizes an evolutionary game approach to analyze the model. Additionally, it investigates the impact of various factors on the participants' strategies and provides relevant policies and recommendations to establish a foundation for a strategic coalition in enterprise pollution control. Sara ^[5] developed a novel framework based on evolutionary game theory to model the dilemma faced by each of the three sectors, including the state, business, and civil society, in deciding between maintaining the status quo or shifting to a new paradigm. In addition, Han ^[6] found that rewarding compliance with commitments can promote compliance with signed contracts, assuming there was sufficient budget to give incentives.

Evolutionary game theory has found widespread application since its development. In this context, a system dynamics model was constructed to investigate a mixed-strategy evolutionary game between a government entity responsible for managing environmental pollution and a firm that generates contamination during its production processes. Remarkably, the results obtained from this study demonstrate the absence of an evolutionary equilibrium when using a static penalty approach ^[7,8]. Furthermore, Wang and Shi ^[9] conducted a study on the evolutionary game model of industrial pollution, focusing on interactions between local governments and enterprises using both static and dynamic punishment mechanisms. It was found that under the dynamic punishment mechanism, the evolutionary path between governments and enterprises tends to converge stably. Additionally, the dynamics of player behavior within an evolutionary game framework involving one government and two competing enterprises were explored by Cai ^[10]. Notably, a system dynamics model was established, and the simulation results revealed a close relationship between the penalty factor ($k$), which represents the limit of the penalty, and the volatility of the dynamic evolutionary process.

Previous research in this field has primarily focused on the internal environment under specific conditions, disregarding the external environment and not fully considering the reality of the situation. However, there are scholars who have recognized the complexity of the system and incorporated the uncertainty of the external environment into their studies. For instance, Chen and Yeh ^[11] developed a model for a population of evolving biological networks as a nonlinear stochastic biological system. This model considered Poisson-driven genetic variations and random environmental fluctuations and discussed the phenotypic robustness and network evolvability of noncooperative and cooperative evolutionary game strategies from a stochastic Nash game perspective. Zhang ^[12] proposed a novel measure to depict biodiversity in stochastic evolutionary dynamics and emphasized the importance of transient dynamics on biodiversity. This approach provided insights into calculating biodiversity under stochastic evolutionary processes. Xu and Yu^[13] utilized stochastic evolutionary game theory to analyze the stability of cooperation among members in the face of external opportunism within a multi-firm alliance context and addressed the impact of stochastic factors on the evolutionary dynamics of cooperation. Quan, Liu, and Chu ^[14] considered the influence of noise under the optional participation mechanism and established a stochastic model for evolutionary public goods games in finite populations. Their study revealed that stochastic and finite-size effects can quantitatively alter the evolutionary dynamics and equilibrium of optional public goods games. Building upon this body of research, this paper aims to establish a pollution control coalition of three enterprises using stochastic evolutionary game theory. It recognizes the importance of incorporating stochastic elements into the analysis. For a comprehensive understanding of game-based approaches to addressing pollution-related problems, readers are referred to works such as ^{[15,16,17,18,19]}.

The remainder of this work is structured as follows: Section 2 introduces the research methods and methods of the evolutionary game. Section 3 examines the construction of the evolutionary game model, the stable equilibrium, and the stability of the equilibrium point. Section 4 constructs the stochastic evolution model and analyzes the stable conditions. Section 5 presents the findings of a numerical simulation of the evolution path of corporate strategy. Section 6 addresses the impact of parameter adjustments on the stable approach, and the results are summarized with conclusions and policy recommendations.

2.   Evolutionary game model

2.1.   Research theory

Given the widespread and relevant problem of environmental pollution, enterprises encounter difficulties in effectively resolving the issue on their own. Moreover, even if they possess the ability to address it independently, the income-cost ratio for completing the task may not be optimal. Therefore, a collaborative approach through binding cooperation between enterprises is more effective. Finus ^[20] introduced the concept of strategic coalitions for enterprise pollution control. In pollution control, a strategic coalition is a collaborative alliance formed by various firms with the purpose of ensuring effective pollution management while lowering investment costs. The coalition requires shared responsibility, coordination, and cooperation, blurring the boundaries between participating companies to a certain extent to work towards a common goal. While the coalition companies collaborate in specific areas, they also maintain their independence in other aspects of operation and management, potentially even competing with one another.

2.2.   Research hypotheses of the model

The hypotheses are described as follows:

(1) Pollution reduction technology research and development and equipment investment have spillover effects, which means that companies in the coalition gain from sharing pollution technology.

(2) The bounded rationality hypothesis in coalition collective: the overall cost of pollution reduction by the alliance should not be greater than the sum of the costs of individual pollution reduction measures.

(3) The enterprise individual rationality hypothesis: the pollution control costs shared by coalition members should not be greater than those borne by non-coalition members.

2.3.   Basic symbol description

There are several variables defined as Table 1:

It is crucial to emphasize some of the relationships between the variables listed above. For businesses, the choice to join a coalition for joint pollution management is based on whether the advantages outweigh the costs. In the model, it was assumed that once an enterprise joins the pollution governance coalition, it has $r_A\pi-C(a) > 0$, $r_B\pi-C(b) > 0$, or $r_C\pi-C(c)) > 0$. The formation of a coalition requires the collective efforts of all enterprises involved. If two enterprises within this group do not join or withdraw from the coalition, even if the other party remains committed to the alliance and makes efforts, the joining enterprise will not receive the benefits of pollution control within the coalition. For example, in the case where only enterprise $A$ joins the coalition and the other two enterprises do not, the enterprise's income would be $\pi_A-C(a)$, and similar scenarios exist for other combinations of enterprise membership.

2.4.   Replicator dynamics analysis

Based on the main assumptions stated above, the strategy sets of both sides of the game are {joining, withdrawing}. The proportion of the adoption of behavioral strategies is as follows: during the initial stage of the game, the probability that enterprise $A$ chooses 'joining' is $x$, 'withdrawing' is $1-x$, the probability that enterprise $B$ chooses 'joining' is $y$, 'withdrawing' is $1-y$, the probability that enterprise $C$ chooses 'joining' is $z$, and 'withdrawing' is $1-z$. In this case, probabilities $x$, $y$, and $z$ are functions of time ^[21,22]. Thus, the strategy portfolios and benefits of the trilateral evolutionary game of the strategic coalition of environmental pollution control are given as in Table 2:

(1) The replicator dynamics equation of enterprise $A$.

According to Table 2, assuming that the expected revenue $f_{A_j}$ and $f_{A_w}$, where $A_j$ and $A_w$ are respectively the expected benefit to the firms $A$ participating and expected benefit to the firms $A$ not participating in the partnership, the average expected revenue $\bar{f}_A$ of the enterprise A's strategies are

Thus, according to ^[23], the average income of enterprise $A$ is expressed as follows:

The replicator dynamics $F(x)$, from ^[24], when enterprise $A$ joins, is described as follows:

Using some stable theorem of differential equations, the authors of this paper can deduce that enterprise $A$'s choice of joining strategy must satisfy the following conditions: $F(x) = 0$ and $\frac{dF(x)}{dx} < 0$. Hence, the stability of the evolution strategies of enterprise $A$ is analyzed as follows:

Ⅰ. When $z = \frac{C(a)-C_A-y\pi r_A}{\pi r_A-y\pi r_A}$, $F(x)\equiv0$, and any level ($x\in[0, 1]$) is in a stable state, the stabilization strategy cannot be determined over time as shown in Figure 1a.

Ⅱ. When $z\neq\frac{C(a)-C_A-y\pi r_A}{\pi r_A-y\pi r_A}$, let $F(x) = 0$, thus $x = 0$ and $x = 1$ are two stable points of enterprise $A$.

The derivative of $F(x)$ with respect to $x$, $\frac{dF(x)}{dx} = (1-2x)(C_A-C(a)+y\pi r_A+z\pi r_A-yz\pi r_A)$. The different situations are analyzed as follows:

a. When $z > \frac{C(a)-C_A-y\pi r_A}{\pi r_A-y\pi r_A}$, and $\frac{dF(x)}{dx}\mid_{x = 0} > 0$, and $\frac{dF(x)}{dx}\mid_{x = 1} < 0$, $x = 1$ is an evolutionary stable strategy as shown in Figure 1b.

b. When $z < \frac{C(a)-C_A-y\pi r_A}{\pi r_A-y\pi r_A}$, $\frac{dF(x)}{dx}\mid_{x = 1} < 0$, and $\frac{dF(x)}{dx}\mid_{x = 1} > 0$, $x = 0$ is an evolutionary stable strategy as shown in Figure 1c.

Proposition 2.1. The probability of enterprise $A$ joining the coalition increases with the increase in the probability of enterprise $B$ and enterprise $C$ joining the coalition, and vice versa.

Proof. We used the derivative dynamic model of enterprise $A$ choosing 'joining' to obtain partial derivatives. The correlation function between the probability $x$ of enterprise $A$ joining and the probability $z$ of joining by enterprise $C$ can be obtained as follows:

When $z > \frac{C(a)-C_A-y\pi r_A}{\pi r_A-y\pi r_A}$, $x = 1$ is the evolutionary stable strategy. When enterprise $C$'s motivation for choosing 'joining' is higher than a certain value, enterprise $A$ is more inclined to joining and obtaining more benefits and the strategy chosen stabilizes at 1. When $z < \frac{C(a)-C_A-y\pi r_A}{\pi r_A-y\pi r_A}$, $x = 0$ is the evolutionary stable strategy. When enterprise $C$'s motivation for choosing 'joining' is lower than a certain value, enterprise $A$ is more inclined to withdraw and save some effort costs, and the strategy chosen stabilizes at 0.

Similarly, the correlation function between the probability of enterprise $A$ joining $x$ and the probability of joining of enterprise $B$ with respect to $y$ is obtained. When $y > \frac{C(a)-C_A-z\pi r_A}{\pi r_A-z\pi r_A}$, $x = 1$ is the evolutionary stable strategy; when enterprise $B$ is inclined to join the coalition, enterprise $A$ would choose to join, and therefore the strategy chosen by enterprise $A$ stabilizes at 1. When $y < \frac{C(a)-C_A-z\pi r_A}{\pi r_A-z\pi r_A}$, $x = 0$ is the evolutionary stable strategy; when enterprise $B$ is inclined not to join the coalition, enterprise $A$ would choose to withdraw, and the strategy chosen by enterprise $A$ stabilizes at 0. □

In summary, when enterprises join the alliance of pollution control strategy, the profit is greater than zero, and as long as one of them has the motivation to join the strategic coalition, the other two sides also have the tendency to join the strategic coalition.

(2) The replicator dynamics equation of enterprise $B$.

According to Table 2, the expected revenue $f_{B_j}$, $f_{B_w}$ and the average expected revenue $\bar{f}_B$ of enterprise B's strategies are

Thus, the average income of enterprise $B$ is expressed as follows:

The replicator dynamics equation when enterprise $B$ is joining is described as follows:

According to the stability theorem of differential equations, enterprise $B$'s choice of joining the strategy must satisfy the following conditions: $F(y) = 0$ and $\frac{dF(y)}{dy} < 0$. The stability of the evolution strategies of enterprise $B$ is analyzed as follows:

Ⅰ. When $x = \frac{C(b)-C_B-z\pi r_B}{\pi r_B-z\pi r_B}$, $F(y)\equiv0$, and any level ($y\in[0, 1]$) is in a stable state, the stabilization strategy cannot be determined over time as shown in Figure 2a.

Ⅱ. When $x\neq\frac{C(b)-C_B-z\pi r_B}{\pi r_B-z\pi r_B}$, let $F(y) = 0$, thus $y = 0$ and $y = 1$ are the two stable points of enterprise $B$.

The derivative of $F(y)$ with respect to $y$ is $\frac{dF(y)}{dy} = (1-2y)(C_B-C(b)+x\pi r_B+z\pi r_B-xz\pi r_B)$. The different situations are analyzed as follows:

a. When $x > \frac{C(b)-C_B-z\pi r_B}{\pi r_B-z\pi r_B}$, $\frac{dF(y)}{dy}\mid_{y = 0} > 0$, and $\frac{dF(y)}{dy}\mid_{y = 1} < 0$, $y = 1$ is an evolutionary stable strategy as shown in Figure 2b.

b. When $x < \frac{C(b)-C_B-z\pi r_B}{\pi r_B-z\pi r_B}$, $\frac{dF(y)}{dy}\mid_{y = 0} < 0$, and $\frac{dF(y)}{dy}\mid_{y = 1} > 0$, $y = 0$ is an evolutionary stable strategy as shown in Figure 2c.

Proposition 2.2. The probability of enterprise $B$ joining the coalition increases with the increase of the probability of enterprise $A$ and enterprise $C$ joining the coalition, and vice versa.

Proof. We used the derivative dynamic model of enterprise $B$ choosing 'joining' to obtain partial derivatives. The correlation function between the probability $y$ of enterprise $B$ joining and the probability $x$ of joining by enterprise $A$ can be obtained as follows:

When $x > \frac{C(b)-C_B-z\pi r_B}{\pi r_B-z\pi r_B}$, $y = 1$ is the evolutionary stable strategy. When enterprise $A$'s motivation for choosing 'joining' is higher than a certain value, enterprise $B$ is more inclined to join and obtain more benefits, and thus the strategy chosen stabilizes at 1. When $x < \frac{C(b)-C_B-z\pi r_B}{\pi r_B-z\pi r_B}$, $y = 0$ is the evolutionary stable strategy. When enterprise $A$'s motivation for choosing 'joining' is lower than a certain value and enterprise $B$ is more inclined to withdraw and save some effort costs, the strategy chosen stabilizes at 0.

Similarly, the correlation function between the probability of enterprise $B$ joining $y$ and the probability of joining of enterprise $C$ with respect to $z$ was obtained. When $z > \frac{C(b)-C_B-x\pi r_B}{\pi r_B-x\pi r_B}$, $y = 1$ is the evolutionary stable strategy; when enterprise $C$ is inclined to join the coalition, enterprise $C$ would choose to join, and therefore the strategy chosen by enterprise $B$ stabilizes at 1. When $z < \frac{C(b)-C_B-x\pi r_B}{\pi r_B-x\pi r_B}$, $y = 0$ is the evolutionary stable strategy; when enterprise $C$ is inclined not to join the coalition, enterprise $B$ would choose to withdraw, and the strategy chosen by enterprise $B$ stabilizes at 0.

(3) The replicator dynamics equation of enterprise $C$.

According to Table 2, the expected revenue $f_{C_j}$, $f_{C_w}$ and the average expected revenue $\bar{f}_C$ of enterprise $C$'s strategies are

Thus, the average income of enterprise $C$ is expressed as follows:

The replicator dynamics equation when enterprise $C$ joins is described as follows:

According to the stability theorem of differential equations, enterprise $C$'s choice of joining strategy must satisfy the following conditions: $F(z) = 0$ and $\frac{dF(z)}{dz} < 0$. The stability of the evolution strategies of enterprise $C$ is analyzed as follows:

Ⅰ. When $x = \frac{C(c)-C_C-y\pi r_C}{\pi r_C-y\pi r_C}$, $F(z)\equiv0$, and any level ($z\in[0, 1]$) is in a stable state, the stabilization strategy cannot be determined over time as shown in Figure 3a.

Ⅱ. When $x\neq\frac{C(c)-C_C-y\pi r_C}{\pi r_C-y\pi r_C}$, let $F(z) = 0$, and thus $z = 0$ and $z = 1$ are the two stable points of enterprise $C$.

The derivative of $F(z)$ with respect to $z$ is $\frac{dF(z)}{dz} = (1-2z)C_C-C(c)+x\pi r_C+y\pi r_C-xy\pi r_C)$. The different situations are analyzed as follows:

a. When $x > \frac{C(c)-C_C-y\pi r_C}{\pi r_C-y\pi r_C}$, $\frac{dF(z)}{dz}\mid_{z = 0} > 0$, and $\frac{dF(z)}{dz}\mid_{z = 1} < 0$, $z = 1$ is an evolutionary stable strategy as shown in Figure 3b.

b. When $x < \frac{C(c)-C_C-y\pi r_C}{\pi r_C-y\pi r_C}$, $\frac{dF(z)}{dz}\mid_{z = 0} < 0$, and $\frac{dF(z)}{dz}\mid_{z = 1} > 0$, $z = 0$ is an evolutionary stable strategy as shown in Figure 3c. □

Proposition 2.3. The probability of enterprise $C$ joining the coalition increases with the increase of the probability of enterprise $A$ and enterprise $B$ joining the coalition, and vice versa.

Proof. The derivative dynamic model of enterprise $C$ choosing 'joining' was used to obtain partial derivatives. The correlation function between the probability $z$ of enterprise $C$ joining and the probability $x$ of joining by enterprise $A$ can be obtained as follows:

When $x > \frac{C(c)-C_C-y\pi r_C}{\pi r_C-y\pi r_C}$, $z = 1$ is the evolutionary stable strategy. When enterprise $A$'s motivation for choosing 'joining' is higher than a certain value, enterprise $C$ is more inclined to join and obtain more benefits, and the strategy chosen stabilizes at 1. When $x < \frac{C(c)-C_C-y\pi r_C}{\pi r_C-y\pi r_C}$, $z = 0$ is the evolutionary stable strategy. When enterprise $A$'s motivation for choosing 'joining' is lower than a certain value, enterprise $C$ is more inclined to withdraw and save some effort costs, and the strategy chosen stabilizes at 0.

Similarly, the correlation function between the probability of enterprise $C$ joining $z$ and the probability of joining of enterprise $B$ with respect to $y$ was obtained. When $y > \frac{C(c)-C_C-x\pi r_C}{\pi r_C-x\pi r_C}$, $z = 1$ is the evolutionary stable strategy; when enterprise $B$ is inclined to join the coalition, enterprise $C$ would choose to join. Therefore, the strategy chosen by enterprise $C$ stabilizes at 1. When $y < \frac{C(c)-C_C-x\pi r_C}{\pi r_C-x\pi r_C}$, $z = 0$ is the evolutionary stable strategy; when enterprise $B$ is inclined not to join the coalition, enterprise $C$ would choose to withdraw and the strategy chosen by enterprise $C$ stabilizes at 0. □

2.5.   Stability of the evolutionary strategies analysis

The stability analysis of the strategy combinations of enterprises $A$, $B$, and $C$ can be carried out through the Jacobian matrix ^[25,26]. The partial derivatives with respect to $x$, $y$, and $z$ are obtained from $F(x), F(y)$, and $F(z)$, respectively, and the Jacobian matrix is given by

where $\alpha = y+z-yz, \beta = x+z-xz$, and $\gamma = x+y-xy$.

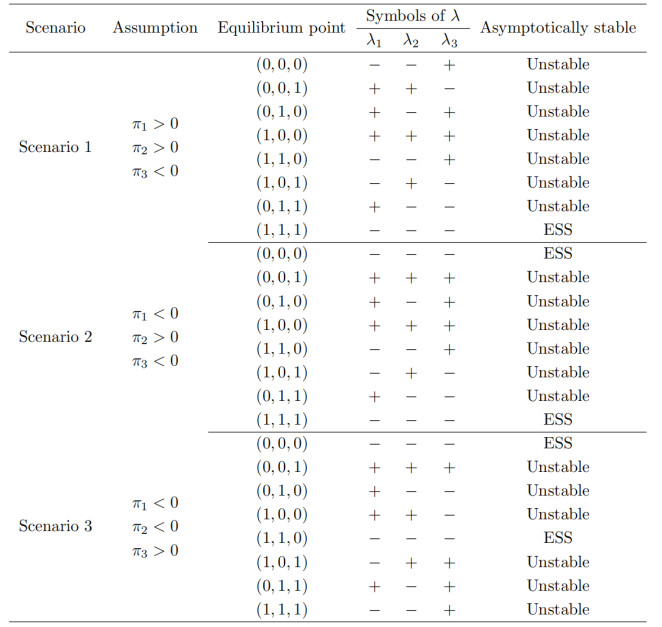
When $F(x) = 0, F(y) = 0$, and $F(z) = 0$, it shows that the game of this evolutionary system achieves a relatively stable equilibrium state, named the 'evolutionary stable strategy (ESS)' ^[8]. The local equilibrium points of the game subject, including enterprises $A$, $B$, and $C$, can be obtained, and the equilibrium point of the local equilibrium point is the equilibrium solution. Then, there are eight equilibrium points. According to Lyapunov's first method ^[27] (pp 531–534) regarding the ESS, the characteristic root of its corresponding Jacobian matrix must be less than 0. In Table 3, the symbols shown in brackets indicate the positive and negative values of the eigenvalues of $J$.

According to Table 3, the positive and negative of some roots are undetermined, so there is a need to discuss the parameters for their uncertainty, which will lead to different results. The analysis is shown in Table 4.

The above equilibrium state analysis shows that, among the eight local equilibrium points, only (0, 0, 0), (1, 1, 0), and (1, 1, 1) are stable points under certain conditions, which is the evolutionary stable strategy, and the corresponding strategies are "withdrawing, withdrawing, withdrawing", "joining, joining, withdrawing", and "joining, joining, joining". According to Table 4, it can be seen that there may be no enterprise coalition, there may be some enterprise coalition, and there may be full enterprise coalition, which is in line with the actual situation.

Next, there is the need to discuss the parameters for their uncertainty, which will lead to different results. Let $\pi_1 = C_C-C_B-\frac{1}{2}wc^2, \pi_2 = C_C-C_B-\frac{1}{2}wc^2+\pi r_C$, and $\pi_3 = C_B-C_C+\frac{1}{2}wc^2-\pi r_C$. Then, according to Lyapunov's first method, there are three possibilities:

Scenario 1 ($\pi_1 > 0, \pi_2 > 0, \pi_3 < 0$): In such a situation, the ESS is (1, 1, 1), and its corresponding evolutionary stabilization strategy is (joining, joining, joining), that is, enterprises $A$, $B$, and $C$ all join the coalition.

Scenario 2 ($\pi_1 < 0, \pi_2 > 0, \pi_3 < 0$): In such a situation, the ESSs are (0, 0, 0) and (1, 1, 1), and its corresponding evolutionary stabilization strategies are (withdrawing, withdrawing, withdrawing) and (joining, joining, joining), that is, enterprises $A$, $B$, and $C$ either all join the coalition or they or do not. There are two stable points, which is not in line with reality and thus should be discarded.

Scenario 3 ($\pi_1 < 0, \pi_2 < 0, \pi_3 > 0$): In such a situation, the ESSs are (0, 0, 0) and (1, 1, 0), and its corresponding evolutionary stabilization strategies are (withdrawing, withdrawing, withdrawing) and (joining, joining, withdrawing), that is, enterprises $A$, $B$, and $C$ either all do not join the coalition or enterprises $A$ and $B$ only join the coalition. There are two stable points, which is not in line with reality and thus should be discarded.

By synthesizing the above three cases, the results are obtained in Table 5.

Table 5 shows the stable points of local equilibria under different conditions. Meanwhile, scenarios 2 and 3 have two evolutionary stable strategies which do not meet the requirements because, according to the actual situation, two stable points cannot appear at the same time in an actual situation. Thus, they are excluded so that the final evolutionary stable strategy is (1, 1, 1).

In brief, when conditions $C_C-C_B-\frac{1}{2}wc^2 > 0, C_C-C_B-\frac{1}{2}wc^2+\pi r_C > 0$, and $C_B-C_C+\frac{1}{2}wc^2-\pi r_C < 0$ are satisfied, (1, 1, 1) is the equilibrium stable point and it is also the optimal equilibrium point. This result is the stable strategy of the system under the condition of internal and external environmental uncertainty. However, due to the complexity of the system and the uncertainty of the external environment, the decision-maker will be disturbed by random factors when making decisions. Such questions as whether strategy (1, 1, 1) is stable and under what conditions it is stable may arise. Therefore, the subsequent section addresses the impact of random interference factors on stability.

Figure 4 shows the dynamic evolution of environmental pollution control behavior of enterprises. According to the above three scenarios, there should be three stable points, $O$, $B$ and $G$, but two stable points $O$ and $B$ appear at the same time, which is not consistent with the actual situation, so there is only one stable point $G$.

3.   Stochastic evolutionary game model and its stability

During the decision-making process, decision-makers encounter a series of uncertain factors, both internal and external. Therefore, the deterministic evolutionary game model cannot fully reflect the actual state of the decision-maker. To address this limitation, Gaussian white noise is added to the system to describe the random interference of the system.

3.1.   Stochastic evolutionary game model

Since $1-x, 1-y$, and $1-z$ in (2.4), (2.9), and (2.14) are nonnegative, respectively, it has no effect on the result of strategy equilibrium evolution. Therefore, for the convenience of discussion, (2.4), (2.9), and (2.14) can be changed to the following dynamic system:

The stochastic dynamical system with high white noise is considered as follows:

where $\sigma$ is the intensity of stochastic disturbance, $\omega(t)$ is one-dimensional standard Brownian motion, $d\omega(t)$ is Gaussian white noise, and $d\omega(t)\sim N(0, \Delta t)$. So, Eqs (3.4)–(3.6) describe the strategy change process of enterprises under random interference. In order to discuss the influence of random disturbance factors on stability, the concept of stability of the zero solution of stochastic differential equations is introduced.

Definition 3.1.^[28]   Let $p > 0$, if $\forall x_0\in[0, 1]$, $x_0$ is the stochastic variable, $x(t, x_0)$ is a solution of Eq (3.4), and it has a negative $p$-th moment lyapunov exponent, i.e., if $\overline{\lim\limits_{t\rightarrow \infty}}t^{-1}\ln E|x(t, x_0)|^p < 0$, then the zero solution of Eq (3.4) is exponentially stable with $p$-moment; if $\overline{\lim\limits_{t\rightarrow \infty}}t^{-1}\ln E|x(t, x_0)|^p > 0$, then the zero solution of Eq (3.4) is exponentially unstable with a $p$-th moment.

Lemma 3.1.^[13]   Consider the following differential equation:

Let there be a smooth function $V(t, x)$ and normal numbers $c_1, c_2$ such that

(1) If there is a normal number $\gamma$ such that $LV(t, x)\leq -\gamma V(t, x)$, then the zero solution of (3.4) is exponentially stable with a $p$-th moment, and $E|x(t, x_0)|^p\leq(c_2/c_1)|x_0|^pe^{rt}$.

(2) If there is a normal number $\gamma$ such that $LV(t, x)\geq \gamma V(t, x)$, then the zero solution of (3.4) is exponentially unstable with a $p$-th moment, and $E|x(t, x_0)|^p\geq(c_2/c_1)|x_0|^pe^{rt}$, where $LV(t, x) = V_t(t, x)+V_x(t, x)f(t, x)+\frac{1}{2}g^2(t, x)V_{xx}(t, x)$.

3.2.   Stability analysis

Proposition 3.1. For the stochastic differential equation (3.4), with $c_1 = c_2 = 1, p = 1, \gamma = 1$, and Lyapunov function $V(t, x) = x(t)$, when

(1) $y(t)+z(t)-y(t)z(t) = 0$ and $1\leq\frac{1}{2}ua^2$, or

(2) $0 < y(t)+z(t)-y(t)z(t)\leq\frac{1+C_A}{r_A\pi}$, $(y(t)+z(t)-y(t)z(t))\pi r_A+1\leq\frac{1}{2}ua^2$, the expected moment of the zero solution is exponentially stable;

(3) $y(t)+z(t)-y(t)z(t) = 0, 1\geq\frac{1}{2}ua^2$, or

(4) $y(t)+z(t)-y(t)z(t) > 0, (y(t)+z(t)-y(t)z(t))\pi r_A+1\geq\frac{1}{2}ua^2$ and $(y(t)+z(t)-y(t)z(t))\geq\frac{1+C_A}{r_A\pi}$, the expected moment of the zero solution is exponentially unstable.

Proof. Consider the stochastic differential equation (3.4). Take the Lyapunov function $V(t, x) = x(t)$. Then, there exist $c_1 = c_2 = 1, p = 1$, and $\gamma = 1$ such that Eq (3.8) in Lemma 3.1 and $LV(t, x) = f(t, x) = x(t)[y(t)\pi r_A+z(t)\pi r_A-\frac{1}{2}ua^2-y(t)z(t)\pi r_A]$. From Lemma 3.1, it can be seen that if there exists $\gamma = 1$, then $LV(t, x)\leq-V(t, x)$, and the zero solution expectation moment of the equation is exponentially stable. So, there is

and we have

because $x(t)\in[0, 1]$, so as long as

at the same time, $r_A\pi-C_A-\frac{1}{2}ua^2\geq0$. Therefore, the discussion is divided into two situations, when $y(t)+z(t)-y(t)z(t) = 0, 1\leq\frac{1}{2}ua^2$, and $LV(t, x)\leq -\gamma V(t, x)$ is obtained; when $y(t)+z(t)-y(t)z(t) > 0, (y(t)+z(t)-y(t)z(t))\pi r_A+1\leq\frac{1}{2}ua^2$ and $(y(t)+z(t)-y(t)z(t))\leq\frac{1+C_A}{r_A\pi}$, $LV(t, x)\leq -\gamma V(t, x)$ is obtained. So, the zero solution of (3.4) is exponentially stable with a $p$-moment.

On the other hand, from Lemma 3.1, it can be seen that if there exists $\gamma = 1$, then $LV(t, x)\geq V(t, x)$, thus the zero solution expectation moment of the equation is exponentially unstable. So, from

it can be obtained that

because $x(t)\in[0, 1]$, so as long as

Similarly, when $y(t)+z(t)-y(t)z(t) = 0, 1\geq\frac{1}{2}ua^2$, or $y(t)+z(t)-y(t)z(t) > 0, (y(t)+z(t)-y(t)z(t))\pi r_A+1\geq\frac{1}{2}ua^2$ can be obtained, and the zero solution of (3.4) is exponentially unstable with a $p$-moment.

Similarly, Propositions 3.2 and 3.3 can be obtained.

Proposition 3.2. For the stochastic differential equation (3.5), with $c_1 = c_2 = 1, p = 1, \gamma = 1$, and Lyapunov function $V(t, y) = y(t)$, when

(1) $x(t)+z(t)-x(t)z(t) = 0$ and $1\leq\frac{1}{2}vb^2$, or

(2) $0 < x(t)+z(t)-x(t)z(t)\leq\frac{1+C_B}{r_B\pi}$, $(x(t)+z(t)-x(t)z(t))\pi r_B+1\leq\frac{1}{2}vb^2$, the expected moment of the zero solution is exponentially stable;

(3) $x(t)+z(t)-x(t)z(t) = 0, 1\geq\frac{1}{2}vb^2$, or

(4) $x(t)+z(t)-x(t)z(t) > 0, (x(t)+z(t)-x(t)z(t))\pi r_B+1\geq\frac{1}{2}vb^2$ and $(x(t)+z(t)-x(t)z(t))\geq\frac{1+C_B}{r_B\pi}$, the expected moment of the zero solution is exponentially unstable.

Proposition 3.3. For the stochastic differential equation (3.6), with $c_1 = c_2 = 1, p = 1, \gamma = 1$, and Lyapunov function $V(t, z) = x(z)$, when

(1) $x(t)+y(t)-x(t)y(t) = 0$ and $1\leq\frac{1}{2}wc^2$, or

(2) $0 < x(t)+y(t)-x(t)y(t)\leq\frac{1+C_C}{r_C\pi}$, $(x(t)+y(t)-x(t)y(t))\pi r_C+1\leq\frac{1}{2}wc^2$, the expected moment of the zero solution is exponentially stable;

(3) $x(t)+y(t)-x(t)y(t) = 0, 1\geq\frac{1}{2}wa^2$, or

(4) $x(t)+y(t)-x(t)y(t) > 0, (x(t)+y(t)-x(t)y(t))\pi r_C+1\geq\frac{1}{2}wc^2$ and $(x(t)+y(t)-x(t)y(t))\geq\frac{1+C_C}{r_C\pi}$, the expected moment of the zero solution is exponentially unstable.

It can be seen from propositions 2.1, 2.2 and 2.3, as long as the parameters satisfy one of the zero solution stability conditions (1) and (2) in propositions 2.1, 2.2 and 2.3, the expected moment of the equilibrium point (1, 1, 1) of the stochastic dynamical system composed of (3.4)-(3.6) is exponentially stable, that is to say, (1, 1, 1) is an evolutionary stable strategy under stochastic interference.

4.   Numerical simulation

4.1.   Evolutionary path analysis

In a three-party game, to visually describe the evolution process of the above differential equations, the dynamic evolution process with different parameters is simulated. In this paper, the evolution path of each enterprise is analyzed by numerical simulation with MATLAB tools.

Let $\pi = 30$, $r_A = \frac{1}{6}$, $r_B = \frac{1}{3}$, $r_C = \frac{1}{2}$, $C_A = 4$, $C_B = 5$, $C_C = 6$, $u = 0.6$, $v = 0.7$, $w = 0.8$, $\pi_A = 4$, $\pi_B = 6$, $\pi_C = 8$, $a = 2$, $b = 3$, and $c = 4$. Meanwhile, it is assumed that the values of these parameters must satisfy the stability conditions previously established. After calculation, it was found that the parameters satisfy the stability conditions of systems (3.4)–(3.6). The simulation results are displayed in Figure 5 and depict the evolutionary process of enterprises joining strategic coalitions. The values of the random interference intensity were set at 0, 0.5, 1, and 2, respectively.

Figure 5 demonstrates that under the influence of random interference, the behavioral strategies of enterprises exhibit fluctuations, primarily due to differences in decision-makers' cognitive, cultural, and technological aspects. As the system's internal and external environment is uncertain, inconsistent judgments and actions occur, resulting in certain instability in behavioral strategy. However, after experiencing a period of fluctuation, the joining strategy becomes stable, aligning with the objective reality.

The evolutionary process illustrated by Figure 5 clearly reveals that the greater the random disturbance intensity, the greater the fluctuation of the decision-maker's behavior strategy. The primary reason for this phenomenon is that, when the random disturbance is significant, the decision-maker cannot accurately anticipate environmental changes.

It can be seen from the figure that the rate at which the decision-maker evolves an equilibrium strategy to join the coalition is roughly the same for different perturbation intensities, which indicates that the decision-maker is aware that joining the coalition can effectively control pollution and obtain higher benefits. Regardless of the initial strategy, the final strategy chosen is to join the coalition for pollution control.

Let $\pi = 24$, $r_A = \frac{1}{6}$, $r_B = \frac{1}{3}$, $r_C = \frac{1}{2}$, $C_A = 4$, $C_B = 5$, $C_C = 6$, $u = 0.6$, $v = 0.7$, $w = 0.8$, $\pi_A = 4$, $\pi_B = 6$, $\pi_C = 8$, $a = 4$, $b = 5$, and $c = 6$. After calculations, it was discovered that the assumptions of the parameters did not meet the stability requirements of systems (3.4)–(3.6). The simulation results are presented in Figure 6, illustrating the evolutionary process of enterprises withdrawing from strategic coalitions. The random interference intensities used were 0, 0.5, 1, and 2, respectively.

As depicted in Figure 6, regardless of the initial strategy, the final strategy is to withdraw from the pollution control strategy coalition and control pollution independently, as the benefits of joining the coalition are less than those of implementing a single pollution control strategy.

In this paper, the evolutionary game model with random disturbance and without random disturbance were considered. It was found that the evolutionary curve with random disturbance fluctuates around the evolutionary curve without random disturbance, which shows that the evolutionary game with random disturbance is more practical. Furthermore, the stability condition of the evolutionary game model with random disturbance is superior to that without, implying that it can surmount various interference factors prevalent in real-life situations.

4.2.   Parameter analysis

From the above analysis, it has been found that there are three evolutionarily stable strategies. The evolutionary trajectory of the game and the ultimate state reached depend heavily on the payment matrix and the initial state of the enterprise. Consequently, changes in certain parameters that impact the payment matrix on both sides can influence the system's convergence in various directions. These parameters exert an influence on game behavior during the process of enterprise evolution by altering costs or revenues.

(1) The initial probabilities

For the sake of exploring the impact of initial probabilities on the evolutionary stable strategy of enterprises, simulation of different initial probabilities of enterprises was performed, changing it between (0, 1) ^[29], and setting the values of other parameters as shown in Table 6.

Through numerical simulation, the overall evolution state of the enterprise under different initial probabilities can be obtained as shown in Figure 7. According to Figure 7, it is evident that the overall stable state of the enterprise is influenced by the initial probability.

For the sake of exploring the impact of initial probability on the evolutionary stable strategy of enterprises further, the discussion has been segmented into three distinct parts. These parts are as follows: the first part consists of enterprises with low initial willingness to form coalitions, the second comprises enterprises with high initial willingness to form coalitions, while the third encompasses enterprises with a mix of initial willingness to form coalitions ^[29].

According to Figure 8, when $x(0) = 0.1, y(0) = 0.2$, and $z(0) = 0.3$, the initial intention of the enterprises is low, the strategy evolution result shown in Figure 8a, and the system finally stabilizes at (0, 0, 0). This means that enterprises do not want to form a pollution strategy control coalition for pollution control, but carry out pollution control alone. Meanwhile, the time for enterprise $C$ to reach the steady state is the shortest, followed by enterprise $B$ and enterprise $A$, which decrease in turn. When $x(0) = 0.7, y(0) = 0.8$, and $z(0) = 0.9$, the initial intention of the enterprises are high, the strategy evolution result shown in Figure 8b, and (1, 1, 1) is the final equilibrium stable point. This means that enterprises are willing to form a pollution strategy control coalition for pollution control. Moreover, for ($x(0) = 0.2, y(0) = 0.7, z(0) = 0.9$) or ($x(0) = 0.9, y(0) = 0.4, z(0) = 0.1$), the initial intention of the enterprises are mixed, the strategy evolution result shown in Figure 8c, d, and (1, 1, 1) is the final equilibrium stable point. It can be found that if one party has a high willingness to form a pollution control strategy coalition, the other two parties will also choose to join the coalition.

The numerical results provide evidence that the ultimate stable state of a company is influenced by its initial probability; specifically, if an enterprise has a higher initial intention. Conversely, if all enterprises have a lower initial intention, they may ultimately choose to pursue pollution control independently rather than forming a coalition.

(2) The sharing profit coefficient

In order to analyze the sensitivity of the sharing profit coefficients ($r_A, r_B, r_C$), other parameters are fixed in the game model. The values of other parameters are set as shown in Table 7, with the results in Figure 9.

As can be seen from Figure 9, enterprise $A$ is greatly affected by the sharing profit coefficient, while enterprise $B$ and enterprise $C$ are less affected by the sharing profit coefficient. According to Figure 9a, when the initial probabilities are 0.8, decreasing opportunity costs will bring about the stable state of enterprise $A$ to be unstable. This illustrates that the willingness of enterprise $A$ to form a pollution strategy control coalition will decrease with the decrease of sharing profit coefficient, even if enterprise $A$ initially had a high willingness. In contrast, when the initial probabilities are 0.2, decreasing the sharing profit coefficient will accelerate enterprise $A$ to not form a coalition. It has no obvious influence on enterprise $B$ or $C$.

(3) The innovation cost coefficient

In order to analyze the sensitivity of the innovation cost coefficients ($u, v, w$), other parameters are fixed in the game model. The values of other parameters are set as shown in Table 8, with the results in Figure 10.

According to Figure 10, it is clear that the innovation cost coefficient has the greatest impact on enterprise $A$, while enterprise $B$ and enterprise $C$ are hardly affected by the innovation cost coefficient. From Figure 10a, when the initial probabilities are 0.8, enterprise $A$ initially had a high willingness to form a coalition, and it is not affected at this time. In contrast, when the initial probabilities are 0.2, enterprise $A$ is affected by the innovation cost coefficient. This illustrates that the willingness of enterprise $A$ to form a pollution strategy control coalition will decrease with the increase of the innovation cost coefficient. Due to the fact that enterprise $A$ has low willingness to form a coalition but the cost coefficient of innovation efforts is high, it finally chooses to withdraw from the coalition and there are no benefits to a firm willing to form an coalition. It has no obvious influence on enterprise $B$ or $C$.

(4) The effort coefficient

In order to analyze the sensitivity of the effort coefficients ($a, b, c$), other parameters are fixed in the game model. The values of each fixed parameter are listed in Table 9, with the results in Figure 11.

According to Figure 11, it can be found that effort coefficient has no effect on the ultimate strategy of the enterprises, but it slows down to a steady speed because effort takes time to accomplish goals. When the initial probability is 0.8, the enterprise is stable at 1, and with the increase of the effort coefficient, the stable speed is slow. Among all enterprises, the effort coefficient has a great impact on enterprise $B$. When the initial probabilities are 0.4, the sensitivity of the enterprises remains unchanged compared to previous findings.

In order to effectively solve the problem of enterprise pollution control, the enterprise pollution control strategic alliance is an effective method. According to the simulation results, the initial probability will directly affect the final stable state of each enterprise. Setting up different initial probabilities reflects the varying preferences among enterprises. By simulating different preferences, it is more helpful to access the real results. Additionally, the influence of other factors such as the shared profit coefficient, innovation cost coefficient, and effort coefficient were also considered in our analysis alongside the initial cooperation probability among enterprises.

5.   Conclusions

This paper establishes a tripartite evolutionary game model of enterprise pollution control, studies the mechanism of the strategic coalition for pollution control by analyzing the replicator dynamics and evolutionary stable strategy, and discusses the influence of other parameters on the strategic coalition for pollution control. This paper identifies that when enterprises form a pollution control strategic coalition, all of their members fully participate in the coalition. However, the assumption of symmetry among the three enterprises is not always accurate, as the actual situation may differ. Therefore, some enterprises may form a coalition, and this puts forward a new model for pollution control coalitions.

Under the condition of a good binding contract, the strategic coalition of environmental pollution control can effectively leverage information sharing among its members, maximize the spill-over effects of technology and capital, and achieve the scale benefits of pollution control. In order to fully mobilize the enthusiasm of enterprises to join the coalition, the following aspects should be considered:

(1) Establishing an effective incentive and punishment mechanism within the coalition is critical for ensuring smooth cooperation and resolving potential disputes among participants. Therefore, an effective reward and punishment mechanism should be established to provide clear guidelines for behavior and promote positive outcomes. Meanwhile, efforts should be made to encourage more participants to join the pollution control coalition.

(2) The government should establish and improve coordination and management mechanisms. In many cases, it is difficult for a mechanism to operate only with internal participants, and external forces may be necessary to facilitate the process. At this time, the involvement of the government becomes crucial.

(3) Citizens are urged to develop social oversight mechanisms for reporting environmental violations, recognizing their responsibility as key stakeholders in the community. With pollution incidents continuing to occur, it is not sufficient to rely solely on governments and businesses to monitor and enforce environmental regulations. Citizens have a crucial role to play in taking responsibility for their own actions and advocating for environmental protection.

(4) To ensure the sustainable operation of the coalition, it is essential to establish a fair and equitable distribution mechanism. As highlighted in the previous analysis, improper profit distribution can lead to the collapse of the coalition, emphasizing the need for a well-designed distribution mechanism that takes into account the interests of all members.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work is supported by Natural Science Foundation of Chongqing (CSTB2022NSCQ-MSX0286, cstc2021jcyj-msxmX0949), Scientific and Technological Research Program of Chongqing Municipal Education Commission (KJZD-K202001201, KJQN202101212), Humanities and Social Sciences program of Chongqing Municipal Education Commission (23SKGH282), Research Center for Sustainable Development of Three Gorges Reservoir Area (2022sxxyjd01).

Conflict of interest

Authors declare no conflicts of interest.