Stochastic analysis of survival and sensitivity in a competition model influenced by toxins under a fluctuating environment

1.   Introduction

The earth's ecosystems are extensively affected by chemical contaminations resulting from a multitude of anthropogenic activities and natural phenomena, which significantly impacts the survival of diverse species and human health, particularly accelerating the extinction of endangered species ^[1]. To safeguard the ecological environment and maintain ecological equilibrium, it is imperative to accurately evaluate the risk posed by environmental toxins on exposed populations. In recent decades, mathematical models have gained widespread recognition as a powerful tool for assessing the risks of chemical contamination. Currently, the majority of population ecological models related to environmental pollution are based on the assumption that population growth rates adhere to the logistic equation ^[2,3,4,5]. However, these models fail to quantitatively analyze the impact of environmental toxins on population capacity. To address this limitation, Thieme ^[6] proposed using the Beverton-Holt equation instead of the logistic equation to describe the population growth rate. This approach can effectively differentiate between various toxins in terms of food uptake, conversion efficiency, and biomass acquisition. Taking into account the influence of toxins on population mortality, ^[7] built a toxin-dependent aquatic ecosystem model based on Thieme's approach and utilized available data to evaluate mercury's effect on rainbow trout.

The aforementioned models are all single-species models, assuming that populations solely absorb toxins from their environment. To investigate the impact of environmental toxins on species interactions, some scholars have extended these single-species models into multi-species ones ^{[8,9,10,11,12]}. For instance, ^[13] established a prey-predator model considering the simultaneous exposure of both prey and predator to environmental toxins, revealing counterintuitive results suggesting that intermediate toxin concentrations could actually increase prey biomass. Peace et al. ^[14] successfully captured the phenomenon known as somatic growth dilution by developing a stoichiometric toxicant-mediated predator-prey model. Recently, Shan and Huang ^[15] proposed a toxin-dependent model to investigate the direct and indirect impacts of environmental toxins on two competing populations:

where the subscript $i$ represents species $i$, with $i, j = 1, 2$, and $i\neq j$; $x_i$ denotes the concentration of population biomass; $y_i$ denotes the body burden; $\alpha_i$ corresponds to the maximum growth rate; $\beta_i$ indicates the impact of toxin on population gain; $\gamma_i$ captures the crowding effect; $k_i$ reflects the influence of toxin on mortality; $m_i$ stands for natural mortality rate; $c_i$ is the competition coefficient; $a_i$ denotes the uptake coefficient; and $\sigma_i$ measures toxin elimination rate, while $T$ refers to environmental toxin concentration.

Considering the significantly higher rate of population metabolism compared to population growth, model (1) can be approximated as a two-dimensional model. To be specific, we introduce the following dimensionless quantities, $\widetilde{x}_i = \gamma_ix_i, \ \widetilde{y}_i = \beta_iy_i$, $\widetilde{t} = \alpha_1t, \ \widetilde{k}_i = \frac{k_i}{\beta_i\alpha_1}$, $\widetilde{m}_i = \frac{m_i}{\alpha_1}, \ \widetilde{\alpha} = \frac{\alpha_2}{\alpha_1}$, $\widetilde{T} = \frac{\beta_1a_1T}{\sigma_1}, \ \widetilde{c}_i = \frac{c_i}{\alpha_1\gamma_j}$, $\widetilde{a} = \frac{\beta_2a_2}{\beta_1a_1}, \ \widetilde{\sigma} = \frac{\sigma_2}{\sigma_1}, \epsilon = \frac{\alpha_1}{\sigma_1}$, then drop the tildes, so that model (1) becomes

Let $\epsilon\rightarrow0$ in (2), then $y_1 = T$, $y_2 = \frac{aT}{\sigma}$. Substituting them into the first two equations in model (2) leads to the following quasi-steady system:

Throughout this paper, we consistently assume that

where $p = \frac{a}{\sigma}$. Otherwise, the study would be meaningless. Under these assumptions, the authors of ^[15] studied the complete dynamics of model (3), revealing that competition outcomes can be influenced in various counterintuitive ways by both the level of toxins and the distinct vulnerabilities exhibited by the two species toward toxins.

In practice, ecosystems typically exist within a stochastic environment. Intuitively, when subjected to relatively minor perturbations, random trajectories tend to exhibit small-amplitude oscillations around deterministic attractors; however, the presence of significant disturbances can potentially lead to the collapse of the entire system ^{[16,17,18,19,20]}. More importantly, intermediate noise intensity can give rise to certain counterintuitive phenomena that lack counterparts in the corresponding deterministic model, such as stochastic resonance ^[21], noise-induced transition ^[22], and noise-enhanced stability ^[23]. The underlying reason for this mainly lies in the multi-stability and high sensitivity of attractors. Research on the effect of noise on multi-stable system can be traced back to ^[24] and has been followed by many researchers recently. Bashkirtseva's team conducted a comprehensive investigation into noise-induced switching and transformation phenomena in multi-stable systems ^{[25,26,27,28]}. Yuan and his collaborators analyzed the stochastic sensitivity of competitive or predator-prey population models ^[29,30,31]. Spagnolo'team studied stochastic and coherence resonances in ecology and other fields ^{[32,33,34,35]}.

Motivated by the above facts, this paper aims to investigate how environmental noise affects the dynamics of toxin-dependent competition model (3). To achieve this objective, we initially utilize the approach proposed in ^[36,37] to develop a stochastic version of model (3) as follows:

where

and where $B_i(t)$ are mutually independent standard Brownian motions, and $\sigma_i$ are the white noise intensities, $i = 1, 2$.

The impact of noise on competition outcomes between two species will be investigated by conducting survival and sensitivity analyses for stochastic model (4). Specifically, a survival analysis will establish sufficient conditions for population extinction and persistence. Furthermore, we will prove the existence of a unique ergodic stationary distribution using Khasminskii's theory in Section 2. Next, we will study the spatial arrangement of random states near the deterministic attractor through applying the stochastic sensitivity function (SSF) technique in Section 3. Lastly, our study concludes with a concise discussion presented in Section 4. Our analysis results show that (ⅰ) large noise is harmful to two competing species and can lead to their extinction; (ⅱ) small noise does not alter the original competition outcomes observed in the model without random disturbance; and (ⅲ) intermediate noise can significantly influence competition outcomes in various ways. In other words, increasing noise intensity may have a positive impact on one species while negatively affecting another. Moreover, increasing noise intensity may enhance coexistence between two species and maintain species diversity by reducing the persistence of dominant species. These findings have significant implications for maintaining ecosystem diversity.

2.   Survival analysis

The initial presentation of fundamental properties is essential for the investigation of the dynamics of model (4).

Lemma 2.1. The given initial valve $(x_1(0), x_2(0))\in\mathbb{R}_{+}^2$ ensures that model (4) possesses a unique solution $(x_1(t), x_2(t))$ for $t\geq 0$. Moreover, it can be guaranteed with probability one that the solution will always remain in $\mathbb{R}_+^2$, i.e., $(x_1(t), x_2(t))\in\mathbb{R}_+^2$ for all $t\geq 0$ almost surely.

Proof. The coefficients of (4) satisfy the local Lipschitz condition but fail to meet the linear growth condition. Consequently, given an initial value $(x_1(0), x_2(0))\in\mathbb{R}_{+}^2$, a unique local solution $(x_1(t), x_2(t))$ exists for $t\in(0, \tau_e]$, where $\tau_e$ is commonly referred to as the explosion time ^[38]. To prove $\tau_e = \infty$ a.s., following the approach in [39, Theorem 3.1], it suffices to construct a nonnegative $C^2$-function $V_1(x_1, x_2)$ that satisfies $\mathcal {L}V_1\leq K$, where $\mathcal {L}$ is a differential operator and $K$ is a constant. To this end, we define the function $V_1$ as follows:

where $n_1 = \frac{m_2n_2}{c_1}$ and $n_2 = \frac{m_1}{c_2}$. Applying Itô's formula, we obtain

Thus, the desired outcome is achieved by employing a similar discourse as presented in ^[39]. □

Lemma 2.2. (see ^[40]) Let $\varphi_i(t)$ $(i = 1, 2)$ be the solution of the stochastic equation

with $\varphi_i(0) = x_i(0)\in\mathbb{R}_+$, where

then, $\varphi_i(t)$ satisfies that

Remark 2.1. From model (4), we know that

which follows from the stochastic comparison theory that $x_i(t)\leq\varphi_i(t) \ a.s.$

2.1.   Extinction and persistence

In this subsection, survival of the two species will be discussed, including extinction and persistence in mean. i.e., the following result is valid based on Lemmas 2.1 and 2.2.

Theorem 2.1. For model (4), denote

(i) If $\max\limits_{i = 1, 2}\{\lambda_i\} < 0$, both species 1 and species 2 go to extinction.

(ii) If $\lambda_i < 0$, $\lambda_j > 0$, $i\neq j$, $i, j = 1, 2$, species $i$ is extinct and species $j$ is persistent in mean.

(iii) If $\min\limits_{i = 1, 2}\{\lambda_i-\vartheta_i\} > 0$, both species 1 and species 2 are persistent in mean, where $\vartheta_1 = \frac{c_1b_2}{d_2}$, $\vartheta_2 = \frac{c_2b_1}{d_1}$.

Remark 2.2. (i) Theorem 2.1 implies that sufficiently small noise will not change the survival of species, while sufficiently large noise will force the entire system to go extinct. Ecologically speaking, large noise is not conducive to maintaining biodiversity.

(ii) Denote

Clearly, $\lambda_i^d < \lambda_i$ $(i = 1, 2)$, implying the possibility that $\lambda_i^d < 0 < \lambda_i$ due to the continuity of $\lambda_i$ in $I_i$. Biologically, this means that when species $i$ is persistent in deterministic model (3) (see [15, Theorem 3.8]), it may be extinct with probability one in stochastic model (4) due to the effect of noise. In other words, noise may influence the competition outcomes of two species.

Proof. By Itô's formula to (4), we have

where $M_i = \sigma_iB_i(t)$, $i = 1, 2$, and $\lim\limits_{t\rightarrow \infty}\frac{M_i}{t} = 0\ a.s.$ by strong law of large numbers.

$(i)$ When $\lambda_1 < 0$, Eq (6) implies that

That is, species 1 converges to $0$ at an exponential rate. Similarly, species 2 goes to extinction under the condition $\lambda_2 < 0$.

$(ii)$ Without loss of generality, we consider the case where $i = 1$ and $j = 2$, then, species 1 is an obvious extinction by case $(i)$, i.e., $\lim\limits_{t\rightarrow \infty}x_1(t) = 0\ a.s.$ Hence, for arbitrary $0 < \epsilon_1 < 1$, there exists a set $\Omega_{\epsilon_1}\subset\Omega$ with $\mathcal{P}(\Omega_{\epsilon_1})\geq1-\epsilon_1$ and a constant $\mathscr{T}_1 = \mathscr{T}_1(\epsilon_1)$ such that $\frac{1}{t}\int_0^tc_2x_1\mathrm{d}s < \epsilon_1,$ for $\omega\in\Omega_{\epsilon_1}$ and $t > \mathscr{T}_1$. By Eq (7), one gets

By [41, Lemma 4] and the arbitrariness of $\epsilon_1$, we obtain

which means that species 2 is persistent in mean.

$(iii)$ By Lemma 2.2, one has $\lim\limits_{t\rightarrow \infty}\frac{1}{t}\int_0^t \varphi_2(s)\mathrm{d}s = \frac{b_2}{d_2}\ a.s.$ In other words, for any arbitrary $0 < \epsilon_2 < 1$, there exists a set $\Omega_{\epsilon_2}\subset\Omega$ with $\mathcal {P}(\Omega_{\epsilon_2})\geq1-\epsilon_2$ and a constant $\mathscr{T}_2 = \mathscr{T}_2(\epsilon_2)$ such that $\frac{1}{t}\int_0^t\varphi_2(s)\mathrm{d}s < \frac{b_2}{d_2}+\epsilon_2$ holds for all $\omega\in\Omega_{\epsilon_2}$ and $t > \mathscr{T}_2$. On the other hand, by Eq (6) and Remark 2.1,

In conjunction with [41, Lemma 4] and the arbitrariness of $\epsilon_2$, this implies that

Similarly, for species 2, we have $\liminf\limits_{t\rightarrow \infty}\frac{1}{t}\int_0^tx_2\mathrm{d}s\geq\frac{\lambda_2-\vartheta_2}{\alpha(1-pT)} > 0\ \ a.s.$ Consequently, both species 1 and species 2 are persistent in mean. □

2.2.   Existence of ergodic stationary distribution

In the following, the existence of ergodic stationary distribution will be investigated, which reflects the long-term stochastic dynamics of model (4). Let us first denote

Using [42, Theorem 4.1], one can prove the following theorem.

Theorem 2.2. Assuming that $\min\limits_{i = 1, 2}\{\lambda_i-\nu_i\} > 0$, a unique and ergodic stationary distribution exists for model (4) given any initial value $(x_1(0), x_2(0))\in\mathbb{R}_+^2$.

Proof. To complete the proof of Theorem 2.2, based on [42, Theorem 4.1], we need to construct a nonnegative $C^2$-function $V_2$ and a bounded closed $U_{\varrho}$ such that $\mathcal {L}V_2\leq-C$ for $(x_1, x_2)\in\mathbb{R}_+^2\backslash U_{\varrho}$, where $C$ is a positive constant.

Let us first define a $C^2$-function $\overline{V}_2$ as

where $b_i$ and $d_i$ $(i = 1, 2)$ are defined as in Lemma 2.2. Obviously, $\overline{V}_2(x_1, x_2)$ is continuous and

where $U_{R} = (\frac{1}{R}, R)\times(\frac{1}{R}, R)$, which implies that $\overline{V}_2(x_1, x_2)$ achieves a lower bound at a point $(\bar{x}_1, \bar{x}_2)$ in the interior of $\mathbb{R}_+^2$. Define the nonnegative $C^2$-function $V_2: \mathbb{R}_+^2\rightarrow \mathbb{R}_+$ as

By Itô's formula, one has

Given that $\min\limits_{i = 1, 2}\{\lambda_i-\nu_i\} > 0$, then

and $\lim\limits_{\mid x\mid\rightarrow \infty}\Theta(x_1, x_2) = -\infty,$ where $\mid x\mid = \sqrt{x_1^2+x_2^2}$. Hence, there exist a positive constant $C$ and a sufficiently small $\varrho$ such that

where $U_{\varrho} = [\varrho, \frac{1}{\varrho}]\times[\varrho, \frac{1}{\varrho}]$. In other words, for any initial value $(x_1(0), x_2(0))\in\mathbb{R}_+^2$, a unique stationary distribution exists for model (4), which is also ergodic. □

3.   Sensitivity analysis

The survival analysis conducted in Section 2 can characterize to some extent how noise affects the dynamics of species. However, these results are crude and do not well reflect the whole effects of noise on species. In this section, some stochastic sensitivity analysis of model (4) is presented, which can fill the gap well.

3.1.   Toxin-dependent single species model

As a basis for further discussion, we first consider the case when only one species without interspecific competition presents in a perturbed environment with toxin. Without loss of generality, suppose that only species $x_1$ is present, then model (4) without interspecific competition is governed by

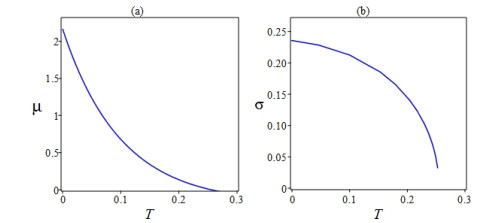
where $\sigma = \sigma_1$. When $\sigma = 0$, model (4) exists two equilibria: $x_1^0 = 0$ (unstable) and $x_1^* = \frac{1-m_1-(1+k_1)T}{m_1+k_1T}$ (stable), then the formula

reflects the sensitivity of $x_1^*$ (see Appendix), as depicted in Figure 1(a). We can see that the sensitivity of $x_1^*$ decreases as the toxin level $T$ increases, suggesting that a higher concentration of toxins in the environment always has a detrimental impact on species survival.

Following $3\sigma$-rule (the fiducial probability $\mathcal {P} = 0.997$), the corresponding confidence interval can be expressed as $(x_1^*-r, x_1^*+r)$ with $r = 3\sigma\sqrt{\mu}$. Furthermore, the critical value of noise intensity can be obtained by $x_1^*-r = 0$,

As depicted in Figure 1(b), the critical value of noise intensity $\sigma^*$ exhibits a decreasing trend with increasing toxin level $T$. Meanwhile, this curve $\sigma^*(T)$ divides the parameter region into two parts: persistence (below) and extinction (above).

In Figure 2, the time series of model (9) (blue) and the boundaries of confidence intervals (red dashed line) are plotted for different noise intensity values. Obviously, as noise intensity increases, the confidence interval expands and the distribution of random states is becoming more and more dispersed. Note that here, $\sigma^* = 0.145$. Figure 2 further shows that when $\sigma < 0.145$, the dispersion of random states is located in the interior of the corresponding confidence interval with probability 0.997, which means that the species is persistent; while for $\sigma > 0.145$, the left boundary of confidence interval is less than zero, suggesting that the survival of species has transformed from persistence to extinction.

3.2.   Two species model with interspecific competition

Taking the parameters of model (3) as in Figure 3, it follows from ^[15] that deterministic model (3) has two types of bistability. As shown in Figure 3(a), exclusion equilibrium $E_1^0$ and coexistence equilibrium $E_l^*$ are asymptotically stable simultaneously. That is, two basins of attraction are separated by the stable manifold (black dashed-dotted) of saddle point $E_r^*$. Obviously, the trajectory with initial value below the separatrix approaches $E_1^0$, whereas the trajectory with initial value above the separatrix converges to $E_l^*$. Figure 3(b) shows another type of bistability, that is, both exclusion equilibria $E_1^0$ and $E_2^0$ are asymptotically stable simultaneously. In this situation, two basins of attraction are separated by the stable manifold of saddle point $E_c^*$.

We now focus on the sensitivity analysis of the stable equilibria $E_1^0$ and $E_l^*$ depicted in Figure 3(a). However, for the exclusion equilibria $E_1^0$ and $E_2^0$ shown in Figure 3(b), a similar analysis can be conducted but is omitted here. The equilibrium $E_l^*$ can be analyzed in two cases.

$(i)$ $\sigma_1 = \sigma_2 = \sigma$. As depicted in Figure 4, the stochastic trajectory of model (4) with an initial value above the separatrix deviates from the deterministic attractor $E_l^*$, subsequently giving rise to a corresponding stochastic attractor. In the presence of small noise, the states of this stochastic attractor tend to concentrate near $E_l^*$; whereas for relatively large noise levels, qualitative changes in dynamics are observed in model (4). More precisely, the stochastic trajectory escapes from the attraction domain of $E_l^*$, subsequently traverses the separatrix, and ultimately enters the attraction domain of $E_1^0$.

The above detailed qualitative analysis can be illustrated clearly by use of SSF technique (see Appendix). To this end, denote $E_l^* = (x_1^*, x_2^*)$ and

where

and

The stochastic sensitivity matrix

can be derived from (A.2) in Appendix A, which satisfies the equation

Here, $w_{11}$ and $w_{22}$, respectively, describe the sensitivity of $E^*$ along the $x_1$-axis and $x_2$-axis, and $w_{12} = w_{21}$ denotes the covariation. The graphs of functions $w_{11}(T)$ and $w_{22}(T)$ are shown in Figure 5. Clearly, $w_{11}(T) > w_{22}(T)$ for each $T\in[0.05, 0.07]$, which shows that the sensitivity of species 1 is large than species 2. Most importantly, the two functions tend to infinity as $T$ approaches $0.05$. This signalizes the possible about noise-induced transitions, which can be visualized by use of confidence ellipses.

The confidence ellipse is a geometrical model describing the configurational arrangement of random states near stable equilibrium. Next, we will illustrate how confidence ellipse can be used to explain the noise-induced transition from persistence to extinction. By Eq (A.4) in Appendix, the corresponding confidence ellipse equation of $E_l^*$ can be expressed by

where $\mathcal {K}^2 = -\ln(1-\mathcal {P})$, and $\mathcal {P}$ is a fiducial probability. In Figure 6, the random states (blue) of model (4) for $\sigma = 0.006$ are plotted, along with the confidence ellipse (green) representing a fiducial probability $\mathcal {P} = 0.95$. It can be observed that the random states are distributed around $E_l^*$ and fall within the interior of confidence ellipse with a probability $\mathcal {P} = 0.95$. This observation, in conjunction with Figure 5, further implies that the dispersion of the random states near $E_l^*$ are influenced by both noise intensity and sensitivity.

The confidence ellipses (solid) in Figure 7 represent the fixed fiducial probability $\mathcal {P} = 0.95$ for three different noise intensity values: $\sigma = 0.004$ (small), $\sigma = 0.0069$ (middle), and $\sigma = 0.01$ (large). It can be observed that when the noise intensity is small, the entire confidence ellipse falls within the attraction domain of $E_l^*$. Consequently, in this scenario, the corresponding random orbit is concentrated near $E_l^*$ as depicted in Figure 4(a). As we increase the noise intensity to a critical value, the confidence ellipse starts expanding and eventually crosses over to occupy the attraction domain of $E_1^0$ after crossing the separatrix (dashed-dotted line). In this case, with a high probability, the corresponding random orbit may leave the attraction domain of $E_l^*$ and form a stochastic attractor near $E_1^0$ as shown in Figure 4(b). The intersection point between the confidence ellipse and separatrix represents an approximate value for this critical intensity denoted by $\sigma^*$. Notably, here we have approximately estimated that $\sigma^*\approx0.0069$. By comparing Figures 7 with 4, it can be concluded that these quantitative analysis results are consistent with direct numerical simulations conducted earlier on this topic. Biologically speaking, noise is not conducive to the coexistence of two species; however, it does confer benefits on the survival of species 1.

$(ii)$ $\sigma_1\neq \sigma_2$. Noise-induced transitions under $\sigma_1\neq \sigma_2$ can be analyzed by means of numerical simulations. In Figure 8, phase trajectories of model (4) with initial value near $E_l^*$ are plotted for two sets of different noise intensity:

Comparing Figures 8(a) with 4(a), we can see that increasing the noise experienced by species 1 but still at a low level can force the state of the system to shift from near $E_l^*$ to near $E_2^0$. This means that noise is not conducive to the coexistence of two species, but species 2 actually benefits from large noise. Similarly, it follows from comparison of Figures 8(b) with 4(a) that further increasing the noise experienced by two species will destroy their coexistence and make both species extinct simultaneously. It seems that the large noise experienced by two species is a disaster for the persistence of the competition system. The appropriate noise intensity can also force the system state to shift from near $E_l^*$ to near $E_r^*$, but its corresponding phase trajectory is not drawn due to the similarity to Figure 8.

In the remaining space of this subsection, we discuss the species 1-only equilibrium $E_1^0$. It is noted that the stochastic sensitivity of $E_1^0$ cannot be analyzed by constructing the corresponding confidence ellipses as in case (ⅰ). Therefore, here we numerically explore the noise-induced phenomenon. Figure 9 shows all possible phase portraits of model (4) with initial value near $E_1^0$ for different noise intensities except the following case: the noise-induced transition from near $E_1^0$ to near $E_r^*$. It can be seen from Figure 9 that the system state can switch from near $E_1^0$ to near any other equilibrium. It is noteworthy that these state transitions are only related to noise intensity, but not to the stability of the equilibrium, which is different from case (ⅰ). It can be seen from these numerical simulations that intermediate noise intensity can promote the coexistence of two competing species by reducing the persistence level of dominant species.

4.   Discussion

To predict the impact of toxic pollutants on aquatic ecosystems, ecologists and mathematicians have recently established a large number of biological mathematical models from different perspectives ^{[8,9,13,14,15]}. These models explicitly incorporate the effects of toxic substances on the survival of aquatic species while not accounting for stochastic fluctuations in the external environment. The ubiquity of environmental noises in aquatic ecosystems arises from the inherent unpredictability of weather, temperature, and various other physical factors that are intricately intertwined within these ecosystems. In this study, we proposed a stochastic toxin-dependent competition model (4) based on the findings of ^[15]. We initially conducted survival analysis and successfully proved the existence of a unique ergodic stationary distribution. From Theorems 2.1 and 2.2, the relationships between the noise intensity and the survival of two species are summarized below:

● When $\sigma_i^2 > \eta_i$, $i = 1, 2$, two species are extinct simultaneously (see Figures 8(b) and 9(d));

● When $\sigma_i^2 > \eta_i$, $\sigma_j^2 < \eta_j$, $i\neq j$, $i, j = 1, 2$, species $i$ is extinct and species $j$ is persistent in mean (see Figures 4(b), 8(a), 9(a), and 9(c));

● When $\sigma_i^2 < \eta_i-2\vartheta_i$, $i = 1, 2$, two species are persistent in mean simultaneously (see Figures 4(a) and 9(b));

● When $\sigma_i^2 < \eta_i-2\nu_i$, $i = 1, 2$, model (4) exists a unique ergodic stationary distribution,

where

The foregoing theoretical analysis shows the impact of noise on two species and estimates the corresponding noise intensity. Due to the limitations of Lyapunov's method, we do not know what happens when $\eta_i-2\vartheta_i < \sigma_i^2 < \eta_i$, $i = 1, 2$. For this reason, we further discussed the stochastic sensitivity of model (4) with the help of the SSF technique and numerical method.

For the single species model (9), we constructed the confidence interval and estimated the critical noise intensity $\sigma^*$. As shown in Figure 2, the critical noise intensity determines the survival of species with probability $\mathcal {P} = 0.997$. For the two species competition model (4), the noise-induced phenomena were studied in detail by different ways. When $\sigma_1 = \sigma_2$, we constructed the confidence ellipse by use of the SSF technique and plotted the sensitivity of attractor to toxin concentration based on stochastic sensitivity matrix, as shown in Figures 5–7. It allows us to see clearly the configurational arrangement of random states near stable equilibrium. Meanwhile, the critical noise intensity was estimated numerically; see Figure 7. Information about the critical noise intensity enables us to predict the conditions of the noise-induced transition. In this case, large noise but still at a low level can force the system state to transform from the coexistence to the species 1-only. When $\sigma_1\neq \sigma_2$, we numerically explored the noise-induced phenomena; see Figures 8 and 9. In this case, the state transitions are only related to the noise intensities $\sigma_1$ and $\sigma_2$, but not to the stability of equilibrium, which is different from the case $\sigma_1 = \sigma_2$.

After theoretical analysis and numerical simulations, it is suggested that noise can significantly influence competition outcomes between two species. Specifically, (ⅰ) high levels of noise are detrimental to the competing species and can lead to their extinction, (ⅱ) low levels of noise do not alter the original competition outcomes in the deterministic model; in this scenario, species survival depends on its initial population size, and (ⅲ) intermediate levels of noise can induce various changes in competition outcomes. Increasing noise intensity may have a positive impact on one species while negatively affecting another due to reduced persistence level and increased resource availability for its competitor. Moreover, higher noise intensity may promote coexistence and maintain species diversity by reducing the persistence level of dominant species. In summary, increasing noise intensity has the potential to reverse competition outcomes between two species. These findings are intriguing and hold significant theoretical implications for ecological resource management.

The model proposed in this paper assumes that environmental noise follows a Gaussian white noise distribution and is directly proportional to the variables. However, in reality, the natural growth of species often encounters abrupt environmental disturbances such as harvesting and earthquakes. Additionally, the growth rates of certain populations exhibit significant variations between summer and winter seasons. These phenomena cannot be adequately captured by white noise alone. Some scholars have proposed alternative types of environmental noise, such as Lévy noise ^[43] and telephone noise ^[44], to better describe these complex dynamics. We acknowledge the importance of investigating these alternatives in future research.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The work was supported by the National Natural Science Foundation of China (No. 12171441), the Scientific Research Team Plan of Zhengzhou University of Aeronautics (No. 23ZHTD01013), the Key Scientific Research Project of Colleges and Universities of Henan Province (No. 24A110012), and the Basic Research Projects of Key Scientific Research Projects Plan in Henan Higher Education Institutions (No. 24ZX008).

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix

Let $B(t) = (B_1(t), \cdots, B_l(t))^{T}$, $t\geq0$ be an $l$-dimensional Brownian motion defined on the complete probability space $(\Omega, \mathcal {F}, \mathcal {P})$ adapted to the filtration $\{\mathcal {F}_{t}\}_{t\geq0}$.

Consider the following stochastic system:

where $x$ is an $n$-dimensional vector, $f(x)$ is an $n$-dimensional vector function, $g(x)$ is an $n\times l$-matrix function, and $\sigma$ is a nonnegative scalar parameter that denotes the noise intensity. Suppose that the corresponding deterministic system of (A.1) has an asymptotically stable equilibrium $x^*$. The stochastic trajectories of (A.1) with initial values near $x^*$ may leave $x^*$ and form a corresponding stochastic attractor with probabilistic density function $\rho(x, \sigma)$, which is governed by the corresponding Kolmogorov-Fokker-Planck (K-P) equation. For one-dimensional model, $\rho(x, \sigma)$ can be solved directly by the K-P equation, but for the multidimensional model, it is difficult to solve it. In this case, it follows from Refs. ^[45,46] that we can write an approximation of this probability distribution as follows:

where $< \cdot, \cdot >$ represents Euclidean scalar product, matrix $W$ denotes the stochastic sensitivity function of equilibrium $x^*$, $\sigma^2W$ is the covariance matrix, and $W$ is a unique solution of the following equation:

where $F = \frac{\partial f}{\partial x}(x^*)$ and $S = g(x^*)g(x^*)^{T}$. With the help of matrix $W$, the corresponding confidence ellipsoid can be constructed as follows (see ^[47]):

where $\mathcal {P}$ is a fiducial probability. The function $\mathcal {K}(\mathcal {P})$ is an inverse function of $\mathcal{P}(\mathcal {K})$, where

For the case $n = 1$, $\mathcal {P}(\mathcal {K}) = \mathrm{erf}(\sqrt{\frac{\mathcal {K}}{2}}), \ \mathrm{erf}(x) = \frac{2}{\sqrt{\pi}}\int_0^x\exp(-t^2)\mathrm{d}t,$ then the corresponding confidence interval is $(x^*-r, x^*+r)$ with $r = \sigma\sqrt{2\mu}\mathrm{erf}^{-1}(\mathcal {P})$, and the stochastic sensitivity $\mu$ can be determined by $\mu = -\frac{g^2(x^*)}{2f'(x^*)}$. It follows from $3\sigma$-rule ^[48] that $r = 3\sigma\sqrt{\mu}$.

For the case $n = 2$, $\mathcal {P}(\mathcal{K}) = 1-\exp(-\frac{\mathcal {K}}{2}), \ \mathcal{K}(\mathcal {P}) = -2\ln(1-\mathcal {P}),$ then the corresponding confidence ellipsoid is

where $\mathcal {K}^2 = \ln\frac{1}{1-\mathcal {P}}$. Similarly, for $n = 3$, $\mathcal {P}(\mathcal {K}) = \mathrm{erf}(\sqrt{\frac{\mathcal {K}}{2}})-\sqrt{\frac{2\mathcal {K}}{\pi}}e^{-\frac{\mathcal {K}}{2}}$; and for $n = 4$, $\mathcal {P}(\mathcal {K}) = 1-\exp(-\frac{\mathcal {K}}{2})(1+\frac{1}{2}\mathcal {K})$.