On a new structure of multi-term Hilfer fractional impulsive neutral Levin-Nohel integrodifferential system with variable time delay

1.   Introduction

Contrary to popular belief, fractional calculus is a more flexible and extraordinarily large field of differentiation compared to classical calculus. In the realm of fractional calculus, numerous definitions of integrals and derivatives exist. The most widely recognized fractional definitions are Caputo and $\mathcal{R.L.}$ ^[1], which have prompted extensive research aimed at extending differential equations of integer orders to fractional domains. Recently, Hilfer ^[2] introduced a general formula that connects the Caputo and $\mathcal{R.L.}$ derivatives. This formulation has garnered significant attention from researchers in the field ^[3,4,5]. In general, fractional calculus can be employed to model each issue of instability phenomena in real life; we refer the researchers to some works that discuss various applications of fractional calculus ^{[6,7,8,9,10,11]}.

The Leivn-Nohel equations offer several advantages in mathematical analyses. They provide a powerful framework for studying the analysis of nonlinear phenomena, exhibit well-posedness properties, and enable the study of stability and convergence. Volterra ^[12] connected a biological application by the convolution Levin-Nohel integrodifferential equation of the following form:

Afterward, in 1954 ^[13], Brownell and Ergen employed Eq (1.1) to interpret the temperature of the reactor generated due to the power circulating-fuel nuclear. Furthermore, the Levin-Nohel systems have important applications in physics and engineering; for instance, these systems can aid in modeling of one-dimensional viscoelasticity such that $k$ represents a relaxation function, and $\mathtt{y}$ acts as the strain. The Levin-Nohel systems have received attention from several researchers. In particular, the stability issue for the Levin-Nohel systems with a constant delay was discussed in ^[14,15]. In 2017, Dung ^[16] established a transfer theorem for the Levin-Nohel systems and the stability conditions by connecting them with the stability conditions of the corresponding functional differential systems. Khelil et al. ^[17] obtained various types of stability for the neutral Levin-Nohel integrodifferential equation by utilizing Krasnoselskii-Burton's fixed point theorem. In 2023 ^[18], the existence, uniqueness, and some types of UH stability were studied for the neutral delay Levin-Nohel integrodifferential equation via Caputo fractional derivative of the following form:

where ${}^{\mathcal{C}}\mathcal{D}^{\alpha}_{0^+}$ is a fractional derivative in the sense of Caputo with a fractional order $\alpha\in(0, 1].$

On the other hand, many physical phenomena have unexpected instantaneous changes in their situation; additionally, some phenomena have time delays in the occurring processes ^{[19,20,21,22]}. Impulsive delay differential equations offer several distinct significance in modeling dynamic systems. They collect delay, sudden, and instantaneous changes, and allow for the exact representation of events, such as impulsive perturbations. Their analysis aids in the understanding of complex phenomena, including control systems, population dynamics, and neural networks with delays. Numerous authors considered the impulsive delay differential systems with a variety of fractional derivatives ^[23,24]. In 2012, Feckan et al. ^[25] used the counterexample technique to show that an essence error appeared in the solution formula for impulsive fractional differential problems in previous studies such as ^[26,27,28]. Then they presented a correct solution formula for a impulsive Caputo fractional Cauchy problem. Wang et al. ^[29] discussed some concepts related to initial and impulsive fractional problems. Anguraj et al. ^[30] investigated sufficient criterion of the existence and uniqueness theorems for a impulsive fractional integro-differential equations. Kharade and Kucche in 2019 ^[31] established uniqueness of an implicit impulsive delay $\psi$-Hilfer fractional problem by utilizing a Banach fixed point, an abstract Gronwall inequality, and Picard operator properties. Then, in 2021 ^[32] the qualitative theorems for a delay impulsive differential system with time delay were studied by utilizing the Gronwall inequality in the $\psi$-$\mathcal{R.L.}$ fractional integral sense and fixed point theorem. Very recently, Chefnaj et al. ^[33] established qualitative results for an impulsive hybrid $\psi$-Caputo fractional differential equation by classical fixed point theorems.

Furthermore, the various types of stabilities have gained attention by many researchers. Specifically, the Ulam-Hyers-Mittag-Leffler (UHML) stability pertains to the behavior of solutions to these equations and is concerned with the existence, uniqueness, and stability of such solutions. Authors in ^[34] studied the UHML stability of solution for delay $\psi$-Hilfer fractional differential system. Authors in ^[35] discussed the UHML stability for a tripled Caputo weighted fractional system via Chebyshev and Bielecki norms. Authors in ^[36] investigated the UHML stability by a Gronwall's inequality and a Picard operator for a non-local $\psi$‑Hilfer Cauchy equation. Thabet et al. ^[37,38] established some types of the UH stability for several fractional systems.

Motivated by the advantages of the Levin-Nohel equations, and inspired by the aforementioned works ^[16,17,18], in the present article, we investigate the existence, uniqueness, and the UHML stability for the following multi-term Hilfer fractional impulsive delay neutral Levin-Nohel integrodifferential (NLNID) system:

where ${}^{\mathcal{H}}\mathcal{D}^{\alpha, \beta}_{0^+}$ is fractional derivative in the Hilfer sense of the arbitrary order $\alpha,$ such that $(0 < \alpha\leq1)$ and type $\beta,$ $(0\leq \beta\leq 1),$ $\mathcal{I}_{0^+}^{1-\gamma}$ is the $\mathcal{R.L.}$ fractional integral of order $(1-\gamma)$, $\alpha\leq\gamma = \alpha+\beta-\alpha\beta,$ $\Delta \, \mathcal{I}_{0^+}^{1-\gamma}\, \mathtt{y}(\mathfrak{u}_i) = \mathcal{I}_{0^+}^{1-\gamma}\, \mathtt{y}(\mathfrak{u}_i^+) - \mathcal{I}_{0^+}^{1-\gamma}\, \mathtt{y}(\mathfrak{u}_i^-), \, \mathcal{I}_{0^+}^{1-\gamma}\, \mathtt{y}(\mathfrak{u}_i^+) = \mathop{\lim}\limits_{\epsilon\to0^+} \mathcal{I}_{0^+}^{1-\gamma}\, \mathtt{y}(\mathfrak{u}_i+\epsilon)$, and $\mathcal{I}_{0^+}^{1-\gamma}\, \mathtt{y}(\mathfrak{u}_i^-) = \mathop{\lim}\limits_{\epsilon\to0^-} \mathcal{I}_{0^+}^{1-\gamma}\, \mathtt{y}(\mathfrak{u}_i+\epsilon)$. Moreover, the functions $\mathtt{f}:\mathbb{J}\times\mathbb{R}^n\to\mathbb{R},$ $\; g_i:\mathbb{R}\to \mathbb{R}$, $k_i, h_i:\mathbb{J}\times\mathbb{J}\to\mathbb{R}, \; \delta_i, \eta_i:\mathbb{J}\to\mathbb{R},$ and $\varphi:[-d, 0]\to\mathbb{R}$ are continuous on their domains, $\delta_i, \eta_i\geq0$; moreover, the space of continuous functions from $[-d, 0]$ to $\mathbb{R}$ is denoted by $\mathcal{C}([-d, 0], \mathbb{R})$, and gifted with the norm $\|\varphi\|_{\mathcal{C}} = \mathop{\sup}\limits_{\mathfrak{u}\in[-d, 0]}|\varphi(\mathfrak{u})|$, where $\varphi\in\mathcal{C}([-d, 0], \mathbb{R})$. Furthermore, similar to Eq (1.1), and for modeling of the one-dimensional viscoelasticity by the system (1.2)–(1.5), the functions $k_i, h_i$ are represented by the multi-term of relaxation functions, and $\mathtt{y}$ acts as the strain.

In what follows, we present the contributions and novelty of this work:

$(i)$ The Levin-Nohel system (1.2)–(1.5) is discussed under a Hilfer fractional derivative, which can be reduced to a Caputo version at $\beta = 1$, $\mathcal{R.L}$ form at $\beta = 0,$ which becomes a first order derivative at $\alpha = 1;$

$(ii)$ The Levin-Nohel system (1.2)–(1.5) is studied with initial impulsive conditions and time delays;

$(iii)$ We establish the existence and uniqueness result for the new multi-term Hilfer fractional impulsive delay NLNID system (1.2)–(1.5), along the UHML stability, by applying the Banach contraction principle, and the generalized Gronwall inequality;

$(iv)$ Additionally, this work discusses the Caputo and $\mathcal{R.L}$ fractional versions of the main proposed system (1.2)–(1.5).

The rest of our work is arranged as follows. Section 2 recalls essential background materials related to fractional calculus. Section 3 is divided into five parts; Part 3.1 derives the corresponding integral equation for the main system (1.2)–(1.5); Part 3.2 proves the existence and uniqueness theorem; Part 3.3 discusses the UHML stability; Part 3.4 deduces the results that are related to the $\mathcal{R.L}$ fractional version; and Part 3.5 presents the results in the sense of the Caputo fractional version. Section 4 is devoted to testing our results using illustrative applications.

2.   Background materials

This part recalls several basic materials for our work analysis throughout this paper. Let us introduce the weighted space of continuous functions as follows:

denotes the weighted Banach space of pieces-wise continuous functions endowed with the supremum norm $\|\mathtt{y}\|_{\mathcal{PC}_{1-\gamma}} = \sup_{\mathfrak{u}\in\mathbb J} |\mathfrak{u}^{1-\gamma} \mathtt{y}(\mathfrak{u})|.$ Moreover, we define the space

equipped with the norm $\|\mathtt{y}\|_{\mathbb Y_{\mathcal{C}, \mathcal{PC}_{1-\gamma}}} = \max\{\|\mathtt{y}\|_{\mathcal{C}}, \|\mathtt{y}\|_{\mathcal{PC}_{1-\gamma}}\}.$ Its easy to show that the space with the norm $(\mathbb Y_{\mathcal{C}, \mathcal{PC}_{1-\gamma}}, \|\mathtt{y}\|_{\mathbb Y_{\mathcal{C}, \mathcal{PC}_{1-\gamma}}})$ represents a Banach space. Furthermore, in similar way, we can define the spaces $\mathbb Y_{\mathcal{C}, \mathcal{PC}_{1-\alpha}}$ and $\mathbb Y_{\mathcal{C}, \mathcal{PC}}$.

Definition 2.1. ^[1] The $\mathcal{R. L.}$ fractional integral of order $\alpha > 0$ for an integrable function $\mathtt{y}$ is given as follows:

Moreover, $\Big(\mathcal{I}_{0^+}^{\alpha} \mathcal{I}_{0^+}^{\beta}\mathtt{y}\Big)(\mathfrak{u}) = \big(\mathcal{I}_{0^+}^{\alpha+\beta} \mathtt{y}\big)(\mathfrak{u}), \alpha, \beta > 0$, and $\mathcal I_{0^+}^{\alpha} \mathfrak{u}^{\zeta-1} = \dfrac{\Gamma(\zeta)}{\Gamma(\zeta+\alpha)} \mathfrak{u}^{\zeta+\alpha-1}, \zeta > 0$.

Definition 2.2. ^[1] The $\mathcal{R. L.}$ fractional derivative of order $\alpha \in (n-1, n]$ for an integrable function $\mathtt{y}$ is given as follows:

where $n = [\alpha]+1, [\alpha]$ is an integer part of $\alpha.$ Furthermore, ${}^{\mathcal{R}}\mathcal D_{0^+}^{\alpha}\mathfrak{u}^{\alpha-1} = 0, \; 0 < \alpha < 1.$

Definition 2.3. ^[2] The Hilfer derivative of fractional order $0 < \alpha\leq1$, and type $0\leq\beta\leq 1$ for a function $\mathtt{y}$ is given as follows:

Remark 2.1. We note that the Hilfer fractional derivative reduces to the $\mathcal{R. L.}$ derivative at ($\beta = 0$), the Caputo derivative at ($\beta = 1$), and the first order derivative when ($\alpha = 1$).

Lemma 2.1. ^[39] Consider $0 < \alpha\leq1$, $0\leq\gamma < 1$, and $\mathtt{y}, \mathcal I_{0^+}^{1-\alpha} \mathtt{y}\in \mathcal C_{1-\gamma}(\mathbb I, \mathbb R)$; then,

(i) $\mathcal{I}_{0^{+}}^\alpha \mathcal{H} \mathcal{D}_{0^{+}}^{\alpha , \beta} \mathtt{y}(\mathfrak{u})=\mathcal{I}_{0^{+}}^\gamma \mathcal{R} \mathcal{D}_{0^{+}}^\gamma \mathtt{y}(\mathfrak{u})=\mathtt{y}(\mathfrak{u})-\frac{\left(\mathcal{I}_{0^{+}}^{1-\gamma} \mathtt{y}\right)(0)}{\Gamma(\gamma)} \mathfrak{u}^{\gamma-1}, \quad \forall \mathfrak{u} \in \mathbb{I}$.

(ii) $^{\mathcal{H}}\mathcal{D}_{0^+}^{\alpha, \beta}\, \mathcal I_{0^+}^{\alpha}\, \mathtt{y}(\mathfrak{u}) = \mathtt{y}(\mathfrak{u}).$

(iii) $^{\mathcal{H}}\mathcal{D}_{0^+}^{\alpha, \beta}\, \mathfrak{u}^{\zeta-1} = 0, \quad 0 < \zeta < 1.$

Lemma 2.2. ^[39] If $0 < \alpha\leq1, f\in \mathcal C_{1-\gamma}(\mathbb I, \mathbb R)$, and $0\leq\gamma < 1$, then

Next, we introduce the generalized Gronwall's inequality as follows.

Lemma 2.3. (Corollary (3), ^[32]) Consider a function $H\in\mathcal{PC}_{1-\gamma}(\mathbb{I}, \mathbb{R}^+)$, which verifies the following relation:

such that $H(\mathfrak{u}), K(\mathfrak{u}), \sigma\in\mathcal{PC}_{1-\gamma}(\mathbb{I}, \mathbb{R}^+)$ are positive, $q$ is a continuous function, and $\lambda_i > 0, (i = \overline{1, n});$ then, one has

where $\mathbb{M}_{\alpha}$ is the Mittag-Leffler law and defined by $\mathbb{M}_{\alpha}(\mathtt{x}) = \mathop{\sum}\limits_{k = 0}^{\infty} \dfrac{\mathtt{x}^{k}}{\Gamma(k\alpha+1)}, \mathtt{x}\in\mathbb C, Re(\alpha) > 0.$

3.   Main results

3.1.   Integral equation of solution

In this part, we introduce an equivalent fractional integral equation, which corresponds to the multi-term Hilfer fractional impulsive delay NLNID system (1.2)–(1.5). Regarding this, we present the following lemma.

Lemma 3.1. Consider $0 < \alpha < 1$, $0\leq \beta\leq 1,$ $\alpha\leq\gamma = \alpha+\beta-\alpha\beta,$ and $p, q: \mathbf{J}\to\mathbb{R}$ are continuous functions. Then, the function $\mathtt{y}\in\mathcal{PC}_{1-\gamma}(\mathbf{J}, \mathbb{R})$ for any $\mathtt{T}\in \mathbf{J},$ is defined by the following:

which is a solution of the fractional equation ${}^{\mathcal{H}}\mathcal{D}^{\alpha, \beta}_{0^+}\, [\mathtt{y}(\mathfrak{u})-p(\mathfrak{u})] = q(\mathfrak{u}), \mathfrak{u}\in\mathbf{J}.$

Proof. The result can be proven by the same manner as the Lemma (3.1) ^[40]. □

Lemma 3.2. The multi-term Hilfer fractional impulsive delay NLNID system (1.2)–(1.5) admits a solution $\mathtt{y}\in \mathbb Y_{\mathcal{C}, \mathcal{PC}_{1-\gamma}}$, if $y$ satisfies the fractional integral equation of the following form:

where

Proof. Let $\mathtt{y}\in \mathbb Y_{\mathcal{C}, \mathcal{PC}_{1-\gamma}}$ verify the multi-term Hilfer fractional impulsive delay NLNID system (1.2)–(1.5). For $\mathfrak{u}\in[0, \mathfrak{u}_1]$, we have the following:

where $\mathcal{G}_{\mathtt{y}}(\mathfrak{u})$ and $\mathcal{F}_{\mathtt{y}}(\mathfrak{u}-\delta_i(\mathfrak{u}))$ are given in (3.3). Now, by applying $\mathcal{I}_{0^+}^{\alpha}$ on both sides of Eq (3.4) and Lemma 2.1, one obtains the following:

Next, if $\mathfrak{u}\in(\mathfrak{u}_1, \mathfrak{u}_2]$, one has the following:

Thus, in view of Lemma 3.1, for $\mathfrak{u}\in(\mathfrak{u}_1, \mathfrak{u}_2],$ we find the following:

Based on Eq (3.5), we obtain

and by substituting it into Eq (3.7), we have

Again, if $\mathfrak{u}\in(\mathfrak{u}_2, \mathfrak{u}_3]$, one has

Therefore, by Lemma 3.1, for $\mathfrak{u}\in(\mathfrak{u}_2, \mathfrak{u}_3],$ we find

From Eq (3.9), we have

Thus, Eq (3.11) becomes

Hence, by continuing in the same way, we get

which is Eq (3.2).

On the another hand, suppose that $\mathtt{y}\in \mathbb Y_{\mathcal{C}, \mathcal{PC}_{1-\gamma}}$ verifies the system (3.2) for $\mathfrak{u}\in\mathbb{J}$; then, we have

By taking ${}^{\mathcal{H}}\mathcal{D}^{\alpha, \beta}_{0^+}$ on both sides of (3.15), and based on Lemma 2.1 (ⅲ), one obtains

which is Eq (1.2). Moreover, according to Eq (3.5), we find

According to Lemma 2.2, this yields that $\mathcal{I}_{0^+}^{1-\gamma}\, \mathtt{y}(0) = \mathtt{y}_0,$ which is Eq (1.4). Additionally, in view of Eq (3.14), for $\mathfrak{u}\in(\mathfrak{u}_i, \mathfrak{u}_{i+1}]$, one has

Again, for $\mathfrak{u}\in(\mathfrak{u}_{i-1}, \mathfrak{u}_{i}]$, one obtains

Then, due to Eqs (3.18) and (3.19), we get

which is Eq (1.3). Hence, the proof is finished. □

3.2.   Existence and uniqueness

In this subsection, we establish the existence and uniqueness result for the multi-term Hilfer fractional impulsive delay NLNID system (1.2)–(1.5). Therefore, we need to introduce the following assumptions:

$(H_1)$ For $\mathtt{y}, \mathtt{x}\in\mathbb Y_{\mathcal{C}, \mathcal{PC}_{1-\gamma}}$, and $\mathfrak{u}\in\mathbb{J},$ there are constants $\ell_i > 0, (i = \overline{1, n})$, such that

where $\mathcal{F}_{\mathtt{y}}(\mathfrak{u}-\delta_i(\mathfrak{u}))$ is defined in (3.3).

$(H_2)$ For $\mathtt{y}, \mathtt{x}\in \in\mathbb Y_{\mathcal{C}, \mathcal{PC}_{1-\gamma}}$ and $\rho_i > 0, (i = \overline{1, n})$, a function $g_i:\mathbb{R}\to \mathbb{R}$ verifies the following identity:

For simplicity, we define the following notations:

Now, in view of Lemma 3.2, we define the mapping $\Xi: \mathbb Y_{\mathcal{C}, \mathcal{PC}_{1-\gamma}} \to \mathbb Y_{\mathcal{C}, \mathcal{PC}_{1-\gamma}}$, as follows:

where $\mathcal{G}_{\mathtt{y}}(\mathfrak{u})$ and $\mathcal{F}_{\mathtt{y}}(\mathfrak{u}-\delta_i(\mathfrak{u}))$ are given in (3.3).

Theorem 3.1. Let $(H_1)$ and $(H_2)$ hold, and if

then the multi-term Hilfer fractional impulsive delay NLNID system (1.2)–(1.5) admits one solution in $\mathbb Y_{\mathcal{C}, \mathcal{PC}_{1-\gamma}}$.

Proof. We prove that a fixed point of the mapping $\Xi$ given in (3.20) is a solution of the proposed system (1.2)–(1.5). To this end, let $\mathtt{y}, \mathtt{x}\in\mathbb Y_{\mathcal{C}, \mathcal{PC}_{1-\gamma}}$ and for any $\mathfrak{u}\in[-d, 0]$, one has

Now, for any $\mathfrak{u}\in\mathbb{J}$, by using $(H_1)$ and $(H_2)$, we have

Thus, by the inequality (3.21), we get

Hence, by the identities (3.22) and (3.23), one finds that

Therefore, due to $\Phi_1 < 1$, the mapping $\Xi$ is a contraction, and because of the Banach theorem, $\Xi$ admits one fixed point in $\mathbb Y_{\mathcal{C}, \mathcal{PC}_{1-\gamma}}$, which is a solution of the multi-term Hilfer fractional impulsive delay NLNID system (1.2)–(1.5) in $\mathbb Y_{\mathcal{C}, \mathcal{PC}_{1-\gamma}}$. □

3.3.   UHML stability

This subsection is devoted to discussing the UHML stability for the multi-term Hilfer fractional impulsive NLNID system (1.2)–(1.3). For this goal, we need to present some basic material which play a key role in our analysis.

Definition 3.1. ^[41,42] We say the multi-term Hilfer fractional impulsive NLNID system (1.2)–(1.3) has the UHML stability with respect to $\mathbb{M}_{\alpha}(\mathfrak{u}^\alpha)$, if for each $\epsilon > 0, \; \exists \, C_{\mathbb{M}_{\alpha}} > 0,$ such that for each $\mathtt{x}\in\mathbb Y_{\mathcal{C}, \mathcal{PC}_{1-\gamma}}$, the following inequalities are satisfied:

where

there is exactly one solution $\mathtt{y}\in\mathbb Y_{\mathcal{C}, \mathcal{PC}_{1-\gamma}}$ for the system (1.2)–(1.3), verifying

Remark 3.1. We would like to declare the following points:

(1) The UH stability and generalized UH are specific cases of the UHML stability; for their definitions see ^[43].

(2) The inequalities in (3.24) have a solution $\mathtt{x}\in\mathbb Y_{\mathcal{C}, \mathcal{PC}_{1-\gamma}}$ if there is a function $\omega\in\mathbb Y_{\mathcal{C}, \mathcal{PC}_{1-\gamma}}$, and the sequence $\{\omega_i\}, (i = \overline{1, n}, )$ depends on $x$, which satisfies the following properties:

(i) $|\omega(\mathfrak{u})|\leq \epsilon\; \mathbb{M}_{\alpha}(\mathfrak{u}^\alpha), \quad \mathfrak{u}\in\mathbb{J}, \quad \sum_{i = 1}^{n}|\omega_i|\leq n\, \epsilon;$

(ii) $^{\mathcal{H}}\mathcal{D}^{\alpha, \beta}_{0^+}\, \left[ \mathtt{x}(\mathfrak{u})- \mathcal{F}_{\mathtt{x}}(\mathfrak{u}-\delta_i(\mathfrak{u}))\right] = \mathcal{G}_{\mathtt{x}}(\mathfrak{u}) +\omega(\mathfrak{u}), \quad \mathfrak{u}\in\mathbb{J};$

(iii) $\Delta \, \mathcal{I}_{0^+}^{1-\gamma}\, \mathtt{x}(\mathfrak{u}_i) = g_i(\mathtt{x}(\mathfrak{u}_i^-))+\omega_i, \quad i = \overline{1, n}.$

Now, we are ready to discuss the UHML stability for the system (1.2)–(1.3).

Theorem 3.2. Let $(H_1)$ and $(H_2)$ hold; then, the multi-term Hilfer fractional impulsive NLNID system (1.2)–(1.3) has UHML stability.

Proof. Consider $\mathtt{x}\in\mathbb Y_{\mathcal{C}, \mathcal{PC}_{1-\gamma}}$ to be a solution of the inequality (3.24); then, based on Lemma 3.2 and Remark 3.1, we get

where $\mathcal{F}_{\mathtt{x}}(\mathfrak{u}-\delta_i(\mathfrak{u}))$ and $\mathcal{G}_{\mathtt{x}}(\mathfrak{u})$ are given (3.25). Furthermore, let $\mathtt{y}\in\mathbb Y_{\mathcal{C}, \mathcal{PC}_{1-\gamma}}$ be a solution of the following system:

Therefore, according to Eq (3.27) and Remark 3.1, for $\mathfrak{u}\in\mathbb{J},$ we obtain

Next, for $\mathfrak{u}\in[-d, 0]$, we have

Moreover, from inequality (3.29), and by utilizing $(H_1)$ and $(H_2)$, for $\mathfrak{u}\in\mathbb J,$ we find

which implies that

Let $w(\mathfrak{u}) = \sup_{\mathfrak{u}\in\mathbb J} |\mathfrak{u}^{1-\gamma} \left(\mathtt{x}(\mathfrak{u})-\mathtt{y}(\mathfrak{u})\right) |$; we find

Based on Lemma 2.1, one has

and yields that

Hence,

where

Thus, in view of (3.30) and (3.31), the multi-term Hilfer fractional impulsive NLNID system (1.2)–(1.3) has UHML stability. □

Corollary 3.1. Let $(H_1)$ and $(H_2)$ hold; then, the multi-term Hilfer fractional impulsive NLNID system (1.2)–(1.3) has UH stability, and consequently a generalized UH stability.

Proof. According to the incremental function $\mathbb{M}_{\alpha}(\cdot)$, the inequality (3.31) becomes

which implies that

where $C_{\mathcal{G}}: = C_{\mathbb{M}_{\alpha}} \mathbb{M}_{\alpha}\big(\zeta \; \mathcal{T}^\alpha \big).$ Furthermore, for $\mathfrak{u}\in[-d, 0]$, one has $\|\mathtt{x}-\mathtt{y}\|_{\mathcal{C}} = 0.$ Thus, we infer that $\|\mathtt{x}-\mathtt{y}\|_{\mathbb Y_{\mathcal{C}, \mathcal{PC}_{1-\gamma}}} \leq \epsilon\; C_{\mathcal{G}},$ this means that the multi-term Hilfer fractional impulsive NLNID system (1.2)–(1.3) has UH stability. As a consequence, if $\psi(\epsilon) = \epsilon\; C_{\mathcal{G}},$ then it has a generalized UH stability. □

3.4.   The $\mathcal{R. L.}$ fractional version

This part aims at discussing the $\mathcal{R. L.}$ version of the Hilfer fractional impulsive delay NLNID system (1.2)–(1.5) at $\beta = 0$, which is given as follows:

which is equivalent to the following Volterra integral equation:

To prove the existence and uniqueness of solutions for the system (3.34)–(3.37), we need the following hypotheses:

$(H_3)$ There are constants $\ell_i > 0, (i = \overline{1, n})$ such that for $\mathtt{y}, \mathtt{x}\in\in\mathbb Y_{\mathcal{C}, \mathcal{PC}_{1-\alpha}}$, and $\mathfrak{u}\in\mathbb{J},$ we have

where $\mathcal{F}_{\mathtt{y}}(\mathfrak{u}-\delta_i(\mathfrak{u}))$ defined in (3.3).

$(H_4)$ For $\mathtt{y}, \mathtt{x} \in\mathbb Y_{\mathcal{C}, \mathcal{PC}_{1-\alpha}}$ and $\rho_i > 0, (i = \overline{1, n})$, a function $g_i:\mathbb{R}\to \mathbb{R}$ verifies the following identity:

Theorem 3.3. Let $(H_3)$ and $(H_4)$ hold, and if

then the $\mathcal{R. L.}$ fractional impulsive delay NLNID system (3.34)–(3.37) admits one solution in $\mathbb Y_{\mathcal{C}, \mathcal{PC}_{1-\alpha}}$.

Proof. The proof can be performed similar to the Theorem 3.1 with $\beta = 0$. □

Theorem 3.4. Let $(H_3)$ and $(H_4)$ be satisfied; then, the $\mathcal{R. L.}$ fractional impulsive NLNID system (3.34)–(3.35) has UHML stability.

Proof. Let $\beta = 0$ within Theorem 3.2; then, the proof is finished. □

Corollary 3.2. Let $(H_3)$ and $(H_4)$ hold; then, the $\mathcal{R. L.}$ fractional impulsive NLNID system (3.34)–(3.35) has UH stability, and consequently a generalized UH stability.

3.5.   The Caputo fractional version

This subsection focuses on the Caputo version of the multi-term Hilfer fractional impulsive delay NLNID system (1.2)–(1.5), at $\beta = 1$, which is given by the following:

which corresponds to the following integral equation:

Regarding the existence and uniqueness of the solutions for the system (3.40)–(3.42), we need the following hypotheses:

$(H_5)$ There are constants $\ell_i > 0, (i = \overline{1, n})$ such that for $\mathtt{y}, \mathtt{x}\in\in\mathbb Y_{\mathcal{C}, \mathcal{PC}}$, and $\mathfrak{u}\in\mathbb{J},$ we have

where $\mathcal{F}_{\mathtt{y}}(\mathfrak{u}-\delta_i(\mathfrak{u}))$ is defined in (3.3).

$(H_6)$ For $\mathtt{y}, \mathtt{x} \in\mathbb Y_{\mathcal{C}, \mathcal{PC}}$ and $\rho_i > 0, (i = \overline{1, n})$, a function $g_i:\mathbb{R}\to \mathbb{R}$ verifies the following identity:

Theorem 3.5. Let $(H_5)$ and $(H_6)$ hold, and if

then the Caputo fractional impulsive delay NLNID system (3.40)–(3.42) admits one solution in $\mathbb Y_{\mathcal{C}, \mathcal{PC}}$.

Proof. Let $\beta = 1$ within the Theorem 3.1; then, the proof is finished. □

Theorem 3.6. Let $(H_5)$ and $(H_6)$ be satisfied; then, the Caputo fractional impulsive NLNID system (3.40)–(3.41) has UHML stability.

Proof. The proof can be performed similar to Theorem 3.2 with $\beta = 1$. □

Corollary 3.3. Let $(H_5)$ and $(H_6)$ hold; then, the Caputo fractional impulsive NLNID system (3.40)–(3.41) has UH stability, and consequently a generalized UH stability.

Remark 3.2. If $\alpha = 1$ in the system (3.40)–(3.42), then it reduces to the first order impulsive delay NLNID system of the following form:

which corresponds to the following integral equation:

Moreover, the results in the Theorems 3.5, 3.6, and Corollary 3.3 remain valid for the system (3.45)–(3.47), while taking in account that $\alpha = 1$.

4.   Applications

In this section, we provide numerical applications with tables and graphics to test the validity main results.

Now, consider the following multi-term Hilfer fractional impulsive delay NLNID system:

Here, we have

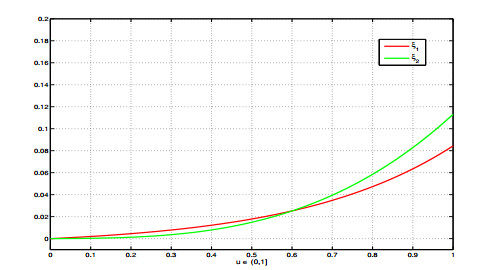
Figure 1, displays the graphics of $\xi_1$ and $\xi_2$ in the interval $\mathfrak{u}\in(0, 1]$, for the system (4.1)–(4.4). In the sequel, we study our application for the following three cases:

The Hilfer fractional version: Let $\alpha = 0.8$ and $\beta = 0.6;$ then $\gamma = 0.875,$ and

Then, $\ell_1 = {\raise0.5ex\hbox{$\scriptstyle {0.5}$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {12}$}}, \, \rho_1 = {\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {8}$}},$ and $\Phi_1: = 0.371274 < 1.$ Hence, the hypotheses $(H_1)$, $(H_2)$, and condition $\Phi_1: = 0.371274. < 1$ of Theorem 3.1 are satisfied; thus, the multi-term Hilfer fractional impulsive NLNID system (4.1)–(4.4) admits one solution in the space $\mathbb Y_{\mathcal{C}, \mathcal{PC}_{1-0.875}}.$ Furthermore, in view of Theorem 3.2, for each $\epsilon > 0$, if $\mathtt{x}\in\mathbb Y_{\mathcal{C}, \mathcal{PC}_{1-0.875}}$ is a solution of the following inequalities:

then there is one solution $\mathtt{y}\in\mathbb Y_{\mathcal{C}, \mathcal{PC}_{1-0.875}}$ of the Hilfer version of system (4.1)–(4.2), which is satisfied that

where $\zeta = 0.197499, \; P = {\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {8}$}}, \; \text{and}\; C_{\mathbb{M}_{0.75}} = 10.7109.$ Therefore, the Hilfer version of system (4.1)–(4.2) has UHML stability. Moreover, by putting $C_{\mathcal{G}}: = C_{\mathbb{M}_{0.75}}\, \mathbb{M}_{0.75}(\zeta \mathfrak{u}^{0.75}),$ and according to Corollary 3.1, we deduce that the Hilfer version of system (4.1)–(4.2) is UH stable, and as a consequence, it has a generalized UH stability.

Figure 2, and Table 1, show that the values of $\Phi_1$ are less than one at various $\alpha\in(0, 1]$ and $\beta\in[0, 1]$, for the system (4.1)–(4.4).

The $\mathcal{R.L.}$ fractional version: Let $\alpha = 0.75$ and $\beta = 0;$ then $\gamma = 0.75,$ and

Then, $\ell_1 = {\raise0.5ex\hbox{$\scriptstyle {0.5}$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {12}$}}, \, \rho_1 = {\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {8}$}},$ and $\Phi_2: = 0.358565 < 1.$ Hence, the hypotheses $(H_3)$, $(H_4)$, and condition $\Phi_2: = 0.358565 < 1$ for Theorem 3.3 are satisfied; thus, the $\mathcal{R.L.}$ version of fractional impulsive NLNID system (4.1)–(4.4) admits one solution in the space $\mathbb Y_{\mathcal{C}, \mathcal{PC}_{1-0.75}}.$ Furthermore, in view of Theorem 3.4, for each $\epsilon > 0$, if $\mathtt{x}\in\mathbb Y_{\mathcal{C}, \mathcal{PC}_{1-0.75}}$ is a solution of the following inequalities:

then there is one solution $\mathtt{y}\in\mathbb Y_{\mathcal{C}, \mathcal{PC}_{1-0.75}}$ of the $\mathcal{R.L.}$ version for the system (4.1)–(4.2), which is satisfied that

where $\zeta = 0.197499, \; P = {\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {8}$}}, \; \text{and}\; C_{\mathbb{M}_{0.75}} = 10.3954.$ Therefore, the $\mathcal{R.L.}$ version for system (4.1)–(4.2) has UHML stability. Moreover, by putting $C_{\mathcal{G}}: = C_{\mathbb{M}_{0.75}}\, \mathbb{M}_{0.75}(\zeta \mathfrak{u}^{0.75}),$ and according to Corollary 3.2, we deduce that the $\mathcal{R.L.}$ version of system (4.1)–(4.2) is UH stable, and as a consequence, it has a generalized UH stability.

The Caputo fractional version: Let $\alpha = 0.75$ and $\beta = 1,$ then $\gamma = 1,$ and

Then, $\ell_1 = {\raise0.5ex\hbox{$\scriptstyle {0.5}$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {12}$}}, \, \rho_1 = {\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {8}$}},$ and $\Phi_3: = 0.381559 < 1.$ Thus, the hypotheses $(H_5)$, $(H_6)$, and condition $\Phi_3: = 0.381559 < 1$ for Theorem 3.5 are satisfied; hence, the Caputo version of the fractional impulsive NLNID system (4.1)–(4.4) admits one solution in the space $\mathbb Y_{\mathcal{C}, \mathcal{PC}}.$ Furthermore, in view of Theorem 3.6, for each $\epsilon > 0$, if $\mathtt{x}\in\mathbb Y_{\mathcal{C}, \mathcal{PC}}$ is a solution of the following inequalities:

then there is one solution $\mathtt{y}\in\mathbb Y_{\mathcal{C}, \mathcal{PC}}$ of the Caputo version for the system (4.1)–(4.2), which is satisfied that

where $\zeta = 0.197499, \; P = {\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {8}$}}, \; \text{and}\; C_{\mathbb{M}_{0.75}} = 10.9686.$ Therefore, the Caputo version for system (4.1)–(4.2) has UHML stability. Moreover, by putting $C_{\mathcal{G}}: = C_{\mathbb{M}_{0.75}}\, \mathbb{M}_{0.75}(\zeta \mathfrak{u}^{0.75}),$ and according to Corollary 3.3, we deduce that the Caputo version of system (4.1)–(4.2) is UH stable, and as a consequence, it has a generalized UH stability.

Figure 3, and Table 2, display the values of $\Phi_2$ and $\Phi_3$ are less than one at various $\alpha\in(0, 1]$ and specific values of $\beta = 0$ and $\beta = 1$ respectively, for system (4.1)–(4.4).

5.   Conclusions

This paper focused on investigating a new structure of the Hilfer NLNID system (1.2)–(1.5) under initial and instantaneous impulse conditions with variable time delays. The existence and uniqueness results were established by applying the Banach contraction principle. Moreover, the UHML stability was proven by employing the generalized Gronwall's inequality and nonlinear analysis issues. As a consequence, the UH stability and generalized UH were deduced as special cases of UHML stability. Additionally, this paper was enhanced by discussing the $\mathcal{R.L.}$ and Caputo fractional types of the proposed system (1.2)–(1.5). Finally, numerical simulations with tables and graphics were provided to test the exactitude of our findings. The results of this work give us a deep understanding of those applications that are connected with the Levin-Nohel equations, especially those that cause instantaneous impulses and time delays. In the future, our focus will be on studying sufficient conditions of positive solutions for the NLNID system involving the Hilfer-like fractional difference on discrete time scale ^[44].

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This study is supported via funding from Prince Sattam bin Abdulaziz University project number (PSAU/2024/R/1445). The author T. Abdeljawad would like to thank Prince Sultan University for the support through TAS research group. The authors express their gratitude dear unknown referees for their helpful suggestions which improved final version of this paper.

Funding

Pontificia Universidad Católica del Ecuador, Proyecto Título: "Algunos resultados Cualitativos sobre Ecuaciones diferenciales fraccionales y desigualdades integrales" Cod UIO2022.

Availability of data and materials

Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.

Conflict of interest

The authors declare that they have no competing interest.