The objective of this study was to analyze the complex dynamics of a discrete-time predator-prey system by using the piecewise constant argument technique. The existence and stability of fixed points were examined. It was shown that the system experienced period-doubling (PD) and Neimark-Sacker (NS) bifurcations at the positive fixed point by using the center manifold and bifurcation theory. The management of the system's bifurcating and fluctuating behavior may be controlled via the use of feedback and hybrid control approaches. Both methods were effective in controlling bifurcation and chaos. Furthermore, we used numerical simulations to empirically validate our theoretical findings. The chaotic behaviors of the system were recognized through bifurcation diagrams and maximum Lyapunov exponent graphs. The stability of the positive fixed point within the optimal prey growth rate range A1<a<A2 was highlighted by our observations. When the value of a falls below a certain threshold A1, it becomes challenging to effectively sustain prey populations in the face of predation, thereby affecting the survival of predators. When the growth rate surpasses a specific threshold denoted as A2, it initiates a phase of rapid expansion. Predators initially benefit from this phase because it supplies them with sufficient food. Subsequently, resource depletion could occur, potentially resulting in long-term consequences for populations of both the predator and prey. Therefore, a moderate amount of prey's growth rate was beneficial for both predator and prey populations.
Citation: Saud Fahad Aldosary, Rizwan Ahmed. Stability and bifurcation analysis of a discrete Leslie predator-prey system via piecewise constant argument method[J]. AIMS Mathematics, 2024, 9(2): 4684-4706. doi: 10.3934/math.2024226
| [1] | Fatao Wang, Ruizhi Yang, Yining Xie, Jing Zhao . Hopf bifurcation in a delayed reaction diffusion predator-prey model with weak Allee effect on prey and fear effect on predator. AIMS Mathematics, 2023, 8(8): 17719-17743. doi: 10.3934/math.2023905 |
| [2] | Ibraheem M. Alsulami . On the stability, chaos and bifurcation analysis of a discrete-time chemostat model using the piecewise constant argument method. AIMS Mathematics, 2024, 9(12): 33861-33878. doi: 10.3934/math.20241615 |
| [3] | Vinoth Seralan, R. Vadivel, Dimplekumar Chalishajar, Nallappan Gunasekaran . Dynamical complexities and chaos control in a Ricker type predator-prey model with additive Allee effect. AIMS Mathematics, 2023, 8(10): 22896-22923. doi: 10.3934/math.20231165 |
| [4] | Fethi Souna, Salih Djilali, Sultan Alyobi, Anwar Zeb, Nadia Gul, Suliman Alsaeed, Kottakkaran Sooppy Nisar . Spatiotemporal dynamics of a diffusive predator-prey system incorporating social behavior. AIMS Mathematics, 2023, 8(7): 15723-15748. doi: 10.3934/math.2023803 |
| [5] | Na Min, Hongyang Zhang, Xiaobin Gao, Pengyu Zeng . Impacts of hunting cooperation and prey harvesting in a Leslie-Gower prey-predator system with strong Allee effect. AIMS Mathematics, 2024, 9(12): 34618-34646. doi: 10.3934/math.20241649 |
| [6] | A. Q. Khan, Ibraheem M. Alsulami . Discrete Leslie's model with bifurcations and control. AIMS Mathematics, 2023, 8(10): 22483-22506. doi: 10.3934/math.20231146 |
| [7] | Heping Jiang . Complex dynamics induced by harvesting rate and delay in a diffusive Leslie-Gower predator-prey model. AIMS Mathematics, 2023, 8(9): 20718-20730. doi: 10.3934/math.20231056 |
| [8] | Jin Liao, André Zegeling, Wentao Huang . The uniqueness of limit cycles in a predator-prey system with Ivlev-type group defense. AIMS Mathematics, 2024, 9(12): 33610-33631. doi: 10.3934/math.20241604 |
| [9] | Weili Kong, Yuanfu Shao . Bifurcations of a Leslie-Gower predator-prey model with fear, strong Allee effect and hunting cooperation. AIMS Mathematics, 2024, 9(11): 31607-31635. doi: 10.3934/math.20241520 |
| [10] | Yao Shi, Zhenyu Wang . Bifurcation analysis and chaos control of a discrete fractional-order Leslie-Gower model with fear factor. AIMS Mathematics, 2024, 9(11): 30298-30319. doi: 10.3934/math.20241462 |
The objective of this study was to analyze the complex dynamics of a discrete-time predator-prey system by using the piecewise constant argument technique. The existence and stability of fixed points were examined. It was shown that the system experienced period-doubling (PD) and Neimark-Sacker (NS) bifurcations at the positive fixed point by using the center manifold and bifurcation theory. The management of the system's bifurcating and fluctuating behavior may be controlled via the use of feedback and hybrid control approaches. Both methods were effective in controlling bifurcation and chaos. Furthermore, we used numerical simulations to empirically validate our theoretical findings. The chaotic behaviors of the system were recognized through bifurcation diagrams and maximum Lyapunov exponent graphs. The stability of the positive fixed point within the optimal prey growth rate range A1<a<A2 was highlighted by our observations. When the value of a falls below a certain threshold A1, it becomes challenging to effectively sustain prey populations in the face of predation, thereby affecting the survival of predators. When the growth rate surpasses a specific threshold denoted as A2, it initiates a phase of rapid expansion. Predators initially benefit from this phase because it supplies them with sufficient food. Subsequently, resource depletion could occur, potentially resulting in long-term consequences for populations of both the predator and prey. Therefore, a moderate amount of prey's growth rate was beneficial for both predator and prey populations.
As a fundamental component of ecological investigation, the interaction between predator and prey populations in biological ecosystems has long been a subject of interest and analysis among biologists and mathematicians. Predator-prey systems involve the dynamic interaction of two populations, in which the survival of one species (the predators) is dependent on the consumption of another species (the prey). A number of researchers have conducted thorough investigations and analyses of diverse mathematical frameworks that explicate the interrelationships between species. The fundamental objective of these inquiries has been to examine the complex and varied dynamics that are intrinsic to these systems. The primary areas of concern include stability analysis, limit cycles, bifurcations, chaotic phenomena, and associated phenomena [1,2,3,4,5,6,7,8].
The Lotka-Volterra system, which is the classic predator-prey framework, was initially proposed and established by Volterra and Lotka [9,10]. Within the conceptual framework of this system, it is postulated that all components adhere to linear functions, including the growth rate, predator mortality rate, and the transformation of prey biomass into predator reproduction. However, it is crucial to acknowledge that nonlinear components exert a substantial influence on predator-prey dynamics that occur in nature. Scholars have suggested numerous improvements to address the system's inability to incorporate specific real-world events. Leslie and Gower [11,12] introduced the classical Leslie-Gower predator-prey system to provide a comprehensive representation of the real-world scenario. This system incorporates the notion that the predator's environmental carrying capacity is directly proportional to the population density of the prey. Britton [13] suggested the following Leslie's system:
| {dxdt=ax−bx2−cxy,dydt=dy−αy2x, | (1.1) |
where x and y represent the population densities of prey and predator, respectively. The parameter a denotes the intrinsic growth rate of prey, while b quantifies the strength of competition among individuals of prey. The rate of change due to interaction is represented by the parameter c. Additionally, the intrinsic growth rate of the predator is denoted by d and α signifies the density of prey required to sustain a single predator. All parameters a,b,c,d and α are positive constants.
There are two distinct categories of modeling methodologies, namely, discrete-time systems and continuous-time systems. Much research has been dedicated to examining the nonlinear dynamical characteristics of continuous systems. In contrast, the investigation of discrete systems has been relatively limited. Nevertheless, over time scholars have come to recognize that discrete systems possess distinct dynamical qualities when compared to their continuous counterparts. The discrete-time systems provide the most accurate description of the dynamics exhibited by animals that engage in seasonal reproduction and have nonoverlapping generations. Furthermore, as compared to continuous-time systems, these discrete systems demonstrate much more complicated dynamical patterns [14,15,16,17,18,19,20,21]. Hence, discrete systems possess more attraction in comparison to continuous systems. It is crucial to use suitable numerical techniques for discretizing the continuous systems. The forward Euler strategy [22,23,24,25,26] has been widely used due to its simplicity. However, there needs to be more dynamic consistency when comparing the discrete version to its continuous equivalents. The discrete system produced by the use of the Euler approach lacks realism. Certain parameters and initial values may attribute the presence of negative values for the prey and predator population sizes. Nevertheless, using the piecewise constant argument approach [27,28,29,30] eliminates negative values. Khan et al. [31] investigated the discrete form of the system (1.1) as follows:
| {xn+1=(1+ah)xn−bhx2n−chxnyn,yn+1=(1+dh)xnyn−αhy2nxn. | (1.2) |
They obtained the discretization using the forward Euler technique. They investigated stability analysis and demonstrated the occurrence of the Neimark-Sacker (NS) bifurcation in the system. The authors used the hybrid control methodology to regulate the chaotic behavior in the system. In this study, we use the piecewise constant argument as an alternative method for discretizing the continuous-time system (1.1). By utilizing piecewise constant arguments to solve nonlinear differential equations and considering the regular time interval for the average growth rate in both populations, we can rewrite system (1.1) as follows:
| {1x(t)dxdt=a−bx[t]−cy[t],1y(t)dydt=d−αy[t]x[t], | (1.3) |
where [t] represents the integer part of t and 0<t<∞. Furthermore, integrating system (1.3) on an interval [n,n+1) with n=0,1,2,⋯ yields the following system:
| {x(t)=xne(a−bxn−cyn)(t−n),y(t)=yne(d−αynxn)(t−n). | (1.4) |
Taking t→n+1, we obtain the following discrete-time system:
| {xn+1=xnea−bxn−cyn,yn+1=yned−αynxn. | (1.5) |
The subsequent sections of the paper are structured in the following manner: The objective of Section 2 is to investigate the presence and topological classification of fixed points. Section 3 provides a comprehensive examination of the bifurcation analysis pertaining to the period-doubling (PD) and NS bifurcations occurring at the positive fixed point. Section 4 employs two control methodologies in order to effectively regulate bifurcations and chaos. In order to validate and explicate the theoretical findings, numerical examples are presented in Section 5. The analysis performed in this research is ultimately summarized in Section 6.
The understanding of fixed point stability holds significant importance within the context of a predator-prey system. The fixed points represent equilibrium states wherein the populations of predators and prey have achieved a condition of balance. By conducting an analysis of their stability, we are able to make predictions about the long-term patterns exhibited by these ecological systems, gaining a deeper understanding of the various factors that contribute to the overall dynamics of the ecosystem.
The fixed points for system (1.5) can be obtained by solving
| {x=xea−bx−cy,y=yed−αyx, | (2.1) |
for x and y. It is obtained that system (1.5) has two fixed points E1=(ab,0),E2=(aαcd+bα,adcd+bα).
To classify the fixed points, we employ the following results.
Lemma 2.1. [32] Let Λ(ξ)=ξ2+K1ξ+K0 be the characteristic polynomial of Jacobian matrix computed at fixed point (x,y) and ξ1,ξ2 satisfy Λ(ξ)=0, then (x,y) is a
(1) sink (locally asymptotically stable (LAS)) when |ξ1|<1 along with |ξ2|<1,
(2) source when |ξ1|>1 along with |ξ2|>1,
(3) saddle point (SP) when |ξ1|<1 and |ξ2|>1 (or |ξ1|>1 and |ξ2|<1),
(4) non-hyperbolic point (NHP) when the modulus}of either of ξ1 and ξ2 is one.
Lemma 2.2. [32] Consider the quadratic function Λ(ξ)=ξ2+K1ξ+K0. Suppose that Λ(1)>0. If ξ1 and ξ2 both satisfy the equation Λ(ξ)=0, then
(1) |ξ1|<1 along with |ξ2|<1 if Λ(−1)>0 and K0<1,
(2) |ξ1|<1 and |ξ2|>1 (or |ξ1|>1 and |ξ2|<1) if Λ(−1)<0,
(3) |ξ1,2|>1 if Λ(−1)>0 and K0>1,
(4) |ξ2|≠1 and ξ1=−1 if Λ(−1)=0 and K1≠0,2,
(5) ξ1,ξ2∈C along with |ξ1,2|=1 if K21−4K0<0 and K0=1.
Through simple computations, one can obtain the Jacobian matrix at an arbitrary fixed point (x,y) as follows:
| J(x,y)=[ea−bx−cy(1−bx)−cea−bx−cyxed−yαxy2αx2ed−yαx(x−yα)x]. |
The Jacobian matrix of system (1.5) computed at E1 is shown as follows:
| J(E1)=[1−a−acb0ed]. |
Also, the Jacobian matrix at E2 is given by
| J(E2)=[1−abαcd+bα−acαcd+bαd2α1−d]. | (2.2) |
Proposition 2.1. The boundary fixed point E1 is
(1) never LAS,
(2) a source if a>2,
(3) SP if 0<a<2,
(4) NHP if a=2.
Next, we classify the positive fixed point E2 of system (1.5) according to the above Jacobian matrix and Lemma 2.2. We obtain
| J(E2)=[1−abαcd+bα−acαcd+bαd2α1−d]. | (2.3) |
The characteristic polynomial of J(E2) is
| Λ(ξ)=ξ2+(−2+d+abαcd+bα)ξ+(−1+a)(−1+d)+acdcd+bα. |
It can be obtained through calculations that
| Λ(0)=(−1+a)(−1+d)+acdcd+bα, Λ(−1)=(−2+a)(−2+d)+2acdcd+bα, Λ(1)=ad. |
Theorem 2.1. The following holds for the interior fixed point E2 of the system (1.5):
(1) E2 is a sink if one of the following conditions holds:
(a) d<2 and if one of the following conditions holds:
(i) b+c(−4+d)d2(−2+d)2α≤0 and a<d(cd+bα)cd2+b(−1+d)α,
(ii) b+c(−4+d)d2(−2+d)2α>0 and a<2(−2+d)(cd+bα)cd2+(−2+d)α,
(b) d=2 and a<4c+2bα4c+bα,
(c) 2<d<4,b+c(−4+d)d2(−2+d)2α<0, and
| 2(−2+d)(cd+bα)cd2+(−2+d)α<a<d(cd+bα)cd2+b(−1+d)α, |
(2) E2 is a saddle point if one of the following conditions holds:
(a) 0<d<2,b>cd2(2−d)α, and a>2(−2+d)(cd+bα)cd2+b(−2+d)α,
(b) d>2 and 0<a<2(−2+d)(cd+bα)cd2+b(−2+d)α,
(3) E2 is a source if one of the following conditions holds:
(a) d=2 and a>4c+2bα4c+bα,
(b) d>4 and a>2(−2+d)(cd+bα)cd2+b(−2+d)α,
(c) a>d(cd+bα)cd2+b(−1+d)α and if one of the following conditions holds:
(i) 0<d<2 and b≥cd2(2−d)α,
(ii) 2<d≤4 and b+c(−4+d)d2(−2+d)2α≤0,
(d) d<2,cd2(2−d)α<b<−c(−4+d)d2(−2+d)2α and
| d(cd+bα)cd2+b(−1+d)α<a<2(−2+d)(cd+bα)cd2+b(−2+d)α, |
(e) 2<d≤4,b+c(−4+d)d2(−2+d)2α>0, and a>2(−2+d)(cd+bα)cd2+b(−2+d)α,
(4) E2 is non-hyperbolic point and experiences PD bifurcation if a=A1=2(−2+d)(cd+bα)cd2+b(−2+d)α and if one of the requirements listed below is satisfied:
(a) b+c(−4+d)d2(−2+d)2α<0 and if one of the following conditions holds:
(i) 2<d≤4,
(ii) d<2 and b>cd2(2−d)α,
(b) d∈(0,2)∪(2,4] and b+c(−4+d)d2(−2+d)2α>0,
(c) d>4,
(5) E2 is non-hyperbolic point and experiences NS bifurcation if a=A2=d(cd+bα)cd2+b(−1+d)α and if one of the requirements listed below is satisfied:
(a) d=2,
(b) d∈(0,2)∪(2,4) and b+c(−4+d)d2(−2+d)2α<0.
This section is focused on conducting a comprehensive investigation of the bifurcation phenomenon involving PD and NS bifurcation in the system (1.5) at the positive fixed point E2. In order to obtain a thorough treatment of bifurcation analysis, we recommend that readers refer to [33,34]. The bifurcation holds significant implications for the dynamics of the system, shedding light on scenarios where even slight modifications to parameters yield substantial alterations in the dynamics of predator-prey relationships. In addition, gaining knowledge about PD and NS bifurcations contributes to a deeper comprehension of ecosystem dynamics. This understanding, in turn, facilitates the formulation of effective conservation and management strategies aimed at sustaining the enduring coexistence of predator and prey populations. This study initiates by investigating the PD bifurcation at E2 based on condition (4-c) as presented in Theorem 2.1. By applying a small perturbation δ (|δ|⋘1) to the bifurcation parameter around the critical value A1, the system (1.5) is changed to
| {xn+1=xne(A1+δ)−bxn−cyn,yn+1=yned−αynxn. | (3.1) |
We transform the fixed point E2 to the origin by considering the change of variables un=xn−(a+δ)αcd+bα, vn=yn−(a+δ)dcd+bα. As a result, the system (3.1) is transformed into the following form:
| [un+1vn+1]=[cd2−b(−2+d)αcd2+b(−2+d)α−2c(−2+d)αcd2+b(−2+d)αd2α1−d][unvn]+[F(un,vn,δ)G(un,vn,δ)], | (3.2) |
where
| F(un,vn,δ)=a1u2n+a2u2nvn+a3v2n+a4v3n+a5unv2n+a6unvn+a7u3n+a8unδ+a9vnδ+a10unvnδ+a11u2nδ+a12v2nδ+O((|un|+|vn|+|δ|)4),G(un,vn,δ)=b1v2n+b2unvn+b3v3n+b4u2nvn+b5unv2n+b6u3n+b7u2n+b8v2nδ+b9unvnδ+b10u2nδ+O((|un|+|vn|+|δ|)4), |
| a1=−bcd2cd2+b(−2+d)α, a2=bc2d2cd2+b(−2+d)α, a3=c2(−2+d)αcd2+b(−2+d)α,a4=−c3(−2+d)α3(cd2+b(−2+d)α), a5=c2(cd2−b(−2+d)α)2(cd2+b(−2+d)α), a6=c(−cd2+b(−2+d)α)cd2+b(−2+d)α,a7=b2(3cd2+b(−2+d)α)6(cd2+b(−2+d)α), a8=−bαcd+bα, a9=−cαcd+bα,a10=bcαcd+bα, a11=b2α2cd+2bα, a12=c2α2cd+2bα, |
| b1=cd2+b(−2+d)α4, b2=−d(cd2+b(−2+d)α)2α, b3=−(−3+d)(cd2+b(−2+d)α)224(−2+d)2,b4=−d(4−5d+d2)(cd2+b(−2+d)α)28(−2+d)2α2, b5=(2−4d+d2)(cd2+b(−2+d)α)28(−2+d)2α,b6=(6−6d+d2)(cd3+b(−2+d)dα)224(−2+d)2α3, b7=cd4+b(−2+d)d2α4α2,b8=−(cd2+b(−2+d)α)28(−2+d)(cd+bα), b9=d(cd2+b(−2+d)α)24(−2+d)α(cd+bα), b10=−(cd3+b(−2+d)dα)28(−2+d)α2(cd+bα). |
Next, the system (3.2) is diagonalized through the consideration of the following transformation:
| [unvn]=[(−2+d)αd22cαcd2−2bα+bdα11][enfn]. | (3.3) |
Upon applying the mapping (3.3), the system (3.2) undergoes the alteration as follows:
| [en+1fn+1]=[−100ξ][enfn]+[Γ(en,fn,δ)Υ(en,fn,δ)], | (3.4) |
where
| ξ=−c(−3+d)d2+b(2−3d+d2)αcd2+b(−2+d)α, |
| Γ(en,fn,δ)=c1e2n+c2e3n+c3enfn+c4e2nfn+c5f2n+c6f3n+c7enf2n+c8fnδ+c9enfnδ+c10enδ+c11f2nδ+c12e2nδ+O((|en|+|fn|+|δ|)4),Υ(en,fn,δ)=d1e3n+d2e2n+d3e2nfn+d4enfn+d5f2n+d6f3n+d7enf2n+d8fnδ+d9enδ+d10e2nδ+d11enfnδ+d12f2nδ+O((|en|+|fn|+|δ|)4), |
where the values of coefficients are given in Appendix A. Next, assume that QC is the center manifold of (3.4) intended at origin in a close neighborhood of δ=0. It can be approximated as follows:
| QC={(en,fn,δ)∈R3+|fn=p1e2n+p2enδ+p3δ2+O((|en|+|δ|)3)}, |
where
| p1=d21−ξ, p2=−d91+ξ, p3=0. |
As a result, the system (3.4) is limited to QC in the manner as follows:
| ˜F:=en+1=−en+c1e2n+c10enδ+(c2+c3d21−ξ)e3n−(c8d91+ξ)enδ2+(c12+c8d21−ξ−c3d91+ξ)e2nδ+O((|en|+|δ|)4). | (3.5) |
For the function (3.5) to go through PD bifurcation, it is necessary that the following two quantities possesses nonzero values:
| l1=˜Fδ˜Fenen+2˜Fenδ|(0,0)=2c10, | (3.6) |
| l2=12(˜Fenen)2+13˜Fenenen|(0,0)=2(c21+c2+c3d21−ξ). | (3.7) |
From the previous discussion, we get the following theorem:
Theorem 3.1. Assume that condition (4-c) of Theorem 2.1 holds true. The system (1.5) experiences PD bifurcation at E2 if l1,l2 given in (3.6) and (3.7) are nonzero and a fluctuates in a close neighborhood of A1=2(−2+d)(cd+bα)cd2+b(−2+d)α. Moreover, if l2>0 (respectively, l2<0), then a period-2 orbit of the system (1.5) emerges and it is stable (respectively, unstable).
Next, we proceed to investigate the NS bifurcation at E2 under condition (5-a) stated in Theorem 2.1. By applying a small perturbation δ (|δ|⋘1) to the bifurcation parameter around the critical value A2, the system (1.5) is changed to
| {xn+1=xne(A2+δ)−bxn−cyn,yn+1=yned−αynxn. | (3.8) |
We transform the fixed point E2 to the origin by considering the change of variables un=xn−(a+δ)αcd+bα, vn=yn−(a+δ)dcd+bα. As a result, the system (3.8) is transformed into the following form:
| [un+1vn+1]=[8c2+2bcα(1−2δ)−b2α2(1+δ)(2c+bα)(4c+bα)−cα(4c(1+δ)+bα(2+δ))(2c+bα)(4c+bα)4α−1][unvn]+[F(un,vn)G(un,vn)], | (3.9) |
where
| F(un,vn)=a1u2n+a2u2nvn+a3unv2n+a4v2n+a5v3n+a6u3n+a7unvn+O((|un|+|vn|)4),G(un,vn)=b1v3n+b2u3n+b3u2nvn+b4unv2n+O((|un|+|vn|)4), |
| a1=b(−16c2+4bcα(−2+δ)+b2α2δ)2(2c+bα)(4c+bα), a2=−bc(−16c2+4bcα(−2+δ)+b2α2δ)2(2c+bα)(4c+bα),a3=c2(8c2+2bcα(1−2δ)−b2α2(1+δ))2(2c+bα)(4c+bα), a4=c2α(4c(1+δ)+bα(2+δ))2(2c+bα)(4c+bα),a5=−c3α(4c(1+δ)+bα(2+δ))6(2c+bα)(4c+bα), a6=−b2(−24c2+b2α2(−1+δ)+2bcα(−7+2δ))6(2c+bα)(4c+bα),a7=c(−8c2+b2α2(1+δ)+2bcα(−1+2δ))(2c+bα)(4c+bα), b1=(2c+bα)26(4c+2bα4c+bα+δ)2,b2=−4(2c+bα)23α3(4c+2bα4c+bα+δ)2, b3=2(2c+bα)2α2(4c+2bα4c+bα+δ)2, b4=−(2c+bα)2α(4c+2bα4c+bα+δ)2. |
The characteristic equation of the Jacobian matrix of system (3.9) estimated at origin is
| ξ2−α(δ)ξ+β(δ)=0, | (3.10) |
where
| α(δ)=−bα(4c(1+δ)+bα(2+δ))(2c+bα)(4c+bα), β(δ)=bα(1+δ)+c(2+4δ)2c+bα. |
The complex solutions for (3.10) are calculated as:
| ξ1,2=α(δ)2±i2√4β(δ)−α2(δ). | (3.11) |
Moreover, we obtain
| (d|ξ1|dδ)δ=0=(d|ξ2|dδ)δ=0=4c+bα4c+2bα>0. |
Additionally, it is required that ξk1,2≠1 when δ = 0 for k=1,2,3,4, which corresponds to α(0) ≠ −2,2,0,1. We obtain
| α(0)=−2bα4c+bα<0. |
Moreover, α(0)=−2 is equivalent to c=0, which is not possible. Next, to change (3.9) into normal form at δ=0, we use the following transformation:
| [unvn]=[−2cα4c+bα0−4c4c+bα−12√4−4b2α2(4c+bα)2][XnYn]. | (3.12) |
Upon application of the mapping (3.12), the system (3.9) takes the following form:
| [Xn+1Yn+1]=[−bα4c+bα−12√4−4b2α2(4c+bα)212√4−4b2α2(4c+bα)2−bα4c+bα][XnYn]+[Γ(Xn,Yn)Υ(Xn,Yn)], | (3.13) |
where
| Γ(Xn,Yn)=c1X2nYn+c2XnY2n+c3X2n+c4Y2n+c5XnYn+c6X3n+c7Y3n+O((|Xn|+|Yn|)4),Υ(Xn,Yn)=d1X2nYn+d2XnYn+d3XnY2n+d4X2n+d5Y2n+d6X3n+d7Y3n+O((|Xn|+|Yn|)4), |
and
| c1=8√2c2(c(2c+bα))3/2(4c+bα)3, c2=−4bc3α(2c+bα)(4c+bα)3, c3=4c2(2c+bα)(4c+bα)2,c4=−4c2(2c+bα)(4c+bα)2, c5=−2√2bcα√c(2c+bα)(4c+bα)2, c6=2c2(2c+bα)2(8c+bα)3(4c+bα)3,c7=−148c2(4−4b2α2(4c+bα)2)3/2, d1=−16c4(2c+bα)(4c+bα)3, d2=4bc2α(4c+bα)2,d3=4√2bc3α√c(2c+bα)(4c+bα)3, d4=−4√2c2√c(2c+bα)(4c+bα)2, d5=4√2c2√c(2c+bα)(4c+bα)2,d6=−23√2c(c(2c+bα))3/2(8c+bα)(4c+bα)3, d7=c(160c4+176bc3α+72b2c2α2+14b3cα3+b4α4)3(4c+bα)3. |
The map (3.13) can undergo NS bifurcation if the following quantity is nonzero:
| L=(−Re((1−2ξ1)ξ221−ξ1τ20τ11)−12|τ11|2−|τ02|2+Re(ξ2τ21))δ=0, | (3.14) |
where
| τ20=18(ΓXnXn−ΓYnYn+2ΥXnYn+i(ΥXnXn−ΥYnYn−2ΓXnYn)),τ11=14(ΓXnXn+ΓYnYn+i(ΥXnXn+ΥYnYn)),τ02=18(ΓXnXn−ΓYnYn−2ΥXnYn+i(ΥXnXn−ΥYnYn+2ΓXnYn)),τ21=116(ΓXnXnXn+ΓXnYnYn+ΥXnXnYn+ΥYnYnYn+i(ΥXnXnXn+ΥXnYnYn−ΓXnXnYn−ΓYnYnYn)). |
Therefore, the result derived from the above analysis is as follows:
Theorem 3.2. Suppose that condition (5-a) of Theorem 2.1 holds true. If L given in (3.14) holds a nonzero value, then system (1.5) experiences NS bifurcation at E2 as long as a fluctuates in a close neighborhood of A2=d(cd+bα)cd2+b(−1+d)α. Furthermore, in instances where L is negative (alternatively, positive), the NS bifurcation encountered in system (1.5) at E2 is categorized as supercritical (subcritical), giving rise to the presence of a unique closed invariant curve originating from E2, that is, attracting (repelling).
The aim of optimizing dynamical systems in order to meet particular performance criteria and minimize chaotic behavior is a highly desirable objective. Chaos control techniques are extensively employed in several fields of applied research and engineering. Historically, bifurcations and unstable oscillations have been regarded in a negative light within the field of mathematical biology due to their detrimental impact on the reproductive capacity of biological populations. It is possible to design a controller that may modify the bifurcation features of a nonlinear system in order to achieve specific desired dynamical attributes and effectively control chaos under the effects of PD and NS bifurcations. Multiple strategies exist for the purpose of managing chaos in a discrete-time system. This section is dedicated to examining two distinct control methods, namely, state feedback control and hybrid control approaches.
Initially, the state feedback control strategy, as described in references [35,36], is employed to regulate the chaotic behavior of the system (1.5). The suggested methodology entails the conversion of the chaotic system into a piecewise linear system in order to obtain an optimal controller that effectively reduces the upper limit. Following this, the problem of optimization is carried out subject to certain constraints. The technique described above is utilized in order to attain stabilization of chaotic orbits situated at an unstable fixed point within the system (1.5). The controlled system under consideration for this purpose is as follows:
| {xn+1=xnea−bxn−cyn−Un,yn+1=yned−αynxn, | (4.1) |
where Un=κ1(xn−aαcd+bα)+κ2(yn−adcd+bα) is the feedback controlling force with feedback gains κ1 and κ2. Through simple calculations, it is obtained that for system (4.1) we have
| J(E2)=[−cd(−1+κ1)+b(−1+a+κ1)αcd+bα−κ2−acαcd+bαd2α1−d]. | (4.2) |
The matrix J(E2) has the following characteristic equation:
| ξ2+K1ξ+K0=0, | (4.3) |
where
| K1=cd(−2+d+κ1)+b(−2+a+d+κ1)αcd+bα,K0=cd(d2κ2+α−κ1α+d(−1+a+κ1)α)+bα(d2κ2−(−1+a+κ1)α+d(−1+a+κ1)α)α(cd+bα). |
Let ξ1 and ξ2 be the roots of (4.3), then we have
| ξ1+ξ2=−cd(−2+d+κ1)+b(−2+a+d+κ1)αcd+bα, | (4.4) |
| ξ1ξ2=cd(d2κ2+α−κ1α+d(−1+a+κ1)α)+bα(d2κ2−(−1+a+κ1)α+d(−1+a+κ1)α)α(cd+bα). | (4.5) |
The lines of marginal stability are derived by solving ξ1=±1 and ξ1ξ2=1. These conditions ensure that |ξ1,2|<1. Assume that ξ1ξ2=1, then Eq (4.5) implies that
| L1:(−1+d)κ1+(d2α)κ2+(−1+a)cd2+b(a(−1+d)−d)αcd+bα=0. | (4.6) |
Next, we take ξ1=1 and, utilizing Eqs (4.4) and (4.5), we obtain
| L2:dκ1+(d2α)κ2+ad=0. | (4.7) |
Next, we take ξ1=−1 and, utilizing Eqs (4.4) and (4.5), we obtain
| L3:(−2+d)κ1+(d2α)κ2+cd(4+(−2+a)d)+(−2+a)b(−2+d)αcd+bα=0. | (4.8) |
The stable eigenvalues are enclosed within the triangular region bounded L1,L2 and L3.
Next, we apply the hybrid control approach [37] for controlling chaos through both types of bifurcation effects. The hybrid control technique refers to a methodology that integrates the utilization of state feedback and parameter adjustment in order to achieve stabilization of unstable periodic orbits that are present within the chaotic attractor of a given system. The controlled system of (1.5), when the hybrid control approach is used, becomes
| {xn+1=ρ(xnea−bxn−cyn)+(1−ρ)xn,yn+1=ρyned−αynxn+(1−ρ)yn, | (4.9) |
where ρ∈(0,1). The parameter ρ serves as a control parameter, which balances the influence of the original system (1.5) in comparison to the modified system (4.9). If the value of ρ is negative, it might suggest the reverse impact of the original system (1.5). If the value of ρ is more than 1, it suggests that the original system (1.5) has an intensifying impact on the modified system (4.9), perhaps resulting in impractical or unfeasible outcomes. Systems (4.9) and (1.5) share the same fixed points. We obtain
| J(E2)=[1−abαρcd+bα−acαρcd+bαd2ρα1−dρ], | (4.10) |
then, its characteristic equation is as follows:
| ξ2+K1ξ+K0=0, | (4.11) |
where
| K1=cd(−2+dρ)+bα(−2+aρ+dρ)cd+bα,K0=bα(−1+aρ)(−1+dρ)+cd(1+dρ(−1+aρ))cd+bα. |
Theorem 4.1. The fixed point E2 of the controlled system (4.9) is LAS if
| |K1|<1+K0<2. |
In this section, we provide empirical evidence to support our theoretical conclusions for system (1.5) through the implementation of numerical simulations. The numerical simulations will include the depiction of bifurcation diagrams, phase portraits, time series plots, and graphs illustrating the maximum Lyapunov exponent (MLE).
Example 5.1. We assume that b=0.5,c=0.8,d=2,α=2.5, then system (1.5) experiences NS bifurcation as a varies in small neighborhoods of a2≈1.280899. The positive fixed point is obtained as E2=(1.123596,0.898876) for a=1.280899. The eigenvalues of J(E2) are ξ1,2 = −0.280899±0.959737i with |ξ1,2|=1. Moreover, some careful calculations give
| τ20=0.224618−0.084112i,τ11=−2.77556×10−17+2.498×10−16i,τ02=0.14382−0.191947i,τ21=0.449327−0.076779i. |
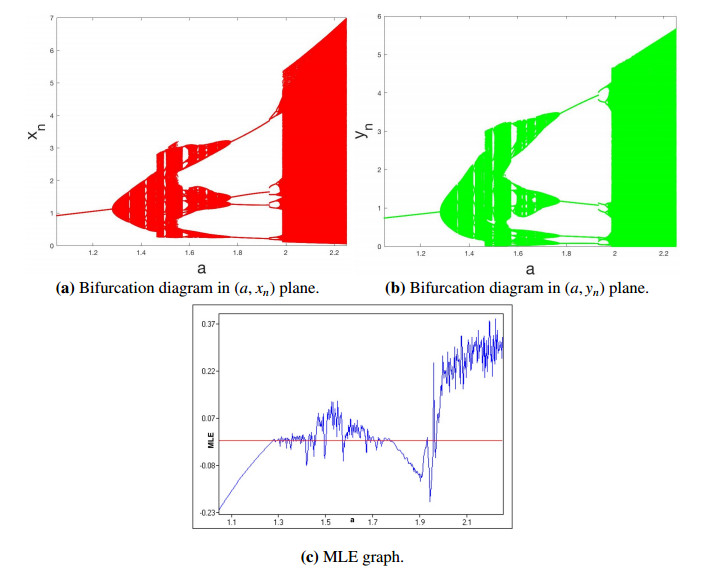
Thus, it is obtained that L=−0.257431<0, which proves the correctness of Theorem 3.2. The bifurcation diagrams of system (1.5) are given in Figure 1(a) and (b), while the MLE is plotted in Figure 1(c) by using initial conditions x0=1.10 and y0=0.90 and varying a∈[1.05,2.25].
Next, Figure 2(a)–(f) show phase portraits of system (1.5) for various values of a. The positive fixed point E2 remains stable when a<1.280899. However, owing to an NS bifurcation, it loses stability at a=1.280899. This results in the formation of an invariant closed curve, the radius of which expands as a grows. Furthermore, the MLE graph demonstrates that negative values of the MLE indicate a range of periodic orbits. For instance, orbit-7 in Figure 2(d), orbit-11 in Figure 2(f), orbit-15 in Figure 2(h), orbit-4 in Figure 2(l) and orbit-8 in Figure 2(m) exhibit this behavior. Conversely, positive MLE values suggest that the system is chaotic. Figure 2(o) and (p) exhibit the presence of strange attractors, indicating the chaotic character that results from positive MLE values.
Example 5.2. We assume that b=0.5,c=0.8,d=3.15,α=2.5, then system (1.5) experiences both PD bifurcation and NS bifurcation as a varies in small neighborhoods of A1≈0.924857 and A2≈1.11764, respectively. The positive fixed point is obtained as E2=(0.613301,0.772759) for a=A1. The eigenvalues of J(E2) are ξ1=−1 and ξ2=−0.45665 with |ξ2|≠1. The positive fixed point is obtained as E2=(0.741142,0.933838) for a=A2. The eigenvalues of J(E2) are ξ1,2 = −0.760285±0.649589i with |ξ1,2|=1. The bifurcation diagrams of system (1.5) are given in Figure 3(a) and (b), while the MLE is plotted in Figure 3(c) by using initial conditions x0=0.60 and y0=0.75 and varying a.
Next, Figure 4(a)–(l) show phase portraits of system (1.5) for various values of a. One can observe that E2 is LAS for 0.924857<a<1.11764, but loses stability at a=0.924857 when the system (1.5) experiences PD bifurcation. For a≥1.11764, the system (1.5) experiences NS bifurcation and an invariant curve emerges from E2, the radius of which grows as a grows. It leads to a strange chaotic attractor presented in Figure 4(l).
Therefore, it can be concluded that the positive fixed point E2 of the system (1.5) exhibits stability when the growth rate of the prey population falls within the range (A1,A2). When the growth rate of the prey falls below the threshold value of A1, it experiences difficulties in maintaining its population against predation, leading to a reduction that subsequently affects the survival of predators that rely on it. When the growth rate exceeds the value of A2, rapid growth sustains predators initially but carries the potential for resource exhaustion, therefore affecting both prey and predators over a long period of time.
Subsequently, our objective is to assess the effectiveness of the feedback control strategy. Given the values a=1.15,b=0.5,c=0.8,d=3.15, and α=2.5, together with the initial conditions x0=0.60 and y0=0.75 for the controlled system (4.1), the marginal stability lines may be determined as follows:
| L1:κ2=−0.022978−0.541698κ1, |
| L2:κ2=−0.912698−0.793651κ1, |
and
| L3:κ2=−0.141068−0.289746κ1. |
The stability region of system (4.1) is shown in Figure 5(a), which is bounded by lines L1,L2 and L3. The instability of the fixed point E2 of system (1.5) has been shown for the specified parametric values. The system described by Eq (4.1) is analyzed using feedback gains κ1=−3.01 and κ2=1.60. Figure 5 illustrates the graph of xn as shown in Figure 5(c), yn as shown in Figure 5(d), and the phase portrait as presented in Figure 5(b) for the system (4.1). Hence, it may be inferred that the use of the feedback control approach seems to be efficacious in managing bifurcation and chaos.
The effectiveness of the hybrid control strategy will now be assessed. We assume ρ=0.95, b = 0.5, c=0.8,d=3.15,α=2.5 and vary a for the controlled system (4.9). If 0.897012<a<1.183794, the positive fixed point E2 is LAS. One can observe that the stability region has been expanded. The bifurcation diagrams are presented in Figure 6(a) and (b) by using initial conditions x0=0.60, y0 = 0.75 and varying a∈[0.20,1.20].
Our study focused on a discrete-time system, which provided a more accurate depiction of animal dynamics in seasonal reproduction with nonoverlapping generations. These discrete systems, in comparison to continuous-time systems, displayed more detailed and rich dynamical patterns, making them more attractive. When discretizing continuous systems, it was critical to use proper numerical approaches. In this paper, we used the piecewise constant argument methodology to discretize the system (1.1), leading to a discrete system (1.5) that consistently preserved positive solutions. This approach presented a benefit in comparison to the Euler method, which was susceptible to producing negative solutions, thereby posing challenges for population systems. This study conducted a comprehensive analysis of the existence and stability of fixed points, focusing specifically on local bifurcations that occur at the positive fixed point. It was observed that our system (1.5) undergoes bifurcations in both PD and NS at a positive fixed point, whereas prior investigations [31] only reported NS bifurcations. Hybrid control and feedback control techniques were employed to effectively manage bifurcation and disorder within the system denoted as (1.5). In order to validate our theoretical findings, we employed numerical simulations that incorporated a range of graphical representations, such as time series plots, phase portraits, bifurcation diagrams, and MLE graphs.
It can be inferred that the stability of the positive fixed point E2 is maintained when the prey population growth rate lies within the interval (A1,A2). In situations where the prey's growth rate fell below a certain threshold value denoted as A1, it encountered challenges in sustaining its population in the face of predation, resulting in a decline that ultimately impacts the viability of predators dependent on it. When the growth rate exceeded the value of A2, rapid growth sustained predators initially but carried the potential for resource exhaustion, therefore affecting both prey and predators over a long period of time.
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
This study is supported via funding from Prince Sattam bin Abdulaziz University project number (PSAU/2023/R/1445).
All authors declare no conflicts of interest in this paper.
| c1=−2c(cd2+b(−2+d)α)c(−4+d)d2+b(−2+d)2α, c2=(cd2+b(−2+d)α)2(cd2(16−24d+4d2+d3)+b(−2+d)4α)6(−2+d)2d4(c(−4+d)d2+b(−2+d)2α), |
| c3=−c(cd3+b(−4+d2)α)c(−4+d)d2+b(−2+d)2α, c4=2c(−1+d)(cd2+b(−2+d)α)(c(−2+d)d2+b(−2−2d+d2)α)(−2+d)d2(c(−4+d)d2+b(−2+d)2α), |
| c5=−(cd2(c3d4(12−6d+d2)+bc2d2(−16+36d−18d2+3d3)α+3b2c(−2+d)3dα2+b3(−2+d)3α3))/(2(cd2+b(−2+d)α)2(c(−4+d)d2+b(−2+d)2α)), |
| c6=(cd2(cd+bα)2(c3d4(8+8d−5d2+d3)+bc2(−2+d)2d2(6−7d+3d2)α+b2c(−2+d)2(−12+12d−11d2+3d3)α2+b3(−3+d)(−2+d)3α3))/(12(cd2+b(−2+d)α)3(c(−4+d)d2+b(−2+d)2α)), |
| c7=(c(3c3d4(8−4d+d2)+bc2d2(−40+72d−40d2+9d3)α+b2cd(−48+72d−44d2+9d3)α2+b3(−8+24d−16d2+3d3)α3))/(4(cd2+b(−2+d)α)(c(−4+d)d2+b(−2+d)2α)), |
| c8=−cd3c(−4+d)d2+b(−2+d)2α, c9=2cd(cd2+b(−2+d)α)c(−4+d)d2+b(−2+d)2α, |
| c10=−(cd2+b(−2+d)α)2(cd+bα)(c(−4+d)d2+b(−2+d)2α), c11=cd2(cd+bα)(cd3+b(−2+d)2α)4(cd2+b(−2+d)α)(c(−4+d)d2+b(−2+d)2α), |
| c12=(cd2+b(−2+d)α)2(cd3+b(−2+d)2α)2(−2+d)d2(cd+bα)(c(−4+d)d2+b(−2+d)2α), |
| d1=−(8−11d+3d2)(cd2+b(−2+d)α)33(−2+d)d4(c(−4+d)d2+b(−2+d)2α), d2=(−2+d)(cd2+b(−2+d)α)2c(−4+d)d4+b(−2+d)2d2α, |
| d3=−(cd2+b(−2+d)α)2(cd(8−7d+2d2)+b(4−7d+2d2)α)2d3(c(−4+d)d2+b(−2+d)2α), |
| d4=(c2d3(8−5d+d2)+bc(−2+d)2d(−3+2d)α+b2(−2+d)3α2)c(−4+d)d3+b(−2+d)2dα, |
| d5=(c4d6(8+8d−6d2+d3)+4bc3d4(4−12d+16d2−7d3+d4)α+2b2c2(−2+d)2d2(−4+12d−12d2+3d3)α2+4b3c(−2+d)4(−1+d)dα3+b4(−2+d)5α4)/(4(cd2+b(−2+d)α)2(c(−4+d)d2+b(−2+d)2α)), |
| d6=−(cd+bα)2(c4d6(64−44d+22d2−7d3+d4)+2bc3d4(−96+164d−130d2+62d3−17d4+2d5)α+6b2c2(−2+d)3d2(−6+6d−4d2+d3)α2+2b3c(−2+d)4(−6+6d−7d2+2d3)α3+b4(−3+d)(−2+d)5α4))/(24(cd2+b(−2+d)α)3(c(−4+d)d2+b(−2+d)2α), |
| d7=−(c4d7(28−16d+3d2)+4bc3d4(16−40d+44d2−19d3+3d4)α+2b2c2(−2+d)2d2(−12+28d−30d2+9d3)α2+4b3c(−2+d)2d(−8+16d−13d2+3d3)α3+b4(−2+d)3(4−10d+3d2)α4))/(8d2(cd2+b(−2+d)α)(c(−4+d)d2+b(−2+d)2α)), |
| d8=cd3c(−4+d)d2+b(−2+d)2α, d9=(cd2+b(−2+d)α)2(cd+bα)(c(−4+d)d2+b(−2+d)2α), |
| d10=−(cd2+b(−2+d)α)3d2(cd+bα)(c(−4+d)d2+b(−2+d)2α), d11=−(cd2+b(−2+d)α)(cd3+b(−2+d)2α)2(c(−4+d)d3+b(−2+d)2dα), |
| d12=−(cd+bα)(c2d4(8−4d+d2)+2bc(−2+d)3d2α+b2(−2+d)4α2)8(cd2+b(−2+d)α)(c(−4+d)d2+b(−2+d)2α). |
| [1] |
A. Kashyap, Q. Zhu, H. Sarmah, D. Bhattacharjee, Dynamical study of a predator-prey system with Michaelis-Menten type predator-harvesting, Int. J. Biomath., 16 (2023), 2250135. http://dx.doi.org/10.1142/S1793524522501352 doi: 10.1142/S1793524522501352

|
| [2] |
M. Ghori, P. Naik, J. Zu, Z. Eskandari, M. Naik, Global dynamics and bifurcation analysis of a fractional-order SEIR epidemic model with saturation incidence rate, Math. Method. Appl. Sci., 45 (2022), 3665–3688. http://dx.doi.org/10.1002/mma.8010 doi: 10.1002/mma.8010

|
| [3] |
W. Lu, Y. Xia, Multiple periodicity in a predator-prey model with prey refuge, Mathematics, 10 (2022), 421. http://dx.doi.org/10.3390/math10030421 doi: 10.3390/math10030421

|
| [4] |
A. Matouk, Chaos and bifurcations in a discretized fractional model of quasi-periodic plasma perturbations, Int. J. Nonlin. Sci. Num., 23 (2022), 1109–1127. http://dx.doi.org/10.1515/ijnsns-2020-0101 doi: 10.1515/ijnsns-2020-0101

|
| [5] |
E. González-Olivares, A. Rojas-Palma, Limit cycles in a Gause-type predator-prey model with sigmoid functional response and weak Allee effect on prey, Math. Method. Appl. Sci., 35 (2012), 963–975. http://dx.doi.org/10.1002/mma.2509 doi: 10.1002/mma.2509

|
| [6] |
A. Elsadany, Q. Din, S. Salman, Qualitative properties and bifurcations of discrete-time Bazykin-Berezovskaya predator-prey model, Int. J. Biomath., 13 (2020), 2050040. http://dx.doi.org/10.1142/S1793524520500400 doi: 10.1142/S1793524520500400

|
| [7] |
D. Sen, S. Ghorai, M. Banerjee, A. Morozov, Bifurcation analysis of the predator-prey model with the allee effect in the predator, J. Math. Biol., 84 (2022), 7. http://dx.doi.org/10.1007/s00285-021-01707-x doi: 10.1007/s00285-021-01707-x

|
| [8] |
A. Suleman, R. Ahmed, F. Alshammari, N. Shah, Dynamic complexity of a slow-fast predator-prey model with herd behavior, AIMS Mathematics, 8 (2023), 24446–24472. http://dx.doi.org/10.3934/math.20231247 doi: 10.3934/math.20231247

|
| [9] |
A. Lotka, Elements of physical biology, Nature, 116 (1925), 461. http://dx.doi.org/10.1038/116461b0 doi: 10.1038/116461b0

|
| [10] |
V. Volterra, Fluctuations in the abundance of a species considered mathematically, Nature, 118 (1926), 558–560. http://dx.doi.org/10.1038/118558a0 doi: 10.1038/118558a0

|
| [11] |
P. Leslie, Some further notes on the use of matrices in population mathematics, Biometrika, 35 (1948), 213–245. http://dx.doi.org/10.2307/2332342 doi: 10.2307/2332342

|
| [12] |
P. Leslie, A stochastic model for studying the properties of certain biological systems by numerical methods, Biometrika, 45 (1958), 16–31. http://dx.doi.org/10.2307/2333042 doi: 10.2307/2333042

|
| [13] | N. Britton, Essential mathematical biology, London: Springer, 2003. http://dx.doi.org/10.1007/978-1-4471-0049-2 |
| [14] |
M. Zhao, C. Li, J. Wang, Complex dynamic behaviors of a discrete-time predator-prey system, J. Appl. Anal. Comput., 7 (2017), 478–500. http://dx.doi.org/10.11948/2017030 doi: 10.11948/2017030

|
| [15] |
S. Rana, Dynamics and chaos control in a discrete-time ratio-dependent Holling-Tanner model, J. Egypt. Math. Soc., 27 (2019), 48. http://dx.doi.org/10.1186/s42787-019-0055-4 doi: 10.1186/s42787-019-0055-4

|
| [16] |
P. Baydemir, H. Merdan, E. Karaoglu, G. Sucu, Complex dynamics of a discrete-time prey-predator system with Leslie type: Stability, bifurcation analyses and chaos, Int. J. Bifurcat. Chaos, 30 (2020), 2050149. http://dx.doi.org/10.1142/s0218127420501497 doi: 10.1142/s0218127420501497

|
| [17] |
S. Akhtar, R. Ahmed, M. Batool, N. Shah, J. Chung, Stability, bifurcation and chaos control of a discretized Leslie prey-predator model, Chaos Soliton. Fract., 152 (2021), 111345. http://dx.doi.org/10.1016/j.chaos.2021.111345 doi: 10.1016/j.chaos.2021.111345

|
| [18] |
P. Naik, Z. Eskandari, H. Shahraki, Flip and generalized flip bifurcations of a two-dimensional discrete-time chemical model, Mathematical Modelling and Numerical Simulation with Applications, 1 (2021), 95–101. http://dx.doi.org/10.53391/mmnsa.2021.01.009 doi: 10.53391/mmnsa.2021.01.009

|
| [19] | Z. Eskandari, Z. Avazzadeh, R. Ghaziani, B. Li, Dynamics and bifurcations of a discrete-time Lotka-Volterra model using nonstandard finite difference discretization method, Math. Method. Appl. Sci., in press. http://dx.doi.org/10.1002/mma.8859 |
| [20] |
P. Naik, Z. Eskandari, Z. Avazzadeh, J. Zu, Multiple bifurcations of a discrete-time prey-predator model with mixed functional response, Int. J. Bifurcat. Chaos, 32 (2022), 2250050. http://dx.doi.org/10.1142/s021812742250050x doi: 10.1142/s021812742250050x

|
| [21] |
P. Naik, Z. Eskandari, A. Madzvamuse, Z. Avazzadeh, J. Zu, Complex dynamics of a discrete-time seasonally forced SIR epidemic model, Math. Method. Appl. Sci., 46 (2023), 7045–7059. http://dx.doi.org/10.1002/mma.8955 doi: 10.1002/mma.8955

|
| [22] |
W. Liu, D. Cai, Bifurcation, chaos analysis and control in a discrete-time predator-prey system, Adv. Differ. Equ., 2019 (2019), 11. http://dx.doi.org/10.1186/s13662-019-1950-6 doi: 10.1186/s13662-019-1950-6

|
| [23] |
Y. Li, F. Zhang, X. Zhuo, Flip bifurcation of a discrete predator-prey model with modified Leslie-Gower and Holling-type iii schemes, Math. Biosci. Eng., 17 (2020), 2003–2015. http://dx.doi.org/10.3934/mbe.2020106 doi: 10.3934/mbe.2020106

|
| [24] |
Rajni, B. Ghosh, Multistability, chaos and mean population density in a discrete-time predator-prey system, Chaos Soliton. Fract., 162 (2022), 112497. http://dx.doi.org/10.1016/j.chaos.2022.112497 doi: 10.1016/j.chaos.2022.112497

|
| [25] |
A. Yousef, A. Algelany, A. Elsadany, Codimension one and codimension two bifurcations in a discrete Kolmogorov type predator-prey model, J. Comput. Appl. Math., 428 (2023), 115171. http://dx.doi.org/10.1016/j.cam.2023.115171 doi: 10.1016/j.cam.2023.115171

|
| [26] |
A. Khan, I. Alsulami, Complicate dynamical analysis of a discrete predator-prey model with a prey refuge, AIMS Mathematics, 8 (2023), 15035–15057. http://dx.doi.org/10.3934/math.2023768 doi: 10.3934/math.2023768

|
| [27] |
A. Tassaddiq, M. Shabbir, Q. Din, H. Naaz, Discretization, bifurcation, and control for a class of predator-prey interactions, Fractal Fract., 6 (2022), 31. http://dx.doi.org/10.3390/fractalfract6010031 doi: 10.3390/fractalfract6010031

|
| [28] |
S. Lin, F. Chen, Z. Li, L. Chen, Complex dynamic behaviors of a modified discrete Leslie-Gower predator-prey system with fear effect on prey species, Axioms, 11 (2022), 520. http://dx.doi.org/10.3390/axioms11100520 doi: 10.3390/axioms11100520

|
| [29] |
P. Naik, Z. Eskandari, M. Yavuz, J. Zu, Complex dynamics of a discrete-time Bazykin-Berezovskaya prey-predator model with a strong Allee effect, J. Comput. Appl. Math., 413 (2022), 114401. http://dx.doi.org/10.1016/j.cam.2022.114401 doi: 10.1016/j.cam.2022.114401

|
| [30] |
R. Ahmed, M. Rafaqat, I. Siddique, M. Arefin, Complex dynamics and chaos control of a discrete-time predator-prey model, Discrete Dyn. Nat. Soc., 2023 (2023), 8873611. http://dx.doi.org/10.1155/2023/8873611 doi: 10.1155/2023/8873611

|
| [31] |
A. Khan, I. Alsulami, Discrete Leslie's model with bifurcations and control, AIMS Mathematics, 8 (2023), 22483–22506. http://dx.doi.org/10.3934/math.20231146 doi: 10.3934/math.20231146

|
| [32] | A. Luo, Regularity and complexity in dynamical systems, New York: Springer, 2012. http://dx.doi.org/10.1007/978-1-4614-1524-4 |
| [33] | J. Guckenheimer, P. Holmes, Nonlinear oscillations, dynamical systems, and bifurcations of vector fields, New York: Springer, 1983. http://dx.doi.org/10.1007/978-1-4612-1140-2 |
| [34] | S. Wiggins, Introduction to applied nonlinear dynamical systems and chaos, New York: Springer, 1990. http://dx.doi.org/10.1007/978-1-4757-4067-7 |
| [35] | G. Chen, X. Dong, From chaos to order: methodologies, perspectives and applications, Singapore: World Scientific, 1998. http://dx.doi.org/10.1142/3033 |
| [36] |
C. Lei, X. Han, W. Wang, Bifurcation analysis and chaos control of a discrete-time prey-predator model with fear factor, Math. Biosci. Eng., 19 (2022), 6659–6679. http://dx.doi.org/10.3934/mbe.2022313 doi: 10.3934/mbe.2022313

|
| [37] |
X. Luo, G. Chen, B. Wang, J. Fang, Hybrid control of period-doubling bifurcation and chaos in discrete nonlinear dynamical systems, Chaos Soliton. Fract., 18 (2003), 775–783. http://dx.doi.org/10.1016/s0960-0779(03)00028-6 doi: 10.1016/s0960-0779(03)00028-6

|
| 1. | Parvaiz Ahmad Naik, Zohreh Eskandari, Mehmet Yavuz, Zhengxin Huang, Bifurcation results and chaos in a two-dimensional predator-prey model incorporating Holling-type response function on the predator, 2024, 0, 1937-1632, 0, 10.3934/dcdss.2024045 | |
| 2. | A. M. Madian, M. F. Elettreby, M. M. A. El-sheikh, A. A. El-Gaber, Dynamical and Phase Analyses on Chaos Control of Discrete Predator–Prey Systems of Mixed Holling Types with Density-Dependent Birth Rates, 2024, 34, 0218-1274, 10.1142/S0218127424501712 | |
| 3. | Allah Ditta, Parvaiz Ahmad Naik, Rizwan Ahmed, Zhengxin Huang, Exploring periodic behavior and dynamical analysis in a harvested discrete-time commensalism system, 2025, 13, 2195-268X, 10.1007/s40435-024-01551-z |