Solutions and local stability of the Jacobsthal system of difference equations

1.   Introduction

Difference equations and their systems have long been instrumental in addressing classical challenges within combinatorics, probability, and time series analysis. These challenges span a spectrum of problems, including doubly AutoRegressive ^[1], bilinear ^[2,3,4,5,6], bilinear-Generalized AutoRegressive Conditional Heteroskedasticity ^[7,8], threshold GARCH ^[9], logGARCH ^[10,11], and stochastic volatility ^[12]. The quest for practical solutions to these scientific dilemmas underscores the paramount importance of acquiring closed-form formulas for the solutions, serving as intricate models for the problems at hand. The exploration of closed-form solutions for difference equations and systems has a rich history, rooted in seminal works such as ^{[13,14,15,16]}. Subsequent literature dedicated to difference equations, as well as broader topics like calculus, numerical mathematics, combinatorics, and economics, has delved into these subjects in depth (see, for instance, ^{[17,18,19,20]}). While recent years have witnessed a resurgence of interest within the mathematical community, with the field steadily expanding and evolving (refer to ^{[21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37]} and related citations), the increased utilization of computers, particularly leveraging symbolic algebra packages, has played a pivotal role in fueling this renewed interest, facilitating a diverse range of computations. Consequently, the question of solvability for difference equations and their systems has emerged as an intriguing subject, given that many of these equations remain practically or theoretically unsolvable. Some scholars strive to, at a minimum, identify specific constants, which in turn prove invaluable in scrutinizing and elucidating the long-term behavior of solutions to these equations and systems (see, for example, ^[38,39]). Various methodologies exist for studying the prolonged behavior of solutions, as exemplified by works such as ^{[23,40,41,42,43,44,45,46,47,48,49,50,51]}. For practical applications of closed-form formulas, one may refer to sources like ^{[17,18,52,53,54]}.

An early example of a nonlinear difference equation with a comprehensively derived closed-form solution is the bilinear equation

where $\alpha_{1}, \; \alpha_{2}, \; \alpha_{3}, \; \alpha_{4}, \; \Omega_{0} \in\mathbb{R}$, and $\alpha_{3}^{2}+\alpha_{4}^{2}\neq0.$ This equation, commonly known as the Riccati difference equation, has been extensively studied in the literature. Over the last two decades, numerous papers have been published on such equations, systems, or systems derived from them associated with number sequences, including Fibonacci, Lucas, Padovan, Tetranacci, Horadam, Pell, Jacobsthal, and Jacobsthal-Lucas sequences (see citations in ^{[29,30,48,55,56,57,58,59,60,61]} and references therein). Fibonacci numbers as well as Jacobsthal sequences remain of great interest for researchers due to their theoretical richness and applications. The Fibonacci sequence in particular is an inexhaustible source of interesting identities, constituting one of the most famous numerical sequences in mathematics. Similar statements apply to Jacobsthal sequences, which scientists have utilized for their fundamental theory and applications (see citations in ^{[62,63,64,65]}). In computer science, for instance, Jacobsthal numbers have been employed in conditional instructions to change the flow of program execution. The properties of these numbers were first summarized by Horadam.

In this paper, we extend the investigation of the solvability of a bilinear system of difference equations, where the coefficients are dependent on the Jacobsthal sequence. We provide general solutions using the Jacobsthal sequence. To achieve this objective, we examine the ensuing $m-$dimensional system of difference equations:

and the initial values $\Omega_{-v}^{\left(j\right) }, \; j\in\left\{ 1, ..., s\right\}, \; v\in\left\{ 0, ..., m\right\}$.

Motivated by the above-mentioned investigations on solvability systems of difference equations, the aim of this paper is to provide detailed theoretical explanations for obtaining closed-form formulas and representations for the general solutions of Eq $\left(1.1\right)$ and give natural proofs of the results. We also demonstrate the main results on the long-term behavior, particularly local stability, of the solutions to Eq $\left(1.1\right)$.

2.   Main results

To tackle the solution of the system $\left(1.1\right)$, we need to leverage the insights provided by the following lemmas.

Lemma 2.1. The recurrence relation for the Jacobsthal sequence is governed by a homogeneous linear difference equation with constant coefficients:

with initial conditions $J_{0} = 0\ $and $J_{1} = 1$. The closed-form expressions for the Jacobsthal numbers are elegantly given as $J_{k} = \left(\alpha ^{k}-\beta^{k}\right) /\left(\alpha-\beta\right)$, where $\alpha = 2$ and $\beta = -1$. This yields significant relations for $n, \; p\in\mathbb{N},$

● $J_{p+n} = J_{p}J_{n+1}+2J_{p-1}J_{n}$,

● $J_{n}^{2} = \left(-2\right) ^{n-1}+J_{n-1}J_{n+1}$,

● $2J_{n-1}+J_{n+1} = j_{n}$,

where $(j_{n})$ represents the Lucas-Jacobsthal sequence.

Lemma 2.2. Consider the homogeneous linear difference equation with constant coefficients

with initial conditions $\Psi_{0}, \; \Psi_{-1}\in\mathbb{R}^{\ast}$, then, the solution is given by:

where $2\lambda_{i} = j_{k}+\left(-1\right) ^{i-1}\sqrt{j_{k}^{2}+12\beta ^{k}j_{k}+4}, \; i = 1, \; 2,$ and $(j_{k}, \; k\geq0)$ represents the Lucas-Jacobsthal sequence.

Proof. The difference equation $\left(2.1\right)$ is typically solved using the characteristic polynomial:

where $\lambda_{1}$ and $\lambda_{2}$ are the roots of this equation, linked to the Lucas-Jacobsthal number. The closed form of the general solution for Eq $\left(2.1\right)$ is given by

where $\Psi_{0}, \; \Psi_{-1}$ are initial values such that

and we have

After some calculations, we obtain:

Thus the lemma is proven. □

Lemma 2.3. Consider the following rational difference equation,

then, the solution is given by:

Proof. Using the change of variables $\Phi_{n} = J_{k+1}+2J_{k}\Omega_{n}, \forall n\geq0$, we can express $\left(2.2\right)$ as

Furthermore, if $\Phi_{n} = \left. \Psi_{n}\right/ \Psi_{n-1}, \forall n\geq0$, we obtain $\Psi_{n+1}-j_{k}\Psi_{n}-\left(-2\right) ^{k}\Psi_{n-1} = 0, \; \forall n\geq0.$ By Lemma 2.2, the closed form of the general solution for Eq $\left(2.3\right)$ is given by:

then,

Therefore, the lemma is proven. □

2.1.   On the system $\left(2.4\right)$

In this subsection, we examine the following system of $1$st-order difference equations:

Now, utilizing the last difference equation in $\left(2.4\right)$, we obtain:

Similarly, we get:

and recursively for the above, we can get

System $\left(2.4\right)$ can be expressed as the following rational difference equation of $s^{th}-$order:

Let $\Omega_{n}\left(i\right) = \Omega_{sn+i}, \; i\in\left\{ 0, \text{ }1, \text{ }..., \text{ }s-1\right\}.$ For this, we have

By Lemma 2.3, the closed form of the general solution of Eq $\left(2.5\right)$ is easily obtained. In the following corollary:

Corollary 2.1. Let $\left\{ \Omega_{n}, \mathit{\text{}}n\geq0\right\}$ be a solution of Eq $\left(2.5\right)$, then, for $i\in\left\{ 0, \mathit{\text{}}1, \mathit{\text{}}..., \mathit{\text{}}s-1\right\}$,

where $(J_{k}$, $k\geq0)$ is the Jacobsthal sequence.

Through the above discussion, we can introduce the following theorem:

Theorem 2.1. Let $\left\{ \Omega_{n}^{\left(1\right) }, \mathit{\text{}}\Omega _{n}^{\left(2\right) }, \mathit{\text{}}..., \mathit{\text{}}\Omega_{n}^{\left(s\right) }, \mathit{\text{}}n\geq0\right\}$ be a solution of the system $\left(2.4\right)$, then, for all $n\geq0$,

for $i\in\left\{ 0, \mathit{\text{}}1, \mathit{\text{}}..., \mathit{\text{}}s-1\right\}$, $l\in\left\{ 1, \mathit{\text{}}..., \mathit{\text{}}s\right\} \ $where $(J_{k}$, $k\geq0)$ is the Jacobsthal sequence.

Proof. From Corollary 2.1, for $i\in\left\{ 0, \text{ }1, \text{ }..., \text{ }s-1\right\}$, $l\in\left\{ 1, \text{ }..., \text{ }s\right\}$, we have

and by system $\left(2.4\right)$, we get

Now, using $\Omega_{i}^{\left(1\right) }$, $i\in\left\{ 0, \text{ }1, \text{ }..., \text{ }s-1\right\}$, $l\in\left\{ 1, \text{ }..., \text{ }s\right\}$, we obtain

then,

The theorem is proved. □

2.2.   On the system $\left(1.1\right)$

In this article, we study the system $(1.1)$, which is an extension of system $(2.4).$ Therefore, the system $(1.1)$ can be written as follows:

for $u\in\left\{ 0, \text{ }1, \text{ }..., \text{ }m\right\}.$ Now, using the following notation for all $n\geq0$,

we can get $\left(m+1\right) -$systems similar to system $(2.4)$,

for $u\in\left\{ 0, \text{ }1, \text{ }..., \text{ }m\right\}.$ Through the above discussion, we can introduce the following theorem:

Theorem 2.2. Let $\left\{ \Omega_{n}^{\left(1\right) }, \mathit{\text{}}\Omega _{n}^{\left(2\right) }, \mathit{\text{}}..., \mathit{\text{}}\Omega_{n}^{\left(s\right) }, \mathit{\text{}}n\geq0\right\}$ be a solution of system $\left(1.1 \right)$, then, for $u\in\left\{ 0, \mathit{\text{}}1, \mathit{\text{}}..., \mathit{\text{}}m\right\}$, $i\in\left\{ 0, \mathit{\text{}}1, \mathit{\text{}}..., \mathit{\text{}}s-1\right\}$, $l\in\left\{ 1, \mathit{\text{}}..., \mathit{\text{}}s\right\}$,

where $(J_{k}$, $k\geq0)$ is the Jacobsthal sequence$.$

2.3.   Local stability of positive solutions of $(1.1)$

In the following, we will study the local stability character of the solutions of system $(1.1)$. Obviously, the unique positive equilibrium of system $(1.1)$ is

where $\gamma = \left(1-\sqrt {7}\right) /4$ and $\underline{1}_{\left(s\right) }$ denotes the vector of order $s\times1$ whose entries are ones. Let the functions $\Gamma _{j}:\left(0, +\infty\right) ^{s\left(m+1\right) }\rightarrow \left(0, +\infty\right)$, $j\in\left\{ 1, \text{ }..., \text{ }s\right\}$ be defined by

where $\underline{y}_{0:m} = \left(y_{0}, \text{ }y_{1}, \text{ }..., \text{ }y_{m}\right) ^{\prime}.$ To facilitate the study, it is customary to linearize the system $(1.1)$ around the equilibrium point $E$. Introducing the vectors $\underline{Y}_{n}^{\prime}: = \left(\left(\underline{Y}_{n}^{\left(1\right) }\right) ^{\prime}, \text{ }\left(\underline{Y}_{n}^{\left(2\right) }\right) ^{\prime}, \text{ }..., \text{ }\left(\underline{Y}_{n}^{\left(s\right) }\right) ^{\prime}\right) \ $where $\underline{Y}_{n}^{\left(j\right) } = \left(y_{n}^{\left(j\right) }, \text{ }y_{n-1}^{\left(j\right) }, \text{ }..., \text{ } y_{n-m}^{\left(j\right) }\right)$, $j\in\left\{ 1, \text{ }..., \text{ }s\right\}$, we obtain the following representation

where

with $O_{(k, l)}$ denoting the matrix of order $k\times l$ whose entries are zeros. For simplicity, we set $O_{(k)}: = O_{(k, k)}$ and $\underline{O} _{(k)}: = O_{(k, 1)}$, and $I_{\left(m\right) }$ is the $m\times m$ identity matrix. We summarize the above discussion in the following theorem:

Theorem 2.3. The positive equilibrium point $E$ is locally asymptotically stable.

Proof. After some preliminary calculations, the characteristic polynomial of $\Lambda_{m}$ is given by:

where

then

According to Rouche's Theorem, all zeros of $\chi_{1}\left(\lambda\right) -\chi _{2, k}\left(\lambda\right) = 0$ lie in the unit disc $\left\vert \lambda\right\vert < 1.$ Thus, the positive equilibrium point $E$ is locally asymptotically stable. □

3.   Numerical simulation results

For the purpose of numerical solutions, we provide illustrative examples to visually validate the theoretical outcomes for each system under consideration in this manuscript.

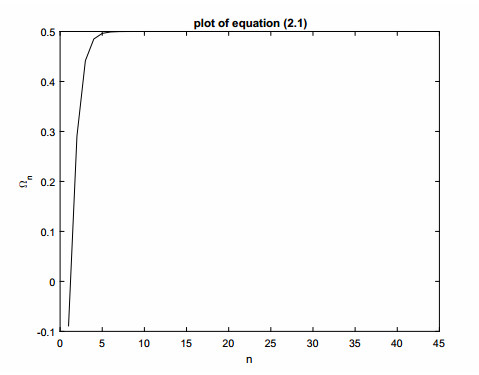
Illustrative Example 1: The figure below depicts the numerical solution of Eq $(2.2)$ when $k = 2$ under specified initial condition $\Omega_{0} = -0.09$ (refer to Figure 1).

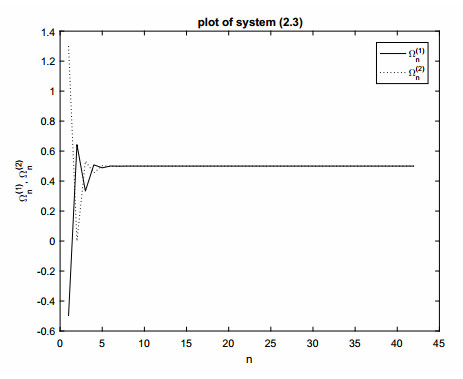
Illustrative Example 2: The figure below depicts the numerical solution of system $(2.4)$ when $k = s = 2$ under specified initial conditions $\Omega_{0}^{\left(1\right) } = -0.5$ and $\Omega_{0}^{\left(2\right) } = 1.3$ (refer to Figure 2).

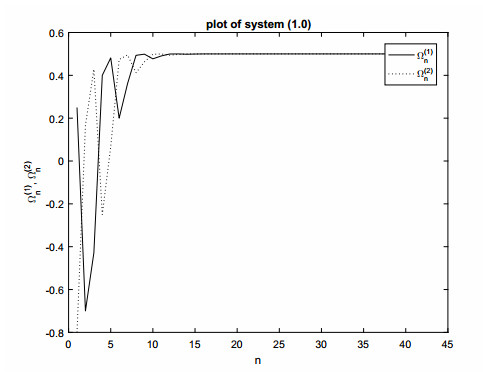
Illustrative Example 3: The figure below depicts the numerical solution of system $(1.1)$ when $k = s = 2$ and $m = 1$ under specified initial conditions $\Omega_{-1}^{\left(1\right) } = 1/4$, $\Omega _{0}^{\left(1\right) } = -0.7$, $\Omega_{-1}^{\left(2\right) } = -0.8$, and $\Omega_{0}^{\left(2\right) } = 1/6$ (refer to Figure 3).

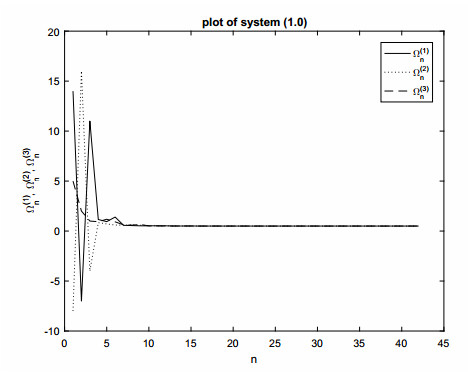
Illustrative Example 4: The figure below depicts the numerical solution of system $(1.1)$ when $m = k = 2$ and $s = 3$ under specified initial conditions $\Omega_{-2}^{\left(1\right) } = 14$, $\Omega _{-1}^{\left(1\right) } = -7$, $\Omega_{0}^{\left(1\right) } = 11$, $\Omega_{-2}^{\left(2\right) } = -8, \; \Omega_{-1}^{\left(2\right) } = 16, \; \Omega_{0}^{\left(2\right) } = -4, \; \Omega_{-2}^{\left(3\right) } = 5, \; \Omega_{-1}^{\left(3\right) } = 2$, and $\Omega_{0}^{\left(3\right) } = 1$ (refer to Figure 4).

4.   Conclusions

In this paper, we have conducted a detailed analysis of the system $(1.1)$, building upon the foundational concepts introduced in system $(2.4)$. Our primary focus was on the positive equilibrium state denoted as $E$. Our investigation into the local stability of the system around the equilibrium point $E$ has yielded significant results. Utilizing Rouché's theorem, we have established the local asymptotic stability of the positive equilibrium. This insight enhanced our comprehension of the system's behavior in the vicinity of positive equilibrium states. The implications of our findings extend to the broader realm of dynamical systems and stability within applied mathematics.

By offering a comprehensive analysis of the system's stability, this study established a solid foundation for future research endeavors, and contributed to the advancement of mathematical understanding. Ultimately, this investigation represents a meaningful contribution to the field of mathematical dynamics. The outcomes presented herein serve as a springboard for further exploration and research initiatives.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through the Small Groups Project under grant number R.G.P.1/138/44.

Conflict of interest

All authors declare no conflicts of interest in this paper.