Finite-time anti-synchronization of a 6D Lorenz systems

1.   Introduction

Great progress has been made in the field of chaos research since Edward Lorenz's pioneering discovery of the first chaotic system in 1963 ^[16]. In all different fields, such as secure communication, biological systems, image encryption, biomedical engineering, information processing, chemical reactions, economic systems, and so on, the growing importance of chaos systems has been extensively known by researchers ^[11,12,24]. Synchronized systems are ubiquitous and play a very key part in a lot of different aspects, including nervous systems ^[4,21,30], climate changes ^[5,10], optomenchanical systems ^[14] and quantum networks ^[20]. So far, the synchronization and anti-synchronization of master-slave chaotic systems (MSCSS) have been in-depth investigated; for example, we can refer to these published articles ^{[6,27,28,29,38]}, where, the Lyapunov function method was used to study the synchronization for their respective MSCSS; in ^[33], the graph theory was used to study the synchronization ^[17] for fractional-order MSCSS, the LMI was used to study the synchronization for their respective MSCSS; in ^[32,39], the stability theory was used to research the synchronization for their respective MSCSS.

The exponential and asymptotic synchronization of systems cannot guarantee that the system is bounded in a finite time. However, in practical application, in order to better control the dynamics, it is the best thing that the convergence rate of the dynamics should be in a finite time spantum. Hence, the study of finite-time synchronization (FTS) and FTAS is of very important theoretical meaning.

So far, some research works have been achieved on the FTS and FTAS for the MSCSS. In ^[2], the predefined-time synchronization of two MSCSS was investigated. By using the FTST, designing two controllers, and using inequality skills, some new criteria were obtained to assure that two nonidentical MSCSS realize predefined-time synchronization. In ^[31], according to the variable-order fractional type Mittag-Leffler stability theorem, a fractional-order derivative was applied to a sliding surface, and suitable adaptive laws were devised to address uncertainties and disturbances. By using a variable-order fractional control strategy, a new criterion was developed to guarantee the FTS for the systems. In ^[19], the authors studied the FTS subject of fractional order chaotic systems (FOCSS) with different structures. By adopting the FTST, they established some criteria for the synchronization of the FOCSS. In article ^[7], employing the sliding-mode control, the authors introduced a finite-time adaptive synchronization method to achieve the generalized projective synchronization of fractional order (FO) memristors or chaotic systems with unknown parameters. The sufficient condition for the sliding-mode surface can be reached by the synchronization error system in finite time by using the Lyapunov functional method. Paper ^[15] introduced a novel fuzzy event-triggered control method for uncertain FOCSS without input delay. First, fuzzy logic systems were utilized to deal with immeasurable systematic information. Second, FO command filters were incorporated to circumvent the problem of "complexity explosion" in back-stepping controller construction. Finally, a sequence of FO finite-time compensation signals was cited to counteract the adverse influence of input delay rapidly. Furthermore, a novel practical finite-time chaos synchronization criterion was proposed. Paper ^[9] explored the topic of FTSN of FO simplest two-component chaotic oscillations operating at high frequency. On the basis of the Lyapunov function, an adaptive feedback controller was designed to achieve the FTS of two oscillators. The FTS of chaotic systems with different dimensions and secure communication was researched in ^[18]. In ^[23], the FTS problem of nonlinear delayed FO MSCSS was studied. By developing a robust, quantized, stochastic, reliable control protocol, the FTS was achieved for the discussed MSCSS via LMI. In ^[13], by using the FTST, a synchronization control scheme was designed to achieve the FTS for the discussed MSCSS.

In ^[1], the anti-synchronization of an MS6DLSS was studied via analytical skills and numerical simulations, including critical points, stability, Lyapunov exponents, time phase portraits, and circuit implementation. However, the studies on the FTS and FTAS for the discussed MS6DLLS have not been found.

Up to now, the FTS and FTAS for MSCSS have been explored often by employing the FTST ^[8,13,18,19], Lyapunov function method ^{[7,9,13,15,22]}, LMI ^[23] and graph theory ^[17]. Since, up to now, the studies on the FTAS for the MS6DLSS have not been found, this inspires us to research the FTAS for the MS6DLSS. In addition, on the basis of the above considerations, we propose the following questions: How to use the different methods from above to study the FTAS for MS6DLLS? How to design the controllers to achieve the FTAS for the considered MS6DLLS?

In our article, without applying the existing study methods on the FTAS for the considered MS6DLSS, by introducing new study methods–using the negative definition of the quadratic form of the matrix and using the properties of quadratic inequalities of one variable–two novel criteria are obtained on the FTAS for the considered MS6DLLS, which develops and improves the study fields of the FTS and FTAS for MSCSS. It is a fact that the results on FTAS for dynamical systems obtained by applying LMI are so complicated that they cannot easily be verified. Since the FTST is a traditional theorem that has been deeply applied to studying the FTS and FTAS, if one always uses it to study the FTS and FTAS, it is impossible that the novel results will be published. One of the advantages of our methods is that by using the properties of quadratic inequalities of one variable and using the negative definiteness of the quadratic form of the matrix, more concise and easily verified results than those in the existing papers on the FTAS for the MSCSS can be obtained. The other of the advantages of our method is that our methods can be used to study the FTS for many dynamical systems expressed by differential equations.

Thus, the main contributions of this article include the following three aspects:

1) The negative definiteness of the quadratic form of the matrix is used to study the FTAS of MS6DLLS, which is a novel study work;

2) The properties of quadratic inequalities of one variable are used to study the FTAS for the MS6DLLS;

3) Two new criteria on the FTAS of the MS6DLLS are obtained.

2.   Preliminaries

The authors in ^[1] proposed the following master 6d Lorenz systems (continuous real variable hyperchaotic model):

and the slave 6D Lorenz systems as follows:

where $x_i(t), i = 1, 2, 3, 4, 5, 6$ are the control functions that will be designed later, $(m_1(t), m_2(t), m_3(t)$, $m_4(t)$, $m_5(t)$, $m_6(t))^T$, and $(n_1(t), n_2(t), n_3(t), n_4(t), n_5(t), n_6(t))^T$, respectively, are real variables in the master 6D Lorenz systems and the slave 6D Lorenz systems, and the parameters $a_1, b_1, c_1, p_1, q_1, r_1, h_1$ are positive constants. Defining the error functions as $u_i(t) = m_i(t)+n_i(t), i = 1, 2, 3, 4, 5, 6$, then the error system can be described as:

Now, by designing the control functions $x_i(t), i = 1, 2, 3, 4, 5, 6$, and employing the control skills, we will study the FTAS for systems (2.1) and (2.2).

Definition 2.1. The systems (2.1) and (2.2) are said to reach FTAS if for each solution of system (2.1) and system (2.2) denoted by $[m_1(t), m_2(t), \cdots, m_5(t), m_6(t)]^T$, and $[n_1(t), n_2(t), \cdots, n_5(t)$, $n_6(t)]^T,$ there is a positive constant $T$ which depends on the initial values of the error system (2.3) such that for $i = 1, 2, \cdots, 5, 6,$

In order to prove the FTAS for systems (2.1) and (2.2), we only need to prove

Lemma 2.1. Symmetric matrix $A = \left(\begin{array}{cccccc} a_{11}&a_{12}&a_{13}&a_{14}&a_{15}&a_{16}\\ a_{21}&a_{22}&a_{23}&a_{24}&a_{25}&a_{26}\\ a_{31}&a_{32}&a_{33}&a_{34}&a_{35}&a_{36}\\ a_{41}&a_{42}&a_{43}&a_{44}&a_{45}&a_{46}\\ a_{51}&a_{52}&a_{53}&a_{54}&a_{55}&a_{56}\\ a_{61}&a_{62}&a_{63}&a_{64}&a_{65}&a_{66}\end{array}\right)$ is negative $(A < 0)$ matrix if and only if $a_{11} < 0, \left|\begin{array}{cc} a_{11}&a_{12}\\ a_{21}&a_{22}\end{array}\right| > 0, \left|\begin{array}{ccc} a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33}\end{array}\right| < 0, \left|\begin{array}{cccc} a_{11}&a_{12}&a_{13}&a_{14}\\ a_{21}&a_{22}&a_{23}&a_{24}\\ a_{31}&a_{32}&a_{33}&a_{34}\\ a_{41}&a_{42}&a_{43}&a_{44}\end{array}\right| > 0,$ $\left|\begin{array}{ccccc} a_{11}&a_{12}&a_{13}&a_{14}&a_{15}\\ a_{21}&a_{22}&a_{23}&a_{24}&a_{25}\\ a_{31}&a_{32}&a_{33}&a_{34}&a_{35}\\ a_{41}&a_{42}&a_{43}&a_{44}&a_{45}\\ a_{51}&a_{52}&a_{53}&a_{54}&a_{55}\end{array}\right| < 0, \left|\begin{array}{cccccc} a_{11}&a_{12}&a_{13}&a_{14}&a_{15}&a_{16}\\ a_{21}&a_{22}&a_{23}&a_{24}&a_{25}&a_{26}\\ a_{31}&a_{32}&a_{33}&a_{34}&a_{35}&a_{36}\\ a_{41}&a_{42}&a_{43}&a_{44}&a_{45}&a_{46}\\ a_{51}&a_{52}&a_{53}&a_{54}&a_{55}&a_{56}\\ a_{61}&a_{62}&a_{63}&a_{64}&a_{65}&a_{66}\end{array}\right| > 0.$

Proof: The proof is well known and it is omitted.

Lemma 2.2. If $\hat{a} > 0, \hat{b}^2-4\hat{a}\hat{c} < 0,$ then $\hat{a}x^2+\hat{b}x+\hat{c} > 0, \forall x\in R.$

Proof: The proof is known well, and it is omitted.

Lemma 2.3. If $\hat{a} < 0, \hat{b}^2-4\hat{a}\hat{c} < 0,$ then $\hat{a}x^2+\hat{b}x+\hat{c} < 0, \forall x\in R.$

Proof: The proof is well known, and it is omitted.

3.   Main results

The control functions in system (2.3) are designed as follows:

and

where $\eta > 0, \eta_3 > 0, \eta_2 > 0, \eta_1 > 0, \lambda_i\; (i = 1, 2, \cdots, 6)$ are positive constants.

Theorem 3.1. The systems (2.1) and (2.2) can realize the FTAS by utilizing the designed controllers (3.1) if the following conditions are satisfied:

$(k_1) \quad 0.25(a_1+c_1)^2-a_1 < 0;$

$(k_2) \quad 0.25+(h_1-\xi_1)[a_1-0.25(a_1+c_1)^2] < 0;$

$(k_3) \quad 0.5(p_1+r_1+a_1)-0.125(a_1+c_1+q_1)^2 < 0;$

$(h_1-\xi_1)\Big[0.25p_1(a_1+c_1)^2+0.25r_1^2-a_1(p_1-0.25q_1^2)-0.25q_1r_1(a_1+c_1)\Big] > 0;$

$(k_4) \quad 0.25r_1^2(h_1-\xi_1)-a_1p_1(h_1-\xi_1)-0.25(a_1+p_1+r_1) < 0.$

Remark 3.1. $k_1$ implies $4a_1 > (a_1+c_1)^2.$

Proof: A Lyapunov function is considered as follows: $N(t) = \frac{1}{2}\Big[u_1^2(t)+u_2^2(t)+u_3^2(t)+u_4^2(t)+u_5^2(t)+u_6^2(t)\Big].$ When $u_6(t) = 0,$ the Lyapunov function $N(t) = \sum\limits_{i = 1}^5u_i(t)$ is constructed. The proof in the case when $u_6(t) = 0$ is the special case of the following proof. Hence, it is omitted. Without loss of generalization, we assume that $u_6(t)\not = 0.$ By utilizing system (2.3), we obtain

where $Y = [u_1(t), u_2(t), u_3(t), u_4(t), u_5(t), u_6(t)]^T$, and

Due to $(k_1), (k_2), (k_3)$ and $(k_4)$, we get $a_1 > 0, b_1 > 0, c_1 > 0, r_1 > 0, h_1 > 0, q_1 > 0$

It is clear that

Since $-0.5(p_1+r_1+a_1)+0.125(a_1+c_1+q_1)^2 > 0,$ then

and because of $(h_1-\xi_1)\Big[0.25p_1(a_1+c_1)^2-a_1(p_1-0.25q_1^2)+0.25r_1^2-0.25q_1r_1(a_1+c_1)\Big] > 0,$ then

Substituting (3.9)–(3.10) into (3.8) gives

From $(k_3)$ and $(k_4)$, we get

By (3.4)–(3.7), (3.11), and (3.12), we get $B < 0.$

Namely,

Substituting (3.13) into (3.3) gives

Integrating (3.14) over $[0, t]$ gives

When $t\geq \bar{t}_1 = \frac{N(0)}{\eta} > 0,$ by (3.15), we get $0\leq N(t)\leq 0, t\geq \bar{t}_1.$

Namely,

Namely,

This ends the argument of Theorem 3.1.

Theorem 3.2. The systems (2.1) and (2.2) can gain the FTAS by utilizing the constructed controllers (3.2) if the following conditions are satisfied:

$(l_1) \quad \lambda_1 > 2, \lambda_2 > 1, \lambda_3 > 1,$

$(2-\lambda_1)b_1^2(1-\lambda_2)-(\lambda_3-1)\Big\{(2-\lambda_1)(a_1-1+q_1+r_1)^2+(1-\lambda_2)[(c_1-a_1+r_1)^2+4(2-\lambda_1)\eta_1]\Big\} < 0.$

$(l_2) \quad (1-q_1)^2\lambda_5+16\lambda_6\Big[(1-p_1)^2\lambda_4^2+\lambda_4\lambda_5(1+h_1)^2-\lambda_4\lambda_5\eta_2\Big] < 0.$

Proof: A Lyapunov function is considered as follows:

By utilizing system (2.3), we get

Next, we prove that

and

By $(l_1)$, we get

Multiplying (3.17) with $(2-\lambda_1)(1-\lambda_2)$ gives

Namely,

Due to $\lambda_1 > 2, \lambda_2 > 1, \lambda_3 > 1,$ then

Via (3.18) and (3.19), by using Lemma 2.2, we get

Multiplying (3.20) with $16(2-\lambda_1)$ leads to

Since $\lambda_1 > 2, \lambda_2 > 1,$ then $-4(1-\lambda_2)(2-\lambda_1) < 0.$

From which, via (3.20) and (3.21), by utilizing Lemma 2.3, we get

from which, together with $2-\lambda_1 < 0,$ it follows that

Because of $(l_2)$, we have

Multiplying (3.23) with $\lambda_4^2\lambda_5$ yields

which, together with $-4\lambda_4^2\lambda_5\lambda_6 < 0$ yields

namely,

Which, together with $-4\lambda_4\lambda_5 < 0,$ we obtain

Because of $-\lambda_4 < 0,$ we have from (3.25)

Substituting (3.23) and (3.26) into (3.16) gives

Integrating (3.27) from $0$ to $t$ results in

When $t\geq t = \bar{t}_2 = \frac{M(0)}{\eta_3}$, by (3.28), we get $0\leq M(t)\leq0.$

Namely,

This ends the argument of Theorem 3.2.

Remark 3.2. In ^[1], anti-synchronization of the MS6DLLS was studied by utilizing analytical skills and numerical simulations, including critical points, stability, Lyapunov exponents, time phase portraits, and circuit implementation. However, the studies on the FTAS for the discussed MS6DLLS have not been found. In this article, by using new study methods, the innovative results on the FTAS for the MS6DLLS are established. This develops the study fields of synchronization for MSCSS.

Remark 3.3. So far, the results on FTAS of the MSCSS are obtained often by employing the Lyapunov function way ^[3,25,26,34], LMI ^[23], and FTST ^[8,13,18,19]. In this article, two new study methods are cited to study the FTAS of the MS6DLSS. Namely, by utilizing the properties of the quadratic form of the matrix and utilizing the negative definiteness of the quadratic form of the matrix, two innovative results on FTAS of the discussed MS6DLLS are gotten. One of the advantages of our methods is that the more concise and easily verified conditions than those in the existing papers on FTS can be obtained for the MSCSS. The other of the advantages of our methods is that our methods can be used to study the FTS and FTAS for many dynamical systems.

Remark 3.4. So far, the results on the FTS for neural networks have been obtained mainly by using FSST, the integral inequality method ^[35,36], and the maximum-valued method ^[37]. So, our study methods on the FTAS for MSCSS are different from those used in NNS ^[35,36,37].

Remark 3.5. In the proof of Theorem 3.1, from computing the $N'(t),$ in order to offset the nonlinear items of the error system (2.3), the negative items of the nonlinear items have been designed in the control (3.1). In the proof of Theorem 3.2, in order to use Lemmas 2.2 and 2.3 to realize the FTAS for the MSCSS, the items $u_i^2(t)(i = 1, 2, 3, 4, 5, 6), n_1^2(t), m_i^2(t)(i = 1, 2, 3)$ have to be designed in the control (3.2).

4.   Numerical examples

In this section, two examples are given for showing the validity of our results.

Example 4.1. We are concerned with the system (2.1), the system (2.2) with (3.1) for $a_1 = 0.12, \; r_1 = 0.1, p_1 = 0.1, \; c_1 = 0.1, \; q_1 = 0.77, \; h_1 = 0.1, \; \xi_1 = 100, \; b_1 = 1, \; \eta = 1.$ So, $a_1 > 0.25(a_1+c_1)^2+0.5a_1(1+r_1+q_1), \; 0.25[1-0.5(1+r_1+q_1)]+(h_1-\xi_1)\Big(a_1[1-0.5(1+r_1+q_1)]-0.25(a_1+c_1)^2\Big) < 0, \; (-1+r_1+q_1)(0.5q_1-p_1-r_1-a_1)-0.5(a_1+c_1)^2 < 0, \; h_1-\xi_1 > 0, \; \Big[ 0.25r_1^2+a_1(-p_1+0.5q_1)\Big](-1+r_1+q_1)+0.5(-p_1+0.5q_1)(a_1+c_1)^2 < 0, \; 0.5(1+r_1) < q_1.$

Thus, by Theorem 3.1, the systems (2.1) and (2.2) can achieve the FTAS utilizing (3.1). In our example, without utilizing the past study methods in ^{[4,7,8,17,22]}, the controllers in our paper are quite different from those in ^{[1,4,7,19,31]}, so our result in Example 4.1 on FTAS cannot be dealt with their methods in ^{[1,4,8,17,31]}.

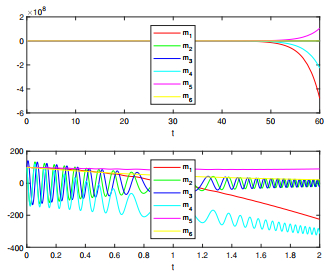
The curves of variables $m_i(t), i = 1, 2, 3, 4, 5, 6$ are shown in the following Figure 1, the curves of variables $n_i(t), i = 1, 2, 3, 4, 5, 6$ are shown in the following Figure 2, the error curves of drive-response system $u_i(t) = m_i(t)+n_i(t), i = 1, 2, 3, 4, 5, 6$ are shown in the following Figure 3.

Example 4.2. We are concerned about the systems (2.1) and (2.2) with (3.2) for $a_1 = 0.3, \; c_1 = 0.4, \; b_1 = 0.2, \; r_1 = 0.3, \; p_1 = 0.5, \; q_1 = 0.4, \; h_1 = 0.1, \; \eta_1 = 0.4, \; \eta_2 = 1.8, \; \eta_3 = 5, \; \lambda_1 = 2.4, \; \lambda_2 = 1.3, \; \lambda_3 = 1.3, \; \lambda_4 = 0.4, \; \lambda_5 = 0.5, \; \lambda_6 = 0.5.$ So, $\lambda_1 > 2, \; \lambda_2 > 1, \; \lambda_3 > 1, \; (2-\lambda_1)b_1^2(1-\lambda_2)-(\lambda_3-1)\Big\{(2-\lambda_1)(a_1-1+q_1+r_1)^2+(1-\lambda_2)[(c_1-a_1+r_1)^2+4(2-\lambda_1)\eta_1]\Big\} < 0, \; (1-q_1)^2\lambda_5+16\lambda_6\Big[(1-p_1)^2\lambda_4^2+\lambda_4\lambda_5(1+h_1)^2-\lambda_4\lambda_5\eta_2\Big] < 0.$ Thus, by Theorem 3.2, the systems (2.1) and (2.2) can attain the FTAS employing the controllers (3.2). In our discussion, without utilizing the past study methods in ^{[1,4,7,19,31]}, the controllers in our paper are very different from those in ^[4], the asymptotic synchronization was explored, while in our paper, the FTAS is considered, so our result in example 4.2 on FTAS cannot be dealt with the results of their methods in ^{[4,7,8,17,22]}.

The curves of variables $m_i(t), i = 1, 2, 3, 4, 5, 6$ are shown in the following Figure 4; the curves of variables $n_i(t), i = 1, 2, 3, 4, 5, 6$ are shown in the following Figure 5, the error curves of error system $u_i(t) = m_i(t)+n_i(t), i = 1, 2, 3, 4, 5, 6$ are shown in the following Figure 6.

5.   Conclusions

In this article, without adopting the past method, such as the LMI approach and FTST, by using the properties of the quadratic inequalities of one variable and utilizing the negative definiteness of the quadratic form of the matrix, two novel criteria assuring the FTAS for the discussed MSFOCSS are established. Our study method and results enriched and developed the study fields for FTAS of the MSCSS.

Use of Generative-AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Author contributions

Hu Tang: conceptualization, methodology, software, validation, formal analysis, writing-review and editing, project administration; Kaiyu Liu: conceptualization, methodology; Zhengqiu Zhang: conceptualization, methodology, validation, formal analysis, investigation, writing-original draft preparation. All authors have read and agreed to the published version of the manuscript.

Conflict of interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

Data availability statement

All data included in this study are available upon request by contact with the corresponding author.