Feasible robust Liu estimator to combat outliers and multicollinearity effects in restricted semiparametric regression model

1.   Introduction

The semiparametric regression model (SRM) is an appropriate tool to model a data set when the type of relationship between the dependent variable and some of the explanatory variables is linear parametric, but the link function of the dependent variable with other explanatory variables is not clear ^[1,2,3]. Consider the set of observations denoted as ${(y}_{1}, {\boldsymbol{x}}_{1}^{\mathrm{\top }}, {t}_{1})$, ..., ${(y}_{n}, {\boldsymbol{x}}_{n}^{\mathrm{\top }}, {t}_{n})$, which conform to the semiparametric regression model defined by

where ${y}_{i}$ is the value of the response variable for ith observation, ${\boldsymbol{x}}_{i}^{\mathrm{\top }} = \left({x}_{i1}, ..., {x}_{ip}\right)$represents a vector of explanatory variables, $\boldsymbol{\beta } = ({\beta }_{1}, ..., {\beta }_{p}{)}^{\mathrm{\top }}$ denotes a vector of the unknown parameters, and the ${t}_{i}\text{'}s$ are the observed points that match the boundaries of the domain $D\subset \mathbb{R}$ ^[4,5,6]. It is generally assumed that the unknown function $f(.)$ is a smooth function, while the ${\varepsilon }_{i}\text{'}s$ represent random errors that are considered to be independent of both $({x}_{i}, {t}_{i})$.

Since the semiparametric regression models combine both parametric and nonparametric components, the response variable depends on the explanatory variables in a linear form but has a nonlinear relationship with other explanatory variables, which are more flexible than standard linear regression models according to (1.1) ^[7,8,9]. There are different ways to estimate $\beta$ and $f(.)$. Some of the most important methods were introduced by ^[10,11].

The presence of nearly linear dependency among the columns of the design matrix $\boldsymbol{X} = ({\boldsymbol{x}}_{1}, ..., {\boldsymbol{x}}_{n}{)}^{\mathrm{\top }}$ is known as multicollinearity, and it is an issue that might arise in regression analysis. In this case, the matrix $\boldsymbol{S} = {\boldsymbol{X}}^{{\top }}\boldsymbol{X}$ contains one or more small eigenvalues, causing the regression coefficient estimations to be large in absolute value. The condition number is an effective measure for detecting the presence of multicollinearity. The matrix S is ill-conditioned under multicollinearity because its condition number tends to an extremely large value. Multicollinearity makes the ordinary least-squares estimator (OLSE) perform badly. Also, multicollinearity in data may cause confidence intervals to be too large for either the individual parameters or their linear mixes, which may lead to inaccurate predictions. Applying shrinkage estimators is widely used as an effective solution to address the issues arising from multicollinearity ^{[12,13,14,15]}. In this study, the shrinkage estimator, suggested by Liu ^[16], is applied to solve the problem of multicollinearity. Liu ^[16] combined the Stein type estimator with the conventional ordinary ridge regression estimator to derive the Liu estimator, as described in ^[17,18]. Other alternative approaches to addressing the issue of multicollinearity can be found in ^[19,20,21].

Besides the multicollinearity problem, another typical issue that arises in regression analysis is the presence of outliers, which are observations that do not follow the pattern of the main bulk of the data. Outliers can cause problems like inflated sums of squares, estimate bias, p-value confusion, and more. To combat these problems, robust regression methods are used. The ordinary least-squares estimator is known to be extremely affected by outliers, so the least trimmed squares approach is used to estimate both components of SRM in this research.

The breakdown point of an estimator is the fundamental measurement that is used to evaluate its robustness. This breakdown point concept refers to the percentage of outlying observations (up to 50 percent) that can contaminate the estimation promiscuously. In computational geometry, the investigation of effective algorithms for robust estimation methods has been an important field of study. Several researchers have examined the robust least median of squares (LMS) method, which is the hyperplane that minimizes the squared residual median ^[22]. Although the LMS estimator has been the subject of most publications on robust estimation in the field of linear models, Rousseeuw and Leroy ^[23] noted that LMS is not the optimal option due to its statistical features. They asserted that selecting the least trimmed squares is the better alternative option because both LTS and LMS have the same breakdown point, approximately 50%, but the objective function of LTS is smoother than LMS. Also, since LTS converges more quickly and is distributed asymptotically normally ^[22], it has superior statistical efficiency. For these reasons, LTS is a better choice as a starting point for two-step robust estimators such as the MM-estimator ^[24].

The main focus of this paper is to study a feasible generalized robust Liu estimator in a restricted semiparametric regression model. The organization of this article is as follows: Section 2 contains the classical estimator of a restricted semiparametric regression model based on the kernel method. After reviewing the concepts of Liu and least trimmed squares approaches in a semiparametric regression model, a new feasible robust Liu estimator in a restricted semiparametric regression model is suggested, and then its asymptotic bias and distributional covariance are derived in Section 3.Based on the obtained results, the feasible generalized robust Liu estimator is compared with the classical one in terms of the mean squared error. In Section 4, the efficiencies of the proposed estimators are assessed through Monte Carlo simulation experiments as well as with a real-world data example. Finally, some important findings are concluded in Section 5.

2.   Feasible type of the classical estimators in RSRM

The estimators conform to certain restrictions in classical estimators. Let us examine the semiparametric regression model

where $\boldsymbol{y} = ({y}_{1}, ..., {y}_{n}{)}^{\mathrm{\top }}, \boldsymbol{X} = ({\boldsymbol{x}}_{1}, ..., {\boldsymbol{x}}_{n}{)}^{\mathrm{\top }}, f\left(\boldsymbol{t}\right) = \left(f\right({t}_{1}), ..., f({t}_{n}){)}^{\mathrm{\top }}, \boldsymbol{\varepsilon } = ({\varepsilon }_{1}, ..., {\varepsilon }_{n}{)}^{\mathrm{\top }}.$

Generally, we assume that $\boldsymbol{\varepsilon }$ is a vector of disturbances that follows a distribution with $E\left(\boldsymbol{\varepsilon }\right) = {\bf{0}}$ and $E\left({\boldsymbol{\varepsilon }}^{{\top }}\boldsymbol{\varepsilon }\right) = {\sigma }^{2}\boldsymbol{V}$, where ${\sigma }^{2}$ is an unknown parameter and $\boldsymbol{V}$ is a symmetric and positive definite matrix. To estimate the linear part of model (2.1), we first remove the non-parametric effect by detrending. Given the assumption that β is known, a natural non-parametric estimator of f (.) is

in which k(.) is a kernel function. Following ^[25], by substituting $\widehat{f}$(t) for $f\left(\boldsymbol{t}\right)$ in Eq (2.1), the model may be reduced to

where $\widetilde {\boldsymbol{y}} = \left({\boldsymbol{I}}_{\boldsymbol{n}}-\boldsymbol{K}\right)\boldsymbol{y}$, $\widetilde {\boldsymbol{X}} = \left({\boldsymbol{I}}_{\boldsymbol{n}}-\boldsymbol{K}\right)\boldsymbol{X}$, and $\boldsymbol{K}$ is the smoother matrix with $\left(i, j\right)$-th component ${K}_{\omega }\left({t}_{i}, {t}_{j}\right)\mathrm{i}\mathrm{n}\; \mathrm{w}\mathrm{h}\mathrm{i}\mathrm{c}\mathrm{h}\;{K}_{\omega }\left( \cdot \right)$ is a kernel function of order $m$ with bandwidth parameter $\omega$. We can simply use the following transformations to change model (2.2) into a standard regression model by multiplying ${\boldsymbol{V}}^{-1/2}$ on the both sides as follows:

where $\stackrel{˘}{\boldsymbol{y}} = {\boldsymbol{V}}^{-1/2}\widetilde {\boldsymbol{y}}$, $\stackrel{˘}{\boldsymbol{X}} = {\boldsymbol{V}}^{-1/2}\widetilde {\boldsymbol{X}}$, and $\stackrel{˘}{\boldsymbol{\varepsilon }} = {\boldsymbol{V}}^{-1/2}\boldsymbol{\varepsilon }.$ Now, the estimation of $\boldsymbol{\beta }$ is performed using the generalized least-squares estimator (GLSE), which is known to be the best linear unbiased estimator

where $\boldsymbol{C} = {\widetilde {\boldsymbol{X}}}^{\mathrm{\top }}{\boldsymbol{V}}^{-1}\widetilde {\boldsymbol{X}}$.

In applications, the matrix V is not known. Therefore, ${\widehat{\boldsymbol{\beta }}}_{GLS}$ in Eq (2.3) is not applicable because it is a function of covariance matrix (V) which is not known. To solve this issue, we have to utilize a two-stage process and implement a feasible generalized least-squares estimator (FGLSE) by replacing the unknown parameter V with a suitable estimator ^[26], $\boldsymbol{S} = \frac{1}{n-p}(\widetilde {\boldsymbol{y}}-\widetilde {\boldsymbol{X}}{\widehat{\boldsymbol{\beta }}}_{LS}){\left(\widetilde {\boldsymbol{y}}-\widetilde {\boldsymbol{X}}{\widehat{\boldsymbol{\beta }}}_{LS}\right)}^{{\top }}$, which is a consistent estimator, as follows:

where ${\boldsymbol{C}}_{F} = {\widetilde {\boldsymbol{X}}}^{{\top }}{\boldsymbol{S}}^{-1}\widetilde {\boldsymbol{X}}$, and ${\widehat{\boldsymbol{\beta }}}_{LS}$ is the ordinary least-squares estimator ${\left({\widetilde {\boldsymbol{X}}}^{{\top }}\widetilde {\boldsymbol{X}}\right)}^{-1}{\widetilde {\boldsymbol{X}}}^{{\top }}\widetilde {\boldsymbol{y}}$. As demonstrated in Zellner ^[26], ${\widehat{\boldsymbol{\beta }}}_{FGLS} = {\widehat{\boldsymbol{\beta }}}_{GLS}+{O}_{p}\left({n}^{-1}\right)$, and consequently ${\surd n(\widehat{\boldsymbol{\beta }}}_{FGLS}-\beta)$ and ${\surd n(\widehat{\boldsymbol{\beta }}}_{FGLS}-\beta)$have the same normal asymptotical distribution, and so ${\mathrm{V}\mathrm{a}\mathrm{r}(\widehat{\boldsymbol{\beta }}}_{FGLS}) = {\boldsymbol{C}}_{F}^{-1}+o({n}^{-1})$, where ${O}_{p}\left({n}^{-1}\right)$ indicates an amount which is of order ${n}^{-1}$ in probability and $o\left({n}^{-1}\right)$ indicates a quantity of a higher order of smallness than ${n}^{-1}$.

Interestingly, another method to handle the strong and extremely strong multicollinearity problems is to obtain the estimators under particular constraints on the unknown parameters, which may be exact or stochastic (see ^[27,28,29] for more details). By applying some constraints on the parameter space of the linear part, Durbin ^[30], Theil and Goldberger ^[31], and Theil ^[32] proposed the ordinary mixed estimator (OME) for the vector of the regression coefficient. Assume that we had prior knowledge regarding $\beta$ in the sense of non-stochastic exact constraints ^[33,34,35], as follows:

where R is a known matrix $q\times \; \mathrm{p}$ of prior information of rank $q < p$ and r is a known $q\times \; 1$ vector. This restriction should come from an outside source (it might be determined, for example, by an outside source of information or an expert). Thus, when the regression parameters are restricted by a space of linear constraints non-stochastically represented by independent prior information, we provide the instruments necessary to compute the risk of estimators. Next, the performances of the new constrained estimators and the classical estimators may be compared under certain conditions. We show that the innovative constrained estimators outperform the classical ones in terms of least-risk functions, assuming linear restrictions. In these circumstances, certain non-sample information (a previous constraint on the parameters) may exist; they are often presented to the model as constraints. Compared to typical estimators, the restricted estimation performs better, and so, in this work, the restricted semiparametric regression model (RSRM) is fitted to the data set. The feasible generalized least-squares restricted estimator (FGLSRE) is derived by imposing a linear restriction as follows:

As it is known, the covariance matrix estimation of ${\widehat{\boldsymbol{\beta }}}_{FGLS}$ is equal to ${\sigma }^{2}{\boldsymbol{C}}_{F}^{-1}$. So, the FGLSE and its covariance matrix are significantly influenced by the features of matrix ${\boldsymbol{C}}_{F}$. The FGLS estimators gain susceptibility to various errors when ${\boldsymbol{C}}_{F}$ is ill-conditioned. Also, some of the estimations of the regression coefficients, for instance, might have incorrect signs or be statistically insignificant; this could lead to unstable estimators, which are characterized by large confidence intervals for the specific parameters. Making valid statistical inferences becomes challenging in the presence of these errors, and so a biased estimation technique is introduced and utilized for RSRM under the multicollinearity problem.

3.   Feasible robust Liu estimator in RSRM

Multicollinearity leads to ${\boldsymbol{X}}^{{\top }}\boldsymbol{X}$ being ill-conditioned with a large condition number. When the signal to noise ratio ${\boldsymbol{\beta }}^{{\top }}\boldsymbol{\beta }/{\sigma }^{2}$ is small and the condition number of ${\boldsymbol{X}}^{{\top }}\boldsymbol{X}$ is large, the least-squares estimator is most severely affected by multicollinearity. In this situation, the high level of data noise is enlarged by ${\left({\boldsymbol{X}}^{{\top }}\boldsymbol{X}\right)}^{-1}$, making the least-squares estimator highly unstable. To solve this drawback, Hoerl and Kennard ^[36] proposed the ridge estimator ${\widehat{\boldsymbol{\beta }}}_{k} = {({\boldsymbol{X}}^{{\top }}\boldsymbol{X}+k\boldsymbol{I})}^{-1}{\boldsymbol{X}}^{{\top }}\boldsymbol{y}$ in the standard linear regression model $\boldsymbol{y} = \boldsymbol{X}\boldsymbol{\beta }+\boldsymbol{\varepsilon }$ with $E\left(\boldsymbol{\varepsilon }\right) = {\bf{0}}$ and $E\left({\boldsymbol{\varepsilon }}^{{\top }}\boldsymbol{\varepsilon }\right) = {\sigma }^{2}\boldsymbol{I}$, and it has become the most often used method for combating the multicollinearity problem that causes the least squares estimator to fail. Indeed, the ridge method solves the multicollinearity problem by adding a small non-stochastic constant k to the diagonal elements of ${\boldsymbol{X}}^{{\top }}\boldsymbol{X}$ to decrease its condition number. In practical use, the biasing parameter k in ridge approach is typically rather modest. It is obvious that the condition number of ${\boldsymbol{X}}^{{\top }}\boldsymbol{X}+k\boldsymbol{I}$ is a decreasing function of k. Thus, high values of k are needed to achieve small-scale control over the condition number of ${\boldsymbol{X}}^{{\top }}\boldsymbol{X}+k\boldsymbol{I}$. Because of this, the small k selected in practice may not be sufficiently big to solve the severe multicollinearity problem of ${\boldsymbol{X}}^{{\top }}\boldsymbol{X}$. So, the resultant ridge estimation may still be unstable since ${\boldsymbol{X}}^{{\top }}\boldsymbol{X}+k\boldsymbol{I}$ has remained ill-conditioned. Furthermore, despite its practical effectiveness, the ridge estimator is a complicated function of k. Although the Stein-type estimator ${\widehat{\boldsymbol{\beta }}}_{c} = {c\left({\boldsymbol{X}}^{{\top }}\boldsymbol{X}\right)}^{-1}{\boldsymbol{X}}^{{\top }}\boldsymbol{y}$ is a linear function of c, the shrinkage of each element of ${\widehat{\boldsymbol{\beta }}}_{c}$ is the same. To address these issues, Liu ^[12] proposed a new biased estimator ${\widehat{\boldsymbol{\beta }}}_{d} = {({\boldsymbol{X}}^{{\top }}\boldsymbol{X}+\boldsymbol{I})}^{-1}{(\boldsymbol{X}}^{{\top }}\boldsymbol{y}+d\widehat{\boldsymbol{\beta }}$) by combining the advantages of the ridge and Stein-type estimators, which effectively solved the problem of ill-conditioning in standard regression model, where 0 < d < 1 is a biasing parameter and $\widehat{\boldsymbol{\beta }} = {\left({\boldsymbol{X}}^{{\top }}\boldsymbol{X}\right)}^{-1}{\boldsymbol{X}}^{{\top }}\boldsymbol{y}$. It is obvious that when d = 1, ${\widehat{\boldsymbol{\beta }}}_{d}$ = $\widehat{\boldsymbol{\beta }}$.

According to ^[12] the mean squared error (MSE) of the Liu estimator is obtained by

where ${\alpha }_{j}^{2}$ corresponds to the jth element of $\boldsymbol{\alpha } = {\boldsymbol{\varGamma }}^{{\top }}\boldsymbol{\beta }$ and $\boldsymbol{\varGamma }$ is an orthogonal matrix such that ${\boldsymbol{C}}_{F} = \boldsymbol{\varGamma }\boldsymbol{\varLambda }{\boldsymbol{\varGamma }}^{\boldsymbol{\top }}$, in which $\boldsymbol{\varLambda } = diag\left({\lambda }_{1}, ..., {\lambda }_{p}\right)$ contains the eigenvalues of matrix ${\boldsymbol{C}}_{F}.$ Consequently, the biasing parameter d is chosen by minimizing $MSE\left({\widehat{\boldsymbol{\beta }}}_{d}\right)$ as follows:

where ${\widehat{\sigma }}_{FGLS}^{2}$ and ${\widehat{\alpha }}_{jFGLS}^{2}$ are the unbiased estimators of ${\sigma }^{2}$ and ${\alpha }_{j}$ based on FGLSE, respectively, i.e., ${\widehat{\sigma }}_{FGLS}^{2} = \frac{1}{n-p}{\left(\boldsymbol{y}-\widetilde {\boldsymbol{X}}{\widehat{\boldsymbol{\beta }}}_{FGLS}\right)}^{{\top }}{\boldsymbol{S}}^{-1}\left(\boldsymbol{y}-\widetilde {\boldsymbol{X}}{\widehat{\boldsymbol{\beta }}}_{FGLS}\right)$ and ${\widehat{\boldsymbol{\alpha }}}_{FGLS} = {{\boldsymbol{\varGamma }}^{{\top }}\widehat{\boldsymbol{\beta }}}_{FGLS}$.

The feasible generalized least-squares Liu estimator (FGLSLE) can be extended by ^[37,38,39] as follows:

where ${\boldsymbol{F}}_{d} = ({\boldsymbol{C}}_{F}+\boldsymbol{I}{)}^{-1}\left({\boldsymbol{C}}_{F}+d\boldsymbol{I}\right)$.

Based on the fact that ${\boldsymbol{F}}_{d}$ and ${\boldsymbol{C}}_{F}^{{\bf{-1}}}$ are commutative, the feasible generalized least-squares restricted Liu estimator (FGLSRLE) can be obtained for RSRM as follows ^[40,41,42]:

Lemma 3.1. If β satisfies the linear restriction Rβ = r, then the properties (bias, covariance, and mean squared error) of the suggested estimator can be calculated directly as follows:

where $\boldsymbol{H} = {\boldsymbol{C}}_{F}^{-1}\left(\boldsymbol{I}-{\boldsymbol{R}}^{\mathrm{\top }}{\left(\boldsymbol{R}{\boldsymbol{C}}_{F}^{-1}{\boldsymbol{R}}^{\mathrm{\top }}\right)}^{-1}\boldsymbol{R}{\boldsymbol{C}}_{F}^{-1}\right)$.

Theorem 3.1. The MSE of FGLSRLE under the linear restriction Rβ = r can be given by

where ${m}_{jj}$ is the jth diagonal element of the matrix $\boldsymbol{M} = {\boldsymbol{\varGamma }}^{{\top }}\boldsymbol{H}\boldsymbol{\varGamma }$.

Proof. Using $({\boldsymbol{C}}_{\boldsymbol{F}}+\boldsymbol{I}{)}^{-1} = \boldsymbol{\varGamma }(\boldsymbol{\varLambda }+\boldsymbol{I}{)}^{-1}{\boldsymbol{\varGamma }}^{{\top }}$ and $\left({\boldsymbol{C}}_{F}+d\boldsymbol{I}\right) = \boldsymbol{\varGamma }\left(\boldsymbol{\varLambda }+d\boldsymbol{I}\right){\boldsymbol{\varGamma }}^{{\top }}$, we can write

Also, from $({\boldsymbol{C}}_{F}+\boldsymbol{I}{)}^{-2} = \boldsymbol{\varGamma }(\boldsymbol{\varLambda }+\boldsymbol{I}{)}^{-2}{\boldsymbol{\varGamma }}^{{\top }}$, we have

So, the proof is completed. ■

As an important result of Theorem 3.1, the optimal value of the biasing parameter d can be obtained by differentiating the MSE function of GLSRLE as a function of d (same as $g$(d)) with respect to d, and solve it by setting the derivative equal to zero to extract the optimal value of d. Via direct calculation, we have

So, it can be written

According to the fact that ${g}^{{{'}}{{'}}}\left(d\right)$ is positive for all values of d, we can conclude the obtained extremum value of d minimizes the MSE function of GLSRLE. Now, for practical aspects, the following estimator can be used for the optimal d in applications:

where ${\widehat{\sigma }}_{FGLSR}^{2}$ and ${\widehat{\alpha }}_{jFGLSR}^{2}$ are the unbiased estimators of ${\sigma }^{2}$ and ${\alpha }_{j}$ based on GLSRE, respectively, i.e., ${\widehat{\sigma }}_{FGLSR}^{2} = \frac{1}{n-(p+q)}{\left(\boldsymbol{y}-\widetilde {\boldsymbol{X}}{\widehat{\boldsymbol{\beta }}}_{FGLSR}\right)}^{{\top }}{\boldsymbol{S}}^{-1}\left(\boldsymbol{y}-\widetilde {\boldsymbol{X}}{\widehat{\boldsymbol{\beta }}}_{FGLSR}\right)$ and ${\widehat{\boldsymbol{\alpha }}}_{FGLSR} = {{\boldsymbol{\varGamma }}^{{\top }}\widehat{\boldsymbol{\beta }}}_{FGLSR}$, in which

As was mentioned earlier, outlier observations have the potential to significantly corrupt the least-squares estimators and all of the estimators based on it due to their significant impact on the objective function. The robust regression approach is a broad term that encompasses various estimating approaches. Least trimmed squares is a robust regression method introduced by ^[43]. LTS seeks to tackle this issue by minimizing the sum of the lowest h squared residuals following the removal of a specific percentage of extreme values. In this case, h serves as a threshold, and the proportion of the outlying data is represented by the ratio α = (n − h)/n.

Typically, the value of h can be taken as h = [[n(1 − α)]], where [[x]] stands for the ceiling of x. Some other authors suggest to take $h = \left[n/2\right]+\left[(p+1)/2\right]$, $h = \left[n\left(1-\alpha \right)\right]+\left[\alpha \left(p+1\right)\right]$, $\mathrm{o}\mathrm{r}h = \left[n\left(1-\alpha \right)\right]+1$ (see ^[44]). The LTS estimator is computed by solving the $\left(\begin{array}{c}n\\ h\end{array}\right)$ total least-squares fits combinations of the index set {1, ..., n}. Thus, for large values of sample size, finding the global minimum in the objective function of the LTS method takes time and space. To accelerate the process of finding the solution (LTS fit), we use an analogue of the FAST-LTS algorithm extended by ^[24].

Let ${z}_{i}$ represent the indicator variable that signifies whether or not observation $i$ is regarded as a normal observation. The optimization problem of a feasible robust estimator based on the LTS approach in RSRM can be developed as follows:

where Z is the diagonal matrix with diagonal elements $\boldsymbol{z} = {({z}_{1}.\dots., {z}_{n})}^{\top }$, ${e = (1.\dots.1)}_{n\times 1}^{\mathrm{\top }}$, and $h$is a positive integer. The resultant estimator is the feasible generalized least trimmed squares restricted estimator (FGLTSRE), which is provided by

where ${\boldsymbol{C}}_{F}\left(\boldsymbol{z}\right) = {\widetilde {\boldsymbol{X}}}^{{\top }}{\boldsymbol{S}}^{-1/2}{\boldsymbol{Z}\boldsymbol{S}}^{-1/2}\widetilde {\boldsymbol{X}}\;\mathrm{a}\mathrm{n}\mathrm{d}\;{\widehat{\boldsymbol{\beta }}}_{FGLTS}\left(\boldsymbol{z}\right) = {{\boldsymbol{C}}_{F}\left(z\right)}^{-1}{\widetilde {\boldsymbol{X}}}^{{\top }}{\boldsymbol{S}}^{-1/2}{\boldsymbol{Z}\boldsymbol{S}}^{-1/2}\widetilde {\boldsymbol{y}}$.

Now, we aim to implement the robust estimators obtained previously via the Liu idea to extract the novel feasible robust Liu estimator that is resistant to the existence of multicollinearity and outliers in the data set. The feasible generalized least trimmed squares restricted Liu estimator (FGLTSRLE) for RSRM using a two stages estimator for d and β can be extended as follows:

where ${\lambda }_{j}\left(\boldsymbol{z}\right)$ is the jth eigenvalue of matrix ${\boldsymbol{C}}_{F}\left(\boldsymbol{z}\right) = \boldsymbol{\varGamma }\left(\boldsymbol{z}\right)\boldsymbol{\varLambda }\left(\boldsymbol{z}\right){\boldsymbol{\varGamma }\left(\boldsymbol{z}\right)}^{{\top }}$, ${m}_{jj}\left(\boldsymbol{z}\right)$ is the jth diagonal element of the matrix $\boldsymbol{M}\left(\boldsymbol{z}\right) = {\boldsymbol{\varGamma }\left(\boldsymbol{z}\right)}^{{\top }}\boldsymbol{H}\left(\boldsymbol{z}\right)\boldsymbol{\varGamma }\left(\boldsymbol{z}\right)$ in which $\boldsymbol{H}\left(\boldsymbol{z}\right) = {\boldsymbol{C}\left(\boldsymbol{z}\right)}^{-1}\left(\boldsymbol{I}-{\boldsymbol{R}}^{\mathrm{\top }}{\left({\boldsymbol{C}\left(\boldsymbol{z}\right)}^{-1}{\boldsymbol{R}}^{\mathrm{\top }}\right)}^{-1}{\boldsymbol{R}\boldsymbol{C}\left(\boldsymbol{z}\right)}^{-1}\right)$, ${\widehat{\alpha }}_{jFGLTSR}^{2}\left(\boldsymbol{z}\right)$ is the jth element of ${\widehat{\boldsymbol{\alpha }}}_{FGLTSR}\left(\boldsymbol{z}\right) = {\boldsymbol{\varGamma }}^{{\top }}{\widehat{\boldsymbol{\beta }}}_{FGLTSR}\left(\boldsymbol{z}\right)$, and ${\boldsymbol{F}}_{{\widehat{d}}_{LTS}}\left(\boldsymbol{z}\right) = ({\boldsymbol{C}}_{F}\left(\boldsymbol{z}\right)+\boldsymbol{I}{)}^{-1}\left({\boldsymbol{C}}_{F}\left(\boldsymbol{z}\right)+{\widehat{d}}_{LTS}\boldsymbol{I}\right)$.

Theorem 3.2. The estimation of the MSE of the suggested estimator (5.2) under the linear restriction Rβ = r can be given by

Proof. The proof directly follows by mimicking the proof of Theorem 3.1. ■

Lemma 3.2. The covariance matrix of estimator ${\widehat{\boldsymbol{\beta }}}_{FGLTSRL}\left(d.\boldsymbol{z}\right)$ is smaller compared to the covariance of estimator ${\widehat{\boldsymbol{\beta }}}_{FGLTSR}\left(\boldsymbol{z}\right)$ if and only if

where $\tau = \frac{1}{1+d}$ and the ${\mu }_{ii}$'s are the eigenvalues of matrix $\boldsymbol{H}{\left(\boldsymbol{z}\right)}^{-1}\boldsymbol{N}\left(\boldsymbol{z}\right)$, in which $\boldsymbol{N}\left(\boldsymbol{z}\right) = {\boldsymbol{C}}_{F}\left(\boldsymbol{z}\right)\boldsymbol{H}\left(\boldsymbol{z}\right)+\boldsymbol{H}\left(\boldsymbol{z}\right){\boldsymbol{C}}_{F}\left(\boldsymbol{z}\right)$.

Proof. The covariance matrix of the mentioned estimators can be written as

So, the difference ${\Delta }^{\mathrm{*}} = \mathrm{C}\mathrm{o}\mathrm{v}\left({\widehat{\boldsymbol{\beta }}}_{FGLTSR}\left(\boldsymbol{z}\right)\right)-\mathrm{C}\mathrm{o}\mathrm{v}\left({\widehat{\boldsymbol{\beta }}}_{FGLTSRL}\left(d.\boldsymbol{z}\right)\right)$ can be expressed as follows:

where $\boldsymbol{U}\left(\boldsymbol{z}\right) = {\left({\boldsymbol{C}}_{F}\left(\boldsymbol{z}\right)+\boldsymbol{I}\right)}^{-1}$, $\tau = \frac{1}{1+d}$, and $\boldsymbol{N}\left(\boldsymbol{z}\right) = {\boldsymbol{C}}_{F}\left(\boldsymbol{z}\right)\boldsymbol{H}\left(\boldsymbol{z}\right)+\boldsymbol{H}\left(\boldsymbol{z}\right){\boldsymbol{C}}_{F}\left(\boldsymbol{z}\right)$ is a symmetric matrix. Since $\boldsymbol{H}\left(\boldsymbol{z}\right) = \boldsymbol{L}{\left(\boldsymbol{z}\right)}^{\mathrm{\top }}\boldsymbol{L}\left(\boldsymbol{z}\right)$, in which

and $\mathrm{R}\mathrm{a}\mathrm{n}\mathrm{k}\left(\boldsymbol{L}\left(\boldsymbol{z}\right)\right) = p-q < n$, then $\boldsymbol{H}\left(\boldsymbol{z}\right)$ is a positive definite matrix. Therefore, a nonsingular matrix Q exists such that ${\boldsymbol{Q}}^{\mathrm{\top }}\boldsymbol{H}\left(\boldsymbol{z}\right)\boldsymbol{Q} = \boldsymbol{I}$ and ${\boldsymbol{Q}}^{\mathrm{\top }}\boldsymbol{N}\left(\boldsymbol{z}\right)\boldsymbol{Q} = \boldsymbol{P}\left(\boldsymbol{z}\right)$, where $\boldsymbol{P}\left(\boldsymbol{z}\right)$ is a diagonal matrix and its diagonal elements are the roots of the polynomial equation $\left|\boldsymbol{H}{\left(\boldsymbol{z}\right)}^{-1}\boldsymbol{N}\left(\boldsymbol{z}\right)-\mu \boldsymbol{I}\right| = 0$ (see Graybill ^[45], pp. 408; and Harville ^[46] pp. 563), and so we have

where $\boldsymbol{I}+\tau \boldsymbol{P}\left(\boldsymbol{z}\right) = \mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}(1+\tau {\mu }_{11}, \dots, 1+\tau {\mu }_{pp})$. And, since $\boldsymbol{N}\left(\boldsymbol{z}\right) = {\boldsymbol{C}}_{F}\left(\boldsymbol{z}\right)\boldsymbol{H}\left(\boldsymbol{z}\right)+\boldsymbol{H}\left(\boldsymbol{z}\right){\boldsymbol{C}}_{F}\left(\boldsymbol{z}\right)\ne {\bf{0}}$, then at least one of diagonal elements of $\boldsymbol{P}\left(\boldsymbol{z}\right)$ is nonzero. Assume ${\mu }_{ii} < 0$ for at least one i. Then, the positive definiteness of $\boldsymbol{I}+\tau \boldsymbol{P}\left(\boldsymbol{z}\right)$ is ensured by

As a result, for every i = 1, ..., p, $1+\tau {\mu }_{ii} > 0$, and $\boldsymbol{I}+\tau \boldsymbol{P}\left(\boldsymbol{z}\right)$ is a positive definite matrix. Therefore, ${\Delta }^{*}$ is turned into a positive definite matrix. It is now clear that, if and only if (3.15) fulfills the criteria, ${\widehat{\boldsymbol{\beta }}}_{FGLTSRL}\left(d.\boldsymbol{z}\right)$ has a smaller variance than ${\widehat{\boldsymbol{\beta }}}_{FGLTSR}\left(\boldsymbol{z}\right)$. ■

Next the necessary and sufficient condition is provided under which the FGLTSRLE in RSRM is preferable to the FGLTSRE in the sense of the mean squared error matrix (MSEM). The following lemma is required for the demonstration of the forthcoming theorem.

Lemma 3.3. (Farebrother ^[47]) Let A be an p×p positive definite matrix, b be an (p×1) nonzero vector, and δ a positive scalar value. Then, δA−bb^⊤ is non-negative if and only if ${\bf{b}}^{{\top }}{\bf{A}}^{-1}{\bf{b}}\le {\rm{ \mathsf{ δ} }}$.

Theorem 3.3. Let us be given the estimator ${\widehat{\boldsymbol{\beta }}}_{FGLTSRL}\left(d.\boldsymbol{z}\right)$ under the linear regression model with true restrictions Rβ = r. ${\widehat{\boldsymbol{\beta }}}_{FGLTSRL}\left({\widehat{d}}_{LTS}.\boldsymbol{z}\right)$ is MSEM superior to ${\widehat{\boldsymbol{\beta }}}_{FGLTSR}\left(\boldsymbol{z}\right)$ if and only if

where $\boldsymbol{G}\left(\boldsymbol{z}\right) = \boldsymbol{H}\left(\boldsymbol{z}\right)+\tau \boldsymbol{N}\left(\boldsymbol{z}\right)$.

Proof. We prove the necessary and sufficient conditions for the MSEM difference $\Delta = \mathrm{M}\mathrm{S}\mathrm{E}\mathrm{M}\left({\widehat{\boldsymbol{\beta }}}_{FGLTSR}\left(\boldsymbol{z}\right)\right)-\mathrm{M}\mathrm{S}\mathrm{E}\mathrm{M}\left({\widehat{\boldsymbol{\beta }}}_{FGLTSRL}\left(d.\boldsymbol{z}\right)\right)$, where

According to the proof of Lemma 3.2., the difference $\Delta$ can be expressed as follows:

where $\boldsymbol{G}\left(\boldsymbol{z}\right) = \boldsymbol{H}\left(\boldsymbol{z}\right)+\tau \boldsymbol{N}\left(\boldsymbol{z}\right)$. Now, by using Lemma 3.3 and supposing that condition (3.15) is met, it is concluded that $\Delta$ is positive definite if and only if

■

Theorem 3.4. Let us be given the estimator ${\widehat{\boldsymbol{\beta }}}_{FGLSRL}\left(d\right)$ under the linear regression model with true restrictions Rβ = r. ${\widehat{\boldsymbol{\beta }}}_{FGLSRL}\left(d\right)$ is MSEM superior to ${\widehat{\boldsymbol{\beta }}}_{FGLSR}$ if and only if

where $\boldsymbol{G} = \boldsymbol{H}+\tau \boldsymbol{N}$ and $\boldsymbol{N} = {\boldsymbol{C}}_{F}\boldsymbol{H}+\boldsymbol{H}{\boldsymbol{C}}_{F}$.

Proof. The desired result is simply obtained, similar to the proof of Theorem 3.4. ■

4.   Illustrative experiments

To demonstrate the advantages of the improved techniques that have been proposed for the restricted semiparametric regression model in the presence of the multicollinearity and outlier problems simultaneously, we examine the theoretical findings using some numerical experiments in this section. We evaluate the performance of the proposed techniques in both a real-world data set and Monte Carlo simulation schemes.

4.1.   The Monte Carlo simulation studies

We conduct a numerical analysis to evaluate the precision of our robust estimators for RSRM when dealing with contaminated data sets with outliers and multicollinearity. In each replication, the regressors are randomly generated using the following structure: Indeed, in order to reach the various levels of multicollinearity, we used the approach proposed by ^[48,49], in which the explanatory variables were constructed using a device with 150 observations and ${10}^{3}$ iterations, based on the model described below:

where ${z}_{ij}$ are independent standard normal pseudo-random variables, and $\gamma$ is chosen such that the correlation between any two explanatory variables is equal to ${\gamma }^{2}$. These variables are subsequently normalized to ensure that ${\boldsymbol{X}}^{{\top }}\boldsymbol{X}$ and ${\boldsymbol{X}}^{{\top }}\boldsymbol{y}$ are in correlation forms. Four distinct sets of correlation values are investigated, specifically for $\gamma = \; 0.25, 0.50, \; 0.75, \; \mathrm{a}\mathrm{n}\mathrm{d}\; 0.95$. For the dependent variable, n observations are then calculated by

where

in which

and

where ${\chi }_{m}^{2}\left(\delta \right)$ represents the m-degree of freedom non-central Chi-squared distribution with non-centrality parameter δ. The primary motivation behind selecting such structure for producing the error terms is to corrupt the data set and assess the resistance of the suggested techniques. In fact, we designated the last n−h error terms as independent non-central Chi-squared distributed random variables and the first h error terms as dependent normal random variables. The non-centrality parameter leads to that the outliers lie on one side of the real regression model and bias the non-robust estimations. For the restriction, we consider the following stochastic linear restrictions:

For estimating the nonparametric part of model (4.1), f (.), the weight proposed by ^[50] with the Gaussian kernel is used as follows:

Also, the cross-validation (C.V.) approach is applied for obtaining the optimum value of bandwidth $\omega$, which minimizes the C.V. criterion.

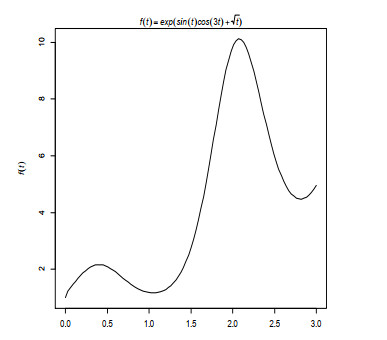
The non-parametric component of model (4.1) is presented in Figure 1. This wavy function is challenging to predict and offers a useful example for testing the proposed estimation techniques. All calculations were performed with R 4.3.1, the statistical software program. Tables 1–14 present a summary of the results. After iterating the process for all simulations, the minimum, maximum, mean, median, and standard deviation values of MSEs for the linear and non-linear estimators were reported in Tables 1 & 2, respectively, where

in which $\hat{\beta}_{(i)}^{(\mathrm{m})}$ and $\hat{f}_{({\rm{i}})}^{(\mathrm{m})}$ are the ith estimators of the linear and non-linear parts (i = 1, ..., 4) obtained in the mth iteration for all of the four proposed approaches, and $\|\boldsymbol{v}\|_2^2 = \sum_{i = 1}^q v_i^2$ for $\boldsymbol{v} = ({v}_{1}, ..., {v}_{p}{)}^{\mathrm{\top }}$. Also, PCDO is the percentage of the contaminated data with outliers (PCDO = 100 ×$\frac{n-h}{n}$%).

Figure 2 shows the estimations of the non-linear part of model (4.1) using the proposed methods. In this figure, the nonparametric function is estimated by the kernel method after estimation of the linear part of model (4.1) by FGLSRE, FGLTSRE, FGLSRLE, and FGLTSRLE, respectively. To save space, the results have been only reported for n = 150 with PCDO = 25%, 33%, and 50%, and $\gamma = 0.95$. From Figure 2, it is evident that the non-robust methods are completely corrupted by the outliers, especially for large values of PCDO.

4.2.   Real-world data analysis

We analyze the hedonic pricing of housing features in order to motivate the challenge of linearly restricted estimations in the semiparametric regression model. Lot size has a big impact on housing costs. Ho ^[51] fit this data set using semiparametric least squares. The information is based on 92 detached houses that were sold in the Ottawa region in 1987. Here is how the variables are defined: The sale price (SP) is the dependent variable, while the lot size (lot area = LT), square footage of housing (SFH), average neighborhood income (ANI), distance to the highway (DHW), garage availability (GAR), and fireplace (FP) are the independent variables. At first, the pure parametric model is fit as follows:

We use the added-variable charts to intuitively determine the parametric and nonparametric components of the model (see Sheather ^[52] for more details). Added-variable plots allow us to examine each predictor's influence graphically after adjusting for the effects of the other explanatory variables. Based on the analysis of the added-variable plot (Figure 3), we identify ANI as a nonparametric component. Therefore, the SRM is specified accordingly:

The "mctest" package in R is used to detect multicollinearity in the design matrix, producing the following results. The Farrar-Glauber test and other pertinent tests for multicollinearity are provided.

The correlation graphs are displayed in Figure 4 for the real data set. It is evident from the output above and Figure 4 that the independent variables in the real data set under investigation exhibit substantial multicollinearity. So, to address the multicollinearity issue, the suggested estimating techniques must be used.

The restriction $\boldsymbol{R}\boldsymbol{\beta } = \boldsymbol{r}$ may be identified as follows based on a basic investigation of the semiparametric regression model (4.2) using a robust Liu estimator:

Now, the linear hypothesis $\boldsymbol{R}\boldsymbol{\beta } = \boldsymbol{r}$ is examined in the framework of the restricted semiparametric regression model (4.2). The test statistic is computed as follows under $\boldsymbol{R}\boldsymbol{\beta } = \boldsymbol{r}$:

where ${\widehat{\bf{\Sigma }}}_{\widehat{\boldsymbol{\beta }}} = {\widehat{s}}^{2}{\left({\widetilde {\boldsymbol{X}}}^{{\top }}{\boldsymbol{S}}^{-1}\widetilde {\boldsymbol{X}}\right)}^{-1}$, in which ${\widehat{s}}^{2} = \frac{1}{n-p}{\left(\boldsymbol{y}-\widetilde {\boldsymbol{X}}{\widehat{\boldsymbol{\beta }}}_{FGLS}\right)}^{{\top }}{\boldsymbol{S}}^{-1}\left(\boldsymbol{y}-\widetilde {\boldsymbol{X}}{\widehat{\boldsymbol{\beta }}}_{FGLS}\right)$. Consequently, the restricted estimators are obtained. Table 15 shows a brief evaluation of the proposed estimators. In this table, the values of $\mathrm{M}\widehat{\mathrm{S}}\mathrm{E}\; \mathrm{a}\mathrm{n}\mathrm{d}\; {\mathrm{R}}^{2}$ are calculated, in which ${\mathrm{R}}^{2} = 1-\frac{\mathrm{R}\mathrm{S}\mathrm{S}}{{\mathrm{S}}_{\mathrm{Y}\mathrm{Y}}}$ is the coefficient of determination of the model, where $\mathrm{R}\mathrm{S}\mathrm{S} = {\sum }_{i = 1}^{n}{({y}_{i}-{\widehat{y}}_{i})}^{2}$ is the residual sum of squares and ${\widehat{y}}_{i} = {x}_{i}\widehat{\beta }+\widehat{f}{(t}_{i})$. Compared to the other procedures, FGLTSRLE seems to be accurately effective based on the results that were obtained.

Following the proposed estimations of the linear component of the model (4.2), the estimations on the non-parametric function by kernel smoothing is shown in Figure 5. For estimation of the nonparametric effect, at first we estimated the parametric effects by one of the proposed methods, and then the kernel approach was applied to fit ${SP}_{i}-{x}_{i}^{\mathrm{\top }}\widehat{\beta }$on ${ANI}_{i}, i = 1, \dots, n$ for all proposed linear estimators, where ${x}_{i}^{\mathrm{\top }} = ({LT}_{i}, {SFH}_{i}, {FP}_{i}, {DHW}_{i}, {GAR}_{i})$. Table 15 and Figure 5 demonstrate how the Liu type of robust and non-robust estimators outperform non-Liu forms in both parametric and nonparametric estimations due to the presence of multicollinearity in the design matrix. Furthermore, robust estimators outperform non-robust estimators in model prediction since the data set contains some outlier observations.

5.   Conclusions

In this research, Liu and non-Liu types of the feasible generalized restricted robust estimator are suggested in a semiparametric regression model when some additional linear constraints held on the linear parameter space and the variance matrix of the error terms were unknown. We introduced robust Liu estimators in the presence of multicollinearity among column vectors of the design matrix of a semiparametric regression model and outliers in the data set. We also introduced some new estimators of d by minimizing the mean squared error of the proposed estimators. After extracting the MSEM superiority condition of a feasible generalized least trimmed squares restricted Liu estimator over a non-Liu type based on some theorems, comprehensive Monte-Carlo simulation experiments and a real data analysis were conducted to evaluate the effectiveness of the suggested estimators. The numerical experiments illustrated that the suggested methods can be effectively implemented to predict the dependent variable of restricted SRMs without being affected by the corruptive impact of multicollinearity or outlier issues. As a good topic for future research, it is proposed to derive the asymptotic distribution of the proposed estimator by the interested authors (see ^[53,54] for more details).

Author contributions

W. B. Altukhaes: Methodology, Software, Validation, Formal analysis, Investigation, Resources, Data curation, Writing-original draft preparation, Writing-review and editing, Visualization, Funding acquisition; M. Roozbeh: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Resources, Data curation, Writing-original draft preparation, Writing-review and editing, Visualization, Project administration; N. A. Mohamed: Conceptualization, Methodology, Validation, Formal analysis, Investigation, Resources, Data curation, Visualization, Supervision, Funding acquisition. All authors have read and agreed to the published version of the manuscript.

Acknowledgments

The first author would like to thank the Deanship of Scientific Research at Shaqra University for supporting this work. The second author thank the Research Council of Semnan University for its support. The second and third authors would like to thank the Ministry of Higher Education Malaysia for their support in funding this research through the Fundamental Research Grant Scheme (Project No.: FP072-2023) awarded to Nur Anisah Mohamed and Mahdi Roozbeh.

The authors would like to thank the three anonymous reviewers and handling editor for their valuable comments and corrections to an earlier version of this paper, which significantly improved the quality of our work.

Conflicts of Interest

The authors declare no conflict of interest.