A novel two-grid Crank-Nicolson mixed finite element method for nonlinear fourth-order sin-Gordon equation

1.   Introduction

It is well known that the problem of reducibility and stability of Sobolev norms for quasi-periodically forced linear operators on the torus is a classical one in the theory of infinite dimensional dynamical systems, which has received new attention in the past few years. Roughly speaking, given a linear operator with coefficients that depend on time in a quasi-periodic way, we say that it is reducible if there exists a bounded change of variables depending quasi-periodically on time (say mapping $H^s\rightarrow H^s$ for all times), which makes its coefficients constant. Actually, the notion of reducibility has been first introduced for ordinary differential equations (ODEs), going back to Bogolyubov ^[11] and Moser ^[32]. Also, there is a large literature around the reducibility of ODEs by means of the KAM tools. Regarding recent developments in this direction, we invite the reader to consult ^{[4,16,22,25,26]} and the references therein. Such kind of reducibility results for PDEs using KAM machinery have been well developed, see ^{[7,8,9,10,13,18,21,30,31]}. Due to the large amount of work in reducible KAM theory for non linear partial differential equations (PDEs), we do not list them, and refer to the introduction in ^[20] for more details.

Investigating the reducibility of linear operators is important when reducibility problems of nonlinear PDEs are considered. Very recently, Feola et al. ^[20] considered the reducibility of linear equations of the form

on the torus $x\in \mathbb{T}^d$ where $\omega\in \mathbb{R}^\nu$ and $\zeta\in\mathbb{R}^d$ are parameters (and the dependence on these parameters is denoted by the corresponding subscripts) while $a_{(\omega, \zeta)}\in C^\infty(\mathbb{T}^{\nu+d}, \mathbb{R}^d).$ They proved that if for any $s_1\in \mathbb{Z}_+$ large enough and $\|a\|_{s_1} = \|a_{(\omega, \zeta)}\|_{H^{s_1}(\mathbb{T}^{\nu+d}, \mathbb{R}^d)}$ small enough, then there exists a Borl set $\mathcal{O}_\infty\subset \mathcal{O}_0$ (a bounded domain in $\mathbb{R}^{\nu+d}$) with positive Lebesgue measure such that for any $(\omega, \zeta)\in \mathcal{O}_\infty,$ there is a quasi-periodic family of bounded and invertible linear operators $\Psi(\omega t) = \Psi_{\omega, \zeta}(\omega t)$ and the equation (1.1) is reduced by $v = \Psi(\omega t)^{-1}[u]$ into constant coefficients

where $|m_{\omega, \zeta}-\zeta| = O(\|a\|_{s_1})$ uniformly in $(\omega, \zeta)\in\mathcal{O}_0,$ see Theorem 1 in ^[20]. As a direct consequence, the Sobolev norms of the solutions of the Cauchy problem associated to (1.1) are controlled uniformly in time. The main strategies in ^[20] are divided into two steps: Firstly, the problem of reducing equations (1.1) to constant coefficients, by the identification between first order operators and vector fields, can be formulated as the problem of finding a family of diffeomorphism $\Psi_\xi\, :\, \theta\mapsto\theta+h_\xi(\theta)$ that conjugates a weakly perturbed constant vector field

on $\mathbb{T}^{\nu+d}$ to constant Diophantine vector fields $\alpha_\xi\cdot\partial_\theta.$ Here, $\xi$ is a parameter ranging in a bounded domain $\mathcal{O}\subset\mathbb{R}^{\nu+d}$ and $f_\xi, \, h_\xi\in C^\infty(\mathbb{T}^{\nu+d}, \mathbb{R}^{\nu+d}).$ In other words, the authors obtained a new version of J. Moser's theorem on straightening vector fields on tori (called the tame Moser theorem), see Theorem 2 in ^[20]. Second, the tame Moser theorem is proven via an iterative KAM-type scheme in the Sobolev spaces $H^s.$ Approximations by analytic functions are not used. Instead, the authors approached the problem in the spirit of the Nash-Moser theory, where one employs interpolation and smoothing estimates in order to control the loss of regularity due to the presence of small divisors.

Consider two classes of first order, linear quasi-periodically forced PDEs as the following:

where $x\in \mathbb{T}^m, \, \, \omega\in \mathbb{R}^d, \, \, \xi\in \mathcal{O}\subset\mathbb{R}^m$, $f\, :\, \mathbb{T}^{m+d}\rightarrow \mathbb{R}^m$ and $u_0\, :\, \mathbb{T}^{m}\rightarrow \mathbb{R}$ are both $C^\omega$ functions, and

where $x\in \mathbb{T}, \, \, \omega\in \mathbb{R}^d, \, \, \rho\in \mathbb{R}$, $f\, :\, \mathbb{T}^{1+d}\rightarrow \mathbb{R}$ and $u_0\, :\, \mathbb{T}\rightarrow \mathbb{R}$ are both $C^\omega$ functions. We say (1.2) and (1.3) satisfy the Cauchy problem with initial condition $u(x, 0) = u_0(x)$ if $u(x, t)$ is the solution of (1.2) and (1.3) and satisfies $u(x, 0) = u_0(x)$. Furthermore, we say this Cauchy problem is stable if the norm of $u(x, \cdot)$ can be controlled by the norm of $u_0(x)$ for each $t\in \mathbb{R}$. Inspired by the works in ^[20], we study the stability of the Cauchy problem of (1.2) and (1.3) in analytic Sobolev norm under multi-Liouvillean forced frequency. To this end, we have to discuss the rotations reducibility^* of PDEs

*Equation (1.4) is said to be rotations reducible, if there exists a quasi-periodic transformation $u = \Phi(\omega t)[v]$ such that system (1.4) is transformed into $\partial_t v+m(\omega t, \xi))\cdot \partial_x v = 0$ and $m$ is close to constant.

and

since it is quite difficult to study the reducibility of PEDs in the case of Liouvillean forced frequency, and such rotations reducibility is able to ensure the stability of solutions of Cauchy problems (1.2) and (1.3). See Theorems 3.1 and 3.2 in Section 3 for more detail. As done in ^[20], we use the identification between derivation operators and vector fields in order to change rotations reducible for PDEs (1.4) and (1.5) into a corresponding rotations reducible for analytic vector field on $\mathbb{T}^{m+d}$

and for analytic vector field on $\mathbb{T}^{1+d}$

Under appropriate hypotheses on the size of $f,$ rotations reducibility of vector field (1.6) or (1.7) follows a KAM-type iterative scheme with multidimensional Liouvillean forced frequency in the analytic Sobolev spaces $H^s.$ See Propositions 1 and 2 in Section 3 for more detail; these results can be regarded as the generalization of V.I. Arnold's ^[1] $C^\omega$ reducible result on analytic vector fields in the case of Diophantine frequency to $C^\infty$ rotations reducible in the case of multidimensional Liouvillean forced frequency.

Let us briefly review recent developments in KAM theory with Liouvillean forced frequency. In 2011, Avila et al. ^[4] considered the following linear skew-products

where $\alpha\in \mathbb{R}$ and $A :\mathbb{T} \rightarrow SL(2;\mathbb{R})$ is analytic, and gave a KAM scheme for the rotations reducibility of $SL(2;\mathbb{R})$ cocycles with Liouvillean frequency by using the technique of continued fractions. Subsequently, X. Hou and J. You ^[24] further proved that a quasi-periodic linear differential equation (1.8) in $sl(2, \mathbb{R})$ with two frequencies $(1, \alpha)$ is almost reducible provided that the coefficients are analytic and close to a constant. In the case that $\alpha$ is Diophantine, they got the non-perturbative reducibility. Reducibility and the rotations reducibility for an arbitrary irrational $\alpha$ under some assumption on the rotation number were also obtained. For more references, see ^{[38,39,40,41,42,43,44]}. Starting from the works ^[4] and ^[24], the question of reducibility on quasi-periodically forced systems beyond Diophantine or Brjuno condition ^† has been one of the central themes of the subject---when can the dynamics of a given system be related to those of a linear model, as for example periodic or quasi-periodic motion on a torus? However, very little is known about reducibility (or linearization) of quasi-periodically forced nonlinear flows on a $m$-dimensional torus under a non-resonance condition on forced frequency weaker than the Diophantine or Brjuno condition.

^†If there exist $\gamma > 0$ and $\tau > d$ such that

then we say the frequency $\omega$ satisfies Diophantine conditions. Slightly weaker than Diophantine conditions can be often required as Brjuno conditions, which are defined by

If the frequency $\omega$ does not satisfy Brjuno condition, we call it Liouvillean.

An analytic quasi-periodically forced (qpf) $m$-torus flow is the flow

defined by an analytic vector field of the form

where $f : \mathbb{T}^m\times\mathbb{T}^d\rightarrow \mathbb{R}^m$ is analytic, and $\omega\in \mathbb{R}^d$ is rationally independent. We denote by $(\omega, f)$ the flow of the vector field (1.9) for simplicity. Recently, in the case of $m = 1,$ Krikorian et al. ^[27] proved that the flow $(\omega, \rho+f)$ with $\omega = (1, \alpha),$ where $f:\mathbb{T}\times \mathbb{T}^2\rightarrow \mathbb{R}$ is analytic, $\alpha$ satisfies not super-Liouvillean condition

with $\{\frac{p_{n}}{q_{n}}\}$ being the continued fraction approximate to $\alpha$ and its rotation number $\rho_f$ is Diophantine with respect to the basic frequency $\omega$ ^‡, is $C^\infty$ rotations reducible provided that $f$ is sufficiently small. Their inspiration comes from reducibility theory of quasi-periodic $SL(2, \mathbb{R})$ cocycle ^{[2,3,4,5,6,14,15,19,24]} and their breakthrough is solving a homological equations of variable coefficient taking advantage of diagonally dominant operators. This work generalizes the linear result ^[4,24] to general nonlinear quasi-periodically forced circle flows. Subsequently, using the same Liouvillean non-resonant condition, i.e., $\omega = (1, \alpha)$ satisfies not super-Liouvillean condition (1.10), J. Wang and J. You ^[35] proved the boundedness of solutions for non-linear quasi-periodic differential equations. In addition, there are many interesting works on the Stoker's problem (existence of response solutions) for nonlinear mechanical models with Liouvillean forced frequency. Since the Stoker's problem is different from that of the reducible problem, its Liouvillean forced frequency can be much weaker. Readers can consult ^{[12,29,36,43]} for related results.

^‡that is

with $\gamma > 0$ and $\tau > 2$.

All the above reducible results about quasi-periodically forced (qpf) flows with Liouvillean forced frequency are mainly concerned with two-dimensional frequency. However, for multidimensional Liouvillean forced frequency, the theory of high-dimensional continued fractions is not completely satisfactory. Thus, we must look for more appropriate methods to deal with the case of multidimensional Liouvillean forced frequency. In this direction, there are some works on ODEs or PDEs, see ^{[12,34,37,38]}. In particular, Xu et al. ^[38] provided quasi-periodic solutions for Hamiltonian PDE with frequency vector $\omega = (\overline{\omega}_{1}, \overline{\omega}_{2})\in\mathbb{R}^{2}\times\mathbb{R}^{d-2}$, $\overline{\omega}_{1} = (1, \alpha)$, $\alpha\in\mathbb{R}\backslash\mathbb{Q},$ which is called weak Liouvillean frequency, i.e., for $\gamma > 0, \tau > d+1,$ there is

where $\{\frac{p_{n}}{q_{n}}\}$ is the continued fraction approximate to $\alpha.$ We note that in (1.11) only $\overline{\omega}_{1}$ is allowed to be Liouvillean, not the entire frequency $\omega$.

In the case of multidimensional Liouvillean forced frequency, a key step the stability of the Cauchy problem (1.2) or (1.3) is to study rotations reducibility of the qpf $m$-torus flow $(\omega, \rho+f).$ Even under Brjuno conditions, this problem becomes more complex in higher-dimensional tori ($m\geq 2$) because there is no conception of rotation number in higher-dimensional tori. The corresponding conception are rotation vectors, which are highly relying on the orbit of flow. In most cases, the rotation vector is not unique but a set. Thus, it is difficult to classify the quasi-periodically forced tori using the characters of rotation vector. In the case $m\geq 1$, $d\geq2$, W. Si and J. Si^[33] proved that the qpf flow $(\omega, \rho+f)$, where $\rho\in \mathbb{R}^m$, $f:\mathbb{T}^m\times \mathbb{T}^d\rightarrow \mathbb{T}^m$ is analytic and $(\omega, \rho)$ satisfies the Brjuno-Rüssmann's non-resonant condition

is $C^\omega$ reducible provided that $f$ is sufficiently small and satisfies some non-degeneracy condition (see ^[33] for the definition of $\Delta$).

In this paper, we will prove that, in the case $m\geq1$ and $d\geq 2$, the analytic qpf $m$-torus flow $(\omega, \xi+f)$ can be $C^\infty$ rotations reducible when $\omega$ possesses finite uniform Diophantine exponent (see (2.3) below), $f$ is sufficiently small and $\xi\in\mathcal{O}_\gamma$, where $\mathcal{O}_\gamma\subset \mathcal{O}$ is Cantor subset of compact set $\mathcal{O}$ in $\mathbb{R}^m$ with positive Lebesgue measure. In the case $m = 1$ and $d\geq 2$, the analytic qpf circle flow $(\omega, \rho+f)$ can be $C^\infty$ rotations reducible when $\omega$ possesses finite uniform Diophantine exponent (see (2.3) below), its rotation number $\rho_f$ is Diophantine with respect to the forced frequency $\omega$, and $f$ is sufficiently small.

Essentially, the Liouvillean property in multidimensional Liouvillean frequency (1.11) comes from $2$-dimensional frequency $\bar \omega_1$. In this paper, we introduce multidimensional Liouvillean frequency by using finite uniform Diophantine exponent, which can holistically describe the Liouvillean property of a frequency. We can also prove that our Liouvillean frequency set contains all the Liouvillean frequencies in (1.11). This is the main novelty of our paper.

The rest of this paper is organized as follows. In Section 2, we introduce some notations, definitions, and relevant concepts, which will be used subsequently. In Section 3, we first introduce the results of rotations reducibility for qpf $m$-torus flow $(\omega, \xi+f)$ in the case $m\geq1$ and $d\geq 2$ and qpf circle flow $(\omega, \rho+f)$ in the case $m = 1$ and $d\geq 2,$ i.e., Proposition 3.1 and Proposition 3.2. Then we give the proof of the main result, Theorem 1. In Section 4, we give the proof of Propositions 3.1 and 3.2. In Section 5, we give an Appendix that introduces the definition of CD-bridge.

2.   Preliminaries

In this section, we first give some notations, definitions, and relevant concepts, which will be used subsequently..

2.1.   Analytic function space

Denote by $\mathbb{Z}$ and $\mathbb{Z}_+$ the sets of integers and positive integers, respectively. Let $\mathbb{T}^l = \mathbb{R}^l/2\pi\mathbb{Z}^l$ be the standard $l$-dimensional real torus. Given $m\in \mathbb{Z}_+$, we consider a real valued function $f\in L^2(\mathbb{T}^d, \mathbb{R}^m)$

We define the sets

For an analytic function $f(\varphi) = \sum_{k\in \mathbb{Z}^d}f_ke^{{\rm i}\langle k, \varphi\rangle}$ defined in $W_{r}(\mathbb{T}^d)$, we define the spaces of analytic functions

where $r > 0$. For any $N > 0,$ we define the truncation and projection operators $\mathcal{T}_N$, $\mathcal{R}_N$ on $H^{r, a}$

If we consider two variables $(\theta, \varphi)\in \mathbb{T}^{m+d}$, we may consider a real valued function $f(\theta, \varphi)\in L^2(\mathbb{T}^{m+d}, \mathbb{R}^m)$ as a $\varphi$-dependent family of functions $f(\theta, \cdot)\in L^2(\mathbb{T}^{m}, \mathbb{R}^m)$ with the Fourier series expansion

In this case, we describe the spaces of analytic functions defined in $W_{s, r}(\mathbb{T}^m\times \mathbb{T}^d)$

where $s > 0$, $r > 0$. It is clear that the spaces $H^{r}$ and $H^{s, r}$ are Banach algebra under their norms, see ^[28]. Fix $m\in \mathbb{Z}_+$ and let $\mathcal{O}$ be a compact subset of $\mathbb{R}^m.$ For a function $f:\mathcal{O}\rightarrow H^{r}$, we define the norm of $f$ as

where

For a function $f:\mathcal{O}\rightarrow H^{s, r}$, we define the norm of $f$ as

where

Here, the derivative with respect to $\xi$ is in the sense of Whitney.

For an analytic function $f(\theta, \phi)$ defined in $W_{s, r}(\mathbb{T}^m\times \mathbb{T}^d)$, its supremum norm is defined by

By the attenuation of Fourier coefficients $f_l^k$, i.e., $|f_l^k|\leq |f|_{s, r}e^{|l|s+|k|r}$, one can check that

In addition, one can easily check that $|f|^2_{s, r}\leq \|f\|^2_{s, r}$, which implies $\|f\|_{s, r} = |f|_{s, r}$.

2.2.   Diffeomorphisms of the torus

Consider a diffeomorphisms of the $m$-dimensional torus

where $h:\mathbb{T}^m \rightarrow \mathbb{R}^m$ is an analytic function with $\|h\|_s\leq 1/2$. We denote the inverse of $\Phi$ by

with $\tilde h$ an analytic function. Using the same notation, we denote transformations like (2.1) with the corresponding linear operators acting on $H^{r}$ as

Similarly, we consider the action of $\Phi$ on the vector fields on $\mathbb{T}^m$ by the pushforward. Explicitly, we denote by $T(\mathbb{T}^m)$ the tangent space of $\mathbb{T}^m$.

Now given a vector field $X:\mathbb{T}^m\rightarrow T(\mathbb{T}^m)$

its pushforward is

2.3.   Linear operators

A $C^\omega$ vector field $X(\theta) = \sum_{j = 1}^m X_j(\theta)\frac{\partial }{\partial \theta_j}$ induces a linear operator acting on the space of functions $f :\mathbb{T}^m \rightarrow \mathbb{R}$, that we denote by $X(\theta)\cdot \partial_\theta = \sum_{j = 1}^m X_j(\theta)\frac{\partial }{\partial \theta_j}$. More precisely, the action of such a linear operator is given by

2.4.   The fibred rotation number

We consider the case of $m = 1.$ Suppose $(\omega, f)$ is a qpf circle flow defined by

Let

be the fibred rotation number associated with $(\omega, f)$, where $\hat\Phi_\varphi^t(\hat\theta):\mathbb{R}_+^1\times \mathbb{R}^1\times \mathbb{T}^d\rightarrow \mathbb{R}^1$, via $(t, \hat \theta, \varphi)\mapsto\hat\Phi_\varphi^t(\hat\theta)$ denotes the lift of the flow $(\omega, f)$ of the first variable $\theta$. The limit exists and is independent of $(\hat\theta, \varphi)$ ^[23]. As a direct consequence of the definition, we have the following well-known results:

Lemma 2.1. (^[23]) Let $\omega\in\mathbb{R}^d, \, \, \rho\in\mathbb{R}$ and $\|f(\theta, \varphi)\|_{C^0}\leq \epsilon$, then

Lemma 2.2. (^[23]) Suppose $(\omega, f)$ is a qpf circle flow and $H\in C_0(\mathbb{T}\times\mathbb{T}^d, \mathbb{T}\times\mathbb{T}^d)$ is a homeomorphism homotopic to the identity that projects to the identity on the second factor. Then the fibred rotation numbers of $(\omega, f)$ and $H\circ(\omega, f)\circ H^{-1}$ are the same.

2.5.   Uniform Diophantine exponent

In this subsection, we recall the definition of uniform Diophantine exponent of forced frequency $\omega_0\in\mathbb{R}^d$ introduced in ^[17].

• Recall the Diophantine exponent denoted by $\omega(\omega_0)$ that the supremum of all positive real numbers $\kappa$ such that there exists $k\in \mathbb{Z}^d\setminus \{0\}$ and $|\langle k, \omega_0 \rangle| \leq |k|^{-\kappa}$.

• Recall the uniform Diophantine exponent denoted by $\hat \omega(\omega_0)$ that the supremum of all positive real numbers $\kappa$ such that for any sufficiently large $N$, there exists $k\in \mathbb{Z}^d\setminus \{0\}$ such that $|k|\leq N$ and $|\langle k, \omega_0 \rangle | \leq N^{-\kappa}$. In other words, if we define the set

then $\hat \omega(\omega_0) = \sup S$.

By the definitions of $\hat \omega(\omega_0)$ and $\omega(\omega_0)$, one obtains that $\hat \omega(\omega_0)\leq \omega(\omega_0)$, and while $\omega(\omega_0)$ measures how small linear forms with integer coefficients of a given size can become when evaluated at $\omega_0$. It is clear that if $\omega(\omega_0) < \infty$ then $\omega_0$ is Diophantine vector and if $\omega(\omega_0) = \infty$ then $\omega_0$ is not Diophantine vector. For uniform Diophantine exponent $\hat\omega(\omega_0)$, if $\hat\omega(\omega_0) = \infty$, then $\omega_0$ is not Diophantine vector. But if $\hat\omega(\omega_0) < \infty$, then $\omega_0$ also contains Liouvillean frequency. For example, $\hat\omega(\omega_0)$ is always finite if $\omega_0 = (1, \alpha)$ with $\alpha\in \mathbb{R}\setminus\mathbb{Q}$ because $|\langle k, \omega_0 \rangle| > {1}/{2q_n},$ for $0 < |k|\leq q_n,$ where $\frac{p_{n}}{q_{n}}$ is the continued fraction approximated to $\alpha$.

In this paper, we strengthen the condition $\hat\omega(\omega_0) < \infty$ to exist a $\tau_1$ and an increasing sequence $K_n$ such that

where the sequence $\{K_n\}_{n\geq 0}$ satisfies

(1) For the given constant $\tau_1 > 0$, there exists a positive constant $M > d/2$ such that

(2) There exists a positive constant $N$ such that

Remark 2.1. Assumptions (2.4) and (2.5) are really technical conditions summarized from not super-Liouvillean condition in ^[27]. This property can also be reflected in high dimensional Liouvillean frequencies. One of the purposes of this paper is an observation of this property in higher dimensions.

2.6.   Liouvillean frequency vectors

Definition 2.1 (Diophantine condition). Given a frequency $\omega\in \mathbb{R}^d$, we call $\omega$ Diophantine if there exists a sequence $\{K_n\}_{n\geq 0}$ with $K_n = K_{n-1}^{\widehat{\beta}}$ and $1 < \widehat{\beta} < 2$ such that

where $\gamma\in(0, 1)$, $\tau_1 > d-1$.

Definition 2.2 ($MN\tau_1$-admissibility). For a given sequence $\{K_n\}_{n\geq 0}$, $N, \tau_1 > 0$ and $M > d/2$, we call $\{K_n\}_{n\geq 0}$ is ($MN\tau_1$)-admissible if it satisfies the inequalities (2.4) and (2.5). The set of all such sequences is denoted by

Definition 2.3 (Liouvillean vectors set). For given $K = \{K_n\}_{n\geq 0}\in \mathcal{K}(\tau_1, M, N),$ we define the set

where $D\in\mathbb{R}^d$ is compact and $C$ is a positive number. Setting

we call $\mathcal{L}$ Liouvillean vectors set.

We will show that the set $\mathcal{L}$ allows many Liouvillean vectors. In the following discussions, we always assume $C\equiv1$ occurring in the frequency set (2.6) without loss of generality.

Remark 2.2. If frequency $\omega_0$ belongs to Liouvillean vectors set $\mathcal{L}$, then convergence speed of small divisor tending to $0$ can be much faster than Diophantine case that is because if $\omega_0\in \mathcal {L}$, $K_{n+1} = \mathcal{O}(e^{K_n})$ increases much faster than the Diophantine case $K_{n+1} = \mathcal{O}({K_n}^{\widehat{\beta}})$.

Remark 2.3. We can prove that all the vectors in $\mathcal{L}$ have finite uniform Diophantine exponent. In fact, by definition of $\omega_0$, we have that if $\omega_0\in \mathcal{L},$ then there exists $K$, which is ($MN\tau_1$)-admissible, such that $\omega_0\in {O}_K$. For the set $S$ defined in (2.2), it is clear that $S$ is no-empty because $0\in S,$ and it has the following two characters:

1. If $\kappa_1\in S$, then $\kappa\in S$ for all $\kappa\leq \kappa_1$. That is because if $\kappa_1\in S$, then for all $N$ large enough, there exists $k\in \mathbb{R}^d\backslash \{0\}$, $0 < |k|\leq N$, such that $|\langle k, \omega_0 \rangle|\leq N^{-\kappa_1}$, which implies $|\langle k, \omega_0 \rangle|\leq N^{-\kappa}$ for all $\kappa\leq \kappa_1$. Thus, $\kappa\in S$.

2. If $\kappa_1\notin S$, then $\kappa\notin S$ for all $\kappa\geq\kappa_1$. That is because if $\kappa_1\notin S$, then there exists $N$ large enough, for all $k\in \mathbb{R}^d\backslash \{0\}$, $0 < |k|\leq N$, such that $|\langle k, \omega_0 \rangle| > N^{-\kappa_1}$, which implies $|\langle k, \omega_0 \rangle| > N^{-\kappa}$ for all $\kappa\geq \kappa_1$. Thus, $\kappa\notin S$.

Moreover, $\omega_0\in O_K$, then $\tau_1\notin S$. Thus $0 \leq\hat\omega(\omega_0) = \sup S\leq \tau_1$.

Remark 2.4. Now, we illustrate that the Liouvillean vectors set $\mathcal{L}$ allows many Liouvillean vectors.

In two-dimensional case, we consider $\omega = (1, \alpha)$ in $\mathbb{R}^2.$ Let $\mathcal{A} = 8$ and $(Q_n)_{n\in\mathbb{N}}$ be the selected subsequence in Lemma A.1 of Appendix. By Corollary 2.1 in ^[27], if $\beta(\alpha) < \infty$ we have the following claims:

(1) $Q_n > Q_{n-1}^{\mathcal{A}}$. That is because for $n = 1$, it is clear that $Q_1 > Q_0^{\mathcal{A}}$ since $Q_0 = 1$. If $n\geq 2$ and $\overline Q_{n-1}\leq Q_{n-1}^\mathcal{A}$, then one has $Q_n\geq \overline Q_{n-1}\geq Q_{n-1}^{\mathcal{\mathcal{A}}}$. If $n\geq 2$ and $\overline Q_{n-1} > Q_{n-1}^\mathcal{A}$, then $(\overline Q_{n-1}, Q_n)$ and $(Q_n, Q_{n+1})$ are both $CD(\mathcal{A}, \mathcal{A}, \mathcal{A}^3)$ bridges. Thus, we get $Q_n > Q_{n-1}^{\mathcal{A}}$.

(2) $\ln Q_{n+1} < Q_n^{U}$, where $U = \beta(\alpha)+\frac{4\ln\mathcal{A}}{\ln2}$. That is because

which implies $\ln Q_{n+1} < Q_n^{U}$.

We also have $\langle k, \omega \rangle \geq \frac{1}{2Q_{n}}$ for all $0 < |k| < Q_n$, which implies $\omega\in \cup_{K\in \mathcal{K}(1, \mathcal{A}, U)}O_K$. Thus $\mathcal{L}$ includes some frequencies beyond Brjuno in two-dimensional case.

In multidimensional case, $\mathcal{L}$ includes all the frequency satisfying condition (1.11). That is because if $\omega = (\overline{\omega}_{1}, \overline{\omega}_{2})\in\mathbb{R}^{2}\times\mathbb{R}^{d-2}$ satisfies condition (1.11), then

and

where $(Q_n)_{n\in\mathbb{N}}$ is the selected subsequence in Lemma A.1 of Appendix. If $\tau_1 = \max\{1, \tau\}$, then $\omega\in \cup_{K\in \mathcal{K}(\tau_1, \mathcal{A}, U)}O_K,$ and so $\omega\in\mathcal{L}.$

3.   Reducibility

For any integer $m\geq1$ and $d\geq2,$ we have the following Proposition.

Proposition 3.1. Let $\mathcal{O}$ be a bounded closed set in $\mathbb{R}^m$ not containing zero, $r > 0$, $s > 0$, $\tau > m+d-1$, $\gamma > 0$, $\omega\in\mathcal{L}$ and $\xi\in \mathcal{O}.$ Consider a $C^1$-smooth family of vector fields on $\mathbb{T}^{m+d}$

where $f(\cdot; \xi)\in H^{s, r}(W_{s, r}(\mathbb{T}^m\times \mathbb{T}^d), \mathbb{R}^m)$. Then, there exists a sufficiently small constant $\epsilon = \epsilon(\tau, \tau_1, \gamma, s, r,$ $M, N, \mathcal{O})$ such that if

then there exists a set

where $\rho_{\infty}(\xi):\mathcal{O}_{\infty}\rightarrow \mathbb{R}^m$ is a $C^1$ function and there exists a map

which is $C^\infty$-smooth in $\varphi$, analytic in $\theta$ and $C^1$-smooth in $\xi$, so that for all $\xi\in \mathcal{O}_{\infty}$ the pushforward of vector fields $X$ by diffeomorphism $\Psi:(\varphi, \theta)\mapsto (\varphi, \theta+h(\theta, \varphi)) = (\varphi, \widehat\theta)$ is

where $m_{\infty}:\mathbb{T}^d\times\mathcal{O}_{\infty}\rightarrow \mathbb{R}^m$, $(\varphi, \xi)\mapsto m_{\infty}(\varphi, \xi)$ is $C^1$-smooth in $\xi$, analytic in $\varphi$ and for each $\xi\in\mathcal{O}_{\infty}$ satisfies

For $m = 1$ and any integer $d\geq2,$ we have the following Proposition.

Proposition 3.2. Let $\rho\in \mathbb{R}$, $\omega\in\mathcal{L}$, $r > 0$, $s > 0$, $\tau > d$ and $\gamma > 0.$ We consider a vector field on $\mathbb{T}^{d+1}$

where $f(\theta, \varphi)\in H^{s, r}(W_{s, r}(\mathbb{T}\times \mathbb{T}^d), \mathbb{R}^m)$. Assume that $\tilde\rho(\omega, \rho+f(\theta, \varphi)) = \rho_f\in DC_\omega(\gamma, \tau)$ in the sense

Then there exists a sufficiently small constant $\epsilon = \epsilon(\tau, \tau_1, \gamma, s, r, M, N)$ such that if $\|f(\theta, \varphi)\|_{s, r}\leq \epsilon,$ and there exists a map

which is $C^\infty$-smooth in $\varphi$, analytic in $\theta$, so that the pushforward of vector fields $X$ by diffeomorphism $\Psi:(\varphi, \theta)\mapsto (\varphi, \theta+h(\theta, \varphi)) = (\varphi, \widehat\theta)$ is

where $m_{\infty}(\varphi)$ is $C^\infty$-smooth in $\varphi$ and satisfies

Remark 3.1. The proof of Proposition 3.1 or Proposition 3.2 is based on a KAM iterative scheme under the assumption that forced frequency has finite uniform Diophantine exponent. As we know, the results existing in the literature deal with two-dimensional frequency, and exploit the theory of continued fractions to control the small divisor problem. The results in this paper extend the analysis to higher dimensional frequency with finite uniform Diophantine exponent, allowing a class of Liouvillean frequencies. More specifically, Proposition 1 can be regarded as a generalization of the work in ^[20] from Diophantine frequency to Liouvillean frequency and work in ^[33] from Brjuno frequency to Liouvillean frequency, while Theorem 3.1 can be regarded as a generalization of the work in ^[27] from two-dimensional not super-Liouvillean forced frequency to high-dimensional forced frequency with finite uniform Diophantine exponent. The overall strategy of this paper comes from the literature ^[27,33], but the method is still in the spirit of ^[4,17,24], which, however, has to overcome essential obstructions in techniques for dealing with the questions considered here.

Remark 3.2. Compared with the results in ^[20], which reduce the variables $(\theta, \varphi)$, our results only reduce variable $\theta$ because of the difficulty from Liouvillean frequency. Even so, the analytic norms of the solutions of the Cauchy problem can also be controlled uniformly in time. This is the following Theorem 1.

Theorem 1. Let $\omega\in \mathcal{L}$ and consider the transport equation

Then if $f(\cdot; \xi)\in H^{s, r}(W_{s, r}(\mathbb{T}^m\times \mathbb{T}^d), \mathbb{R}^m)$ is $C^1$-smooth with respect to $\xi$ and (3.1) is fulfilled, for $\xi\in \mathcal{O}_\infty$ (see (3.2)), under the change of variable $u = \Psi(\omega t)[v] = v(x+h(x, \omega t))$ defined in (3.3), the $PDE$ (3.5) transforms into the equation with coefficients independent of spatial variable $x$

As a consequence, for $u_0\in H^{\frac{s}{2}}$, the only solution of the Cauchy problem

satisfies $\|u(x, t)\|_{\frac{s}{4}}\leq \|u_0(x)\|_{\frac{s}{2}}$ for any $t\in \mathbb{R}$, i.e., this Cauchy problem is stable.

Proof. Let $\omega\in \mathcal{L}$ and $\xi\in \mathcal{O}_\infty$. Under the change of coordinates $u = \Psi(\omega t)[v] = v(x +h(x, \omega t))$, the equation transforms (3.5) into the PDE

In view of Proposition 3.1, one obtains that

where

Let $v = \sum_{l\in \mathbb{Z}^m}v_l(t)e^{{\rm i}\langle l, x\rangle}$. Such a PDE with coefficients independent of a spatial variable can be integrated explicitly, implying that for any $l\in\mathbb{Z}^m$, $v_l(t) = v_l(0)e^{{\rm i}\langle \xi+\int_0^t m_{\infty}(\omega s)ds, l \rangle}$ and

By Proposition 3.1 and inverse mapping theorem, we get $\Psi(\omega t)^{-1}[u] = u(x+\tilde h(x, \omega t))$, where

with $\sigma = s/12$. Then, given $u_0(x)\in H^{s}(\mathbb{T}^m, \mathbb{R})$, one gets that for each $t\in \mathbb{R}$

This completes the proof. □

Similarly, we can prove the following theorem by using Proposition 3.2.

Theorem 2. Let $\rho\in \mathbb{R}$ and $\omega\in \mathcal{L}$ and consider the transport equation

Then, if $\tilde\rho(\omega, \rho+f(\theta, \varphi)) = \rho_f\in DC_\omega(\gamma, \tau)$, $f\in H^{s, r}(W_{s, r}(\mathbb{T}\times \mathbb{T}^d), \mathbb{R})$ and $\|f(\theta, \varphi)\|_{s, r}\leq \epsilon,$ under the change of variable $u = \Psi(\omega t)[v] = v(x+h(x, \omega t))$ defined in (3.4), the $PDE$ (3.6) transforms into the equation with coefficients independent of spatial variable $x$

As a consequence, for $u_0\in H^{\frac{s}{2}}$, the only solution of the Cauchy problem

satisfies $\|u(x, t)\|_{\frac{s}{4}}\leq \|u_0(x)\|_{\frac{s}{2}}$ for any $t\in \mathbb{R}$, i.e., this Cauchy problem is stable.

4.   Proofs of Propositions 3.1 and 3.2

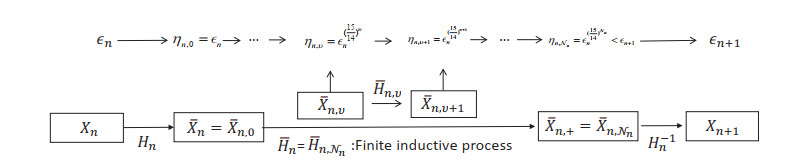
In this section, we give the proofs of Propositions 3.1 and 3.2 by a modified KAM iterative scheme. To better understand this iterative scheme, we draw a block diagram as follows:

4.1.   Proof of Proposition 1

Since $\omega\in \mathcal{L},$ we assume that $M, N, \tau_1$ are defined as in (2.3). And we take $c$ and $\alpha$ satisfying $c > \frac{16\alpha (3\tau+2+\frac{d}{2})}{\tau N}$ and $\max\{\frac{M(2\tau_1-d-2)}{2M-d}, 1\} < \alpha < M.$ For $r_0$, $s_0$, $\gamma > 0$, $\tau > m+d-1,$ we suppose $K_0 > 0$ large enough such that

and $\epsilon_0$ is sufficiently small. We further define the following sequences for $n\geq 1:$

Let

where $T^{(n-1)} = (\frac{\gamma^3}{32\epsilon_{n-1}^{\frac{1}{2}}})^{\frac{1}{3\tau+2+\frac{d}{2}}}$ and ${O}_{-1} = \mathcal{O}$.

4.1.1.   One KAM step

In $(n-1)$-th step, the vector fields $X_{n-1}$ can be written as

where $\xi\in{O}_{n-1}$, $[g_{n-1}]_{\varphi} = 0$ and

In what follows, we divide KAM step into three parts. In the proof, we do not write $\xi$ explicit for simplicity if there is no confusion. First, we give a Lemma that is used to eliminate the lower-frequency terms.

Lemma 4.1. If we denote $\bar s_n = s_{n-1}-\frac{\Delta_n}{3}$, $\bar r_n = \frac{r_0}{K_n^\alpha}$, then there exists $h_{n-1}(\varphi)$ with $\|h_{n-1}(\varphi)\|_{\bar r_n, {O}_{n-1}}\leq K_n^{\frac{M\tau_1+(d+1)\alpha}{M}}$, such that the transformation $H_{n-1}:\theta = \overline\theta+h_{n-1}(\varphi)(\mod 2\pi)$ conjugates the vector fields (4.3) into

where

Proof. Using transformation $\theta = \bar\theta+h_{n-1}(\varphi)(\mod 2\pi)$, the vector field (4.3) becomes

The vector field (4.5) becomes

where $\tilde f_{n-1}(\bar\theta, \varphi) = \rho_{n-1}+\mathcal{R}_{K_n}g_{n-1}(\varphi)+f_{n-1}(\bar\theta+h_{n-1}(\varphi), \varphi)$, if homological equation $\partial_\omega h_{n-1}(\varphi) = \mathcal{T}_{K_n}g_{n-1}(\varphi)$ is solvable. In view of $|\langle k, \omega\rangle| > \frac{1}{K_n^{\tau_1}}$ for all $|k|\leq K_n$, one can check that

since $K_{n-1} < K_n^{\frac{1}{M}}$ and $\epsilon_0$ sufficiently small. In order to control $f_{n-1}(\bar\theta+h_{n-1}(\varphi), \varphi)$, we should illustrate that ${\rm Im} h_{n-1}(\varphi)$ can be well controlled. Let $\varphi = \varphi_1+{\rm i} \varphi_2$ for $\varphi_1\in \mathbb{T}^{d}$ and $\varphi_2\in \mathbb{R}^d$ and define

Notice that $g_{n-1}(\varphi)$ is real analytic, which implies ${\rm Im} h_{n-1}^1(\varphi_1) = 0$. Since $\frac{1}{K_j^{\frac{\alpha (2m-d)-M(2\tau_1-d-2)}{2M}}}$ goes to zero much faster than $\Delta_j$, we can assume $\frac{1}{K_j^{\frac{\alpha (2m-d)-M(2\tau_1-d-2)}{2M}}} < \frac{\Delta_j}{3}$ for all $j\geq 0$ without loss of generality. Thus, applying Cauchy-Schwarz inequality, we can get

Letting $\bar g_{n-1}(\varphi) = \mathcal{R}_{k_n}g_{n-1}(\varphi)$ and $\bar f_{n-1}(\bar\theta, \varphi) = f_{n-1}(\bar\theta+h_{n-1}(\varphi), \varphi)$, we have

if $K_0 > (2c\tau N\ln K_0)^{\frac{2M}{M-\alpha}}.$ The proof is completed.

□

In what follows, we should make the perturbation smaller taking advantage of diagonally dominant operators such that the order of perturbation reach that of the next KAM step. But we can not achieve this using one transformation. So we have to make several transformations. We give the following Lemma.

Lemma 4.2. Denote $r_{n+} = \frac{r_0}{2K_n^\alpha}$, $s_{n+} = \bar s_n-\frac{\Delta}{3}$. Under the assumptions of Lemma 4.1 and $\xi \in O_{n-1}$, there exists a transformation $\overline {H}_{n-1}$ with estimates

such that $\overline H_{n-1}$ conjugates the vector field (4.4) to

with

Proof. In order to find $\overline H_{n-1}$, we divide $\overline H_{n-1}$ into $\mathcal N$ transformations where $\mathcal{N}$ is determined later. Letting $\tilde r = \bar r_n = \frac{r_0}{K_n^\alpha}$, $\tilde s = \bar s_n = s_{n-1}-\frac{\Delta}{3}$, $\tilde \eta = 2\epsilon_{n-1}$, we define the following sequences

In the proof, we do not write $n$ explicitly for simplicity. At $(\nu-1)$-th step, we write vector field as

where

Applying transformation $\phi_{\nu-1}:(\bar\theta_{\nu-1}, \varphi) = (\bar\theta_\nu+h_{\nu}(\bar\theta_\nu, \varphi), \varphi)$, the vector field (4.7) becomes

where $\bar g_{\nu}(\varphi) = \bar g_{\nu-1}(\varphi)+[\bar f_{\nu-1}(\bar\theta_{\nu}, \varphi)]_{\bar\theta_\nu},$ if the homological equation

is solved. Since homological equation (4.9) may have no analytic solution, we solve its approximate equation for each $1\leq i\leq m$.

Let

In order to solve equation (4.10), it is equivalent to solve

for $0 < |l| < T_\nu$.

For any fixed $l$, (4.11) can be written as a matrix equation

where

with $\bar g_{\nu, k}$ being the Fourier coefficients of Fourier expansion of $\bar g_\nu(\varphi)$. If we denote

for any $r'\leq \bar r_n,$ then we have

where

Letting $\mathcal N = [2^nc_1\tau N\ln K_n]+1$ with $c_1 = \frac{c}{ 16(3\tau+2+\frac{d}{2})\ln3}-\frac{\alpha}{ \tau N\ln3},$ we have

since $\epsilon_0$ sufficiently small. In view of $\xi\in O_{n-1}$ and (4.12), we get

for all $0 < |k|+|l| < T_\nu$, $|l|\neq 0$. Meanwhile, since the $(k_1, k_2)$-th variable of $\tilde G_{l, r'}$ is ${\rm i}e^{(|k_1|-|k_2|)r'}\langle l, \bar g_{\nu, k_1-k_2}\rangle,$ we obtain that

which implies the diagonally dominant operators $\tilde A_{l, r'}+\tilde G_{l, r'}$ have a bounded inverse and the following estimate

for $r' = \tilde r_{\nu-1}-\sigma_\nu$. One can check that

since $\epsilon_0$ sufficiently small. And the error

satisfies

Now, the system (4.8) becomes

where $\bar g_{\nu}(\varphi) = \bar g_{\nu-1}(\varphi)+[\bar f_{\nu-1}(\bar\theta_{\nu}, \varphi)]_{\bar\theta_{\nu}}$ and

By the mean value theorem and Cauchy estimate, we have for each $\xi\in O_{n-1}$ that

where $s\in (0, 1)$. This implies

Since $1\leq \nu\leq \mathcal{N}$, we should estimate $\bar f_{\mathcal{N}}(\bar\theta_{\mathcal{N}}, \varphi)$. First, we have the following estimate

By (2.5), we have

in view of $\epsilon_0 < e^{-2c\tau N}.$ Let $\bar\theta_{\mathcal{N}} = \bar\theta_+$ and

for $1\leq \nu\leq \mathcal{N}$. Then, $\overline H_\nu(\bar\theta_{\nu}, \varphi)$ is analytic in $W_{\tilde s_\nu, \tilde r_\nu}(\mathbb{T}^m\times \mathbb{T}^d)$ and

where $\pi:\mathbb{T}^m\times \mathbb{T}^d\rightarrow \mathbb{T}^m$ denotes the natural projection to the first variable. If we rewrite $\overline H_{\mathcal{N}}(\bar\theta_{+}, \varphi) = (\bar\theta_++\tilde h(\bar\theta_+, \varphi)\mod 2\pi, \varphi)$, then we have

In conclusion, let $\tilde s_{\mathcal{N}} = s_{n+}$, $\tilde r_{\mathcal{N}} = r_{n+}$, $\bar g_{\mathcal{N}}(\varphi) = \bar g_{n-1, +}(\varphi)$ and $\bar f_{\mathcal{N}}(\bar\theta_{+}, \varphi) = \bar f_{n-1, +}(\bar\theta_{+}, \varphi)$. Then $\overline H_{n-1} = \overline H_{\mathcal{N}}(\bar\theta_{+}, \varphi)$ conjugates (4.4) to

with the estimates

□

The following Lemma is the end of one KAM step.

Lemma 4.3. Under the assumptions of Lemma 4.1 and Lemma 4.2, there exists $\widetilde{H}_{n-1}$ with estimates

such that $\widetilde H_{n-1}$ conjugates vector field (4.3) to

with the following estimates

Proof. In the Lemma 4.1, we eliminate the non-resonant terms of $g_{n-1}(\varphi)$ and, as a result, the transformation we obtain is not close to the identity. In order to get rotations reducibility results, we need to inverse the first step, which means conjugating back by the transformation of the first step. Applying the inverse transformation $H_{n-1}^{-1}$:

the vector field (4.6) can be conjugated to

where $\rho_n = \rho_{n-1}+[\bar g_{n-1, +}(\varphi)]_{\varphi}$ and

We have

which implies $\|g_n(\varphi)\|_{r_n, O_{n-1}}\leq 4\tilde\epsilon_n$. And it is obvious that

Let $\widetilde H_{n-1} = H_{n-1}\circ\overline H_{n-1}\circ H^{-1}_{n-1}$, then $\widetilde H_{n-1} = \theta_++\tilde h(\theta_+-h_{n-1}(\varphi), \varphi)$. By (4.14), we have

4.1.2.   Iteration lemma

Lemmas 4.1, 4.2, and 4.3 can be summarized as the following iterative lemma.

Lemma 4.4. Suppose $\omega\in\mathcal{L}$ and $\gamma_n$, $r_n$, $s_n$, $\epsilon_n$ are defined in (4.1) for $n\geq 0$. Let $\epsilon_0$ sufficiently small. Then the following holds for all $n\geq 1$: If the vector field

satisfies

where $[g_{n}(\varphi, \xi)]_{\varphi} = 0$ and

Then there exists a subset $O_{n+1}\subset O_n,$ where

with

and a change of variables $\widetilde H_n:\mathbb{T}^m\times\mathbb{T}^d\rightarrow \mathbb{T}^m\times\mathbb{T}^d$ with estimates

such that it transforms the vector field (4.15) to

with

and $[g_{n+1}(\varphi, \xi)]_{\varphi} = 0$.

Proof. Actually, Lemma 4.4 is an immediate corollary of Lemmas 4.1-4.3. The only point we need to illustrate is the definition of $O_{n+1}$. If $\xi\in O_{n}$ and $0 < |k|+|l|\leq T^{(n)}$, then

Thus, by the definition of (4.16), we have

which satisfies the definition (4.2). □

4.1.3.   Measure estimation

By the definition of $O_n$, we get $\mathcal{O}_\gamma = \bigcap_{n\geq 0}O_n$.

By (4.16), we have

In what follows, we start to estimate the measure of set $\Gamma_{kl}^{n+1}(\gamma_{n+1}).$ In view of

and $\frac{d\rho_0(\xi)}{d\xi} = I$, we have

It follows from Lemma 1.2 in ^[33] that

Then, we have the following estimation

provided $\tau > m+d-1$.

4.1.4.   Convergence

Select $\epsilon_0$ sufficiently small and $r_0 = r$, $s_0 = s$. If $\rho\in \mathcal{O} = \bigcap_{n\geq 0}O_n$ and $\|f\|_{s, r, \mathcal{O}_{\gamma}} < \epsilon_0$, then the vector field

is $C^{\infty}$ rotations linearizable. We can use Lemma 4.2 to system (4.17). Thus we can get $H_0\in H^{s_{1}, r_{1}, a}$ which conjugates (4.17) to

with

Then we apply Lemma 6 inductively, we can get $\widetilde H_i\in H^{s_{i+1}, r_{i+1}, a}$, $i = 1, \cdots, n,$ such that $H^{(n)} = \widetilde H_0\circ \widetilde H_1\circ\cdots\circ \widetilde H_n$ conjugates (4.17) to

with

And we have

which implies

By the definition of $(\epsilon_n)_{\mathbb{N}}$, we know that for any $j\in \mathbb{Z}_+^{m+d},$ there exists $N\in \mathbb{N}$, such that for any $n\geq N$, we have $8(\frac{4K_{n+1}^\alpha}{r_0})^{|j|}\epsilon_n^{\frac{3}{4}}\leq \epsilon_n^{\frac{1}{2}}$. By the Cauchy estimates, if we denote $x: = (\theta, \varphi)\in \mathbb{T}^{m+d}$, we have

for any $n > N-1$. This guarantees the limit $\lim_{n\rightarrow \infty}H^{(n)}$ belongs to $C^\infty$.

Finally, let $\rho_\infty(\xi) = \lim_{n\rightarrow \infty}\rho_n(\xi)$, $m_{\infty}({\varphi, \xi}) = \lim_{n\rightarrow \infty}g_{n}(\varphi, \xi)$ and $\Psi = (\lim_{n\rightarrow \infty}H^{(n)})^{-1}$, the proof of Proposition 3.1 is completed.

4.2.   Proof of Proposition 2

In this section, we give the proof of Proposition 3.2. Since the proof process is very similar to ^[27], we only write the relevant lemma and the key points of proof that are different from Proposition 3.1. Readers can combine Proposition 3.2 with ^[27] for more detailed analysis.

Let $N$ $r_0$, $s_0$, $\gamma > 0$, $M > d/2$ $\tau > d$. Suppose $K_0 > 0$ large enough such that

where $c > \frac{16\alpha (3\tau+2+\frac{d}{2})}{\tau N}$ and $\max\{\frac{M(2\tau_1-d-2)}{2M-d}, 1\} < \alpha < M.$ $\epsilon_0$ is sufficiently small. For given $r_0$, $s_0$, $\epsilon_0$, we define some sequences depending on $r_0$, $s_0$, $\epsilon_0$ for $n\geq 1$:

where $\max\{\frac{M\tau_1}{M-d-1}, 1\} < \alpha < M$.

4.2.1.   One KAM step

In $(n-1)$-th step, vector field can be written as

where

Similar to Proposition 3.1, we can get the following Lemmas.

Lemma 4.5. Denote $\bar s_n = s_{n-1}-\frac{\Delta_n}{3}$, $\bar r_n = \frac{r_0}{K_n^\alpha}$, then there exists $h_{n-1}(\varphi)$ with $\|h_{n-1}(\varphi)\|_{\bar r_n}\leq K_n^{\frac{M\tau_1+(d+1)\alpha}{M}}$, such that transformation $H_{n-1}:\theta = \overline\theta+h_{n-1}(\varphi)(\mod 2\pi)$ conjugates the vector field (4.19) into

where

Proof. Using transformation $\theta = \bar\theta+h_{n-1}(\varphi)(\mod 2\pi)$, system (4.19) becomes

where $\tilde f_{n-1}(\bar\theta, \varphi) = \rho_{f}+[g_{n-1}(\varphi)]+\mathcal{R}_{k_n}g_{n-1}(\varphi)+f_{n-1}(\bar\theta+h_{n-1}(\varphi), \varphi)$, if homological equation $\partial_\omega h_{n-1}(\varphi) = \mathcal{T}_{K_n}g_{n-1}(\varphi)-[g_{n-1}(\varphi)]$ is solvable. Then, we have

By Lemma 2.2, we know $\rho(\omega, \tilde f_{n-1}(\bar\theta, \varphi)) = \rho_f$. By Lemma 2.1, we know that

Letting $\bar g_{n-1}(\varphi) = [g_{n-1}(\varphi)]_{\varphi}+\mathcal{R}_{k_n}g_{n-1}(\varphi)$ and $\bar f_{n-1}(\bar\theta, \varphi) = f_{n-1}(\bar\theta+h_{n-1}(\varphi), \varphi)$, we have

□

Lemma 4.6. Denote $r_{n+} = \frac{r_0}{2K_n^\alpha}$, $s_{n+} = \bar s_n-\frac{\Delta}{3}$. Under the assumptions of Lemma 4.5, there exists $\overline {H}_{n-1}$ with estimates

such that $\overline H_{n-1}$ conjugates (4.20) to

with

Proof. Taking advantage of $(\omega, \rho_f)$ being Diophantine, we can obtain this Lemma immediately using the same process of Lemma 4.2. The detail proof is omitted here. □

Lemma 4.7. Under the assumptions of Lemma 4.5 and Lemma 4.6, there exists $\widetilde{H}_{n-1}$ with estimates

such that $\widetilde H_{n-1}$ conjugates (4.20) to

with

Proof. Applying the inverse transformation $H_{n-1}^{-1}$:

the system (4.23) can be conjugated to

where

We have

which implies $\|g_n(\varphi)\|_{r_n, O_{n-1}}\leq 4\tilde\epsilon_n$. Thus

Let $\widetilde H_{n-1} = H_{n-1}\circ\overline H_{n-1}\circ H_{n-1}^{-1}.$ By (4.21) and (4.22), we get (4.24) and (4.25) hold. □

4.2.2.   Iteration lemma

Lemmas 4.5, 4.6, and 4.7 can be summarized as the following iterative lemma. We do not give the proof because it can be seen in ^[27].

Lemma 4.8. Suppose $\omega\in \mathcal{L}$, $\tilde\rho(\omega, \rho+f(\theta, \varphi)) = \rho_f\in DC_\omega(\gamma, \tau)$ and $r_n$, $s_n$, $\epsilon_n$ are defined in (4.18) for $n\geq 0$. Let $\epsilon_0$ be sufficiently small. Then the following holds for all $n\geq 1$: If the system

satisfies

then there exists a change of variables $\widetilde H_n:\mathbb{T}\times\mathbb{T}^d\rightarrow \mathbb{T}\times\mathbb{T}^d$ with estimates

such that it transforms the system (4.26) to

with

4.2.3.   Convergence

Let $\epsilon_0$ be sufficiently small and $r_0 = r$, $s_0 = s$. If $\tilde\rho(\omega, \rho+f) = \rho_f\in DC_\omega(\gamma, \tau)$ and $\|f\|_{s, r, \mathcal{O}_{\gamma}} < \epsilon_0/2$, then the vector field

can be written as

where $\tilde f(\theta, \varphi) = \rho-\rho_f+f(\theta, \varphi)$. We can use Lemma 4.6 to system (4.27). Thus we can get $\widetilde H_0\in H^{s_1, r_1, a},$ which conjugates (4.27) to

with

Then we apply Lemma 4.8 inductively, we can get $\widetilde H_i\in H^{s_{i+1}, r_{i+1}, a}$, $i = 1, \cdots, n,$ such that $H^{(n)} = \widetilde H_0\circ \widetilde H_1\circ\cdots\circ \widetilde H_n$ conjugates (4.27) to

with

And we have

which implies

By the definition of $(\epsilon_n)_{n\in\mathbb{N}}$, we know that for any $j\in \mathbb{Z}_+^{1+d},$ there exists $N\in \mathbb{N}$, such that for any $n\geq N$, we have $8(\frac{4K_{n+1}^\alpha}{r_0})^{|j|}\epsilon_n^{\frac{3}{4}}\leq \epsilon_n^{\frac{1}{2}}$. By the Cauchy estimates, if we denote $x: = (\theta, \varphi)\in \mathbb{T}^{1+d}$, we have

for any $n > N-1$. This guarantees the limit $\lim_{n\rightarrow \infty}H^{(n)}$ belongs to $C^\infty$.

Finally, let $m({\varphi}) = \lim_{n\rightarrow \infty}g_{n}(\varphi)$ and $\Psi = (\lim_{n\rightarrow \infty}H^{(n)})^{-1}$, the proof of Proposition 3.1 completed.

Author contributions

Xinyu Guan: Methodology, Writing-original draft; Nan Kang: Validation(equal), Writing-review & editing (equal). All authors have read and approved the final version of the manuscript for publication.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments (All sources of funding of the study must be disclosed)

Xinyu Guan was partially supported by the National Natural Science Foundation of China (Grant No. 12301201) and the Shandong Provincial Natural Science Foundation, China (Grant No. ZR2023QA055).

Conflict of interest

The authors declare that there is no conflict of interest in this paper.

A.   Appendix

We give the conception of continued fraction expansion and $CD$-bridge. Let $\alpha\in (0, 1)$ be irrational and ${\rm int}(\bullet)$ denote the integer part of $\bullet$. Define that $a_0 = 0$, $\alpha_0 = \alpha$, and inductively for $k\geq 1$,

We also define that $p_0 = 0$, $p_1 = 1$, $q_0 = 1$, $q_1 = a_1$, and recursively,

Then $(q_n)$ is the sequence of denominators of the best rational approximation for $\alpha$. It satisfies

and

where $\|x\|_{\mathbb{T}}$ is defined by $\|x\|_{\mathbb{T}} = \inf_{p\in\mathbb{Z}}|x-p|.$

For each $\alpha\in \mathbb{R}/\mathbb{Q}$, in the sequel we will fix a particular subsequence $(q_{n_k})$ of the denominators of the best rational approximations for $\alpha$, which for simplicity will be denote by $(Q_k)$. Denote the sequences $(q_{n_{k}+1})$ and $(p_{n_k})$ by $(\overline{Q}_{k})$ and $(P_k)$ respectively. Now, we introduce the concept of a $CD$-bridge which first appeared in ^[4].

Definition A.1. Let $0 < \mathcal{A}\leq \mathcal{B}\leq \mathcal{C}.$ We say that the pair of denominators $(q_l, q_n)$ forms a $CD(\mathcal{A}, \mathcal{B}, \mathcal{C})$ bridge if

• $q_{i+1}\leq q_i^{\mathcal{A}}, \; \forall i = l, \ldots, n-1$,

• $q_l^{\mathcal{C}}\geq q_n\geq q_{l}^{\mathcal{B}}$.

Lemma A.1. For each $\mathcal{A}\geq 1$, there exists a subsequence $(Q_k)$ such that $Q_0 = 1$, and for each $k\geq 0$, $Q_{k+1}\leq \overline Q_{k}^{\mathcal{A}^4}$, and either $\overline Q_k\geq Q_k^{\mathcal{A}},$ or the pairs $(\overline Q_{k-1}, Q_k)$ and $(Q_k, Q_{k+1})$ are both $CD(\mathcal{A}, \mathcal{A}, \mathcal{A}^3)$ bridges.

The proof can be seen in ^[4].