Some systems were recently put forth by Nguyen et al. as models for studying the interaction of long and short waves in dispersive media. These systems were shown to possess synchronized Jacobi elliptic solutions as well as synchronized solitary wave solutions under certain constraints, i.e., vector solutions, where the two components are proportional to one another. In this paper, the exact periodic traveling wave solutions to these systems in general were found to be given by Jacobi elliptic functions. Moreover, these cnoidal wave solutions are unique. Thus, the explicit synchronized solutions under some conditions obtained by Nguyen et al. are also indeed unique.
Citation: Bruce Brewer, Jake Daniels, Nghiem V. Nguyen. Exact Jacobi elliptic solutions of some models for the interaction of long and short waves[J]. AIMS Mathematics, 2024, 9(2): 2854-2873. doi: 10.3934/math.2024141
| [1] | Mansour Shrahili, Mohamed Kayid . Laplace transform ordering of bivariate inactivity times. AIMS Mathematics, 2022, 7(7): 13208-13224. doi: 10.3934/math.2022728 |
| [2] | Miaomiao Zhang, Bin Lu, Rongfang Yan . Ordering results of extreme order statistics from dependent and heterogeneous modified proportional (reversed) hazard variables. AIMS Mathematics, 2021, 6(1): 584-606. doi: 10.3934/math.2021036 |
| [3] | Mingxia Yang . Orderings of the second-largest order statistic with modified proportional reversed hazard rate samples. AIMS Mathematics, 2025, 10(1): 311-337. doi: 10.3934/math.2025015 |
| [4] | Mohamed Kayid . Dynamic multivariate quantile inactivity time and applications in investigation of a treatment effect. AIMS Mathematics, 2024, 9(11): 30000-30014. doi: 10.3934/math.20241449 |
| [5] | Bin Lu . Stochastic comparisons of second-order statistics from dependent and heterogeneous modified proportional (reversed) hazard rates scale models. AIMS Mathematics, 2024, 9(4): 8904-8919. doi: 10.3934/math.2024434 |
| [6] | Bin Lu, Rongfang Yan . Ordering results of second order statistics from random and non-random number of random variables with Archimedean copulas. AIMS Mathematics, 2021, 6(6): 6390-6405. doi: 10.3934/math.2021375 |
| [7] | Refah Alotaibi, Hassan Okasha, Hoda Rezk, Abdullah M. Almarashi, Mazen Nassar . On a new flexible Lomax distribution: statistical properties and estimation procedures with applications to engineering and medical data. AIMS Mathematics, 2021, 6(12): 13976-13999. doi: 10.3934/math.2021808 |
| [8] | Tie Li, Zhengcheng Zhang . Generalized conditional spacings and their stochastic properties. AIMS Mathematics, 2024, 9(9): 23909-23923. doi: 10.3934/math.20241162 |
| [9] | Li Zhang, Rongfang Yan . Stochastic comparisons of series and parallel systems with dependent and heterogeneous Topp-Leone generated components. AIMS Mathematics, 2021, 6(3): 2031-2047. doi: 10.3934/math.2021124 |
| [10] | Tabassum Naz Sindhu, Zawar Hussain, Naif Alotaibi, Taseer Muhammad . Estimation method of mixture distribution and modeling of COVID-19 pandemic. AIMS Mathematics, 2022, 7(6): 9926-9956. doi: 10.3934/math.2022554 |
Some systems were recently put forth by Nguyen et al. as models for studying the interaction of long and short waves in dispersive media. These systems were shown to possess synchronized Jacobi elliptic solutions as well as synchronized solitary wave solutions under certain constraints, i.e., vector solutions, where the two components are proportional to one another. In this paper, the exact periodic traveling wave solutions to these systems in general were found to be given by Jacobi elliptic functions. Moreover, these cnoidal wave solutions are unique. Thus, the explicit synchronized solutions under some conditions obtained by Nguyen et al. are also indeed unique.
The inactivity time of a lifetime unit, also known as the reversed residual life or past lifetime, has involved many studies in different contexts with an increasing interest in the literature (see, e.g., Finkelstein [10], Kayid and Ahmad [20], Ahmad et al. [1], Kayid and Izadkhah [23], Khan et al. [26] and Khan et al. [25]). The inactivity time has been mainly used in reliability and furthermore it has also been useful to describe the behavior of lifetime random variables in survival retrospective studies when dealing with past events or situations showing the improvement/deteriorate of the lifetime of a system over a period of time (Andersen et al. [2]); and some applications have been discovered in risk theory, and econometrics (Eeckhoudt and Gollier [9], Kijima and Ohnishi [27], and Ma [31]).
Based on the concept of inactivity time, various types of stochastic orders, inequalities and associated properties have been developed rapidly over the years, resulting in a large body of literature (cf. Nanda et al. [36], Kayid and Ahmad [20], Izadkhah and Kayid [17] and Kayid et al. [22]).
In the context of survival analysis numerous models have been introduced in the literature to model lifetime data. The Cox's proportional hazards (PHR) model is one of the reputable models among other models. Bennett [7] introduced the proportional odds model and following this model Li and Zhao [29] then developed the mixture model. Zahedi [43] presented the proportional mean residual life model on the basis of the proportionality of two mean residual life functions and then Gupta and Kirmani [12] and Nanda et al. [37] studied some reliability properties in this model. Gupta et al. [13] proposed the proportional reversed hazards (PRH) model in contrast to the PHR model as a competitive for lehmann alternatives. They studied the monotonicity of the failure rate function in the case of their model. Di Crescenzo [8] presented several implications involving various stochastic orders and aging properties in reliability theory for the PRH model. Later, Gupta and Gupta [15] further concentrated on the structure of the PRH model and discussed some possible applications of the model. For example, some aging properties of the model were investigated. Li and Li [28] introduced a mixture PRH model and focused on some stochastic comparisons and aging properties regarding this model. Badía and Berrade [4] developed some properties of mean inactivity time (MIT) function and reversed hazard rate (rhr) function for mixtures. Asadi and Berred [3] proposed a new reliability model based on the proportionality of two mean inactivity time functions called proportional mean inactivity time model (PMIT). The monotonicity property of the variance of the inactivity time in the PMIT model has been obtained by Toomaj and Di Crescenzo [41]. In the context of this model a useful characterization related to the parallel systems was obtained. They proved that if the PMIT model and the PRH model coincide with each other then a family of distributions is characterized. By some examples, they have indicated the usefulness of the PMIT model. Recently, Rezaei [39] focused on the PMIT model to study some reliability properties and some implications of stochastic orders and aging notions between random variables that follow the model. Extended mixture model arising from the PMIT model is introduced in Badía and Cha [5]. Preservation properties of some stochastic orders and aging classes of lifetime distributions under this mixture model has been obtained by Rezaei [39]. Negative dependence properties between two variables constipating the PMIT model have also been acquired in Rezaei [39]. Recently, relative ageing properties of distributions in frailty and resilience models based on the MIT function as well as other related reliability measures have been developed by Misra and Francis [34].
In a dynamic mean inactivity time model, more information about common closure properties with respect to stochastic changes may be sought. Dependencies among random variables constituting the model and preservation properties of stochastic orders under the framework of the model can be developed. This paper addresses this issue and clarify further aspects of the mean inactivity time frailty models in general and a weighted proportional mean inactivity time in particular for future studies in this direction. We present the mixture distribution which is arisen from the frailty models. In mixture models, we focus on the dependence structure between the variable that gives amounts in overall population and the mixing random variable. We finally apply the model on a real data set and also carry out a simulation study.
Before closing this section for ease of reference we give some preliminary notions that will be used throughout the paper. Let Xi be a non-negative random variable (rv) with probability density function (pdf) ϕi, cumulative distribution function (cdf) Φi, and survival function (sf) ˉΦi≡1−Φi, for i=1,2. The rhr function of Xi is given by ri(t)=(Φi(t))−1ϕi(t) for i=1,2. The MIT function, for the random variable Xi which has finite mean, is mi(t)=(Φi(t))−1∫t0Φi(x)dx, t>0 for i=1,2.
Definition 1.1. The random variable X1 is said to be smaller than X2 in the:
(i) Likelihood ratio order (denoted by X1≤lrX2), if ϕ2(t)/ϕ1(t) is non-decreasing in t>0.
(ii) Reversed hazard order (denoted by X1≤rhrX2) if r1(t)≤r2(t), for all t≥0; or equivalently if Φ2(t)/Φ1(t) is non-decreasing in t on (0,∞).
(iii) Mean inactivity time order (denoted by X1≤mitX2) if m1(t)≥m2(t), for all t>0; or equivalently if
| ∫t0Φ2(x)dx∫t0Φ1(x)dxisnon−decreasingint>0. |
(iv) Usual stochastic order (denoted by X1≤stX2) if ˉΦ1(t)≤ˉΦ2(t) for all t≥0.
(v) Strong mean inactivity time order (denoted by X1≤smitX2),
| ∫t0xΦ2(x)dx∫t0xΦ1(x)dxisnon−decreasingint>0. |
(vi) Increasing concave order (denoted by X1≤icvX2), if ∫t0Φ2(x)dx≤∫t0Φ1(x)dx for all t≥0.
The following chain of implications explains the relations of stochastic orders in Definition 1.1.
| X1≤lrX2→X1≤rhrX2→X1≤stX2↓↘X1≤smitX2→X1≤mitX2→X1≤icvX2. |
The hazard rate (hr) function of Xi is given by hi(t)=(ˉΦi(t))−1ϕi(t) for i=1,2. The mean residual lifetime (MRL) function for Xi with finite mean, is given by Mi(t)=(ˉΦi(t))−1∫∞tΦi(x)dx, t>0 for i=1,2. The following definition presents stochastic orders that are related to the residual lifetime Xit=(Xi−t|Xi>t) in place of the inactivity time Xi(t)=(t−Xi|Xi≤t) for i=1,2.
Definition 1.2. The random variable X1 is said to be smaller than X2 in the:
(i) Hazard rate order (written as X1≤hrX2) if h1(t)≥h2(t), for all t≥0; or equivalently if ˉΦ2(t)/ˉΦ1(t) is non-decreasing in t on (0,∞).
(ii) Mean residual lifetime order (written as X1≤mrlX2) if M1(t)≤M2(t), for all t>0; or equivalently if
| ∫∞tˉΦ2(x)dx∫∞tˉΦ1(x)dxisnon−decreasingint>0. |
(iii) Increasing convex order (written as X1≤icxX2), if ∫∞tˉΦ2(x)dx≤∫∞tˉΦ1(x)dx for all t≥0.
For more details and descriptions, one may refer to Shaked and Shanthikumar [40], Müller and Stoyan [35], and Kayid and Ahmad [20]. The following chain of implications explains the relations of stochastic orders in Definitions 1.1 and 1.2.
| X1≤lrX2→X1≤hrX2→X1≤stX2↓↓X1≤mrlX2→X1≤icxX2. |
Two notions of total positivity and reverse regularity are defined below according to Karlin [19].
Definition 1.3. δ(x,y)≥0 is said to be totally positive of order 2 (abbreviated by TP2) in (x,y)∈χ×γ, whenever
| |δ(x1,y1)δ(x1,y2)δ(x2,y1)δ(x2,y2)| ≥0, | (1.1) |
for all x1≤x2∈χ and y1≤y2∈γ, in which χ and γ are two real subsets of R.
Remark 1.4. If the direction of the inequality given in (1.1) is reversed, then δ(x,y) is said to be reverse regular of order 2 (abbreviated by RR2). By convention, a/0=+∞, for any a>0 and a/0=0 when a=0. It is thus not hard to conclude that, β(x,y) is TP2 (RR2) if δ(x2,y)/δ(x1,y) is increasing (decreasing) in y∈γ, for all x1≤x2∈χ, or equivalently if, δ(x,y2)/δ(x,y1) is increasing (decreasing) in x∈χ, for each y1≤y2∈γ.
Throughout this paper, the phrase "increasing" means "monotone non-decreasing" and the term "decreasing" stands for "monotone non-increasing". The random variables under consideration are assumed to have absolutely continuous distribution functions and we suppose further that the random variables are non-negative in the sense that the left limit, at the point 0, of their cumulative distribution functions is 0.
To fix the idea, consider a random MIT m(t,V) at a time t, where V is a random factor of an individual which is randomly taken from the population. The conditional cumulative distribution function (cdf) of the lifetime T given V=v is
| F(t|v)=P(T≤t|V=v) | (2.1) |
and the conditional of T given V=v is f(t|v). Therefore, the conditional MIT of T given V=v is
| m(t,v)=∫t0F(x|v)dxF(t|v),t≥0, | (2.2) |
for all v for which F(t|v)>0, where F(t|v) is the conditional cdf of T given that V=v as defined earlier in (2.1). For the sake of completeness, a closely related measure known as the reversed failure rate (rfr) function of T given V=v is given by
| r(t|v)=f(t|v)F(t|v),t≥0, | (2.3) |
which is connected to the MIT function as
| r(t|v)=1−∂∂tm(t,v)m(t,v),t≥0. | (2.4) |
By inversion formula, when r(t|v) is known, the conditional cdf F(⋅|v) can be obtained via
| F(t|v)=exp{−∫+∞tr(x|v)dx},t≥0. | (2.5) |
Hence, in the sprit of (2.4) and (2.5) the conditional cdf F(⋅|v) is characterized as
| F(t|v)=exp{−∫∞t(1−∂∂xm(x,v)m(x,v))dx},t≥0. | (2.6) |
The relation (2.6) between the cdf and the MIT function of a random variable could also be achieved as in Finkelstein (2002) by considering the MIT function m(t,v) in place of the MIT of the original distribution.
It is quite well-known that (see, e.g., Kayid and Izadkhah (2018)) m(t,v) is valid as the MIT of a lifetime random variable for a given v>0 and, therefore, (2.6) is a valid distribution function whenever
(ⅰ) m(t,v)>0 for all t>0 and for all v, and m(0,v)=0.
(ⅱ) ∂∂tm(t,v)<1, for all t≥0.
(ⅲ) ∫+∞t(1−∂∂τm(τ,v)m(τ,v))dτ<∞, for all t>0.
(ⅳ) ∫+∞0(1−∂∂τm(τ,v)m(τ,v))dτ=∞.
The association of t and v in m(t,v) in different possible ways may trigger the construction of dynamic MIT-based models. For example, in the PMIT model one has m(t,v)=vm0(t) where m0(t) is the baseline MIT function (see, e.g., Asadi and Berred [3], Rezaei [39], Mansourvar and Asadi [32] and Hooti et al. [16]). In this context, a general semiparametric model is m(t,v)=ψ(m0(t),v) in which ψ is an appropriate selected bivariate function under which m(t,v) is valid as an MIT function. For instance, in contrast to the additive mean residual life model which is a quite valid model (see, e.g., Kayid et al. [21]) the additive mean inactivity time model m(t,v)=m0(t)+v is not valid since m(0,v)>0 which contradicts latter part in the condition (i) above.
In the framework of some well-known applied semiparametric models in survival analysis each of which is a source of association of t and v in m(t,v), the following examples illustrate the formation and the exhibition of the MIT function. The baseline distribution F is chosen to be the (no-aging) exponential distribution in each case.
Example 2.1. Consider the proportional odds model ˉF(x|v)=vˉF(x)/(1−ˉvˉF(x)) with ˉv=1−v,v>0 where the baseline is exponential distribution with mean μ. Thus, the implied cdf is F(x|v)=(ex/μ−1)/(ex/μ−ˉv). As stated in Marshall and Olkin [33] this is a two-parameter competitor of the Weibull and the Gamma distributions. The mean inactivity time (2.2) for v≠1 has the closed form
| m(t,v)=(etμ−ˉv)(t+μvln(1−ˉvetμ−ˉv))ˉv(etμ−1). | (2.7) |
However, for v=1 we know that ˉF(x|v)=ˉF(x)=e−xμ. The limit of (2.7) as v approaches 1 is
| m(t,1−)=t1−e−tμ−μ | (2.8) |
which is exactly the MIT of the exponential distribution with mean μ. Figure 1 plots the graph of m(t,v) for different values of tilt parameter v. If v≠1 the expression in (2.7) is valid and for v=1 the mean inactivity time is as given in (2.8).
Example 2.2. Consider the proportional hazard rates model ˉF(x|v)=ˉFv(x),v>0 where the baseline is exponential distribution with mean μ. Therefore, the implied sf is ˉF(x|v)=e−xv/μ. This is the sf of the exponential distribution with mean μ/v. Hence, from (2.8) for all v>0 we have
| m(t,v)=t1−e−tvμ−μv. | (2.9) |
Figure 2 plots the graph of m(t,v) in (2.9) for different values of v.
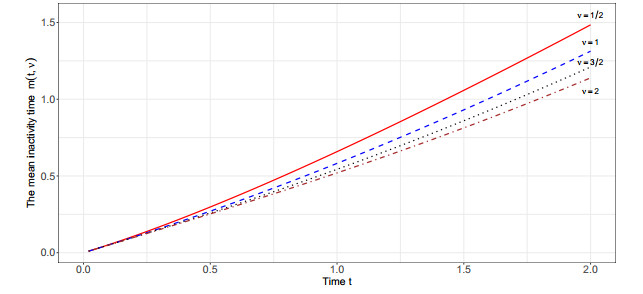
Example 2.3. In the proportional reversed hazard rates model it holds that F(x|v)=Fv(x),v>0 in which ˉF(x)=e−x/μ which concludes that F(x|v)=(1−e−x/μ)v. For all v>0,
| m(t,v)=μ∫1e−t/μ(1−y)vydy(1−e−t/μ)v. | (2.10) |
In general, the mean inactivity time function does not have a closed form in this case. However, for some rational values of v it may have a closed form. For instance when v=1/2 we get
| m(t,v)=m(t,12)=t+μln(2−e−tμ)√1−e−tμ−2μ√1−e−tμ. |
and v=3/2 we obtain
| m(t,v)=m(t,32)=−23μ−2μ1−e−tμ+μln(1+√1−e−tμ1−√1−e−tμ)(1−e−tμ)32. |
For v=2, we have
| m(t,v)=t+2μe−tμ−μ2e−2tμ−32μ(1−e−tμ)2. |
Figure 3 plots the graph of m(t,v) in (2.10) for v=1/2,1,3/2,2.
Example 2.4. In the proportional mean residual life model we have
| ˉF(t|v)=(∫∞tˉF(x)dx)1+1vμ1+1vˉF(t). |
By taking ˉF(x)=e−x/μ as the baseline distribution it reduces to ˉF(x|v)=e−x/vμ,v>0. For all v>0,
| m(t,v)=t1−e−tvμ−vμ. | (2.11) |
Figure 4 exhibits the graph of m(t,v) in (2.11) for values v=1/2,1,3/2,2.
Remark 2.1. In the proportional mean inactivity time model it holds that (cf. Eq (3.2) in Hooti et al. [16])
| F(t|v)=F(t)(∫t0F(x)dx∫F−1(1)0F(x)dx)1v−1,0<v<1, |
where F−1(p)=sup{x|F(x)≤p}. However, as for many standard distributions with finite mean μ including the exponential distribution, ∫F−1(1)0F(x)dx=+∞ thus the proportional mean inactivity time model in such cases does not induce a proper distribution function (see, e.g., Hooti et al. [16]).
We will consider mixture of distribution (2.6) with respect to v which is a realization of V where we assume that T and V, denote the resultant (overall population) and the random factor (of individuals) in the population which have cdf's F and G, respectively. The associated density functions will also be denoted by f and g, respectively. Having the random factor to be realized as V=v, the conditional MIT function of the random variable T is given by
| m(t|v)=m(t,v),t≥0, | (2.12) |
where v is the frailty associated with an individual. In (2.12), m(t∣v) denotes the MIT of the conditional random variable X∣V=v which can be defined as
| m(t|v)=E(t−T|T≤t,V=v). |
The frailty V is basically considered to be unobservable and hence the individual level model in (2.6) is unobservable. The random variable V is the mixing random variable. It is, therefore, reasonable to consider the population model below in which the mean inactivity time is considered to be that of a randomly drawn individual:
| F∗(t)=E[F(t|V)]=∫+∞−∞F(t|v)dG(v), | (2.13) |
where F(t|v) is as given in (2.6). The unconditional pdf of T is also given by
| f∗(t)=E[f(t|V)]=∫∞−∞f(t|v)dG(v). | (2.14) |
The functions (2.13) and (2.14) are known as the population-level distribution function and the population-level density function, respectively.
According to Li et al. [30], the reversed hazard rate of the general mixture model (2.13) is given by
| r∗(t)=∫+∞−∞f(t|v)g(v)dv∫+∞−∞F(t|v)g(v)dv=∫+∞−∞r(t|v)g(v|T≤t), |
where g(v|T≤t) is the conditional pdf of V given that T≤t which is given by
| g(v|T≤t)=F(t|v)g(v)∫+∞−∞F(t|v)g(v)dv |
and
| G(v|T≤t)=P(V≤v|T≤t)=∫v−∞F(t|v)g(v)dv∫+∞−∞F(t|v)g(v)dv |
is the corresponding distribution function. It is remarkable that G(v|T≤t) converges to G(v) as t→∞. The conclusion is that r∗(t)=E(r(t|V)|T≤t).
The population level mean inactivity time function is given by
| m∗(t)=∫t0F∗(x)F∗(t)dx,t>0. | (2.15) |
The following result shows that the mean inactivity time at time t in the dynamic population is the average of the individual mean inactivity time among the lives left before time t.
Theorem 2.5. The population level mean inactivitytime function is the expected value of m(t∣V) with respect to the conditional density of thefrailty random variable V given T≤t. That is m∗(t)=E[m(t∣V)∣T≤t].
Proof. Note that the conditional pdf of V given T≤t is given by
| g(v|T≤t)=∂∂vP(V≤v,T≤t)P(T≤t)=∂∂v∫v0P(T≤t|V=u)dG(u)F(t)=∂∂v∫v0F(t|u)g(u)duF(t)=F(t|u)g(u)F(t),t>0,v>0. | (2.16) |
In view of (2.16), by using the Fubini Theorem it follows from (2.15) that
| m∗(t)=∫t0∫∞0F(x|v)h(v)dvdxF(t)=∫∞0∫t0F(x|v)g(v)dxdvF(t)=∫∞0∫t0F(x|v)dxF(t|v)F(t|v)g(v)F(t)dv=∫∞0m(t|v)g(v|T≤t)dv=E[m(t|V)|T≤t]. | (2.17) |
This section includes some closure properties of the model with respect to some dependence structures. According to Nelsen [38], the following notions of dependence are proposed.
Definition 3.1. (i) The random variables X and Y have positive [negative] likelihood ratio dependence (PLRD [NLRD]) structure if their joint density f(x,y) is TP2 (RR2) in (x,y).
(ii) The random variable X is stochastically increasing [decreasing] in Y (SI(X|Y) [SD(X|Y)]) if F(x∣y) is non-increasing [non-decreasing] in y, for all x.
(iii) The random variables X and Y are left corner set decreasing [increasing] (LCSD [LCSI]) if P(X≤x,Y≤y) is TP2 (RR2) in (x,y).
(iv) The random variable X is left tail decreasing [increasing] in Y (LTD(X|Y) [LTI(X|Y)]) if P(X≤x∣Y≤y) is decreasing [increasing] in y, for all x.
It is well-known in the literature that
| PLRD(X,Y)[NLRD(X,Y)]⇒LCSD(X,Y)[LCSI(X,Y)]⇒LTD(X∣Y)[LTI(X∣Y)] |
and that
| PLRD(X,Y)[NLRD(X,Y)]⇒SI(X∣Y)[SD(X∣Y)] |
The dependence structure between the unconditional random variable T with cdf (2.13) and the frailty variable V with cdf G may be explainable in terms of the deterministic notions of dependence reported in Definition 3.1 and sufficient conditions on the shape of the individual-indexed MIT function m(t|v) can be obtainable. We will assume, for simplicity, that m(t|v) is twice differentiable with respect to t and differentiable with respect to v.
Definition 3.2. (a) Let (i) m(t|v) and ∂2m(t|v)/∂t2 be decreasing in v, for all t≥0 such that ∂m(t|v)/∂t is decreasing (resp. increasing) in v, for all t≥0 and let (ii) m(t|v) be RR2 in (t,v) and let m(t|v) be convex (resp. concave) in t≥0, for all v. Then T and V are PLRD.
(b) Let (i) m(t|v) and ∂2m(t|v)/∂t2 be increasing in v, for all t≥0 such that ∂m(t|v)/∂t is increasing (resp. decreasing) in v, for all t≥0 and let (ii) m(t|v) be TP2 in (t,v) and let m(t|v) be convex (resp. concave) in t≥0, for all v. Then T and V are NLRD.
Proof. By Definition 4(ⅲ) in Hooti et al. [16] and from Definition 3.1(ⅰ) T and V are PLRD if, and only if, ∂2ln(f(t|v))/∂v∂t≥0, ∀t≥0,∀v. Denote m′(t,v)=∂m(t|v)/∂t and m″. From (2.6), we get
| f(t|v) = \frac{1-m'(t,v)}{m(t,v)}exp\left(-\int_t^{\infty}\frac{1-m'(x,v)}{m(x,v)}\; dx \right) |
from which one has
| \begin{align*} \frac{\partial}{\partial t}\ln(f(t|v))& = \frac{1-m'(t,v)}{m(t,v)}-\frac{m'(t,v)}{m(t,v)}-\frac{m''(t,v)}{1-m'(t,v)}\\ & = \frac{1-2m'(t,v)}{m(t,v)}-\frac{m''(t,v)}{1-m'(t,v)}\\ & = \frac{1}{m(t,v)}-2\frac{\partial}{\partial t} \ln(m(t,v))-\frac{m''(t,v)}{1-m'(t,v)}. \end{align*} |
Therefore,
| \begin{align*} \frac{\partial^2}{\partial v \partial t}\ln(f(t|v))& = \frac{\partial}{\partial v}\frac{1}{m(t,v)}-2\frac{\partial^2}{\partial v \partial t}\ln(m(t,v))\\ &-\frac{\frac{\partial}{\partial v}m''(t,v)}{1-m'(t,v)}-\frac{m''(t,v)\frac{\partial}{\partial v} m'(t,v)}{(1-m'(t,v))^2}. \end{align*} |
To prove assertion (a), from assumptions we have for all t\geq 0 and for all v , (\partial/\partial v)(1/m(t, v))\geq 0, \partial^2 \ln(m(t, v))/\partial v \partial t \leq 0, (\partial/\partial v) m''(t, v)\leq 0 , (\partial/\partial v)m'(t, v) \leq (resp. \geq) 0 and m''(t, v)\geq (resp. \leq) 0 thus using the last identity above one gets (\partial^2)/(\partial v \partial t)\ln(f(t|v))\geq 0 , for all t\geq 0 and for all v, i.e., T and V are PLRD. To present a proof for assertion (b), we similarly conclude by assumptions that for all t\geq 0 and for all v , (\partial/\partial v)(1/m(t, v))\leq 0, \partial^2 \ln(m(t, v))/\partial v \partial t \geq 0, (\partial/\partial v) m''(t, v)\geq 0 , (\partial/\partial v)m'(t, v) \geq (resp. \leq) 0 and m''(t, v)\geq (resp. \leq) 0 thus it follows that (\partial^2)/(\partial v \partial t)\ln(f(t|v))\leq 0 , for all t\geq 0 and for all v, i.e., T and V are NLRD.
In the following theorem sufficient conditions for weaker dependencies are presented.
Definition 3.3. Let m(t|v) be decreasing (increasing) in v, for all t\geq 0 so that m(t|v) be RR _2 (TP _2 ) in (t, v) . Then
(i) T is stochastically increasing (decreasing) in V .
(ii) T and V are LCSD (LCSI) and also LTD (LTI).
Proof. By virtue of (2.6), one writes
| F(t|v) = P(T\leq t|V = v) = \exp\left(-\int_t^{\infty} \left(\frac{1}{m(x,v)}-\frac{\partial}{\partial x}\ln(m(x,v))\right)dx\right) |
for the cdf of T given V = v (individual-level present frailty) and denotes the cdf of T given V\leq v (individual-level past frailty) by
| F^{\ast}(t|v) = P(T\leq t|V\leq v) = \int_{-\infty}^{v}\frac{F(t|y)g(y)}{G(v)}dy |
To have SI(T|V) ( SD(T|V) ) a necessary and sufficient condition is that
| \partial \ln(F(t|v))/\partial v \geq (\leq) 0 |
for all t\geq 0 and for all v and that T and V are LCSD (LCSI) if, and only if, \partial^2 \ln(F^{\ast}(t|v))/\partial t \partial v \geq (\leq) 0 for all t\geq 0 and for all v . To indicate the first dependency statement, we write
| \frac{\partial}{\partial v}\ln(F(t|v)) = \int_t^{+\infty} \left(\frac{\partial^2}{\partial v\partial x}\ln(m(x,v))-\frac{\partial}{\partial v}\frac{1}{m(x,v)}\right)dx |
which is non-negative (non-positive) by assumption and hence the proof of (i) is completed. To have the second dependency property we see that
| \partial^2 \ln(F^{\ast}(t|v))/\partial t \partial v \geq (\leq) 0 |
holds whenever
| f(t|v)F(t|y)\geq (\leq)f(t|y)F(t|v)\; \; for\; all\; y\leq v, |
which holds if and only if r(t|v)\geq (\leq) r(t|y) for all y\leq v . It is known from (2.4) that if m(t|v) be decreasing (increasing) in v, for all t\geq 0 so that m(t|v) be RR _2 (TP _2 ) in (t, v) then r(t|v) is increasing (decreasing) in v . Hence the results immediately follow.
The following lemma which is due to Foschi and Spizzichino [11] makes Theorem 3.1 applicable to conclude some stochastic comparisons of individual-level (conditional) random variables in the mean inactivity time frailty model. This may reveal further aspects of association of T and V in the model.
Lemma 3.4. (i) The random variables T and V have positive [negative] likelihood ratio dependence(PLRD [NLRD]) structure iff T|V = v_1 \leq_{lr} (\geq_{lr}) T|V = v_2 , for all v_1 \leq v_2.
(ii) The random variable T is stochastically increasing [decreasing] in X (SI( T|V )[SD( T|V )]) iff T|V = v_1 \leq_{st} (\geq_{st}) T|V = v_2, for all v_1 \leq v_2.
(iii) The random variables T and V are left corner set decreasing [increasing](LCSD [LCSI]) iff T|V\leq v_1 \leq_{rhr} (\geq_{rhr}) T|V\leq v_2, for all v_1 \leq v_2.
(iv). The random variable T is left tail decreasing [increasing] in V (LTD( T|V )[LTI( T| V )]) iff T|V\leq v_1 \leq_{st} (\geq_{st}) T|V\leq v_2, for all v_1 \leq v_2.
Lemma 3.4 is useful to interpret the results of Theorem 3.1 and Theorem 3.2 which has been originally stated for dependencies in terms of stochastic orders between special conditional random variables. The interpretation will be more detailed when the model is applied to a context where T and V have physical senses.
The dynamic MIT model proposed in Section 2 stands as a general frailty model with the bivariate MIT function m(t, v) as the underlying unique characteristic of the distribution. The feature of association between t (time) and v (frailty) in m(t, v) has an important role in the model to conclude further implications. Thus, a search for proper choices of this function is worth as the reader of the paper may seek it also. As argued previously, any function (t, v)\mapsto m(t, v) having an arbitrary shape cannot be an MIT function which is in turn a difficulty in theoretical case. The multiplicative association m(t, v) = m_1(v)m_2(t) (in which m_1 and m_2 are two proper non-negative functions) is a typical instance of the general dynamic MIT model which proposes a weighted model as a particular case (which is also a generalization of the commonly used PMIT model in literature) by which a number of regular properties of the MIT function such as the TP_2 property and the RR_2 property is induced being important for developing ordering properties in the model as will be seen in the sequel.
To develop the properties of proportional models in reliability and survival analysis some weighted versions of models have been considered in the literature recently. For example, Jarrahiferiz et al. [18] have proposed the weighted proportional hazards model and Kayid et al. [24] have studied the weighted proportional reversed hazard rates model. The definition of a weighted version of the proportional mean inactivity time model is therefore a natural extension but the model is still a partial model. It is ordinarily pointed out, as illustrated also in Section 2, that there is a baseline mean inactivity time m_0(t) , say, on which a model about a response variable is constructed. Let us assume that \gamma(\cdot) is a non-negative function which is continuous so that
| \begin{equation} m(t|v) = v\gamma(t)m_0(t) . \end{equation} | (4.1) |
The association of t and v in the individual-level mean inactivity time function is multiplicative and \gamma plays the role of capturing further variations due to time in the PMIT model where m(t|v) = vm_0(t) which has already been defined and analyzed in the literature (see, e.g., Asadi and Berred [3] and Rezaei [39]). Unlike the PMIT model in the WPMIT model the resulting cdf does not have a closed expression. Based on (2.6), the conditional cdf of T given V = v is
| \begin{equation} F(t|v) = \frac{\gamma(\infty)m_0(\infty)}{\gamma(t)m_0(t)}e^{-\frac{1}{v}\int_t^{\infty} \frac{dx}{\gamma(x)m_0(x)}} = \frac{U'(t)}{U'(\infty)}\exp\left(-\frac{U(t)}{v}\right), \end{equation} | (4.2) |
where U(t) = \int_t^{\infty} dx/(\gamma(x)m_0(x)) and U' denotes the derivative of U . The associated pdf is also obtained as
| \begin{align} f(t|v)& = \frac{\partial}{\partial t}\left( \frac{U'(t)}{U'(\infty)}e^{-\frac{U(t)}{v}}\right) \\ & = \frac{U''(t)}{U'(\infty)}e^{-\frac{U(t)}{v}}-\frac{(U'(t))^2}{vU'(\infty)}e^{-\frac{U(t)}{v}} \\ & = \frac{1}{U'(\infty)}\left(U''(t)-\frac{(U'(t))^2}{v}\right)e^{-\frac{U(t)}{v}}, \end{align} | (4.3) |
in which U'' is the second derivative of U . The expression in the right hand side of (4.3) has to be positive. It is known that
| U(t) = v\int_t^{\infty} \frac{dx}{m(x|v)},\; U'(t) = -\frac{v}{m(t|v)},\; U''(t) = -v\frac{\partial}{\partial t} \frac{1}{m(t|v)}. |
Thus, we can write
| \begin{align*} U''(t)-\frac{(U'(t))^2}{v}& = -v\frac{\partial}{\partial t} \frac{1}{m(t|v)}-\frac{v}{m^2(t|v)}\\ & = -v\left(\frac{\partial}{\partial t}\frac{1}{m(t|v)}+\frac{1}{m^2(t|v)}\right)\\ & = -\frac{v}{m(t|v)}\left(\frac{\partial}{\partial t}\log\left(\frac{1}{m(t|v)}\right)-\frac{m'(t|v)}{m(t|v)}\right)\\ & = -\frac{v}{m^2(t|v)} (1-m'(t|v))\leq 0,\; \;{\rm{ for\; all }}\; t\geq 0, \end{align*} |
where the last inequality holds because m'(t|v) < 1 for all t\geq 0 . Now, since U'(\infty) < 0 hence
| \frac{1}{U'(\infty)}\left(U''(t)-\frac{(U'(t))^2}{v}\right)\geq 0,\; \;{\rm{ for\; all }}\; t\geq 0. |
The model given in (4.1) is a model with multiplicative effects of time and frailty as m(t|v) = a(t)b(v) in which a(\cdot) and b(\cdot) are non-negative functions product of them fulfilling the properties of a mean inactivity time function as enumerated in Section 2. In the model (4.1) we have a(t) = \gamma(t)m_0(t) and b(v) = v . The model is, hereafter, called the weighted proportional mean inactivity time (WPMIT) model.
Conditions under which (4.1), for a given v > 0 , is valid as an MIT function so that (4.2) stands as a valid distribution function are derived below:
(ⅰ) \gamma(t) > 0 , for all t > 0 .
(ⅱ) \frac{\partial}{\partial t}(\gamma(t)m_0(t)) < 1/v, for all t\geq 0 .
(ⅲ) \frac{U'(\infty)}{U'(t)}e^{U(t)/v} < \infty , for all t > 0 .
(ⅳ) \frac{U'(\infty)}{U'(0^{+})}e^{U(0^{+})/v} = \infty ,
where U(0^{+}) and U'(0^{+}) denote the right limit of U and U', respectively, at the point 0.
The following example illustrates an appropriate situation where the WPMIT model stands valid. Let F_0 be the baseline distribution function in the model with MIT function m_0 . Note that U(\infty) and U'(\infty) in all previous statements is replaced with U(u_{T_0}) and U'(u_{T_0}) in which u_{T_0} = \sup\{t\geq 0| F_0(t) < 1\} which applies for both finite and infinite supports for non-negative random variables.
Example 4.1. Let T_0 be an exponential random variable with mean one and with MIT function m_0 which is given by (see e.g., (2.8))
| m_0(t) = \frac{t}{1-e^{-t}}-1. |
Suppose that \gamma(t) = (2t-1+e^{-2t})/(4(1+e^{-t})(t-1+e^{-t})) . Then if v = 2, we get
| m(t|v) = m(t|2) = \frac{t}{1-e^{-2t}}-\frac{1}{2} |
which is the MIT function of an exponential random variable with mean \mu = 1/2 . We can see that (i) \gamma(t) > 0 for all t > 0 . We know that for any a > 0 , e^{-at} > 1-at for all t\geq 0 ; thus for all t\geq 0 we have that (t-1+e^{-t}) > 0 and that (2t-1+e^{-2t}) > 0 which concludes that \gamma(\cdot) is a positive function on (0, +\infty) . We also see that the condition (ii) holds true because
| \frac{\partial}{\partial t}(\gamma(t)m_0(t)) = \frac{1-e^{-2t}-2te^{-2t}}{2(1-e^{-2t})^2} < \frac{1}{2} |
is equivalent to 1-e^{-2t} < 2t for all t > 0 as stated in case (i). For condition (iii) after some calculation we get
| \frac{U'(\infty)}{U'(t)}e^{U(t)/v} = \frac{1}{1-e^{-2t}} |
which is finite for any t > 0 . The condition (iv) also easily follows since
| \frac{U'(\infty)}{U'(0^{+})}e^{U(0^{+})/v} = \lim\limits_{t\rightarrow 0^{+}}\frac{U'(\infty)}{U'(t)}e^{U(t)/v} = \lim\limits_{t\rightarrow 0^{+}}\frac{1}{1-e^{-2t}} = \infty. |
The heterogeneity is usually left to be unexplained in many problems in nature. The amount and even the distribution function of the random frailty V cannot be determined accurately. The mixture of the family of the proportional mean inactivity time has been initially considered by Badía and Cha [5] and they developed some bending properties of the mean inactivity time (see, e.g., Theorem 4(d) and Example 6 in Badía and Cha [5]). The importance of studying the influence of the heterogeneity caused solely by the frailty on the distribution of the response variable T in the WPMIT model. To evaluate the effect of variation of frailty variable one considers V_i for i = 1, 2 as the frailty associated with the i th population under consideration. We shall assume that V_i has an absolutely continuous cdf G_i with corresponding density function g_i . The corresponding response variable is denoted by T_i . In the spirit of (4.2), the unconditional cdf of T_i which represents a typical mixture model is as follows:
| \begin{equation} F_{i}^{*}(t) = \int_0^{\infty} \frac{U'(t)}{U'(\infty)}\exp\left(-\frac{U(t)}{v}\right)\; dG(v) = \frac{U'(t)}{U'(\infty)} E(\exp\left(-\frac{U(t)}{V_i}\right)). \end{equation} | (4.4) |
The dependence structure of T and V inspires aspects of stochastic relation among the random variables T and V . In accordance with Theorems 3.1 and 3.2 the dependence structure in MIT frailty models depends on the shape (behaviour) of the mean inactivity time m(t|v) and its partial derivatives. In the WPMIT model, to realize the dependency between the frailty V and the random variable T which has cdf
| \begin{equation} F(t) = \frac{U'(t)}{U'(\infty)} E\left[\exp\left(-\frac{U(t)}{V}\right)\right] \end{equation} | (4.5) |
one can apply Theorem 3.1(b). It is known that m(t|v) = v\gamma(t)m_0(t) is TP _2 and also RR _2 in (t, v) and that m(t|v) is increasing in v for all t\geq 0 . If \gamma(t)m_0(t) is increasing and convex in t\geq 0 then by Theorem 3.1(b) T and V are NLRD and also SD, LCSI and LTI. In addition, according to the parenthetical part of Theorem 3.2, which can be particularly applied in the cases where, in contrast to the previous case, \gamma(t)m_0(t) is not increasing and convex in t\geq 0 , T and V are LCSI and also LTI. The population distribution function (4.5) can be reduced to a specific individual in the population at the fixed frailty level V = v_0 whenever G(v) = 0 for all v < v_0 and G(v) = 1 for all v\geq v_0 , i.e. if P(V = v_0) = 1 which means that V is degenerate in v_0 > 0 .
To present further aspects of the stochastic relation of V and T , we can study how the stochastic orders between V_1 and V_2 are translated to the (same or different) stochastic orders among T_1 and T_2 . From the foregoing discussions, it is deduced that since V has a negative effect on the response variable T in the WPMIT model, thus it is expected that stochastic variation of V in one direction induces stochastic variation of T in another direction. In general, there is no compelling reason, other than mathematical tractability, to choose a the distribution of V . Thus, it is particularly important to investigate how the probability distribution of the overall random variable responds to variations in the probability distribution of the frailty. Stochastic comparison that translates the order between two frailty random variables into that between the corresponding overall variables helps in understanding the effect of mis-specification of the frailty distribution.
Recently, Xu and Li [42] proved that the (likelihood ratio) lr order, the hr order and rhr order between two frailty variables imply the lr order, the rhr order, and the hr order between the corresponding population variables, respectively. Gupta and Kirmani [14] conducted stochastic comparisons of frailty models arising from different choices of the distribution of frailty. They established that an increase in the frailty random variable in terms of the lr order tends to decrease the population random variable in the hr order.
Here, we demonstrate that the MIT order and the increasing concave (icv) order between two frailty variables imply the mrl order and the usual stochastic order of the corresponding population variables, respectively.
The main result about stochastic order relations in the WPMIT model is presented here. We assume that V_i and T_i for i = 1, 2 are non-negative random variables with absolutely continuous distribution functions.
Theorem 4.1. Let m(t|v) = v\gamma(t)m_0(t) such that U(t) = \int_t^{\infty}(1/\gamma(x)m_0(x))dx is twice differentiable in t . Suppose the conditions given in Remark 5 of Badía and Cha [5] for interchanging derivatives and integrals hold.
(ⅰ) If m(t|v) is increasing and convex in t > 0 for all v > 0 , then V_1 \leq_{lr} V_2 implies T_1 \geq_{lr} T_2.
(ⅱ) V_1 \leq_{st} V_2 implies T_1 \geq_{st} T_2.
(ⅲ) V_1 \leq_{hr} V_2 implies T_1 \geq_{rhr} T_2.
(ⅳ) Let F(t|v) be convex in v > 0 for all t\geq 0 . Then V_1 \leq_{mrl} V_2 implies T_1 \geq_{smit} T_2 and hence T_1 \geq_{mit} T_2.
(ⅴ) Let F(t|v) be convex in v > 0 for all t\geq 0 . Then V_1 \leq_{icx} V_2 implies T_1 \geq_{icv} T_2.
Proof. (ⅰ) By considering (4.3), it suffices to prove that
| f_i^{*}(t) = \int_{0}^{\infty} f(t|v)dG_i(v) = \int_{0}^{\infty}\frac{1}{U'(\infty)}\left(U''(t)-\frac{(U'(t))^2}{v}\right)e^{-\frac{U(t)}{v}}g_i(v)dv |
is RR _2 in (i, t) when i = 1, 2 and t\geq 0 . Since V_1\leq_{lr} V_2 thus g_i(v) is TP _2 in (i, v) when i = 1, 2 and v > 0 . If f(t|v) is RR _2 in (t, v) as t\geq 0 and v > 0 thus by general composition theorem in Karlin [19] we deduce that f_i^{*}(t) is RR _2 as a function of i = 1, 2 and t > 0 . We intend to prove that f(t|v) is RR _2 in (t, v) within the domain. Let us observe that
| \frac{\partial^2}{\partial t \partial v} \log(e^{-\frac{U(t)}{v}}) = \frac{U'(t)}{v^2} < 0,\; \; \;{\rm{ for\; all }}\;t > 0 |
which by appealing to Definition 4(iii) in Hooti et al. [16] implies that the function e^{-U(t)/v} is RR _2 in (t, v) when t\geq 0 and v > 0 . Denoting by \overset{sign}{ = } the equality in sign, we have
| \frac{d}{dv} \frac{U''(t_2)-(U'(t_2))^2/v}{U''(t_1)-(U'(t_1))^2/v}\overset{sign}{ = } U''(t_1)(U'(t_2))^2-U''(t_2)(U'(t_1))^2 |
which is non-positive for all 0\leq t_1 \leq t_2 when U(t) is convex in t\geq 0 , if, and only if, U''(t)/(U'(t))^2 is increasing in t\geq 0 . We have U'(t) = -v/m(t|v) and also that U''(t)/(U'(t))^2 = v^{-1}m'(t|v) . Thus the required conditions hold from assumption. Therefore, we proved that (U'(\infty))^{-1}(U''(t)-v^{-1}(U'(t))^2) is RR _2 in (t, v) when t\geq 0 and v > 0 . It is known that the product of two RR _2 functions is itself another RR _2 function and develop that f(t|v) which is the product of two RR _2 functions (U'(\infty))^{-1}(U''(t)-v^{-1}(U'(t))^2) and e^{-U(t)/v} is RR _2 in (t, v)\in [0, \infty)\times (0, \infty).
(ⅱ) It is clear that m(t|v) = v\gamma(t) m_0(t) is increasing in v , for all t\geq 0 and m(t|v) is TP _2 in (t, v) and thus according to Theorem 3.2(i) SD(T|V) holds by which
| F(t|v_1) = P(T\leq t|V = v_1)\leq P(T\leq t|V = v_2) = F(t|v_2),\; \; \;{\rm{ for\; all }}\;v_1\leq v_2. |
We showed that F(t|v) is increasing in v > 0 for all t\geq 0 . The assumption V_1 \leq_{st} V_2 yields \int_{a}^{\infty} d(G_2(v)-G_1(v))\geq 0 for all a\geq 0 . Thus, by Lemma 7.1(a) in Barlow and Proschan [6], \int_{-\infty}^{\infty} F(t|v)d(G_2(v)-G_1(v))\geq 0 for all t\geq 0 , i.e. F_2^{*}(t)\geq F_1^{*}(t), for all t\geq 0 and hence the result follows.
(ⅲ) The proof obtains if F_i^{*}(t) is TP _2 in (i, t) when i = 1, 2 and t\geq 0 . The partial derivatives of F(t|v) with respect to t and also v exist and they are continuous. We have
| \frac{\partial}{\partial v}F(t|v) = \frac{\partial}{\partial v}\left(\frac{U'(t)}{U'(\infty)}\exp\left(-\frac{U(t)}{v}\right)\right) = \frac{U'(t)U(t)}{U'(\infty)v^2}e^{-\frac{U(t)}{v}}, |
which is non-negative from Theorem 3.2(i). Integration by parts provides that
| \begin{align*} F_i^{*}(t)& = \int_{0}^{\infty} F(t|v)g_i(v)\; dv\\ & = l-u+\int_0^{\infty}\frac{U'(t)U(t)}{U'(\infty)v^2}e^{-\frac{U(t)}{v}} \bar{G}_i(v)dv\\ & = \int_0^{\infty}\frac{U'(t)U(t)}{U'(\infty)v^2}e^{-\frac{U(t)}{v}} G_i(v)dv, \end{align*} |
where
| l = \lim\limits_{v\rightarrow 0} F(t|v)\bar{G}_i(v) = \lim\limits_{v\rightarrow 0} \frac{U'(t)}{U'(\infty)}\exp\left(-\frac{U(t)}{v}\right)\bar{G}_i(v) = 0 |
and since \bar{G}_i(+\infty) = 0, i = 1, 2 thus
| u = \lim\limits_{v\rightarrow \infty} F(t|v)\bar{G}_i(v) = \lim\limits_{v\rightarrow \infty} \frac{U'(t)}{U'(\infty)}\exp\left(-\frac{U(t)}{v}\right)\bar{G}_i(v) = 0. |
It is evidently seen that (U'(t)U(t)/U'(\infty)v^2)e^{-U(t)/v} is RR _2 in (t, v) when t\geq 0 and v > 0 . It is also verified that V_1 \leq_{hr} V_2 if, and only if, \bar{G}_i(v) is TP _2 in (i, v) when i = 1, 2 and v > 0 which holds by assumption. The result is proved by applying the general composition theorem of Karlin [19].
(ⅳ) We need to show that \int_0^t xF_i^{*}(x)\; dx is TP _2 in (i, t) when i = 1, 2 and t\geq 0 . The partial derivative of \Lambda(t, v) = \int_0^t xF(x|v)\; dx with respect to v is
| \frac{\partial}{\partial v}\Lambda(t,v) = \int_0^{t}x\frac{\partial}{\partial v}F(x|v)\; dx = \int_0^t \frac{xU'(x)U(x)}{U'(\infty)v^2}e^{-\frac{U(x)}{v}}\; dx |
which is non-negative since for all x\geq 0 and v > 0 ,
| \frac{\partial}{\partial v}F(x|v) = \frac{U'(x)U(x)}{U'(\infty)v^2}e^{-\frac{U(x)}{v}}\geq 0. |
We also can get
| \frac{\partial^2}{\partial v^2}\Lambda(t,v) = \int_0^{t}x\frac{\partial^2}{\partial v^2}F(x|v)\; dx, |
where
| \frac{\partial^2}{\partial v^2}F(x|v) = \frac{U(x)U'(x)e^{-\frac{U(x)}{v}}}{v^3U'(\infty)}\left(\frac{U(x)}{v}-2\right). |
We can see by using integration by parts that
| \begin{align*} \int_0^t xF_i^{*}(x)\; dx& = \int_0^{\infty}\left(\int_0^{t} xF(x|v)dx \right)g_i(v)\; dv\\ & = l-u+\int_0^{\infty}\bar{G}_i(v)\left(\frac{\partial}{\partial v}\Lambda(t,v)\right)\; dv\\ & = \int_0^{\infty}\bar{G}_i(v)\left(\frac{\partial}{\partial v}\Lambda(t,v)\right)\; dv, \end{align*} |
in which, according to proof of (iii),
| l = \lim\limits_{v\rightarrow 0} \bar{G}_i(v) \Lambda(t,v) = \int_0^t \lim\limits_{v\rightarrow 0} \frac{U'(x)}{U'(\infty)}\exp\left(-\frac{U(x)}{v}\right)\bar{G}_i(v)\; dx = 0 |
and also
| u = \lim\limits_{v\rightarrow \infty} \bar{G}_i(v)\Lambda(t,v) = \int_0^t \lim\limits_{v\rightarrow \infty}\frac{U'(x)}{U'(\infty)}\exp\left(-\frac{U(x)}{v}\right)\bar{G}_i(v)\; dx = 0. |
Once again, integration by parts yields
| \begin{align*} \int_0^{\infty}\bar{G}_i(v)\left(\frac{\partial}{\partial v}\Lambda(t,v)\right)\; dv& = l^{*}-u^{*} +\int_0^{\infty} \left(\int_0^v \bar{G}_i(y)dy \right)\left(\frac{\partial^2}{\partial v^2}\Lambda(t,v)\right)\; dv\\ & = \int_0^{\infty} \left(\int_0^v \bar{G}_i(y)dy \right)\left(\frac{\partial^2}{\partial v^2}\Lambda(t,v)\right)\; dv, \end{align*} |
where
| \begin{align*} l^{*}& = \lim\limits_{v\rightarrow 0} \left(\int_v^{\infty}\bar{G}_i(y)dy\right)\frac{\partial}{\partial v}\Lambda(t,v)\\ & = \int_0^t \lim\limits_{v\rightarrow 0} \frac{xU'(x)U(x)}{v^2U'(\infty)}\exp\left(-\frac{U(x)}{v}\right)\left(\int_v^{\infty}\bar{G}_i(y)dy\right)\; dx = 0 \end{align*} |
and further, since E(V_i) < \infty provides that \int_v^{\infty} \bar{G}_i(y)dy\rightarrow 0 as v\rightarrow \infty , thus
| \begin{align*} u^{*}& = \lim\limits_{v\rightarrow \infty} \left(\int_v^{\infty}\bar{G}_i(y)dy\right)\frac{\partial}{\partial v}\Lambda(t,v)\\ & = \int_0^t \lim\limits_{v\rightarrow \infty}\frac{xU'(x)U(x)}{v^2U'(\infty)}\exp\left(-\frac{U(x)}{v}\right)\left(\int_v^{\infty}\bar{G}_i(y)dy\right)\; dx = 0. \end{align*} |
From assumption, \int_v^{\infty}\bar{G}_i(y)dy is TP _2 in (i, v) when i = 1, 2 and v > 0 . It can also be checked that \partial^2 \Lambda(t, v)/\partial v^2 is RR _2 in (t, v) when t\geq 0 and v > 0 . Thus by the general composition formula of Karlin [19] the result follows.
(ⅴ) It suffices to prove that \int_0^t F_2^{*}(x)dx \geq \int_0^t F_1^{*}(x)dx for all t\geq 0 . As in the proof of assertion (ⅳ) we have
| \int_0^t F_i ^{*}(x) dx = \int_0^{\infty} \left(\frac{\partial}{\partial v}\Theta(t,v)\right)\bar{G}_i(v)dv, |
where \Theta(t, v) = \int_0^t F(x|v) dx . From the assumption it holds that V_1\leq_{icx}V_2 which is equivalent to
| \int_{a}^{\infty} \bar{G}_2(v)dv \geq \int_{a}^{\infty} \bar{G}_2(v)dv,\; \;{\rm{ for\; all }}\;\; a\geq 0. |
Since F(x|v) is convex in v > 0 for all x\geq 0 thus (\partial/\partial v)\Theta(t, v) is a non-decreasing function in v, for all t\geq 0 , thus by Lemma 7.1(a) in Barlow and Proschan [6], for all t\geq 0 we obtain
| \int_0^t F_2^{*}(x)dx-\int_0^t F_1^{*}(x)dx = \int_0^{\infty} \left(\frac{\partial}{\partial v}\Theta(t,v)\right)d\left(\int_v^{\infty} \bar{G}_1(y)dy -\int_v^{\infty} \bar{G}_2(y)dy \right)\geq 0. |
The proof of the theorem is complete.
In this section, we apply the WPMIT model to a real data set and also carry out a simulation study to demonstrate the proficiency of the model. From a study argued by Siddiqui and Gehan [44] the survival times T_1, T_2, \ldots, T_{43} for patients suffering from chronic granulocytic leukemia, with t = 0 taken as the date of diagnosis, are available as follows:
| \begin{array}{cccccccccccc} 7 & 47 & 58&74& 177& 232& 273& 285& 317& 429 &440\\ 445& 455& 468& 495& 497& 532&571& 579& 581 &650& 702 \\ 715& 779& 881& 900& 930& 968& 1077& 1109 &1314&1334& 1367\\ 1534& 1712& 1784& 1877& 1886& 2045& 2056& 2260& 2429& 2509. \end{array} |
Let us consider T_0 as a random variable with Rescaled Power distribution with CDF F_0(t) = \left(\frac{t}{\eta}\right)^{\theta} for 0 < t < \eta in which \theta > 0 and also \eta > 0 and we denote it by T_0\sim RP(\theta, \eta) . The MIT of T_0 is obtained as m_0(t) = \frac{t}{\theta+1} for 0\leq t\leq \eta . For values of t < 0 and values of t > \eta we take, conventionally, m_0(t) = 0 . To assign the baseline distribution, we take \theta = 2 and \eta = 2700 and further, to build the MIT of response variable we assume that \gamma(t) = I[t \leq \eta^{\ast}] where I[A] is the indicator of the set A and \eta^{\ast} < 2700 . Then the random variable T with MIT m(t|v, \eta^{\ast}) = \frac{t}{\theta'+1}I[t\leq \eta^{\ast}], in which \theta' = \frac{2701}{v}-1 with v < 2701 . Hence, T_{i}\sim RP\left(\frac{2701}{v}-1, \eta^{\ast}\right) for i = 1, 2, \ldots, 43 . The formation of the baseline distribution is, therefore, preserved under the WPMIT model. The maximum likelihood estimation (MLE) of (v, \eta^{\ast}) is derived as:
| \widehat{\eta^{\ast}} = T_{(43)} = \max\{T_1,T_2,\ldots,T_{43}\} = 2509 |
and
| \widehat{v} = \frac{2701}{1+\ln(T_{(43)}) -\frac{1}{43}\sum_{i = 1}^{43} \ln(T_i)} = 1112.315. |
Now, we perform a simulation study on the WPMIT model. To build a a regression model on the basis of the WPMIT model, suppose that the baseline distribution is exponential with mean one which, as discussed in Example 1, has MIT m_0(t) = \frac{t}{1-e^{-t}}-1 . Let us choose \gamma(t) = \left(k(t)\right)^{\theta} where \theta > 0 and k(t) = \frac{2t-1+e^{-2t}}{(1+e^{-t})(t-1+e^{-t})} . We generate a sample of size n = 200 from the baseline distribution using the function runif in R. We first generate U_1, U_2, \ldots, U_{200} from U(0, 1) . Then, T_i = -\ln(U_i), i = 1, 2, \ldots, 200 follows the baseline distribution. The associated MIT function at T_i is m_0(T_i) = \frac{T_i}{1-e^{-T_i}}-1, i = 1, 2, \ldots, 200. If we denote by T the random variable with MIT function m(t|v, \theta) = v\gamma(t)m_0(t) then at time point T_i it is given by m(T_i|v, \theta) = v\left(k(T_i)\right)^{\theta}m_0(T_i), i = 1, 2, \ldots, 200. To examine the accuracy of the model, we take v = \frac{1}{2} and \theta = 1 and also set M_i = \ln(m_0(T_i)) and S_i = \ln(m(T_i|v, \theta)) . Then the linear model W_i = \ln(v)+\theta \ln\left(k(T_i)\right)+M_i+\varepsilon_i in which \varepsilon_1, \varepsilon_2, \ldots, \varepsilon_{200} are errors and constituting a random sample from normal distribution with mean 0 and variance 0.002 . The model Z_i = W_i-M_i = \ln(v)+\theta \ln\left(k(T_i)\right)+\varepsilon_i , i = 1, 2, \ldots, 200 is known as a simple linear regression model with unknown parameters v and \theta . By applying the method of least squares, estimations for v and \theta are acquired as
| \hat{\theta} = \frac{\sum_{i = 1}^{200} Z_i ln\left(k(T_i)\right)-\frac{\sum_{i = 1}^{200} Z_i \sum_{i = 1}^{200} \ln\left(k(T_i)\right)}{200}}{\sum_{i = 1}^{200} \ln^2(\left(k(T_i)\right))-\frac{\left( \sum_{i = 1}^{200} \ln(\left(k(T_i)\right))\right)^2}{200}} |
and
| ln(\hat{v}) = \frac{\sum_{i = 1}^{200} Z_i}{200}-\frac{\hat{\theta}\sum_{i = 1}^{200} \ln(k(T_i))}{200}. |
By using the simulated values T_1, T_2, \ldots, T_{200} , the amounts of estimations are \hat{v} = 0.4990268 and \hat{\theta} = 1.002384 .
The results on the PMIT model in the literature are limiting as further refined stochastic aspects of the model have been lacking. In this paper, a general MIT frailty model in which the frailty variable V (in the population level) with possible realization v (in the individual level) takes a new dimension of the model into consideration contributed to have advanced perspectives on the model. The association between the lifetime variable in the population and the random frailty which can be quantified partially through dependence concepts PLRD (NLRD), SI(SD), LCSD (LCSI) and LTD (LTI) was characterized which further concluded that, in most cases, the dependence structure induced is negative and the direction of the stochastic variation of frailty variable has to be in opposite of the direction of the stochastic variation of the lifetime variable. Therefore, a negative influence of frailty verbile on the magnitude of the population lifetime is appreciated by the model. This property was, later on, established and examined in a particular model where the effect of time and frailty on the MIT is considered to be multiplicative, using the theory of stochastic orderings including the lr order, the usual stochastic order, the rhr order, the (strong) MIT order and the icv order. The new multiplicative model is called the WPMIT model. In the final part of the paper, this model was applied on a real data set and provided maximum likelihood estimations of the parameters. To authenticate the WPMIT model as a regression model, a simulation process of the model was also carried out to estimate the parameters by using least squares method.
The authors are grateful to two anonymous reviewers for their useful comments and suggestions which lead to this improved version. This work is supported by Researchers Supporting Project number (RSP-2021/392), King Saud University, Riyadh, Saudi Arabia.
There is no conflict of interest declared by the authors.
| [1] |
N. V. Nguyen, C. Y. Liu, Some models for the interaction of long and short waves in dispersive media. Part Ⅰ: Derivation, Water Waves, 2 (2020), 327–359. https://doi.org/10.1007/s42286-020-00038-6 doi: 10.1007/s42286-020-00038-6

|
| [2] |
C. Y. Liu, N. V. Nguyen, Some models for the interaction of long and short waves in dispersive media. Part Ⅱ: Well-posedness, Commun. Math. Sci., 21 (2023), 641–669. https://dx.doi.org/10.4310/CMS.2023.v21.n3.a3 doi: 10.4310/CMS.2023.v21.n3.a3

|
| [3] |
B. Deconinck, N. V. Nguyen, B. L. Segal, The interaction of long and short waves in dispersive media, J. Phys. A Math. Theor., 49 (2016), 415501. https://doi.org/10.1088/1751-8113/49/41/415501 doi: 10.1088/1751-8113/49/41/415501

|
| [4] |
T. Kawahara, N. Sugimoto, T. Kakutani, Nonlinear interaction between short and long capillary-gravity waves, J. Phys. Soc. Japan, 39 (1975), 1379–1386. https://doi.org/10.1143/JPSJ.39.1379 doi: 10.1143/JPSJ.39.1379

|
| [5] | C. Liu, N. V. Nguyen, B. Brewer, Explicit synchronized solitary waves for some models for the interaction of long and short waves in dispersive media, Adv. Differ. Equ., In press. |
| [6] | B. Brewer, C. Liu, N.V. Nguyen, Cnoidal wave solutions for some models for the interaction of long and short waves, In press. |
| [7] | M. A. Krasnosel'skii, Positive solutions of operator equations, Gronigan: P. Noordhoff Ltd., 1964. |
| [8] | M. A. Krasnosel'skii, Topological methods in the theory of nonlinear integral equations, London: Pergamon, 1964. |
| [9] |
H. Q. Chen, Existence of periodic traveling-wave solutions of nonlinear, dispersive wave equations, Nonlinearity, 17 (2004), 2041–2056. https://doi.org/10.1088/0951-7715/17/6/003 doi: 10.1088/0951-7715/17/6/003

|
| [10] |
H. Q. Chen, M. Chen, N. V. Nguyen, Cnoidal wave solutions to Boussinesq systems, Nonlinearity, 20 (2007), 1443–1461. https://doi.org/10.1088/0951-7715/20/6/007 doi: 10.1088/0951-7715/20/6/007

|
| [11] |
N. V. Nguyen, Existence of periodic traveling-wave solutions for a nonlinear Schrödinger system: a topological approach, Topol. Methods Nonlinear Anal., 43 (2016), 129–155. https://doi.org/10.12775/TMNA.2014.009 doi: 10.12775/TMNA.2014.009

|
| [12] |
M. Chen, Exact solutions of various Boussinesq systems, Appl. Math. Lett., 11 (1998), 45–49. https://doi.org/10.1016/S0893-9659(98)00078-0 doi: 10.1016/S0893-9659(98)00078-0

|
| [13] |
M. Chen, Exact traveling-wave solutions to bidirectional wave equations, Int. J. Theor. Phys., 37 (1998), 1547–1567. https://doi.org/10.1023/A:1026667903256 doi: 10.1023/A:1026667903256

|
| [14] |
J. L. Bona, M. Chen, J. C. Saut, Boussinesq equations and other systems for small-amplitude long waves in nonlinear dispersive media. Ⅰ: Derivation and linear theory, J. Nonlinear Sci., 12 (2002), 283–318. https://doi.org/10.1007/s00332-002-0466-4 doi: 10.1007/s00332-002-0466-4

|
| [15] |
J. L. Bona, M. Chen, J. C. Saut, Boussinesq equations and other systems for small-amplitude long waves in nonlinear dispersive media: Ⅱ. The nonlinear theory, Nonlinearity, 17 (2004), 925–952. https://doi.org/10.1088/0951-7715/17/3/010 doi: 10.1088/0951-7715/17/3/010

|
| 1. | Mansour Shrahili, Mohamed Kayid, Antonio Di Crescenzo, Reliability Analysis of the Proportional Mean Departure Time Model, 2022, 2022, 2314-4785, 1, 10.1155/2022/7349598 |