On the existence, stability and chaos analysis of a novel 4D atmospheric dynamical system in the context of the Caputo fractional derivatives

Asharani J. Rangappa; Chandrali Baishya; Reny George; Sina Etemad; Zaher Mundher Yaseen; Asharani J. Rangappa; Chandrali Baishya; Reny George; Sina Etemad; Zaher Mundher Yaseen

doi:10.3934/math.20241386

AIMS Mathematics

2024, Volume 9, Issue 10: 28560-28588. doi: 10.3934/math.20241386

Previous Article Next Article

Research article

On the existence, stability and chaos analysis of a novel 4D atmospheric dynamical system in the context of the Caputo fractional derivatives

1.
Department of Studies and Research in Mathematics, Tumkur University, Tumakuru 572103, Karnataka, India
2.
Department of Mathematics, College of Science and Humanities in Al-Kharj, Prince Sattam bin Abdulaziz University, Al-Kharj 11942, Saudi Arabia
3.
Department of Mathematics, Azarbaijan Shahid Madani University, Tabriz, Iran
4.
Mathematics in Applied Sciences and Engineering Research Group, Scientific Research Center, Al-Ayen University, Nasiriyah 64001, Iraq
5.
Civil and Environmental Engineering Department, King Fahd University of Petroleum & Minerals, Dhahran 31261, Saudi Arabia

Received: 07 August 2024 Revised: 13 September 2024 Accepted: 26 September 2024 Published: 09 October 2024
MSC : 26A33, 34A12, 37L05, 60H10

In this study, changes in westerly waves and their connections to increased global warming under the influence of greenhouse gases were investigated via a Caputo fractional four-dimensional atmospheric system. The idea of the existence of chaotic behavior in the westerly wind's motion was depicted. It has been noted that westerlies are becoming stronger due to rising air temperatures. An analysis of the existence, uniqueness, boundedness, stability of equilibrium points, and conservative behavior of the solutions was conducted. To prove the existence of chaos in the modified model, the Lyapunov exponents, Poincaré map, and bifurcation were computed. A sliding mode controller to control the chaos in this novel fractional-order system was designed, and conditions for the global stability of the controlled system with and without external disturbances and uncertainties were derived. The finite-time interval for the system to reach the sliding surface was computed. The developed controller's performance was evaluated with respect to both commensurate and non-commensurate fractional derivatives. In each scenario, the impact of fractional orders was investigated. Numerical simulations were used to support theoretical statements about how the controller affects the system.

Keywords:

Citation: Asharani J. Rangappa, Chandrali Baishya, Reny George, Sina Etemad, Zaher Mundher Yaseen. On the existence, stability and chaos analysis of a novel 4D atmospheric dynamical system in the context of the Caputo fractional derivatives[J]. AIMS Mathematics, 2024, 9(10): 28560-28588. doi: 10.3934/math.20241386

Related Papers:

[1]	Muhammad Imran Liaqat, Sina Etemad, Shahram Rezapour, Choonkil Park . A novel analytical Aboodh residual power series method for solving linear and nonlinear time-fractional partial differential equations with variable coefficients. AIMS Mathematics, 2022, 7(9): 16917-16948. doi: 10.3934/math.2022929
[2]	Yousef Jawarneh, Humaira Yasmin, M. Mossa Al-Sawalha, Rasool Shah, Asfandyar Khan . Numerical analysis of fractional heat transfer and porous media equations within Caputo-Fabrizio operator. AIMS Mathematics, 2023, 8(11): 26543-26560. doi: 10.3934/math.20231356
[3]	Azzh Saad Alshehry, Naila Amir, Naveed Iqbal, Rasool Shah, Kamsing Nonlaopon . On the solution of nonlinear fractional-order shock wave equation via analytical method. AIMS Mathematics, 2022, 7(10): 19325-19343. doi: 10.3934/math.20221061
[4]	M. Mossa Al-Sawalha, Osama Y. Ababneh, Rasool Shah, Nehad Ali Shah, Kamsing Nonlaopon . Combination of Laplace transform and residual power series techniques of special fractional-order non-linear partial differential equations. AIMS Mathematics, 2023, 8(3): 5266-5280. doi: 10.3934/math.2023264
[5]	Imran Talib, Md. Nur Alam, Dumitru Baleanu, Danish Zaidi, Ammarah Marriyam . A new integral operational matrix with applications to multi-order fractional differential equations. AIMS Mathematics, 2021, 6(8): 8742-8771. doi: 10.3934/math.2021508
[6]	Yousef Jawarneh, Humaira Yasmin, Abdul Hamid Ganie, M. Mossa Al-Sawalha, Amjid Ali . Unification of Adomian decomposition method and ZZ transformation for exploring the dynamics of fractional Kersten-Krasil'shchik coupled KdV-mKdV systems. AIMS Mathematics, 2024, 9(1): 371-390. doi: 10.3934/math.2024021
[7]	Chang Phang, Abdulnasir Isah, Yoke Teng Toh . Poly-Genocchi polynomials and its applications. AIMS Mathematics, 2021, 6(8): 8221-8238. doi: 10.3934/math.2021476
[8]	Shazia Sadiq, Mujeeb ur Rehman . Solution of fractional boundary value problems by $\psi$ -shifted operational matrices. AIMS Mathematics, 2022, 7(4): 6669-6693. doi: 10.3934/math.2022372
[9]	Zahra Pirouzeh, Mohammad Hadi Noori Skandari, Kamele Nassiri Pirbazari, Stanford Shateyi . A pseudo-spectral approach for optimal control problems of variable-order fractional integro-differential equations. AIMS Mathematics, 2024, 9(9): 23692-23710. doi: 10.3934/math.20241151
[10]	Abdul Hamid Ganie, Fatemah Mofarreh, Adnan Khan . A novel analysis of the time-fractional nonlinear dispersive K(m, n, 1) equations using the homotopy perturbation transform method and Yang transform decomposition method. AIMS Mathematics, 2024, 9(1): 1877-1898. doi: 10.3934/math.2024092

Abstract

1. Introduction

Fractional calculus is a branch of mathematical analysis that generalizes integration and differentiation to arbitrary orders. Its origins can be traced back to the speculations of G. W. Leibniz in 1695 and L. Euler in 1730. Despite a long history, fractional calculus and the corresponding fractional differential equations (FDEs) are only gaining attention and popularity now. Different definitions of fractional derivatives exist, such as Riemann-Liouville, Caputo, Grunwald-Letnikov, Weyl, Marchaud, and Prabhakar. The history of this topic is available in ^[1,2,3]. Fractional calculus has several practical applications in various functional sciences, engineering, and technology fields. These include economics ^[4], chaotic systems ^[5], viscoelastic materials dynamics ^[6], electrochemical processes ^[7], traffic models in fluid dynamics ^[8], and optics ^[9]. Fractional derivatives are also helpful in describing the history profile and heritable properties of various constituents and practices. Furthermore, several researchers have investigated the existence and uniqueness of solutions for FDEs ^[2,3]. Additionally, because most fractional differential equations lack exact analytical solutions, approximate and numerical techniques, including semi-analytical methods, are widely employed to address fractional differential models. These methods include the homotopy analysis method ^[10], the variational iteration technique ^[11], Adams methods ^[12], Multi-Step Methods ^[13], Haar wavelet method ^[14], as well as several others ^{[15,16,17,18]}.

The Adomian decomposition method (ADM) ^[19] has seen extensive use over the past decades in solving a broad range of different types of equations. Originally introduced by George Adomian in the 1980s, the method has experienced numerous developments, modifications, and improvements. For further details regarding the convergence and stability of the ADM in its application to different types of equations, see ^{[20,21,22,23]}. The extended review by Duan et al. ^[24] covers the method and its applications to fractional differential equations; see also ^[25,26].

In recent times, ADM has been extensively used to provide analytical approximate solutions for linear and nonlinear fractional differential equations ^[27,28,29]. The ADM has been improved in several ways to enhance its accuracy, speed, and computational efficiency. These modifications have also made it adaptable to different types of functional equations. The upgraded ADM has shown significant progress by rapidly converging to a series solution compared to the standard ADM. It has also proven to be computationally efficient in various models, which is crucial for researchers in applied science ^[30,31,32]. Modifications to the ADM have produced notable results and offer flexibility in solving complex higher-order equations. However, in specific cases, explicitly solving definite integrals with parameters in the domain, or even performing approximate numerical integrations for specific right-hand terms, is not possible. As a result, it becomes essential to approximate these right-hand terms using series expansions before applying the ADM. Orthogonal functions are highly esteemed in areas such as numerical methods and approximation theory.

However, in relation to their practical applications. Wazwaz et al. were the first to propose approximating right-hand terms using the Taylor series before applying the ADM ^[33]. Later, Hosseini ^[34] introduced the combination of ADM with the first kind of Chebyshev polynomials, demonstrating the effectiveness and reliability of this method for both linear and nonlinear equations. Following this, Liu ^[35] incorporated Legendre polynomials into the ADM and conducted a comparative analysis with the previously used Chebyshev polynomials. Furthermore, in ^[36], it was observed that using the second kind of Chebyshev polynomials with the ADM improved estimation accuracy, outperforming the first kind. Another approach for approximating right-hand terms, as suggested in ^[37], is through Gegenbauer and Jacobi polynomials. Finally, in ^[38], a study comparing Chebyshev, Legendre, and Laguerre polynomials found that Legendre polynomials were superior estimators to Chebyshev polynomials, contradicting earlier findings.

The present manuscript proposes several modification procedures for the standard ADM aimed at solving initial-value problems of fractional order. These procedures leverage the application of orthogonal polynomials, which play a crucial role in approximation theories. Specifically, we will explore the use of Legendre polynomials and Chebyshev polynomials of both the first and second kinds to develop enhanced modification methods for the standard ADM. Additionally, a comparative analysis will be conducted to evaluate the accuracy and efficiency of the proposed approach. The primary advantage of the proposed modification lies in its high level of accuracy, along with fewer computational steps and reduced complexity in the calculations.

The organization of the manuscript is as follows: Section 2 recalls some basics on fractional calculus and formulation and basic features of the Taylor series and orthogonal polynomials, Section 3 outlines the modified approaches to the fractional differential equations, Section 4 applies the constructed scheme on certain test models, while Section 5 presents some concluding notes.

2. Main concepts and theorems

In the current section, we present some definitions and properties of the fractional calculus. Further, we discuss the formulation and basic features of the Taylor series and orthogonal polynomials.

2.1. Basic definitions and properties of the fractional calculus

Definition 2.1. For a function $y(x)\in C([a, b])$ and $a < x < b$ , the Riemann-Liouville fractional integral operator of order $\alpha > 0$ is defined as ^[1,2]

$\begin{eqnarray} I^{\alpha}_{a}y(x) = \frac{1}{\Gamma(\alpha)}\int_{a}^{x}y(t)(x-t)^{\alpha-1}dt. \end{eqnarray}$

(2.1)

Note from the above that for $\alpha = 0,$ we have $I^{0}_{a}y(x) = y(x),$ which is the identity operator. Additionally, when $\alpha \in \mathbb{N}$ , then $I^{\alpha}_{a}y(x)$ coincides with that classical integral.

Definition 2.2. For $y(x)\in C([a, b])$ , the Caputo fractional derivative of order $\alpha > 0$ is defined by ^[1,2]

$\begin{equation} D^{\alpha}_{*}y(x) = \begin{cases} I^{m-\alpha}y^{(m)}(x),\; \; m-1 < \alpha < m,\\ \frac{d^{m}}{dt^{m}}y(t),\; \; \alpha = m. \end{cases} \end{equation}$

(2.2)

In the following, we will outline some important properties for the fractional differential and integral operators based on the aforementioned definitions ^[1,2].

$\begin{equation} I^{\alpha}_{a}I^{\beta}_{a}y(x) = I^{\alpha+\beta}y(x),\; \; \alpha, \beta\geq 0. \end{equation}$

(2.3)

ii)

$\begin{equation} I^{\alpha}_{a}D^{\alpha}_{*}y(x) = y(x)-\sum\limits_{k = 0}^{m-1}y^{(k)}(0^{+})\frac{x^{k}}{\Gamma(k+1)}, \end{equation}$

(2.4)

where $m-1 < \alpha\leq m.$

iii)

$\begin{equation} I^{\alpha}_{a}x^{n} = \frac{\Gamma(n+1)}{\Gamma(\alpha+n+1)}x^{n+\alpha}, \ x > 0, \end{equation}$

(2.5)

where $\ m-1 < \alpha\leq m, \ n > -1.$

iv)

$\begin{equation} D^{\alpha}_{*}C = 0, \text{ where } C \text{ is a real constant.} \end{equation}$

(2.6)

v).

$\begin{equation} D^{\alpha}_{*}x^{n} = \begin{cases} \ 0, \qquad \qquad\qquad n < m-1,\\ \frac{\Gamma(n+1)}{\Gamma(n+1-\alpha)}x^{n-\alpha},\qquad \; n\geq m-1.\\ \end{cases} \end{equation}$

(2.7)

In this study, we are solving fractional differential equations in the Caputo sense. We have chosen the Caputo definition to solve the fractional differential equations because it allows us to obtain a unique and exact solution by specifying additional initial conditions for the fractional equation. The Caputo definition is widely accepted as it enables defining initial conditions related to the integer derivatives of the derived functions in the considered models. It is worth noting that many studies have extensively explored the geometric interpretation of fractional derivatives.

2.2. The structure and fundamental characteristics of the Taylor series and orthogonal polynomials

In this study, we focus on the function $g(x)$ , referred to as the "source term". Our goal is to approximate this term using various methods to reduce computational complexity and simplify the solution process. The significance of orthogonal functions in estimation theory and numerical methods is well known. Therefore, these functions and polynomials are utilized in this study to further enhance the accuracy of the standard Adomian decomposition method (ADM). We begin by applying the Taylor series expansion to the source term $g(x)$ , for an arbitrary positive integer $l$ , as follows:

$\begin{equation} g_{Taylor}(x)\approx \sum\limits_{k = 0}^{l-1} \frac{g^{(k)}(0)}{k!}x^{k}. \end{equation}$

(2.8)

Thus, in the subsequent sections, we have developed a series of Adomian modification methods using orthogonal polynomials. In particular, we employed orthogonal polynomials such as Legendre and the first and second kinds of Chebyshev polynomials.

$(1)$ Chebyshev's polynomials of the first kind

The first kind of Chebyshev polynomial $T_k (x)$ expanding $g(x)$ is

$\begin{equation} g{T}(x)\approx \sum\limits_{k = 0}^{l-1} a_{k}T_{k}(x), \end{equation}$

(2.9)

where

$\begin{equation} \begin{cases} T_{0}(x) = 1,\\ T_{1}(x) = x,\\ T_{2}(x) = 2x^{2}-1, \text{and in general}, \\ T_{k+1}(x) = 2xT_{k}-T_{k-1}, k\geq 1,\\ \end{cases} \end{equation}$

(2.10)

and

$\begin{equation} a_{0} = \frac{1}{\pi} \int_{-1}^{1} \frac{g(0.5x+0.5)}{\sqrt{1-x^2}}T_{0}(x)dx, \end{equation}$

(2.11)

$\begin{equation} a_{i} = \frac{2}{\pi} \int_{-1}^{1} \frac{g(0.5x+0.5)}{\sqrt{1-x^2}}T_{i}(x)dx. \end{equation}$

(2.12)

$(2)$ Chebyshev's polynomials of the second kind

Similarly, we employ Chebyshev polynomials of the second kind to approximate the source term $g(x)$ , rather than using Chebyshev polynomials of the first kind, as shown below:

$\begin{equation} g{U}(x)\approx \sum\limits_{k = 0}^{l-1} b_{k}U_{k}(x), \end{equation}$

(2.13)

where

$\begin{equation} \begin{cases} U_{0}(x) = 1,\\ U_{1}(x) = 2x,\\ U_{2}(x) = 4x^{2}-1, \text{and in general}, \\ U_{k+1}(x) = 2xU_{k}-U_{k-1}, k\geq 1,\\ \end{cases} \end{equation}$

(2.14)

and

$\begin{equation} b_{k} = \frac{2}{\pi} \int_{-1}^{1} g(0.5x+0.5){\sqrt{1-x^2}}U_{k}(x)dx. \end{equation}$

(2.15)

Finally, to introduce a modification method utilizing Legendre polynomials, we represent the source term $g(x)$ as a series expansion of Legendre polynomials as follows.

$(3)$ Legendre's polynomials

$\begin{equation} g{P}(x)\approx \sum\limits_{k = 0}^{l-1} c_{k}P_{k}(x), \end{equation}$

(2.16)

where

$\begin{equation} \begin{cases} P_{0}(x) = 1,\\ P_{1}(x) = -x+1,\\ P_{2}(x) = \frac{3}{2}x^2-\frac{1}{2},\\ P_{3}(x) = \frac{5}{2}x^3-\frac{3}{2}x,\\ \vdots \end{cases} \end{equation}$

(2.17)

and

$\begin{equation} c_{k} = \frac{2k+1}{\pi} \int_{-1}^{1} g(0.5x+0.5)P_{k}(x)dx. \end{equation}$

(2.18)

3. Modified Adomian decomposition method

This section introduces modified Adomian decomposition methods with some orthogonal polynomials for addressing initial-value problems (IVPs) of nonhomogeneous fractional differential equations.

We consider the initial-value problem (IVP) for a nonlinear fractional differential equation as shown below:

$\begin{equation} D^{\alpha}_{*} y(x)+Ry(x)+Ny(x) = g(x) ,\; \; \mathrm{\alpha} > 0. \end{equation}$

(3.1)

$\begin{equation*} y^{k}(0) = c_{k}, \quad k = 0,1,2,...,m-1, \quad m-1 < \alpha < m. \end{equation*}$

In the above equation, $y(x)$ is the unknown function, $D^{\alpha}_{*}$ is the Caputo fractional derivative operator of high order $\alpha,$ which is easily invertible, $N$ is the nonlinear operator, $R$ is the remaining linear operator, which might include other Caputo fractional derivative operators $D^{v}_{*}$ ( $v < \alpha$ ), and $g$ is the given source function.

To solve the above initial-value problem (IVP), the approach involves applying the operator $I^{\alpha}$ on both sides of (3.1), which is indeed the inverse operator of $D^{\alpha}_{*},$ and further make use of (2.4) to obtain

$\begin{equation} I^{\alpha}[D^{\alpha}_{*} y(x)+Ry(x)+Ny(x)] = I^{\alpha}[g(x)] . \end{equation}$

(3.2)

$\begin{equation} y(x) = \sum\limits_{k = 0}^{m-1}c_{k}\frac{x^{k}}{k!}+[I^{\alpha}g(x)]-[I^{\alpha}Ry(x)]-[I^{\alpha}Ny(x)]. \end{equation}$

(3.3)

Alternatively, by expressing the latter equation in accordance with the Adomian decomposition method, we arrive at the following formulation:

$\begin{equation} \sum\limits_{n = 0}^{\infty} y_{n}(x) = \sum\limits_{k = 0}^{m-1}c_{k}\frac{x^{k}}{k!}+[I^{\alpha}g(x)]-[I^{\alpha}R \sum\limits_{n = 0}^{\infty}y_{n}(x)]-[I^{\alpha}\sum\limits_{n = 0}^{\infty}A_{n}(x)], \end{equation}$

(3.4)

where the $A_{n}$ 's are the Adomian polynomials, which are to be computed using the following compacted formula:

$\begin{equation*} A_{n} = \frac{1}{n!}\frac{d^{n}}{d\lambda^{n}}\left[N\left(\sum\limits_{i = 0}^{\infty}\lambda^{i}y_{i}\right)\right]_{\lambda = 0}, \quad n = 0,1,2,\dots. \end{equation*}$

The recurrence relation for $y(x)$ can be established by simply defining:

$\begin{equation} \begin{cases} \quad y_{0}(x) = \sum_{k = 0}^{m-1}c_{k}\frac{x^{k}}{k!}+I^{\alpha}[g(x)],\\ \quad y_{n}(x) = -I^{\alpha}R[y_{n-1}(x)] -I^{\alpha}[A_{n-1}], \quad n \geq 1.\\ \end{cases} \end{equation}$

(3.5)

This approach follows the structure outlined below, resulting in the corresponding recursive solution.

$(1)$ Modification method via Taylor's series

$\begin{equation} \begin{cases} \quad y_{0}(x) = \sum_{k = 0}^{m-1}c_{k}\frac{x^{k}}{k!}+I^{\alpha}[\sum_{k = 0}^{l-1} \frac{g^{(k)}(0)}{k!}x^{k}],\\ \quad y_{n}(x) = -I^{\alpha}R[y_{n-1}(x)] -I^{\alpha}[A_{n-1}], \quad n \geq 1.\\ \end{cases} \end{equation}$

(3.6)

$(2)$ Modification method via the first kind of Chebyshev's polynomials

$\begin{equation} \begin{cases} \quad y_{0}(x) = \sum_{k = 0}^{m-1}c_{k}\frac{x^{k}}{k!}+I^{\alpha}[\sum_{k = 0}^{l-1} a_{k}T_{k}(x)],\\ \quad y_{n}(x) = -I^{\alpha}R[y_{n-1}(x)] -I^{\alpha}[A_{n-1}], \quad n \geq 1.\\ \end{cases} \end{equation}$

(3.7)

$(3)$ Modification method via the seconed kind of Chebyshev's polynomials

$\begin{equation} \begin{cases} \quad y_{0}(x) = \sum_{k = 0}^{m-1}c_{k}\frac{x^{k}}{k!}+I^{\alpha}[\sum_{k = 0}^{l-1} b_{k}U_{k}(x)],\\ \quad y_{n}(x) = -I^{\alpha}R[y_{n-1}(x)] -I^{\alpha}[A_{n-1}], \quad n \geq 1.\\ \end{cases} \end{equation}$

(3.8)

$(4)$ Modification method via Legendre's polynomials

$\begin{equation} \begin{cases} \quad y_{0}(x) = \sum_{k = 0}^{m-1}c_{k}\frac{x^{k}}{k!}+I^{\alpha}[\sum_{k = 0}^{l-1} c_{k}P_{k}(x)],\\ \quad y_{n}(x) = -I^{\alpha}R[y_{n-1}(x)] -I^{\alpha}[A_{n-1}], \quad n \geq 1.\\ \end{cases} \end{equation}$

(3.9)

Considering the rapid convergence of the decomposition series, it will be demonstrated through a representative example that only a small number of terms are needed to achieve an accurate solution. Subsequently, a comparison will be made between the approximate $y(x)$ and those derived from Taylor expansion, Chebyshev expansion, and Legendre expansion. This comparison aims to validate both the accuracy of the obtained solution and the efficacy of the proposed method.

Algorithm 1 Coding algorithm for the modification method of the ADM

1: Input: Define the problem and the source term

$g(x)$ .
2: Step 1: Apply the operator

$I^{\alpha}$ on both sides of the problem.
3: Step 2: Expand

$g(x)$ using a Taylor series or using Legendre and Chebyshev polynomials.
4: Step 3: Apply the Adomian decomposition method (ADM) for further modification.
5: Step 4: Derive the recursive solution based on the approximation.
6: Step 5: Compute the numerical results.
7: Output: Recursive solution to the problem.

4. Numerical applications

This section makes use of some test IVPs to ascertain the effectiveness of the proposed recursive schemes numerically for the classes of the fractional differential equations. All calculations are performed, and the plots are generated by using Maple 22 with 8 digits precision.

Example 4.1. Consider the following inhomogeneous fractional differential equation ^[39]:

$\begin{equation} D^{\alpha}_{*}y(x)+y(x) = \sin(x), \ \ y(0) = 0. \end{equation}$

(4.1)

$\begin{equation*} 0 < \alpha \leq 1 ,\; \; \; \; x \in [0,1]. \end{equation*}$

The exact solution of the above problem when $\alpha = 1$ is

$\begin{equation} y(x) = \frac{-1}{2}\cos(x)+\frac{1}{2}\sin(x)+\frac{1}{2}e^{-x}. \end{equation}$

(4.2)

In the above equation, $y(x)$ is the unknown function, $D^{\alpha}_{*}$ is the Caputo fractional derivative operator of high order $\alpha$ , and $g(x) = \sin(x)$ .

To solve the above IVP, we apply the operator $I^\alpha$ to both sides of the IVP to get:

$\begin{equation} I^{\alpha} [D^{\alpha}_{*}y(x)]+I^{\alpha}[y(x)] = I^{\alpha}[\sin(x)], \end{equation}$

(4.3)

$\begin{equation} y(x)-y(0)+I^{\alpha}[y(x)] = I^{\alpha}[\sin(x)]. \end{equation}$

(4.4)

Applying the standard Adomian decomposition method yields the following result:

$\begin{equation} \sum\limits_{n = 0}^{\infty}y_{n}(x)+I^{\alpha}[\sum\limits_{n = 0}^{\infty}y_{n}(x)] = I^{\alpha}[\sin(x)]. \end{equation}$

(4.5)

The recurrence relation for $y(x)$ can be established by simply defining:

$\begin{equation} \begin{cases} y_{0}(x) = I^{\alpha}[\sin(x)],\\ y_{n}(x) = -I^{\alpha}[y_{n-1}(x)],\; \; \forall n\geq 1. \end{cases} \end{equation}$

(4.6)

It is essential to implement the suggested modifications while dealing with the complex source term associated with the $sin(x)$ term in computations. It is important to recognize that directly applying the ADM has certain disadvantages, such as a large computation size, extended computation time, and complicated computation of the remaining terms since it relies on the first term. Considering the preceding discussion, we propose the following formulations to relieve these issues.

● The expansion of $g(x) = \sin (x)$ using the Taylor series $l = 6$ is

$\begin{equation} \begin{cases} y_{0}(x) = I^{\alpha}[\sum_{k = 0}^{5} \frac{g^{(k)}(0)}{k!}x^{k}] = I^{\alpha}[x-\frac{1}{6} x^{3}],\\ y_{n}(x) = -I^{\alpha}[y_{n-1}(x)],\; \; \forall n\geq 1, \end{cases} \end{equation}$

(4.7)

such that upon summing the above components yields the following series solution:

$\begin{equation} y_{Taylor}(x) = \frac{x^{\alpha+1}}{\Gamma(\alpha+2)}-\frac{x^{\alpha+3}}{\Gamma(\alpha+4)}+\frac{x^{2\alpha+1}}{\Gamma(2\alpha+2)}+\dots \end{equation}$

(4.8)

● The expansion of $g(x) = \sin (x)$ using the first kind of Chebyshev polynomials $l = 6$ is

$\begin{equation} \begin{cases} y_{0}(x) = I^{\alpha}[\sum_{k = 0}^{5} a_{k}T_{k}(x)]\\ = I^{\alpha}[3.0908 \times 10^{-7}+0.99997898x+0.0023523x^{2}-0.16761545x^{3}+0.001633897x^{4}\\+0.0072373478x^{5} ],\\ y_{n}(x) = -I^{\alpha}[y_{n-1}(x)],\; \; \forall n\geq 1, \end{cases} \end{equation}$

(4.9)

such that their summation results in

$\begin{equation} yT(x) = \frac{3.0908 \times 10^{-7}x^{\alpha}}{\Gamma(\alpha+1)}+\frac{0.99997898x^{\alpha+1}}{\Gamma(\alpha+2)}+\frac{0.0047046x^{\alpha+2}}{\Gamma(\alpha+3)}+\dots \end{equation}$

(4.10)

● The expansion of $g(x) = \sin (x)$ using the second kind of Chebyshev polynomials $l = 6$ is

$\begin{equation} \begin{cases} y_{0}(x) = I^{\alpha}[\sum_{k = 0}^{5} b_{k}U_{k}(x)]\\ = I^{\alpha}[1.00504 \times10^{-6}+0.99996781x+0.00028067x^{2}-0.16767393x^{3}+0.001648541x^{4}\\+0.0072481459x^{5} ],\\ y_{n}(x) = -I^{\alpha}[y_{n-1}(x)],\; \; \forall n\geq 1, \end{cases} \end{equation}$

(4.11)

which results in the subsequent series solution:

$\begin{equation} yU(x) = \frac{1.00504 \times10^{-6}x^{\alpha}}{\Gamma(\alpha+1)}+\frac{0.99996781x^{\alpha+1}}{\Gamma(\alpha+2)}+\frac{0.00056134x^{\alpha+2}}{\Gamma(\alpha+3)}+\dots \end{equation}$

(4.12)

● The expansion of $g(x) = \sin (x)$ using Legendre polynomials $l = 6$ is

$\begin{equation} \begin{cases} y_{0}(x) = I^{\alpha}[\sum_{k = 0}^{5} c_{k}P_{k}(x)]\\ = I^{\alpha}[6.6871\times10^{-7}+0.99997284x+0.0002611x^{2}-0.16764828x^{3}+0.00164224x^{4}\\+0.007243161x^{5} ],\\ y_{n}(x) = -I^{\alpha}[y_{n-1}(x)],\; \; \forall n\geq 1, \end{cases} \end{equation}$

(4.13)

that sums to the following:

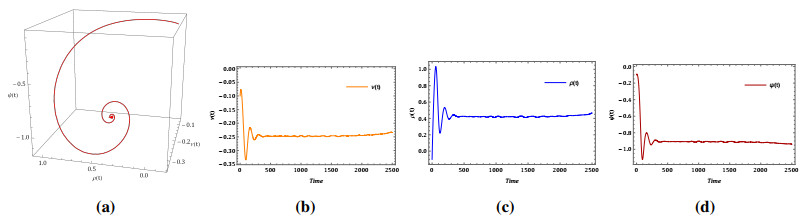
$\begin{equation} yP(x) = \frac{6.6871\times10^{-7}x^{\alpha}}{\Gamma(\alpha+1)}+\frac{0.99997284x^{\alpha+1}}{\Gamma(\alpha+2)}+\frac{0.0005222x^{\alpha+2}}{\Gamma(\alpha+3)}+\dots \end{equation}$

(4.14)

Additionally, in the following , we present an analysis of the simulated error difference for the orthogonal polynomial with $n = 5$ , compared to the exact solution of the problem with $\alpha = 1$ . In addition, we have visually represented the obtained solution for the IVP in the –, showcasing the graphical visualization for various values of $\alpha$ .

Table 1. Comparison of the proposed modified ADM's solution to the exact solution for Example (4.1).

$x$	$\|exact-y_{Taylor}\|$	$\|exact-yP(x)\|$	$\|exact-y{T}(x)\|$	$\|exact-y{U}(x)\|$
0	0	0	0	0
0.2	9.3 $\times 10^{-8}$	1.9 $\times 10^{-8}$	2.0 $\times 10^{-8}$	1.3 $\times 10^{-8}$
0.4	5.373 $\times 10^{-6}$	9.0 $\times 10^{-9}$	1.4 $\times 10^{-8}$	8.0 $\times 10^{-9}$
0.6	5.965 $\times 10^{-5}$	4.3 $\times 10^{-7}$	4.2 $\times 10^{-7}$	4.2 $\times 10^{-7}$
0.8	3.2628 $\times 10^{-4}$	3.76 $\times 10^{-6}$	3.77 $\times 10^{-6}$	3.76 $\times 10^{-6}$
1	1.21277 $\times 10^{-3}$	2.2040 $\times 10^{-5}$	2.2030 $\times 10^{-5}$	2.201 $\times 10^{-5}$

| Show Table

DownLoad: CSV

Figure 1. The exact solution and proposed modified ADM of Example (4.1) for different values of

$\alpha$ .

DownLoad: Full-Size Img PowerPoint

Example 4.2. Let us make consideration of the nonlinear inhomogeneous fractional IVP as follows ^[40]:

$\begin{equation} D^{\alpha}_{*}y(x)+2y(x)-y^{3}(x) = \sin(x)\cos^{2}(x), \ \ y(0) = 0,y'(0) = 1. \end{equation}$

(4.15)

$\begin{equation*} 0 < \alpha \leq 2 ,\; \; \; \; x \in [0,1]. \end{equation*}$

The exact solution of the above problem when $\alpha = 2$ is

$\begin{equation} y(x) = \sin(x). \end{equation}$

(4.16)

In the above equation, $y(x)$ is the unknown function, $D^{\alpha}_{*}$ is the Caputo fractional derivative operator of high order $\alpha$ , $y^{3}(x)$ is a nonlinear term, and $g(x) = \sin(x)\cos^{2}(x)$ .

To solve the above IVP, we apply the operator $I^\alpha$ to both sides of the IVP to get:

$\begin{equation} I^{\alpha} [D^{\alpha}_{*}y(x)]+I^{\alpha}[2y(x)]-I^{\alpha}[y^{3}(x)] = I^{\alpha}[\sin(x)\cos^{2}(x)], \end{equation}$

(4.17)

$\begin{equation} y(x)-y(0)-y'(0)x+I^{\alpha}[2y(x)]-I^{\alpha}[y^{3}(x)] = I^{\alpha}[\sin(x)\cos^{2}(x)]. \end{equation}$

(4.18)

Applying the standard Adomian decomposition method yields the following result:

$\begin{equation} \sum\limits_{n = 0}^{\infty}y_{n}(x)-x+I^{\alpha}[2\sum\limits_{n = 0}^{\infty}y_{n}(x)]-I^{\alpha}[\sum\limits_{n = 0}^{\infty}A_{n}] = I^{\alpha}[\sin(x)\cos^{2}(x)], \end{equation}$

(4.19)

where $A_{n}$ are the Adomian polynomials for nonlinear term $y^3 (x)$ which when computed iteratively takes the following form:

$\begin{equation} \begin{split} A_0& = y_{0}^{3},\\ A_1& = 3(y_0)^{2}y_1,\\ A_2& = 3(y_0)^{2}y_2+3y_{1}^{2}y_0,\\ A_3& = 3(y_{0})^{2}y_3+6y_0y_1y_2+y_{1}^{3},\\ & \vdots\\ \end{split} \end{equation}$

(4.20)

The recurrence relation for $y(x)$ can be established by simply defining:

$\begin{equation} \begin{cases} y_{0}(x) = x+I^{\alpha}[\sin(x)\cos^{2}(x)],\\ y_{n}(x) = -I^{\alpha}[2y_{n-1}(x)]+I^{\alpha}[A_{n-1}(x)],\; \; \forall n\geq 1. \end{cases} \end{equation}$

(4.21)

To simplify the complexity of $g(x) = \sin(x)\cos^{2}(x)$ , we recommend using the following formulations:

● The expansion of $g(x) = \sin (x)\cos^{2}(x)$ using the Taylor series $l = 6$ is

$\begin{equation} \begin{cases} y_{0}(x) = x+I^{\alpha}[\sum _{k = 0}^{5} \frac{g^{(k)}(0)}{k!}x^{k}] = x+I^{\alpha}[x-\frac{7}{6} x^{3}],\\ y_{n}(x) = -I^{\alpha}[2y_{n-1}(x)]+I^{\alpha}[A_{n-1}(x)],\; \; \forall n\geq 1, \end{cases} \end{equation}$

(4.22)

leading to the following series solution:

$\begin{equation} y_{Taylor}(x) = \frac{x^{\alpha+1}}{\Gamma(\alpha+2)}-\frac{7x^{\alpha+3}}{\Gamma(\alpha+4)}+\frac{x^{2\alpha+1}}{\Gamma(2\alpha+2)}+\dots \end{equation}$

(4.23)

● The expansion of $g(x) = \sin (x)\cos^{2}(x)$ using the first kind of Chebyshev polynomials $l = 6$ is

$\begin{equation} \begin{cases} y_{0}(x) = x+I^{\alpha}[\sum_{k = 0}^{5} a_{k}T_{k}(x)]\\ = x+I^{\alpha}[0.0001117718+0.99203869x+0.09116705x^{2}-1.5421702x^{3}+0.67021928x^{4}\\+0.034394566x^{5} ],\\ y_{n}(x) = -I^{\alpha}[2y_{n-1}(x)]+I^{\alpha}[A_{n-1}(x)],\; \; \forall n\geq 1, \end{cases} \end{equation}$

(4.24)

that sums to the following:

$\begin{equation} yT(x) = \frac{0.0001117718x^{\alpha}}{\Gamma(\alpha+1)}+\frac{0.99203869x^{\alpha+1}}{\Gamma(\alpha+2)}+\frac{0.18233410x^{\alpha+2}}{\Gamma(\alpha+3)}+\dots \end{equation}$

(4.25)

● The expansion of $g(x) = \sin (x)\cos^{2}(x)$ using the second kind of Chebyshev polynomials $l = 6$ is

$\begin{equation} \begin{cases} y_{0}(x) = x+I^{\alpha}[\sum _{k = 0}^{5} b_{k}U_{k}(x)]\\ = x+I^{\alpha}[0.0003936422+0.9875480x+0.10989235x^2-1.570291x^3+0.68366181x^4\\+0.034844186x^5 ],\\ y_{n}(x) = -I^{\alpha}[2y_{n-1}(x)]+I^{\alpha}[A_{n-1}(x)],\; \; \forall n\geq 1, \end{cases} \end{equation}$

(4.26)

that leads to the following series solution:

$\begin{equation} yU(x) = \frac{0.0003936422x^{\alpha}}{\Gamma(\alpha+1)}+\frac{0.9875480x^{\alpha+1}}{\Gamma(\alpha+2)}+\frac{0.21978470x^{\alpha+2}}{\Gamma(\alpha+3)}+\dots \end{equation}$

(4.27)

● The expansion of $g(x) = \sin (x)\cos^{2}(x)$ using Legendre polynomials $l = 6$ is

$\begin{equation} \begin{cases} y_{0}(x) = x+I^{\alpha}[\sum _{k = 0}^{5} c_{k}P_{k}(x)]\\ = x+I^{\alpha}[0.0002485684+0.98967633x+0.1012779x^{2}-1.5574782x^{3}+0.6775396x^{4}\\+0.034636179x^{5} ],\\ y_{n}(x) = -I^{\alpha}[2y_{n-1}(x)]+I^{\alpha}[A_{n-1}(x)],\; \; \forall n\geq 1, \end{cases} \end{equation}$

(4.28)

which totals to the following:

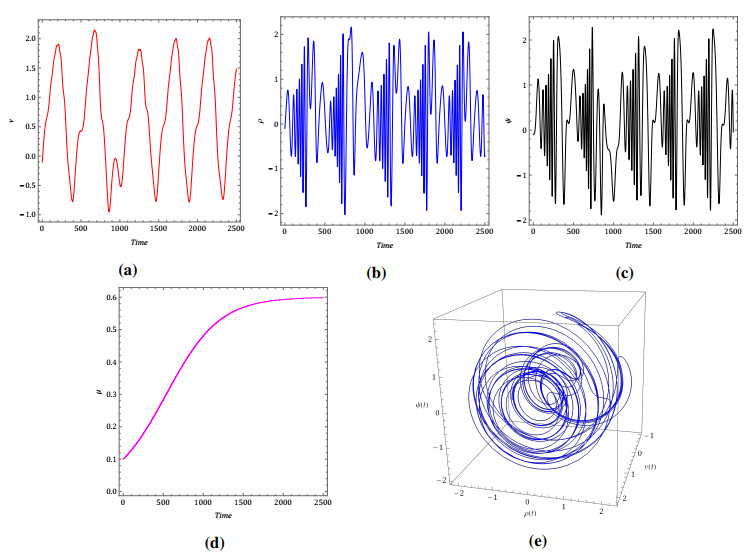
$\begin{equation} yP(x) = \frac{0.0002485684x^{\alpha}}{\Gamma(\alpha+1)}+\frac{0.98967633x^{\alpha+1}}{\Gamma(\alpha+2)}+\frac{0.2025558x^{\alpha+2}}{\Gamma(\alpha+3)}+\dots \end{equation}$

(4.29)

In the following , we present an analysis of the simulated error difference for the orthogonal polynomial with $n = 5$ , compared to the exact solution of the problem with $\alpha = 2$ . Further, we graphically visualize the obtained solution for the IVP in –, showcasing the various visualizations for different values of $\alpha$ .

Table 2. Comparison of the proposed modified ADM's solution to the exact solution for Example (4.2).

$x$	$\|exact-y_{Taylor}\|$	$\|exact-y{P}(x)\|$	$\|exact-y{T}(x)\|$	$\|exact-y{U}(x)\|$
0	0	0	0	0
0.2	1.54 $\times 10^{-7}$	2.447737 $\times 10^{-7}$	9.41263 $\times 10^{-7}$	7.65213 $\times 10^{-7}$
0.4	1.93662 $\times 10^{-5}$	1.517810 $\times 10^{-7}$	2.74701 $\times 10^{-7}$	1.62808 $\times 10^{-6}$
0.6	3.21843 $\times 10^{-4}$	1.600035 $\times 10^{-7}$	5.02968 $\times 10^{-7}$	2.27452 $\times 10^{-6}$
0.8	2.32654 $\times 10^{-3}$	3.882715 $\times 10^{-7}$	1.81022 $\times 10^{-6}$	2.5491 $\times 10^{-6}$
1	1.06477 $\times 10^{-2}$	7.837075 $\times 10^{-6}$	9.06708 $\times 10^{-6}$	4.60779 $\times 10^{-6}$

| Show Table

DownLoad: CSV

Figure 2. The exact solution and proposed modified ADM of Example (4.2) for different values of

$\alpha$ .

DownLoad: Full-Size Img PowerPoint

Based on the provided illustration and the outcomes obtained through analyses and comparisons, we can conclude that incorporating orthogonal polynomials such as Chebyshev, Legendre, and Taylor series can significantly enhance the performance of the ADM. Comparison between the standard ADM and Taylor series with Legendre and Chebyshev polynomials shows that the latter provide more accurate estimations.

4.1. Special application

Consider the fractional order forced Duffing-van der Pol oscillator equation as follows

$\begin{equation} D^{\alpha}_{*}y(x)-\mu(1-y^{2}(x))y'(x)+ay(x)+by^{3}(x) = f\cos(\omega x), \ \ y(0) = 1,\; y'(0) = 0. \end{equation}$

(4.30)

$\begin{equation*} 1 < \alpha \leq 2 ,\; \; \; \; x \in [0,1]. \end{equation*}$

● (Single-well $a > 0, b > 0$ ). $a = b = 0.5$ , $\mu = 0.1$ , $f = 0.5$ , and $\omega = 0.79$ .

● (Double-well $a < 0, b > 0$ ). $a = -0.5, b = 0.5$ , $\mu = 0.1$ , $f = 0.5$ , and $\omega = 0.79$ .

● (Double-hump $a > 0, b < 0$ ). $a = 0.5, b = -0.5$ , $\mu = 0.1$ , $f = 0.5$ , and $\omega = 0.79$ .

To solve Eq (4.30) using the modification method of the ADM, we apply the previously outlined algorithm as follows:

$\begin{equation} y(x)-1-I^{\alpha}[\mu y'(x)]+I^{\alpha}[y^{2}(x)y'(x)]+I^{\alpha}[ay(x)]+I^{\alpha}[by^{3}(x)] = I^{\alpha}[f\cos(\omega x)], \end{equation}$

(4.31)

such that when the ADM is deployed reveals

$\begin{equation} \sum\limits_{n = 0}^{\infty} y_{n}(x)-1- I^{\alpha}\bigg[\mu \sum\limits_{n = 0}^{\infty}y_{n}'(x)\bigg]-I^{\alpha}\bigg[\sum\limits_{n = 0}^{\infty}A_{n}(x)\bigg]+I^{\alpha}\bigg[a\sum\limits_{n = 0}^{\infty}y_{n}(x)\bigg]+I^{\alpha}\bigg[ b\sum\limits_{n = 0}^{\infty}B_{n}(x)\bigg] = I^{\alpha}\bigg[f\cos(\omega x)\bigg], \end{equation}$

(4.32)

where ${A_n}$ and $B_{n}$ are Adomian polynomials corresponding to the nonlinear terms $y^{2}(x)y'(x)$ and $y^{3}(x)$ respectively, defined as follows:

$\begin{equation} \begin{split} A_{0}& = y_{0}\! \left(x\right)^{2} \left(\frac{d}{d x} y_{0}\! \left(x\right)\right),\\ A_{1}& = 2 y_{0}\! \left(x\right) \left(\frac{d}{d x} y_{0}\! \left(x\right)\right) y_{1}\! \left(x\right)+y_{0}\! \left(x\right)^{2} \left(\frac{d}{d x} y_{1}\! \left(x\right)\right),\\ A_{2}& = y_{1}\! \left(x\right)^{2} \left(\frac{d}{d x} y_{0}\! \left(x\right)\right)+2 y_{0}\! \left(x\right) \left(\frac{d}{d x} y_{1}\! \left(x\right)\right) y_{1}\! \left(x\right)+2 y_{0}\! \left(x\right) \left(\frac{d}{d x} y_{0}\! \left(x\right)\right) y_{2}\! \left(x\right)+y_{0}\! \left(x\right)^{2} \left(\frac{d}{d x} y_{2}\! \left(x\right)\right),\\ & \vdots\\ \end{split} \end{equation}$

(4.33)

$\begin{equation} \begin{split} B_{0}& = y_{0}\! \left(x\right)^{3},\\ B_{1}& = 3\cdot y_{0}\! \left(x\right)^{2}\cdot y_{1}\! \left(x\right),\\ B_{2}& = 3\cdot y_{0}\! \left(x\right)\cdot y_{1}\! \left(x\right)^{2}+3\cdot y_{0}\! \left(x\right)^{2}\cdot y_{2}\! \left(x\right),\\ & \vdots\\ \end{split} \end{equation}$

(4.34)

Moreover, the formal recursive relationship for the governing fractional IVP is obtained as follows:

$\begin{equation} \begin{cases} y_{0}(x) = 1+I^{\alpha}\bigg[f\cos(\omega x)\bigg],\\ y_{n}(x) = I^{\alpha}\bigg[\mu y_{n-1}'(x)\bigg]-I^{\alpha}\bigg[A_{n-1}(x)\bigg]-I^{\alpha}\bigg[ay_{n-1}(x)\bigg]-I^{\alpha}\bigg[ bB_{n-1}(x)\bigg], n\geq 1. \end{cases} \end{equation}$

(4.35)

In the subsequent discussion, to avoid the complexity of calculating the source term $f\cos(\omega x)$ , we will apply the proposed modification methods to solve the governing equation of the forced Duffing-van der Pol oscillator. We will first introduce the classical Taylor series approach, followed by the proposed schemes. The solution will be represented based on the respective modifications as follows: $y_{Taylor}(x)$ for the Taylor series expansion, $yP(x)$ for the Legendre series expansion, and $yT(x)$ and $yU(x)$ for the first and second kind of Chebyshev series expansion.

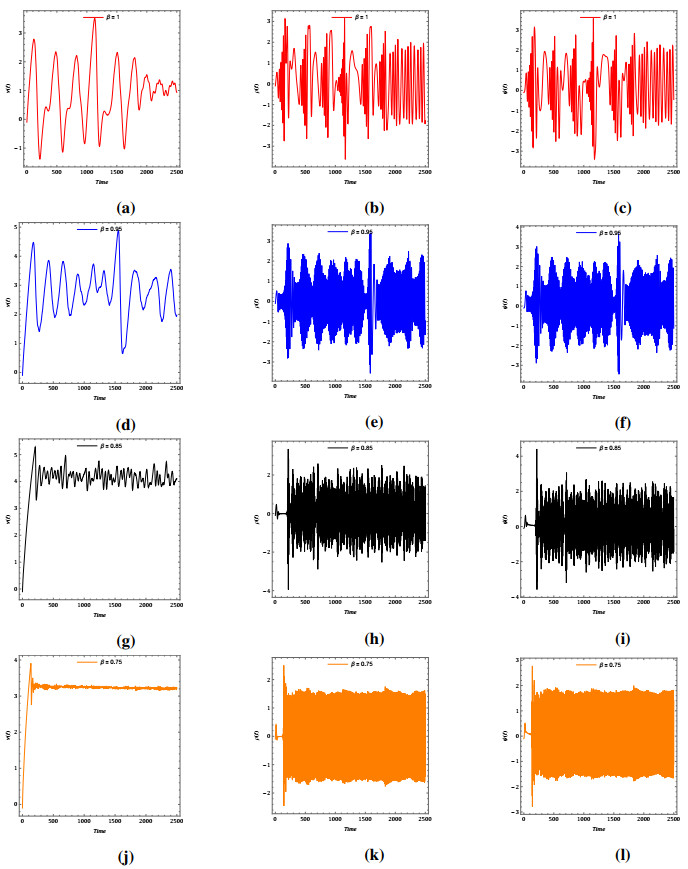
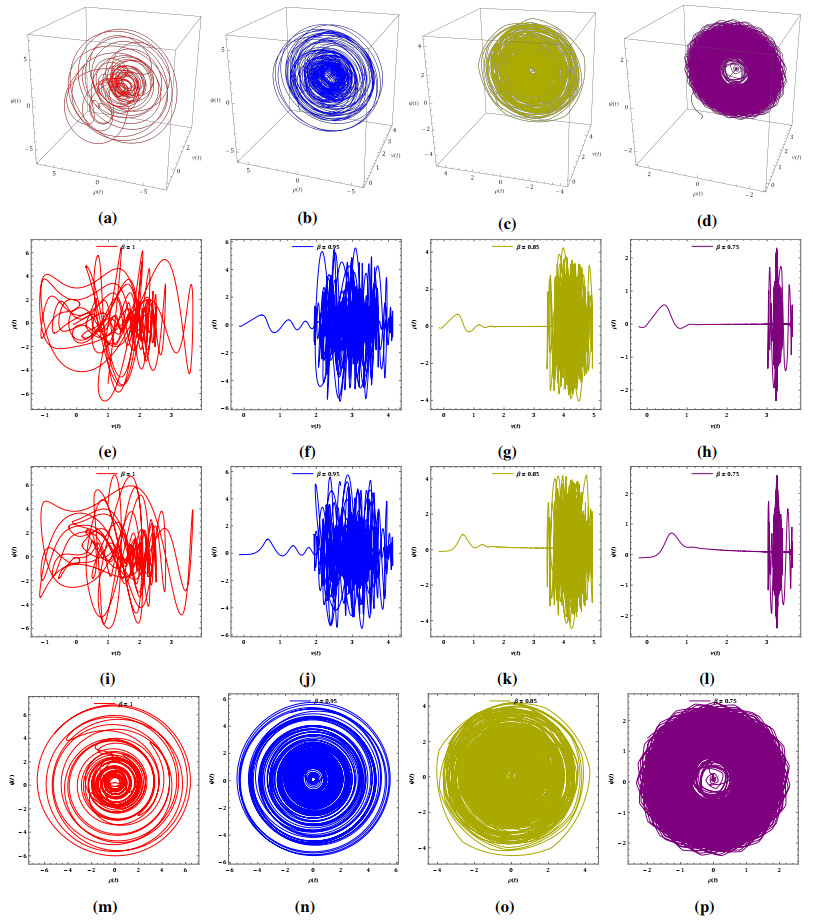
4.1.1. Single-well situation

The recursive formula for the fractional problem (4.30) in this case is given by:

$\begin{equation} \begin{cases} y_{0}(x) = 1+I^{\alpha}\bigg[\frac{1}{2}\cos(0.79 x)\bigg],\\ y_{n}(x) = I^{\alpha}\bigg[0.1 y_{n-1}'(x)\bigg]-I^{\alpha}\bigg[A_{n-1}(x)\bigg]-I^{\alpha}\bigg[\frac{1}{2}y_{n-1}(x)\bigg]-I^{\alpha}\bigg[ \frac{1}{2}B_{n-1}(x)\bigg], n\geq 1. \end{cases} \end{equation}$

(4.36)

● Modification method via Taylor's series

The source term $g(x) = \frac{1}{2}\cos(0.79 x)$ will be expanded for $l = 6$ in the following manner:

$\begin{equation} g_{Taylor}(x) = \frac{1}{2}- 0.156025000 x^{2}+ 0.00811460020 x^{4}+\mathrm{O}\! \left(x^{6}\right). \end{equation}$

(4.37)

This yields the subsequent iterative components.

$\begin{equation} \begin{split} y_{0}(x)& = 1+I^{\alpha}\bigg[\frac{1}{2}- 0.156025000 x^{2}+ 0.00811460020 x^{4}\bigg],\\ y_{1}(x)& = I^{\alpha}\bigg[0.1 y_{0}'(x)\bigg]-I^{\alpha}\bigg[A_{0}(x)\bigg]-I^{\alpha}\bigg[\frac{1}{2}y_{0}(x)\bigg]-I^{\alpha}\bigg[ \frac{1}{2}B_{0}(x)\bigg],\\ \vdots \end{split} \end{equation}$

(4.38)

such that upon summing the above components yields the following series solution:

$\begin{equation} y_{Taylor} = 1+\frac{x^{\alpha}}{2\Gamma(\alpha+1)}-\frac{ 0.312050000x^{2+\alpha}}{\Gamma(\alpha+3)}+\frac{0.1947504048x^{4+\alpha}}{\Gamma(\alpha+5)}+\dots \end{equation}$

(4.39)

● Modification method via Chebyshev's polynomials of the first kind

We Proceed by expanding the source term $g(x)$ in the following manner:

$\begin{equation} \begin{split} gT(x)& = 0.500000002- 5.3\times 10^{-8} x- 0.156023884 x^{2}- 7.0081\times 10^{-6} x^{3}\\&+ 0.00813387558 x^{4}- 0.000025329921 x^{5}- 0.000154945607 x^{6}. \end{split} \end{equation}$

(4.40)

Therefore, the solution components are as follows:

$\begin{equation} \begin{split} y_{0}(x)& = 1+I^{\alpha}\bigg[gT(x)\bigg],\\ y_{1}(x)& = I^{\alpha}\bigg[0.1 y_{0}'(x)\bigg]-I^{\alpha}\bigg[A_{0}(x)\bigg]-I^{\alpha}\bigg[\frac{1}{2}y_{0}(x)\bigg]-I^{\alpha}\bigg[ \frac{1}{2}B_{0}(x)\bigg],\\ \vdots \end{split} \end{equation}$

(4.41)

which results in the subsequent series solution:

$\begin{equation} yT(x) = 1+\frac{0.500000002x^{\alpha}}{\Gamma(\alpha+1)}-\frac{5.3\times 10^{-8} x^{\alpha+1}}{\Gamma(\alpha+2)}-\frac{0.312047768x^{2+\alpha}}{\Gamma(3+\alpha)}+\dots \end{equation}$

(4.42)

● Modification method via Chebyshev's polynomials of the second kind

We begins by expressing the source term $g(x)$ in the following manner:

$\begin{equation} \begin{split} gU(x)& = 0.500000004- 1.30\times 10^{-7} x- 0.156023427 x^{2}- 8.0266\times 10^{-6} x^{3}\\&+ 0.00813475220 x^{4}- 0.000025461710 x^{5}- 0.000155053667 x^{6}. \end{split} \end{equation}$

(4.43)

This gives the following iterative solutions:

$\begin{equation} \begin{split} y_{0}(x)& = 1+I^{\alpha}\bigg[gU(x)\bigg],\\ y_{1}(x)& = I^{\alpha}\bigg[0.1 y_{0}'(x)\bigg]-I^{\alpha}\bigg[A_{0}(x)\bigg]-I^{\alpha}\bigg[\frac{1}{2}y_{0}(x)\bigg]-I^{\alpha}\bigg[ \frac{1}{2}B_{0}(x)\bigg],\\ \vdots \end{split} \end{equation}$

(4.44)

that sums to the following:

$\begin{equation} yU(x) = 1+\frac{0.500000004x^{\alpha}}{\Gamma(\alpha+1)}-\frac{1.3\times 10^{-7} x^{\alpha+1}}{\Gamma(\alpha+2)}-\frac{ 0.312046854x^{2+\alpha}}{\Gamma(3+\alpha)}+\dots \end{equation}$

(4.45)

● Modification method via Legendre's polynomials

Now, the expansion of the source term $g(x)$ using Legendre polynomials gives:

$\begin{equation} \begin{split} gP(x)& = 0.500000004- 1.43\times 10^{-7} x- 0.156023485 x^{2}- 7.7201\times 10^{-6}x^{3}\\&+ 0.00813440004 x^{4}- 0.000025402532 x^{5}- 0.000155003233 x^{6}. \end{split} \end{equation}$

(4.46)

This gives the following iterative solutions:

$\begin{equation} \begin{split} y_{0}(x)& = 1+I^{\alpha}\bigg[gP(x)\bigg],\\ y_{1}(x)& = I^{\alpha}\bigg[0.1 y_{0}'(x)\bigg]-I^{\alpha}\bigg[A_{0}(x)\bigg]-I^{\alpha}\bigg[\frac{1}{2}y_{0}(x)\bigg]-I^{\alpha}\bigg[ \frac{1}{2}B_{0}(x)\bigg],\\ \vdots \end{split} \end{equation}$

(4.47)

that sums to the following:

$\begin{equation} yP(x) = 1+\frac{0.500000004x^{\alpha}}{\Gamma(\alpha+1)}-\frac{1.43\times 10^{-7} x^{\alpha}}{\Gamma(\alpha+1)}-\frac{ 0.31204696x^{2+\alpha}}{\Gamma(3+\alpha)}+\dots \end{equation}$

(4.48)

4.1.2. Double-well situation

The recursive formula for the fractional problem (4.30) in this case is given by:

$\begin{equation} \begin{cases} y_{0}(x) = 1+I^{\alpha}\bigg[\frac{1}{2}\cos(0.79 x)\bigg],\\ y_{n}(x) = I^{\alpha}\bigg[0.1 y_{n-1}'(x)\bigg]-I^{\alpha}\bigg[A_{n-1}(x)\bigg]+I^{\alpha}\bigg[\frac{1}{2}y_{n-1}(x)\bigg]-I^{\alpha}\bigg[ \frac{1}{2}B_{n-1}(x)\bigg], n\geq 1. \end{cases} \end{equation}$

(4.49)

Therefore, without further details, we provide the corresponding solution by applying the proposed modification methods for $l = 6$ , following the same procedure as in the single-well situation, as outlined below.

$\begin{equation} y_{Taylor} = 1+\frac{x^{\alpha}}{2\Gamma(\alpha+1)}-\frac{ 0.312050000x^{2+\alpha}}{\Gamma(\alpha+3)}+\frac{0.1947504048x^{4+\alpha}}{\Gamma(\alpha+5)}-\frac{2.60389834\times 10^{-14}x^{6+\alpha}}{\Gamma(7+\alpha)}+\dots \end{equation}$

(4.50)

(4.51)

(4.52)

(4.53)

4.1.3. Double-hump situation

The recursive formula for the fractional problem (4.30) in this case is given by:

$\begin{equation} \begin{cases} y_{0}(x) = 1+I^{\alpha}\bigg[\frac{1}{2}\cos(0.79 x)\bigg],\\ y_{n}(x) = I^{\alpha}\bigg[0.1 y_{n-1}'(x)\bigg]-I^{\alpha}\bigg[A_{n-1}(x)\bigg]-I^{\alpha}\bigg[\frac{1}{2}y_{n-1}(x)\bigg]+I^{\alpha}\bigg[ \frac{1}{2}B_{n-1}(x)\bigg], n\geq 1. \end{cases} \end{equation}$

(4.54)

Furthermore, without loss of generality, using the same approach as in the above situations, we present the corresponding solutions by applying the proposed modification methods for $l = 6$ .

$\begin{equation} \begin{split} y_{Taylor}& = 1+\frac{x^{\alpha}}{2\Gamma(\alpha+1)}-\frac{ 0.312050000x^{2+\alpha}}{\Gamma(\alpha+3)}-\frac{ 8.249652602\times 10^{-6}x^{3+\alpha}}{\Gamma(4+\alpha)}\\&+\frac{0.1947504048x^{4+\alpha}}{\Gamma(\alpha+5)}-\frac{2.60389834\times 10^{-14}x^{6+\alpha}}{\Gamma(7+\alpha)}+\dots \end{split} \end{equation}$

(4.55)

$\begin{equation} \begin{split} yT(x)& = 1+\frac{0.500000002x^{\alpha}}{\Gamma(\alpha+1)}-\frac{5.3\times 10^{-8} x^{\alpha+1}}{\Gamma(\alpha+2)}-\frac{0.312047768x^{1+\alpha}}{\Gamma(2+\alpha)}-\frac{0.001388888891x^{2+\alpha}}{\Gamma(3+\alpha)} \\&+\frac{ 0.0008680555500x^{2+\alpha}}{\Gamma(3+\alpha)}-\frac{ 4.803621032\times 10^{-10}x^{4+\alpha}}{\Gamma(5+\alpha)}+\dots \end{split} \end{equation}$

(4.56)

$\begin{equation} \begin{split} yU(x)& = 1+\frac{0.500000004x^{\alpha}}{\Gamma(\alpha+1)}-\frac{1.3\times 10^{-8} x^{\alpha+1}}{\Gamma(\alpha+2)}-\frac{0.312047768x^{1+\alpha}}{\Gamma(2+\alpha)}-\frac{0.001388888891x^{2+\alpha}}{\Gamma(3+\alpha)} \\&+\frac{ 0.0008680555792x^{2+\alpha}}{\Gamma(3+\alpha)}-\frac{ 4.8036971329\times 10^{-10}x^{4+\alpha}}{\Gamma(5+\alpha)}+\dots \end{split} \end{equation}$

(4.57)

$\begin{equation} \begin{split} yP(x)& = 1+\frac{0.500000004x^{\alpha}}{\Gamma(\alpha+1)}-\frac{1.43\times 10^{-7} x^{\alpha}}{\Gamma(\alpha+1)}-\frac{ 0.31204696x^{2+\alpha}}{\Gamma(3+\alpha)}-\frac{0.001388888913x^{1+\alpha}}{\Gamma(\alpha+2)}+\\&+\frac{0.0008680555792x^{2+\alpha}}{\Gamma(3+\alpha)}+\frac{ 4.805407763\times 10^{-10}x^{4+\alpha}}{\Gamma(5+\alpha)}+\dots \end{split} \end{equation}$

(4.58)

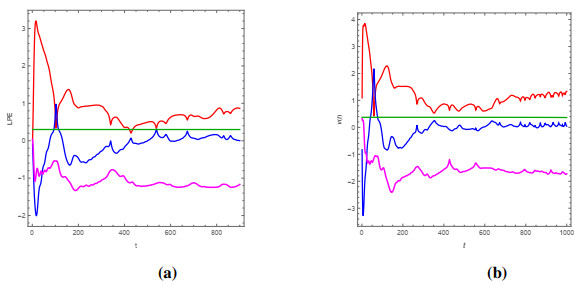
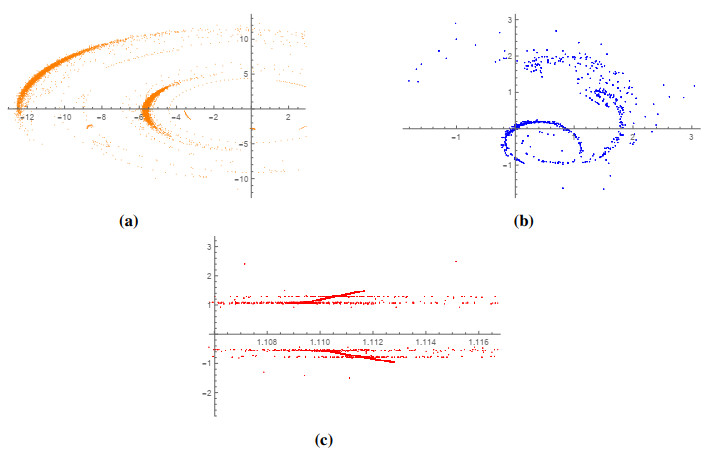
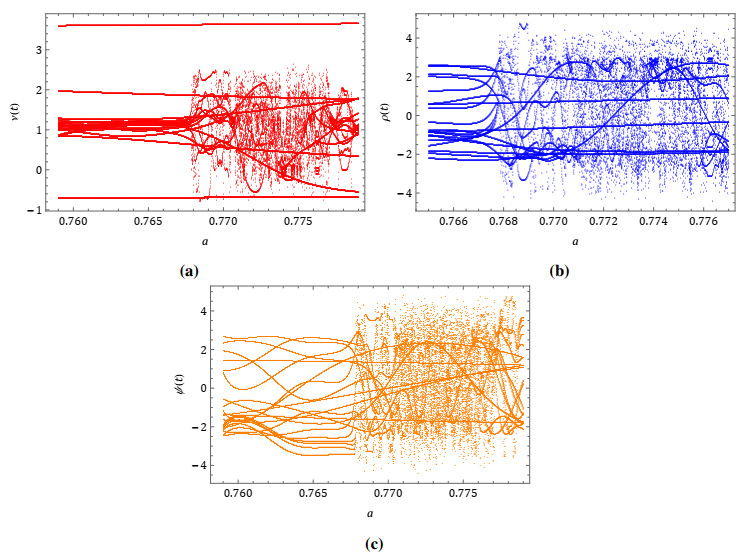
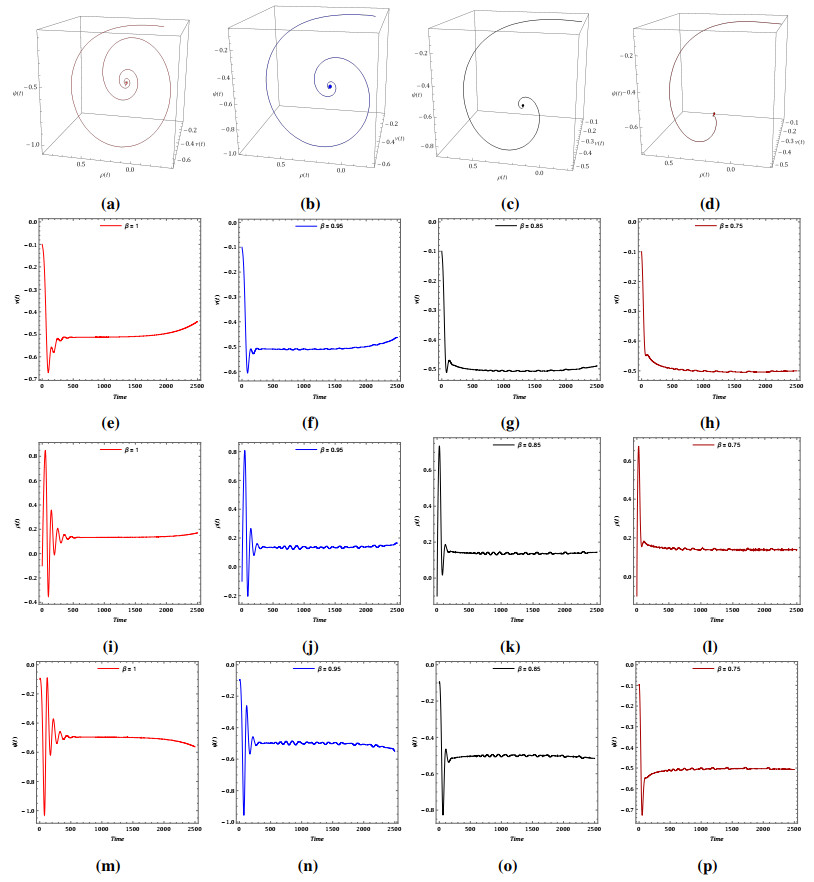
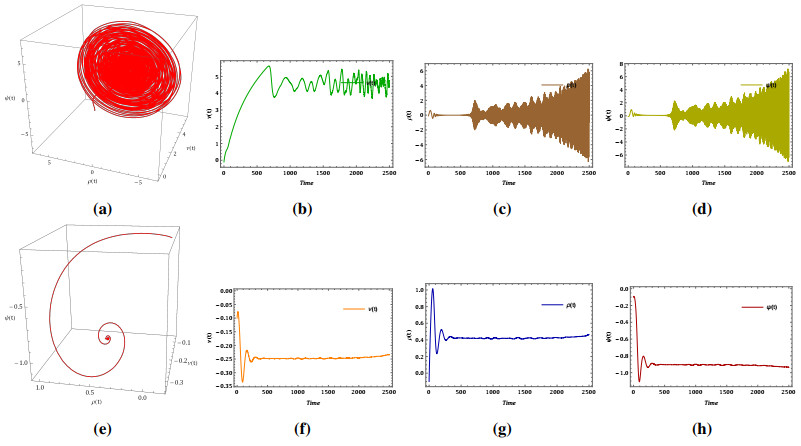
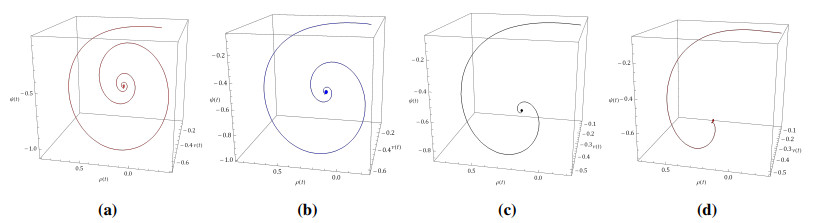
The results obtained using the modification method of the ADM with $l = 6$ for three different scenarios (single-well, double-well, and double-hump) are presented in Tables 4, , and , respectively. In this analysis, we set the fractional order of the problem to $\alpha = 2$ . The numerical results are compared with those from the variational iteration method (VIM) ^[41], the ultraspherical wavelets method (UWM) ^[42], the fourth-order Runge-Kutta (RK) method, and Bernoulli wavelet method (BWM) ^[43], see Tables 3, 5, and 7, respectively. In addition, CPU times of the presented method are listed in Tables 4, 6, and 8. Figure 3 shows the obtained numerical solutions by the presented modification method of the ADM.

Table 3. Single-well situation: Comparison of numerical solutions for

$\alpha = 2$ .

$x$	VIM	UWM	RK-4	BWM
0.0	1.00000000	1.00000000	1.00000000	1.00000000
0.1	0.99750286	0.99750276	0.99750272	0.99750285
0.2	0.99004534	0.99004513	0.99004504	0.99004516
0.3	0.97772778	0.97772579	0.97772567	0.97772579
0.4	0.96071284	0.96070262	0.96070236	0.96070247
0.5	0.93922114	0.93918360	0.93918299	0.93918309
0.6	0.91352389	0.91341578	0.91341497	0.913415063
0.7	0.88393496	0.88367502	0.88367344	0.88367350
0.8	0.85080112	0.85052195	0.85024907	0.85024912
0.9	0.81449135	0.81343957	0.81343631	0.81343635
CPU time	–	–	–	0.047

| Show Table

DownLoad: CSV

Table 4. Single-well situation: Comparison of the modification method for

$\alpha = 2$ .

$x$	$y_{Taylor}$	$yT(x)$	$yU(x)$	$yP(x)$
0.0	1.00000000	1.00000000	1.00000000	1.00000000
0.1	0.997511148	0.997511148	0.997511148	0.997511148
0.2	0.990111067	0.990111067	0.990111067	0.990111067
0.3	0.977945843	0.977945843	0.977945842	0.977945843
0.4	0.961217057	0.961217047	0.961217046	0.961217047
0.5	0.940171867	0.940171858	0.940171846	0.940171859
0.6	0.915091741	0.915091701	0.915091690	0.915091693
0.7	0.886280168	0.886280013	0.886279999	0.886280002
0.8	0.854049540	0.854049049	0.854049037	0.854049041
0.9	0.818704518	0.818703259	0.818703244	0.818703257
CPU time	0.0489	0.0696	0.06844	0.0781

| Show Table

DownLoad: CSV

Table 5. Double-well situation: Comparison of numerical solutions for

$\alpha = 2$ .

$x$	VIM	UWM	RK-4	BWM
0.0	1.00000000	1.00000000	1.00000000	1.00000000
0.1	1.00249660	1.00249669	1.00249670	1.00249660
0.2	1.00994530	1.00994542	1.00994545	1.00994536
0.3	1.0222113	1.02222174	1.02222179	1.02222170
0.4	1.03911114	1.03911446	1.03911459	1.03911450
0.5	1.06030866	1.06032214	1.06032231	1.06032223
0.6	1.08540584	1.08544887	1.08544906	1.08544898
0.7	1.11388470	1.11400072	1.11400108	1.11400100
0.8	1.14510669	1.14538393	1.14538468	1.14538460
0.9	1.17830101	1.17890570	1.17890664	1.17890656
CPU time	–	–	–	0.062

| Show Table

DownLoad: CSV

Table 6. Double-well situation: Comparison of the modification method for

$\alpha = 2$ .

$x$	$Y_{Taylor}$	$yT(x)$	$yU(x)$	$yP(x)$
0.0	1.00000000	1.00000000	1.00000000	1.00000000
0.1	1.00248830	1.00248830	1.00248830	1.00248830
0.2	1.00987939	1.00987939	1.00987939	1.00987939
0.3	1.02200111	1.02200111	1.02200111	1.02200111
0.4	1.03859815	1.03859814	1.03859814	1.03859814
0.5	1.05932967	1.05932966	1.05932965	1.05932966
0.6	1.08376731	1.08376727	1.08376726	1.08376726
0.7	1.11139358	1.11139342	1.11139341	1.11139341
0.8	1.14160208	1.14160159	1.14160158	1.14160158
0.9	1.17369994	1.17369868	1.17369867	1.17369868
CPU time	0.0489	0.0696	0.06844	0.0781

| Show Table

DownLoad: CSV

Table 7. Double-hump situation: Comparison of numerical solutions for

$\alpha = 2$ .

$x$	VIM	UWM	RK-4	BWM
0.0	1.00000000	1.00000000	1.00000000	1.00000000
0.1	1.00250077	1.00250086	1.00250078	1.00250077
0.2	1.01001232	1.01001258	1.01001240	1.01001236
0.3	1.02256255	1.02256352	1.02256311	1.02256305
0.4	1.04019982	1.04020320	1.04020266	1.04020259
0.5	1.06299669	1.06300878	1.06300754	1.06300746
0.6	1.09105590	1.09109104	1.09108901	1.09108890
0.7	1.12451829	1.12460856	1.12460496	1.12460473
0.8	1.16357278	1.16377964	1.16377494	1.16377462
0.9	1.20846809	1.20890608	1.20890103	1.20890063
CPU time	–	–	–	0.171

| Show Table

DownLoad: CSV

Table 8. Double-hump situation: Comparison of the modification method for

$\alpha = 2$ .

$x$	$Y_{Taylor}$	$yT(x)$	$yU(x)$	$yP(x)$
0.0	1.00000000	1.00000000	1.00000000	1.00000000
0.1	1.00249245	1.00249245	1.00249245	1.00249245
0.2	1.00994585	1.00994585	1.00994585	1.00994585
0.3	1.02233836	1.02233836	1.02233836	1.02233836
0.4	1.03966877	1.03966876	1.03966876	1.03966876
0.5	1.06196079	1.06196078	1.06196077	1.06196078
0.6	1.08927009	1.08927005	1.08927004	1.08927004
0.7	1.12169449	1.12169433	1.12169432	1.12169432
0.8	1.15938728	1.15938678	1.15938677	1.15938677
0.9	1.20257483	1.20257354	1.20257353	1.20257354
CPU time	0.0489	0.0696	0.06844	0.0781

| Show Table

DownLoad: CSV

Figure 3. Comparison of numerical solutions for the fractional IVP (4.30).

DownLoad: Full-Size Img PowerPoint

5. Conclusions

This study investigates the application of the Taylor series, Legendre polynomials, and both the first and second kinds of Chebyshev polynomials within the Adomian decomposition method (ADM) for solving initial-value problems (IVPs) of fractional differential equations. The findings demonstrate the efficiency and accuracy of these approaches. Additionally, the study presents several modification methods for the ADM, highlighting the critical role of orthogonal polynomials in numerical analysis. Among the nonlinear inhomogeneous IVPs tested, the Legendre polynomial methods exhibited the lowest error rates. Given their computational benefits, these methods are recommended for fractional-order IVP models in scientific and engineering applications. Furthermore, the results obtained can be extended or generalized to various types of fractional differential equations and their associated operators.

Author contributions

Mariam Al-Mazmumy: Conceptualization, methodology, investigation, software, writing review & editing; Maryam Ahmed Alyami: Methodology, investigation, writing review & editing; Mona Alsulami: Methodology, investigation, writing review & editing; Asrar Saleh Alsulami: Formal analysis, methodology, investigation, writing original draft preparation, software, writing review & editing; Saleh S. Redhwan: Writing review & editing. All authors have read and approved the final version of the manuscript for publication.

Acknowledgments

The authors would like to thank the editor and referees for their comments and suggestions, which improved the presentation of the original manuscript.

Conflict of interest

The authors declare that they have no conflict of interest.

References

[1]	J. E. Skinner, M. Molnar, T. Vybiral, M. Mitra, Application of chaos theory to biology and medicine, Integr. Physiol. Behav. Sci., 27 (1992), 39–53. https://doi.org/10.1007/bf02691091 doi: 10.1007/bf02691091
[2]	Y. Liu, Circuit implementation and finite-time synchronization of the 4D Rabinovich hyperchaotic system, Nonlinear Dyn., 67 (2012), 89–96. https://doi.org/10.1007/s11071-011-9960-2 doi: 10.1007/s11071-011-9960-2
[3]	M. E. Sahin, Z. G. Cam Taskiran, H. Guler, S. E. Hamamci, Application and modeling of a novel 4D memristive chaotic system for communication systems, Circuits Syst. Signal Process., 39 (2020), 3320–3349. https://doi.org/10.1007/s00034-019-01332-6 doi: 10.1007/s00034-019-01332-6
[4]	E. N. Lorenz, Irregularity: a fundamental property of the atmosphere, Tellus A, 36A (1984), 98–110. https://doi.org/10.3402/tellusa.v36i2.11473 doi: 10.3402/tellusa.v36i2.11473
[5]	Y. Yu, Dynamical analysis of a low-order model representing Hadley circulation, J. Beijing Jiaotong Univ., 30 (2006), 50–53.
[6]	I. Podlubny, Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications, Academic Press, 1998.
[7]	N. Sene, Analysis of a four-dimensional hyperchaotic system described by the Caputo-Liouville fractional derivative, Complexity, 2020 (2020), 8889831. https://doi.org/10.1155/2020/8889831 doi: 10.1155/2020/8889831
[8]	Y. Cao, Y. Kao, J. H. Park, H. Bao, Global Mittag-Leffler stability of the delayed fractional-coupled reaction-diffusion system on networks without strong connectedness, IEEE Trans. Neural Networks Learn. Syst., 33 (2022), 6473–6483. https://doi.org/10.1109/TNNLS.2021.3080830 doi: 10.1109/TNNLS.2021.3080830
[9]	R. N. Premakumari, C. Baishya, M. K. A. Kaabar, Dynamics of a fractional plankton-fish model under the influence of toxicity, refuge, and combine-harvesting efforts, J. Inequal. Appl., 2022 (2022), 137. https://doi.org/10.1186/s13660-022-02876-z doi: 10.1186/s13660-022-02876-z
[10]	S. Vaidyanathan, A. T. Azar, Analysis and control of a 4-D novel hyperchaotic system, In: A. Azar, S. Vaidyanathan, Chaos modeling and control systems design: studies in computational intelligence, Springer, Cham, 581 (2015), 3–17. https://doi.org/10.1007/978-3-319-13132-0_1
[11]	L. O. Chua, M. Itoh, L. Kocarev, K. Eckert, Chaos synchronization in Chua's Circuit, J. Circuits Syst. Comput., 3 (1993), 93–108. https://doi.org/10.1142/S0218126693000071 doi: 10.1142/S0218126693000071
[12]	D. Baleanu, S. S. Sajjadi, J. H. Asad, A. Jajarmi, E. Estiri, Hyperchaotic behaviors, optimal control, and synchronization of a nonautonomous cardiac conduction system, Adv. Differ. Equ., 2021 (2021), 157. https://doi.org/10.1186/s13662-021-03320-0 doi: 10.1186/s13662-021-03320-0
[13]	U. E. Kocamaz, B. Cevher, Y. Uyaroǧlu, Control and synchronization of chaos with sliding mode control based on cubic reaching rule, Chaos Soliton. Fract., 105 (2017), 92–98. https://doi.org/10.1016/j.chaos.2017.10.008 doi: 10.1016/j.chaos.2017.10.008
[14]	Y. Kao, Y. Li, J. H. Park, X. Chen, Mittag-Leffler synchronization of delayed fractional memristor neural networks via adaptive control, IEEE Trans. Neural Networks Learn. Syst., 32 (2021), 2279–2284. https://doi.org/10.1109/TNNLS.2020.2995718 doi: 10.1109/TNNLS.2020.2995718
[15]	C. Baishya, M. K. Naik, R. N. Premakumari, Design and implementation of a sliding mode controller and adaptive sliding mode controller for a novel fractional chaotic class of equations, Results Control Optim., 14 (2024), 100338. https://doi.org/10.1016/j.rico.2023.100338 doi: 10.1016/j.rico.2023.100338
[16]	A. Moufid, N. Bennis, A multi-modelling approach and optimal control of greenhouse climate, In: S. El Hani, M. Essaaidi, Recent advances in electrical and information technologies for sustainable development, Advances in Science, Technology & Innovation, Cham: Springer, 2019,201–208. https://doi.org/10.1007/978-3-030-05276-8_22
[17]	R. N. Premakumari, C. Baishya, M. E. Samei, M. K. Naik, A novel optimal control strategy for nutrient-phytoplankton-zooplankton model with viral infection in plankton, Commun. Nonlinear Sci. Numer. Simul., 137 (2024), 108157. https://doi.org/10.1016/j.cnsns.2024.108157 doi: 10.1016/j.cnsns.2024.108157
[18]	S. Vaidyanathan, Global stabilisation of control systems using a new sliding mode control method and its application to a general type of synchronisation for chaotic systems, Int. J. Model. Identif. Control, 40 (2022), 1–10. https://doi.org/10.1504/IJMIC.2022.124067 doi: 10.1504/IJMIC.2022.124067
[19]	M. K. Naik, C. Baishya, R. N. Premakumari, M. E. Samei, Navigating climate complexity and its control via hyperchaotic dynamics in a 4D Caputo fractional model, Sci. Rep., 14 (2024), 18015. https://doi.org/10.1038/s41598-024-68769-x doi: 10.1038/s41598-024-68769-x
[20]	M. Roohi, S. Mirzajani, A. Basse-O'Connor, A no-chatter single-input finite-time PID sliding mode control technique for stabilization of a class of 4D chaotic fractional order laser systems, Mathematics, 11 (2023), 21. https://doi.org/10.3390/math11214463 doi: 10.3390/math11214463
[21]	Y. Kao, C. Wang, H. Xia, Y. Cao, Projective synchronization for uncertain fractional reaction-diffusion systems via adaptive sliding mode control based on finite-time scheme, In: Analysis and control for fractional-order systems, Singapore: Springer, 2024,141–163. https://doi.org/10.1007/978-981-99-6054-5_8
[22]	Y. Cao, Y. Kao, Z. Wang, X. Yang, J. H. Park, W. Xie, Sliding mode control for uncertain fractional order reaction-diffusion memristor neural networks with time delays, Neural Networks, 178 (2024), 106402. https://doi.org/10.1016/j.neunet.2024.106402 doi: 10.1016/j.neunet.2024.106402
[23]	Y. Kao, Y. Cao, X. Chen, Global Mittag-Leffler synchronization of coupled delayed fractional reaction-diffusion Cohen-Grossberg neural networks via sliding mode control, Chaos, 32 (2022), 113123. https://doi.org/10.1063/5.0102787 doi: 10.1063/5.0102787
[24]	P. J. Roebber, Climate variability in a low-order coupled atmosphere-ocean model, Tellus A, 47 (1995), 473–494. https://doi.org/10.3402/tellusa.v47i4.11534 doi: 10.3402/tellusa.v47i4.11534
[25]	A. Chakraborty, P. Veeresha, Effects of global warming, time delay and chaos control on the dynamics of a chaotic atmospheric propagation model within the frame of Caputo fractional operator, Commun. Nonlinear Sci. Numer. Simul., 128 (2024), 107657. https://doi.org/10.1016/j.cnsns.2023.107657 doi: 10.1016/j.cnsns.2023.107657
[26]	R. N. Premakumari, C. Baishya, P. Veeresha, L. Akinyemi, A fractional atmospheric circulation system under the influence of a sliding mode controller, Symmetry, 14 (2022), 2618. https://doi.org/10.3390/sym14122618 doi: 10.3390/sym14122618
[27]	J. Singh, R. Agrawal, K. S. Nisar, A new forecasting behavior of fractional model of atmospheric dynamics of carbon dioxide gas, Partial Differ. Equ. Appl. Math., 9 (2024), 100595. https://doi.org/10.1016/j.padiff.2023.100595 doi: 10.1016/j.padiff.2023.100595
[28]	S. Etemad, S. K. Ntouyas, I. Stamova, J. Tariboon, On solutions of two post-quantum fractional generalized sequential Navier problems: an application on the elastic beam, Fractal Fract., 8 (2024), 236. https://doi.org/10.3390/fractalfract8040236 doi: 10.3390/fractalfract8040236
[29]	T. Kanwal, A. Hussain, İ. Avcı, S. Etemad, S. Rezapour, D. F. M. Torres, Dynamics of a model of polluted lakes via fractal-fractional operators with two different numerical algorithms, Chaos Soliton. Fract., 181 (2024), 114653. https://doi.org/10.1016/j.chaos.2024.114653 doi: 10.1016/j.chaos.2024.114653
[30]	P. Y. Dousseh, C. Ainamon, C. H. Miwadinou, A. V. Monwanou, J. B. C. Orou, Chaos in a financial system with fractional order and its control via sliding mode, Complexity, 2021 (2021), 4636658. https://doi.org/10.1155/2021/4636658 doi: 10.1155/2021/4636658
[31]	C. T. Deressa, S. Etemad, S. Rezapour, On a new four-dimensional model of memristor-based chaotic circuit in the context of nonsingular Atangana-Baleanu-Caputo operators, Adv. Differ. Equ., 2021 (2021), 444. https://doi.org/10.1186/s13662-021-03600-9 doi: 10.1186/s13662-021-03600-9
[32]	N. D. Phuong, F. M. Sakar, S. Etemad, S. Rezapour, A novel fractional structure of a multi-order quantum multi-integro-differential problem, Adv. Differ. Equ., 2020 (2020), 633. https://doi.org/10.1186/s13662-020-03092-z doi: 10.1186/s13662-020-03092-z
[33]	A. Amara, S. Etemad, S. Rezapour, Approximate solutions for a fractional hybrid initial value problem via the Caputo conformable derivative, Adv. Differ. Equ., 2020 (2020), 608. https://doi.org/10.1186/s13662-020-03072-3 doi: 10.1186/s13662-020-03072-3
[34]	H. Najafi, S. Etemad, N. Patanarapeelert, J. K. K. Asamoah, S. Rezapour, T. Sitthiwirattham, A study on dynamics of CD4⁺ T-cells under the effect of HIV-1 infection based on a mathematical fractal-fractional model via the Adams-Bashforth scheme and Newton polynomials, Mathematics, 10 (2022), 1366. https://doi.org/10.3390/math10091366 doi: 10.3390/math10091366
[35]	H. L. Li, L. Zhang, C. Hu, Y. L. Jiang, Z. Teng, Dynamical analysis of a fractional-order predator-prey model incorporating a prey refuge, J. Appl. Math. Comput., 54 (2017), 435–449. https://doi.org/10.1007/s12190-016-1017-8 doi: 10.1007/s12190-016-1017-8
[36]	H. Wang, Y. Yu, G. Wen, Dynamical analysis of the Lorenz-84 atmospheric circulation model, J. Appl. Math., 2014 (2014), 296279. https://doi.org/10.1155/2014/296279 doi: 10.1155/2014/296279
[37]	A. T. Azar, S. Vaidyanathan, Chaos modeling and control systems design, Vol. 581, Springer International Publishing, Springer Cham, 2015. https://doi.org/10.1007/978-3-319-13132-0
[38]	M. F. Danca, Lyapunov exponents of a discontinuous 4D hyperchaotic system of integer or fractional order, Entropy, 20 (2018), 337. https://doi.org/10.3390/e20050337 doi: 10.3390/e20050337
[39]	Z. Liu, J. Li, X. Di, A new hyperchaotic 4D-FDHNN system with four positive lyapunov exponents and its application in image encryption, Entropy, 24 (2022), 900. https://doi.org/10.3390/e24070900 doi: 10.3390/e24070900
[40]	G. P. Williams, Chaos theory tamed, 1 Ed., CRC Press, 1997. https://doi.org/10.1201/9781482295412
[41]	K. Diethelm, An algorithm for the numerical solution of differential equations of fractional order systems, Electron. Trans. Numer. Anal., 5 (1997), 1–6.
[42]	N. Sene, Introduction to the fractional-order chaotic system under fractional operator in Caputo sense, Alexandria Eng. J., 60 (2021), 3997–4014. https://doi.org/10.1016/j.aej.2021.02.056 doi: 10.1016/j.aej.2021.02.056
[43]	K. Deng, C. Azorin-Molina, S. Yang, C. Hu, G. Zhang, L. Minola, et al., Changes of southern hemisphere westerlies in the future warming climate, Atmos. Res., 270 (2022), 106040. https://doi.org/10.1016/j.atmosres.2022.106040 doi: 10.1016/j.atmosres.2022.106040

This article has been cited by:

Peng E, Tingting Xu, Linhua Deng, Yulin Shan, Miao Wan, Weihong Zhou, Solutions of a class of higher order variable coefficient homogeneous differential equations, 2025, 20, 1556-1801, 213, 10.3934/nhm.2025011

Reader Comments

Your name:*

Email:*
© 2024 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)