1.
Introduction
The main contribution of this paper is the introduction of a novel invariant of a monomial ideal, termed its signature, which can be thought of as a type of canonical form of its incidence matrix, and the proof that two monomial ideals with the same signature have essentially the same irreducible decomposition.
In general, monomial ideals are central objects in commutative algebra through which a fruitful bridge has been established between commutative algebra and combinatorics; see, for instance, [1,2,3] and the references contained there. In particular, the irreducible decomposition of a monomial ideal has played an important role in combinatorial commutative algebra. It has an increasing number of applications, from pure mathematics to biology. Its applications in pure mathematics go from the integer programming gap, the Frobenius problem, secants of monomial ideals, tropical convex hulls and cyclic polytopes, differential powers of monomial ideals, and in biology as the reverse engineering of biochemical networks; see, for instance, the references contained in [4]. There are also available efficient specialized algorithms to compute the irredundant irreducible decomposition of a monomial ideal; see, for instance, [4,5].
The irreducible decomposition of an ideal is very close to its primary decomposition, in which primary ideals are replaced by irreducible ideals. One difference with a primary decomposition is that the irreducible decomposition is unique and generally simpler to compute. Moreover, when the ideal is monomial, several aspects of the irreducible decomposition can be simplified, leading us naturally toward a more combinatorial context. The primary decomposition of an ideal, introduced by Lasker and Noether, is one of the seminal ideas of commutative algebra. It was inspired by the fact that any ring element can be factorized as the product of some irreducible factors, such as in the Fundamental Theorem of Arithmetic for the ring of integers at the beginning of the 1900s. A key fact to factorizing an ideal is that it is more convenient to consider the intersection of irreducible ideals instead of its product, as in the factorization of integers.
Let's fix some of the notation that we will use throughout the paper. Let S=k[x] be a polynomial ring over a field k and variables x={x1,…,xn}. Here, we will stress the bijection between the variables in S and the elements of [n]={1,…,n} via the correspondence between xi and i. Moreover, this bijection can be extended to a bijection between multisets in [n], monomials in k[x], and vectors in Nn. The first one can be obtained with the map that sends the multiset A of [n] to the monomial xA=∏a∈Axa in S, and the second one can be obtained by the map that sends the monomial xa=∏ni=1xaii to the vector a=(a1,…,an) in Nn. When no confusion arises, we will identify monomials in k[x], vectors in Nn, and multisets in [n]. This provides a bridge between commutative algebra, polyhedral geometry, and combinatorics, enriching the interaction between these areas.
In this sense, the set of monomials Mon(S) of S corresponds to the elements in Nn. Moreover, antichains G in Nn (that is, a set G={g1,…,gq}⊂Nn which are incomparable gi⊥gj by pairs with respect to the order ≤ of Nn) corresponds to minimal generating sets of monomial ideals in S. Thus, given an antichain G in Nn, let IG=⟨xg1,…,xgq⟩⊂S be its antichain ideal, which is simply another way of saying monomial ideals. We use the term antichain ideal to refer to a monomial ideal since the former emphasizes that the order in Nn plays a crucial role in studying these ideals.
It is well-known that each monomial ideal I in S is minimally generated by a finite set of generators xG={xg1,…,xgq}. Moreover, xG is a minimal generating set of a monomial ideal if and only if G is an antichain in Nn. Although the algebraic properties of a monomial ideal do not depend on the order of its generators, throughout the paper, we are always assuming that the elements of G are ordered. This is similar to the difference between a linear transformation and its matrix representation; unlike the linear transformation, the latter depends on the chosen base.
In Section 2, we recall what the irreducible decomposition of a monomial ideal means. More precisely, we will use the ideals generated by the power of a single variable as basic blocks and the union and intersection as operations between them; we get that any monomial ideal has an irreducible decomposition; see Eq (2.1).
After that, we introduce the novel concept of ∞-cover of the antichain, which generalizes the concept of minimal vertex cover for graphs.
Definition 2.8. An ∞-cover of the antichain G is a vector c∈Nn∞, N∞=N∪{∞}, such that for any
Moreover, it is called maximal whenever it is maximal with respect to the order ≤ in Nn∞.
This leads to the following combinatorial description of the irredundant irreducible decomposition of an antichain ideal IG in terms of the set T(G) of its maximal ∞-covers.
Theorem 2.12. If G is an antichain in Nn, then
is the irredundant irreducible decomposition of the antichain ideal IG.
In Section 3, we introduce the central concept of this paper, the signature of a monomial ideal. Roughly speaking, the signature of a monomial ideal is a matrix that encodes the way the minimal generators of the ideal are ordered for each variable separately. More precisely, given a vector c∈Nn, its content is the vector cont(c)=(m0,…,mr) that contains its different entries in ascending order and its signature is given by
Definition 3.5. The signature of a monomial ideal IG, denoted by σ(IG), is the matrix obtained from its incidence matrix BG by replacing its rows with their corresponding signatures.
The main result of this paper gives us a description of the irredundant irreducible decomposition of any monomial with signature σ in terms of the irredundant irreducible decomposition of the antichain ideal Iσ of σ. Given a vector c∈Nn, the support of c is given by supp(c)={i∈[n]:ci≠0}.
Theorem 3.11. If σ is a signature, IG is a monomial ideal with signature σ and m=gcd(gi∈G), then
is the irredundant irreducible decomposition of IG for some Jσ⊆∏qi=1supp(gi) and mGJ=⟨x(g1)J1J1,…,x(gq)JqJq⟩ for J∈Jσ.
In Section 4, we explore Alexander duality in the context of the signature. If τ0 is the matrix that encodes the irredundant irreducible decomposition of the antichain ideal associated with a signature σ and interchanging the zero entries by ∞, σ∨ and τ∨0 are the matrices obtained from σ and τ by reversing the order on its entries (see Definition 4.3), respectively, then the content of its rows is preserved.
Theorem 4.5. Let σ be the signature of a monomial ideal without the power of a variable as a generator. If si, ti, ui and vi are the i-rows of σ, τ0, σ∨, and τ∨0, respectively, then
This leads to show that Alexander duality behaves well with respect to signature.
Theorem 4.12. Let σ be a signature with no column with only one nonzero entry and DG be the decomposition matrix of the antichain ideal of G. Then, σ(DG)=τ0 if and only if σ(IG)=σ.
Therefore, it is natural to extend Alexander duality between monomial ideals with the same signature.
We finish this paper by posing a pair of conjectures that claim that monomial ideals with the same signature have essentially the same minimal free resolution and that their quotient modules share at least a common regular sequence. These pair of conjectures give us an insight into the possible usefulness of the signature of a monomial ideal.
Conjecture 5.2. Let I and J be monomial ideals with the same signature. If d is the depth of I, then there exists a sequence h1,…,hd of polynomials such that it is a regular sequence of both S/I and S/J.
Before establishing the second conjecture, we must introduce the concept of poset resolution. Given a minimal free resolution F∙={Fi,di}pi=0 of a monomial ideal, its poset resolution is a decorated graded poset P∙ given by a triplet (P,s,m), where P=(F,≤) is the graded poset on the generators of each of the free modules Fi, where u∈Fi−1 is covered by v∈Fi whenever di(v)=∑w∈Fi−1sww with 0≠su∈k for some 1≤i≤p. The function s comes from the edges of the Hasse diagram of P to the field k given by the coefficient of the term su in
and m:F→Mon(S) is the function that takes the monomial with the multidegree of v.
Conjecture 5.3. If I and J are monomial ideals with the same signature, then there exists a poset resolution P∙=(P,s,m) of I such that P′∙=(P,s,m′) is a poset resolution of J for some m′.
2.
Irredundant irreducible decomposition of a monomial ideal
We begin by recalling what the irreducible decomposition of a monomial ideal means. The reader can consult, for instance, Section 3 of [6] for a very accessible exposition of the subject.
Although many of the ideas included in this section are found (explicitly or implicitly) in the literature, the way they are presented here differs from how they are commonly presented. More importantly, it provides a point of view that will be useful for our purposes, and we believe it contains some new ideas. For instance, one of the novel elements introduced here is the maximal ∞-cover of an antichain, which generalizes the concept of the minimal vertex cover of a graph.
A monomial ideal has at least two minimal ways to be represented. The most common form of these, which gives rise to its name, is as the ideal generated by a set of monomials. A second way is the so-called irreducible decomposition, which expresses it as the intersection of ideals generated by the powers of some subsets of variables, called irreducible.
In what follows, we will show that all the monomials in a monomial ideal I can be obtained from ideals generated by the power of a single variable as basic blocks and the union and intersection as operations between them. Given an ideal I in the polynomial ring S, let Mon(I) denote its set of monomials. We recall that any monomial ideal is determined by its set of monomials. That is, if I and J are monomial ideals of S, then I=J if and only if Mon(I)=Mon(J).
The irreducible decomposition of a monomial ideal can begin with the following very simple observation: the ideal generated by the monomial xg is equal to
where supp(g)={i∈[n]:gi≠0} is the support of g. Moreover, since the set of monomials of the antichain ideal IG is equal to Mon(IG)=Mon(⟨xg1,…,xgq⟩)=⋃qk=1Mon(⟨xgk⟩), then
Distributing the union over the intersection, we get that
and therefore
We remark that each J is a vector in [n]q. Thus, using this very simple observation, we have proved that any monomial ideal has at least one irreducible decomposition. However, the decomposition given in (2.1) has several redundancies. The simplest of which is that the factors
can have powers on the same variable. This can be easily solved by recalling that ⟨xa,xb⟩=⟨xmin{a,b}⟩. More precisely:
Definition 2.1. Given J∈∏qi=1supp(gi)⊆[n]q, let GJ∈Nn be such that
where m=⟨x1,…,xn⟩ and ma=⟨{xaii:ai>0}⟩ for any a∈Nn.
To simplify the notation, let ΠG=∏qi=1supp(gi). Thus, by Definition 2.1, establish a mapping from ΠG to Nn that sends J to GJ.
Remark 2.2. In the definition of ma there are only considered positive powers of the variables.
Thus, the decomposition (2.1) can be simplified as
A second type of redundancy that appears in this decomposition is that, in general, many of the factors in (2.2) are not necessary; that is, we can omit them from the intersection preserving IG. This leads us to introduce the concept of irredundancy of an irreducible decomposition.
Definition 2.3. An irreducible decomposition with factors Q={Q1,…,Qm} of an ideal I is called irredundant whenever
and redundant otherwise.
Although irreducible decompositions of a monomial ideal are not necessarily unique, it is not difficult to check that an irredundant irreducible decomposition must be unique.
The irreducible decomposition given in (2.2) has |ΠG|=∏qi=1|supp(gi)| factors, which can be huge. Even so, there exist cases where it is actually irredundant. For instance, let IqK2=⟨x1x2,x3x4,…,x2q−1x2q⟩ be the edge ideal of the disjoint union of q edges. It can be checked that |ΠqK2|=∏qi=1|supp(gi)|=2q and its irredundant irreducible decomposition is equal to
where E(qK2)={v1v2,v3v4,…,v2q−1v2q}.
In order to get an irredundant irreducible decomposition from (2.2), we need to omit the factors that are not minimal with respect to the inclusion of sets. In the literature, several strategies to achieve this can be found. In our case, we choose to use the partially ordered extended natural numbers Nn∞.
2.1. The partially ordered extended natural numbers ¯Nn.
Let ¯N=N∪{∞} be the extended natural numbers and ≤ be the extension on it of the usual order in N with a≤∞ for any a∈N. The reader can think of ¯N as a type of compactification of N. In a similar way, let ¯Nn be the set of vectors of size n with entries in ¯N, and ≤ be the partial order on ¯Nn induced by ≤ componentwise. Additionally, let N∞=¯N∖0.
Consider (¯Nn,≤) instead of only (Nn,≤), at least in our case, to do this has some advantages. For instance, it is not difficult to check that for a and b in Nn (see, for instance, [7,Proposition 1.4] for a very similar result),
where c∞∈¯Nn is obtained from c∈Nn by exchanging its zero entries by ∞. In a similar way, in this context it is very simple to describe the complement of Mon(ma) in Mon(S) as
Remark 2.4. In the same way that it is natural to consider that x0i=1, it is also natural to consider that ⟨x∞i⟩=0 because 0⊊⋯⊊⟨xni⟩⊊⋯⊊⟨x2i⟩⊊⟨xi⟩.
Since xa=0 for any a∈Nn∞ with some entry equal to ∞ and ma=S for any a∈Nn with some entry equal to 0, then from here on when we write xa we are assuming that a∈Nn and when we write ma we are assuming that a∈Nn∞. This convention is also adopted in [4], which helps distinguish between irreducible ideals and ideals generated by a monomial. This is a glimpse of a duality between 0 and ∞ into the two ways of expressing a monomial ideal, as generated by monomials and as the intersection of irreducible ideals.
Remark 2.5. If a∈Nn∞, then ma=⟨xa11,…,xann⟩=⟨{xaii:ai<∞}⟩≠S, which is equivalent to the previous definition of an irreducible ideal given in 2.1 for a0, where a0 is obtained from a by exchanging its ∞ entries by zero.
Besides, in this new context, the containment relation between two irreducible ideals is expressed simply as
and Mon(ma)c={xb:b+1≤a}. In what follows, we characterize when an intersection of irreducible ideals is irredundant.
Lemma 2.6. If T⊂Nn∞, then T is an antichain in (Nn∞,≤) if and only if
is irredundant.
Proof. We will proceed by contradiction, that is, we will assume that ⋂a∈Tma is redundant. The decomposition ⋂a∈Tma is redundant if and only if there exists b∈T such that ⋂a∈Tma=⋂a∈T∖bma if and only if ⋂a∈TMon(ma)=⋂a∈T∖bMon(ma) if and only if
if and only if
if and only if there exists a∈T∖b such that b≤a if and only if T is not an antichain of (Nn∞,≤), which is a contradiction. □
Remark 2.7. If A is a subset of Nn∞ whose elements are maximal with respect to the order in Nn∞, then A is an antichain in (Nn∞,≤). Thus, taking only maximal elements of T from the decomposition (2.2), we can get an irredundant irreducible decomposition of an antichain ideal.
2.2. maximal ∞-covers
In this subsection, we will express the irredundant irreducible decomposition of a monomial ideal in combinatorial terms. More precisely, we generalize the concept of a minimal vertex cover given in graph theory, which we call a maximal ∞-cover, to the context of monomial ideals.
Definition 2.8. An ∞-cover of the antichain G is a vector c∈Nn∞ such that for any
Moreover, it is called maximal whenever it is maximal with respect to the order ≤ in Nn∞.
It is well-known that the concept of minimal vertex cover has played a significant role in graph theory and combinatorial commutative algebra; see, for instance, [3] and [8], respectively. To make reading easier, we recall that a minimal vertex cover of a graph G is a set of vertices C such that it is incident (or covers) to all the edges of G, which is also minimal with respect to the inclusion of sets.
Since the edge ideal of a graph is the antichain ideal of the characteristic vectors of its edges and a≤b for a,b∈{0,1}n if and only if b∞≤a∞. Then, it is not difficult to check that a∈Nn is the characteristic vector of a minimal vertex cover of the graph G if and only if a∞∈Nn∞ is a maximal ∞-cover of G.
In what follows, we characterize the maximal ∞-cover of a given antichain. Recalling Definition 2.1, for any J∈ΠG, let GJ∈Nn be such that
In other words,
and therefore we have that GJ is always an ∞-cover of G. We recall that when i≠Jk for all 1≤k≤q, then (GJ)i=∞. Moreover, as shown in the following lemma, every maximal ∞-cover of an antichain G is of this form.
Lemma 2.9. Let G be an antichain in Nn. If c∈Nn∞ is a maximal ∞-cover of G, then there exists J∈ΠG such that
Proof. To start, we will prove that for any 1≤i≤n such that ci≠∞, there exists 1≤ki≤q such that ci=(gki)i. Otherwise, assume that ci≠(gk)i for some 1≤i≤n and for any 1≤k≤q. Thus, let 1≤j≤q such that ci<(gj)i and (gk)i∉[ci,(gj)i−1] for any 1≤k≤q.
Now, let ei be the vector of size n whose entries are zero, except its i-th entry, which equals one. It is not difficult to check that if c is an ∞-cover of G, then also c+ei is an ∞-cover of G, which is a contradiction to the maximality of c.
Let J be a vector in [n]q such that Jki=i and its other entries are defined using any of the values i already added to J. Moreover, for all i∈[n], we have 0≠ci≤(gk)i. Since c is an ∞-cover, then J it is well defined and c=GJ. We remark that J is not necessarily unique. □
Remark 2.10. In the proof of [7,Proposition 1.2], one can find similar arguments to those used in the proof of Lemma 2.9.
Note that the converse of Lemma 2.9 is not necessarily true; that is, although always GJ is an ∞-cover, it is not necessarily maximal. For instance, if
then G(1,2)=(1,2) is not maximal because G(2,1)=(2,3)≥(1,2)=G(1,2).
Remark 2.11. Moreover, if J≠K∈ΠG, then not necessarily GJ≠GK. That is, different J's can define the same ∞-cover of G. For instance, if IG is the edge ideal of the complete graph with three vertices K3 with g1=(1,1,0), g2=(0,1,1), and g3=(1,0,1), then G(1,2,1)=G(2,2,1)=(1,1,∞), which correspond to the minimal vertex cover {v1,v2} of K3.
Lemma 2.9 gives an insight into how maximal ∞-covers of G are related to the irreducible factors of the irreducible decomposition of IG given in (2.2).
We are now ready to generalize the classical result, which gives an irredundant irreducible decomposition of the edge ideal of a graph in terms of its minimal vertex covers [9,p. 279]. Let T(G) be the set of maximal ∞-covers of an antichain G.
Theorem 2.12. If G is an antichain in Nn, then
is the irredundant irreducible decomposition of the antichain ideal IG.
Proof. Since ma⊆mb if and only if a≥b, we get the result by applying Lemmas 2.6 and 2.9 to the irreducible decomposition given in (2.2). □
This result is similar to [5,Proposition 3], which establishes a bijection between the maximal standard monomial of S/I and the irredundant irreducible components of I. However, Theorem 2.12 is more direct and less mysterious in the way that it works. Even more important, it generalizes the result that describes the irredundant irreducible decomposition of an edge ideal IG in terms of the minimal vertex covers of G.
The next example illustrates before constructions.
Example 2.13. Let G={(2,0,2),(0,2,0),(1,1,3)} be an antichain in N3 and
be its antichain ideal. Thus, the decomposition (2.1) has the next six factors
which can be simplified to
On the other hand, since (2,2,3)⪈(1,2,2) and (0,2,2)⪈(0,1,2), then ⟨x21,x22,x33⟩⊊⟨x1,x22,x23⟩ and ⟨x22,x23⟩⊊⟨x2,x23⟩. That is, ⟨x1,x22,x23⟩ and ⟨x2,x23⟩ are redundant and, therefore,
is the irredundant irreducible decomposition of IG because (1,2,∞), (2,1,∞), (∞,2,2), and (2,2,3) are an antichain in N3∞. Moreover, it is not difficult to check that these last vectors are the maximal ∞-covers of G.
Since the concept of primary decomposition has played a significant role in commutative algebra, we finish this section by recalling how to recover the primary decomposition of a monomial ideal from its irreducible decomposition. We recall that a monomial ideal is primary if and only if it is generated by the powers and some monomials in a set of variables.
2.3. The primary decomposition of a monomial ideal
It is not difficult to recover the primary decomposition of a monomial ideal from its irreducible decomposition. To get the primary factors, we only need to intersect the irreducible factors with the same radical, which is very simple to check. The next example illustrates this procedure.
Example 2.14. Let IG be the monomial ideal given in Example 2.13. Thus,
is its irredundant irreducible decomposition. Since ⟨x1,x22⟩ and ⟨x21,x2⟩ have the same radical ideal ⟨x1,x2⟩ and ⟨x1,x22⟩∩⟨x21,x2⟩=⟨x21,x1x2,x22⟩,
is its primary decomposition.
3.
The signature of a monomial ideal
In this section, we will introduce the central concept of this paper, the signature of a monomial ideal. Roughly speaking, the signature of a monomial ideal is a matrix that encodes the way the minimal generators of the ideal are ordered for each variable separately. Although the signature is a simple concept, many of the algebraic and combinatorial properties of the monomial ideals with the same signature are surprisingly preserved.
After introducing the signature formally, we will show that given a signature σ, there exists a polyhedral cone Pσ such that its integral points correspond to the monomial ideals with signature σ. Even more important, we will give a description of the irredundant irreducible decomposition of any monomial with signature σ in terms of the irredundant irreducible decomposition of the antichain ideal Iσ of σ.
Before defining the signature, we need to introduce the incidence matrix of a monomial ideal, which is another way to represent a monomial ideal as a matrix. Here, we will use the matrix representations of a monomial ideal and its irredundant irreducible decomposition instead of its usual representations because it is more convenient to work with.
Definition 3.1. The incidence matrix of an antichain G (or of the antichain ideal IG) is the matrix whose columns are its vectors.
That is, the columns of BG are indexed by the minimal generators of IG, and their rows are indexed by the variables of the polynomial ring S.
Remark 3.2. A matrix is the incidence matrix of a monomial ideal whenever its entries are nonnegative integers and its columns form an antichain. Moreover, it is not difficult to check that there exists a bijection between the set of monomial ideals in S and the set of nonnegative integer matrices whose columns form an antichain.
Now, the content of a nonnegative integer vector c∈Nn, denoted by cont(c), is the vector that contains its different entries in ascending order. Note that a vector and its content do not necessarily have the same dimension. When the content of a vector is equal to (0,1,2,…,r) for some r∈N, we say that it is tight. That is, a tight vector can be thought of as a vector without gaps.
Definition 3.3. A nonnegative integer matrix B is row-tight or simply tight whenever its rows are tight.
The following example illustrates previous concepts.
Example 3.4. Let G={(0,5,9),(2,2,1),(1,2,9)} be an antichain in N3. Then the incidence matrix of G is given by
Besides, it is not difficult to check that cont(r2)=(2,5) and, therefore, BG is not row-tight.
We are now almost ready to define the signature of a matrix. However, given a vector c in Nn with cont(c)=(m0,…,mr) its signature is the vector in Nn given by
Thus, by definition, the signature of a vector is a tight vector.
Definition 3.5. The signature of a monomial ideal IG, denoted by σ(IG), is the matrix obtained from its incidence matrix BG by replacing its rows with their corresponding signatures.
Similarly, it can be defined the signatures of any nonnegative integer matrix. For instance, if B is the matrix given in Example 3.4, then its signature it is equal to
As we mentioned before, the signature is a very simple concept; even calculating it is straightforward. Actually, the computational complexity of calculating it is linear. However, as we will show in the following, many of the algebraic and combinatorial properties of the monomial ideals with the same signature are surprisingly preserved.
Remark 3.6. Getting a monomial ideal with the same signature as a given one is very simple. For instance, it is not difficult to check that the ideal obtained from IG by replacing each variable with a power of it has the same signature as IG.
Again, in general, a matrix is not necessarily tight, but its signature always is. Clearly, if B is tight, then σ(B)=B. The idea behind the signature is that looking at each variable of the minimal generators only matters by the relative position of its powers.
The next result shows that the signature of a monomial ideal is well-defined. That is, it preserves the fact that the columns of a matrix form an antichain.
Lemma 3.7. The columns of a nonnegative integer matrix B form an antichain if and only if the columns of its signature σ are also an antichain.
Proof. It follows from the fact that a≤b if and only if ai≤bi for all 1≤i≤n and Bi,j≤Bi,k if and only if σi,j≤σi,k for all 1≤i≤n and 1≤j≠k≤q. □
From here on, when we say matrix, we mean a nonnegative integer matrix whose columns form an antichain unless otherwise stated. In a similar way, when we say a signature, we mean a tight matrix. Thus, Lemma 3.7 implies that if σ is a signature, then the columns of any matrix with signature σ form an antichain.
In what follows, we will define a polyhedral cone Pσ whose integral points correspond to the monomial ideals with signature σ.
3.1. The polyhedral cone of a signature
Monomial ideals with the same signature can easily be characterized as those whose incidence matrix are the integral points of a polyhedral cone. More precisely, given a signature σ, let
Many of the inequalities used here are clearly redundant. The polyhedral cone Pσ can be defined alternatively as (without redundant inequalities): Bi,j≥0 for all 1≤i≤n and 1≤j≤q, Bi,j=Bi,k if and only if σi,j=σi,k and Bi,j≤Bi,k+1 for all 1≤i≤n and 1≤j≠k≤q such that σi,k=σi,j+1.
The next result establishes that there is a bijection between integral points of the polyhedral cone Pσ and monomial ideals with signature σ.
Proposition 3.8. If σ is a signature and B is a nonnegative integral matrix, then σ(B)=σ if and only if B is an integral point of the polyhedral cone Pσ.
Proof. It is followed directly from the definition of the signature and Lemma 3.7. □
Directly for the definition of Pσ, it is not difficult to get a formula for its dimension in terms of the content of the rows of σ.
Proposition 3.9. If σ is a signature and (r1,…,rq) are its rows, then
The next example illustrates previous concepts.
Example 3.10. If σ=[12100200122000101243] is a signature, then
is the polyhedral cone associated to σ and its dimension is equal to 14=3+3+3+5.
In what follows, we will show that all the monomials ideal with the same signatures have essentially the same irredundant irreducible decomposition.
3.2. The irreducible decomposition of a monomial ideal with a given signature
In this subsection, we give a description of the irredundant irreducible decomposition of the monomial ideals with signature σ in terms of the irredundant irreducible decomposition of the antichain ideal Iσ of σ.
We need some definitions before establishing our main result. By Lemma 2.9 we have that any maximal ∞-cover of Iσ is equal to σJ for some J∈ΠGσ, where Gσ=(g1,…,gq) are the columns of σ. Thus, there exists Jσ⊆ΠGσ such that
is the irredundant irreducible decomposition of Iσ. In other words, T(Gσ)={(Gσ)J:J∈Jσ}. We recall again that Jσ is not necessarily unique. Finally, given an integer nonnegative matrix B, let gcd(B)∈Nn given by
where b1,…,bq are the columns of B. That is, gcd(B)i=min{Bi,j:1≤j≤q}.
Theorem 3.11. If σ is a signature, IG is a monomial ideal with signature σ and m=gcd(BG), then
is the irredundant irreducible decomposition of IG.
Proof. By Theorem 2.12, we only need to prove that
To begin, it is clear that miei is a maximal ∞-cover of G if and only if mi>0. On the other hand, GJ is always an ∞-cover for any J∈ΠG.
The rest follows by using similar arguments to those used in the proof of Lemma 3.7. □
Now, it is not difficult to check that
where ik is such that (BG)k,ik=min{(BG)Ji,i:Ji=k}. Thus, mGJ can be expressed as the irreducible ideal whose exponent on each variable is some entry of the matrix BG.
The next example illustrates the previous process for obtaining the irredundant irreducible decomposition of a monomial ideal with a given signature.
Example 3.12. Let σ=[12100200122000101243] be the signature given in Example 3.10 and
be its antichain ideal. Using Macaulay2 [10], we obtain that
is its irredundant irreducible decomposition. Moreover, it is not difficult to check that
That is, Jσ={(1,1,1,2,2),(1,1,1,4,4),(1,1,1,4,2),(1,1,1,4,3),(2,4,4,4,4),(3,4,4,4,4),(2,1,4,4,4),(3,1,4,4,4)} is a subset of ΠGσ such that ⋂J∈JσmσJ is the irredundant irreducible decomposition of Iσ.
Now, if B=[b1,1b1,2b1,300b2,100b2,4b2,5b3,1000b3,50b4,2b4,3b4,4b4,5]∈Pσ and B is the set of columns of B, then
Thus, by Theorem 3.11,
is the irredundant irreducible decomposition of the antichain ideal
where b1,1=b1,3 and b2,1=b2,5, b1,1,b2,1,b3,1,b1,2,b4,2,b4,3,b2,4,b4,4,b3,5,b4,5∈N+.
In the most general case, if B=[b1,1b1,2b1,3b1,4b1,5b2,1b2,2b2,3b2,4b2,5b3,1b3,2b3,3b3,4b3,5b4,1b4,2b4,3b4,4b4,5]∈Pσ, we need to add the factors ⟨xbi,jii⟩ for which bi,ji>0 to get the irredundant irreducible decomposition of the antichain ideal
where m=gcd(G)=xb1,41xb2,22xb3,23xb4,14. Let us recall that b1,4=b1,5, b2,2=b2,3 and b3,2=b3,3=b3,4.
Thus, it is very simple to calculate the irredundant irreducible decomposition of an antichain ideal from the irredundant irreducible decomposition of its signature.
To simplify the notation, we will encode the irredundant irreducible decomposition on its incidence matrix.
Definition 3.13. Given an antichain G, its irredundant irreducible decomposition matrix (or simply decomposition matrix) is the matrix whose columns are the exponents of the irreducible factors of the irredundant irreducible decomposition ⋂pi=1mdi of IG.
We recall that the entries of DG are in Nn∞. In a similar way to the definition of the signature of a monomial ideal, the signature of a matrix D with entries in Nn∞ is defined as σ(D)=σ(D0)∞.
Again, similar to the Lemma 3.7, we get the following result:
Lemma 3.14. If D is a matrix with entries in Nn∞, then its columns are an antichain in Nn∞ if and only if the columns of its signature σ(D) are also an antichain in Nn∞.
Proof. It follows by using similar arguments to those used in the proof of Lemma 2.6. □
We end this section with an example that illustrates previous concepts.
Example 3.15. Following with Example 3.12, we have that
Moreover, if B=[bi,j]∈Pσ, then
whenever gcd(B)=0, and it is not difficult to check that σ(DB)=Dσ. Note that the columns of Dσ are antichains in Nn∞; however, the columns of (Dσ)0 are not necessarily antichains in Nn. For instance, (d1)0=(1,1,0,0)≤(2,2,0,2)=(d5)0 and d1=(1,1,∞,∞)≰(2,2,∞,2)=d5.
On the other hand, if gcd(B)≥1, then gcd(B)=(b1,4,b2,2,b3,2,b4,1) and
4.
Alexander duality
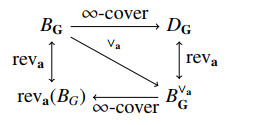
Alexander duality has become an important tool in the study of monomial ideals. In this section, after recalling Alexander duality in monomial ideals as in [7], we extend it to the space of polyhedral cones associated with signatures and use it to prove some properties of signatures. The way it is presented here is slightly different from how it is presented in [7], more consistent with our purposes. Roughly speaking, from our point of view, Alexander dual of the antichain IG is the monomial ideal whose incidence matrix is obtained from DG by reversing the order of the entries in each of its rows.
We will try to convince the reader that an essential part of Alexander duality relies on the order in Nn as well as the reversing and the minimal-maximal duality. There exist several ways to reverse the order of the entries in each row of a matrix; one of the most simple is the one used in [7], which subtracts all nonzero entries from a given constant. In what follows, we will present a slightly more general adaptation of this construction, where additionally we interchange the zero entries with infinity. In [7], a big enough number is used instead of using infinity as an entry in the factors of the irredundant irreducible decomposition.
Given a matrix D of size n×p with entries in N∞ and a∈Nn, its a-reversing matrix is given by
In [7], the a-reversing operation is used as a column operation on DG; however, in our context, it is more clear to see as an operation over its rows. It is not difficult to check that the entries of reva(D) are nonnegative if and only if a≥lcm(D), where lcm(D)i=max{Di,j: for all 1≤j≤q such that Di,j≠∞}.
Definition 4.1. The Alexander dual I∨aG with respect to a≥lcm(BG) of the antichain ideal IG is the monomial ideal whose incidence matrix is equal to the a-reversing, denoted by B∨aG, of the irredundant irreducible decomposition matrix DG of IG.
By Theorem 3.11, it is not difficult to check that lcm(BG)≥lcm(DG) and, therefore, the Alexander dual I∨aG is indeed a monomial ideal. Each monomial ideal has many of Alexander duals. Indeed, for any a∈Nn such that a≥lcm(BG) we have one of them. On the other hand, it is not difficult to check that all of Alexander duals of a given monomial ideal have the same signature. Moreover, all the Alexander duals of the Alexander duals (I∨aG)∨b has the same signature as IG. That is, Alexander duality sent integral points in Pσ to integral points in Pσ∨a for a=lcm(BG). It is for this reason that it is natural to consider Alexander duality on the polyhedral cones Pσ instead of a single monomial ideal.
The a-reversing operation preserves the fact that the columns of the matrix are an antichain in Nn∞. Thus, since the columns of DG are an antichain in Nn∞, then it is not difficult to check that the columns of B∨aG also are an antichain in Nn. That is, the columns of B∨aG correspond to the minimal generators of I∨aG. For instance, following Example 3.15, we get that
for a=lcm(BG)=(2,2,2,4). To make the notation simpler, when there is no confusion, we write B∨G instead B∨aG for a=lcm(BG).
Moreover, the a-reversing operation interchanges the fact that the columns of DG are maximal to the fact that the columns of B∨aG are minimal with respect to the order ≤ in Nn. In a similar way, it also interchanges the fact that the columns of BG are minimal to the fact that the columns of reva(BG) are maximal with respect to the order ≤ in Nn∞.
Thus, it is very simple to get that the functor defined by a-reversing operation is contravariant with respect to taking the irredundant irreducible decomposition.
Theorem 4.2 (Corollary 2.14 [7]). Let G be an antichain in Nn and a≥lcm(BG), then reva(BG) is the irredundant irreducible decomposition matrix of B∨aG (see the commutative diagram given in Figure 1).
Proof. Let c be a column of DG, that is, c is a maximal ∞-cover of G. A vector c is ∞-cover of G whenever for any g∈G there exists 1≤j≤n such that cj≤gj. Moreover, the fact that c being maximal implies that for any 1≤j≤n, such that cj≠∞ there exists g∈G such that cj≤gj (moreover, it can be stated that the g satisfies that ci≰gi for any i≠j).
Since reva(g)j≤reva(c)j, it follows that reva(g) is an ∞-cover of the columns of B∨aG=reva(DG). Additionally, it is maximal because reva interchanges minimality and maximality (see Figure 2(a)). Finally, the result follows by Theorem 2.12. □
It is not difficult to check that Theorem 4.2 can be easily generalized for any reversing function.
Definition 4.3. A function f:A→¯N for some A⊆¯N with the zero and infinity, is called reversing whenever rev(0)=∞, rev(∞)=0, and
Given a matrix D with entries in N and rows ri for 1≤i≤n, let cont(D)=⋃ni=1cont(ri).
Corollary 4.4. Let G be an antichain in Nn and rev be a reversing function for cont(BG)∪cont(DG), then rev(BG) is the irredundant irreducible decomposition matrix of rev(DG).
In order to simplify the notation, let
see Figure 2(b).
In what follows, we will show that the content of the rows of the matrices σ and τ and their duals σ∨ and τ∨ are equal when σ is the signature of a monomial ideal without the power of a variable as a generator.
Theorem 4.5. Let σ be the signature of a monomial ideal without the power of a variable as a generator. If si, ti, ui, and vi are the i-rows of σ, τ0, σ∨, and τ∨0, respectively, then
Proof. For any r∈¯N, let cont+(r)=cont(r)∩N+ be its positive content and a=lcm(σ). To start, by Theorem 4.2 we have that τ∨ is the decomposition matrix of σ∨; see Figure 2(b). Thus, by Theorem 3.11 we have that cont+(ti)⊆cont+(si) and cont+(vi)⊆cont+(ui).
Since cont(si)={0,1,…,ai} and vi=revai(si)0, then cont(vi)=cont(si)={0,1,…,ai}. Moreover, since ui=revai(ti)0, then
and, therefore, cont+(si)=cont+(ti)=cont+(ui)=cont+(vi)={1,…,ai} for all 1≤i≤n. Lastly, if 0∉cont(ti), then 0∉cont(ui). Applying Theorem 3.11 to Iσ∨, we get that τ∨0 has a column with only one nonzero entry, and therefore Iσ has a generator which is the power of a variable; a contradiction. □
Remark 4.6. Using similar arguments to those used in the proof of Theorem 4.5, it can be proved it is true whenever one of the matrices σ, τ0, σ∨, and τ∨0 is a signature.
Example 4.7. Let σ be a nonnegative matrix, τ be its decomposition matrix, σ∨ the Alexander dual of σ and τ∨ be its decomposition matrix as shown in Figure 3. Besides, let si, ti, ui, and vi be the i-rows of σ, τ0, σ∨, and τ∨0, respectively.
Since σ is a signature and σ∨ is not a signature, then it cannot be removed the hypothesis that the monomial ideal does not have minimal generators that are the power of a variable in the Theorem 4.5. Moreover, 0∈cont(v1)⊈cont(u1), proving that not necessarily the content of a row of a nonnegative integer matrix is contained in the corresponding row of its decomposition matrix.
Since xai is a minimal generator of an antichain ideal IG if and only if a=max(G)i, then xi divides the generators of its Alexander dual I∨G but not x2i and, therefore, the positive content of its i-th row has no gaps. The generators in a monomial ideal that are the power of a variable play a dual role to the factors which are the power of a variable in its irreducible decomposition. For instance, if (σ∨)′ is the signature of σ∨, then its Alexander dual σ′ corresponds to the original monomial ideal without the generators that are the power of a variable, as shown in Figure 3.
By the symmetry between σ and σ∨ and between τ0 and τ∨0, it is not difficult to prove that any one of them are signatures without a column with only one nonzero entry, then the others are also a signature.
Corollary 4.8. If any of the σ, τ0, σ∨, and τ∨0 are a signature with no column with only one nonzero entry, then the others are also a signature.
In consequence, if any of the σ, τ0, σ∨, and τ∨0 is a signature, then
If the matrices BG and DG are considered as vectors in Rnq and Rnp, then Theorem 3.11 can be interpreted as that there exists a linear transformation T:Rnq→Rnp such that T(BG)=DG. Moreover, the entries of the matrix representation of the linear transformation T are either zero or one.
Corollary 4.9. Let G be an antichain with no generator equal to the power of a variable, and BG and DG be its incidence and decomposition matrices, respectively. If ri and si are the rows of BG and (DG)0, respectively, then
Proof. Let σ be the signature of IG and τ=σ((DG)0). It is not difficult to check that there exists f:cont(σ)→cont(BG) such that f(σi,j)=(BG)i,j. Considering the matrices BG and DG as vectors in Rnq and Rnp, by Theorem 3.11, there exists a linear transformation T:Rnq→Rnp such that T(BG)=DG and whose matrix representation has only zero and one entries. Thus, f(τi,j)=(DG)i,j, as shown Figure 4.
Let r′i and s′i be the rows of σ and τ, respectively. By Theorem 4.5, cont(r′i)=cont(s′i) for all 1≤i≤n, and, therefore,
for all 1≤i≤n. □
Since, as we have seen in Subsection 2.3, the primary decomposition of a monomial ideal can be obtained by intersecting the factors of the irreducible decomposition with the same radical, then it is not complicated to check that a monomial ideal with the same signature has essentially the same primary decomposition.
Remark 4.10. It is important to note that throughout the article, a fixed order is used over the variables and generators of the monomial ideal.
On the other hand, given a signature σ, let
be a face of the polyhedral cone Pσ whose integral points correspond to the monomial ideals with signature σ with irredundant irreducible decomposition that does not contain a factor of the form ⟨xgcd(B)ii⟩. As the next result shows, it is not difficult to calculate the dimension of P0σ in terms of the dimension of Pσ.
Proposition 4.11. If σ is a signature, then dim(P0σ)=dim(Pσ)−n.
Proof. By the definition of P0σ we have that dim(P0σ)=∑ni=1(|cont(ri)|−1)=dim(Pσ)−n, where (r1,…,rq) are the rows of σ. □
In a similar way, let
In other words, Pτ∩Znp={D∈Matn,p(N∞∖0):σ(D)=τ}. It is not difficult to check that Pτ can be identified with the polyhedral cone Pτ0=(Pτ)0.
As the following result proves that there exists a depth relation between P0σ and Pτ.
Theorem 4.12. Let σ be a signature with no column with only one nonzero entry and DG be the decomposition matrix of the antichain ideal of G. Then σ(DG)=τ0 if and only if σ(IG)=σ.
Proof. It follows directly from Corollary 4.9. □
In other words, there exists a bijection between P0σ and Pτ. Thus, we get that P0σ and (Pτ)0 have the same dimension.
Corollary 4.13. If σ is a signature, then dim(P0σ)=dim(Pτ0).
Thus, it is natural to consider that any monomial ideal whose incidence matrix is in P0σ is an Alexander dual of a monomial ideal whose incidence matrix is in Pτ0.
5.
Future work
We finish by posing a pair of conjectures, stating that monomial ideals with the same signature have essentially the same minimal free resolution and that their quotient modules share at least a common regular sequence. These conjectures put into perspective the depth of the concept of the signature of a monomial ideal.
5.1. Regular sequences
In what follows, we recall what a regular sequence of an S-module means. Given a module M over a ring S, we say that nonzero element r of M is regular whenever rm≠0M for all m∈M∖0M. In other words, r is regular whenever it is not a zero divisor of M. Moreover, a sequence h1,…,hd of polynomials in S is called regular in M whenever
and ⟨h1,…,hd⟩M≠M. The depth of M, denoted by depth(M), is the maximal length of its regular sequences.
We begin by raising the weakest version of our conjectures, which claims that the depth of the quotient module of a monomial ideal is preserved under the signature.
Conjecture 5.1. If I and J are monomial ideals with the same signature, then
A stronger version claims that the S-modules S/I and S/J have a common regular sequence.
Conjecture 5.2. Let I and J be monomial ideals with the same signature. If d is the depth of I, then there exists a sequence h1,…,hd of polynomials such that it is a regular sequence of both S/I and S/J.
A stronger version of the previous conjecture asserts that this common regular sequence can be chosen with linear forms.
5.2. Minimal free resolutions
Roughly speaking, a graded free resolution of a finitely generated graded S-module M is a sequence F∙={Fi,di}pi=0 of graded free modules Fi and homogeneous homomorphism di:Fi+1→Fi such that
is an exact complex, that is, Im(di)=Ker(di−1) for all 1⩽i⩽p, Im(π)=M, and Ker(dp)=0. Besides, it is called minimal whenever
see for instance [11,Section I.7]. When M=S/I for some ideal I, F0=S, and we say that F∙ is a minimal free resolution of the ideal I. Although there are many ways to grade an S-module, the most common are with the standard grading and the standard multigrading. To simplify the notation, from here on, when we say multigraded minimal free resolution, we mean that it is graded with the standard multigrading and when we say graded minimal free resolution, we mean that it is graded with the standard grading.
Alternative ways exist to represent a minimal free resolution. For instance, in [12], the minimal resolution of a monomial ideal is encoded as the sequence M∙={Mi}pi=1 of the matrix representation of the differentials di. Thus, it is clear that the entries of these matrices are terms in S and M1 is a matrix with only one row whose entries are the minimal generators of the ideal. To establish what it means that two monomial ideals have essentially the same minimal free resolution, we will introduce a new way of representing it, which we will call its poset resolution.
The poset resolution of a multigraded minimal free resolution F∙={Fi,di}pi=0 of a monomial ideal is what we call decorated graded poset P∙. More precisely, a decorated poset means a triplet (P,s,m), where P=(F,≤) is the graded poset on the generators of each of the free modules Fi, where u∈Fi−1 is covered by v∈Fi whenever di(v)=∑w∈Fi−1sww with 0≠su∈k for some 1≤i≤p. The second element of the triplet P∙ is the function from the edges of the Hasse diagram H of P to the field k given by the coefficient of the term su in di(v)=∑w∈Fi−1sww. Finally,
is the function that takes the monomial with the multidegree of v. The concept of poset resolution was developed during the Ph.D. studies of Javier A. Moreno and David C. Molano; see in [13,14].
Conjecture 5.3. If I and J are monomial ideals with the same signature, then there exists a poset resolution P∙=(P,s,m) of I such that P′∙=(P,s,m′) is a poset resolution of J for some m′.
According to the previous conjectures, the signature is an invariant fine enough to preserve some of the most important algebraic properties of a monomial ideal.
6.
Conclusions
The signature of a monomial ideal is introduced. It is proved that two monomial ideals with the same signature have essentially the same irreducible decomposition. Moreover, using Alexander duality, it is proved that the irredundant irreducible decomposition matrix of a monomial ideal whose incidence matrix is tight is also tight. This leads to enlarging the monomial ideals, which are considered Alexander Duals of a given monomial ideal. Additionally, it is conjectured that monomial ideals with the same signature have essentially the same minimal free resolution and that their quotient modules share at least a common regular sequence.
Author contributions
J.I, D.S.M., C.E.V. and R.H.V. contributed equally to this work regarding conceptualization, methodology, formal analysis, investigation, software, writing—original draft preparation, writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Acknowledgments
The first and second authors were partially supported by a Conahcyt Ph.D. scholarship. The third and fourth authors were partially supported by SNII, México. We used Macaulay2 [10] to perform the computations. The authors would like to thank the anonymous referees for their helpful comments.
Conflict of interest
The authors declare no conflicts of interest.









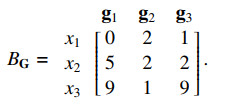

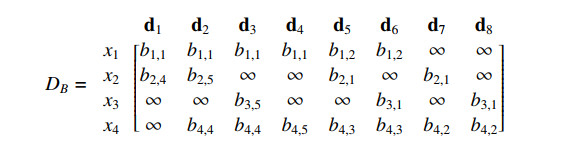
 DownLoad:
DownLoad:






