Functions of bounded ${\bf (2, k)}$-variation in 2-normed spaces

1.   Introduction

In 1881, Jordan ^[12] discovered in the work of Dirichlet the notion of function of bounded variation and proved that, for this class of functions, the Fourier conjecture is valid. He also showed that the function $f\colon [a, b]\to \mathbb{R}$ has bounded variation on $[a, b]$ if and only if $f$ is the difference of monotone functions (nowadays, this result is known as Jordan's Representation Theorem).

The notion of function of bounded variation has been studied and generalized in different contexts, studying different structures and properties in spaces with research interest. For example, Chistyakov in ^[4,5,6] studied a concept of a function of bounded generalized variation in the sense of Jordan-Riesz-Orlicz for functions $f\colon [a, b]\to X$, where $X$ is a normed or metric space. More recently, the notion of functions of bounded variation in spaces with indefinite metric was introduced by Ferrer, Guzmán, Naranjo ^[10]. Furthermore, functions of bounded variation have multiple applications in various fields, for example, in image processing, Brokman, Burger, Gilboa ^[1] presented an analysis of the total-variation (TV) on non-Euclidean parametrized surfaces, a natural representation of the shapes used in 3D graphics. Among the results achieved in this research is a new method to generalize the convexity of sets from the plane to surfaces, derived by characterizing the TV eigenfunctions on surfaces. Additionally, Bugajewska, Bugajewski, Hudzik ^[2] investiged solutions of nonlinear Hammerstein and Volterra-Hammerstein integral equations in the space of functions of bounded $\phi$-variation in the sense of Young. Later, Bugajewska, Bugajewski, Lewicki ^[3] explored the superposition operator and solutions to non linear integral equations in spaces of functions of generalized bounded $\phi$-variation. In the field of nonlinear analysis, Xie, Liu, Li, Huang ^[18] examined the bounded variation capacity (BV capacity) and characterized the Sobolev-type inequalities associated with BV functions within a general framework of strictly local Dirichlet spaces with a doubling measure, utilizing the BV capacity.

On the other hand, the notion of a 2-normed vector space was introduced in 1963 by Siegfried Gähler ^[11] as a generalization of normed spaces. It has continued to be studied by several authors, among which the following stand out: White ^[17], who introduced the concept of 2-Banach space; Diminnie ^[8,9], which generated numerous results in the context of these spaces; and Lewandowska ^[14], who studied some properties of bounded 2-linear operators in a 2-normed set, endowed the set of bounded 2-linear operators of a norm, and proved the Banach-Steinhaus theorem for a family of bounded 2-linear operators.

In this paper, we extend the notion of bounded variation function in normed spaces to 2-normed spaces, endow the set of functions of bounded variation in 2-normed spaces with a norm, and extend the main properties of such functions. Moreover, in 2-normed spaces, we construct several examples of functions of bounded variation and prove the most relevant results for such functions.

2.   Research gap

Spaces with 2- inner product and spaces with 2-norm are extensions of spaces with inner product and normed spaces, respectively. So far, the theory of functions of bounded variation has not been studied in this context. Considering the historical importance of classical bounded variation functions, we consider that the lack of a detailed study of bounded variation functions in these new spaces provides a significant gap in the mathematical literature, preventing that the classical results of bounded variation functions from being extended to these more general spaces. Knowing that classical bounded variation functions have multiple applications, we consider that the exploration of bounded variation functions in spaces with 2-inner product and 2-normed product is as an important opportunity for the development of functional analysis and other related areas. In our research work, we aim to address this gap and answer two key questions:

(ⅰ) How to give a definition of bounded variation that allows to successfully relate the classical theory of functions of bounded variation to functions of bounded variation in 2-normed spaces?

(ⅱ) How appropriate are the concepts of $(2, k)$-variation and functions of bounded $(2, k)$-variation to formally extend some classical results of functions of bounded variation to 2-normed spaces?

3.   Preliminaries

Definition 3.1. ^[11,15] Let $X$ to be a complex vector space of dimension $d$, where $2\leq d\leq \infty$. A 2-norm on $X$ is a function $\|\cdot, \cdot\|:X \times X\to\mathbb{R}$ that satisfies the following four conditions:

$(2N_1)$ $\|x, y\| = 0$ if and only if $x$ and $y$ are linearly dependent;

$(2N_1)$ $\|x, y\| = \|y, x\|$;

$(2N_1)$ $\|x, \alpha y\| = |\alpha|\|x, y\|$, for all $\alpha \in \mathbb{C}$;

$(2N_1)$ $\|x, y+z\| \leq \|x, y\|+\|x, z\|$.

If $\|\cdot, \cdot\|$ is a 2-norm for $X$, then the pair $(X, \|\cdot, \cdot\|)$ is called a 2-norm space.

Next, we will see an introductory example of 2-normed spaces.

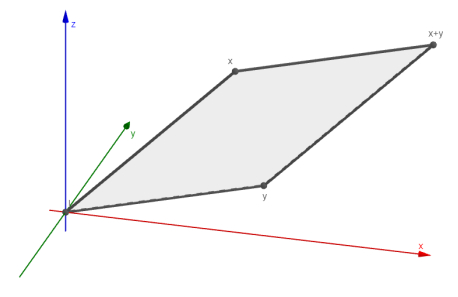
Example 3.1. (Example 2-normed space) The set of all ordered triples of real numbers, $\mathbb{R}^3$, equipped with the function $\|\cdot, \cdot\|_{\Delta}\colon \mathbb{R}^3\times \mathbb{R}^3\to \mathbb{R}$, defined by

it is a 2-norm (see Figure 1).

Indeed, let us see that $\|\cdot, \cdot\|_{\Delta}$ satisfies the conditions of being a norm for $\mathbb{R}^3$.

Recall that the area of the parallelogram generated by points three points $A, B, C\in\mathbb{R}^3$ is given by

Let $\mathbf{x}, \mathbf{y}, \mathbf{z}\in \mathbb{R}^3$ and $\alpha\in \mathbb{R}$.

$(2N_1)$ $(\Rightarrow)$ If $\|\mathbf{x}, \mathbf{y}\|_{\Delta} = 0$, then $\frac{\|\mathbf{x}\times \mathbf{y}\|}{2} = 0$, i.e., $\mathbf{x}\times \mathbf{y} = \mathbf{0}$, which implies that $\{\mathbf{x}, \mathbf{y}\}$ is linearly dependent.

$(\Leftarrow)$ If $\{\mathbf{x}, \mathbf{y}\}$ is linearly dependent, then $\mathbf{x}\times \mathbf{y} = \mathbf{0}$, therefore $0 = \frac{\|\mathbf{0}\|}{2} = \frac{\|\mathbf{x}\times \mathbf{y}\|}{2} = \|\mathbf{x}, \mathbf{y}\|_{\Delta}$.

$(2N_2)$ $\|\mathbf{x}, \mathbf{y}\|_{\Delta} = \frac{\|\mathbf{x}\times \mathbf{y}\|}{2} = \frac{\|-(\mathbf{y}\times \mathbf{x})\|}{2} = \frac{\|\mathbf{y}\times \mathbf{x}\|}{2} = \|\mathbf{y}, \mathbf{x}\|_{\Delta}.$

$(2N_3)$ $\|\mathbf{x}, \alpha \mathbf{y}\|_{\Delta} = \frac{\|\mathbf{x}\times \alpha \mathbf{y}\|}{2} = \frac{\|\alpha(\mathbf{x}\times \mathbf{y})\|}{2} = \left|\alpha\right|\frac{\|\mathbf{x}\times \mathbf{y}\|}{2} = |\alpha |\cdot\|\mathbf{x}, \mathbf{y}\|_{\Delta}$.

$(2N_4)$ $\|\mathbf{x}, (\mathbf{y}+\mathbf{z})\|_{\Delta} = \frac{\|\mathbf{x}\times (\mathbf{y}+\mathbf{z})\|}{2} = \frac{\|(\mathbf{x}\times \mathbf{y})+(\mathbf{x}\times \mathbf{z}))\|}{2}\le \frac{\|(\mathbf{x}\times \mathbf{y})\| +\|(\mathbf{x}\times \mathbf{z}))\|}{2} = \|\mathbf{x}, \mathbf{y}\|_{\Delta}+\|\mathbf{x}, \mathbf{z}\|_{\Delta}$.

Proposition 3.1. ^[11] Let $(X, \|\cdot, \cdot\|)$ be 2-norm space. For all $x, y, z \in X$ and $\alpha \in \mathbb{C}$, it follows that:

$(1)$ $\|x, y\|\geq 0$.

$(2)$ $\|x, y+\alpha x\| = \|x, y\|$.

Definition 3.2. ^[7] Let X be a complex vector space of dimension $d \geq 2$. A 2-inner product is a function

that satisfies the following conditions:

$(2\text{I}_1)$ $\left(x_{1}+x_{2}, y | z\right) = \left(x_{1}, y | z\right)+\left(x_{2}, y | z\right)$.

$(2\text{I}_1)$ $(x, x | z) = (z, z | x)$;

$(2\text{I}_1)$ $(y, x | z) = \overline{(x, y | z)}$;

$(2\text{I}_1)$ $(\alpha x, y | z) = \alpha(x, y | z)$ for all $\alpha \in \mathbb{C}$;

$(2\text{I}_1)$ $(x, x | z) \geq 0$ and $(x, x | z) = 0$ if and only if $x$ and $z$ are linearly dependent.

The pair $(X, (\cdot, \cdot | \cdot))$ is called a 2-inner product space (or pre-2-Hilbert space).

Remark 3.1. Note that in $(2\text{I}_{3})$, $(y, x | z) = \overline{(x, y | z)}$. If $y = x$, we obtain $(x, x | z) =$ $\overline{(x, x | z)}$, which guarantees $(x, x | z) \in \mathbb{R}$.

Proposition 3.2. ^[7] Let $(X, \langle\cdot, \cdot\rangle)$ be space with inner product. Then, the following expression defines a 2-inner product on $X$.

This 2-inner product is called a standard 2-inner product and guarantees that every inner product space can be viewed as a 2-inner product space.

Proposition 3.3. ^[7] Let $(X, (\cdot, \cdot | \cdot))$ be space with 2-inner product and $x, y, z \in X.$ Then, it holds that:

The inequality above is the analogue of the Cauchy-Schwarz inequality in spaces with inner product.

Remark 3.2. Given a space with 2-inner product $\left(H, (\cdot, \cdot|\cdot)\right)$, we can define a 2-norm for $H$, called the induced 2-norm of the 2-inner product given by

Example 3.2. Let us consider $\mathbb{C}^{3}$ with the usual inner product. We can induce a 2-inner product from this inner product by the function

According to Remark 3.2, the function

is a 2-norm. Then,

Remark 3.3. According to ^[17], given $(X, \|\cdot, \cdot\|)$ is a 2-normed space, the application $\|\cdot, \cdot\|\colon X\times X\to \mathbb{R}$ is continuous. In particular, given $k\in X$, the function $\|\cdot, k\|\colon X\to \mathbb{R}$ is continuous.

Definition 3.3. Let $(X, \|\cdot, \cdot\|)$ be a 2-normed space, $k\in X$, $[a, b]$ a closed interval. A function $f\colon [a, b]\to X$ is said to be $(2, k)$-bounded, if there exists $\alpha\in\mathbb{R}^+$ such that for all $x\in[a, b]$, it satisfies $\|f(x), k\|\le \alpha$.

Definition 3.4. ^[17] A sequence $\left\{x_{n}\right\}_{n \in\mathbb{N}}$ in a 2-normed space $X$ is called a convergent sequence if there exists a $x \in X$ such that the $\lim_{n\to\infty} \left\|x_{n}-x, y\right\| = 0$ for all $y \in X$. If $\left\{x_{n}\right\}_{n \in\mathbb{N}}$ converges to $x$, we write $x_{n} \to x$ and we call $x$ the limit of $\left\{x_{n}\right\}_{n \in\mathbb{N}}$.

Definition 3.5. ^[13] Let $(X, \|\cdot, \cdot\|)$ be a 2-normed space, $k\in X$. A sequence $\left\{x_{n}\right\}_{n \in\mathbb{N}}$ in $X$ is called $k$-Cauchy if for all $\epsilon > 0$, there exists $N\in\mathbb{N}$, such that if $m, n > N$, then $\left\|x_{n}-x_{m}, k\right\| < \epsilon$.

Definition 3.6. ^[13] A 2-normed vector space in which every $k$-Cauchy sequence is a convergent sequence is called a $(2, k)$-Banach space.

Definition 3.7. ^[14] A space with 2-inner product $\left(\mathcal{H}, (\cdot, \cdot |\cdot)\right)$ is said to be a 2-Hilbert space if it is complete with respect to the 2-norm induced by the 2-inner product. We reserve the letter $\mathcal{H}$ for 2-Hilbert spaces.

4.   Main results

4.1.   Bounded variation in 2-normed spaces

We now introduce the notion of $(2, k)$-variation of a function in 2-normed spaces.

Definition 4.1. ($(2, k)$-Variation of a function) Let $(X, \|\cdot, \cdot\|)$ be a 2-normed space, $k\in X$, $[a, b]$ a closed interval, and $f\colon [a, b]\to X$ a function. The $(2, k)$-variation of $f$ over $[a, b]$ denoted by $V_a^b(f, X, k)$, is as:

Clearly, $V_a^b(f, X, k)\ge 0$.

Theorem 4.1. Let $(X, \|\cdot, \cdot\|)$ be a 2-normed space, $k, l\in X$, $\alpha \in \mathbb{C}$ and $f\colon [a, b]\to X$ a function. Then, we have that:

$(i)$ $V_a^b(\alpha f, X, k) = | \alpha | V_a^b(f, X, k)$.

$(ii)$ $V_a^b(f+g, X, k)\leq V_a^b(f, X, k)+V_a^b(g, X, k)$.

$(iii)$ $V_a^b(f, X, k+l)\leq V_a^b(f, X, k)+V_a^b(f, X, l)$.

Proof. Let $P = \{t_0, t_1, \cdots, t_n\}$ be a partition for the interval $[a, b]$. Using Definition 4.1, we obtain that

Therefore, $V_a^b(\alpha f, X, k) = | \alpha | V_a^b(f, X, k)$.

Therefore, $V_a^b(f+g, X, k)\leq V_a^b(f, X, k)+V_a^b(g, X, k).$

Remark 4.1. Note that, in particular, for the constant function $g(t) = \lambda k$, where $\lambda\in \mathbb{C}$, we have that

This proves that $V_a^b(f, X, k+l)\leq V_a^b(f, X, k)+V_a^b(f, X, l)$. □

4.2.   Functions of bounded variation in 2-normed spaces

Next, we introduce the notion of a function of bounded $(2, k)$-variation in 2-normed spaces.

Definition 4.2. Let $(X, \|\cdot, \cdot\|)$ be a 2-normed space and $k\in X$. A function $f\colon [a, b]\to X$ is said to be of bounded $(2, k)$-variation on $[a, b]$ if $V_a^b(f, X, k)$ is finite; in other words, if there exists a constant $c\in \mathbb{R}^{+}$ such that $V_a^b(f, X, k)\le c$.

The set of all functions of bounded $(2, k)$-variation on $[a, b]$ are denoted by $BV([a, b], 2, k)$; in other words,

Example 4.1. Consider the 2-normed space $(\mathbb{C}^{3}, \|\cdot, \cdot\|)$ given in Example 3.2. Let us see that $f\colon [a, b]\to \mathbb{C}^3$ defined by $f(x) = (xi, 2xi, 3xi)$ is of bounded $(2, k)$-variation.

Consider $P = \{a, t_1, \cdots, t_{n-1}, b\}$ a partition of $[a, b]$.

On one side

Thus,

Then, $\langle f(t_j)-f(t_{j-1}), f(t_j)-f(t_{j-1})\rangle$ is equal to

On the other hand,

In addition,

Thus, we obtain that

Taking $\sqrt{14(|k_{1}|^2+|k_{2}|^2+|k_{3}|^2)-\left|\overline{k_1}+2\overline{k_2}+3\overline{k_3}\right|^{2}} = M$, we have that

Taking $2M(b-a) = \xi$, we have that

Therefore $f\colon [a, b]\to \mathbb{C}^3$ is of bounded $(2, k)$-variation.

In the following result, it is shown that a bounded variation function in an inner product space can be considered as a function of bounded $(2, k)$-variation with respect to the induced standard 2-inner product space.

Proposition 4.1. Let $\left(X, \langle \cdot, \cdot \rangle\right)$ be a space with an inner product, $k\in X$ and $f\colon [a, b]\to X$ a function. If $f$ is of bounded variation on $\left(X, \langle \cdot, \cdot \rangle\right)$, then $f$ is of bounded $(2, k)$-variation under the 2-norm induced by the standard 2-inner product.

Proof. Let $P = \{t_0, t_1, \cdots, t_n\}\in\mathcal{P}([a, b])$. Consider the 2-norm defined in Example 3.2. If $f$ is of bounded variation in $\left(X, \langle \cdot, \cdot \rangle\right)$, then there exists $\alpha\in \mathbb{R}^+$ such that

Then,

Thus,

Therefore, $f$ is of bounded $(2, k)$-variation with the standard 2-inner product. □

Proposition 4.2. Let $(X, \|\cdot, \cdot\|)$ be a 2-normed space, $k\in X$ and $f\colon [a, b]\to X$ a function of bounded $(2, k)$-variation on $[a, b]$. If $V_a^b(f, X, k) = 0$, then $f(x) = mk+\frac{1}{2}(f(a)+f(b))$ for all $x\in (a, b)$.

Proof. Suppose that $V_a^b(f, X, k) = 0$, i.e.,

Hence, for any participation of $[a, b]$, we have

Consider $x\in(a, b)$. Then, in particular, for the partition $P = \{a, x, b\}$ of $[a, b]$. By (4.1), we have that

Thus,

Therefore,

That is, there exist $\alpha, \beta \in \mathbb{C}$ non-null, such that

Then,

Thus,

Therefore, $f(x) = mk+\frac{1}{2}(f(a)+f(b))$ for all $x\in (a, b)$. □

Theorem 4.2. Let $(X, \|\cdot, \cdot\|)$ be a 2-normed space and $k\in X$. If $f\colon [a, b]\to X$ is a function of bounded $(2, k)$-variation, then $f$ is $(2, k)$-bounded.

Proof. Since $f$ is of bounded $(2, k)$-variation, then there exists $M > 0$ such that

Consider $x\in(a, b)$ and also consider the partition $P = \{a, x, b\}$ of $[a, b]$. Then, in particular,

Then,

Taking $M+\|f(a), k\|+\|f(b), k\| = \alpha$, we have that

Thus, there exists $\alpha\in\mathbb{R}^+$ such that for all $x\in[a, b]$, we have that $\|f(x), k\|\le \alpha$. Therefore, $f$ is $(2, k)$-bounded. □

The reciprocal of the above theorem is not always true.

Example 4.2. Let us consider the space $\left(\mathbb{C}^{3}, \| \cdot, \cdot\|\right)$ and the 2-norm defined in Example 3.2 by

Let us see that $f\colon [\sqrt{11}, 4]\to\mathbb{C}^3$ defined by

and $k = (0, -i, -i)\in \mathbb{C}^{3}.$

Lets see that $f$ is $(2, k)$-bounded, but it is not of bounded $(2, k)$-variation.

Indeed, if $t$ is rational,

Now,

In addition,

Also,

Therefore,

Hence,

Therefore, $\|f(t), (0, -i, -i)\|\leq \sqrt{2}$ for all $t \in [\sqrt{11}, 4].$ Thus, $f$ is $(2, k)$-bounded in $[\sqrt{11}, 4]$.

Now, let us see that $f$ is not of $(2, k)$-bounded variation.

Consider $t_{0} = \sqrt{11},$ since between any two reals there exists a rational and an irrational number, we can choose $t_{1}$ as a rational number between $\sqrt{11}$ and $4,$ $t_{2}$ as an irrational number between $t_{1}$ and $4,$ $t_{3}$ as a rational number between $t_{2}$ and $4,$ and so on; $t_{2j}$ would be an irrational number between $t_{2j-1}$ and $4,$ $t_{2j+1}$ would be a rational number between $t_{2j}$ and $4$. Finally we choose $t_{n} = 4.$ Then,

Note that a partition of the interval $[\sqrt{11}, 4]$ was constructed starting with $\sqrt{11}$ and then alternating between rational and irrational numbers until it ends at $4,$ for which $V_{\sqrt{11}}^{4}(f, \mathbb{C}^{3}, (0, -i, -i))$ is not finite. Therefore, $f$ is not of bounded $(2, k)$-variation in $(\mathbb{C}^3, \|\cdot, \cdot\|).$

4.3.   Algebra of functions of bounded variation in 2-normed spaces

Theorem 4.3. Let $(X, \|\cdot, \cdot\|)$ be a 2-normed space, $k\in X$ and $f, g\colon [a, b]\to X$ functions of bounded $(2, k)$-variation on $[a, b]$. Then, $\alpha f$ and $f+g$ are also functions of bounded $(2, k)$-variation over $[a, b]$.

Proof. Since $f$ and $g$ are of bounded $(2, k)$-variation, then there exist $\lambda, \beta \in\mathbb{R}^+$ such that

and

(ⅰ) From Theorem 4.1 we have that

Also, $|\alpha|\in\mathbb{R}^+$, thus

Taking $|\alpha|\lambda = \sigma$,

Therefore, $\alpha f$ is of bounded $(2, k)$-variation on $[a, b]$.

Remark 4.2. Note that if we take $\alpha = -1$, then $-f$ is also of bounded $(2, k)$-variation.

(ⅱ) Consider $P\in\mathcal{P}[a, b]$. Taking $\lambda+\beta = \sigma$, we have that

Therefore, $f+g$ is of bounded $(2, k)$-variation on $[a, b]$. □

Remark 4.3. From the theorem above, it follows that the set $BV([a, b], X, k)$ is a vector space.

Theorem 4.4. Let $(X, \|\cdot, \cdot\|)$ be a 2-normed space, $k\in X$, $f\colon [a, b]\to X$ a function of bounded $(2, k)$-variation on $[a, b]$ and $c\in(a, b)$. Then, it is satisfied that $f$ is of bounded $(2, k)$-variation in $[a, c]$ and in $[c, b]$. Furthermore, $V_a^c(f, X, k)+V_c^b(f, X, k)\le V_a^b(f, X, k)$.

Proof. If $f$ is of bounded $(2, k)$-variation, then there exists $M > 0$ such that for any partition $P$ of $[a, b]$ it follows that

Let us consider the partition $P = \{a, t_1, t_2, t_3, \cdots, t_{n-1}, b\}.$ Since $c\in(a, b)$, then

Then,

Therefore, $M$ is an upper bound of the set

Then,

Therefore, $f$ is of bounded $(2, k)$-variation on the interval $[a, c]$. Similarly, it is proved that $f$ is of bounded $(2, k)$-variation on the interval $[c, b]$.

Let us consider $t\in (a, b]$ and the partitions $\Pi_{[a, c]}, \Pi_{[c, b]}$, given by:

and

As $\Pi_{[a, c]}\subset \Pi_{[a, b]}$ and $\Pi_{[c, b]}\subset \Pi_{[a, b]}$, it follows that

Where the supremum is chosen over the set of all partitions $\Pi_{[a, b]}$.

Consequently, by Definition 4.1., we conclude that

□

Proposition 4.3. The following relation $\sim$ defined in $BV([a, b], 2, k)$ is an equivalence relation.

Proof. ⅰ) There exists $0\in \mathbb{C}$ such that $f-f = 0k$, so $f\sim f$. Therefore, $\sim$ is reflexive.

ⅱ) If $f\sim g$, then $f-g = \alpha k$ for some $\alpha \in \mathbb{C}$, then, there exists $\beta = -\alpha \in \mathbb{C}$ such that $g-f = \beta k$, so $g\sim f$. Therefore, $\sim$ is symmetric.

ⅲ) If $f\sim g$ and $g\sim h$, then, there exists $\lambda, \gamma \in \mathbb{C}$ such that $f-g = \lambda k$ and $g-h = \gamma k$, then $f-h = \gamma k +\lambda k$, so $f-h = (\gamma +\lambda) k$, where $\gamma +\lambda\in \mathbb{C}$ so $f\sim h$. Therefore, $\sim$ is transitive.

□

By virtue of the proposition above, the equivalence class of $f\in BV([a, b], 2, k)$ under the relation $\sim$ is given by:

In addition,

Remark 4.4. $[f+g] = [f]+[g]$ and $\lambda [f] = [\lambda f]$.

Remark 4.5. The set of all equivalence classes under the relation $\sim$ given in Proposition 4.3 will be noted by $\mathcal{BV}_k^{\sim}[a, b]$. This is

Next, we will endow the set $\mathcal{BV}_k^{\sim}[a, b]$ of functions of $(2, k)$-bounded variation of a norm.

Theorem 4.5. Let $(X, \|\cdot, \cdot\|)$ be a 2-normed space, $k\in X$. The functional $\|\cdot\|_{\mathcal{BV}_k^{\sim}[a, b]}\colon \mathcal{BV}_k^{\sim}[a, b]\to \mathbb{R}$ defined by

is a norm for the set $\mathcal{BV}_k^{\sim}[a, b]$.

Proof. Let $[f], [g] \in \mathcal{BV}_k^{\sim}[a, b]$ and $\lambda\in\mathbb{C}$, then

$(N_{1})$ From the definition of 2-norm and $(2, k)$-variation, we have that $\|f(a), k\|\ge 0$, $\|f(b), k\|\ge 0$ and $V_a^b(f, X, k)\ge0$, obtaining that

$(N_{2})$ $(\Longrightarrow)$ Let us suppose that $\left\|\left[f\right]\right\|_{\mathcal{BV}_k^{\sim}[a, b]} = 0$, then

Then, $\|f(a), k\| = 0$, $\|f(b), k\| = 0$ and $V_a^b(f, X, k) = 0$. Thus

for some $\alpha, \beta\in \mathbb{C}$. From $V_a^b(f, X, k) = 0$, using Proposition 4.2 and taking into account that $f(a) = \alpha k$ and $f(b) = \beta k$, we have that for all $t\in [a, b]$, there exists $\gamma\in\mathbb{C}$ such that $f(t) = \gamma k$.

Therefore, $f\sim 0$. Then, $[f] = [0]$.

$(\Longleftarrow)$ Lets suppose that $[f] = [0]$, since $f\in [f] = [0]$, then $f\in [0]$; in other words, there exists $\gamma \in \mathbb{C}$ such that $f(x)-0 = \gamma k$ for all $x\in[a, b]$, so

Therefore, $\left\|\left[f\right]\right\|_{\mathcal{BV}_k^{\sim}[a, b]} = 0$.

$(N_{3})$

$(N_{4})$ As $\mathcal{BV}_k^{\sim}[a, b]$ is a vector space, then, $[f]+[g]\in \mathcal{BV}_k^{\sim}[a, b]$. Also,

Therefore, $\left\|\left[f\right]+\left[g\right]\right\|_{\mathcal{BV}_k^{\sim}[a, b]}\le \left\|\left[f\right]\right\|_{\mathcal{BV}_k^{\sim}[a, b]}+\left\|\left[g\right]\right\|_{\mathcal{BV}_k^{\sim}[a, b]}$. Thus, it is proved that $\|\cdot\|_{\mathcal{BV}_k^{\sim}[a, b]}$ is a norm for $\mathcal{BV}_k^{\sim}[a, b]$. □

Proposition 4.4. Let $f, g\in \mathcal{BV}_k^{\sim}[a, b]$. If $f\sim g$, then $\left\|\left[f\right]\right\|_{\mathcal{BV}_k^{\sim}[a, b]} = \left\|\left[g\right]\right\|_{\mathcal{BV}_k^{\sim}[a, b]}$.

Proof. If $f\sim g$, then there exists $\alpha \in \mathbb{C}$ such that $f-g = \alpha k$. Thus,

□

Theorem 4.6. If $(X, \|\cdot, \cdot\|)$ is a $(2, k)$-Banach space, then the space $\left(\mathcal{BV}_k^{\sim}[a, b], \|\cdot\|_{\mathcal{BV}_k^{\sim}[a, b]}\right)$ of all functions of bounded $(2, k)$-variation on $[a, b]$, is a Banach space.

Proof. Let $\left\{[f_{n}]\right\}_{n\in \mathbb{N}}$ a Cauchy sequence in $\left(\mathcal{BV}_k^{\sim}[a, b], \|\cdot\|_{\mathcal{BV}_k^{\sim}[a, b]}\right)$ and $\epsilon > 0$. Then, there exists $N\in \mathbb{N}$ such that if $m, n \geq N$, we have that

Since $\left\{\left[f_{n}\right]\right\}_{n\in \mathbb{N}}$ is of Cauchy, then it is bounded, so there exists $M\in \mathbb{R}^+$ such that for all $n\in \mathbb{N}$

From (4.2) we have that

Thus,

which ensures that $\left\{f_{n}(a)\right\}_{n\in \mathbb{N}}$ and $\left\{f_{n}(b)\right\}_{n\in \mathbb{N}}$ are sequences $k$-Cauchy at $(X, \|\cdot, \cdot\|)$.

On the other hand, from the inequality (4.4), we have that

Suppose $t\in (a, b)$. Let us consider the partition $P = \{a, t, b\}.$ Using the Definition 4.1 and the inequality (4.5), we have

From this, we have that

Then,

Thus,

As a result, the sequence $\left\{f_{n}(t)\right\}_{n \in\mathbb{N}}$ is a uniform sequence $k$-Cauchy in $X$.

Since $X$ is $(2, k)$-Banach, there exists a function $f\colon [a, b] \to X$ such that:

Consequently, for all $\epsilon > 0$ and $t\in [a, b]$, there exists $N\in\mathbb{N}$ such that if $n\ge N$ we have that

Similarly, from (4.5), we obtain

In other words,

Let us see that $[f]\in \mathcal{BV}_k^{\sim}[a, b]$.

Using the inequalities (4.7) and (4.3), we have that for all $\epsilon > 0$, $\sum\limits_{j = 1}^{n}\left\|f(t_{j})-f(t_{j-1}), k\right\| < \epsilon+M$. So, $\sum\limits_{j = 1}^{n}\left\|f(t_{j})-f(t_{j-1}), k\right\|\le N.$ Hence $[f]\in \mathcal{BV}_k^{\sim}[a, b]$.

Now, of the inequalities (4.6) and (4.7) we have $\|(f_{n}-f)(a), k\| < \epsilon$, $\|(f_{n}-f)(b), k\| < \epsilon$ and $V_a^b(f_{n}-f, X, k) < \epsilon$. Therefore,

Thus, $\{[f_n] \}_{n \in\mathbb{N}}$ converges to $[f]$ with the norm $\|\cdot\|_{\mathcal{BV}_k^{\sim}[a, b]}$. Therefore, the set $\mathcal{BV}_k^{\sim}[a, b]$ of all functions of bounded $(2, k)$-variation in $[a, b]$ is a Banach space. □

5.   Conclusions

The notion of a function of bounded $(2, k)$-variation in 2-normed spaces presented in Definition 4.2 is a generalization of the functions of bounded variation in normed spaces. Moreover, any function of bounded variation in a space with inner product is a function of bounded $(2, k)$-variation in the 2-normed space induced by the standard 2-inner product (Proposition 4.1). In this context, we envision that the functions of generalized bounded $\phi$-variation on spaces with inner product can be viewed as functions of generalized bounded $\phi$-variation in the context of the theory of spaces with 2-inner product. Therefore, we believe that the results obtained by Bugajewska et al. in ^[2,3] can be extended to the context of the theory of 2-normed spaces. On the other hand, if $f$ a function of $(2, k)$-variation null on $[a, b]$, then the restriction of $f$ to the interval $(a, b)$, ${f} |_{(a, b)}$, is of the form $mk+\frac{1}{2}(f(a)+f(b))$ (Proposition 4.2). Also, every function of bounded $(2, k)$-variation is $(2, k)$-bounded, but the reciprocal is not true in general, as can be seen in the counterexample (Example 4.2). The set of functions of bounded $(2, k)$-variation over a $(2, k)$-Banach space is a Banach space (Theorem 4.6).

Yazdi, Zarei, Adumene, Abbassi and Rahnamayiezekavat ^[19] characterized and addressed uncertainty in digitized process systems, which are essential and unavoidable today. These must be integrated with the design, control, and modeling supports of feasible and optimal engineering systems. The classical theory of functions of bounded variation represents an effective option to address these problems. For example, Weerasinghe ^[16] considered an infinite horizon discounted cost minimization problem for a one-dimensional stochastic differential equation model. Although the operating cost function is not necessarily convex, sufficient conditions are obtained to guarantee zero-control optimality due to the inclusion of a functions of bounded variation process. Considering that classical functions of bounded variation can be viewed as functions of bounded $(2, k)$-variation, our study represents a novel option for conducting research such as ^[16,19].

Author contributions

Cure Jaffeth, Ferrer Kandy and Ferrer Osmin: Conceptualization, methodology, validation, software, writing-original draft, writing-review & editing. All authors contributed equally to the manuscript. All authors have read and approved the final version of the manuscript for publication.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare that they have no conflict of interest in this work.