Bifurcation, chaotic behavior and solitary wave solutions for the Akbota equation

1.   Introduction

In recent years, chaos theory [1,2] has been widely applied in fields such as physics, chemistry, biology, economics, and control. Chaotic behavior [3,4,5] is a complex and interesting stochastic behavior in chaos theory, and it is highly sensitive to initial conditions. Specifically, when there is a slight disturbance in the initial conditions of the system, as the system evolves over time, its orbit will deviate from the original orbit and the system will exhibit chaotic behavior. In recent years, with the development of nonlinear dynamics, it has been found that two-dimensional planar dynamical systems can exhibit orbital properties with chaotic behavior under small disturbances [6], that is, the orbital properties of the system will show chaotic behavior. Obviously, chaotic behavior is universal, and research has shown that studying chaotic behavior has broad application prospects, for example, the Chen system, the Lorentz system, and Duffing system. Current researches have shown that the theory and methods of chaos apply to many fields such as natural science and engineering technology [7,8,9,10]. Moreover, research on nonlinear dynamics has shown that the Lyapunov exponent is an important measure for qualitatively characterizing complex systems. As it is well known, the positive or negative Lyapunov exponent can characterize a dynamical system as chaotic or stable.

Nonlinear partial differential equations (NLPDEs) [11,12,13,14,15,16,17] can be used to simulate nonlinear problems from fields such as physics, chemistry, biology, electronic communication, and engineering technology [18,19,20,21,22,23,24,25]. Moreover, in recent years, researchers have conducted extensive research on NLPDEs. Particularly, many experts have been devoted to the study of bifurcation, chaotic behavior, and solitary waves of NLPDEs, and some very important results have been reported. However, research on the bifurcation, chaotic behavior, and solitary waves of more complex NLPDEs are still in the enlightenment stage. Based on the research of chaos theory mentioned above, this article will consider the study of bifurcation, chaotic behavior, and solitary waves of the Akbota equation, which is described as follows [26,27]:

where $v = v(x, t)$ and $u = u(x, t)$ represent a real values function and a complex function, respectively. $\alpha$, $\beta$, and $\gamma$ are the arbitrary constants. When $\alpha = 0$, the Akbota equation becomes the Kuralay equation. When $\beta = 0$, the Akbota equation becomes the well-known Schrödinger equation. The Akbota equation is an integrable coupled partial differential equation, which was proposed in the study of the Heisenberg ferromagnetic equation. This equation has significant theoretical implications for studying nonlinear phenomena in magnets, nonlinear optics, and curve and surface geometry. In [26], Faridi and collaborators gave the optical soliton solutions of Eq (1.1) by using an explicit approach. In [27], Mathanaranjan and Myrazakulov studied the optical soliton solutions of Eq (1.1) by using the extended auxiliary equation method. However, the analysis of the dynamic behavior of Eq (1.1) has not yet been reported. Moreover, a more general Jacobian function solution has not been provided. Therefore, in this article, we will use the method of planar dynamical system analysis to analyze the dynamic behavior of the two-dimensional dynamical system of the equation and its perturbation system.

The remaining part of this article is arranged as follows: In Section 2, the phase portraits of the dynamical system are plotted. Moreover, the phase portraits, sensitivity analysis, and Lyapunov exponent of its perturbation system are discussed. In Section 3, the solitary wave solutions of the Akbota equation are constructed. In Section 4, the graph of the obtained solution is plotted. In Section 5, a brief conclusion is given.

2.   Qualitative analysis

2.1.   Mathematical derivation

Firstly, we consider a wave transformation

where $U(\xi)$ and $V(\xi)$ are the wave's amplitude components. $\delta$, $k$, and $w$ are constants.

Substituting Eq (2.1) into Eq (1.1), we obtain the imaginary component

From Eq (2.4), we have

Integrating Eq (2.3), we can obtain the relationship between $U(\xi)$ and $V(\xi)$ as follows

Substituting Eqs (2.5) and (2.6) into Eq (2.2), we can also obtain the real part

where $(\alpha-\beta\delta)\beta\neq0$.

2.2.   Bifurcation analysis

When $\frac{dU}{\xi} = q$, we can obtain the dynamic system of Eq (2.7) as

with Hamiltonian function

where

$h$ is an integral constant.

Let

$f(U)$ has three equilibrium points of system (2.8), which are $(0, 0)$, $\left(\sqrt{\frac{r_{1}}{r_{3}}}, 0\right)$, and $\left(-\sqrt{\frac{r_{1}}{r_{3}}}, 0\right)$. The Jacobian of system (2.8) is

Thus, the eigenvalue is obtained when the equilibrium points of system (2.8) are $E_{j}(U_{j}, 0)$ ($j = 0, 1, 2$)

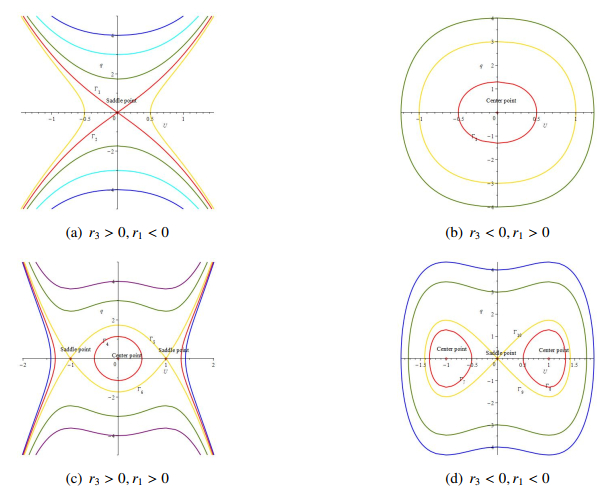
By using the theory of planar dynamical systems, we know that the equilibrium point $E_{j}(U_{j}, 0)$ of system (2.8) is the saddle point when $f'(U_{j}) > 0$, the equilibrium point $E_{j}(U_{j}, 0)$ of system (2.8) is the center point when $f'(U_{j}) < 0$, the equilibrium point $E_{j}(U_{j}, 0)$ of system (2.8) is the degenerate point when $f'(U_{j}) = 0$, where $j = 0, 1, 2$. Using mathematical software, we have drawn the planar phase portrait of (2.8) as shown in Figure 1.

From Figure 1, it can be seen that the orbit corresponding to curve $\Gamma_{1}$, $\Gamma_{9}$, and $\Gamma_{10}$ is the homoclinic, the orbit of curve $\Gamma_{3}$, $\Gamma_{4}$, $\Gamma_{7}$, and $\Gamma_{8}$ is the periodic, and the orbit to curve $\Gamma_{5}$ and $\Gamma_{6}$ is heteroclinic. The homoclinic orbit of the dynamical system (2.8) corresponds to the solitary wave of Eq (1.1). Heteroclinic orbits correspond to twisted or anti-twisted waves. Periodic orbits correspond to periodic waves. Therefore, through the analysis of planar dynamic systems, we can obtain various types of wave solutions for Eq (1.1).

2.3.   Perturbed dynamical system

By adding a periodic disturbance to system (2.8), we can present a two-dimensional dynamical system with periodic disturbances [28,29,30],

where $A$ and $\varpi$ represent the amplitude and the frequency of system (2.12), respectively.

Remark 2.1. The Lyapunov exponent is an important tool for describing the dynamic properties of a nonlinear system. When the maximum Lyapunov exponent is greater than zero, the system (2.12) is considered chaotic. When the maximum Lyapunov exponent is greater than zero, the system (2.12) is stable. In Figures 2 and 3, we respectively depict the qualitative behavior of system (2.12). In Figure 4, we present the bifurcation diagram of system (2.12). In Figure 5, we plot the maximum Lyapunov exponent of system (2.12).

3.   Solitary wave solutions of Eq (1.1)

After assuming that $h_{0} = H(0, 0) = 0$, $h_{1} = H\left(\pm\sqrt{\frac{r_{1}}{r_{3}}}, 0\right) = \frac{r_{1}^{2}}{4r_{3}}$, we construct the solitary wave solutions of Eq (1.1) by the theory of planar dynamical system.

Case 1. $r_{1} > 0$, $r_{3} > 0$, $0 < h < \frac{r_{1}^{2}}{4r_{3}}$. System (2.8) can be rewritten as

where

Substituting (3.1) into $\frac{dU}{d\xi} = q$ and integrating it, the Jacobian function solutions of Eq (1.1) are presented

Case 2. $r_{1} > 0$, $r_{3} > 0$, $h = \frac{r_{1}^{2}}{4r_{3}}$. When $\Upsilon_{1h}^{2} = \Upsilon_{2h}^{2} = \frac{r_{1}}{r_{3}}$, the solitary wave of Eq (1.1) can be derived

Case 3. $r_{1} < 0$, $r_{3} < 0$, $\frac{r_{1}^{2}}{4r_{3}} < h < 0$. System (2.8) can be rewritten as

where

Similar to the situation in Section 3.1, we can also obtain, the Jacobian function solutions for Eq (1.1),

Case 4. $r_{1} < 0$, $r_{3} < 0$, $h = 0$. If $\Upsilon_{3h}^{2} = \frac{2r_{1}}{r_{3}}$ and $\Upsilon_{4h}^{2} = 0$, the solitary wave of Eq (1.1) can be derived

Case 5. $r_{1} < 0$, $r_{3} < 0$, $h > 0$. System (2.8) can be rewritten as

where

Similar to the situation in Section 3.1, the Jacobian function solutions of Eq (1.1) can be derived

4.   Graphical analysis

In this section, we plot the modular length of the solution of $u_{1}(x, t)$, $u_{2}(x, t)$, and $u_{4}(x, t)$ including a 3D graph, 2D graph, and counter graph as shown in Figures 6–8, respectively. From Figure 6, the solution $u_{1}(x, t)$ is a Jacobian function solution, which is a periodic function solution. The solution $u_{2}(x, t)$ in Figure 7 is a dark soliton solution. The solution $u_{4}(x, t)$ in Figure 8 is a bright soliton solution.

5.   Conclusions

In this article, we study the dynamic behavior and solitary wave solutions of the Akbota equation from magnets, nonlinear optics, curve, and surface geometry. We transform the Akbota equation into a two-dimensional planar dynamical system by controlling the parameters $h$, $r_1$, and $r_3$ of the two-dimensional dynamical system, and use mathematical software to draw the planar phase portraits of the system. From the plane phase portrait, we can easily observe the orbital properties of the dynamic system. What's more, we add a periodic disturbance term to the two-dimensional dynamical system and draw two-dimensional phase diagrams, three-dimensional phase portraits, sensitivity analysis diagrams, bifurcation diagrams, and Lyapunov exponent diagrams. Through the above dynamic analysis, we present the dynamic behavior of the disturbance system. Moreover, we also combine the definition of Jacobian functions and the analysis method of planar dynamical systems to obtain the solitary wave solution of the Akbota equation and draw its three-dimensional, two-dimensional, and contour maps. Through the research in this article and compared with existing literature, we not only obtain the dynamic behavior of the two-dimensional dynamical system of the Akbota equation and its perturbation system, but also the solitary wave solution of the Akbota equation. This study has significant theoretical value for understanding the dynamic behavior of the Akbota equation and the transmission of solitary wave solutions in nonlinear optical fibers.

Author contributions

Zhao Li: Writing-Review & Editing; Writing-Original Draft; Formal Analysis; Shan Zhao: Software. Both authors have read and approved the final version of the manuscript for publication.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare no conflicts of interest.