On random force correction for large time steps in semi-implicitly discretized overdamped Langevin equations

1.   Introduction

The limited time step size in molecular dynamics (MD) simulations is a major barrier to simulating long-time behaviors of various biological processes, even if coarse-grained molecular models are applied. The limitation originates from the large stiffnesses of strong bonds. In most cases, these strong interactions are necessary to maintain the basic structure of molecules, but the associated small fluctuations do not seem to be essential for molecular deformations of interest. In continuum mechanics, we can overcome the barrier with the use of implicit time integration schemes ^[1], where the Hessian matrix of the potential function is used to prevent the amplification of oscillations associated with its large eigenvalues. However, the complicated landscapes of MD potential functions hamper the use of implicit schemes because Newton iteration is unstable ^[2]. In our previous work ^[3], we introduced a semi-implicit Hessian correction scheme using only the positive parts of Hessian matrices of elemental potentials to avoid instabilities. This scheme allowed us to use time steps 50–800 times larger than those in the explicit Euler-Maruyama (EM) time integration scheme ^[4]. However, further increases in the time step created considerable errors in the conformational distributions even though the molecular structures were not destroyed.

In this paper, we focus on the damping effect of the Hessian matrix on the fluctuations caused by random forces. In the overdamped Langevin (OL) equation, the increment of the random variable $\boldsymbol{X}$ is given by

where $\boldsymbol{G}$ is a positive-definite matrix representing the friction, $\boldsymbol{F}\left(\boldsymbol{X}\right)$ is the force as a function of $\boldsymbol{X}$, and $\boldsymbol{\varXi }$ is the random force satisfying $\left\langle{\boldsymbol{\varXi }dt}\right\rangle =$ 0. We use differential forms and their discrete approximations according to the Itô calculus, as in (1.1), throughout this article. The increment of the probability density function is determined by the averages:

Here, the first equation represents advection by the force $\boldsymbol{F}\left(\boldsymbol{X}\right)$. The second equation represents the diffusion of the probability density function. Therefore, the random force is the source of diffusion, which is damped by the friction. In the explicit EM scheme, (1.1) is directly discretized for a finite time interval $h$as

to obtain the increment $\Delta \boldsymbol{X} = \boldsymbol{X}\left(t+h\right)-\boldsymbol{X}\left(h\right)$. Therefore, the impact of the friction coefficient $\boldsymbol{G}$ on the fluctuation of the numerical solution is estimated by replacing $dt$ with $h$ in (1.2). If $\boldsymbol{F}\left(\boldsymbol{X}+\Delta \boldsymbol{X}\right)$ can be approximated with a positive-semidefinite matrix $\boldsymbol{K}\left(\boldsymbol{X}\right)$ as

the following semi-implicit scheme may be applied to enable the use of a large time interval $h$:

In this case, the variance is given by

If there are eigenvalues of $h\boldsymbol{K}$ that are much greater than those of $\boldsymbol{G}$, the damping by $h\boldsymbol{K}$ may underestimate the diffusion. In this study, we pursue a correction scheme for the random force in the semi-implicit EM scheme to shift the diffusion toward the desired direction and magnitude. Comparing (1.3) and (1.5), the coefficient $\boldsymbol{G}+h\boldsymbol{K}\left(\boldsymbol{X}\left(t\right)\right)$ on the left-hand side of (1.5) can be regarded as a modified friction coefficient. Therefore, a natural strategy would appear to involve correcting the random force ${\boldsymbol{\varXi }}_{h}$ on the right-hand side to be consistent with the modified friction.

We begin our analysis with a linear overdamped Langevin (OL) equation with a positive semidefinite matrix $\boldsymbol{K}$. Through comparison of the numerical solution obtained by the implicit scheme with the analytical solution, we find an appropriate correction to the random force of the form $h\boldsymbol{K}$, where $h$ is the time interval of the temporal discretization. Next, we extend the idea of random force correction to nonlinear OL equations using the Hessian matrix instead of $\boldsymbol{K}$ in the linear case. We derive a discrete Fokker-Planck (FP) equation from the semi-implicitly discretized OL equation with a random force correction. Here, we see that the correction of the random force corresponds to the addition of artificial friction associated with the Hessian matrix. Finally, we validate the proposed semi-implicit scheme on the entropic elasticity problem of the freely jointed chain model.

Grønbech-jensen and Doniach ^[5] proposed a semi-implicit scheme for the OL equation in which strong bonded interactions are constrained. Though their approach is limited to infinitely stiff bonds, our approach can analyze the effects of the magnitude of strong bonded interactions on the stochastic behavior of molecules, as shown in our numerical experiments. Sweet et al. ^[6] applied a friction matrix constructed by normal mode partitioning of a mass reweighted Hessian matrix for the underdamped Langevin (UL) equation. Their scheme requires the computation of all eigenvectors of the mass reweighted Hessian matrix to perform the projections on the two subspaces spanned by the low- and high-frequency modes, whereas our scheme requires only the inversion in solving (1.5) and the construction of the additional random forces constructed from the elemental Hessian matrices of the individual strong bonds. This configuration enables faster computations.

2.   Preliminary analysis of the linear problem

To determine the essence of the discrepancy of implicit scheme for large times, we start our discussion with a linear OL equation:

where $\gamma$ is the friction coefficient, $\boldsymbol{K}$ is a positive semidefinite matrix, and $\boldsymbol{\varXi }\left(t\right)$ is the random force vector satisfying

with the Boltzmann constant ${k}_{B}$ and the temperature $T$. Here, $\boldsymbol{I}$ is the identity matrix, and the tensor product $\boldsymbol{a}\otimes \boldsymbol{b}$ of two vectors $\boldsymbol{a}$ and $\boldsymbol{b}$ can be identified with the square matrix $\boldsymbol{a}{\boldsymbol{b}}^{T}$. For a given initial solution $\boldsymbol{X}\left(t\right)$ at $t$, the analytical solution $\boldsymbol{X}\left(t+h\right)$ at $t+h$ is as follows:

Here, the variance of the integrated random force on the right-hand side is calculated using (2.2) to be

Here, we assume ${x}^{-1}\left(\exp x-1\right)$ = 1 at $x$ = 0 for the null space of $\boldsymbol{K}$. Let us analyze the relationship between the exact solution at $t+h$ in (2.3) and the temporally discretized solution of the implicit scheme defined as

where ${\widehat{\boldsymbol{\varXi }}}_{h}\left(t\right)$ is the discrete random force at $t$ given later. The above equation can be rewritten as

Here, the matrix $\left(\boldsymbol{I}+{\gamma }^{-1}h\boldsymbol{K}\right)$ on the right-hand side can be regarded as the first order Taylor expansion of $\mathrm{e}\mathrm{x}\mathrm{p}\left({\gamma }^{-1}h\boldsymbol{K}\right)$ in (2.3). Furthermore, if we additionally take the first order Taylor expansion of ${\gamma }^{-1}h\boldsymbol{K}$ in the last term of (2.4), the following condition to be imposed on the random force ${\widehat{\boldsymbol{\varXi }}}_{h}\left(t\right)$ is derived:

Namely, the addition of $h\boldsymbol{K}$ to the identity matrix $\gamma \boldsymbol{I}$, which is used in the explicit EM scheme, may improve the accuracy of implicit schemes. This suggests that the random force should be corrected using the Hessian matrix in semi-implicit schemes for nonlinear problems as well. In other words, the proposed implicit scheme can be regarded as the EM scheme with the random force satisfies (2.7), where $h\boldsymbol{K}$ plays the role of the artificial friction.

Note that the accuracy of the approximation of (2.4) to (2.7) is ensured only for the low frequency components of small eigenvalues of ${\gamma }^{-1}h\boldsymbol{K}$. However, we are interested in using time steps much larger than that of the stability condition for explicit schemes, i.e.,

where $\rho \left(\boldsymbol{K}\right)$ is the spectral radius of $\boldsymbol{K}$. According to (2.4), we cannot expect high accuracy for the high-frequency components for a single time step. However, if the high frequency components are damped over $k$ steps ($k\gg 1)$, the temporal change of the stochastic distribution may be correctly obtained. To see this damping effect, we compare the numerical solution after the $k$ steps to the analytical solution. First, we split the analytical solution at $t+kh$ into the stochastic part ${\boldsymbol{X}}_{S}$ and the deterministic part ${\boldsymbol{X}}_{D}$, where $\boldsymbol{X} = {\boldsymbol{X}}_{S}+{\boldsymbol{X}}_{D}$, and the two parts are given by

Here, the variance of ${\boldsymbol{X}}_{S}\left(t+kh\right)$ is calculated as

Here, we assume ${x}^{-1}\left(1-\exp \left(-x\right)\right)$ = 1 at $x$ = 0 for the null space of $\boldsymbol{K}$. Similarly, the numerical solution after $k$ steps is split as ${\widehat{\boldsymbol{X}}}_{k} = {\widehat{\boldsymbol{X}}}_{S, k}+{\widehat{\boldsymbol{X}}}_{D, k}$, where the stochastic part ${\widehat{\boldsymbol{X}}}_{S, k}$ and deterministic part ${\widehat{\boldsymbol{X}}}_{D, k}$ are given by

Here, ${\widehat{\boldsymbol{\varXi }}}_{h, l} = {\widehat{\boldsymbol{\varXi }}}_{h}\left(t+lh\right)$ is the random force applied at the $(l+1)$-th step. From the decorrelation of these random forces and (2.7), the variance of ${\widehat{\boldsymbol{X}}}_{S, k}$ is

Thus, the difference between (2.10) and (2.12) can be evaluated by taking the difference of the following two functions, where $x = {\gamma }^{-1}h\boldsymbol{K}$:

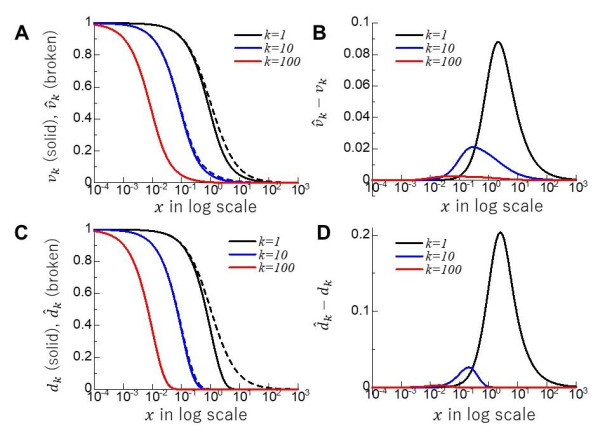
The two functions and their differences are depicted in Figure 1A and B for $k =$1, 10, and 100. The damping effects for $x\gg o\left(1\right)$ are clearly shown for both the functions and the differences. Similarly, the deterministic parts in (2.9) and (2.11) can be evaluated using the functions defined by

In Figure 1C and D, the same trends as in the stochastic parts are observed.

Figure 1.  Functions representing the solution updates after $k$ steps of the implicit scheme. The variance functions of the stochastic part are depicted for the analytical solutions (${v}_{k}$: solid lines) and the discrete implicit solutions (${\widehat{v}}_{k}$: broken lines) in A. The differences ${\widehat{v}}_{k}-{v}_{k}$ are depicted in B. The functions of the deterministic part are depicted for the analytical solutions (${d}_{k}$: solid lines) and the discrete implicit solutions (${\widehat{d}}_{k}$: solid lines) in C. The differences ${\widehat{d}}_{k}-{d}_{k}$ are depicted in D.

DownLoad: Full-Size Img PowerPoint

A comparison with the EM scheme

will further elucidate the effects of the implicit scheme. In this case, the stochastic and deterministic parts of the numerical solution are represented as

The variance of the stochastic part is calculated as

In Figure 2, the following functions representing the evolution of solutions are compared with their analytical counterparts for $0 < x < 2$, where convergence is ensured:

As in the implicit case, the numerical error around $x = O\left(1\right)$ is damped as $k$ increases.

Figure 2.  Functions representing the solution updates after $k$ steps of the EM scheme. The variance functions of the stochastic part are depicted for the analytical solutions (${v}_{k}$: solid lines) and the discrete implicit solutions (${\check{v}}_{k}$: broken lines) in A. The differences ${\check{v}}_{k}-{v}_{k}$ are depicted in B. The functions of the deterministic part are depicted for the analytical solutions (${d}_{k}$: solid lines) and the discrete implicit solutions (${{\check{d}}_{k}}_{k}$: solid lines) in C. The differences ${\check{d}}_{k}-{d}_{k}$ are depicted in D.

DownLoad: Full-Size Img PowerPoint

3.   Modification of friction for nonlinear problems

We consider numerical time integration schemes of the nonlinear OL equation for $n$ particles in three-dimensional space:

where $\boldsymbol{G}$ is a $3n\times 3n$positive diagonal matrix representing the friction coefficients imposed on the $n$ particles, $U\left(\boldsymbol{X}\right)$ is a potential function, and $\boldsymbol{\varXi }\left(t\right)$ is a random vector satisfying

The potential function consists of bonded and nonbonded interactions, and the thermal effects of the implicit solvent are approximated by the random force. The limitation on the time step size comes from the large eigenvalues of the Hessian matrix $\boldsymbol{H} = {\partial }^{2}U/{\partial \boldsymbol{X}}^{2}$. These large eigenvalues originate from the strong bonded interactions. Because the inversion of a banded matrix consisting of elemental Hessian matrices of the strong bonded interactions is computationally efficient, the use of a semi-implicit method is natural. In the following, we start with the EM scheme, and modify the friction coefficient and the random force to enable a large time interval.

In accordance with the Ito integral for a constant time interval $h$ as in the EM scheme, we must update the particle coordinates ${\boldsymbol{X}}_{h}$ from $t$ to $t+h$ as follows:

where the right-hand side involves the force $-dU/d\boldsymbol{X}$ at $t$ and the discrete random force satisfies

When applying the above scheme to MD simulations, we encounter a severe restriction of the time interval $h$ owing to the stability condition:

In our previous work ^[3], we introduced a semi-implicit Hessian correction scheme (SimHec) with the intention of replacing $-\frac{dU}{d\boldsymbol{X}}\left({\boldsymbol{X}}_{h}\left(t\right)\right)$ in (3.3) by a linear approximation of $-\frac{dU}{d\boldsymbol{X}}\left({\boldsymbol{X}}_{h}\left(t+h\right)\right)$ as follows:

Here, $\widetilde{\boldsymbol{H}}\left(\boldsymbol{X}\right)$ is a $3n\times 3n$ symmetric matrix designed to approximate the positive part of the Hessian matrix of $U$ at $\boldsymbol{X}$. Based on the derivation of (2.7), we regard the coefficient $h\widetilde{\boldsymbol{H}}\left({\widetilde{\boldsymbol{X}}}_{h}\left(t\right)\right)$ on the left-hand side of (3.6) as the artificial friction and apply the corrected random force as follows:

where the additional random force ${\widetilde{\boldsymbol{\varXi }}}_{h}\left(t\right)$ satisfies the conditions

Here, the first condition indicates that the additional random force ${\widetilde{\boldsymbol{\varXi }}}_{h}$ must be uncorrelated with the original random force ${\boldsymbol{\varXi }}_{h}\left(t\right)$, and the second condition corresponds to the consistency of the additional random force and the artificial friction $h\widetilde{\boldsymbol{H}}$. From these conditions, we can easily derive the consistency condition of the total friction ${\widehat{\boldsymbol{G}}}_{h}\left({\widehat{\boldsymbol{X}}}_{h}\left(t\right)\right) = \boldsymbol{G}+h\widetilde{\boldsymbol{H}}\left({\widehat{\boldsymbol{X}}}_{h}\left(t\right)\right)$ and the total random force ${\widehat{\boldsymbol{\varXi }}}_{h}\left(t\right) = {\boldsymbol{\varXi }}_{h}\left(t\right)+{\widetilde{\boldsymbol{\varXi }}}_{h}\left(t\right)$, which is

In the following, we discuss the meaning of this consistency condition in the context of the probability density. Hereafter, we refer to this method as the "semi-implicit Hessian correction scheme with random force correction" (SimHec-RC).

4.   Impact of random force correction on probability density

As shown in the literature ^[7,8,9], the property (3.2) of the random force is key to deriving the FP equation when applying the Ito integral to the OL Eq (3.1). Here, we trace the process from the OL equation to the FP equation based on the discrete temporal integration of SimHec-RC.

In SimHec-RC, the update ${\Delta \widehat{\boldsymbol{X}}}_{h} = {\widehat{\boldsymbol{X}}}_{h}\left(t+h\right)-{\widehat{\boldsymbol{X}}}_{h}\left(t\right)$ is performed as follows:

Therefore, we obtain

Here, we have derived the second equation assuming (3.9) as follows:

Note that the higher order products of ${{\widehat{\boldsymbol{G}}}_{h}\left({\widehat{\boldsymbol{X}}}_{h}\right)}^{-1}{\widehat{\boldsymbol{\varXi }}}_{h}h$ are $\boldsymbol{O}\left({h}^{2}\right)$. If we replace the modified random force ${\widehat{\boldsymbol{\varXi }}}_{h}\left(t\right)$ with the original random force ${\boldsymbol{\varXi }}_{h}\left(t\right)$ as in the original SimHec in (3.6), the second term is replaced by

Here, $\left\langle{{\Delta \widetilde{\boldsymbol{X}}}_{h}\otimes {\Delta \widetilde{\boldsymbol{X}}}_{h}}\right\rangle$ differs by the factor $\boldsymbol{G}{{\widehat{\boldsymbol{G}}}_{h}\left({\widetilde{\boldsymbol{X}}}_{h}\left(t\right)\right)}^{-1}$from $\left\langle{{\Delta \widehat{\boldsymbol{X}}}_{h}\otimes {\Delta \widehat{\boldsymbol{X}}}_{h}}\right\rangle$ in (4.2). Below, we evaluate the impact of this difference on the probability density functions produced by these discrete stochastic processes.

From (4.2), we can derive the discrete version of Ito's lemma ^[10] for any smooth function $f$ using Taylor expansion:

Here, the average $\left\langle{*}\right\rangle$ is taken over the discrete stochastic processes from $t$ to $t+h$, and the symbol –8–8represents the dot product of two vectors or two matrices. Let ${\widehat{P}}_{h}\left({\widehat{\boldsymbol{X}}}_{h}, t\right)$ be the probability density function of SimHec-RC in (3.7). Then, we have the following relationship between the integrals over the conformation spaces ${\widehat{\mathrm{\Omega }}}_{h}\left(t\right)$ and ${\widehat{\mathrm{\Omega }}}_{h}\left(t+h\right)$ at times $t$ and $t+h$, respectively:

Here, the averaging operation $\left\langle{f\left({\widehat{\boldsymbol{X}}}_{h}+{\Delta \widehat{\boldsymbol{X}}}_{h}\right)}\right\rangle$ on the left-hand side is taken over ${\Delta \widehat{\boldsymbol{X}}}_{h}$. By using Eq (4.6) followed by Eq (4.5) and applying integration by parts, we obtain the following equations:

Because the above equation holds for any smooth function $f$, we obtain

This is a discrete version of the FP equation in which ${\widehat{\boldsymbol{G}}}_{h}\left(\boldsymbol{X}\right)$ corresponds to the friction coefficients. Similarly, from (4.4), we obtain the following equation for the probability density function ${\widetilde{P}}_{h}\left(\boldsymbol{X}, t\right)$ for the stochastic process given by SimHec in (3.6) without the random force correction:

Here, we see that the dispersion is overdamped by a factor of ${{\widehat{\boldsymbol{G}}}_{h}\left(\widetilde{\boldsymbol{X}}\left(t\right)\right)}^{-1}\boldsymbol{G}$ compared with (4.8). The advantage of the random force correction is clear when ${\widehat{\boldsymbol{G}}}_{h}$ is a constant matrix. The term inside the brackets on the right-hand side of (4.8) is rewritten as

Thus, we see that the probability density of the FP equation converges to the Boltzmann distribution, i.e.,

Equation (4.10) also suggests that the accuracy of the obtained time transients of the distribution depends on the magnitude of $\left\|\frac{d}{d\boldsymbol{X}}:{{\boldsymbol{G}}_{h}}^{-1}\right\|$. Therefore, it may be important to minimize $\left\|\frac{d}{d\boldsymbol{X}}\widetilde{\boldsymbol{H}}\right\|$ in the construction of $\widetilde{\boldsymbol{H}}$. Physically, $\frac{d}{d\boldsymbol{X}}:{{\boldsymbol{G}}_{h}}^{-1}\ne 0$ means that the thermal effect of the solvent depends on the conformation $\boldsymbol{X}$. Thus, the probability density does not converge to the Boltzmann distribution in thermal equilibrium for a finite $h$.

5.   Combining the artificial friction matrix and random force

Here, we consider combining the $\widetilde{\boldsymbol{H}}\left(\boldsymbol{X}\right)$ and ${\widetilde{\boldsymbol{\varXi }}}_{h}$ that satisfy the conditions in (3.8). In general, the potential function $U\left(\boldsymbol{X}\right)$ in MD is given as a sum of elemental potentials between two, three, or four particles, as follows:

where ${\boldsymbol{P}}_{k}$ represents projection onto the subspace ${\Omega }_{k}$ of the subset of particles for which the potential ${V}_{k}$ is defined. For every potential ${V}_{k}$, if we can construct ${\widetilde{\boldsymbol{H}}}_{k}$ and ${\widetilde{\boldsymbol{\varXi }}}_{k, h}$ on ${\Omega }_{k}$ such that the conditions

are fulfilled, then it is straightforward to show that the sums

satisfy the conditions in (3.8). Here, we identify ${\widetilde{\boldsymbol{H}}}_{k}$ and ${\widetilde{\boldsymbol{\varXi }}}_{k, h}$ on the subspace ${\Omega }_{k}$ with ${{\boldsymbol{P}}_{k}}^{T}{\widetilde{\boldsymbol{H}}}_{k}{\boldsymbol{P}}_{k}$ and ${{\boldsymbol{P}}_{k}}^{T}{\widetilde{\boldsymbol{\varXi }}}_{k, h}$ on the total space, respectively, for the sake of simplicity. We can realize the uncorrelatedness of random forces between different elemental potentials using sequences of uncorrelated random numbers. Therefore, the remaining problems are (ⅰ) constructing ${\widetilde{\boldsymbol{H}}}_{k}$ for ${V}_{k}$, and (ⅱ) constructing a ${\widetilde{\boldsymbol{\varXi }}}_{k, h}\left(t\right)$ that fulfills the condition:

As an example, we consider the potential $V\left({\boldsymbol{x}}_{1}, {\boldsymbol{x}}_{2}\right) = \varphi \left({r}_{\mathrm{1, 2}}\right)$, which is a function of the distance ${r}_{\mathrm{1, 2}} = \left\|{\boldsymbol{x}}_{2}-{\boldsymbol{x}}_{1}\right\|$. In this case, the Hessian matrix is

where the matrices ${\boldsymbol{A}}_{\mathrm{1, 2}}$ and ${\boldsymbol{B}}_{\mathrm{1, 2}}$ are defined as

with the unit vector

Note that the matrices ${\boldsymbol{A}}_{\mathrm{1, 2}}$ and ${\boldsymbol{B}}_{\mathrm{1, 2}}$ satisfy

Therefore, for two given positive coefficients $\widetilde{\alpha }$ and $\widetilde{\beta }$ which may depend on ${r}_{\mathrm{1, 2}}$, a pair of ${\widetilde{\boldsymbol{H}}}_{\mathrm{1, 2}}$ and ${\widetilde{\boldsymbol{\varXi }}}_{h}$ satisfying Eq (5.4) can be given as

with the normalized Gaussian noise satisfying

From (5.8), the eigenspaces of ${\boldsymbol{H}}_{\mathrm{1, 2}}$ are composed of those of ${\boldsymbol{A}}_{\mathrm{1, 2}}$ and ${\boldsymbol{B}}_{\mathrm{1, 2}}$. The null space is spanned by the parallel displacements $\left[\begin{array}{c}d\\ d\end{array}\right], {}_{}{}^{\forall }\boldsymbol{d}$. The eigenspace of ${\boldsymbol{A}}_{\mathrm{1, 2}}$ is spanned by the vector $\left[\begin{array}{c}n\\ -n\end{array}\right]$, which corresponds to oscillation along $\boldsymbol{n}$. The eigenspace of ${\boldsymbol{B}}_{\mathrm{1, 2}}$ is spanned by the vectors $\left[\begin{array}{c}m\\ -m\end{array}\right], \boldsymbol{m}\perp \boldsymbol{n},$ which corresponds to the rotation about the center $\left({\boldsymbol{x}}_{1}+{\boldsymbol{x}}_{2}\right)/2$ (Figure 3). Because the nonzero eigenvalues of ${\boldsymbol{A}}_{\mathrm{1, 2}}$ and ${\boldsymbol{B}}_{\mathrm{1, 2}}$ are equal to 2, the nonzero eigenvalues of ${\boldsymbol{H}}_{\mathrm{1, 2}}$ are $2\ddot{\varphi }\left({r}_{\mathrm{1, 2}}\right)$ and $2\dot{\varphi }\left({r}_{\mathrm{1, 2}}\right)/{r}_{\mathrm{1, 2}}$. In a case of a bond between a pair of adjacent particles $(i, i+1)$,

The coefficient of ${\boldsymbol{B}}_{\mathrm{1, 2}}$ in (5.2) is negative for $r < {r}_{0}$. In this paper, we replace $\left(r-{r}_{0}\right)/r$ with a nonnegative constant ${b}_{B}$ as follows:

Hereafter, we refer to the parameter ${b}_{B}$ as SimHec(${b}_{B})$ or SimHec-RC(${b}_{B})$. In the following, a nearly optimal parameter is chosen for each approach.

Figure 3.  Eigenvectors of ${\boldsymbol{A}}_{\mathrm{1, 2}}$ and ${\boldsymbol{B}}_{\mathrm{1, 2}}$. Parallel displacements (green arrows) span the null space. Oscillations in the direction of $\boldsymbol{n}$ (red arrows) span the eigenspace of ${\boldsymbol{A}}_{\mathrm{1, 2}}$. Rotations represented by $\boldsymbol{m}$ orthogonal to $\boldsymbol{n}$ (blue arrows) span the eigenspace of ${\boldsymbol{B}}_{\mathrm{1, 2}}$.

DownLoad: Full-Size Img PowerPoint

6.   Validation on entropic elasticity problems

To test the efficiency and the accuracy of SimHEC-RC, we simulated the entropic elasticity of a freely jointed chain consisting of $n$ particles ($n = 100)$ with potential

We adopted the parameters of the coarse-grained protein model CafeMol ^[11], which only considers the position of a single bead at the ${C}_{\alpha }$ position for each residue in the polymer chain. A friction coefficient of ${\gamma }_{i} = 168.7\mathrm{C}\mathrm{a}\mathrm{f}\mathrm{e}\mathrm{M}\mathrm{o}\mathrm{l}\mathrm{T}\mathrm{i}\mathrm{m}\mathrm{e}\cdot\ \mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}/\left(\mathrm{m}\mathrm{o}\mathrm{l}\ Å^{2}\right)$ was used. This value was derived by assuming the viscosity of water: $8\times {10}^{-4}\mathrm{k}\mathrm{g}/\left(\mathrm{m}\ \mathrm{s}\right)$, and the radius ${r}_{+1}$ of the amino acids: 3.82 Å. The time unit in CafeMol (CafeMolTime) is approximately 49 fs. A value of ${c}_{B} = 110.4\ \mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}/\left(\mathrm{m}\mathrm{o}\mathrm{l}\ Å^{2}\right)$ was used for all bonds; the limitation on the time step size of the EM scheme due to the bond stiffness was estimated as $h\le \gamma /{2c}_{B} =$0.76 CafeMolTime.

First, we examined the accuracy for a transient problem where one end of the straight chain was released (Figure 4A). In this numerical test, one end ${\boldsymbol{x}}_{1}$ was always fixed, and the other end ${\boldsymbol{x}}_{n}$ was released at $t = 0.$ The trajectories of the coordinates of ${\boldsymbol{x}}_{n}$ in the stretched direction were analyzed using the numerical results of 64 samples. We observed that the time transients of edge coordinate averages with 64 samples and 256 samples were almost identical in SimHec-RC with $h = 100$. Therefore, we performed the comparisons with 64 samples. The EM scheme with $h = 0.5$ shows a severe discrepancy (Figure 4B). The SimHec and SimHec-RC schemes were compared with the EM scheme with $h = 0.125$ (Figure 4C). The accuracy of SimHec deteriorated as the time step $h$ increased. The shortening speed decreased with excessive friction as shown in (4.4) and (4.9). However, SimHec-RC retained its accuracy by correcting the random force.

Figure 4.  Time transients of the free end of the freely jointed chain. The averages of the free end coordinates of 64 samples are plotted. (A) Examples of the chain shape at various times. (B) The averaged coordinates of the free end calculated using EM schemes with $h =$ 0.25 (broken pink), 0.5 (broken green), and $h =$0.125 (black). (C) The coordinates of the free end as calculated using SimHec-RC (red) and SimHec (blue) schemes are compared with those using the EM scheme with $h =$ 0.125 (broken black) for $h =$ 10 (left panel), 100 (center panel), and 1000 (right panel). In SimHec-RC, ${b}_{B} =$0.0 was adopted for $h =$ 10, and ${b}_{B} =$0.01 was adopted for $h =$ 100 and 1000.

DownLoad: Full-Size Img PowerPoint

To confirm the accuracy for multiple steps as estimated in Figures 1 and 2, we examined the distributions of $\left(x, y\right) = \left(r\cos \theta, r\sin \theta \right)$, where $r$ and $\theta$ are defined using the changes of ${\boldsymbol{x}}_{i+nd}-{\boldsymbol{x}}_{i}$ from $t$ to $t+kh$ as follows:

In Figure 5, we compared the distributions superposed for all pairs $(i, i+nd)$ with $nd$ = 10 obtained using the EM scheme with $h = 0.125$ and SimHec-RC(0.01) with $h = 100$. There are substantial differences between the $k =$1 and 10 cases of SimHec-RC and their counterparts, namely, the $k =$800 and 8000 cases of the EM scheme. However, as expected from Figure 1A and B, the difference is diminished for $k = 100.$

Figure 5.  Distributions of changes of ${\boldsymbol{x}}_{i+10}-{\boldsymbol{x}}_{i}$ in the EM scheme (top) with $h$ = 0.125 and SimHec-RC(0.01) (bottom) with $h$ = 100 for $kh$ = 100 (left), 1000 (center), and 10000 (right). Red indicates high concentration. The same color scale is used in each plot with the same time interval $kh$.

DownLoad: Full-Size Img PowerPoint

Note that $hk$ = 10⁴CafeMolTime ~ 0.5 ns is much smaller than the total time 10⁷ CafeMolTime ~ 0.5 μs, which needed to be reduced to close to zero (Figure 4).

Next, we evaluated the force acting on the end ${\boldsymbol{x}}_{n}$ trapped by the spring at the position ${\boldsymbol{p}}_{L} = {\left[n{r}_{+1}, \mathrm{0, 0}\right]}^{T}$ as

In the numerical experiment, we adopted ${K}_{a}$ = 0.1$\ \mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}/\left(\mathrm{m}\mathrm{o}\mathrm{l}\ Å^{2}\right)$. In Figure 6A, the average values of the force

computed over the time range $\left[\mathrm{0, 5}\times {10}^{9}\right]$CafeMolTime (~[0, 0.25]s) for a single process are compared with the values calculated using the explicit scheme with $h = 0.25$. The EM scheme with $h = 0.5$ shows a severe discrepancy (Figure 6B) as in the case of shortening of the free end. In Figure 6C, we compared the average force as computed by SimHec and SimHec-RC, where ${c}_{B}$ and ${K}_{a}$ were increased by factors of one hundred and ten, respectively, with the theoretical values in the limit of ${c}_{B}\to \infty$:

where the Langevin function $F$ is given by

Figure 6.  Entropic elasticity (A) Average values of the force $\left\langle{{f}_{1}}\right\rangle$ acting on the end point (bottom), and the difference compared with the EM scheme with $h$ = 0.25 (top). SimHec-RC (red) and SimHec (blue) are compared with EM with $h$ = 0.25 (black points) for $h$ = 10 (left panel), 100 (center panel), and 1000 (right panel). (B) EM with $h$ = 0.5 (green) is compared with $h =$ 0.25 (black). (C) SimHec-RC (red) and SimHec (blue) for the highly stiff bond parameter ${c}_{B} = 110.4\times 100\ \mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}/\left(\mathrm{m}\mathrm{o}\mathrm{l}\ Å^{2}\right)$ are compared with the theoretical limit where ${c}_{B}\to \infty$.

DownLoad: Full-Size Img PowerPoint

7.   Computational efficiency

To assess the computational efficiency, we compared the overhead of SimHec-RC with that of EM. The overheads consist of the cost of computing the elemental Hessian matrices, the random force corrections, and the linear solutions. The computation times per time step for EM, SimHec, and SimHec-RC were 3.2, 16.9, and 22.6 μs, respectively, for a simulation of 100 particles using an Intel(R) Xeon(R) Gold 6448Y (4.1 GHz) single core processor. In the linear solution, the band structure with bandwidth 5 was exploited in the Cholesky factorization. The overhead of SimHec-RC was larger than that of SimHec owing to the random force correction. Comparing EM with $h$ = 0.25 and SimHec-RC with $h$ = 100 (resp. $h$ = 1000), we found a speedup of a factor of 56.6 (resp. 566).

8.   Conclusions and future work

In this study, we analyzed the relationship between the corrected Hessian matrix in a semi-implicit scheme and the random force concerning the accuracies for both the linear problem and the derived FP equations of the nonlinear problem. The proposed correction to the random force worked well for the simple MD problem involving bonded interactions. Although our approach is potentially extendable to more general potentials with bond angles and dihedral angles ^[3], the appropriate corrections to the Hessian matrix must be developed to avoid negative eigenvalues.

Author contributions

Toshiaki Hisada designed the project; Takumi Washio and Akihiro Fujii developed the semi-implicit Hessian correction scheme with random force correction, ran the simulations, analyzed the simulation data, and wrote the manuscript with input from Toshiaki Hisada; Takumi Washio developed the simulation code with input from Akihiro Fujii and Toshiaki Hisada. All authors contributed to the article and approved the submitted version.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by MEXT as "Program for Promoting Researches on the Supercomputer Fugaku–8(Project ID: hp230216). We thank Edanz (https://jp.edanz.com/ac) for editing a draft of this manuscript.

Conflict of interest

The authors declare no conflict of interest.