The generalized scale mixtures of asymmetric generalized normal distributions with application to stock data

1.   Introduction

In the wake of the swift progression of technology over recent decades, a noteworthy proliferation of diverse data types has ensued. A salient feature inherent in many of these datasets is their proclivity toward heavy tails and marked skewness, thereby rendering conventional univariate distributions inadequately applicable. Consequently, considerable scholarly focus has been directed toward the formulation of robust distributions adept at effectively modeling such intricately structured data.

Andrews and Mallows (1974) ^[1] and West (1987) ^[2] proposed a scale mixtures of normal (SMN) distributions with the following stochastic representation

where $\mu\in\mathbb{R}$ is the location parameter, $Z \sim N(0, \sigma^{2})$, and $U$ is a positive random variable independent with $Z$. The SMN distributions provide great flexibility in modeling not only asymmetric but also heavy-tailed datasets. Although SMN distributions are attractive, when facing asymmetric population with strong skewness and heavy-tailed behavior simultaneously in practice, SMN distribution appears overwhelming. To cope with this problem, Branco and Dey (2001) ^[3] constructed the scale mixtures of skew-normal (SMSN) distribution by replacing the normal distribution of Eq (1.1) to the skew-normal distribution. This class of distributions not only contains the entire family of SMN distributions, but also accounts for asymmetry and heavy tails simultaneously. Ferreira, Lachos, and Bolfarine (2020)^[4] pointed out that scale mixtures of the skew normal distribution can offer much-needed flexibility by combining both skewness and heavy tails. Basso (2010) ^[5] developed an EM-type algorithm to obtain the maximum likelihood estimation for the SMSN family and derived the observed information matrix. Kim and Genton (2011) ^[6] obtained the characteristic functions for the SMSN family by means of the simple stochastic representation. Lin et al. contributed a great deal of important work for scale mixture models based on the skew-normal distribution, which has been found to be effective in the treatment of heavy-tailed data involving asymmetric behaviors ^[7,8,9]. Mahdavi et al. ^[10] obtained the maximum likelihood estimation for scale-shape mixtures of flexible generalized skew normal distributions via EM-type algorithms.

The utilization of the skew normal distribution in the aforementioned study is rooted in the seminal work of Azzalini (1985) ^[11]. However, it is essential to recognize the limitations of this distribution when confronted with highly skewed and leptokurtic data, as its ability to accurately fit such data may be constrained by the range of the skewness and kurtosis coefficients. To explore more recent advancements in the field of skew normal distribution, we recommend consulting the works of ^{[12,13,14,15,16]}. Acknowledging these limitations, it becomes imperative to develop alternative forms of skew normal distributions that can accommodate a broader spectrum of diverse data. One approach in this direction was introduced by Fernandez and Steel (1988) ^[17], who incorporated a skew parameter into a symmetric distribution. This innovation enabled the regulation of the probability density functions in both the positive and negative orthants, offering enhanced flexibility. Another notable contribution is the work of Zhu (2009) ^[18], who proposed the asymmetric exponential power distribution by introducing a skew parameter into the exponential power distribution. Zhu further demonstrated the consistency, asymptotic normality, and efficiency of the maximum likelihood estimation for this distribution. These advancements signify important strides in the development of alternative skew normal distributions that can better accommodate complex data patterns.

In this work, we have introduced an asymmetric generalized normal (AGN) distribution by incorporating a skew parameter into the generalized normal (GN) distribution ^[19]. This extension provides a flexible framework for modeling various types of data exhibiting asymmetric behavior and heavy-tailed characteristics. However, in many practical scenarios, the observed data often exhibits strongly heavy tails and significant skewness. To address this challenge, we turn our attention to the family of generalized scale mixtures of the asymmetric generalized normal (GSMAGN) distributions. This family represents a generalization of traditional scale mixtures, wherein we replace the power $-\frac{1}{2}$ of the scale factor in Eq (1.1) with any power $-\frac{1}{\beta}$, with $\beta > 0$. By employing this generalization, we gain greater flexibility in capturing the complexities present in the data and better accommodate the wide range of tail and skewness behaviors encountered in practical applications.

The rest of this paper will be organized as follows. In section two, some definitions and essential properties of the GSMAGN family are summarized. In section three, the explicit expression for moments of order statistics from the GSMAGN family are obtained under independent identically distributed (IID) cases. In section four, an efficient and tractable EM-type algorithm to obtain the maximum likelihood estimation of parameters is established. In section five, the consistency properties of the estimates and the estimation of standard errors are demonstrated. In section six, a simulation study is implemented to assess the performance of the proposed algorithm. In section seven, two real dataset analyses are presented to demonstrate the feasibility of the proposed model. Finally, conclusions are noted in section eight.

2.   The generalized scale mixtures of asymmetric generalized normal distributions

2.1.   Definition and properties

Definition 2.1. Let the random variable $X$ with the following probability density function (pdf) be

where $\Gamma(\cdot)$ denotes the gamma function, $\mu\in \mathbb{R}$ is a location parameter, $\sigma > 0$ is a scale parameter, $\kappa > 0$ is the skewness parameter and $\beta > 0$ is a shape parameter. We say that the random variable $X$ follows an AGN distribution, denoted by $X\sim AGN(\mu, \sigma, \kappa, \beta)$. In particular, if $\kappa = 1$, the AGN distribution becomes a GN distribution ^[19] denoted by $GN(\mu, \sigma, \beta)$.

Definition 2.2. A random variable $Y$ is in the GSMAGN family if its stochastic representation is given by

where $X\sim AGN(0, 1, \kappa, \beta)$, $\mu$ is the location parameter, $k(\cdot)$ is a weight function, and $U$ is a random variable.

If $U = u$, then $Y\mid U = u\sim AGN(\mu, [k(U)]^{1/\beta}\sigma, \kappa, \beta)$ and the pdf of $Y$ is given by

where $H(\cdot; \boldsymbol{\alpha})$ is the cumulative distribution function (CDF) of $U$ indexed by parameter $\boldsymbol{\alpha}$. To imbue the proposed distributions that have some compelling mathematical properties to facilitate statistical inference, usually the weight function will be chosen for $k(u) = \frac{1}{u}$.

Proposition 2.1. If $Y\sim GSMAGN(\mu, \sigma, \kappa, \alpha, \beta)$, then the stochastic representation of $Y$ can be written as follows

where $U\sim H(\cdot; \boldsymbol{\alpha})$, $Z\sim Gamma(1/\beta, 1)$, $I$ is a discrete random variable with probability mass function $f_I = \frac{\kappa^2}{1+\kappa^2}\mathbf{1}_{\{I = -\kappa\}}+\frac{1}{1+\kappa^2}\mathbf{1}_{\{I = 1/\kappa\}}$, and $U, I, Z$ are independent of each other.

Proposition 2.2. If $Y\sim GSMAGN(\mu, \sigma, \kappa, \alpha, \beta)$, then

In particular, the expectation and variance of the random variable $Y$ are respectively given by

Proof. See Appendix Part 1. □

2.2.   Examples of the GSMAGN distributions

(ⅰ) AGN distribution

In this case $U = 1$, the CDF of $Y$ is

where $\mathit{\boldsymbol{\gamma}}(\alpha; x) = \frac{1}{\varGamma(\alpha)}\int_{0}^{x}t^{\alpha-1}e^{-t} \mathrm{d}t$ denotes the lower incomplete gamma function.

(ⅱ) Asymmetric generalized $t$ distribution (AGT)

In this case we consider $U\sim Gamma(\alpha, \beta)$ ($\boldsymbol{\alpha} = (\alpha, \beta)$ for $H(u; \mathit{\boldsymbol{\alpha}})$) and the pdf of $Y$ is given by

and the CDF of $Y$ can be represented as

where

${\mathrm{B}}(\cdot, \cdot)$ denotes the beta function, $I(a, b;x) = \frac{1}{ {\mathrm{B}}(a, b)}\int_{0}^{x}t^{a-1}(1-t)^{b-1} \mathrm{d}t$ denotes the incomplete beta function, and $\alpha, \beta > 0$ are two shape parameters, then we say that the random variable $Y$ follows AGT distribution, denoted by $Y\sim AGT(\mu, \sigma, \kappa, \alpha, \beta)$.

Corollary 2.1. If $Y\sim AGT(\mu, \sigma, \kappa, \alpha, \beta)$, then

In particular, the expectation and variance of $Y$ are respectively given by

Proposition 2.3. If $Y\sim AGT(\mu, \sigma, \kappa, \alpha, \beta)$, then $U| Y = y\sim Gamma\bigg(\alpha+\frac{1}{\beta}, {\bigg[\frac{1}{\beta}+\frac{1}{2}\bigg(\kappa^{ \mathrm{sign}(y-\mu)}\frac{|y-\mu|}{\sigma}\bigg)^\beta\bigg]}^{-1}\bigg)$.

Proof. See Appendix Part 1. □

(ⅲ) Asymmetric generalized slash distribution (AGSL)

In this case, we have $U\sim Beta(\alpha, 1)$ and the pdf of $Y$ is given by

All parameters play the same role as in AGT distribution, then we say that the random variable $Y$ follows an AGSL distribution, denoted by $Y\sim AGSL(\mu, \sigma, \kappa, \alpha, \beta)$.

Proposition 2.4. If $Y\sim AGSL(\mu, \sigma, \kappa, \alpha, \beta)$, then the pdf of $U\mid Y = y$ is given by

Proof. See Appendix Part 1. □

(ⅳ) Contaminated asymmetric generalized normal distribution (CAGN)

In this case, $U$ is a discrete random variable taking one of two states with the following probability mass function

It follows immediately that the pdf of the random variable $Y$ is given by

and the CDF of $Y$ is

where

Proposition 2.5. If $Y\sim CAGN(\mu, \sigma, \kappa, \lambda, \alpha, \beta)$, the pdf of $U\mid Y = y$ for $0 < \lambda < 1$ is given by

Proof. See Appendix Part 1. □

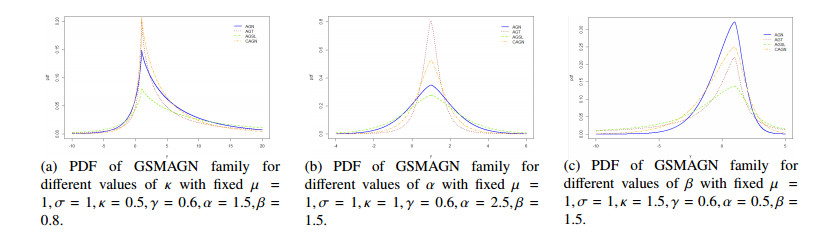
Figure 1 illustrates the pdf of the GSMAGN family under three distinct scenarios, providing valuable insights into the impact of the shape parameters ($\alpha$ and $\beta$) on the pdf's shape. The chosen values of $\alpha$ and $\beta$ exert a decisive influence on the characteristics of the density. When $\alpha$ and $\beta$ assume smaller values (Figure 1a and 1c), the resulting densities exhibit longer tails and greater leptokurtosis. Conversely, larger values of $\alpha$ and $\beta$ (Figure 1b) lead to contrasting effects. Notably, the shape parameter $\beta$ has a predominant impact on the distribution's shape, while the parameter $\alpha$ governs the behavior of the tail. Moreover, all three subfigures demonstrate that the AGSL distribution possesses thicker tails compared to the other three distributions. Consequently, the AGSL distribution exhibits a favorable advantage in modeling observations characterized by skewness and heavy tails.

3.   Order statistics

In the following, we provide the moments of order statistics generating from $GSMAGN(0, 1, \kappa, \boldsymbol{\alpha}, \beta)$ distribution under IID case.

3.1.   Order statistics of AGN

Proposition 3.1. Let $X_1, X_2, \cdots, X_n$ be a random sample of size $n$ from $AGN(0, 1, \kappa, \beta)$, and $X_{1:n}, X_{2:n}, \cdots, X_{n:n}$ are corresponding order statistics. The $m_{th}$ moments of the largest order statistic is given by

where

Proof. See Appendix Part 2. □

The Lauricella function of type A (see, for example, Exton(1978)^[20]) is defined as

where $(f)_k = f(f+1)\cdots(f+k-1)$ denotes the ascending factorial.

We also acquire the moments of the largest order statistic by means of the Lauricella function of type A.

Proposition 3.2. If $X \sim AGN(0, 1, \kappa, \beta)$, and $X_{1:n}, X_{2:n}, \cdots, X_{n:n}$ are the order statistics, then the $m_{th}$ moments of the largest order statistic is given by

Proof. See Appendix Part 2. □

3.2.   Order statistics of AGT

Proposition 3.3. If $X \sim AGT(0, 1, \kappa, \alpha, \beta)$, $\frac{1}{\beta}$ is an integer, and $X_{1:n}, X_{2:n}, \cdots, X_{n:n}$ are the order statistics, then the $m_{th}$ moments of the largest order statistic $X_{n:n}$ is given by

where ${T_v}(1/\beta, 0) = 1$, ${T_v}(1/\beta, 1) = {C_v}, \; v = 0, 1, \cdots, (1/\beta)$, and $C_v = (-1)^v\binom{1/\beta-1}{v}\frac{1}{\alpha+v}$. For $n > 2$, ${T_v}\left({\frac{1}{\beta }, n - 1} \right) = \sum\limits_{i = 0}^v {{C_i}} {T_{v - i}}\left({\frac{1}{\beta }, n - 2} \right), v = 0, 1, \cdots, (1/\beta)(n-1).$

Proof. See Appendix Part 2. □

The formula for computing the m-th moments of the order statistics given in Proposition 3.3 is only applicable to the case that $1/\beta$ is an integer. We derive a general representation of the m-th moments of order statistics without restrictions on $\beta$.

Introduced by Exton (1978) ^[20], the generalized Kampe de Feriet function is defined by

where $a = (a_1, a_2, \cdots, a_A)$, $b_i = (b_{i, 1}, b_{i, 2}, \cdots, b_{i, B})$, $c = (c_1, \cdots, c_C)$, $d_i = (d_{i, 1}, \cdots, d_{i, D})$, for $i = \; 1, 2, \cdots, n$ and $((f))_k = ((f_1, f_2, \cdots, f_p))_k = (f_1)_k\cdots(f_p)_k$, $(f_i)_k = f_i(f_i+1)\cdots(f_i+k-1)$.

By using the the generalized Kampe de Feriet function, we derive the following proposition:

Proposition 3.4. If $1/\beta$ is a real non-integer, the $m$-th moments of order statistics $X_{n:n}$ from $AGT(0, 1, \kappa, \alpha, \beta)$ can be computed by the following convergent expression

where

Proof. See Appendix Part 2. □

3.3.   Order statistics of CAGN

The relationship between order statistics from CAGN distribution and AGN distribution can be stated as follows

Proposition 3.5. If $Y\sim CAGN(0, 1, \kappa, \lambda, \alpha, \beta)$, $X\sim AGN(0, 1, \kappa, \alpha, \beta)$, then we have

Proof. See Appendix Part 2. □

4.   Parameter estimation via the EM-type algorithm

In this section, an EM-type algorithm to determine the MLEs for the parameters of the $GSMAGN(\mu, \sigma, \kappa, \boldsymbol{\alpha}, \beta)$ family is established.

Originally proposed by Dempster et al. (1977) ^[21], the EM algorithm has garnered significant attention as a powerful tool for handling estimation challenges in situations involving incomplete data. This algorithm offers numerous exceptional advantages. For a more comprehensive understanding of this subject, we highly recommend referring to the monograph by Lange (2013) ^[22]. A notable extension of the EM algorithm is the ECM algorithm introduced by Meng and Rubin (1993) ^[23]. The ECM algorithm not only preserves the desirable property of monotonic convergence exhibited by the Q-function in the classical EM algorithm but also facilitates faster convergence rates.

Invoking Proposition 2.1, the hierarchical representation for the GSMAGN model can be described as

Let $Y = (y_1, \ldots, y_n)^T$ denote the observed data, $U = (u_1, \ldots, u_n)^T$ on behalf of the corresponding latent variable. Combining $Y$, $U$ together we obtain the complete data denoted by $W = (Y, U)$. Let $\varTheta = (\mu, \sigma, \kappa, \boldsymbol{\alpha})^T$ represent the vector of parameters, then the complete log-likelihood function can be expressed as follows

Prior to outlining the precise steps of the estimation algorithm, it is imperative to highlight a crucial aspect. We adopt the assumption that the shape parameter $\beta$ remains constant, and the optimal value for this parameter can be determined through the PLA. By integrating the ECM algorithm with the PLA, the computational speed and overall efficiency of the algorithm are significantly enhanced. Consequently, under this assumption, the parameter vector $\theta_i$ is transformed into $\theta_i = (\mu_i, \sigma_i, \alpha_i)$ throughout the subsequent sections of this paper.

It is well known that the EM framework is an iterative algorithm consisting of two steps, namely, the expectation step (E-step) and the maximization step (M-step).

E-step: Given the observed data set $Y$ and parameter estimation values ${\hat{\Theta}}^{(h)}$ of the $h$-th iteration, the aim of this step involves calculation of several necessary conditional expectations. The so-called Q-function is expressed by

where $A_{1j}(Y, \hat{\varTheta}^{(h)}) = \mbox{E}[U_j\mid Y, \hat{\varTheta}^{(h)}]$, $A_{2j}(Y, \hat{\varTheta}^{(h)}) = \mbox{E}[\ln U_j\mid Y, \hat{\varTheta}^{(h)}]$, and $B_{j}(Y, \hat{\varTheta}^{(h)}) = \mbox{E}[\ln h(U_j; \boldsymbol{\alpha})\mid Y, \hat{\varTheta}^{(h)}]$.

For different members of the GSMAGN family, the crucial conditional expectations are calculated as follows

● For AGT

where $\hat{c}_{j}^{(h)} = \frac{1}{2}\bigg(\kappa^{ \mathrm{sign}(y_j-\hat{\mu}^{(h)})}\frac{|y_j-\hat{\mu}^{(h)}|}{\hat{\sigma}^{(h)}}\bigg)^{\beta}$, and $\varphi(\cdotp)$ is the Digamma function.

● For AGSL

● For CAGN

In the EM algorithm, the M-step needs to maximize the conditional expectation obtained by the E-step and the suggested framework can be briefly described as follows

(1) According to the theory of robust statistics ^[24], $\hat{\mu}^{(h+1)}$ can be updated through the following expression

where $\omega_{j}(Y, \varTheta) = { \kappa^{\beta \mathrm{sign}(y_j-\mu)}|y_j-\mu|^{\beta-2}A_{1j}(Y, \varTheta)},$

(2) Update $\hat{\sigma}^{(h+1)}$ by the following equation

where $\hat{\varTheta}^{\ast(h)} = (\hat{\mu}^{(h+1)}, \hat{\sigma}^{(h)}, \hat{\kappa}^{(h)}, \hat{\mathit{\boldsymbol{\alpha}}}^{(h)})$.

(3) Update $\hat{\kappa}^{(h+1)}$ by the following equation

such that $\varTheta^{\ast\ast(h)} = (\hat{\mu}^{(h+1)}, \hat{\sigma}^{(h+1)}, \hat{\kappa}^{(h)}, \hat{\mathit{\boldsymbol{\alpha}}}^{(h)})$ and $[x]^+ = max\{x, 0\}$, $[x]^- = [-x]^+$.

(4) Regarding $\hat{\alpha}^{(h+1)}$

● For AGT: Update $\hat{\alpha}^{(h+1)}$ as the root of

where $\hat{\varTheta}^{\ast\ast\ast(h)} = (\hat{\mu}^{(h+1)}, \hat{\sigma}^{(h+1)}, \hat{\kappa}^{(h+1)}, \hat{\mathit{\boldsymbol{\alpha}}}^{(h)})$.

● For AGSL: Update $\hat{\alpha}^{(h+1)}$ by

● For CAGN: Update $\hat{\alpha}^{(h+1)}$ by

Remark 4.1. For AGN, an interative procedure presented below to update $\hat{\beta}^{(h+1)}$ is also recommended

where

For a prescribed value $\varepsilon > 0$, if the value of the actual log-likelihood function $L(Y\mid\varTheta)$ of two successive iterations statifies $|L(Y\mid\hat{\varTheta}^{(h+1)})/L(Y\mid\hat{\varTheta}^{(h)})-1| < \varepsilon$, then the iterative process is broken up. In our study, the tolerance $\varepsilon$ is set equal to $10^{-5}$.

It is well known that the starting value plays a decisive role in the implementation of the EM-type algorithm. As a result, the following steps are recommended to find reasonable starting value.

Notes on implementation

● Random sample generation: From the stochastic representation in Proposition 2.1, the following procedures are recommended to generate random samples from GSMAGN.

Step 1: Generate $U\sim H(u; \boldsymbol{\alpha})$ and set $Z\sim Gamma(1/\beta, 1)$.

Step 2: Generate $W\sim U(0, 1)$. If $W\leq\frac{1}{1+\kappa^2}$, set $I = \frac{1}{\kappa}$; else set $I = -\kappa$.

Step 3: Set $Y = \mu+\sigma U^{-\frac{1}{\beta}}I (2Z)^{\frac{1}{\beta}}$ and return $Y$.

● Initialization: The initial value for $\hat{\mu}^{(0)}$, $\hat{\sigma}^{(0)}$ and $\hat{\kappa}^{(0)}$ can be computed by

(1) For AGT and AGSL: Compute the initial guess $\hat{\alpha}^{(0)}$ through the following equation

(2) For CAGN: The initial value for $\alpha$ and $\lambda$ are uniformly generated in $(0, 1)$.

Choosing the value of $\beta$

Step 1: Run the AGN model and obtain an estimate $\tilde{\beta}$ that can be referenced, then consider grids of values $\{\check{\beta}_{(1)}, \ldots, \check{\beta}_{(R)}\}$ that contain $\tilde{\beta}$ (the initial value for $\beta$ can be obtained from the moment estimator).

Step 2: Substitute each $\beta_{(q)}$ into the Q-function to acquire simultaneous estimation for the unknown parameters denoted by $\hat{\theta}^{(q)}_i$ via the ECM algorithm. After that, calculate the value of the corresponding log-likelihood function through Eq (4.1).

Step 3: Repeat Step 2 and then interpolate on $\beta$ values and derive $\breve{\beta}$ which maximizes the trace of the value of the log-likelihood function.

5.   Consistency properties

5.1.   Existence and consistency of the MLE

Lemma 5.1. If $X\sim{\mathrm{d}}P_\theta(x) = f(x; \theta){\mathrm{d}}\mu(x), \theta = (\theta_1, \cdots, \theta_s), x = (x_1, \cdots, x_n)$ are a $n$ identically distributed $f(x; \theta)$ random variable, then parameter space $\Theta$ is an open set in $\mathbb{R}^s$. Assume that

(1) If $\theta_1 \neq \theta_2$, then $P_{\theta_1} \neq P_{\theta_2}$.

(2) For $\forall x$ in the range of $X$, $f(x, \theta) > 0$, and has a continuous first partial derivative with respect to $\theta$.

(3) For $\forall \theta_0 \in \Theta$, there exists a neighborhood $U_{\theta_0} \subset \Theta$ and a positive function $G(x)$ if $\theta, \theta^{'}$ in $U_{\theta_0}$, we have $\mid{\mathrm{ln}}f(x; \theta^{'})-{\mathrm{ln}}f(x; \theta)\mid\leq G(x)\parallel\theta^{'}-\theta\parallel$, and ${\mathrm{E}}_{\theta_0}[G(X)] < \infty.$

For $\theta_0 \in \Theta$, when $n\rightarrow \infty$, there exists a solution $\hat{\theta}$ to likelihood equation (a.s.)

and the solution $\hat{\theta}$ is strongly consistent.

Theorem 5.1. If $Y\sim GSMAGN(\mu, \sigma, \kappa, \alpha, \beta)$, $\mathbf{y} = (y_1, y_2, \ldots, y_n)$ is random sample from population $Y$, where $\theta \in \tilde{\Theta} = \{(\mu, \sigma, \kappa, \alpha, \beta): \mu \in \mathbb{R}, \sigma \in \mathbb{R}^{+}, \kappa \in \mathbb{R}^{+}, \alpha \in \mathbb{R}^{+}, \beta \in \mathbb{R}^{+}\}$, the maximum likelihood estimator $\hat{\theta}$ of $\theta$ satisfies

Proof. See Appendix Part 3. □

5.2.   Estimation of standard errors

The observed information matrix of the GSMAGN distribution is computed by

It is well known that, under some regularity conditions, the covariance matrix of the maximum likelihood estimators $\mathbf{\hat{\Theta}}$ can approximated by the inverse of $\mathbf{I_0(\Theta|y)}$. We evaluate

Following the results of Basso^[5], the individual score can be described as $\mathbf{\hat{s}}_i = \frac{\partial L(\Theta|y_i)}{\partial \Theta}|_{\Theta = \hat\Theta}$, where $\mathbf{\hat{s}}_i = ({\hat{s}}_{\mu}, {\hat{s}}_{\sigma}, {\hat{s}}_{\kappa}, {\hat{s}}_{\boldsymbol{\alpha}})$. The elements in $\mathbf{\hat{s}}_i$ are given by

$D_{\mu}(f(y_i; \Theta))$ denotes the derivation of the density function with respect to $\mu$, and $D_{\sigma}(f(y_i; \Theta))$, $D_{\kappa}(f(y_i; \Theta))$ and $D_{\boldsymbol{\alpha}}(f(y_i; \Theta))$ are defined by analogy. Let

After some algebraic computation, let $A_i = \kappa^{ \mathrm{sign}(y_i-\mu)}\frac{|y_i-\mu|}{\sigma}$ and we obtain

$D_{\boldsymbol{\alpha}}(f(y_i; \Theta))$ depends on each particular case mentioned in section 2. The components of the score vector are given in Appendix Part 3.

6.   Simulation study

In this section, we conduct Monte Carlo simulations and the performance of the proposed algorithm is assessed via Bias and mean squared error (MSE) under different censoring schemes and parameter values. These two measures will be computed with 1500 replications at the same time and they are defned as follows:

Without losing the generality, we consider sample sizes $n = 50,100,300,500,800, 1000$, and change the values of the shape parameter $\beta$. To be more specific, in order to study the influence of sample variability on the estimation effects of proposed method, we consider the cases where $\beta = 1.5$ and $\beta = \; 2.5$, and for each case of $\beta$, the remaining parameter $(\mu, \sigma, \kappa, \alpha)$ is taken to be equal to (10, 2.5, 1.5, 3.5).

Figures 2 and 3 exhibit the Bias and MSE plots for the parameter estimates of the AGN, AGT, AGSL, and CAGN distributions across varying sample sizes. Based on the observations drawn from these two pictures, the following findings can be elucidated:

(1) It is evident that both the Bias and MSE of the parameters for the different sub-models (AGN, AGT, AGSL, CAGN) diminish and converge to zero as the sample sizes increase. This convergence implies that the estimates obtained through the proposed EM-type algorithm adhere to the desirable asymptotic properties, signifying consistency.

(2) Notably, when employing the proposed EM-type algorithm, the parameters $\kappa$ and $scale$ demonstrate relatively minor Bias across all sample sizes. Additionally, the MSE of the $\kappa$ parameter exhibits significant sensitivity to changes in sample size.

(3) Furthermore, Figures 2 and 3 reveal that the estimated performance of the EM algorithm for the AGT and AGSL distributions closely approximates that of these two distributions.

(4) Conversely, the results indicate that the estimation method faces the challenge of dependency on distribution complexity. Comparing the maximum likelihood estimates of the four distributions within the GSMAGN family, it becomes evident that the EM-type algorithm effectively estimates the parameters of the AGN distribution. However, for the CAGN distribution, which possesses a relatively larger number of parameters, the Bias and MSE of $\sigma$ and $\beta$ are relatively substantial, resulting in less stable estimates.

Through a comparative analysis of Figures 2 and 3, it becomes apparent that as the value of $\beta$ increases, the Bias and MSE of the parameter estimates decrease for all four distributions overall. This observation indicates that the EM-type algorithm for maximum likelihood estimation is more suitable for distributions with lower leptokurtosis.

7.   Application

In order to facilitate the empirical investigation, datasets encompassing the S&P 500 Composite Index (S&P 500) and the Shanghai Stock Exchange Composite Index (SSEC) indices, spanning from January 2, 1998 to June 18, 2023 were diligently compiled. These datasets were acquired from the esteemed source, https://finance.yahoo.com. A total of 6,408 samples were drawn from the S&P 500 and SSEC indices at corresponding time points to enable a comprehensive comparative analysis. Within the scope of this study, the return ($R_t$) in period $t$ is defined as $R_t = \; 100(\ln P_t - \ln P_{t-1})$, where $P_t$ (for $t = 1, 2, \dots, N$) represents the level of the S&P 500 and SSEC indices at time $t$.

As elucidated by Wen et al. (2022) ^[25], notwithstanding divergent summary statistics between the S&P 500 and SSEC indices, both datasets deviate from the assumptions associated with a normal distribution. Furthermore, both sets of data exhibit characteristics such as heavy-tailedness, leptokurtosis, and left-skewness.

To assess the adequacy of the proposed GSMAGN family, fitting procedures were conducted for the AGN, AGT, AGSL, and CAGN distributions using the S&P 500 and SSEC datasets separately. The estimation of distribution parameters was executed using the EM-type algorithm, as expounded in section four. To evaluate the goodness of fit for the four distributions and various metrics, including observed log-likelihood (l), Akaike information criterion (AIC), Bayesian information criterion (BIC), and the Efficient determination criterion (EDC), were employed. The fitting results were consolidated and presented in Tables 1 (for the S&P 500 dataset) and 2 (for the SSEC dataset). The ultimate values of the shape parameter $\beta$ of the GSMAGN family were determined by the trace of the PLA, as presented in Figures 4 and 5.

Upon scrutinizing Table 1, with a focus on the AIC and BIC criteria, it is discerned that the AGSL distribution consistently outperforms the other three distributions in fitting the S&P 500 dataset. Subsequently, the AGT distribution emerges as the next best-fitting alternative, indicating its substantial advantage when fitting data characterized by skewness and leptokurtic behavior. Turning attention to Table 2, considering the AIC, BIC, EDC, and log-likelihood values, it is deduced that the GSMAGN family surpasses the alternative models in terms of goodness of fit for the SSEC dataset.

To visually illustrate the fitting results, Figure 6 depicts histograms of the datasets alongside corresponding fitted densities. Notably, the fitted curves of AGT, AGSL and CAGN closely align with the contours of the histograms, attesting to the model's proficiency in capturing pertinent information inherent in the observations.

8.   Conclusions

This paper introduced a distribution family named GSMAGN, which holds significant relevance in the fitting of complex data characterized by skewness and heavy tails. The study focused on examining the properties of this family and deriving the explicit expression for the moment of order statistics. This expression serves as a valuable tool for parameter estimation based on the order statistics. To enhance the efficiency of parameter estimation for this model, an alternative variant of the EM-type algorithm was established. This variant combined the PLA with the classical ECM algorithm. The proposed method not only improves computational speed but also provides efficient estimations. Furthermore, closed-form expressions of the information matrix, along with the corresponding asymptotic properties of the MLE, were presented for this distribution family. To assess the performance of the proposed estimation method, Monte Carlo simulations were conducted under various scenarios. The results demonstrated that the proposed method satisfies the asymptotic property, and the estimation accuracy improves with larger sample sizes. The feasibility of the proposed methodology was illustrated through two real datasets. The encouraging results obtained in this study motivate us to further delve into the realm of multivariate GSMAGN family for effectively modeling datasets exhibiting asymmetry and heavy-tailedness in the future.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

All authors declare no conflicts of interest in this paper.

Appendix

Part 1: Proofs required for section two

$\bullet$ Proof of Proposition 2.2

According to Proposition 2.1, $Y = \mu+\sigma U^{-\frac{1}{\beta}}I (2Z)^{\frac{1}{\beta}}$, and $U$, $I$, $Z$ are independent of each other, then using the binomial expansion, we can obtain

where $Z\sim Gamma(1/\beta, 1)$, then we can calculate that

and $I$ is a discrete random variable with density function $f_I = \frac{\kappa^2}{1+\kappa^2}\mathbf{1}_{\{I = -\kappa\}}+\frac{1}{1+\kappa^2}\mathbf{1}_{\{I = 1/\kappa\}}$. Thus the $i$th moments of $I$ are

By substituting $\mathrm{E}(I^i)$ and $\mathrm{E}(Z^{\frac{i}{\beta}})$ into the above expression, we can prove Proposition 2.2. In particular, for $m = 1$ and $m = 2$, we obtain $\mathrm{E}(Y)$ and $\mathrm{E}(Y^2)$, respectively. This allows us to derive the expressions for $\mathrm{E}(Y)$ and $\mathrm{Var}(Y)$.

$\bullet$ Proof of Proposition 2.3

For AGT distribution, invoking Eq (2.3), we have

Let $z = \bigg[\frac{1}{2}\bigg(\kappa^{\mbox{sign}(y-\mu)}\frac{|y-\mu|}{\sigma}\bigg)^\beta+\frac{1}{\beta}\bigg]u^\beta$, and we obtain

Hence, we can derive the pdf of AGT distribution.

As a result, by using $f_{U|Y}(u\mid y) = \frac{f_{AGN}(y; \mu, u^{-1/\beta}\sigma, \kappa, \beta)f(u)}{f_{AGT}(y)}$ and after some algebric manipulation, we can obtain Proposition 2.3.

$\bullet$ Proof of Proposition 2.4

For AGSL distribution, we have

let $z = \bigg[\frac{1}{2}\bigg(\kappa^{\mbox{sign}(y-\mu)}\frac{|y-\mu|}{\sigma}\bigg)^\beta\bigg]$, and after some calculation we will derive the pdf of AGSL distribution.

By using $f_{U|Y}(u\mid y) = \frac{f_{AGN}(y; \mu, u^{-1/\beta}\sigma, \kappa, \beta)f(u)}{f_{AGSL}(y)}$ and after some algebric manipulation, we can obtain Proposition 2.4.

$\bullet$ Proof of Proposition 2.5

If $\gamma_i = 1$, then CAGN becomes AGN.

If $0 < \gamma_i < 1$, then the pdf of $U_j$ can be written as

and the conditional pdf of $U_j|Y = y_j$ can be written as

Part 2: Proofs required for Section 3

$\bullet$ Proof of Proposition 3.1

Here, we assume that $X_1, X_2, \cdots, X_n$ are identically distributed $AGN(0, 1, \kappa, \beta)$ samples of size $n$ and $X_{1:n}, X_{2:n}, \cdots, X_{n:n}$ are corresponding order statistics. In the case of $X < 0$, the cdf of $X$ can be evaluated using the power series expansion

Let $b_j = \frac{(-1)^j}{j!(\frac{1}{\beta}+j)}$, for $j = 0, 1, \cdots,$ we have that $b_0 = \beta\neq0$. Consider an integer $s$ order expansion of a power series

where

After that, we can obtain

such that

Let $u = \frac{1}{2}(-\frac{x}{\kappa})^\beta$ and we can easily get

Similarly,

Consequently,

$\bullet$ Proof of Proposition 3.2

If $X\sim AGN(0, 1, \kappa, \beta)$ when $X\leq0$,

Since

we obtain

Denote $H_1(m, n-1, \kappa) = \int_{-\infty}^{0}{x^m[F(x)]^{n-1}f(x)}{\mathrm{d}}x$,

and let $u = \frac{1}{2}(-\frac{x}{\kappa})^{\beta}$, then, $x = -\kappa(2u)^{\frac{1}{\beta}}$, $\frac{{\mathrm{d}}x}{{\mathrm{d}}u} = -\frac{\kappa}{\beta}2^{\frac{1}{\beta}}u^{\frac{1}{\beta}-1}$

Using some algebraic operations, we can obtain

Denote $H_2(m, n-1, \kappa) = \int_{0}^{\infty}{x^m[F(x)]^{n-1}f(x)}{\mathrm{d}}x$.

In the same way, we can obtain

$\bullet$ Proof of Proposition 3.3

If $\frac{1}{\beta}$ is an integer, when $x < 0$ we have

and by binomial expansion we obtain

where $C_i = (-1)^i\binom{1/\beta-1}{i}\frac{1}{\alpha+i}.$

Let $T_v(1/\beta, n-1)$ be the coefficient of $[1+\frac{\beta}{2}(-\frac{x}{\kappa})^\beta]^{-v}$ in the expansion of ${\left\{ {\sum\limits_{i = 0}^{(1/\beta - 1)} {{C_i}} \frac{1}{{{{\left[ {1 + \frac{\beta }{2}{{\left({\frac{{ - x}}{\kappa }} \right)}^\beta }} \right]}^i}}}} \right\}^{n - 1}}$. Clearly, we have ${T_v}(1/\beta, 0) = 1$.

For $v = 0, 1, \cdots, (1/\beta)$,

and for $n > 2$, $v = 0, 1, \cdots, (1/\beta)(n-1)$,

We can calculate every coefficient directly, so ${[F(x)]^{n - 1}}$ can be expressed as

then, we have

and the above expression exists for $\alpha\beta > \frac{m}{n}$. It is not hard to verify the following statement

Consequently,

$\bullet$ Proof of Proposition 3.4

Denote $J(m, n-1, \kappa) = \int_{-\infty}^{0}{x^m[F(x)]^{n-1}f(x)}{\mathrm{d}}x$. When $x < 0$, $\frac{1}{\beta}$ is not an integer and we have

where

Let $C = \frac{2\kappa^{2n-1}}{(2/\beta)^{1+\frac{1}{\beta}}(1+\kappa^2)^n[{\mathrm{B}}(\alpha, 1/\beta)]^n}$, such that, $J(m, n-1, \kappa)$ can be represented as

Let $\frac{\frac{\beta}{2}(-\frac{x}{\kappa})^\beta}{1+\frac{\beta}{2}(-\frac{x}{\kappa})^\beta} = u$, then, the above integral can be converted to

Substituting the above equation into $J(m, n-1, \kappa)$, and using some algebraic operations, we can obtain

It is worth noting that, when $\alpha\beta > \frac{m}{n}$, $B\left(\frac{m+1}{\beta}, \alpha n+\sum_{i = 1}^{n-1}m_i-\frac{m}{\beta} \right) < \Gamma(\frac{m+1}{\beta})$, On the other hand, for a sufficiently large $N$, we can bound that

This means that for a maximum order statistic from $AGT(0, 1, \kappa, \alpha, \beta)$, it's m-th moments always exists.

$\bullet$ Proof of Proposition 3.5

Suppose that $Y\sim ACGN(0, 1, \kappa, \lambda, \alpha, \beta)$, $X\sim AGN(0, 1, \kappa, \alpha, \beta)$, $U$ is a discrete random variable with pdf defined in (2.5), then we have

In view of the independence between $U$ and $X$,

Part 3: Proofs in section five and details to obtain the information matrix

Proof of Theorem 5.1

It is easy to prove that the distributions of the GSMAGN family satisfy item one and two of Lemma 5.1. As a result, our main task is to verify the GSMAGN family satisfies item three under different circumstances.

Let $v = \frac{1}{2}\bigg(\kappa^{ \mathrm{sign}(y-\mu)}\frac{|y-\mu|}{\sigma}\bigg)^{\beta}$. According to Proposition 2.1, we can obtain that $v\stackrel{d}{ = }{U^{-1}Z}$, which illustrates that $\mathrm{E}(v^k) = \mathrm{E}(U^{-k}Z^k)$. Taking the first partial derivation with respect to $\mu, \sigma, \beta, \kappa$,

$\bullet$ For AGN

Take sufficiently small $\epsilon > 0$, $U_{\theta_0} = \{\theta:\parallel\theta_0-\theta\parallel < \epsilon\}\subset\tilde{\Theta}, \forall \theta \in U_{\theta_0}$, then

Let $G(y) = \mathrm{max}\{G_1, G_2, G_3\}+g_1(v)+g_2(v)+g_3(v)+g_4(v)$, for AGN, where $U = 1$, and we can get $\mathrm{E}(v^k) = \mathrm{E}(Z^k), Z\sim Gamma(1/\beta, 1)$, for $\beta > 0$. $\mathrm{E}(v^k) < \infty, k > -\frac{1}{\beta}$, then we have $\mathrm{E}[G(y)] < \infty$.

$\bullet$ For AGT

Take sufficiently small $\epsilon > 0$, $U_{\theta_0} = \{\theta:\parallel\theta_0-\theta\parallel < \epsilon\}\subset\tilde{\Theta}, \forall \theta \in U_{\theta_0}$,

Let $G(y) = \mathrm{max}\{G_1, G_2, G_3, G_4\}+g_1(v)+g_2(v)+g_3(v)$, for AGT, $\mathrm{E}(v^k) = \mathrm{E}(U^{-k}) \mathrm{E}(Z^k)$, where $U\sim Gamma(\alpha, \beta), Z\sim Gamma(1/\beta, 1)$. Invoking Propostion 2, if $\alpha > 1$, $\mathrm{E}(v) < \infty$, and if $\alpha+\frac{1}{\beta} > 1$, $\mathrm{E}(v^{1-\frac{1}{\beta}}) < \infty$, such that, when $\alpha > 1$, we have $\mathrm{E}[G(y)] < \infty$. $\bullet$ For AGSL

where $\gamma(\alpha+\frac{1}{\beta}; v) = \frac{1}{\varGamma(\alpha+1/\beta)}\int_{0}^{v}t^{\alpha+\frac{1}{\beta}-1}e^{-t} \mathrm{d}t$. By taking sufficiently small $\epsilon > 0$, $U_{\theta_0} = \{\theta:\parallel\theta_0-\theta\parallel < \epsilon\}\subset\tilde{\Theta}, \forall \theta \in U_{\theta_0}$, then

Let $G(y) = \mathrm{max}\{G_1, G_2, G_3, G_4\}+g_1(v)+g_2(v)+g_3(v)$. For AGSL, $\mathrm{E}(v^k) = \mathrm{E}(U^{-k}) \mathrm{E}(Z^k)$, where $U\sim Beta(\alpha, 1), Z\sim Gamma(1/\beta, 1)$. Invoking Propostion 2, we can obtain that if $\alpha > 1$, then $\mathrm{E}(v) < \infty$. For $\alpha+\frac{1}{\beta} > 1$, $\mathrm{E}(v^{1-\frac{1}{\beta}}) < \infty$, such that $\alpha > 1$, $\mathrm{E}[G(y)] < \infty$.

$\bullet$ For CAGN

As for CAGN, it can be written as a linear combination of two AGN distributions. According to the above proof, it can be obtained that the MLE of AGN distribution exists and satisfies the strong consistency. Therefore, it can be easily concluded that CAGN satisfies the same property.

Details to obtain information matrix:

$\bullet$ For AGT

and,

$\bullet$ For AGSL

and,

$\bullet$ For CAGN

and,

The information-based approximation (11) is asymptotically applicable. The standard errors of $\hat{\Theta}$ can be obtained through the inverse of the empirical information matrix $\mathbf{I_0(\Theta|y)}$, with a sufficiently large sample size. The accuracy of the estimation can be guaranteed and the complexity of calculation can be reduced.