Derivatives and indefinite integrals of single valued neutrosophic functions

1.   Introduction

Considering the growing ambiguity issues in real life, Zadeh ^[22] first proposed the concept of fuzzy sets in $1965$, which is widely used in various fields because of its strong practicality. The emergence of fuzzy sets is an attempt to alert individuals to the fact that not everything in the world always exhibit black-and-white characteristics. While fuzzy sets are useful for resolving a wide range of practical issues, some uncertainty issues are ignored by the fuzzy information used in one-dimensional membership descriptions. On the other hand, people frequently lack a thorough knowledge of ambiguous concepts due to the limited level of actual research, which means that it is necessary to broaden the scope of conventional fuzzy sets. In order to address this drawback, Atanassov ^[1] created the intuitionistic fuzzy set (IFS) as binary array made up of the membership function $\mu_{A}(x)$ and the non-membership function $\nu_{A}(x)$, where the hesitation $\pi_{A}(x)$ is calculated by the equation $\pi_{A}(x) = 1-\mu_{A}(x)-\nu_{A}(x)$. By making hesitant information independent, Smarandache ^[11] expanded IFS to neutrosophic sets (NS) and named it the indeterminacy membership function. Additionally, a single-valued neutrosophic set (SVNS), a subclass of NS, was proposed by Wang et al. ^[15]. The subtraction and division operators in the fundamental operational laws of neutrosophic numbers were defined by Smarandache ^[13], who also provided certain limitations for these operations. When considering some practical problems, SVNS is closer to the human mind and can better handle ambiguous information, and researchers have examined it extensively in a great deal of work ^{[4,6,10,12,14,16,17,19]}.

It was discovered recently that the majority of the earlier research merely examined how to deal with it by developing certain operations when thinking of the fuzzy set as a discrete constant. It did not cover how the result of the operation will change when the assigned data of the operations change continuously. Thus, the derivatives and differential operations of intuitionistic fuzzy numbers and interval value intuitionistic fuzzy numbers, respectively, were examined by Lei et al. ^[7] and Zhao et al. ^[23]. Yu et al. ^[20] proposed indefinite integrals of generalized intuitionistic multiplicative functions in 2015. Lei et al. ^[8] introduced the essential characteristics of intuitionistic fuzzy calculus in the same year. Derivatives and differentials for multiplicative intuitionistic fuzzy information were discovered in 2017 by Yu et al. ^[21]. Lei et al. ^[9] recently completed work on intuitionistic fuzzy integrals based on Archimedean t-conorms and more work can be seen in references ^[2,3,5,18].

However, to date, there has been no research on the derivatives and integrals of SVNS, which is of great significance for the further development of the calculus theory of SVNS. In fact, we can consider their inverse operations (subtraction and division) based on the addition and multiplication operations between SVNN. After that, we examine their difference quotients in more detail using the real calculus theory. By performing limit calculations on the difference quotient, the derivatives and differentials of SVNF are defined. Furthermore, we investigate some basic features and offer two types of indefinite integrals through solving three ordinary differential equations.

The remainder of this paper is organized as follows. Section 2 reviews the definition and basic operations of SVNS. The change values related to SVNN are proposed in Section 3. The convergence of sequences related to SVNN is introduced in Section 4. Section 5 provides the continuity of SVNF. The derivatives and differentials of SVNF and indefinite integrals of SVNF are discussed in Section 6 and Section 7. In Section 8, the main work of this article is summarized.

2.   Preliminaries

As an extension of the fuzzy set, NS can accurately express more complex fuzzy information. In this section, we review the related definition of NS and their properties.

Definition 2.1. ^[15] Let $X$ be a space of points (objects). A single-valued neutrosophic set (SVNS) $A$ in $X$ is characterized by a truth-membership function $\mu_{A}(x)$, an indeterminacy-membership function $\eta_{A}(x)$ and a falsity-membership function $\nu_{A}(x)$. Then, $A$ can be expressed as

where $\mu_{A}(x)$, $\eta_{A}(x)$, $\nu_{A}(x)\in [0, 1]$, satisfy $0\leq \mu_{A}(x)+\eta_{A}(x)+\nu_{A}(x)\leq3$.

Definition 2.2. ^[15] Let $A = \{ < x, \mu_{A}(x), \eta_{A}(x), \nu_{A}(x) > |x\in X\}$, $B = \{ < x, \mu_{B}(x), \eta_{B}(x), \nu_{B}(x) > |x\in X\}$ be any two single-valued neutrosophic sets, and the relation between them is defined as follows.

(1) $A\subseteq B$ iff $\mu_{A}(x)\leq \mu_{B}(x), \eta_{A}(x)\geq \eta_{B}(x), \nu_{A}(x)\geq \nu_{B}(x)$;

(2) $A = B$ iff $\mu_{A}(x) = \mu_{B}(x), \eta_{A}(x) = \eta_{B}(x), \nu_{A}(x) = \nu_{B}(x)$;

(3) $A^{c} = \{ < x, \nu_{A}(x), 1-\eta_{A}(x), \mu_{A}(x) > |x\in X\}$.

For convenience, a single-valued neutrosophic number (SVNN) can be denoted by $\alpha = (\mu_{\alpha}, \eta_{\alpha}, \nu_{\alpha})$.

Definition 2.3. ^[13] Let $\alpha = (\mu_{\alpha}, \eta_{\alpha}, \nu_{\alpha}), \beta = (\mu_{\beta}, \eta_{\beta}, \nu_{\beta})$ be any two single-valued neutrosophic numbers (SVNNs), and the fundamental operations are defined as follows.

(1) $\alpha\cup\beta = (\max\{\mu_{\alpha}, \mu_{\beta}\}, \min\{\eta_{\alpha}, \eta_{\beta}\}, \min\{\nu_{\alpha}, \nu_{\beta}\})$;

(2) $\alpha\cap\beta = (\min\{\mu_{\alpha}, \mu_{\beta}\}, \max\{\eta_{\alpha}, \eta_{\beta}\}, \max\{\nu_{\alpha}, \nu_{\beta}\})$;

(3) $\alpha\oplus\beta = (\mu_{\alpha}+\mu_{\beta}-\mu_{\alpha}\mu_{\beta}, \eta_{\alpha}\eta_{\beta}, \nu_{\alpha}\nu_{\beta})$;

(4) $\alpha\otimes\beta = (\mu_{\alpha}\mu_{\beta}, \eta_{\alpha}+\eta_{\beta}-\eta_{\alpha}\eta_{\beta}, \nu_{\alpha}+\nu_{\beta}-\nu_{\alpha}\nu_{\beta})$;

(5) $\lambda\alpha = (1-(1-\mu_{\alpha})^{\lambda}, \eta_{\alpha}^{\lambda}, \nu_{\alpha}^{\lambda}), \lambda > 0$;

(6) $\alpha^{\lambda} = (\mu_{\alpha}^{\lambda}, 1-(1-\eta_{\alpha})^{\lambda}, 1-(1-\nu_{\alpha})^{\lambda}), \lambda > 0$.

Numerous approaches have been put out to solve the challenge in order to obtain the techniques for ranking and comparing SVNNs. We simply only discuss two common ranking techniques because the comparison of SVNNs is not the main topic of this paper.

Definition 2.4. ^[6] Let $\alpha = (\mu_{\alpha}, \eta_{\alpha}, \nu_{\alpha}), \beta = (\mu_{\beta}, \eta_{\beta}, \nu_{\beta})$ be any two SVNNs, we denote the partial order as $\alpha\leq\beta$ if and only if $\mu_{\alpha}\leq\mu_{\beta}, \eta_{\alpha}\geq\eta_{\beta}$ and $\nu_{\alpha}\geq\nu_{\beta}$.

Definition 2.5. ^[12] Let $\alpha = (\mu_{\alpha}, \eta_{\alpha}, \nu_{\alpha})$ be a SVNN, then the score functions of $\alpha$ is defined as

the accuracy functions of $\alpha$ is defined as

the certainty functions of $\alpha$ is defined as

Based on the three functions, Smarandache ^[12] demonstrated that a total order on the set of neutrosophic triplets is determined by the score, accuracy, and certainty functions. In the applications of neutrosophic decision-making, this total order is required.

Definition 2.6. ^[12] Let $\alpha = (\mu_{\alpha}, \eta_{\alpha}, \nu_{\alpha}), \beta = (\mu_{\beta}, \eta_{\beta}, \nu_{\beta})$ be any two single-valued neutrosophic numbers, then the score, accuracy, and certainty functions altogether form a total order relationship,

(1) if $s(\alpha) < s(\beta)$, then $\alpha < \beta$,

(2) if $s(\alpha) > s(\beta)$, then $\alpha > \beta$,

(3) if $s(\alpha) = s(\beta)$, then

  (i) if $a(\alpha) < a(\beta)$, then $\alpha < \beta$,

  (ii) if $a(\alpha) > a(\beta)$, then $\alpha > \beta$,

  (iii) if $a(\alpha) = a(\beta)$, then

    (i) if $c(\alpha) < c(\beta)$, then $\alpha < \beta$,

    (ii) if $c(\alpha) > c(\beta)$, then $\alpha > \beta$,

    (iii) if $c(\alpha) = c(\beta)$, then $\alpha = \beta$.

Definition 2.7. ^[6] Let $\alpha_{i} = (\mu_{\alpha_{i}}, \eta_{\alpha_{i}}, \nu_{\alpha_{i}}) (i = 1, 2, \cdots, n)$ be a collection of single-valued neutrosophic sets, $\omega = (\omega_{1}, \omega_{2}, \cdots, \omega_{n})^{T}$ is the weight vector of $\alpha_{i}(i = 1, 2, \cdots, n)$, and $\omega_{i}\in [0, 1]$, $\sum_{i = 1}^{n}\omega_{i} = 1$. Then,

is called the single-valued neutrosophic weighted average operator (SVNWA), and the aggregated value using SVNWA operator is also a SVNN.

Definition 2.8. ^[6] Let $\alpha_{i} = (\mu_{\alpha_{i}}, \eta_{\alpha_{i}}, \nu_{\alpha_{i}}) (i = 1, 2, \cdots, n)$ be a collection of single-valued neutrosophic sets, $\omega = (\omega_{1}, \omega_{2}, \cdots, \omega_{n})^{T}$ is the weight vector of $\alpha_{i}(i = 1, 2, \cdots, n)$, and $\omega_{i}\in [0, 1]$, $\sum_{i = 1}^{n}\omega_{i} = 1$. Then,

is called the single-valued neutrosophic weighted geometric operator (SVNWG), and the aggregated value using SVNWG operator is also a SVNN.

Further, we present two basic operational laws on SVNS, which are the subtraction operation and division operation, respectively. They are significantly important in the discussion that follows.

Definition 2.9. Let $A = \{ < x, \mu_{A}(x), \eta_{A}(x), \nu_{A}(x) > |x\in X\}, B = \{ < x, \mu_{B}(x), \eta_{B}(x), \nu_{B}(x) > |x\in X\}$ be any two single-valued neutrosophic sets, the subtraction and division operations have the following forms.

$A\ominus B = \{ < x, \mu_{A\ominus B}(x), \eta_{A\ominus B}(x), \nu_{A\ominus B}(x) > |x\in X\}$, where

$A\oslash B = \{ < x, \mu_{A\oslash B}(x), \eta_{A\oslash B}(x), \nu_{A\oslash B}(x) > |x\in X\}$, where

Although the subtraction and division operations of single-valued neutrosophic numbers are also described in reference ^[13], it is in fact compatible with this definition.

By Definition 2.9, we know operation $"\ominus"$ is the inverse operation of $"\oplus "$, and operation $"\oslash"$ is the inverse operation of $"\otimes"$. Take $"\ominus "$ for example, Let $\alpha = (\mu_{\alpha}, \eta_{\alpha}, \nu_{\alpha})$ and $\beta = (\mu_{\beta}, \eta_{\beta}, \nu_{\beta})$ be two SVNNs, If they meet the conditions $\mu_{\alpha}\geq \mu_{\beta}, \eta_{\alpha}\leq \eta_{\beta}, \nu_{\alpha}\leq \nu_{\beta}, \eta_{\beta} > 0, \nu_{\beta} > 0$, then $\alpha\ominus\beta$ is still a SVNN. Inversely, $\alpha\ominus\beta$ is not a SVNN if $\alpha$ and $\beta$ don't meet such conditions. In addition, we take account of the closure of the operation by defining $\alpha\ominus\beta = (0, 1, 1)$. However, (0, 1, 1) is almost meaningless.

3.   The change values related to SVNN

For any two real numbers, they can be connected using the four basic operations ($+$, $-$, $\times, \div$), for example, 4 = 8$\div$2, 5 = 2+3. Therefore, it is natural to wonder whether this conclusion holds true in SVNN. In this section, we will discuss this issue. Before that, a basic concept is given.

Definition 3.1. Let $\alpha, \alpha_{0}$ be any two SVNNs, if $\alpha = \alpha_{0}\ast\beta, \beta\in$ SVNNs, where $\ast\in\{\oplus, \ominus, \otimes, \oslash\}$. Then, we call $\alpha$ the change values related to $\alpha_{0} = (\mu_{\alpha_{0}}, \eta_{\alpha_{0}}, \nu_{\alpha_{0}})$.

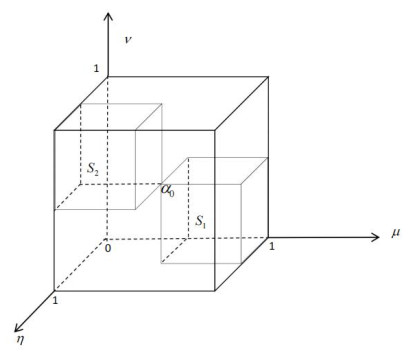
In the three-dimensional coordinate system of Figure 1, we denote $\mathcal{M}$ as a cube area consisted of all SVNNs. Here we divide the entire domain

into several parts, which are related to $\alpha_{0}$ according to basic operational laws.

From Figure 1, $\forall\alpha_{0} = (\mu_{\alpha_{0}}, \eta_{\alpha_{0}}, \nu_{\alpha_{0}})$, if $\alpha = (\mu_{\alpha}, \eta_{\alpha}, \nu_{\alpha})\in S_{1}$, then $\mu_{\alpha}\geq\mu_{\alpha_{0}}, \eta_{\alpha}\leq \eta_{\alpha_{0}}, \nu_{\alpha}\leq \nu_{\alpha_{0}}$. By the definition of the subtraction law, we can get $\alpha\ominus\alpha_{0} = (\frac{\mu_{\alpha}-\mu_{\alpha_{0}}}{1-\mu_{\alpha_{0}}}, \frac{\eta_{\alpha}}{\eta_{\alpha_{0}}}, \frac{\nu_{\alpha}}{\nu_{\alpha_{0}}})\in \mathcal{M}$. That is, for any $\beta\in \mathcal{M}$, we can get $\alpha = \alpha_{0}\oplus\beta\in S_{1}$.

Similarly, if $\alpha = (\mu_{\alpha}, \eta_{\alpha}, \nu_{\alpha})\in S_{2}$, then $\mu_{\alpha}\leq \mu_{\alpha_{0}}, \eta_{\alpha}\geq \eta_{\alpha_{0}}, \nu_{\alpha}\geq \nu_{\alpha_{0}}$. By the definition of the subtraction law, we can get $\alpha_{0}\ominus\alpha = (\frac{\mu_{\alpha_{0}}-\mu_{\alpha}}{1-\mu_{\alpha}}, \frac{\eta_{\alpha_{0}}}{\eta_{\alpha}}, \frac{\nu_{\alpha_{0}}}{\nu_{\alpha}})\in \mathcal{M}$. That is, for any $\beta\in \mathcal{M}$, we can get $\alpha = \alpha_{0}\ominus\beta\in S_{2}$.

If $\alpha = (\mu_{\alpha}, \eta_{\alpha}, \nu_{\alpha})\in S_{2}$, then $\mu_{\alpha}\leq \mu_{\alpha_{0}}, \eta_{\alpha}\geq \eta_{\alpha_{0}}, \nu_{\alpha}\geq \nu_{\alpha_{0}}$. By the definition of the division law, we can get $\alpha\oslash\alpha_{0} = (\frac{\mu_{\alpha}}{\mu_{\alpha_{0}}}, \frac{\eta_{\alpha}-\eta_{\alpha_{0}}}{1-\eta_{\alpha_{0}}}, \frac{\nu_{\alpha}-\nu_{\alpha_{0}}}{1-\nu_{\alpha_{0}}})\in \mathcal{M}$. That is, for any $\beta\in \mathcal{M}$, we can get $\alpha = \alpha_{0}\otimes\beta\in S_{2}$.

If $\alpha = (\mu_{\alpha}, \eta_{\alpha}, \nu_{\alpha})\in S_{1}$, then $\mu_{\alpha}\geq \mu_{\alpha_{0}}, \eta\leq \eta_{\alpha_{0}}, \nu\leq \nu_{\alpha_{0}}$. By the definition of the division law, we can get $\alpha_{0}\oslash\alpha = (\frac{\mu_{\alpha_{0}}}{\mu_{\alpha}}, \frac{\eta_{\alpha_{0}}-\eta_{\alpha}}{1-\eta_{\alpha}}, \frac{\nu_{\alpha_{0}}-\nu_{\alpha}}{1-\nu_{\alpha}})\in \mathcal{M}$. That is, for any $\beta\in \mathcal{M}$, we can get $\alpha = \alpha_{0}\oslash\beta\in S_{1}$.

For the sake of unity, we use $A_{\alpha_{0}}^{*}$, $*\in (\oplus, \ominus, \otimes, \oslash)$, represent the region of change with respect to $\alpha_{0}$ and give the following definition.

Definition 3.2. Let $A_{\alpha_{0}}^{\oplus} = S_{1}, A_{\alpha_{0}}^{\oslash} = S_{1}, A_{\alpha_{0}}^{\ominus} = S_{2}, A_{\alpha_{0}}^{\otimes} = S_{2}$, then we call $A_{\alpha_{0}}^{\oplus}$ the addition region related to $\alpha_{0}$, $A_{\alpha_{0}}^{\ominus}$ the subtraction region related to $\alpha_{0}$, $A_{\alpha_{0}}^{\otimes}$ the multiplication region related to $\alpha_{0}$, $A_{\alpha_{0}}^{\oslash}$ the division region related to $\alpha_{0}$.

To sum up, we know the corresponding parts can be depicted as

Remark 3.1. For Definition 3.2, we can also interpret it this way. Let $\alpha_{1}, \alpha_{2}, \alpha_{3}, \alpha_{4}$ be four SVNNs. When $\alpha_{1}\in A_{\alpha_{0}}^{\oplus}$, we call $\alpha_{1}$ an addition change value related to $\alpha_{0}$. In other words, if $\alpha_{1}\in A_{\alpha_{0}}^{\oplus}$, then there exist a $\beta_{1}\in$ SVNN, such that $\alpha_{1} = \alpha_{0}\oplus\beta_{1}$. Similarly, when $\alpha_{2}\in A_{\alpha_{0}}^{\ominus}$, we call $\alpha_{2}$ a subtraction change value related to $\alpha_{0}$. That is, if $\alpha_{2}\in A_{\alpha_{0}}^{\ominus}$, then there exist a $\beta_{2}\in$ SVNN, such that $\alpha_{2} = \alpha_{0}\ominus\beta_{2}$. When $\alpha_{3}\in A_{\alpha_{0}}^{\otimes}$, we call $\alpha_{3}$ a multiplication change value related to $\alpha_{0}$. That is, if $\alpha_{3}\in A_{\alpha_{0}}^{\otimes}$, then there exist a $\beta_{3}\in$ SVNN, such that $\alpha_{3} = \alpha_{0}\otimes\beta_{3}$. When $\alpha_{4}\in A_{\alpha_{0}}^{\oslash}$, we call $\alpha_{4}$ a division change value related to $\alpha_{0}$. That is, if $\alpha_{4}\in A_{\alpha_{0}}^{\oslash}$, then there exist a $\beta_{4}\in$ SVNN, such that $\alpha_{4} = \alpha_{0}\oslash\beta_{4}$.

4.   The convergence of sequences of SVNN

The definition of a sequence in the field of real numbers is an analogy. We call $\{\alpha_{n}|n\in N^{+}\}$ a sequence of SVNNs if it satisfies $\alpha_{n} = (\mu_{\alpha_{n}}, \eta_{\alpha_{n}}, \nu_{\alpha_{n}})\in$ SVNNs, $n\in N^{+}$.

In order to study and express the single-valued neutrosophic calculus conveniently, here we define a new order of SVNNs.

Definition 4.1. Let $\alpha_{1}$ and $\alpha_{2}$ be any two SVNNs, if there is a SVNN $\beta$, which satisfies $\alpha_{1}\oplus\beta = \alpha_{2}$. Then, we define that $\alpha_{1}$ is less than or equal to $\alpha_{2}$, denoted by $\alpha_{1}\unlhd_{\oplus}\alpha_{2}$ or $\alpha_{1}\unlhd\alpha_{2}$. In particular, $\alpha_{1}\lhd_{\oplus}\alpha_{2}$, if $\beta\neq(0, 1, 1)$.

Definition 4.2. Let $\alpha_{1}$ and $\alpha_{2}$ be any two SVNNs, if there is a SVNN $\beta$, which satisfies $\alpha_{1}\otimes\beta = \alpha_{2}$. Then, we define that $\alpha_{2}$ is less than or equal to $\alpha_{1}$, denoted by $\alpha_{2}\unlhd_{\otimes}\alpha_{1}$ or $\alpha_{2}\unlhd\alpha_{1}$. In particular, $\alpha_{2}\lhd_{\otimes}\alpha_{1}$, if $\beta\neq(1, 0, 0)$.

Based on the partial order, we discuss the sequence of $\alpha_{0}$ from different directions as follows.

Definition 4.3. Let $\{\alpha_{n}|n\in N^{+}\}$ be a sequence of SVNNs, then we call $\{\alpha_{n}\}$ an addition sequence of $\alpha_{0}$, if $\exists N\in N^{+}$, for any $n > N, \alpha_{n}\in A_{\alpha_{0}}^{\oplus}$. Simiarly, if $\exists N\in N^{+}$, for any $n > N, \alpha_{n}\in A_{\alpha_{0}}^{\ominus}$, then we call $\{\alpha_{n}\}$ a subtraction sequence of $\alpha_{0}$. If $\exists N\in N^{+}$, for any $n > N, \alpha_{n}\in A_{\alpha_{0}}^{\otimes}$, then we call $\{\alpha_{n}\}$ a multiplication sequence of $\alpha_{0}$. If $\exists N\in N^{+}$, for any $n > N, \alpha_{n}\in A_{\alpha_{0}}^{\oslash}$, then we call $\{\alpha_{n}\}$ a division sequence of $\alpha_{0}$.

By Definition 4.3, we know that the unlimited elements of different directional sequences are all contained in the corresponding regions. That is, the unlimited elements of a subtraction sequence of $\alpha_{0}$, which are concluded in $A_{\alpha_{0}}^{\ominus}$, and the unlimited elements of a division sequence of $\alpha_{0}$, which are all concluded in $A_{\alpha_{0}}^{\oslash}$.

In the study of the theory of real numbers, the absolute value of their difference between any two numbers $x$ and $y$ is used to describe how approximate they are. Be inspired by this, we will to describe the approaching process of two SVNNs by using these basic operations.

Definition 4.4. Let $\{\alpha_{n}|n\in N^{+}\}$ be an addition sequence of $\alpha_{0}$, then $\lim\limits_{n\rightarrow +\infty}\alpha_{n} = \alpha_{0}^{\oplus}$, if for any $\bar{\varepsilon} = (\mu_{\bar{\varepsilon}}, \eta_{\bar{\varepsilon}}, \nu_{\bar{\varepsilon}}) > (0, 1, 1)$, $\exists N\in N^{+}$, such when $n > N$, we have $\alpha_{n}\ominus\alpha_{0} < \bar{\varepsilon}$. For simplicity, we call $\alpha_{0}$ the addition limit of $\{\alpha_{n}\}$ as $n\rightarrow +\infty$, it can also be denoted by $\alpha_{n}\rightarrow \alpha_{0}^{\oplus}$.

Likewise, we can draw similar conclusions when $\{\alpha_{n}\}$ is a subtraction sequence, a division sequence, or a multiplication sequence of $\alpha_{0}$.

Let $\{\alpha_{n}|n\in N^{+}\}$ be a subtraction sequence of $\alpha_{0}$, then $\lim\limits_{n\rightarrow +\infty}\alpha_{n} = \alpha_{0}^{\ominus}$, if for any $\bar{\varepsilon} = (\mu_{\bar{\varepsilon}}, \eta_{\bar{\varepsilon}}, \nu_{\bar{\varepsilon}}) > (0, 1, 1)$, $\exists N\in N^{+}$, such when $n > N$, we have $\alpha_{0}\ominus\alpha_{n} < \bar{\varepsilon}$. For simplicity, we call $\alpha_{0}$ the subtraction limit of $\{\alpha_{n}\}$ as $n\rightarrow +\infty$, it can also be denoted by $\alpha_{n}\rightarrow \alpha_{0}^{\ominus}$.

Let $\{\alpha_{n}|n\in N^{+}\}$ be a multiplication sequence of $\alpha_{0}$, then $\lim\limits_{n\rightarrow +\infty}\alpha_{n} = \alpha_{0}^{\otimes}$, if for any $\bar{\varepsilon} = (\mu_{\bar{\varepsilon}}, \eta_{\bar{\varepsilon}}, \nu_{\bar{\varepsilon}}) < (1, 0, 0)$, $\exists N\in N^{+}$, such when $n > N$, we have $\alpha_{n}\oslash\alpha_{0} > \bar{\varepsilon}$. For simplicity, we call $\alpha_{0}$ the multiplication limit of $\{\alpha_{n}\}$ as $n\rightarrow +\infty$, it can also be denoted by $\alpha_{n}\rightarrow \alpha_{0}^{\otimes}$.

Let $\{\alpha_{n}|n\in N^{+}\}$ be a division sequence of $\alpha_{0}$, then $\lim\limits_{n\rightarrow +\infty}\alpha_{n} = \alpha_{0}^{\oslash}$, if for any $\bar{\varepsilon} = (\mu_{\bar{\varepsilon}}, \eta_{\bar{\varepsilon}}, \nu_{\bar{\varepsilon}}) < (1, 0, 0)$, $\exists N\in N^{+}$, such when $n > N$, we have $\alpha_{0}\oslash\alpha_{n} > \bar{\varepsilon}$. For simplicity, we call $\alpha_{0}$ the division limit of $\{\alpha_{n}\}$ as $n\rightarrow +\infty$, it can also be denoted by $\alpha_{n}\rightarrow \alpha_{0}^{\oslash}$.

Definition 4.5. Let $\{\alpha_{n}|n\in N^{+}\}$ be a subtraction sequence of $\alpha_{0}$, $\alpha_{n} = (\mu_{\alpha_{n}}, \eta_{\alpha_{n}}, \nu_{\alpha_{n}})$, $\alpha_{0} = (\mu_{\alpha_{0}}, \eta_{\alpha_{0}}, \nu_{\alpha_{0}})$, then $\lim\limits_{n\rightarrow +\infty}\alpha_{n} = \alpha_{0}^{\ominus}\Leftrightarrow \lim\limits_{n\rightarrow +\infty}\mu_{\alpha_{n}} = \mu_{\alpha_{0}}$, $\lim\limits_{n\rightarrow +\infty}\eta_{\alpha_{n}} = \eta_{\alpha_{0}}$, $\lim\limits_{n\rightarrow +\infty}\nu_{\alpha_{n}} = \nu_{\alpha_{0}}$.

For the addition sequence, multiplication sequence and division sequence of $\alpha_{0}$, it can be similarly expressed, which will not be repeated here.

5.   The continuities of SVNF

For any $\alpha = (\mu, \eta, \nu)$ be a SVNN, $G(\alpha) = (f(\mu, \eta, \nu), g(\mu, \eta, \nu), h(\mu, \eta, \nu))$ is a function of $\alpha$. If the function meets $0\leq f(\mu, \eta, \nu)\leq1$, $0\leq g(\mu, \eta, \nu)\leq1$, $0\leq h(\mu, \eta, \nu)\leq1$, and $0\leq f(\mu, \eta, \nu)+ g(\mu, \eta, \nu)+h(\mu, \eta, \nu)\leq3$. Then we call the function $G(\alpha)$ a single-valued neutrosophic function (SVNF) of $\alpha$. Any given SVNF $G(\alpha) = (f(\mu, \eta, \nu), g(\mu, \eta, \nu), h(\mu, \eta, \nu))$ is denoted as $G = (f, g, h)$ for convenience. In this paper, $f, g$ and $h$ are continuous and derivable.

With the help of the problem of continuity of functions in the field of real numbers, we want to discuss the problem whether $G(\alpha)\ominus G(\alpha_{0})$ is still a SVNN when $\alpha\ominus \alpha_{0}$ is a SVNN.

Definition 5.1. Let $\alpha = (\mu, \eta, \nu)$ be a SVNN, $G(\alpha) = (f(\mu, \eta, \nu), g(\mu, \eta, \nu), h(\mu, \eta, \nu))$ be a SVNF of $\alpha$, then we define the following.

(1) The addition area of $G(\alpha)$ at $\alpha_{0}$

(2) The subtraction area of $G(\alpha)$ at $\alpha_{0}$

(3) The multiplication area of $G(\alpha)$ at $\alpha_{0}$

(4) The division area of $G(\alpha)$ at $\alpha_{0}$

In fact, take (3) as an example, $G(\alpha)$ be a SVNF of $\alpha$, by the definition of division operation, we know for $\forall\alpha\in S^{\otimes}(\alpha_{0}, G)$,

from which we can get that $G(\alpha)\oslash G(\alpha_{0})$ is still a SVNN when $\alpha\oslash\alpha_{0}$ is a SVNN.

Similarly, for any $\alpha\in S^{\oplus}(\alpha_{0}, G)$, $G(\alpha)\ominus G(\alpha_{0})$ is still a SVNN when $\alpha\ominus\alpha_{0}$ is a SVNN. For any $\alpha\in S^{\ominus}(\alpha_{0}, G)$, $G(\alpha_{0})\ominus G(\alpha)$ is still a SVNN when $\alpha_{0}\ominus\alpha$ is a SVNN. For any $\alpha\in S^{\oslash}(\alpha_{0}, G)$, $G(\alpha_{0})\oslash G(\alpha)$ is still a SVNN when $\alpha_{0}\oslash\alpha$ is a SVNN. Based on the above discussion, we can get $S^{*}(\alpha_{0}, G)\subseteq A_{\alpha_{0}}^{*}$, where $*\in \{\oplus, \ominus, \otimes, \oslash\}$.

Below, we illustrate the above conclusion with some simple examples.

Example 5.1. (1) Let $G(\alpha) = \alpha = (\mu, \eta, \nu)$, i.e. $f(\mu, \eta, \nu) = \mu, \; g(\mu, \eta, \nu) = \eta, \; h(\mu, \eta, \nu) = \nu$. If $\forall\alpha\in A_{\alpha_{0}}^{\oplus}$, then we can get $\mu\geq\mu_{0}, \eta\leq \eta_{0}, \nu\leq \nu_{0}$. So $\forall\alpha\in A_{\alpha_{0}}^{\oplus}$, we have $0\leq\frac{1-f(\mu, \eta, \nu)}{1-f(\mu_{0}, \eta_{0}, \nu_{0})}\leq1, \; 0\leq\frac{g(\mu, \eta, \nu)}{g(\mu_{0}, \eta_{0}, \nu_{0})}\leq1, \; 0\leq\frac{h(\mu, \eta, \nu)}{h(\mu_{0}, \eta_{0}, \nu_{0})}\leq1$, that is $A_{\alpha_{0}}^{\oplus}\subseteq S^{\oplus}(\alpha_{0}, G)$, then we can get $A_{\alpha_{0}}^{\oplus} = S^{\oplus}(\alpha_{0}, G)$. On the other hand, we can also get $A_{\alpha_{0}}^{\ominus} = S^{\ominus}(\alpha_{0}, G)$, $A_{\alpha_{0}}^{\otimes} = S^{\otimes}(\alpha_{0}, G)$, $A_{\alpha_{0}}^{\oslash} = S^{\oslash}(\alpha_{0}, G)$.

(2) Let $G(\alpha) = \alpha\oplus\beta = (\mu+\mu_{\beta}-\mu\mu_{\beta}, \eta\eta_{\beta}, \nu\nu_{\beta})$, i.e. $f(\mu, \eta, \nu) = \mu+\mu_{\beta}-\mu\mu_{\beta}, \; g(\mu, \eta, \nu) = \eta\eta_{\beta}, \; h(\mu, \eta, \nu) = \nu\nu_{\beta}$. If $\forall\alpha\in A_{\alpha_{0}}^{\ominus}$, then $\mu\leq\mu_{0}, \eta\geq \eta_{0}, \nu\geq \nu_{0}$, we have $0\leq\frac{1-(\mu_{0}+\mu_{\beta}-\mu_{0}\mu_{\beta})}{1-(\mu+\mu_{\beta}-\mu\mu_{\beta})}\leq1, \; 0\leq\frac{\eta_{0}\eta_{\beta}}{\eta\eta_{\beta}}\leq1, \; 0\leq\frac{\nu_{0}\nu_{\beta}}{\nu\nu_{\beta}}\leq1$. So $\forall\alpha\in A_{\alpha_{0}}^{\ominus}$, we can get $0\leq\frac{1-f(\mu_{0}, \eta_{0}, \nu_{0})}{1-f(\mu, \eta, \nu)}\leq1, \; 0\leq\frac{g(\mu_{0}, \eta_{0}, \nu_{0})}{g(\mu, \eta, \nu)}\leq1, \; 0\leq\frac{h(\mu_{0}, \eta_{0}, \nu_{0})}{h(\mu, \eta, \nu)}\leq1$, that is $A_{\alpha_{0}}^{\ominus}\subseteq S^{\ominus}(\alpha_{0}, G)$, then we can get $A_{\alpha_{0}}^{\ominus} = S^{\ominus}(\alpha_{0}, G)$. On the other hand, we can also get $A_{\alpha_{0}}^{\oplus} = S^{\oplus}(\alpha_{0}, G)$, $A_{\alpha_{0}}^{\otimes} = S^{\otimes}(\alpha_{0}, G)$, $A_{\alpha_{0}}^{\oslash} = S^{\oslash}(\alpha_{0}, G)$.

(3) For $G(\alpha) = \lambda\alpha = (1-(1-\mu)^{\lambda}, \eta^{\lambda}, \nu^{\lambda})$, i.e. $f(\mu, \eta, \nu) = 1-(1-\mu)^{\lambda}, \; g(\mu, \eta, \nu) = \eta^{\lambda}, \; h(\mu, \eta, \nu) = \nu^{\lambda}$. If $\forall\alpha\in A_{\alpha_{0}}^{\otimes}$, then $\mu\leq\mu_{0}, \eta\geq \eta_{0}, \nu\geq \nu_{0}$, we have $0\leq\frac{1-(1-\mu)^{\lambda}}{1-(1-\mu_{0})^{\lambda}}\leq1$, $0\leq\frac{1-\eta^{\lambda}}{1-\eta_{0}^{\lambda}}\leq1$, $0\leq\frac{1-\nu^{\lambda}}{1-\nu_{0}^{\lambda}}\leq1$. So $\forall\alpha\in A_{\alpha_{0}}^{\otimes}$, we have $0\leq\frac{f(\mu, \eta, \nu)}{f(\mu_{0}, \eta_{0}, \nu_{0})}\leq1, \; 0\leq\frac{1-g(\mu, \eta, \nu)}{1-g(\mu_{0}, \eta_{0}, \nu_{0})}\leq1, \; 0\leq\frac{1-h(\mu, \eta, \nu)}{1-h(\mu_{0}, \eta_{0}, \nu_{0})}\leq1$, that is $A_{\alpha_{0}}^{\otimes}\subseteq S^{\otimes}(\alpha_{0}, G)$, then we can get $A_{\alpha_{0}}^{\otimes} = S^{\otimes}(\alpha_{0}, G)$. On the other hand, we can also get $A_{\alpha_{0}}^{\oplus} = S^{\oplus}(\alpha_{0}, G)$, $A_{\alpha_{0}}^{\ominus} = S^{\ominus}(\alpha_{0}, G)$, $A_{\alpha_{0}}^{\oslash} = S^{\oslash}(\alpha_{0}, G)$.

In real analysis, after we have learned the limits of the sequence, the continuity of functions is another key topic for discussion, that is whether or not $f(x)-f(x_{0})\rightarrow0$ as $x \rightarrow x_{0}$. In the single-valued neutrosophic environment, if $\alpha\in A_{\alpha_{0}}^{\oplus}$, the problem whether $G(\alpha)\ominus G(\alpha_{0})\rightarrow (0, 1, 1)$ when $\alpha\ominus\alpha_{0}\rightarrow (0, 1, 1)$ is still important. Hence, we will give the definition of continuity of SVNF as follows.

Definition 5.2. Let $G(\alpha)$ be a SVNF of $\alpha_{0}$, then $G(\alpha)$ is continuous in the addition direction at $\alpha_{0}$, denoted by $\lim\limits_{\alpha\rightarrow \alpha_{0}^{\oplus}}G(\alpha) = G(\alpha_{0})$. If it satisfies for any $\bar{\varepsilon} = (\mu_{\bar{\varepsilon}}, \eta_{\bar{\varepsilon}}, \nu_{\bar{\varepsilon}}) > (0, 1, 1)$, $\exists\; \bar{\delta} = (\mu_{\bar{\delta}}, \eta_{\bar{\delta}}, \nu_{\bar{\delta}})$, such for any $\alpha\in S^{\oplus}(\alpha_{0}, G)$ and $(0, 1, 1) < \alpha\ominus\alpha_{0} < \bar{\delta}$ have $G(\alpha)\ominus G(\alpha_{0}) < \bar{\varepsilon}$.

Likewise, we can draw the following parallel conclusions.

Let $G(\alpha)$ be a SVNF of $\alpha_{0}$, then $G(\alpha)$ is continuous in the subtraction direction at $\alpha_{0}$, denoted by $\lim\limits_{\alpha\rightarrow \alpha_{0}^{\ominus}}G(\alpha) = G(\alpha_{0})$. If it satisfies for any $\bar{\varepsilon} = (\mu_{\bar{\varepsilon}}, \eta_{\bar{\varepsilon}}, \nu_{\bar{\varepsilon}}) > (0, 1, 1)$, $\exists\; \bar{\delta} = (\mu_{\bar{\delta}}, \eta_{\bar{\delta}}, \nu_{\bar{\delta}})$, such for any $\alpha\in S^{\ominus}(\alpha_{0}, G)$ and $(0, 1, 1) < \alpha_{0}\ominus\alpha < \bar{\delta}$ have $G(\alpha_{0})\ominus G(\alpha) < \bar{\varepsilon}$.

Let $G(\alpha)$ be a SVNF of $\alpha_{0}$, then $G(\alpha)$ is continuous in the multiplication direction at $\alpha_{0}$, denoted by $\lim\limits_{\alpha\rightarrow \alpha_{0}^{\otimes}}G(\alpha) = G(\alpha_{0})$. If it satisfies for any $\bar{\varepsilon} = (\mu_{\bar{\varepsilon}}, \eta_{\bar{\varepsilon}}, \nu_{\bar{\varepsilon}}) < (1, 0, 0)$, $\exists\; \bar{\delta} = (\mu_{\bar{\delta}}, \eta_{\bar{\delta}}, \nu_{\bar{\delta}})$, such for any $\alpha\in S^{\otimes}(\alpha_{0}, G)$ and $\bar{\delta} < \alpha\oslash\alpha_{0} < (1, 1, 0)$ have $G(\alpha)\oslash G(\alpha_{0}) > \bar{\varepsilon}$.

Let $G(\alpha)$ be a SVNF of $\alpha_{0}$, then $G(\alpha)$ is continuous in the division direction at $\alpha_{0}$, denoted by $\lim\limits_{\alpha\rightarrow \alpha_{0}^{\oslash}}G(\alpha) = G(\alpha_{0})$. If it satisfies for any $\bar{\varepsilon} = (\mu_{\bar{\varepsilon}}, \eta_{\bar{\varepsilon}}, \nu_{\bar{\varepsilon}}) < (1, 0, 0)$, $\exists\; \bar{\delta} = (\mu_{\bar{\delta}}, \eta_{\bar{\delta}}, \nu_{\bar{\delta}})$, such for any $\alpha\in S^{\oslash}(\alpha_{0}, G)$ and $\bar{\delta} < \alpha_{0}\oslash\alpha < (1, 1, 0)$ have $G(\alpha_{0})\oslash G(\alpha) > \bar{\varepsilon}$.

6.   The derivatives and differentials of SVNF

6.1.   The derivatives of SVNF

In this part, we will discuss the derivable conditions of SVNF and the specific form of derivatives. For convenience, we denote $\alpha\oslash\beta$ by $\frac{\alpha}{\beta}$ and denote $\lim\limits_{\alpha^{'}\rightarrow \alpha^{\oplus}}\frac{G(\alpha')\ominus G(\alpha)}{\alpha'\ominus\alpha}$ as $\frac{dG(\alpha)}{d\alpha}$.

Definition 6.1. Let $G(\alpha)$ be a SVNF of $\alpha$. If $\lim\limits_{\alpha^{'}\rightarrow \alpha^{\oplus}}\frac{G(\alpha')\ominus G(\alpha)}{\alpha'\ominus\alpha}$ is a SVNN, then we call $G(\alpha)$ to be derivable in the addition direction of $\alpha$, and the limit value is the derivative of $G(\alpha)$ at $\alpha$.

On the basis of the analysis above, we can get the following theorem.

Theorem 6.1. Let $G(\alpha) = (f(\mu, \eta, \nu), g(\mu, \eta, \nu), h(\mu, \eta, \nu))$ be a SVNF of $\alpha$, then $G(\alpha)$ is derivable in the addition direction of $\alpha$, if and only if

and the derivative of $G(\alpha)$ can be calculated by the following formula

Proof. Let $\alpha' = (\mu+\Delta\mu, \eta+\Delta\eta, \nu+\Delta\nu) = (\mu', \eta', \nu')\in S^{\oplus}(\alpha, G)$, then

$G(\alpha') = (f(\mu+\Delta\mu, \eta+\Delta\eta, \nu+\Delta\nu), g(\mu+\Delta\mu, \eta+\Delta\eta, \nu+\Delta\nu), h(\mu+\Delta\mu, \eta+\Delta\eta, \nu+\Delta\nu)) = (f(\mu', \eta', \nu'), g(\mu', \eta', \nu'), h(\mu', \eta', \nu'))$,

thus,

Now, we simplify the membership function, indeterminacy membership function and the non-membership function respectively, for the membership function

for the indeterminacy membership function

and for the non-membership function

In summary, we can get

where

To ensure that $\frac{dG(\alpha)}{d\alpha}$ is the only determined SVNN, which does not change because of different $\tan\rho, \tan\theta$ and $\tan\tau$. So, it must be satisfied

then $G(\alpha)$ can be expressed by $(f(\mu), g(\eta), h(\nu))$.

The proof is completed. □

Likewise, we can get the derivative of $G(\alpha)$ in the subtraction direction of $\alpha$. When $\alpha'\in S^{\ominus}(\alpha, G)$, then

if $\frac{dG(\alpha)}{d\alpha}$ is a SVNN, then we define it as the derivative of $G(\alpha)$ in the subtraction direction of $\alpha$.

We know that there are the same derivative values in the two different directions if $f, g$ and $h$ are derivables. So we will unify the two directions derivatives into a kind of derivative.

Definition 6.2. Let $\alpha'\in S^{\oplus}(\alpha, G)$ or $\alpha'\in S^{\ominus}(\alpha, G)$. If the SVNF $G(\alpha)$ is derivable in the addition and subtraction directions of $\alpha$, then we call

the subtraction derivative of $G(\alpha)$ at $\alpha$.

Now, let us consider some special examples.

Example 6.1. Let $\alpha = (\mu, \eta, \nu)$ be a SVNN, $G(\alpha)$ be a SVNF of $\alpha$.

(1)$\; {\mathrm{If}}\; G(\alpha) = \alpha_{0} = (\mu_{0},\eta_{0},\nu_{0}), {\mathrm{then}}\; f(\mu) = \mu_{0},g(\eta) = \eta_{0},h(\nu) = \nu_{0}, \frac{dG(\alpha)}{d\alpha} = (0,1,1);$

(2)$\; {\mathrm{If}}\; G(\alpha) = \alpha\oplus\alpha_{0} = (\mu+\mu_{0}-\mu\mu_{0},\eta\eta_{0},\nu\nu_{0}), {\mathrm{then}}\; f(\mu) = \mu+\mu_{0}-\mu\mu_{0},g(\eta) = \eta\eta_{0},h(\nu) = \nu\nu_{0},\\ \frac{dG(\alpha)}{d\alpha} = \left(\frac{1-\mu}{1-\mu-\mu_{0}+\mu\mu_{0}}(1-\mu_{0}),1-\frac{\eta}{\eta\eta_{0}}\eta_{0},1-\frac{\nu}{\nu\nu_{0}}\nu_{0}\right) = (1,0,0);$

(3)$\; {\mathrm{If}}\; G_{1}(\alpha) = \lambda\alpha = (1-(1-\mu)^{\lambda},\eta^{\lambda},\nu^{\lambda}), 0<\lambda<1, {\mathrm{then}}\; f(\mu) = 1-(1-\mu)^{\lambda},g(\eta) = \eta^{\lambda},h(\nu) = \nu^{\lambda},\\ \frac{dG_{1}(\alpha)}{d\alpha} = \left(\frac{1-\mu}{(1-\mu)^{\lambda}}\lambda(1-\mu)^{\lambda-1},1-\lambda,1-\lambda\right) = (\lambda,1-\lambda,1-\lambda).$

${\mathrm{If}}\; G_{2}(\alpha) = \lambda\alpha\oplus\beta = (1-(1-\mu)^{\lambda}(1-\mu_{\beta}),\eta^{\lambda}\eta_{\beta},\nu^{\lambda}\nu_{\beta}), 0<\lambda<1,\\{\mathrm{then}}\; f(\mu) = 1-(1-\mu)^{\lambda}(1-\mu_{\beta}),g(\eta) = \eta^{\lambda}\eta_{\beta},h(\nu) = \nu^{\lambda}\nu_{\beta},\\ \frac{dG_{2}(\alpha)}{d\alpha} = \left(\frac{1-\mu}{(1-\mu)^{\lambda}(1-\mu_{\beta})}\lambda((1-\mu_{\beta})(1-\mu)^{\lambda-1}),1-\frac{\eta}{\eta^{\lambda}\eta_{\beta}}\lambda\eta_{\beta}\eta^{\lambda-1}, 1-\frac{\nu}{\nu^{\lambda}\nu_{\beta}}\lambda\nu_{\beta}\nu^{\lambda-1}\right) = (\lambda,1-\lambda,1-\lambda),\\ {\mathrm{we\; conclude\; that}}\; \frac{dG_{1}(\alpha)}{d\alpha} = (\lambda,1-\lambda,1-\lambda) = \frac{dG_{2}(\alpha)}{d\alpha};$

(4)$\; {\mathrm{If}}\; G(\alpha_{1},\alpha_{2},\cdots,\alpha_{n}) = SVNWA(\alpha_{1},\alpha_{2},\cdots,\alpha_{n}) = \left(1-\prod\limits_{i = 1}^{n}(1-\mu_{\alpha_{i}})^{\omega_{i}},\prod\limits_{i = 1}^{n}\eta_{\alpha_{i}}^{\omega_{i}},\prod\limits_{i = 1}^{n}\nu_{\alpha_{i}}^{\omega_{i}}\right), \\ {\mathrm{that\; is}}\; f(\mu_{\alpha_{i}}) = 1-\prod\limits_{i = 1}^{n}(1-\mu_{\alpha_{i}})^{\omega_{i}},\; g(\eta_{\alpha_{i}}) = \prod\limits_{i = 1}^{n}\eta_{\alpha_{i}}^{\omega_{i}},\; h(\nu_{\alpha_{i}}) = \prod\limits_{i = 1}^{n}\nu_{\alpha_{i}}^{\omega_{i}},\\ {\mathrm{hence}}\; \frac{dG(\alpha_{1},\alpha_{2},\cdots,\alpha_{n})}{d\alpha_{i}} = (\omega_{i},1-\omega_{i},1-\omega_{i}).$

Definition 6.3. Let $G(\alpha)$ be a SVNF of $\alpha$, if $\lim\limits_{\alpha^{'}\rightarrow \alpha^{\oslash}}\frac{G(\alpha')}{ G(\alpha)}\ominus\frac{\alpha'}{\alpha}$ is still a SVNN, then we call $G(\alpha)$ to be derivable in the division direction of $\alpha$, and the limit value is the derivative of $G(\alpha)$ at $\alpha$.

Theorem 6.2. Let $G(\alpha) = (f(\mu, \eta, \nu), g(\mu, \eta, \nu), h(\mu, \eta, \nu))$ be a SVNF of $\alpha$, then $G(\alpha)$ is derivable in the division direction of $\alpha$, if and only if

and the derivative of $G(\alpha)$ can be calculated by the following formula

Likewise, we can get the derivative of $G(\alpha)$ in the multiplication direction of $\alpha$. When $\alpha'\in S^{\otimes}(\alpha, G)$, then

if $\frac{lG(\alpha)}{l\alpha}$ is a SVNN, then we define it as the derivative of $G(\alpha)$ in the multiplication direction of $\alpha$.

We know that there are the same derivative values in the two different directions if $f, g$ and $h$ are derivables. So we will unify the two directions derivatives into a kind of derivative.

Definition 6.4. Let $\alpha'\in S^{\otimes}(\alpha, G)$ or $\alpha'\in S^{\oslash}(\alpha, G)$. If the SVNF $G(\alpha)$ is derivable in the multiplication and division directions of $\alpha$, then we call

the division derivative of $G(\alpha)$ at $\alpha$.

Below let us give some special examples about the division derivative.

Example 6.2. Let $\alpha = (\mu, \eta, \nu)$ be a SVNN, $G(\alpha)$ be a SVNF of $\alpha$.

(1)$\; {\mathrm{If}}\; G(\alpha) = \alpha_{0} = (\mu_{0},\eta_{0},\nu_{0}), {\mathrm{then}}\; f(\mu) = \mu_{0},g(\eta) = \eta_{0},h(\nu) = \nu_{0}, \frac{lG(\alpha)}{l\alpha} = (1,0,0);$

(2)$\; {\mathrm{If}}\; G(\alpha) = \alpha\otimes\alpha_{0} = (\mu\mu_{0},\eta+\eta_{0}-\eta\eta_{0},\nu+\nu_{0}-\nu\nu_{0}), \\ {\mathrm{then}}\; f(\mu) = \mu\mu_{0},g(\eta) = \eta+\eta_{0}-\eta\eta_{0},h(\nu) = \nu+\nu_{0}-\nu\nu_{0},\\ \frac{lG(\alpha)}{l\alpha} = \left(1-\frac{\mu}{\mu\mu_{0}}\mu_{0},\frac{1-\eta}{1-\eta-\eta_{0}+\eta\eta_{0}}(1-\eta_{0}),\frac{1-\nu}{1-\nu-\nu_{0}+\nu\nu_{0}}(1-\nu_{0})\right) = (0,1,1);$

(3)$\; {\mathrm{If}}\; G_{1}(\alpha) = \alpha^{\lambda} = (\mu^{\lambda},1-(1-\eta)^{\lambda},1-(1-\nu)^{\lambda}), 0<\lambda<1,\\ {\mathrm{then}}\; f(\mu) = \mu^{\lambda},g(\eta) = 1-(1-\eta)^{\lambda},h(\nu) = 1-(1-\nu)^{\lambda},\\ \frac{lG_{1}(\alpha)}{l\alpha} = \left(1-\frac{\mu}{\mu^{\lambda}}\lambda\mu^{\lambda-1},\frac{1-\eta}{(1-\eta)^{\lambda}}\lambda(1-\eta)^{\lambda-1}, \frac{1-\nu}{(1-\nu)^{\lambda}}\lambda(1-\nu)^{\lambda-1}\right) = (1-\lambda,\lambda,\lambda).\\ \; \; \; \; \; {\mathrm{If}}\; G_{2}(\alpha) = \alpha^{\lambda}\otimes\beta = (\mu^{\lambda}\mu_{\beta},1-(1-\eta)^{\lambda}(1-\eta_{\beta}),1-(1-\nu)^{\lambda}(1-\nu_{\beta})), 0<\lambda<1, \\ {\mathrm{then}}\; f(\mu) = \mu^{\lambda}\mu_{\beta},g(\eta) = 1-(1-\eta)^{\lambda}(1-\eta_{\beta}), h(\nu) = 1-(1-\nu)^{\lambda}(1-\nu_{\beta}),\\ \frac{lG_{2}(\alpha)}{l\alpha} = \left(1-\frac{\mu}{\mu^{\lambda}\mu_{\beta}}\lambda\mu_{\beta}\mu^{\lambda-1},\frac{1-\eta}{(1-\eta)^{\lambda}(1-\eta_{\beta})}\lambda((1-\eta_{\beta})(1-\eta)^{\lambda-1}),\frac{1-\nu}{(1-\nu)^{\lambda}(1-\nu_{\beta})}\lambda((1-\nu_{\beta})(1-\nu)^{\lambda-1})\right)\\ \; \; \; \; \; \; \; \; \; \; \; \; = (1-\lambda,\lambda,\lambda),\\ {\mathrm{we\; conclude\; that}}\; \frac{lG_{1}(\alpha)}{l\alpha} = (1-\lambda,\lambda,\lambda) = \frac{lG_{2}(\alpha)}{l\alpha};$

(4)$\; {\mathrm{If}}\; G(\alpha_{1},\alpha_{2},\cdots,\alpha_{n}) = SVNWG(\alpha_{1},\alpha_{2},\cdots,\alpha_{n}) = \left(\prod\limits_{i = 1}^{n}\mu_{\alpha_{i}}^{\omega_{i}},1-\prod\limits_{i = 1}^{n}(1-\eta_{\alpha_{i}})^{\omega_{i}},1-\prod\limits_{i = 1}^{n}(1-\nu_{\alpha_{i}})^{\omega_{i}}\right),\\ {\mathrm{that\; is}}\; f(\mu_{\alpha_{i}}) = \prod\limits_{i = 1}^{n}\mu_{\alpha_{i}}^{\omega_{i}},\; g(\eta_{\alpha_{i}}) = 1-\prod\limits_{i = 1}^{n}(1-\eta_{\alpha_{i}})^{\omega_{i}},\; h(\nu_{\alpha_{i}}) = 1-\prod\limits_{i = 1}^{n}(1-\nu_{\alpha_{i}})^{\omega_{i}},\\ {\mathrm{hence\; }}\frac{lG(\alpha_{1},\alpha_{2},\cdots,\alpha_{n})}{l\alpha_{i}} = (1-\omega_{i},\omega_{i},\omega_{i}).$

6.2.   The differentials of SVNF

As a bridge connecting the two modules of derivative and integral, differentiation plays an important role in real analysis and its geometric meaning is expressed as the increment of ordinates on the tangent line, which is an approximation of the increment of the value of the function.

From the discussion above, we define two kinds of derivative operations (the subtraction derivative and the division derivative). Then, there are two kinds of differential operations correspondingly.

Let $G(\alpha)$ be a SVNF of $\alpha$, we denote $\Delta G = G(\alpha_{0}\oplus\Delta\alpha)\ominus G(\alpha_{0})$, then the problem is equal to get the approximate valued of $\Delta G$. Obviously, $\Delta G$ is the function of $\Delta\alpha$, and we attempt to replace $\Delta G$ by a simple function of $\Delta\alpha$ to complete the discussion.

Definition 6.5. For a given SVNN $\alpha = (\mu, \eta, \nu)$, we call $U(\alpha) = \mu$ the take-value function of membership, $W(\alpha) = \eta$ is the take-value function of indeterminacy-membership, and $V(\alpha) = \nu$ is the take-value function of non-membership.

Definition 6.6. Let $G(\alpha)$ be a SVNF of $\alpha$, we define the subtraction differential of $G = G(\alpha)$ as $dG$, and $\Delta\alpha = \alpha\ominus\alpha_{0}$, then the subtraction differential can be expressed as $dG = \frac{dG(\alpha)}{d\alpha}\big|_{\alpha = \alpha_{0}}\otimes\Delta\alpha$.

Theorem 6.3. Let $G(\alpha) = (f(\mu), g(\eta), h(\nu))$ be a SVNF of $\alpha$, in which $f(\mu), g(\eta)$ and $h(\nu)$ are both derivables. For $\alpha\in S^{\oplus}(\alpha_{0}, G)$, we denote $\Delta\alpha = \alpha\ominus\alpha_{0}$ and $\Delta G = G(\alpha)\ominus G(\alpha_{0})$. If $\Delta G\approx dG$, that is

which satisfies the following conditions

Then, we call that $G(\alpha) = (f(\mu), g(\eta), h(\nu))$ is differential, and $\frac{dG(\alpha)}{d\alpha}\big|_{\alpha = \alpha_{0}}\otimes(\alpha\ominus\alpha_{0})$ is the subtraction differential of $G(\alpha)$ at $\alpha_{0}$.

Proof. If $\alpha\in S^{\oplus}(\alpha_{0}, G)$, then we have $\Delta \alpha = \alpha\ominus\alpha_{0} = \left(\frac{\mu-\mu_{0}}{1-\mu_{0}}, \frac{\eta}{\eta_{0}}, \frac{\nu}{\nu_{0}}\right)$, and

so we can get

then

Thus, we have $G(\alpha)\ominus G(\alpha_{0})\approx\frac{dG(\alpha)}{d\alpha}\big|_{\alpha = \alpha_{0}}\otimes(\alpha\ominus\alpha_{0})$, which satisfies

□ In addition, when $\alpha\in S^{\ominus}(\alpha_{0}, G)$, then we have $G(\alpha_{0})\ominus G(\alpha)\approx\frac{dG(\alpha)}{d\alpha}\big|_{\alpha = \alpha_{0}}\otimes(\alpha_{0}\ominus\alpha)$.

Example 6.3. Let $G(\alpha) = \lambda\alpha$, $0 < \alpha < 1$, first, according to the law of operation of SVNN $\lambda(\alpha_{1}\oplus\alpha_{2}) = \lambda\alpha_{1}\oplus\lambda\alpha_{2}$. Second, by Theorem 6.3 $G(\alpha\oplus\Delta\alpha)\ominus G(\alpha)\approx(\lambda, 1-\lambda, 1-\lambda)\otimes\Delta\alpha$, then $G(\alpha\oplus\Delta\alpha)\ominus G(\alpha) = \lambda\Delta\alpha$.

Suppose $\Delta\alpha = (0.03, 0.6, 0.9)$ and $\lambda = 0.5$, then $(\lambda, 1-\lambda, 1-\lambda)\otimes\Delta\alpha = (0.5, 0.5, 0.5)\otimes(0.03, 0.6, 0.9) = (0.015, 0.8, 0.95),$ $\lambda\Delta\alpha = (1-0.97^{0.5}, 0.6^{0.5}, 0.9^{0.5}) = (0.015, 0.775, 0.945)$.

That is to say, we replace $\lambda\Delta\alpha$ with $(\lambda, 1-\lambda, 1-\lambda)\otimes\Delta\alpha$ is approximate obviously.

Example 6.4. Let $\alpha_{1} = (0.3, 0.5, 0.4), \alpha_{2} = (0.4, 0.3, 0.3), \alpha_{3} = (0.6, 0.1, 0.2)$ and $\alpha_{4} = (0.7, 0.2, 0.1)$ be four SVNN, and $\omega = (0.2, 0.3, 0.4, 0.1)^{T}$ be their weight vector. Then

However, in the actual problem situation, decision-makers may make wrong evaluations due to multiple uncertainties as he/she intends to give the value again. Suppose that the new SVNN is $\alpha'_{1} = (0.5, 0.1, 0.2)$, if $\alpha'_{1}\in A^{\oplus}_{\alpha_{1}}$, then $\exists\; \beta_{1}\in SVNN$, such that $\alpha'_{1} = \alpha_{1}\oplus\beta_{1}$. So we can get $\beta_{1} = \alpha'_{1}\ominus\alpha_{1} = (0.286, 0.2, 0.5)$, and

This example shows that when the estimated value changes, differentiation can effectively estimate only the changed value without having to get an exact value.

Definition 6.7. If we define the division differential of $G = G(\alpha)$ as $lG$, and $\nabla\alpha = \alpha\oslash\alpha_{0}$, then we give the concrete form of the division differential by $lG = \frac{lG(\alpha)}{l\alpha}\big|_{\alpha = \alpha_{0}}\oplus\nabla\alpha$.

Theorem 6.4. Let $G(\alpha) = (f(\mu), g(\eta), h(\nu))$ be a SVNF of $\alpha$, in which $f(\mu), g(\eta)$ and $h(\nu)$ are both derivable. For $\alpha\in S^{\otimes}(\alpha_{0}, G)$, we denote $\nabla\alpha = \alpha\oslash\alpha_{0}$ and $\nabla G = G(\alpha)\oslash G(\alpha_{0})$. If $\nabla G\approx lG$, that is

which satisfies the following conditions

Then we call that $G(\alpha) = (f(\mu), g(\eta), h(\nu))$ is differential, and $\frac{lG(\alpha)}{l\alpha}\big|_{\alpha = \alpha_{0}}\oplus(\alpha\oslash\alpha_{0})$ is the division differential of $G(\alpha)$ at $\alpha_{0}$.

Similarly, when $\alpha\in S^{\oslash}(\alpha_{0}, G)$, then we also get $G(\alpha_{0})\oslash G(\alpha)\approx\frac{lG(\alpha)}{l\alpha}\big|_{\alpha = \alpha_{0}}\oplus(\alpha_{0}\oslash\alpha)$.

Example 6.5. Let $G(\alpha) = \alpha^{\lambda}$, $0 < \alpha < 1$, then we have $\frac{G(\alpha\otimes\Delta\alpha)}{G(\alpha)} \approx(1-\lambda, \lambda, \lambda)\oplus\Delta\alpha$. On the one hand, because of the operational laws of SVNN, we have $(\alpha_{1}\otimes\alpha_{2})^{\lambda} = \alpha_{1}^{\lambda}\otimes\alpha_{2}^{\lambda}$, then $\frac{G(\alpha\otimes\Delta\alpha)}{ G(\alpha)} = (\Delta\alpha)^{\lambda}$.

Suppose $\Delta\alpha = (0.8, 0.3, 0.4)$ and $\lambda = 0.2$, then $(1-\lambda, \lambda, \lambda)\oplus\Delta\alpha = (0.8, 0.2, 0.2)\oplus(0.8, 0.3, 0.4) = (0.96, 0.06, 0.08)$, $(\Delta\alpha)^{\lambda} = (0.8^{0.2}, 1-0.7^{0.2}, 1-0.6^{0.2}) = (0.956, 0.069, 0.097)$.

That is to say, we replace $(\Delta\alpha)^{\lambda}$ with $(1-\lambda, \lambda, \lambda)\oplus\Delta\alpha$ is approximate obviously.

Example 6.6. Let $\alpha_{1} = (0.7, 0.1, 0.2), \alpha_{2} = (0.5, 0.4, 0.2), \alpha_{3} = (0.3, 0.4, 0.6)$ and $\alpha_{4} = (0.4, 0.1, 0.3)$ be four SVNN, and $\omega = (0.3, 0.4, 0.1, 0.2)^{T}$ be their weight vector. Then,

Now, a decision maker intends to give the value again. Suppose that the new SVNN is $\alpha'_{2} = (0.9, 0.3, 0.1)$, if $\alpha'_{2}\in A^{\oslash}_{\alpha_{2}}$, then $\exists\; \beta_{2}\in SVNN$, such that $\alpha'_{2} = \alpha_{2}\oslash\beta_{2}$, $\beta_{2} = \alpha_{2}\oslash\alpha'_{2} = (0.556, 0.143, 0.111)$, hence

7.   The indefinite integrals of SVNF

Earlier we discussed the problem of knowing a function and finding its derivative. Conversely, we often encounter the problem of knowing the derivative of a function and finding the original function. We know that the derivative operation and the integral operation are inverse operations of each other, so whether we can get the corresponding indefinite integral formula through the derivative, the conclusion is positive.

Let $\varphi(\alpha) = (f(\mu), g(\eta), h(\nu))$ be a SVNF and $\Phi(\alpha) = (F(\mu), G(\eta), H(\nu))$ be the primitive function of $\varphi(\alpha)$, which satisfies $\frac{d\Phi(\alpha)}{d\alpha} = \varphi(\alpha)$. If we want to get the concrete form of $\Phi(\alpha)$, we need to solve three ordinary differential equations as follows.

solve ordinary differential equations, then

Because of the uniqueness of the solution to the ordinary differential equations, we know that

must be the primitive function of $\varphi(\alpha)$, where $c_{1}, c_{2}, c_{3}$ are three integral constants, which are real number that make $\Phi(\alpha)$ to be a SVNF.

On the contrary, we can verify $\frac{d\Phi(\alpha)}{d\alpha} = \varphi(\alpha)$ according to the derivative of SVNF, which indicates that $\Phi(\alpha)$ is surely the primitive function of $\varphi(\alpha)$.

Definition 7.1. If $\frac{d\Phi(\alpha)}{d\alpha} = \varphi(\alpha)$, and $\varphi(\alpha) = (f(\mu), g(\eta), h(\nu))$ and be a SVNF, then the subtraction indefinite integral of $\varphi(\alpha)$ denoted as $\int\varphi(\alpha)d\alpha$, in which $"\int"$ is the sign of integration, $"\varphi(\alpha)$" is the integrand and $"\alpha$" is the integral variable, then $\int\varphi(\alpha)d\alpha$ must have following form.

where $c_{1}, c_{2}, c_{3}$ are three integral constants, which are real number that make $\int\varphi(\alpha)d\alpha$ to be a SVNF.

Theorem 7.1. Let $\Phi_{1}(\alpha)$ and $\Phi_{2}(\alpha)$ be any two antiderivatives of $\varphi(\alpha)$, and

then we can easily know that there are three real numbers $p_{1}, p_{2}$ and $p_{3}$, which satisfies

Example 7.1. (1) Let $\varphi(\alpha) = (\mu, \eta, \nu)$, that is $f(\mu) = \mu, \; g(\eta) = \eta, \; h(\nu) = \nu$. If we denote $\int\varphi(\alpha)d\alpha = (F(\mu), G(\eta), H(\nu))$, then

where $c_{1}, c_{2}, c_{3}$ are integral constants, such that $\int\varphi(\alpha)d\alpha$ to be a SVNF.

(2) Let $\varphi(\alpha) = (\lambda, 1-\lambda, 1-\lambda)$, that is $f(\mu) = \lambda, \; g(\eta) = 1-\lambda, \; h(\nu) = 1-\lambda$. If we denote $\int\varphi(\alpha)d\alpha = (F(\mu), G(\eta), H(\nu))$, then

where $c_{1}, c_{2}, c_{3}$ are integral constants, such that $\int\varphi(\alpha)d\alpha$ to be a SVNF.

If $c_{1} = c_{2} = c_{3} = 1$, then we can get

That is to say, $\lambda\alpha$ is one of the primitive functions of $\varphi(\alpha) = (\lambda, 1-\lambda, 1-\lambda)$.

Definition 7.2. If $\frac{l\Psi(\alpha)}{l\alpha} = \psi(\alpha)$, and $\psi(\alpha) = (f(\mu), g(\eta), h(\nu))$ and be a SVNF, then the division indefinite integral of $\psi(\alpha)$ denoted as $\int\psi(\alpha)l\alpha$, in which $"\int"$ is the sign of integration, $"\psi(\alpha)$" is the integrand and $"\alpha$" is the integral variable, then $\int\psi(\alpha)l\alpha$ must have following form.

Theorem 7.2. Let $\Psi_{1}(\alpha)$ and $\Psi_{2}(\alpha)$ be any two antiderivatives of $\psi(\alpha)$, and

then we can easily know that there are three real numbers $q_{1}, q_{2}$ and $q_{3}$, which satisfies

Example 7.2. (1) Let $\psi(\alpha) = (\mu, \eta, \nu),$ i.e. $f(\mu) = \mu, \; g(\eta) = \eta, \; h(\nu) = \nu$. If we denote $\int\psi(\alpha)l\alpha = (F(\mu), G(\eta), H(\nu))$, then

where $c_{1}, c_{2}, c_{3}$ are integral constants, such that $\int\psi(\alpha)l\alpha$ to be a SVNF.

(2) Let $\psi(\alpha) = (1-\lambda, \lambda, \lambda)$, i.e. $f(\mu) = 1-\lambda, \; g(\eta) = \lambda, \; h(\nu) = \lambda$. If we denote $\int\psi(\alpha)l\alpha = (F(\mu), G(\eta), H(\nu))$, then

where $c_{1}, c_{2}, c_{3}$ are integral constants, such that $\int\psi(\alpha)l\alpha$ to be a SVNF.

If $c_{1} = c_{2} = c_{3} = 1$, then we can get

That is to say, $\alpha^{\lambda}$ is one of the primitive functions of $\psi(\alpha) = (1-\lambda, \lambda, \lambda)$.

8.   Conclusions

Inspired by the calculus theory of intuitionistic fuzzy functions, in this paper, we first present two basic operations for SVNS, namely the subtraction operation and division operation. Second, we consider the changing value of SVNN as a variable and classify these changed values according to the basic operational laws for SVNN. Based on this, we propose the concept of single-valued neutrosophic function and characterize their derivatives and differential. Finally, by solving ordinary differential equations, we give the specific forms and related properties of two types of indefinite integrals (subtraction indefinite integrals and division indefinite integrals) of SVNF and give several specific examples. Our work lays a solid foundation for further developing the calculus theory of SVNF. In the next work, we will consider the specific form of the definite integral of SVNF and its properties.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence tools in the creation of this article.

Acknowledgments

This work is supported by the National Natural Science Foundation of China (12061607).

Conflict of interest

The authors declare that they have no conflicts of interest.