A conservative exponential integrators method for fractional conservative differential equations

1.   Introduction

Recently, many scholars introduced many fractional differential equations to describe and simulate some phenomena ^[21]. With the emergence of these equations in more and more scientific engineering problems, it is particularly urgent to study theoretical analysis and numerical calculation. However, because the fractional differential equation contains a quasi-differential operator, its memory preserving (nonlocality) gracefully describes the practical problems and causes great difficulties in analysis and calculation. Thus, many numerical schemes are constructed for solving these equations ^[10,23,29]. However, the numerical stability of these traditional methods is poor in long-time numerical simulations.

In recent years, studies indicate that some physical quantities belong to fractional partial differential equations (PDEs), such as the energy and mass ^[12,15,26]. Therefore, it is necessary to develop corresponding algorithms to inherit these quantities. The methods we call the structure-preserving algorithms can inherit inherent properties of systems ^[13], and have better stability than general numerical algorithms. So far, many conservative algorithms have been developed and applied to solve classical differential equations ^[2,18], and have gained remarkable success in theoretical analysis and numerical simulation ^[9,16]. For almost a decade, scholars developed corresponding conservative algorithms for these equations. For instance, Xiao et al. ^[19,25] proposed various conservative difference methods for some conservative equations with fractional Laplacian operators. Wang and Huang ^[26] developed multi-symplectic conservative schemes for the fractional NLS equation. Wang et al. investigated an explicit conservative scheme to conserve the energy of the fractional Hamiltonian wave equation ^[6]. Some related works readers can find in ^[8,27] for more details. However, the linear and nonlinear terms of the equation have not been considered when constructing these conservative numerical algorithms. When the space is densely divided, the linear part will produce great rigidity, and the stability of these structure-preserving algorithms will also be affected.

Many exponential integrator schemes have been developed for solving the stiff systems ^[1,11,20], which can approximate the linear part exactly and provide satisfactory accuracy and stability. In addition, scholars also proposed some conservative exponential integrator schemes for some conservative equations. For example, Cui et al. ^[4] developed a class of exponential energy-preserving schemes for solving the nonlinear Schrödinger (NLS) equation. Li and Wu ^[20] used the discrete gradient method to develop an exponential integrator energy-preserving scheme for conservative equations. For the other structure-preserving exponential integrators schemes, the readers can be referred to ^[3,5,17].

The main goal of the paper is to present a framework to develop a conservative scheme for some fractional PDEs by combining the exponential time difference (ETD) technique and the averaged vector field (AVF) method. The scheme is built upon the Hamiltonian structure of these equations and can be used to solve some fractional Hamiltonian PEDs. In addition, the Fourier pseudo-spectral method is used to approximate fractional Laplacian, and the fast technique based on fast Fourier transformations (FFTs) can be implemented in simulations. Numerical simulations for fractional NLS equations are presented to validate the theoretical analysis of the proposed method.

The outline of the paper is organized as follows. Section 2 introduces fractional Hamiltonian PDEs and uses the Fourier pseudo-spectral method to approximate the equation to obtain a semi-discrete conservative system. Section 3 constructs an exponential time difference averaged vector field (ETD-AVF) scheme for the semi-discrete and discusses the conservation property. In Section 4, Some numerical examples are given to confirm the theoretical results. Some conclusions are obtained in Section 5.

2.   Fractional Hamiltonian PDEs

2.1.   Fractional Hamiltonian systems

The paper aims to construct a conservative exponential time difference averaged vector field scheme for a class of conservative fractional differential equations which can be expressed as an canonical Hamiltonian system

where ${\mathrm{u}}({{\boldsymbol{x}}}, t) = \big(u_1({{\boldsymbol{x}}}, t),$ $u_2({{\boldsymbol{x}}}, t), \cdots, u_{2m}({{\boldsymbol{x}}}, t)\big)^T\in\mathbb{R}^{2m}$, $({{\boldsymbol{x}}}, t)\in\Omega\times[0, T]\subset\mathbb{R}^d\times \mathbb{R}$, and $\frac{\delta \mathcal{H}}{\delta {\mathrm{u}}}$ represents the variational derivative of the Hamiltonian energy functional $\mathcal{H}$ for ${\mathrm{u}}$. To combine ideas of exponential time difference method and energy-preserving method for fractional Hamiltonian systems, we address ourselves to the corresponding $\mathcal{H}$ has the following form

where $(p, q): = \int_{\Omega}pq d {{\boldsymbol{x}}}$, $U({\mathrm{u}})$ is a nonlinear potential. For system (2.2) in $\Omega: = [{-L, L}]\times[-L, L]$ with period $2{L}$, the operator $\mathcal{L}^{\frac{s}{2}}$ ($1 < s\leq 2$) can be defined by ^[24,28]

where ${\alpha}_{k_i} = \frac{k_i\pi}{L} \; (i = 1, 2)$, ${\boldsymbol \alpha}_k: = \sum\limits_{i = 1}^{2}{\alpha}_{k_i}(x_i+L)$, and

Then, we can derive the corresponding equation of system (2.2) by using the variational derivative, namely

2.2.   Fourier pseudo-spectral approximation of spatial derivatives

We employ the Fourier pseudo-spectral method to discrete fractional Laplacian in two-dimension (2D). For 2D case, system $(2.5)$ is truncated on a periodic region $\Omega\in (-L, L)\times (-L, L)$ with ${{{\boldsymbol{x}}}} = (x, y)$, which can be divided by $N \times N$ equal grids, and the corresponding spatial gird points are given by: $\Omega_{h} = \{(x_{j}, y_{k})|j = 0, 1, \cdots, N-1, k = 0, 1, \cdots, N-1\},$ where $x_j = -L+jh = -L+j\frac{2L}{N}, 0\leq j\leq N-1$, $y_k = -L+kh = -L+k\frac{2L}{N}, 0\leq j\leq N-1$, $N$ is a positive even integer. Furthermore, we denote the index sets

and let

be a vector space of grid functions defined on $\Omega_{h}$. Note that the bold ${{{\boldsymbol{i}}}}\in \mathcal{T}_{h}$ refers to an index, while $j$ means the first component of ${{{\boldsymbol{i}}}}$.

Define the interpolation space $S^{p}_N: = {\text {span}}\{g_{j}(x)g_{k}(y), (j, k)\in \mathcal{T}_{h} \}$, where $g_{j}(x)$ and $g_{j}(y)$ are trigonometric polynomial defined by

where $\mu_{1} = \frac{\pi}{L}$, $\mu_{2} = \frac{\pi}{L}$ and

Then, we define the interpolation operator $I_{N}:L^{2}(\Omega)\rightarrow S^{p}_{N}$ by

where

$\widehat{u}_{-N/2} = \widehat{u}_{N/2}$, $\widehat{u}_{-N/2} = \widehat{u}_{N/2}$. Applying the Laplacian operator $\mathcal{L}^{\frac{s}{2}}$ to $I_{N}u(x, y)$ leads to

where ${{{\boldsymbol{u}}}}\in \mathcal{V}_h$, discrete Fourier transform and its inverse are given by

and

Thus, the spectral differentiation matrix of 2D fractional Laplacian can be expressed as

Therefore

The above expression means that the constructed format can be calculated quickly by using the using the two-dimensional FFT technique in $\mathcal{O}(N\log^2 N)$.

Applying the Fourier pseudo-spectral method to approximate the fractional Laplacian, we can obtain a semi-discrete system for system (2.5) as follows

Remark 2.1. We should remark that the spectral differential matrix by using the Fourier pseudo-spectral to discretize fractional Laplacian is a symmetric positive definite matrix, and it is equivalent to classical spectral differential matrix when $s = 2$. Therefore, we can derive that system (2.12) can still preserve the energy in a semi-discrete scene.

Remark 2.2. Note that the proposed method is only for solving canonical Hamiltonian systems. That will prompt me to develop corresponding conservative algorithms for non-canonical fractional Hamiltonian systems.

3.   The ETD-AVF method

3.1.   Construction of the ETD-AVF method

This subsection will give the construction process of a conservative algorithms for system (2.12) on the temporal direction by using the AVF method.

For a positive integer $\mathcal{N}$, we set $\tau = \frac{T}{\mathcal{N}}$ as the time step, and denote $t_n = n\tau$, $n = 0, 1, \cdots, \mathcal{N}$. Both sides of equation (2.12) are multiplied by the exponential factor $\exp(-t J^{-1}\mathcal{D}^{\frac{s}{2}})$ and can obtain the following equivalent system

which can be further rewritten as

Then, we integrate system $(3.2)$ over a single time from $t_{n}$ to $t_{n+1}$ and deduce

where ${\mathrm{V}}: = \tau J^{-1}\mathcal{D}^{\frac{s}{2}}$. We note that many strategies have been applied to approximate the integral in system (3.3) for solving the phase field models. Our aim is to develop the energy-preserving scheme for fractional Hamiltonian system, to this end, we use the d${\bf{G}}$ (denote by $\widetilde{\nabla}_{{{\boldsymbol{z}}}}U(\tilde{{{\boldsymbol{z}}}}, {{\boldsymbol{z}}})$) ^[13] to approximate $\nabla_{{{\boldsymbol{z}}}}U({{\boldsymbol{z}}})$, which satisfies

for all $\tilde{{{\boldsymbol{z}}}}, {{\boldsymbol{z}}}$. For the construction of the ETD-AVF scheme, we take the $\widetilde{\nabla}_{{{\boldsymbol{z}}}}U(\tilde{{{\boldsymbol{z}}}}, {{\boldsymbol{z}}})$ as a combination of the coordinate increment $\widetilde{\nabla}_{{{\boldsymbol{z}}}}U(\tilde{{{\boldsymbol{z}}}}, {{\boldsymbol{z}}})$ and the AVF method, namely

This together with system $(3.3)$, the ETD-AVF method is derived as

where

3.2.   Energy conservation of the ETD-AVF method

This subsection will discuss the energy conservation of the proposed ETD-AVF method, to fix the idea, we first present some lemmas for next proof.

Lemma 3.1. ^[14] For a sufficient smooth function $g(z)$ in the neighborhood of zero ($g(0): = \lim\limits_{z\rightarrow0}g(z)$ when $0$ is a removable singularity), it is can be expressed

and the matrix valued function of the matrix $\mathcal{B}$ is given by

Lemma 3.2. Noticing that the operator $\mathcal{D}^{\frac{s}{2}}$ is symmetric, and the matrix $J^{-1}$ is skew-symmetric. Then, we have

Proof. We first prove property (1). According to Lemma 3.1, we have

Similarly, we can prove property (2) easily.

For property (3), based on the definition of $\phi({\mathrm{V}})$ in formula (3.7), we deduce

Then, one can easily obtain property (4).

Subsequently, we can derive that the commutable properties also hold for properties (5) and (6). For simplicity, we omit it.

Theorem 3.1. The constructed scheme (3.6) can inherit the energy of the system, i.e.

where

Proof. From (3.11), we can obtain

According to ETD-AVF scheme (3.5), we have

Then, based on the skew-symmetry of $J^{-1}\phi({\mathrm{V}})^T+\phi({\mathrm{V}}) J^{-1}$, we deduce

This together with (3.13) implies that

We complete the proof.

4.   Numerical experiments

This section taking the fractional NLS equation as an example to verify the theoretical analysis results of the constructed ETD-AVF scheme. For simplicity, the relative Hamiltonian energy error can be defined by

where $H^{n}$ is the Hamiltonian energy energy at $t = n\tau$. The accuracy can be obtained by the formula

where $\tau_{i}$ is the time step, ${\text {error}}_{i}, ({i} = 1, 2)$ represents the $L^{\infty}$-norm errors with $\tau_{i}$.

4.1.   Fractional NLS equation

We study the fractional nonlinear Schrödinger equation with the form

and the system has the initial condition

where $1 < s \leq 2$, ${\text{i}}^2 = -1$, $\phi({{\boldsymbol{x}}}, t)$ is a complex-valued function with $2L$ as period, $t \in (0, T]$, ${{\boldsymbol{x}}}\in[-L, L]^d\subset \mathbb{ R}^d$ ($d$ = 1, 2) and $\phi_0({{\boldsymbol{x}}})$ is a smooth function. System (4.1) can preserve the following fractional Hamiltonian energy, namely

By setting $\phi = u+{\text{i}}v$, we can rewrite system (4.1) as a pair of real-valued equations

Then, the original energy functional $\mathcal{E}(t)$ is further rewritten as

According to the variational derivative formula ^[7], systems (4.4) and (4.5) can be expressed by the following canonical Hamiltonian system

where ${{\boldsymbol{y}}} = (u, v)^T, J = \left(\begin{array}{cc} 0 & 1 \\ -1 & 0 \end{array} \right)$.

Apply the Fourier pseudo-spectral method to discretize systems (4.4) and (4.5), we can obtain a semi-discrete equation

where $\mathcal{D}^{\frac{s}{2}}$ is the spectral differential matrix by using the Fourier pseudo-spectral method to approximate fractional Lpalacian.

By setting ${{\boldsymbol{y}}}(t) = \big({{\boldsymbol{u}}}(t), {{\boldsymbol{v}}}(t)\big)^T$, ${{\boldsymbol{g}}}\big({{\boldsymbol{u}}}(t), {{\boldsymbol{v}}}(t)\big) = \Big(-\beta({{\boldsymbol{u}}}^2+{{\boldsymbol{v}}}^2){{\boldsymbol{v}}}, \beta({{\boldsymbol{u}}}^2+{{\boldsymbol{v}}}^2){{\boldsymbol{u}}}\Big)^T$ and

and systems (4.7) and (4.8) is further expressed as a compact form

Then, we can obtain a ETD-AVF scheme for system (4.9), namely

where

Theorem 4.1. The constructed ETD-AVF scheme (4.10) can preserve the Hamiltonian energy, i.e.,

where

Proof. The proof process is similar to Theorem 3.1.

In addition, we also compare the proposed schemes with existing scheme in computing efficiency, accuracy and conservation. Thus, we define

● AVF: The traditional AVF scheme for solving the fractional NLS equation.

● ETD-AVF: The constructed ETD-AVF energy-preserving scheme in the paper.

● ETD-SAV: The energy-preserving scheme based on the SAV method ^[17].

4.2.   Simulations of the fractional NLS equation

Example 4.1. This example mainly studies the accuracy and conservation properties of the 1D fractional NLS equation with ${\Omega} = [0, 2\pi]$. The solution of the equation has the form

where $\delta$ is the amplitude, $\theta$ is the wave number. Without loss of generality, we take $\delta = 1$, $\theta = 2$, $s = 1.5, 2$ to demonstrate theoretical analysis results.

In practical calculation, we first take $h = \frac{\pi}{16}$ so that the spatial error has no effect on the measurement of time direction accuracy at $T = 1$. In Table 1, we display the discrete maximum-norm errors and the corresponding convergence rates. From the table we can draw that three schemes have second order accuracy for different $s$ in time, and the errors of the AVF and ETD-AVF schemes are smaller than that of the ETD-SAV scheme. Table 2 presents the spatial errors with $\tau = 10^{-6}$, numerical results show that the three schemes are convergent with arbitrary order spatial accuracy. In addition, as $s$ increases, the spatial errors also increase.

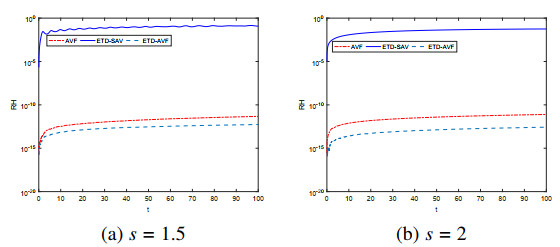
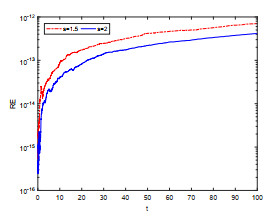
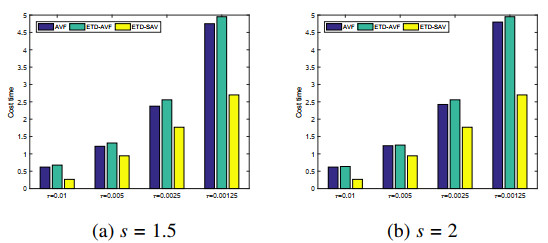
Then, we take $T = 100$ and study the conservation properties of three schemes for solving system (4.1). The relative errors of original energy computed by three schemes for different $s$ in discrete sense are are displayed in Figure 1. As is shown above, the AVF and ETD-AVF method can inherit the Hamiltonian energy, but the ETD-SAV scheme can not. Figure 2 shows that the ETD-SAV scheme conserves the modified energy very well. In Figure 3, we show comparisons on the computational costs of three schemes with $T = 20$. Obviously, we find that the ETD-AVF scheme enjoys the same computational advantages as the AVF scheme, this is because the exponential integral factor can be quickly calculated by FFT technique. Compared with the AVF scheme, the linearly-implicit ETD-SAV scheme reduces the computational cost. Therefore, the proposed method is the best choice to develop conservative schemes to conserve the original energy.

Example 4.2. This example mainly studies system (4.1) in 2D case with

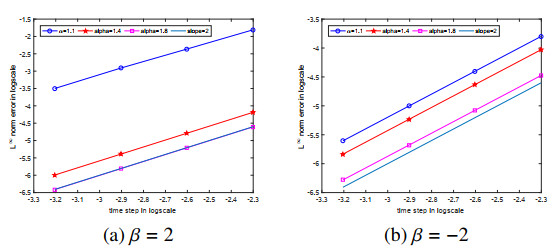
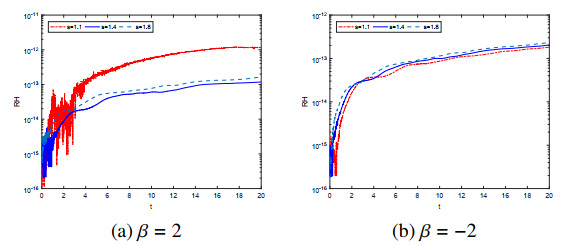
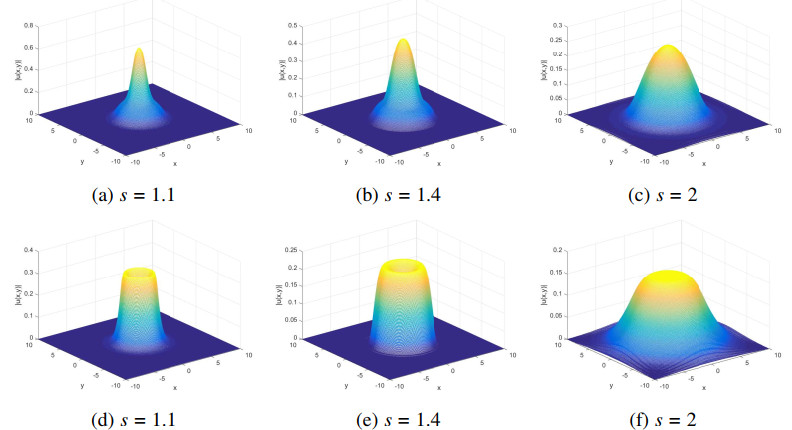
Here, we set $\Omega = [-10, 10]^2$ and take $s = 1.1, 1.4, 1.8$. The parameter $\beta = \pm2$ correspond to the focusing and defocusing case, respectively. We first study the accuracy of the ETD-AVF scheme for the 2D system. The exact solution of system is not given, thus, we compute the numerical errors by using the formula $\lVert e \rVert_{\infty} = \|\phi_{}^{N}(h, \tau)-\phi_{}^{2N}(h, \tau/2)\|_{\infty}$. Figure 4 reveals the proposed scheme has second accuracy with different fractional order $s$ for $\beta = \pm2$. We display the relative energy errors in Figure 5. As the picture shows, the constructed scheme can conserve the discrete Hamiltonian energy. At the last, we define $|u(x, y)| = \sqrt{{{\boldsymbol{u}}}^2+{{\boldsymbol{v}}}^2}$ and give the plots the density function $|u(x, y)|$ with different $s$ in Figure 6. Obviously, we find that the fractional order $s$ affects the shape of the wave. In addition, the focusing case belongs to the lower row of the Figure 6, and the upper row is the defocusing case. The soliton evolution diagram are quite similar to the numerical results proposed in ^[22].

5.   Conclusions

The paper develops an exponential averaged vector field scheme for solving fractional conservative partial differential equations. The derived scheme is built upon the Hamiltonian structure of the equation. The energy conservation and stability of the given method are demonstrated by theoretical proof and numerical experiments. Unfortunately, it is difficult to discuss the convergence of the present scheme because the exponential factor is introduced into the numerical scheme, which makes the new system more complex and challenging to prove the convergence of the proposed scheme. In further work, we will try to prove the convergence of the developed scheme.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (No. 12201071, 12001471), Natural Science Foundation of Henan (No. 212300410323), and the Program for Scientific and Technological Innovation Talents in Universities of Henan Province (No. 22HASTIT018).

Conflict of interest

The authors declare that they have no competing interests.