Existence and stability of fuzzy Pareto-Nash equilibria for fuzzy constrained multi-objective games with fuzzy payoffs

1.   Introduction

Multi-objective games are games with vector-valued payoffs, which were first studied by Zeleny ^[56]. Since then, many scholars have begun to pay attention to multi-objective games; see ^{[16,44,52,54]}. Yu and Yuan ^[52] used Ky Fan's minimax inequality and the Fan-Glicksberg fixed point theorem to study the existence of Pareto equilibria in multi-objective games. Considering the feasible strategy correspondence in the multi-objective game, the constrained multi-objective game can be obtained. Ding ^[15] first proved the existence of Pareto equilibria in constrained multi-objective games by using the quasi-equilibrium existence theorem, and the results were extended in ^[52]. Subsequently, some scholars have focused on the existence of equilibria and the stability of equilibrium sets in constrained multi-objective games; see ^[14,29,41] and references therein.

The main limitation of traditional non-cooperative games is that all data in the game are assumed to be known accurately by the players. In real-world games, players often cannot accurately assess the payoffs of different strategies or their own and other players' preferences. Usually, the uncertainty involved in the game includes fuzziness, randomness and fuzzy randomness.

Zadeh ^[55] first introduced fuzzy set theory. Subsequently, Butnariu ^[8] introduced fuzzy sets in non-cooperative games. Campos ^[9] proposed a fuzzy linear programming method to solve the fuzzy two-player zero-sum matrix game. This method is more suitable for solving the problem that the payoff is a triangular fuzzy number. Based on the literature ^[23,39], Clemente ^[12] introduced the standard fuzzy orders to compare the fuzzy payoffs and studied the Pareto equilibrium of the fuzzy matrix game. Buckley ^[7] used the decision principles of Bellman and Zadeh ^[4] in fuzzy environments to formulate multi-objective non-cooperative games under uncertainty. Kim and Lee ^[25] extended generalized games to generalized fuzzy games and established the existence of fuzzy equilibria for generalized fuzzy games. For generalized games and generalized multi-objective games, in addition to the ambiguity of payoffs, the ambiguity of strategy choice is also studied; see ^[19,24]. For more literature on fuzzy matrix games and generalized fuzzy games; see ^{[6,26,37,40,47]} and references therein.

Since the $\alpha$-cut of a fuzzy number is a compact interval, we need to investigate the properties of fuzzy games with the help of interval analysis. Moore ^[35] systematically introduced the theory of interval analysis for the first time. Subsequently, many scholars further developed the theory of interval arithmetic and interval-valued functions; see ^[1,10,36,42] and references therein. Li et al. ^[28] discussed the weak Pareto-Nash equilibria of generalized interval-valued multi-objective games with fuzzy mappings and gave the existence theorem of weak Pareto-Nash equilibrium. In game theory, the current application of interval analysis is mainly to discuss the existence of equilibria of interval-valued matrix games and their calculation methods; see, e.g., ^{[13,27,28,30]}. Stefanini and Bede ^[42] introduced the concept of $gH$-difference, which is a generalization of $H$-difference. The $gH$-difference is applied to several topics in interval mathematical analysis, such as interval optimization problems ^{[20,21,38,46]}, interval differential equations ^[31,42,43] and so on.

Anderlini and Canning ^[2] established a kind of model with abstract rational function in a general decision environment as follows:

Definition 1.1. A bounded rationality model $\mathcal{M}$ consists of a quadruple $\{\Gamma, X, K, R\}$ with the following interpretation.

(1) $\Gamma$ is a nonempty parameter space;

(2) $X$ is an action space;

(3) $K: \Gamma \times X \rightrightarrows X$ is a feasibility correspondence, and $K$ induces a further correspondence $k: \Gamma \rightrightarrows X$ defined by $k(\gamma) = \{ x \in X\ |\ x \in K(\gamma, x)\}$ for $\gamma \in \Gamma$;

(4) $R: Graph(k) \to \mathbb{R}_+$ is a rationality function with $R(\gamma, x) = 0$ corresponding to perfect rationality, where $Graph(k) = \{(\gamma, x) \in \Gamma \times X \ |\ x \in k(\gamma)\}$ is the graph of $k$.

For any $\gamma \in \Gamma$ and $\epsilon \ge 0$, the set of all $\epsilon$-equilibria of $\gamma$ is defined as $E(\gamma, \epsilon) = \{ x \in k(\gamma)\ |\ R(\gamma, x) \le \epsilon\}$, and $E(\gamma) = E(\gamma, 0) = \{ x \in k(\gamma)\ |\ R(\gamma, x) = 0 \}$ is the set of all equilibria of $\gamma$. The notions of structural stability and robustness to $\epsilon$-equilibria for a bounded rationality model were introduced in ^[2]. A model is structurally stable if the equilibrium set (given fully rational agents) varies continuously with the parameter values of the model. A model is robust to $\epsilon$-equilibria if small deviations from rationality result can lead to only small changes in the equilibrium set. Since then, many researchers began to discuss structural stability and robustness to $\epsilon$-equilibrium for the bounded rationality model. They presented a series of applications to non-cooperative games and fixed point problems; see, e.g., ^{[33,48,49,51,53]}.

Hung et al. ^[24] discussed the existence of fuzzy equilibria in generalized multi-objective games with fuzzy mappings when the payoff space is a Hausdorff topological vector space and investigated the structural stability and robustness of $\epsilon$-equilibrium for this class of games in the framework of bounded rationality. Furthermore, when the payoff space is a Banach space, with the help of an abstract rationality function, a bounded rationality model for generalized multi-objective games with fuzzy mappings was constructed. However, Wang et al. ^[45] pointed out that the space of fuzzy vectors is a quasi-linear space, not a linear space. Therefore, it is impossible to directly obtain the fuzzy constrained multi-objective game with fuzzy payoffs by using the conclusions in ^[24].

Motivated by ^[24,28], we are concerned in this paper with a class of fuzzy constrained multi-objective games with fuzzy payoffs. With the help of the $\alpha$-cuts of fuzzy vectors and the partial order of interval vectors, we establish the partial order of fuzzy vectors. Moreover, the definitions of fuzzy Pareto-Nash equilibrium and fuzzy $\alpha$-Pareto-Nash equilibrium are introduced. Based on Berge's maximum theorem for fuzzy-valued functions (interval-valued functions) and the Fan-Glicksberg fixed point theorem, the existence of a fuzzy Pareto-Nash equilibrium (fuzzy $\alpha$-Pareto-Nash equilibrium) for the FCMGFP is investigated. Furthermore, the bounded rationality model is applied to a new class of FCMGFPs.

This article is organized as follows. In Section 2, we review some basic terminology and related facts. In Section 3, we first discuss the semi-continuity and generalized quasi-concavity for fuzzy vector-valued functions. Moreover, we get Berge's maximum theorem for the fuzzy-vector-valued function. Second, we obtain two existence theorems of fuzzy Pareto-Nash equilibria and fuzzy $\alpha$-Pareto-Nash equilibria for FCMGFPs. These new results directly yield the existence theorems of fuzzy Pareto-Nash equilibria and fuzzy $\alpha$-Pareto-Nash equilibria for fuzzy constrained games with fuzzy payoffs (FCGFPs). In Section 4, we construct the rationality functions for FCMGFPs with the help of the nonlinear scalarization function of interval vectors. A further discussion approaches the structural stability ($(\gamma, \epsilon)$-stability) and the robustness to $\epsilon$-equilibria ($(\gamma, \epsilon)$-robustness) for this class of games. Finally, the conclusion is made in Section 5.

2.   Preliminaries and terminology

Throughout this paper, we write $\mathbb{R}$ for the set of all real numbers, $\mathbb{R}_+$ for the set of all nonnegative real numbers, $\mathbb{N}$ for the set of all natural numbers and $\mathbb{R}^d$ for $d$-dimensional Euclidean space. We recall basic terminology and some related conclusions in this section.

2.1.   Interval vectors and interval-vector-valued functions

We now review the relevant properties of interval vectors and interval vector-valued functions.

2.1.1.   Interval vectors

Let $\mathcal{I}(\mathbb{R})^d$ be the family of all $d$-dimensional interval vectors, and let

where $\mathcal{I}(\mathbb{R}_+)$ is the family of all compact intervals contained in $[0, +\infty)$. For $\boldsymbol{A} = (A_1, \ldots, A_d), \boldsymbol{B} = (B_1, \ldots, B_d) \in \mathcal{I}(\mathbb{R})^d$ and $t \in \mathbb{R}$, $\boldsymbol{A} + \boldsymbol{B} = (A_1 + B_1, \ldots, A_d + B_d)$, and $t \cdot \boldsymbol{A} = (t \cdot A_1, \ldots, t \cdot A_d)$. The $gH$-difference between $\boldsymbol{A}$ and $\boldsymbol{B}$, $\boldsymbol{A} \ominus \boldsymbol{B}$, is defined by $\boldsymbol{A} \ominus \boldsymbol{B} = (A_1 \ominus B_1, \ldots, A_d \ominus B_d)$, where $A_i = [\underline{a}_i, \overline{a}_i]$, $B_i = [\underline{b}_i, \overline{b}_i]$, and $A_i \ominus B_i = [\min\{\underline{a}_i - \underline{b}_i, \overline{a}_i - \overline{b}_i\}, \max\{\underline{a}_i - \underline{b}_i, \overline{a}_i - \overline{b}_i\}]$. In particular, $(-1) \cdot (\boldsymbol{A} \ominus \boldsymbol{B}) = \boldsymbol{B} \ominus \boldsymbol{A}$.

Definition 2.1. (See ^[28]) For $\boldsymbol{A} = (A_1, \ldots, A_d) \in \mathcal{I}(\mathbb{R})^d$, the function $\|\cdot\|_{\mathcal{I}(\mathbb{R})^d} : \mathcal{I}(\mathbb{R})^d \to \mathbb{R}_+$ defined by $\| \boldsymbol{A} \|_{\mathcal{I}(\mathbb{R})^d} = \left(\sum_{i = 1}^d \| A_i \|_{\mathcal{I}(\mathbb{R})}^2 \right) ^{1/2}$ is called a norm on $\mathcal{I}(\mathbb{R})^d$, where $\| A_i \|_{\mathcal{I}(\mathbb{R})} = \max \{ |\underline{a}_i|, |\overline{a}_i| \}$.

The set of all interval vectors $\mathcal{I}(\mathbb{R})^d$ equipped with the norm $\|\cdot\|_{\mathcal{I}(\mathbb{R})^d}$ is a normed quasilinear space with respect to the operations $\{ +, \ominus, .\}$, and $(\mathcal{I}(\mathbb{R})^d, \|\cdot\|_{\mathcal{I}(\mathbb{R})^d})$ is a complete normed quasilinear space. With the topology induced by norm $\| \cdot \|_{\mathcal{I}(\mathbb{R})^d}$ on $\mathcal{I}(\mathbb{R})^d$, it follows that $int \mathcal{I}(\mathbb{R_+})^d = \left\{\boldsymbol{A} = (A_1, \ldots, A_d)\ |\ A_i \in int \mathcal{I}(\mathbb{R}_+), i = 1, \ldots, d \right\}$.

Lemma 2.2. (See ^[28]) For two convergent sequences $\{\boldsymbol{A}^m\}$ and $\{\boldsymbol{B}^m\}$ in $\mathcal{I}(\mathbb{R})^d$,

It is noteworthy that although $+$ is associative in $\mathcal{I}(\mathbb{R})$, for $A, B \in \mathcal{I}(\mathbb{R})$, the interval $(A \ominus B) + B$ is not always equal to $A$. Ghosh et el. ^[21] verified that

Lemma 2.3. For all $\boldsymbol{A}, \boldsymbol{B}, \boldsymbol{C} \in \mathcal{I}(\mathbb{R})^d$, $\|\boldsymbol{A} \ominus \boldsymbol{B}\|_{\mathcal{I}(\mathbb{R})^d} \le \| \boldsymbol{A} \ominus \boldsymbol{C} \|_{\mathcal{I}(\mathbb{R})^d} + \| \boldsymbol{C} \ominus \boldsymbol{B} \|_{\mathcal{I}(\mathbb{R})^d}$.

Proof. See Appendix A.□

Definition 2.4. (See ^[28]) Let $\boldsymbol{A} = (A_1, \ldots, A_d)$ and $\boldsymbol{B} = (B_1, \ldots, B_d)$ be two elements of $\mathcal{I}(\mathbb{R})^d$.

(1) $\boldsymbol{A}$ is said to be dominated by $\boldsymbol{B}$ from below if $\boldsymbol{A} \ominus \boldsymbol{B} \in \mathcal{I}(\mathbb{R_+})^d$, and then we write $\boldsymbol{B} \preceq \boldsymbol{A}$. Otherwise, we write $\boldsymbol{B} \npreceq \boldsymbol{A}$.

(2) $\boldsymbol{A}$ is said to be strictly dominated by $\boldsymbol{B}$ from below if $\boldsymbol{A} \ominus \boldsymbol{B} \in int \mathcal{I}(\mathbb{R_+})^d$, and then we write $\boldsymbol{B} \prec \boldsymbol{A}$. Otherwise, we write $\boldsymbol{B} \nprec \boldsymbol{A}$.

2.1.2.   Interval-vector-valued functions

Let $\mathcal{X}$ be a Hausdorff topological space, and let $F = \{f_1, \ldots, f_d \} : \mathcal{X} \to \mathcal{I}(\mathbb{R})^d$ be an interval-vector-valued function. $F$ is upper semi-continuous (resp., lower semi-continuous) provided that for each $x \in \mathcal{X}$ and for each $\epsilon > 0$, there exists an open neighborhood $o(x)$ of $x$ such that for each $x' \in o(x)$, $F(x') \ominus F(x) \in V_{\epsilon}^d - \mathcal{I}(\mathbb{R_+})^d$ (resp., $F(x') \ominus F(x) \in V_{\epsilon}^d + \mathcal{I}(\mathbb{R_+})^d$), where $V_{\epsilon}^d = \{(A_1, \ldots, A_d)\ |\ A_i \subset (-\epsilon, \epsilon), i = 1, \ldots, d \}$. Furthermore, $F$ is continuous if it is both lower and upper semi-continuous.

Definition 2.5. (See ^[28]) Let $\mathcal{K}$ be a nonempty convex subset of a Hausdorff topological space $\mathcal{Y}$, and let $F = \{f_1, \ldots, f_d \} : \mathcal{K} \to \mathcal{I}(\mathbb{R})^d$ be an interval-vector-valued function. Then, $F$ is said to be generalized $\mathcal{I}(\mathbb{R_+})^d$-quasi-concave on $\mathcal{K}$ provided that for $x_1, x_2 \in \mathcal{K}$, $\boldsymbol{A} \in \mathcal{I}(\mathbb{R})^d$, and for $\lambda \in [0, 1]$, if $\boldsymbol{A} \ominus F(x_i) \notin int \mathcal{I}(\mathbb{R_+})^d$ with $i = 1, 2$, we have $\boldsymbol{A} \ominus F(\lambda x_1 + (1-\lambda) x_2) \notin int \mathcal{I}(\mathbb{R_+})^d$.

Lemma 2.6. (See ^[28]) Let $\mathcal{C}$ be a nonempty compact subset of a Hausdorff topological space $\mathcal{X}$ and $F = \{f_1, \ldots, f_d \} : \mathcal{C} \to \mathcal{I}(\mathbb{R})^d$ be an interval-vector-valued function. If there exists $i \in \{1, \ldots, d\}$ such that $f_i$ is upper semi-continuous on $\mathcal{C}$, then there is $x^* \in \mathcal{C}$ such that $F(x^*) \nprec F(x)$ for all $x \in \mathcal{C}$.

Definition 2.7. (See ^[28]) Let $F = \{f_1, \ldots, f_d \} : \mathcal{K} \subset \mathbb{R} \to \mathcal{I}(\mathbb{R})^d$ be an interval-vector-valued function. Then, $F$ is said to be non-decreasing (resp., non-increasing) on $\mathcal{K}$ if, for $x_1, x_2 \in \mathcal{K}$ and $x_1 < x_2$, we have $F(x_1) \preceq F(x_2)$ (resp., $F(x_2) \preceq F(x_1)$).

Lemma 2.8. (See ^[28]) An interval-vector-valued function $F = \{f_1, \ldots, f_d \} : \mathcal{K} \subset \mathbb{R} \to \mathcal{I}(\mathbb{R})^d$ is non-decreasing (resp., non-increasing) if and only if $\underline{f}_i$ and $\overline{f}_i$ are non-decreasing (resp., non-increasing) for each $i$.

2.2.   Fuzzy sets and fuzzy mapping

Let $X$ denote a universal set. A fuzzy subset $\widetilde{a}$ of $X$ is defined by its membership function $\mu_{\widetilde{a}}: X \to [0, 1]$, which assigns to each element $x \in X$ a real number $\mu_{\widetilde{a}}(x)$ in the interval $[0, 1]$. Especially, $\mu_{\widetilde{a}}(x)$ is the grade of membership of $x$ in the set $\widetilde{a}$. The $\alpha$-cut of $\widetilde{a}$, denoted by $\widetilde{a}^{\alpha}$, is a set defined by $\widetilde{a}^{\alpha} = \{ x \in X \ |\ \mu_{\widetilde{a}}(x) \geq \alpha \}$, when $\alpha \in (0, 1]$, and $\widetilde{a}^0 = cl \{x \in X \ |\ \mu_{\widetilde{a}}(x) > 0 \}$, where $cl$ represents the closure of sets. For more detail, see ^[17,55].

Definition 2.9 (See ^[17]) A fuzzy number $\widetilde{I}$ is a fuzzy set on $\mathbb{R}$, whose membership function $\mu_{\widetilde{I}}(\cdot) : \mathbb{R} \to [0, 1]$ satisfies the following conditions:

(1) $\mu_{\widetilde{I}}(x) = 0$ for all $x \in (- \infty, c]$,

(2) $\mu_{\widetilde{I}}(\cdot)$ is strictly increasing and continuous on $[c, a]$,

(3) $\mu_{\widetilde{I}}(x) = 1$ for all $x \in [a, b]$,

(4) $\mu_{\widetilde{I}}(\cdot)$ is strictly decreasing and continuous on $[b, d]$,

(5) $\mu_{\widetilde{I}}(x) = 0$ for all $x \in [d, + \infty)$,

where $- \infty < c \le a \le b \le d < + \infty$.

As usual, write $\mathcal{F}(\mathbb{R})$ for the family of all fuzzy numbers, and $\mathcal{F}(\mathbb{R})^d$ for the family of all $d$-dimensional fuzzy vectors. We use $\widetilde{\boldsymbol{A}}, \widetilde{\boldsymbol{B}}, \widetilde{\boldsymbol{C}}, \cdots$ to denote the elements of $\mathcal{F}(\mathbb{R})^d$. Given $\widetilde{\boldsymbol{A}} = (\widetilde{A}_1, \ldots, \widetilde{A}_d) \in \mathcal{F}(\mathbb{R})^d$ and $\alpha \in [0, 1]$, the $\alpha$-cut of $\widetilde{\boldsymbol{A}}$ is an interval vector $\widetilde{\boldsymbol{A}}^{\alpha} = (\widetilde{A}_1^{\alpha}, \ldots, \widetilde{A}_d^{\alpha}) \in \mathcal{I}(\mathbb{R})^d$, where $\widetilde{A}_i^{\alpha}$ is the $\alpha$-cut of $\widetilde{A}_i$ for $i = 1, ..., d$.

Let $\mathcal{X}$ and $\mathcal{Y}$ be two Hausdorff topological vector spaces and $X \subset \mathcal{X}$, $Y \subset \mathcal{Y}$ be two nonempty convex subsets. A mapping $\widetilde{S}: X \to \mathcal{F}(Y)$ is called a fuzzy mapping where $\mathcal{F}(Y)$ denotes the collection of fuzzy sets on $Y$. If $\widetilde{S}$ is a fuzzy mapping, $\widetilde{S}(x)$ (denoted by $\widetilde{S}_x$) is a fuzzy set, and $\widetilde{S}_x(y)$ is the membership function of $y$ in $\widetilde{S}_x$.

Definition 2.10. (See ^[11]) A fuzzy mapping $\widetilde{S}: X \to \mathcal{F}(Y)$ is convex if, for every $x \in X$, $y, z \in Y$ and $\lambda \in [0, 1]$, we have $\widetilde{S}_x(\lambda y + (1- \lambda)z) \ge \min \{\widetilde{S}_x(y), \widetilde{S}_x(z) \}$.

Lemma 2.11. (See ^[11]) Let $s: X \to [0, 1]$ be a function. If $\widetilde{S}: X \to \mathcal{F}(Y)$ is convex, and $S: X \rightrightarrows Y$ is defined by $S(x) = (\widetilde{S}_x)^{s(x)}$ for $x \in X$, then $S$ is a correspondence with convex values.

2.3.   Set valued analysis

Let $X$ and $Y$ be two Hausdorff topological spaces and $F: X \rightrightarrows Y$ be a correspondence. $F$ is upper semi-continuous (resp., lower semi-continuous) if, for each $x \in X$ and for each open set $G \subset Y$ with $F(x) \subset G$ (resp., $F(x) \cap G \neq \emptyset$), there exists a neighborhood $o(x)$ of $x$ such that $F(x') \subset G$ (resp., $F(x') \cap G \neq \emptyset$) for each $x' \in o(x)$. $F$ is continuous if it is both lower and upper semi-continuous. The graph of $F$ is $Graph (F) = \{ (x, y) \in X \times Y\ |\ y \in F(x)\}$, and $F$ is closed if $Graph (F)$ is closed on $X \times Y$. For more details, see ^[3,18,22,50].

Lemma 2.12. (See ^[50]) Let $X$ and $Y$ be two Hausdorff topological spaces, and $Y$ be compact. Then, $F: X \rightrightarrows Y$ is upper semi-continuous with nonempty and compact values if and only if it is closed.

Lemma 2.13. (See ^[50]) Let $F, G: X \rightrightarrows Y$ be two correspondences with $F(x) \cap G(x) \neq \emptyset$ for all $x \in X$. If $F$ is closed, and $G$ is upper semi-continuous with nonempty and compact values, then $F \cap G$ is upper semi-continuous.

Theorem 2.14. (Fan-Glicksberg ^[18,22]) Let $\mathcal{V}$ be a locally convex Hausdorff topological vector space, and let $X$ be a nonempty compact subset of $\mathcal{V}$. If $\Phi : X \rightrightarrows X$ is upper semi-continuous with nonempty, convex and compact values, then there exists $x^* \in X$ such that $x^* \in \Phi(x^*)$.

2.4.   Structural stability and robustness

Let us recall the structural stability and robustness of the bounded rationality model according to ^[2,48,49].

Definition 2.15. (See ^[2]) Let $(\Gamma, \rho)$ be a metric space.

(1) The model $\mathcal{M}$ is said to be structurally stable at $\gamma \in \Gamma$ if the equilibrium correspondence $E: \Gamma \times \mathbb{R}_+ \rightrightarrows X$ is continuous at $\gamma \in \Gamma$.

(2) The model $\mathcal{M}$ is said to be robust to $\epsilon$-equilibria at $\gamma \in \Gamma$ if for any $\delta > 0$, there exists $\hat{\epsilon} > 0$ such that $H (E(\gamma', \epsilon), E(\gamma')) < \delta$, for any $\gamma' \in \Gamma$ with $\epsilon < \hat{\epsilon}$ and $\rho(\gamma, \gamma') < \hat{\epsilon}$, where $H$ is the Hausdorff distance defined on $X$.

Definition 2.16. (See ^[34]) Let $(\Gamma, \rho)$ be a metric space.

(1) The model $\mathcal{M}$ is said to be $(\gamma, \epsilon)$-stable if the equilibrium correspondence $E: \Gamma \times \mathbb{R}_+ \rightrightarrows X$ is continuous at $(\gamma, \epsilon) \in \Gamma \times \mathbb{R}_+$.

(2) The model $\mathcal{M}$ is said to be $(\gamma, \epsilon)$-robust if for any $\delta > 0$, there exists $\hat{\epsilon} > 0$ such that $H (E(\gamma', \epsilon), E(\gamma', \epsilon')) < \delta$, for any $(\gamma', \epsilon') \in \Gamma \times \mathbb{R}_+$ with $|\epsilon - \epsilon'| < \hat{\epsilon}$ and $\rho(\gamma, \gamma') < \hat{\epsilon}$, where $H$ is the Hausdorff distance defined on $X$.

In particular, taking $\epsilon' = 0$ in Definition 2.16 (2), we can get the definition of robustness to $\epsilon$-equilibria. A model that is $(\gamma, 0)$-stable is structurally stable, that is, $E: \Gamma \rightrightarrows X$ is continuous at $\gamma \in \Gamma$.

Lemma 2.17. (See ^{[34,48,49,53]}) Let $\Gamma$ be a complete metric space and $X$ be a compact metric space. Let $k: \Gamma \rightrightarrows X$ be an upper semi-continuous correspondence, and let $R: Graph(k) \to \mathbb{R}_+$ be a lower semi-continuous function. For any $\gamma \in \Gamma$, $E(\gamma) \neq \emptyset$,

(1) the correspondence $E: \Gamma \rightrightarrows X$ is upper semi-continuous;

(2) there exists a dense $G_{\delta}$ subset $Q$ of $\Gamma$ such that $\mathcal{M}$ is structurally stable at every $\gamma \in Q$;

(3) if the model $\mathcal{M}$ is structurally stable at $\gamma \in \Gamma$, then $\mathcal{M}$ is robust to $\epsilon$-equilibria at $\gamma \in \Gamma$, and $\mathcal{M}$ is robust to $\epsilon$-equilibria at $\gamma \in Q$;

(4) if $\gamma \in Q$, $\gamma_m \to \gamma$, and $\epsilon_m \to 0$, then $H(E(\gamma_m, \epsilon_m), E(\gamma)) \to 0$;

(5) if $E(\gamma)$ is a singleton set, then $\mathcal{M}$ is structurally stable and robust to $\epsilon$-equilibria at $\gamma \in \Gamma$;

(6) if the model $\mathcal{M}$ is $(\gamma, \epsilon)$-stable, then $\mathcal{M}$ is $(\gamma, \epsilon)$-robust.

3.   Existence of fuzzy Pareto-Nash equilibria

In this section, we focus on the fuzzy Pareto-Nash equilibria of the FCMGFP. We first discuss the semi-continuity and generalized quasi-concavity of fuzzy-vector-valued functions. Then, we obtain Berge's maximum theorem for fuzzy-vector-valued functions. Based on this theorem, we establish two existence theorems of fuzzy Pareto-Nash equilibria and fuzzy $\alpha$-Pareto-Nash equilibria for FCMGFP. Throughout this section, we write $\mathcal{X}$ for a Hausdorff topological space, $\mathcal{Y}$ for a Hausdorff topological vector space and $\mathcal{V}_i$ for a locally convex Hausdorff topological vector space.

3.1.   Fuzzy-vector-valued functions

Let $\widetilde{F} = \{\widetilde{f}_1, ..., \widetilde{f}_d \} : \mathcal{X} \to \mathcal{F}(\mathbb{R})^d$ be a fuzzy-vector-valued function. By the $\alpha$-cuts of fuzzy vectors, we can obtain the interval-vector-valued function $\widetilde{F}^{\alpha} = \{\widetilde{f}_1^{\alpha}, ..., \widetilde{f}_d^{\alpha} \}: \mathcal{X} \times [0, 1] \to \mathcal{I}(\mathbb{R})^d$, defined for $(x, \alpha) \in \mathcal{X} \times [0, 1]$ by $\widetilde{F}^{\alpha}(x) = (\widetilde{f}_1^{\alpha}(x), ..., \widetilde{f}_d^{\alpha}(x))$.

We use the related properties of interval-vector-valued functions to establish the semi-continuity and generalized quasi-concavity of fuzzy-vector-valued functions.

Definition 3.1. A fuzzy-vector-valued function $\widetilde{F} = \{\widetilde{f}_1, ..., \widetilde{f}_d \} : \mathcal{X} \to \mathcal{F}(\mathbb{R})^d$ is upper semi-continuous (resp., lower semi-continuous, continuous) if the corresponding interval-vector-valued function $\widetilde{F}^{\alpha} = \{ \widetilde{f}_1^{\alpha}, ..., \widetilde{f}_d^{\alpha} \} : \mathcal{X} \times [0, 1] \to \mathcal{I}(\mathbb{R})^d$ is upper semi-continuous (resp., lower semi-continuous, continuous).

Remark 3.2. A fuzzy-vector-valued function $\widetilde{F} = \{\widetilde{f}_1, ..., \widetilde{f}_d \} : \mathcal{X} \to \mathcal{F}(\mathbb{R})^d$ is upper semi-continuous (resp., lower semi-continuous, continuous) if and only if each $\widetilde{f}_i : \mathcal{X} \to \mathcal{F}(\mathbb{R})$ is upper semi-continuous (resp., lower semi-continuous, continuous).

Assume that $\mathcal{F}_0(\mathbb{R})$ is the family of all triangular fuzzy numbers. Let $\widetilde{A} = (a, b, c) \in \mathcal{F}_0(\mathbb{R})$ and $\alpha \in [0, 1]$. Then, the $\alpha$-cut of $\widetilde{A}$ is an interval $\widetilde{A}^{\alpha} = [ a + \alpha (b-a), c - \alpha (c - b)]$.

Example 3.3. Consider the fuzzy-vector-function $\widetilde{F}(x) = (\widetilde{f}_1(x), \widetilde{f}_2(x))$, where $\widetilde{f}_1(x) = (2, 3, 4)x + (3, 4, 5)$, and $\widetilde{f}_2(x) = (1, 2, 3)x^2 + (2, 3, 4)$ for $x \in \mathbb{R}$. Since $\widetilde{f}^{\alpha}_1(x) = [2 + \alpha, 4 - \alpha]x + [3 + \alpha, 5 - \alpha]$ and $\widetilde{f}^{\alpha}_2(x) = [1 + \alpha, 3 - \alpha]x^2 + [2 + \alpha, 4 - \alpha]$ are continuous on $\mathbb{R} \times [0, 1]$, $\widetilde{F}$ is a continuous fuzzy-vector-valued function.

Based on the partial order of interval vectors, we use $\alpha$-cuts to establish the following partial order of fuzzy vectors.

Definition 3.4. Let $\widetilde{\boldsymbol{A}}$ and $\widetilde{\boldsymbol{B}}$ be two elements of $\mathcal{F}(\mathbb{R})^d$.

(1) $\widetilde{\boldsymbol{A}}$ is said to be dominated by $\widetilde{\boldsymbol{B}}$ from below if $\widetilde{\boldsymbol{B}}^{\alpha} \preceq \widetilde{\boldsymbol{A}}^{\alpha}$ for all $\alpha \in [0, 1]$, and we rewrite this property as $\widetilde{\boldsymbol{B}} \preceq \widetilde{\boldsymbol{A}}$. Otherwise, we write $\widetilde{\boldsymbol{B}} \npreceq \widetilde{\boldsymbol{A}}$.

(2) $\widetilde{\boldsymbol{A}}$ is said to be strictly dominated by $\widetilde{\boldsymbol{B}}$ from below if $\widetilde{\boldsymbol{B}}^{\alpha} \prec \widetilde{\boldsymbol{A}}^{\alpha}$ for all $\alpha \in [0, 1]$, and we rewrite this property as $\widetilde{\boldsymbol{B}} \prec \widetilde{\boldsymbol{A}}$. Otherwise, we write $\widetilde{\boldsymbol{B}} \nprec \widetilde{\boldsymbol{A}}$.

In particular, when $d = 1$, the partial order $\preceq$ in Definition 3.4 is equivalent to the fuzzy maximum order in ^[32,39]. According to Definitions 2.4 and 3.4, the following lemma is obvious.

Lemma 3.5. For two elements $\widetilde{\boldsymbol{A}}$ and $\widetilde{\boldsymbol{B}}$ of $\mathcal{F}(\mathbb{R})^d$, the following assertions hold:

(1) $\widetilde{\boldsymbol{B}} \preceq \widetilde{\boldsymbol{A}} \ \mathit{\mbox{if and only if}} \ \widetilde{\boldsymbol{A}}^{\alpha} \ominus \widetilde{\boldsymbol{B}}^{\alpha} \in \mathcal{I}(\mathbb{R_+})^d\ for \; all\ \alpha \in [0, 1]$.

(2) $\widetilde{\boldsymbol{B}} \nprec \widetilde{\boldsymbol{A} } \ \mathit{\mbox{if and only if there is}}\ \alpha \in [0, 1]\ \mathit{\mbox{such that}}\ \widetilde{\boldsymbol{A}}^{\alpha} \ominus \widetilde{\boldsymbol{B}}^{\alpha} \notin int\mathcal{I}(\mathbb{R_+})^d$.

Definition 3.6. Let $\mathcal{K}$ be a nonempty convex subset of $\mathcal{Y}$. A fuzzy-vector-valued function $\widetilde{F} = \{ \widetilde{f}_1, ..., \widetilde{f}_d \} : \mathcal{K} \to \mathcal{F}(\mathbb{R})^d$ is said to be generalized quasi-concave on $\mathcal{K}$ provided that for $x_1, x_2 \in \mathcal{K}$ and $\lambda \in [0, 1]$, and for $\widetilde{\boldsymbol{A}} \in \mathcal{F}(\mathbb{R})^d$, if $\widetilde{F} (x_i) \nprec \widetilde{\boldsymbol{A}}$ with $i = 1, 2$, we have

Lemma 3.7. Let $\widetilde{F} = \{ \widetilde{f}_1, ..., \widetilde{f}_d \} : \mathcal{K} \subset \mathbb{R} \to \mathcal{F}(\mathbb{R})^d$ be a fuzzy-vector-valued function. If $\widetilde{F}^{\alpha}: \mathcal{K} \to \mathcal{I}(\mathbb{R})^d$ is non-decreasing (or non-increasing) for each $\alpha \in [0, 1]$, then $\widetilde{F}$ is generalized quasi-concave.

Proof. See Appendix B. □

In Example 3.3, for each $\alpha \in [0, 1]$, since $\underline{\widetilde{f}_1^{\alpha}}(x) = (2 + \alpha)x + (3 + \alpha)$, $\overline{\widetilde{f}_1^{\alpha}}(x) = (4 - \alpha)x + (5 - \alpha)$, $\underline{\widetilde{f}_2^{\alpha}}(x) = (1 + \alpha)x^2 + (2 + \alpha)$ and $\overline{\widetilde{f}_2^{\alpha}}(x) = (3 - \alpha)x^2 + (4 - \alpha)$ are non-decreasing on $[0, +\infty)$, from Lemma 3.7, it follows that $\widetilde{F}$ is generalized quasi-concave on $[0, +\infty)$.

3.2.   Existence of fuzzy Pareto-Nash equilibria

We now consider a fuzzy constrained multi-objective game with fuzzy payoffs (FCMGFP) as follows:

which has the following assumptions:

(1) $N = \{1, 2, ..., n\}$ is a set of players;

(2) $X_i$ is player $i$'s strategy space;

(3) $\widetilde{S}_i:X_{-i}\rightarrow \mathcal{F}(X_i)$ is player $i$'s fuzzy constraint mapping;

(4) $s_i : X_{-i} \to [0, 1]$ is player $i$'s feasible function, where $s_i(x_{-i})$ represent the feasible degree on strategy profile $x_{-i} \in X_{-i}$ for player $i$;

(5) $\widetilde{F}_i = \{\widetilde{f}_1^i, \ldots, \widetilde{f}_d^i\} : X = \prod_{i\in {\rm N}} X_i \to \mathcal{F}(\mathbb{R})^d$ is player $i$'s payoff function.

As usual, for each player $i \in N$, write

where the latter is endowed with the product topology.

Definition 3.8. A point $x^* = (x_i^*, x_{-i}^*) \in X$ is called a fuzzy Pareto-Nash equilibrium of $\gamma$ if for each $i \in N$, $\widetilde{S}_{i x_{-i}^*}(x_i^*) \ge s_i(x_{-i}^*)$, and for each $u_i$ with $\widetilde{S}_{i x_{-i}^*}(u_i) \ge s_i(x_{-i}^*)$, we have

Definition 3.9. Let $\alpha = (\alpha_1, \dots, \alpha_n) \in [0, 1]^n$. A point $x^* = (x_i^*, x_{-i}^*) \in X$ is called a fuzzy $\alpha$-Pareto-Nash equilibrium of $\gamma$ if for each $i \in N$, $\widetilde{S}_{i x_{-i}^*}(x_i^*) \ge s_i(x_{-i}^*)$, and for each $u_i$ with $\widetilde{S}_{i x_{-i}^*}(u_i) \ge s_i(x_{-i}^*)$, we have

where $[0, 1]^n = [0, 1] \times \dots \times [0, 1]$.

For $\alpha = (\alpha_1, \dots, \alpha_n) \in [0, 1]^n$, we observed that a fuzzy $\alpha$-Pareto-Nash equilibrium of $\gamma$ must be a fuzzy Pareto-Nash equilibrium of $\gamma$, but a fuzzy Pareto-Nash equilibrium of $\gamma$ is not necessarily a fuzzy $\alpha$-Pareto-Nash equilibrium of $\gamma$.

Using the fuzzy mapping $\widetilde{S}_i$ and the corresponding feasibility function $s_i$, we consider the correspondence $S_i : X_{-i} \rightrightarrows X_i$ as follows: For all $x_{-i} \in X_{-i}$,

In what follows, $S_i$ is called a correspondence induced by the fuzzy mapping $\widetilde{S}_i$. Then, a strategy profile $x^* = (x_i^*, x_{-i}^*) \in X$ is called a fuzzy Pareto-Nash equilibrium of $\gamma$ if for each $i\in N$, $x_i^* \in S_i(x_{-i}^*)$, and for each $u_i \in S_i (x_{-i}^*)$, $\widetilde{F}(x_i^*, x_{-i}^*) \nprec \widetilde{F}_i(u_i, x_{-i}^*)$. A strategy profile $x^* = (x_i^*, x_{-i}^*) \in X$ is called a fuzzy $\alpha$-Pareto-Nash equilibrium of $\gamma$ if for each $i\in N$, $x_i^* \in S_i(x_{-i}^*)$, and for each $u_i \in S_i (x_{-i}^*)$,

In order to prove the existence of fuzzy Pareto-Nash equilibria, we need the following lemma.

Theorem 3.10. Let $\mathcal{X}_1$ and $\mathcal{X}_2$ be two Hausdorff topological spaces, let $\widetilde{F} = \{\widetilde{f}_1, \ldots, \widetilde{f}_d \}: \mathcal{X}_1 \times \mathcal{X}_2 \to \mathcal{F}(\mathbb{R})^d$ be a continuous fuzzy-vector-valued function, and let $S: \mathcal{X}_2 \rightrightarrows \mathcal{X}_1$ be a continuous correspondence with nonempty and compact values. Moreover, for all $y \in \mathcal{X}_2$, let

Then $\Phi: \mathcal{X}_2 \rightrightarrows \mathcal{X}_1$ is an upper semi-continuous correspondence with nonempty and compact values.

Proof. Let $y \in \mathcal{X}_2$, and then

where $\Phi_{\alpha}(y) = \{x \in S(y)\ |\ \widetilde{F}^{\alpha}(u, y) \ominus \widetilde{F}^{\alpha}(x, y) \notin int\mathcal{I}(\mathbb{R_+})^d, \ \mbox{for all}\ u \in S(y) \}$.

Since $S(y)$ is nonempty and compact. Meanwhile, the continuity of $\widetilde{F}$ yields that of each $\widetilde{f}_i^{\alpha}$. So, from Definition 2.4 and Lemma 2.6, it follows that $\Phi_{\alpha}(y) \neq \emptyset$ for each $\alpha \in [0, 1]$. Consequently, $\Phi(y) \neq \emptyset$.

Next, we verify the compactness of $\Phi(y)$. Since $\Phi(y)$ and $S(y)$ are compact, and $\Phi(y) \subset S(y)$, we need only to show that $\Phi(y)$ is closed. For this aim, consider a net $\{x^{\tau}\}_{\tau \in D} \subset \Phi(y)$ having the properties $x^{\tau} \to x$ and $x \notin \Phi(y)$. Then, there exists $u_0 \in S(y)$ such that

Since $x^{\tau} \in \Phi(y)$, from (3.4) there is $\alpha_{\tau} \in [0, 1]$ such that for all $u \in S(y)$,

Furthermore, there is a subnet $\{\alpha_{\tau'}\}$ of $\{\alpha_{\tau}\}$ such that $\alpha_{\tau'} \to \alpha \in [0, 1]$. From the compactness of $S(y)$ and $u_0 \in S(y)$, there is a net $\{u^{\tau}\}_{\tau \in D}$ such that $u^{\tau} \in S(y)$ and $u^{\tau} \to u_0$. Then, from the continuity of $\widetilde{F}$, (3.6) and Lemma 2.2, it follows that

which contradicts the formula (3.5). Therefore, $\Phi(y)$ is compact.

Finally, we prove that $\Phi$ is upper semi-continuous. Note that

and by Lemma 2.13, we turn to verify the closeness of the correspondence $T: \mathcal{X}_2 \rightrightarrows \mathcal{X}_1$, which is defined for $y \in \mathcal{X}_2$ by

For this aim, assume that $\{y^{\tau}\}_{\tau \in D} \subset \mathcal{X}_2$ with $y^{\tau} \to y$, and $x^{\tau} \in T(y^{\tau})$ with $x^{\tau} \to x \in \mathcal{X}_1$. It suffices to show that $x \in T(y)$.

We argue by contradiction and assume $x \notin T(y)$. Then, there exists $u_0 \in S(y)$, such that

On the other hand, since $x^{\tau} \in T(y^{\tau})$, this implies that $x^{\tau} \in \mathcal{X}_1$, and for all $u \in S(y^{\tau})$, we have $\widetilde{F}(x^{\tau}, y^{\tau}) \nprec \widetilde{F}(u, y^{\tau})$. In other words, there is $\alpha_{\tau} \in [0, 1]$, such that

Furthermore, there is a subnet $\{\alpha_{\tau'}\}$ of $\{\alpha_{\tau}\}$ such that $\alpha_{\tau'} \to \alpha \in [0, 1]$. Guaranteed by the lower semi-continuity of $S$, there is a net $\{u^{\tau}\}_{\tau \in D}$ such that $u^{\tau} \in S(y^{\tau})$ and $u^{\tau} \to u_0$. Then, from the continuity of $\widetilde{F}$, (3.8) and Lemma 2.2, it follows that

which contradicts the formula (3.7). Hence, $\Phi$ is closed. The proof is completed.□

A special result of Theorem 3.10 is the following corollary, which was first proved by Li et al. ^[28].

Corollary 3.11. Let $\mathcal{X}_1$ and $\mathcal{X}_2$ be two Hausdorff topological spaces, let $F = \{f_1, \ldots, f_d \}: \mathcal{X}_1 \times \mathcal{X}_2 \to \mathcal{I}(\mathbb{R})^d$ be a continuous interval-vector-valued function, and let $S: \mathcal{X}_2 \rightrightarrows \mathcal{X}_1$ be a continuous correspondence with nonempty and compact values. Moreover, for each $y \in \mathcal{X}_2$, let

Then, $\Phi : \mathcal{X}_2 \rightrightarrows \mathcal{X}_1$ is an upper semi-continuous correspondence with nonempty compact values.

It is noted that for the case $d = 1$ in Corollary 3.11, if $F: \mathcal{X}_1 \times \mathcal{X}_2 \to \mathbb{R}$ is continuous, and $S: \mathcal{X}_2 \rightrightarrows \mathcal{X}_1$ is a continuous correspondence with nonempty and compact values, then Corollary 3.11 becomes Berge's maximum theorem (see ^[5]).

Theorem 3.12. Let $\gamma = (X_i, \widetilde{S}_i, s_i, \widetilde{F}_i)_{i \in N}$ be an FCMGFP, where $X_i$ is a nonempty, convex and compact subset of $\mathcal{V}_i$. Then, $\gamma$ has at least one fuzzy Pareto-Nash equilibrium if the following conditions are fulfilled: For each $i \in N$,

(1) $\widetilde{S}_i$ is a convex fuzzy mapping, and $S_i$ is continuous with nonempty and compact values;

(2) there is $k_i \in \{1, \dots, d\}$ such that $\widetilde{f}^i_{k_i}: X \to \mathcal{F}(\mathbb{R})$ is continuous;

(3) for each $x_{-i} \in X_{-i}$, $x_i \mapsto \widetilde{f}^i_{k_i}(x_i, x_{-i})$ is generalized quasi-concave.

Proof. Let $\Phi: X \rightrightarrows X$ be the correspondence defined for $x = (x_1, ..., x_n) \in X$ by

Here, for $i \in N$ and $x_{-i} \in X_{-i}$, we have

According to Theorem 3.10, each $\Phi_i: X_{-i} \rightrightarrows X_i$ is upper semi-continuous with nonempty compact values.

Next, we verify the convexity of $\Phi_i (x_{-i})$. For this aim, let $a_1, a_2 \in \Phi_i(x_{-i})$ and $\lambda \in [0, 1]$. That is, for $a_1, a_2 \in S_i(x_{-i})$ and for all $u_i \in S_i(x_{-i})$, it follows that

Since the fuzzy mapping $\widetilde{S}_i$ is convex, from Lemma 2.11 it follows that $S_i(x_{-i})$ is convex. So, $\lambda a_1 + (1- \lambda)a_2 \in S_i(x_{-i})$. Since $x_i \mapsto \widetilde{f}^i_{k_i}(x_i, x_{-i})$ is generalized quasi-concave, we have

That is, $\lambda a_1 + (1- \lambda)a_2 \in \Phi_i(x_{-i})$. Therefore, $\Phi_i(x_{-i})$ is convex.

Recall that each $\Phi_i$ is upper semi-continuous with nonempty convex compact values, and so is $\Phi$. According to Theorem 2.14, there exists $x^* \in X$ such that $x^* \in \Phi(x^*)$. In other words, for each $i \in N$, $x_i^* \in S_i(x_{-i}^*)$, and for all $u_i \in S_i(x_{-i}^*)$, $\widetilde{f}^i_{k_i}(x_i^*, x_{-i}^*) \nprec \widetilde{f}^i_{k_i}(u_i, x_{-i}^*)$, that is, $\widetilde{F}_i(x_i^*, x_{-i}^*) \nprec \widetilde{F}_i(u_i, x_{-i}^*)$. This completes the proof.□

It should be noted that if, for each $i \in N$, $\widetilde{F}_i : X \to \mathbb{R}^d$ and $s_i(x_{-i}) = 1$ ($x_{-i} \in X_{-i}$) in Theorem 3.12, then the FCMGFP becomes a constrained multi-objective game (see ^[48]). When each player has only one objective in an FCMGFP, the FCMGFP degenerates into a fuzzy constrained game with fuzzy payoffs (FCGFP). Letting $d = 1$ within Theorem 3.12, we obtain the following corollary.

Corollary 3.13. Let $\gamma' = (X_i, \widetilde{S}_i, s_i, \widetilde{f}_i)_{i\in N}$ be an FCGFP, where $X_i$ is a nonempty, convex and compact subset of $\mathcal{V}_i$. Then, $\gamma'$ has at least one fuzzy Pareto-Nash equilibrium if the following conditions are fulfilled: For each $i \in N$,

(1) $\widetilde{S}_i$ is a convex fuzzy mapping, and $S_i$ is continuous with nonempty and compact values;

(2) $\widetilde{f}_i : X \to \mathcal{F}(\mathbb{R})$ is a continuous fuzzy-valued function;

(3) for each $x_{-i} \in X_{-i}$, $x_i \mapsto \widetilde{f}_i(x_i, x_{-i})$ is generalized quasi-concave.

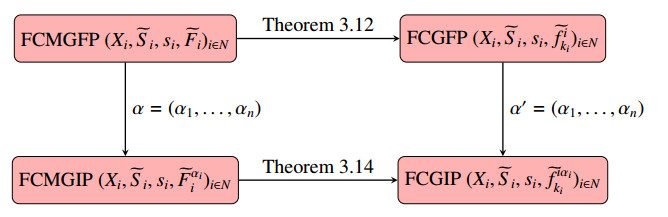
Through Theorem 3.12 and Corollary 3.13, we can get the following conclusion that a fuzzy Pareto-Nash equilibrium of FCMGFP $(X_i, \widetilde{S}_i, s_i, \widetilde{F}_i)_{i \in N}$ must be a fuzzy Pareto-Nash equilibrium of a certain FCGFP $(X_i, \widetilde{S}_i, s_i, \widetilde{f}^i_{k_i})_{i\in N}$ ($k_i \in \{1, \dots, d\}$). Therefore, the fuzzy Pareto-Nash equilibria of FCMGFP can be transformed into the fuzzy Pareto-Nash equilibria of the FCGFP.

Theorem 3.14. Let $\gamma = (X_i, \widetilde{S}_i, s_i, \widetilde{F}_i)_{i \in N}$ be an FCMGFP, where $X_i$ is a nonempty, convex, and compact subset of $\mathcal{V}_i$, and let $\alpha = (\alpha_1, \dots, \alpha_n) \in [0, 1]^n$. Then, $\gamma$ has at least one fuzzy $\alpha$-Pareto-Nash equilibrium if the following conditions are fulfilled: For each $i \in N$,

(1) $\widetilde{S}_i$ is a convex fuzzy mapping, and $S_i$ is continuous with nonempty and compact values;

(2) there is $k_i \in \{1, \dots, d\}$ such that $\widetilde{f}^{i \alpha_i}_{k_i}: X \to \mathcal{I}(\mathbb{R})$ is continuous;

(3) for each $x_{-i} \in X_{-i}$, $x_i \mapsto \widetilde{f}^{i \alpha_i}_{k_i}(x_i, x_{-i})$ is generalized $\mathcal{I}(\mathbb{R}_+)$-quasi-concave.

Proof. By Corollary 3.11 and the proof method of Theorem 3.12, we prove Theorem 3.14.□

In real-world games, decision makers often determine the membership degrees of each player's fuzzy payoffs according to their needs, that is, determine the $\alpha$-cuts of fuzzy vectors. Given an $\alpha = (\alpha_1, \dots, \alpha_n) \in [0, 1]^n$, we can obtain a corresponding fuzzy constrained multi-objective game with interval payoffs (FCMGIP) $(X_i, \widetilde{S}_i, s_i, \widetilde{F}_i^{\alpha_i})_{i \in N}$ from $(X_i, \widetilde{S}_i, s_i, \widetilde{F}_i)_{i \in N}$ in Theorem 3.14. When each player has only one objective in an FCMGIP, the FCMGIP degenerates into a fuzzy constrained game with interval payoffs (FCGIP). Letting $d = 1$ within Theorem 3.14, we obtain the following corollary.

Corollary 3.15. Let $\gamma' = (X_i, \widetilde{S}_i, s_i, \widetilde{f}_i)_{i \in N}$ be an FCGFP, where $X_i$ is a nonempty, convex and compact subset of $\mathcal{V}_i$, and let $\alpha = (\alpha_1, \dots, \alpha_n) \in [0, 1]^n$. Then, $\gamma'$ has at least one fuzzy $\alpha$-Pareto-Nash equilibrium if the following conditions are fulfilled: For each $i \in N$,

(1) $\widetilde{S}_i$ is a convex fuzzy mapping, and $S_i$ is continuous with nonempty and compact values;

(2) there is $k_i \in \{1, \dots, d\}$ such that $\widetilde{f}^{\alpha_i}_{i}: X \to \mathcal{I}(\mathbb{R})$ is continuous;

(3) for each $x_{-i} \in X_{-i}$, $x_i \mapsto \widetilde{f}^{\alpha_i}_{i}(x_i, x_{-i})$ is generalized $\mathcal{I}(\mathbb{R}_+)$-quasi-concave.

According to Theorems 3.12 and 3.14, Corollaries 3.13 and 3.15, we can get that the fuzzy Pareto-Nash equilibrium and fuzzy $\alpha$-Pareto-Nash equilibrium of an FCMGFP can be transformed into weak Pareto-Nash equilibrium of an FCGIP. The specific relationship is shown in Figure 1. It should be noted that the membership degrees $\alpha$ and $\alpha'$ of fuzzy payoffs can be the same or different in Figure 1.

Example 3.16. Consider a two-player fuzzy constrained multi-objective game with fuzzy payoffs $(X_i, \widetilde{S}_i, s_i, \widetilde{F}_i)_{i \in \{1, 2\}}$ as follows: For $i = 1, 2$,

(1) $X_i = [0, 3]$,

(2) $\widetilde{S}_i: [0, 3] \to \mathcal{F}([0, 3])$ is player $i$'s fuzzy constraint mapping given by

and

(3) $s_i: [0, 3] \to [0, 1]$ is defined by $s_1(x_2) = \frac{1}{2}$ and $s_2(x_1) = \frac{3}{4}$, for $x_1, x_2 \in [0, 3]$, that is, the feasible degree on strategy $x_2 \in [0, 3]$ is $\frac{1}{2}$ for player 1, and the feasible degree on strategy $x_1 \in [0, 3]$ is $\frac{3}{4}$ for player 2.

(4) $\widetilde{F}_i: [0, 3] \times [0, 3] \to \mathcal{F}_0(\mathbb{R})^2$ is the triangular fuzzy-vector-valued function given for $(x_1, x_2) \in [0, 3] \times [0, 3]$ by

where

For such a game, the conditions within Theorem 3.12 are satisfied.

First, for $i = 1, 2$, it is not difficult to verify the convexity of $\widetilde{S}_i$. The correspondence $S_i: [0, 3] \rightrightarrows [0, 3]$ induced by the fuzzy mapping $\widetilde{S}_i$ is precisely given by

Obviously, $S_i$ is continuous with nonempty convex compact values.

Second, for all $(x_1, x_2, \alpha) \in [0, 2] \times [1, 3] \times [0, 1]$, observe that

We see that $\underline{\widetilde{f}_{11}^{\alpha}}(x_1, x_2) = (2 + \alpha)x_1 - (3 + \alpha) x_2$ and $\overline{\widetilde{f}_{11}^{\alpha}}(x_1, x_2) = (4 - \alpha) x_1 - (5 - \alpha) x_2$ are both continuous. So, $\widetilde{f}_{11}^{\alpha}$ is continuous. Similarly, we can also verify the continuity of $\widetilde{f}_{21}^{\alpha}$. According to Definition 3.1, the second condition of Theorem 3.12 is fulfilled.

Finally, for $\alpha \in [0, 1]$, by Lemma 2.6, $x_1 \mapsto \widetilde{f}_{11}^{\alpha}(x_1, x_2)$ is non-decreasing for each $x_2 \in [1, 3]$, and $x_2 \mapsto \widetilde{f}_{21}^{\alpha}(x_1, x_2)$ is non-decreasing for each $x_1 \in [0, 2]$. From Lemma 3.7, the considered game also fulfills the last condition of Theorem 3.12. By calculation, we can deduce that $(2, 3)$ is a fuzzy Pareto-Nash equilibrium of the game $(X_i, \widetilde{S}_i, s_i, \widetilde{f}_{i1})_{i \in \{1, 2\}}$.

In fact, for $\alpha \in [0, 1]$, $u_1 \in [0, 2]$, $u_2 \in [1, 3]$, we immediately arrive at the following consequences:

Furthermore, for all $u_1 \in [0, 2]$, $u_2 \in [1, 3]$, $\widetilde{f}_{11}(2, 3) \nprec \widetilde{f}_{11}(u_1, 3)$, and $\widetilde{f}_{21}(2, 3) \nprec \widetilde{f}_{21}(2, u_2)$. From Definition 3.8, $(2, 3)$ is a fuzzy Pareto-Nash equilibrium of the game $(X_i, \widetilde{S}_i, s_i, \widetilde{f}_{i1})_{i \in \{1, 2\}}$.

Similarly, $\widetilde{f}_{12}^{\alpha}$ and $\widetilde{f}_{22}^{\alpha}$ are continuous. At the same time, for $\alpha \in [0, 1]$, by Lemma 2.8, $x_1 \mapsto \widetilde{f}_{12}^{\alpha}(x_1, x_2)$ is non-increasing for each $x_2 \in [1, 3]$, and $x_2 \mapsto \widetilde{f}_{22}^{\alpha}(x_1, x_2)$ is non-increasing for each $x_1 \in [0, 2]$. For all $u_1 \in [0, 2]$, $u_2 \in [1, 3]$,

that is, $\widetilde{f}_{12}(0, 1) \nprec \widetilde{f}_{12}(u_1, 1)$, and $\widetilde{f}_{22}(0, 1) \nprec \widetilde{f}_{22}(1, u_2)$. Hence, $(0, 1)$ is a fuzzy Pareto-Nash equilibrium of the game $(X_i, \widetilde{S}_i, s_i, \widetilde{f}_{i2})_{i \in \{1, 2\}}$. In the same way, we can verify that $(2, 1)$ and $(0, 3)$ are two fuzzy Pareto-Nash equilibria of the games $(X_i, \widetilde{S}_i, s_i, \widetilde{f}_{ii})_{i \in \{1, 2\}}$ and $(X_i, \widetilde{S}_i, s_i, \widetilde{f}_{ij (j \neq i)})_{i \in \{1, 2\}}$. Therefore, $(2, 3)$, $(0, 1)$, $(2, 1)$ and $(0, 3)$ are four fuzzy Pareto-Nash equilibria of the game $(X_i, \widetilde{S}_i, s_i, \widetilde{F}_i)_{i \in \{1, 2\}}$. □

Remark 3.17. For any given $\alpha = (\alpha_1, \alpha_2) \in [0, 1]^2$, from Definition 3.9, $(2, 3)$, $(0, 1)$, $(2, 1)$ and $(0, 3)$ are not only four fuzzy Pareto-Nash equilibria of $(X_i, \widetilde{S}_i, s_i, \widetilde{F}_i)_{i \in \{1, 2\}}$ but also four fuzzy $\alpha$-Pareto-Nash equilibria of $(X_i, \widetilde{S}_i, s_i, \widetilde{F}_i)_{i \in \{1, 2\}}$ in Example 3.16.

4.   Stability of the fuzzy Pareto-Nash equilibria set

The last section presents a comprehensive discussion on a bounded rationality model for FCMGFPs. First, we construct a metric space of all FCMGFPs with fuzzy Pareto-Nash equilibria. Then, we verify the completeness of the metric space. Furthermore, with the help of the nonlinear scalarization function, we introduce a rationality function for FCMGFP. Finally, we prove that the structural stability ($(\gamma, \epsilon)$-stability) of this model implies its robustness to $\epsilon$-equilibria ($(\gamma, \epsilon)$-robustness).

4.1.   The metric space of all FCMGFPs with fuzzy Pareto-Nash equilibria

For each $i \in N$, let $(X_i, d_i)$ be a compact metric space, and let $\Gamma$ be the set of all FCMGFPs, where each $\gamma = (X_i, \widetilde{S}_i, s_i, \widetilde{F}_i)_{i \in N}$ satisfies the following conditions:

(1) $S_i: X_{-i} \rightrightarrows X_i$ is a continuous correspondence with nonempty and compact values induced by $\widetilde{S}_i$;

(2) $\widetilde{F}_i: X \to \mathcal{F}(\mathbb{R})^d$ is continuous on $X$ with

(3) there exists $x = (x_1, \ldots, x_n) \in X$, for each $i \in N$, $x_i \in S_i(x_{-i})$, and for each $u_i \in S_i (x_{-i}^*)$, $\widetilde{F}(x_i^*, x_{-i}^*) \nprec \widetilde{F}_i(u_i, x_{-i}^*)$.

Denote by $E(\gamma)$ all fuzzy Pareto-Nash equilibria of $\gamma \in \Gamma$. Clearly, $E : \Gamma \rightrightarrows X$ is a correspondence, and $E(\gamma) \neq \emptyset$.

For $\gamma_j = (X_i, S_{i j}, \widetilde{F}_{i j})_{i \in N} \in \Gamma$ with $j = 1, 2$, define

where $H_i$ denotes the Hausdorff distance on $K_0(X_i)$, the set of all nonempty compact subsets in $X_i$. It is easy to show that $(\Gamma, \rho)$ is a metric space.

Lemma 4.1. The metric space $(\Gamma, \rho)$ is complete.

Proof. Let $\{\gamma_m\}_m$ be a Cauchy sequence in $\Gamma$, where $\gamma_m = (X_i, S_{i m}, \widetilde{F}_{i m})_{i \in N}$ for each $m \in \mathbb{N}$. Then, for $\epsilon > 0$, there is $Z \in \mathbb{N}$ such that for all $m, p > Z$,

Associated with each $i \in N$ are the following consequences. First, for each $(x, \alpha) \in X \times [0, 1]$, the sequence $\{\widetilde{F}_{i m}^{\alpha}(x)\}_m$ is a Cauchy sequence in $\mathcal{I}(\mathbb{R})^d$. Second, for each $x_{-i} \in X_{-i}$, the sequence $\{S_{i m}(x_{-i})\}_m$ is a Cauchy sequence in $X_i$.

In order to prove the existence of a limit $\gamma \in \Gamma$ of $\{\gamma_m\}_m$, we divide our proof into three steps in the following.

Step Ⅰ. We show that there is $S_i: X_{-i} \rightrightarrows X_i$ such that $S_{i m} \to S_i$, and $S_i$ is continuous with convex compact values on $X_{-i}$.

From the completeness of $(K_0(X_i), H_i)$, there is $S_i: X_{-i} \rightrightarrows X_i$ such that $S_{i m}(x_{-i}) \to S_i(x_{-i})$ for all $x_{-i} \in X_{-i}$. Recall that each $S_{i m}$ is continuous with convex compact values on $X_{-i}$, and so is $S_i$.

Step Ⅱ. We prove that there is $\widetilde{F}_i: X \to \mathcal{F}(\mathbb{R})^d$ such that $\widetilde{F}_{i m} \to \widetilde{F}_i$, and $\widetilde{F}_i$ is continuous on $X$ with

Since $(\mathcal{I}(\mathbb{R})^d, \|\cdot \|_{\mathcal{I}(\mathbb{R})^d})$ is complete, for each $\alpha \in [0, 1]$, there is $\widetilde{F}_i^\alpha : X \to \mathcal{I}(\mathbb{R})^d$ such that $\widetilde{F}_{i m}^{\alpha}(x) \to \widetilde{F}_i^{\alpha}(x)$ for all $x \in X$.

As for the continuity of $\widetilde{F}_i$ on $X$, notice that for any $\{ (x^m, \alpha^m) \}_m \subset X \times [0, 1]$, we have

Since $\widetilde{F}_{i m}^{\alpha} (x)$ is continuous on $X \times [0, 1]$, by Lemma 2.3, we have

That is, $\widetilde{F}_i$ is continuous for all $i \in N$.

Finally, (4.1) follows from the estimate

together with the convergence $\widetilde{F}_{i m}^{\alpha}(x) \to \widetilde{F}_i^{\alpha}(x)$ for all $(x, \alpha) \in X \times [0, 1]$.

Step Ⅲ. We now verify that there exists $x^* \in X$, for each $i \in N$, $x_i^* \in S_i(x_{-i}^*)$, and for each $u_i \in S_i (x_{-i}^*)$, $\widetilde{F}(x_i^*, x_{-i}^*) \nprec \widetilde{F}_i(u_i, x_{-i}^*)$.

In fact, from $\{\gamma_m \}_m \subset \Gamma$ it follows that there exists a sequence $\{ x^m \}_m \subset X$ such that each $x^m$ is a fuzzy Pareto-Nash equilibrium of $\gamma_m$. In other words, for each $i \in N$, $x_i^m \in S_{i m}(x_{-i}^m)$, and for each $u_i \in S_{i m}(x_{-i}^m)$, $\widetilde{F}_{i m}(x_i^m, x_{-i}^m) \nprec \widetilde{F}_{i m}(u_i, x_{-i}^m)$. That is, there is $\alpha_{im} \in [0, 1]$ such that for each $u_i \in S_{i m}(x_{-i}^m)$,

Because of the compactness of $X$, without loss of generality, we may assume $x^m \to x^* \in X$. Since

from the continuity of $S_i$, it follows that $H_i(S_{i m}(x_{-i}^m), S_i(x_{-i}^*)) \to 0$ as $m \to \infty$. Thus, we have

which implies that $x_i^* \in S_i(x_{-i}^*)$.

For all $u_i \in S_i(x_{-i}^*)$, we note that the sets $S_i(x_{-i}^*)$ and $S_{i m}(x_{-i}^*)$ are both compact. Thus, from the convergence $S_{i m}(x_{-i}^m) \to S_i(x_{-i}^*)$, there is $u_i^m \in S_{i m} (x_{-i}^m)$ such that $u_i^m \to u_i$ as $m \to \infty$. Then, by (4.2), we obtain

Moreover, there is a subsequence of $\{\alpha_{im}\}$ such that $\alpha_{im} \to \alpha_i$ (for the sake of simplicity, $\{\alpha_{im}\}$ also denotes its subsequence). Since $\widetilde{F}_{im}$ is continuous, from Lemma 2.3, it follows that

Thus, as $m \to \infty$,

Similarly, it can be verified that as $m \to \infty$,

Then, combining (4.4), (4.6) and (4.7), finish Step Ⅲ. The proof is completed.□

4.2.   The bounded rationality model for FCMGFPs

In order to construct the bounded rationality model for FCMGFPs, we first establish a nonlinear scalarization function for an interval vector by the Minkowski functional. This nonlinear scalarization function yields a principle of constructing bounded rationality functions.

Definition 4.2. For any fixed $\boldsymbol{e} = (e_1, \dots, e_d) \in int \mathcal{I}(\mathbb{R}_+)^d$, the nonlinear scalarization function $\xi_{\boldsymbol{e}} : \mathcal{I}(\mathbb{R})^d\to \mathbb{R}_+$ is defined for $\boldsymbol{A} = (A_1, \dots, A_d) \in \mathcal{I}(\mathbb{R})^d$ by

Clearly, $\xi_{\boldsymbol{e}}(\boldsymbol{A}) = \min \{\xi_{e_1}(A_1), \dots, \xi_{e_d}(A_d) \}$.

Lemma 4.3. The nonlinear scalarization function $\xi_{\boldsymbol{e}} : \mathcal{I}(\mathbb{R})^d\to \mathbb{R}_+$ has the following properties:

(1) $\xi_{\boldsymbol{e}}$ is positively homogeneous and continuous.

(2) $\xi_{\boldsymbol{e}}(\boldsymbol{A}) \le r$ if and only if $\boldsymbol{A} \notin r \cdot \boldsymbol{e} + int \mathcal{I}(\mathbb{R}_+)^d$.

Proof. See Appendix C.□

Next, we consider the bounded rationality model for FCMGFPs $\mathcal{M} = \{\Gamma, X, K, R\}$ as follows:

(1) $(\Gamma, \rho)$ is a complete metric space;

(2) $X$ is a compact metric space;

(3) $K: \Gamma \times X \rightrightarrows X$ is defined by

for all $(\gamma, x) \in \Gamma \times X$;

(4) $k: \Gamma \rightrightarrows X$ is defined by

for all $\gamma \in \Gamma$;

(5) $R: Graph(k) \to \mathbb{R}_+$ is a rationality function, given by choosing $e \in int \mathcal{I}(\mathbb{R}_+)^d$ and then for each $x \in k(\gamma)$ defining

It is clear that $R(\gamma, x) \ge 0$ for each $\gamma \in \Gamma$ and $x \in k(\gamma)$. From Lemma 4.3, $R(\gamma, x) = 0$ if and only if $x$ is a fuzzy Pareto-Nash equilibrium of $\gamma$.

For any $\gamma \in \Gamma$ and $\epsilon \ge 0$, the set of all $\epsilon$-equilibria of $\gamma$ is defined as

Lemma 4.4. Let $\gamma \in \Gamma$ and $\epsilon \ge 0$ with $x \in k(\gamma)$. Then, $x \in E(\gamma, \epsilon)$ if and only if for each $i \in N$, there is $\alpha_i \in [0, 1]$ such that for all $u_i \in S_i(x_{-i})$,

Consequently, $E(\gamma, 0) = \{ x\in k(\gamma)\ |\ R(\gamma, x) = 0\} \neq \emptyset$ is the set of fuzzy Pareto-Nash equilibria of $\gamma$.

Proof. Assume that $x \in E(\gamma, \epsilon)$, i.e., $R(\gamma, x) \le \epsilon$. Then,

So, for each $i \in N$, there is $\alpha_i \in [0, 1]$ such that $\xi_e(\widetilde{F}_i^{\alpha_i}(u_i, x_{-i}) \ominus \widetilde{F}_i^{\alpha_i}(x_i, x_{-i})) \le \epsilon$ for all $u_i \in S_i(x_{-i})$. Using Lemma 4.3, we obtain (4.8).

Conversely, if, for each $i \in N$, there is $\alpha_i \in [0, 1]$ such that (4.8) holds for all $u_i \in S_i(x_{-i})$, then from Lemma 4.3, $\xi_e(\widetilde{F}_i^{\alpha_i}(u_i, x_{-i}) \ominus \widetilde{F}_i^{\alpha_i}(x_i, x_{-i})) \le \epsilon$ for all $u_i \in S_i(x_{-i})$, and thus, $R(\gamma, x) \le \epsilon$.□

Theorem 4.5. The bounded rationality model for FCMGFPs $\mathcal{M} = \{\Gamma, X, K, R\}$ has the following properties:

(1) The correspondence $E: \Gamma \rightrightarrows X$ is upper semi-continuous;

(2) there exists a dense $G_{\delta}$ subset $Q$ of $\Gamma$ such that $\mathcal{M}$ is structurally stable at every $\gamma \in Q$;

(3) if the model $\mathcal{M}$ is structurally stable at $\gamma \in \Gamma$, then $\mathcal{M}$ is robust to $\epsilon$-equilibria at $\gamma \in \Gamma$, and $\mathcal{M}$ is robust to $\epsilon$-equilibria at $\gamma \in Q$;

(4) if $\gamma \in Q$, $\gamma_n \to \gamma$ and $\epsilon_n \to 0$, then $H(E(\gamma_n, \epsilon_n), E(\gamma)) \to 0$;

(5) if $E(\gamma)$ is a singleton set, then $\mathcal{M}$ is structurally stable and robust to $\epsilon$-equilibria at $\gamma \in \Gamma$;

(6) if the model $\mathcal{M}$ is $(\gamma, \epsilon)$-stable, then $\mathcal{M}$ is $(\gamma, \epsilon)$-robust.

To prove Theorem 4.5, we need the following lemmas.

Lemma 4.6. The correspondence $k: \Gamma \rightrightarrows X$ is upper semi-continuous.

Proof. According to Lemma 2.12, we only need to show that $k$ is closed on $\Gamma$. That is, the set $\text{Graph}(k) = \{(\gamma, x) \in \Gamma \times X\ |\ x \in k(\gamma)\}$ is closed on $\Gamma \times X$.

Assume that $\{(\gamma_m, x^m)\}_m \subset \text{Graph}(k)$ with $(\gamma_m, x^m) \to (\gamma, x)$. We turn to show that $(\gamma, x) \in \text{Graph}(k)$. From the completeness of $(\Gamma, \rho)$, it follows that $\gamma \in \Gamma$. Meanwhile, by $x^m \in k(\gamma_m)$, we obtain $x_i^m \in S_{i m} (x^m_{-i})$ for all $i \in N$. Moreover, in the same way as the proof of (4.3), we get $x_i \in S_i(x_{-i})$ for all $i \in N$. Thus, $x \in k(\gamma)$ and $(\gamma, x) \in \text{Graph}(k)$.□

Lemma 4.7. The rationality function $R$ is lower semi-continuous at $(\gamma, x)$ for any $(\gamma, x) \in \Gamma \times X$.

Proof. Let $r \in \mathbb{R}$, and we aim to prove the closeness of the lower level set

Suppose that $\{(\gamma_m, x^m)\}_m \subset \Gamma \times X$ with $R(\gamma_m, x^m) \le r$ for all $m$, and $(\gamma_m, x^m) \to (\gamma, x)$. We turn to show that $R(\gamma, x) \le r$.

Since $R(\gamma_m, x^m) \le r$, for each $i \in N$, there is $\alpha_i \in [0, 1]$ such that

Meanwhile, note that the sets $S_i(x_{-i})$ and $S_{i m}(x_{-i}^m)$ are both compact. For any $u_i \in S_i(x_{-i})$, from $S_{i m}(x_{-i}^m) \to S_i(x_{-i})$, there exists $u_i^m \in S_{i m}(x_{-i}^m)$ such that $u_i^m \to u_i$. Combining this with (4.9), we obtain

By an argument analogous to the proof of (4.5), we can derive that

and

Using the continuity of $\xi_e$, (4.11) and (4.12), let $m \to \infty$ within (4.10), and we get

By the definition of $R$, it follows that

The proof is completed.□

Proof of Theorem 4.5. Combining Lemma 2.17 with Lemmas 4.1, 4.6 and 4.7, we can directly obtain Theorem 4.5.

5.   Conclusions

In this paper, we investigate a new class of fuzzy constrained multi-objective games with fuzzy payoffs. First, by $\alpha$-cuts of fuzzy vectors, we establish the partial order of fuzzy vectors as well as the continuity and generalized quasi-concavity of fuzzy vector-valued functions. Second, we prove Berge's maximum theorem for fuzzy vector-valued functions (Theorem 3.10). Combining our result with the Fan-Glicksberg fixed point theorem leads to two existence theorems of fuzzy Pareto-Nash equilibria and fuzzy $\alpha$-Pareto-Nash equilibria for FCMGFPs (Theorems 3.12 and 3.14). Finally, through a nonlinear scalar method, we construct the bounded rationality model $\mathcal{M}$, a class of FCMGFPs with bounded rational functions. After verifying the lower semi-continuity of the bounded rational function, a series of relevant conclusions about the structural stability ($(\gamma, \epsilon)$-stability) and the robustness to $\epsilon$-equilibria ($(\gamma, \epsilon)$-robustness) of the model are proved (Theorem 4.5). The results obtained in this paper are generalizations and extensions of relevant conclusions in some of the literature, such as in ^{[24,28,44,48,52]}. In the future, we will focus on the application of FCMGFPs in practical problems. In addition, when considering mixed strategies, the multi-objective bi-matrix game with fuzzy payoffs is a special case of the two-player multi-objective game with fuzzy payoffs. The conditions for the existence and the specific calculation method of fuzzy Pareto-Nash equilibrium for this game are the issues we will discuss in the future. This paper discussed the stability of the FCMGFP in the framework of bounded rationality. Next, we intend to study the general stability of fuzzy Pare-Nash equilibrium for the FCMGFP from the perspective of essential stability.

Appendix A. Proof of Lemma 2.3.

Proof. Let $\boldsymbol{A} = (A_1, \ldots, A_d)$, $\boldsymbol{B} = (B_1, \ldots, B_d)$, $\boldsymbol{C} = (C_1, \ldots, C_d)$, by (2.1) and the Minkowski inequality, we get

Appendix B. Proof of Lemma 3.7.□

Proof. Let $\widetilde{\boldsymbol{A}} \in \mathcal{F}(\mathbb{R})^d$, let $x_1, x_2 \in X$, and let $\lambda \in [0, 1]$. Suppose that

We only need to prove that

From (5.1), there are $\alpha_1, \alpha_2 \in [0, 1]$ such that

We will discuss the following two cases.

Case 1: $x_1 \le x_2$. Since $\widetilde{F}^{\alpha_1}$ is non-decreasing, we have $\widetilde{F}^{\alpha_1}(x_1) \preceq \widetilde{F}^{\alpha_1}(\lambda x_1 + (1-\lambda) x_2)$. From $\widetilde{F}^{\alpha_1}(x_1) \nprec \widetilde{\boldsymbol{A}}^{\alpha_1}$, it follows that $\widetilde{F}^{\alpha_1}(\lambda x_1 + (1-\lambda) x_2) \nprec \widetilde{\boldsymbol{A}}^{\alpha_1}$.

Case 2: $x_1 > x_2$. Since $\widetilde{F}^{\alpha_2}$ is non-decreasing, we have $\widetilde{F}^{\alpha_2}(x_2) \preceq \widetilde{F}^{\alpha_2}(\lambda x_1 + (1-\lambda) x_2)$. From $\widetilde{F}^{\alpha_2}(x_2) \nprec \widetilde{\boldsymbol{A}}^{\alpha_2}$, it follows that $\widetilde{F}^{\alpha_2}(\lambda x_1 + (1-\lambda) x_2) \nprec \widetilde{\boldsymbol{A}}^{\alpha_2}$.

As mentioned for the above two cases, (5.2) holds. If $\widetilde{F}^{\alpha}$ is non-increasing for each $\alpha \in [0, 1]$, (5.2) holds by similar argument. The proof is completed.□

Appendix C. Proof of Lemma 4.3.

Proof. (1) Let $\boldsymbol{e} = ([\underline{e}_1, \overline{e}_1], \dots, [\underline{e}_d, \overline{e}_d])$ and $\boldsymbol{A} = ([\underline{a}_1, \overline{a}_1], \dots, [\underline{a}_d, \overline{a}_d])$. For each $t > 0$,

which shows the positive homogeneity of $\xi_{\boldsymbol{e}}$.

In what follows, we verify the continuity of $\xi_{\boldsymbol{e}}$. If

then there is $i$ such that $[\underline{a}_i, \overline{a}_i] \notin int \mathcal{I}(\mathbb{R}_+)$, and thus the definition of $\xi_{\boldsymbol{e}}$ implies that $\xi_{\boldsymbol{e}}(\boldsymbol{A}) = 0$. Consequently, for $\epsilon > 0$, taking $\delta = \min\{\epsilon \cdot \underline{e}_1, \dots, \epsilon \cdot \underline{e}_d\}$, we see that $\xi_{\boldsymbol{e}}(\boldsymbol{A}') < \epsilon$ for all $\boldsymbol{A}' \in o(\boldsymbol{A}, \delta)$. As for the case

from the fact that $[\underline{a}_i, \overline{a}_i] \in int \mathcal{I}(\mathbb{R}_+)$ for all $i$, together with the definition of $\xi_{\boldsymbol{e}}$, it follows that

Then, for $\epsilon > 0$, taking $\delta = \min\{\epsilon \cdot \underline{e}_1, \dots, \epsilon \cdot \underline{e}_d\}$, we see that $|\xi_{\boldsymbol{e}}(\boldsymbol{A}')- \xi_{\boldsymbol{e}}(\boldsymbol{A})| < \epsilon$ for all $\boldsymbol{A}' \in o(\boldsymbol{A}, \delta)$.

(2) Let $\xi_{\boldsymbol{e}}(\boldsymbol{A}) = r'$. If $r' \le r$, then the definition of $\xi_{\boldsymbol{e}}$ implies that $\boldsymbol{A} \notin r' \cdot \boldsymbol{e} + int \mathcal{I}(\mathbb{R}_+)^d$, and thus, $\boldsymbol{A} \notin r \cdot \boldsymbol{e} + int \mathcal{I}(\mathbb{R}_+)^d$ for all $r' < r$. Conversely, if $\boldsymbol{A} \notin r \cdot \boldsymbol{e} + int \mathcal{I}(\mathbb{R}_+)^d$, then the definition of $\xi_{\boldsymbol{e}}$ implies that $\xi_{\boldsymbol{e}}(\boldsymbol{A}) \le r$.□

Acknowledgments

The authors are indebted to the two reviewers for their thoughtful comments and suggestions that have helped to significantly improve the quality and presentation of our research.

The authors would also like to express their gratitude for the support from the National Natural Science Foundation of China (Nos. [72031009], [12171378]) and Excellent Youth Foundation of Hubei Scientific Committee (No. 2020CFA079).

Conflict of interest

The authors declared that they have no conflicts of interest to this work.