1.
Introduction
In 1965, Zadeh [56] presented fuzzy set theory. Later, Atanasov [10] generalized the notion of a fuzzy set and added the notion of an intuitionistic fuzzy set. One of the underlying issues of fuzzy arithmetic and fuzzy decision-making is the ranking of fuzzy numbers. Before the decision-maker can act, fuzzy numbers should be ranked. Real numbers can be ordered linearly by the connection ≤ or ≥, however, and fuzzy numbers do not have this type of disparity. Because a probable distribution depicts fuzzy numbers, they could also overlap, making it challenging to determine whether one fuzzy number is either larger or smaller than another. A ranking component, which outlines each fuzzy number further into a real line in which a natural order persists, is an efficient method to order the fuzzy numbers. Ramesh [49] compares the notion of ranking function for making comparisons of normal fuzzy numbers.
Abbasbandy and Hajjari [1] developed an innovative method for classifying trapezoidal fuzzy numbers. Wang and Kerre [52] proposed ordering features for fuzzy quantities. Angelov [8] adhered the Bellman and Zadeh [12] fuzzy optimization approach to intuitionistic fuzzy optimization. Numerous authors, including Jana and Roy [30], Mahapatra et al. [35], Dubey et al. [20], Mukherjee and Basu [39] have investigated the issue of optimization in an intuitionistic fuzzy background. One initiative to model the decision-making challenge with ambiguous quantities is to treat such imprecise quantities as intuitionistic fuzzy numbers. Consequently, the analogy of fuzzy numbers is required in the intuitionistic fuzzy optimisation problem. To create ranking systems for intuitionistic fuzzy numbers, comparisons of these erroneous numbers are necessary.
Between intuitionistic fuzzy sets, Atanassov identified four fundamental distances: "The Hamming, normalised Hamming, Euclidean, and normalised Euclidean distances". Szmidt and Kacprzyk [51] added to this principle and suggested a new definition of distance between intuitionistic fuzzy sets. Wang and Xin [53] also investigated the striking similarities and detachments between intuitionistic fuzzy sets by presenting some new axioms. Besides this, Nayagam et al. [41] and Nehi [42] also have investigated the ranking of intuitionistic fuzzy numbers. Li [34] defined and implemented a ratio methodology for triangular intuitionistic fuzzy numbers to MADM. In literature, there are additional ranking techniques that have been developed by authors like Kumar and Kaur [33], Zhang and Yu [57], Esmailzadeh and Esmailzadeh [22] and Papakostas et al. [44]. By adding the valuation and ambiguity indexes of a trapezoidal intuitionistic fuzzy number, De and Das [19] were capable of describing a ranking function.
The centroid approach of ranking intuitionistic fuzzy numbers was introduced by Nishad et al. [43]. Bharati and Singh [13,14] have explored intuitionistic fuzzy multiple objective programming and implemented it in agricultural planning and control. In a two-stage time-minimizing transportation concern, Bharati and Malhotra [15] used intuitionistic fuzzy sets. A novel algorithm for ranking intuitionistic fuzzy digits using the centroid method was put forth by Prakash et al. [45]. Mitchell [37] introduced some techniques for ranking intuitively fuzzy numbers. To use the intuitionistic fuzzy number's anticipated interval, Grzegorzewski [26] suggested a ranking and having-to-order method for intuitionistic fuzzy numbers. This is entirely predicated on the possible values for the fuzzy number first presented in Chiao [17]. An approach for ranking fuzzy numbers using the circumcenter of centroids and an indicator of modality was presented by Rao and Shankar [46]. Nasseri et al. [40] introduce an addition to using the circumcenter of centroids to rank fuzzy numbers with the aid of an area method. Roseline and Amirtharaj [50] presented intinuistic fuzzy numbers using distance methods that rely on the circumcenter of centroids.
Additionally, Yager [54,55] expanded upon the idea of PFS and introduced a new definition known as a q-rung orthopair fuzzy set (q-ROFS). Chen [16] suggested m-polar FS, while Zhang [57] established bipolar FS and its relationships. Akram [2] investigated the theory, procedures, and applications of m-polar F graphs in DM. Riaz and Hashmi [47] proposed the cutting-edge idea of a linear Diophantine fuzzy set (LDFS). The research on LDFSs has recently expanded significantly. Iampan et al. [29] researched linear Diophantine fuzzy Einstein aggregation operators, spherical linear Diophantine fuzzy, and linear Diophantine fuzzy relations concerning decision-making issues. Developed a fresh method for the COVID-19 q-linear Diophantine fuzzy emergency decision support system. Algebraic linear Diophantine fuzzy structures were researched by Kamac [31]. Khan et al. [32] use triangular linear Diophantine fuzzy numbers to solve linear and quadratic equations. There are several authors who studied different applications of generalized fuzzy set models, for instance, Ali et al. [3,4,5,6], Ashraf et al. [9], Ayub et al. [11], Das and Granados [18], Farid et al. [23], Gupta et al. [27], Hashmi et al. [28], Mahmood et al. [36], Mohammad et al. [38] and Riaz and Farid [48].
The domain principle of intuitionistic fuzzy set (IFS), interval-valued intuitionistic fuzzy set (IVIFS), Pythagorean fuzzy set (PFS), interval-valued Pythagorean fuzzy set (IVPFS) and q-rung orthopair fuzzy set (q-ROFS) have several actual applications in diverse fields. But researchers found some limitations to apply these concepts in much uncertain problems due to some issues related to membership and non-membership grades. For instance, in all these theories the researchers cannot choose 1 for membership and 1 for no-membership, if someone choose 1 for membership and 1 for no-membership the 1q+1q>1. In order to remedy the issues, firstly, Riaz and Hashmi introduce the novel idea of linear Diophantine fuzzy set (LDFS). In LDFS concept, they use the reference parameters similar to membership and non-membership grades makes it most accommodating in the direction of modeling uncertainties in actual existence issues. This research proposes a novel circumcenter-based algorithm for ranking LD fuzzy numbers. A trapezoid is initially divided into three segments in a trapezoidal LD fuzzy number, with the first, second, and third parts consecutively being a triangle, a rectangle, and a triangle. Next, the centroids of each of these three components are computed and their circumcenters. To rank LD fuzzy numbers, a ranking algorithm is lastly specified as the circumcenter position plus the original position. The centroid of the trapezoid, which serves as the trapezoid's balance point, is used as a point of reference in most ranking algorithms suggested in the literature. But since all of the centroids' vertices are fairly different from this point, the centroids' circumcenter could be considered a significantly balanced location.
2.
Preliminaries and basic definitions
This section is dedicated to reviewing some fundamental ideas essential for comprehending the dominant model.
Definition 2.1. [56] Consider a non-empty set X as the universe of discourse. Then a fuzzy set ξ in X is defined as follows:
where μξ(θ):X⟶[0,1] is the membership degree.
Definition 2.2. [24] A fuzzy set ξ defined on the universe set X is said to be normal iff μξ(θ)=1.
Definition 2.3. [21] A fuzzy set ξ of universe set X is said to be convex iff
Definition 2.4. [21] A fuzzy set ξ of universe set X is a fuzzy number iff ξ is normal and convex on X.
A real fuzzy number ξ is described as any fuzzy subset of the real line R with membership function μξ(θ) possessing the following properties:
● μξ is a continuous mapping from R to the closed interval [0,1].
● ξ is normalized : there exist t∈R such that μξ(t)=1.
● Convexity of ξ: i.e., u,w∈R, if t≤u≤w, then μξ(u)≥min{μξ(t),μξ(w)}.
● Boundness of support: i.e., ∃S∈R and ∀t∈R, if |t|≥S, then μξ(t)=0.
Definition 2.5. [10] An intuitionistic fuzzy set ϖ in X defined by
where αϖ:X⟶[0,1] and βϖ:X⟶[0,1] are the membership degree and non-membership degree, respectively, with the condition:
The hesitation degree of IFS ϖ defined in X is denoted as πϖ(θ). It is determined by the following expression:
Definition 2.6. [47] Let X be the universe. A linear Diophantine fuzzy set (LDFS) £R on X is defined as follows:
where ζτR(θ),ηυR(θ),α(θ),β(θ)∈[0,1] such that
The hesitation part can be written as
where ϱ is the reference parameter.
Definition 2.7. [47] An absolute LDFS on X can be written as
and empty or null LDFS can be expressed as
Definition 2.8. [47] Let £R={(θ,⟨ζτR(θ),ηυR(θ)⟩,⟨α(θ),β(θ)⟩):θ∈X} be an LDFS. For any constants s,t,u,v∈[0,1] such that 0≤su+tv≤1 with 0≤u+v≤1, define the (⟨s,t⟩,⟨u,v⟩)-cut of £R as follows:
Definition 2.9. [32] A LDF number £R is
● a LDF subset of the real line R,
● normal, i.e., there is any θ0∈R such that ζτR(θ0)=1, ηυR(θ0)=0, α(θ0)=1, β(θ0)=0,
● convex for the membership functions ζτR and α, i.e.,
● concave for the nonmembership functions ηυR and β, i.e.,
Definition 2.10. Let £R be a trapezoidal LDFN (TrapLDFN) on R with the following membership functions (ζτR and α) and non-membership functions (ηυR and β):
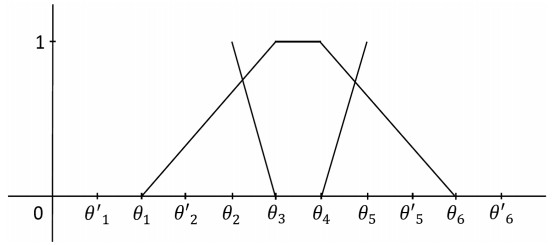
where θ1≤θ2≤θ3≤θ4≤θ5≤θ6 for all x∈R. The figure of (θ1,θ2,θ3,θ4,θ5,θ6) is shown in Figure 1.
where θ′1≤θ′2≤θ3≤θ4≤θ′5≤θ′6 for all x∈R. The figure of (θ′1,θ′2,θ3,θ4,θ′5,θ′6) is shown in Figure 2.
The figure of £RTrapLDFN is shown in Figure 3.
Definition 2.11. Consider a TrapLDFN £RTrapLDFN={(θ1,θ2,θ3,θ4,θ5,θ6)(θ′1,θ′2,θ3,θ4,θ′5,θ′6). Then
(i) s-cut set of £RTrapLDFN is a crisp subset of R, which is defined as follows
(ii) t-cut set of £RTrapLDFN is a crisp subset of R, which is defined as follows
(iii) u-cut set of £RTrapLDFN is a crisp subset of R, which is defined as follows
(iv) v-cut set of £RTrapLDFN is a crisp subset of R, which is defined as follows
We can denote the (⟨s,t⟩,⟨u,v⟩)-cut of £RTrapLDFN={(θ1,θ2,θ3,θ4,θ5,θ6)(θ′1,θ′2,θ3,θ4,θ′5,θ′6) by
We denote the set of all TrapLDFN on R by £RTrapLDFN(R).
3.
Centroid method for ranking of trapaziodal LDFNs
In this part, we determine the centroid location of the trapezoidal linear Diaphontine fuzzy number (TrapLDFN). The geometric core of a trapezoidal Linear diophantine fuzzy number is used in the process of ranking TrapLDFNs with a centroid index. Values on the horizontal and vertical axes correlate to the geometric centre.
Consider a TrapLDFN £RTrapLDFN={(θ1,θ2,θ3,θ4,θ5,θ6)(θ′1,θ′2,θ3,θ4,θ′5,θ′6), whose membership function can be defined as follows:
Where
are called the sides of TrapLDFN, where fLA, gRA, f′LA and g′RA are non-decreasing and fRA, gLA, f′RA and g′LA are non-increasing functions. Therefore the inverse functions of fLA, fRA, gLA, gRA, f′LA, f′RA, g′LA and g′RA exist which are also of the same nature. Let
be the inverse functions of fLA, fRA, gLA, gRA, f′LA, f′RA, g′LA and g′RA respectively. Then, hLA, hRA, kLA, kRA, h′LA, h′RA, k′LA and k′RA should be integrable on R. In the case of the above defined TrapLDFN, the above inverse functions can be analytically expressed as follows:
The centroid point of the TrapLDFN is determined as follows. First we find ζτR(x) and ηυR(x), also see the Figure 4.
Similarly, we find α(x) and β(x), also see the Figure 5.
Next, we find ζτR(y) and ηυR(y), also see the Figure 6.
Similarly, we find α(y) and β(y), also see the Figure 7.
Then (⟨ζτR(x),ζτR(y)⟩,⟨α(x),α(y)⟩;⟨ηυR(x),ηυR(y)⟩,⟨β(x),β(y)⟩) gives the centroid of the TrapLDFN.
Definition 3.1. The ranking function of the TrapLDFN A is defined by
which is the Eculidean distance.
As a special case, if in a TrapLDFN, we let θ3=θ4, then we will get a triangular LDFN with parameters θ1≤θ2≤θ3≤θ4≤θ5≤θ6 and θ′1≤θ′2≤θ3≤θ4≤θ′5≤θ′6. It is denoted by £RTriLDFN={(θ1,θ2,θ3,θ5,θ6)(θ′1,θ′2,θ3,θ′5,θ′6). The centroids of the membership functions and non-membership functions of the triangular LDFN respectively are defined as
and
Definition 3.2. The ranking function of the triangular LDFN A is defined by
which is the Eculidean distance.
Example 3.3. Consider two TriLDFNs A={(3,5,7,8,13)(1,4,7,10,14) and B={(1,3,9,10,13)(0,4,9,13,15). Then using the proposed method we find ℜ(A),
Also
Now,
Now, by using the proposed method we find ℜ(B),
Also
Now,
As ℜ(A)<ℜ(B)⟹A<B.
4.
Ranking of trapaziodal LDFNs using circumcenter of centroids
A trapezoid's centroid is regarded as the shape's equilibrium position. The linear Diophantine fuzzy number's membership function trapezoid is divided into three planar figures. These three plane figures are in order, a triangle, a rectangle, and another triangle. The point of reference for defining the ordering of linear Diophantine fuzzy numbers is the circumcenter of the centroids of these three plane figures. Each centroid point (G1 of a triangle, G2 of a rectangle, and G3 of a triangle) is a balancing point for each unique planar figure, and the circumcenter of these centroid points is equidistant from each vertex, which is why this point was chosen as a point of reference (which are centroids). As a result, this point would serve as a more accurate reference point than the trapezoid's centroid.
Take into consideration the trapezoidal linear Diophantine fuzzy number
The centroids of the three plane figures that make up the ζτR(x) are G1=(θ1+2θ33,13),G2=(θ3+θ42,12) and G3=(2θ4+θ63,13) and membership function are G1=(θ1+2θ33,13),G2=(θ3+θ42,12) and G3=(2θ4+θ63,13)) are non-collinear and form a triangle. Since the equation of line G1G3 is y=13 and G2 does not lie on line G1G3. Figure 8 displays the circumcenter of the centroids of ζτR(x).
Likewise, the centroids of the three plane figures that make up the membership function of α(x) are, in a similar manner, G′1=(θ′2+2θ33,13),G′2=(θ3+θ42,12) and G′3=(2θ4+θ′53,13). G′2 does not fall on the line G′1G′3, and its equation is y=13. G′1,G′2and G′3 are therefore non-collinear and form a triangle. Figure 9 displays the circumcenter of the centroids of α(x).
Finding the triangle's circumcenter is our next task. The general equation for a triangle's circumcentre with the coordinates (x1,y1), (x2,y2) and (x3,y3) is
where
The circumcenter ˆSA(ζτR(x))(¯x0,¯y0) of the triangle with vertices G1, G2 and G3 (as shown in Figure 8) of the membership function of the trapezoidal LDFN A={(θ1,θ2,θ3,θ4,θ5,θ6)(θ′1,θ′2,θ3,θ4,θ′5,θ′6) is
Also, the circumcenter ˆSA(α(x))(¯x′0,¯y′0) of the triangle with vertices G′1, G′2and G′3 (as shown in Figure 9) is
Separate the TrapLDFN trapezoid of non-membership functions into three plane figures as well. Again, a triangle, a rectangle, and a triangle successively make up these three plane figures. Additionally, the centroids of the three plane figures that make up the non-membership function ηνR(x) are G11=(θ2+2θ33,23), G12=((θ3+θ4)2,12) and G13=((2θ4+θ53,23) correspondingly. The line G11G13 is has the equation y=23, and G12 does not fall on this line.
G11 ,G12 and G13 are therefore not collinear and form a triangle. Figure 10 displays the circumcenter of the centroids of ηνR(x). And the circumcenter ˆSA(ηνR(x)) of the triangle formed by the vertices G11 ,G12 and G13 of the non-membership function of the trapezoidal LDFN £RTrapLDFN={(θ1,θ2,θ3,θ4,θ5,θ6)(θ′1,θ′2,θ3,θ4,θ′5,θ′6) is
Similarly, the centroids of the three plane figures of nonmembership function β(x) are G1′1=(θ′1+2θ33,23), G1′2=((θ3+θ4)2,12) and G1′3=((2θ4+θ′63,23) respectively. Equation of the line G1′1G1′3 is y=23 and G1′2 does not lie on the line G1′1G1′3. Therefore G1′1,G1′2 and G1′3 (as shown in Figure 11) are non-collinear and they form a triangle. The circumcenter of centroids of β(x) is
Definition 4.1. The ranking function of the trapezoidal LDFN A={(θ1,θ2,θ3,θ4,θ5,θ6)(θ′1,θ′2,θ3,θ4,θ′5,θ′6) for membership function and non-membership function are defined as RA(ζτR(x))=√¯x20+¯y20 , RA(α(x))=√¯x′20+¯y′20 and RA(ηνR(x))=√¯x12+¯y12, RA(β(x))=√¯x′21¯+y′21, then
As an exception, if we allow θ3=θ4 in a TrapLDFN, we will obtain a triangular LDFN with the parameters θ1≤θ2≤θ3≤θ4≤θ5≤θ6 and θ′1≤θ′2≤θ3≤θ4≤θ′5≤θ′6. It is indicated by £RTriLDFN={(θ1,θ2,θ3,θ5,θ6)(θ′1,θ′2,θ3,θ′5,θ′6). The circumcenters of the centroids for the triangular LDFN's membership function and nonmembership function are defined as follows.
and
Example 4.2. Consider two TriLDFN A= {(2,4,5,7,9)(1,3,5,8,10) and B={(3,5,7,8,9)(2,4,7,9,9). Then using the proposed method we find ℜ(A),
Also,
Now,
Now, using the proposed method we find ℜ(B),
Also,
Now,
As ℜ(A)<ℜ(B)⟹A<B.
5.
Conclusions
The linear Diophantine fuzzy numbers have been identified in this research. In this study, we discovered the circumcenter of centroids of the membership function and non-membership function of a linear Diophantine fuzzy number. We also suggested a distance approach for ranking the linear Diophantine fuzzy number depending on the circumcenter of centroids. The suggested method gives the precise organization of linear Diophantine fuzzy numbers. It may be used to rank the linear Diophantine fuzzy numbers in order to deal with various fuzzy optimization issues. This method can be implemented to rank trapezoidal in addition to triangular fuzzy numbers and their counterparts. The following areas may be covered by our future projects:
(ⅰ) Linear programming problems;
(ⅱ) Differential equations;
(ⅲ) Game theory;
(ⅳ) Transportation problems;
(ⅴ) Differential games.
Acknowledgements
The authors would like to express their sincere thanks to the anonymous reviewers for their careful reading and constructive comments.
Conflict of interest
The authors of this paper declare that they have no conflict of interest.









 DownLoad:
DownLoad: