Pricing of vulnerable options based on an uncertain CIR interest rate model

1.   Introduction

Probability theory and uncertainty theory are two axiomatic mathematical systems that model uncertain phenomena. Probability theory is based on frequency. Traditionally, probability theory has been used to describe uncertain events, such as the price of the underlying asset in financial derivatives. If your distribution function is close enough to the frequency, using probability theory is fine. In fact, when we can only get small samples or no samples, the distribution function may deviate far from the real frequency. In this case, using probability theory may lead to counterintuitive results. The relevant content can be seen in Chapter 1 of ^[18]. Furthermore, as early as 1979, Kahneman and Tversky ^[12] pointed out that people always overestimate the probability of impossible events. Thus people always hope that experts in the field will give the belief degree of an event. In order to rationally deal with the belief degree, Liu ^[13] founded the uncertainty theory which is an axiomatic mathematical system based on normality, duality, subadditivity and product axioms in 2007. Nowadays uncertainty theory has become a branch of mathematics concerned with the analysis of belief degree. The forward development of a discipline is inseparable from the joint efforts of many scholars (see ^{[4,13,14,15,16,28]}).

In 2009, Liu ^[15] introduced the uncertainty theory into the financial field and proposed an uncertain stock model that follows uncertain differential equations driven by the geometric Liu process. Peng and Yao ^[22] gave a class of uncertain stock models with mean reversion. Dai et al. ^[8] gave a nonlinear uncertain stock model. In addition, Yu ^[29] studied uncertain stock models with jumps and Chen et al. ^[] also proposed an uncertain stock model with periodic dividends. Many option pricing formulas have been obtained using the above uncertain stock models.

In recent years, with the development of the financial market, hedging and avoiding financial risk have become more and more important, and various types of options have emerged. Default risk, also known as credit risk, comes from the possibility of the default of loan borrowers, bond issuers and derivative counterparties. In general, it has been assumed that options have no default risk when options are traded on an organized exchange. However, the rapid growth in the over-the-counter options has motivated increased attention to the implications of counterparty credit risk. The holders of over-the-counter options are exposed to potential credit risk due to the possibility of their counterparty being unable to make the necessary payments at the expiration date. In 1987, Johnson and Stulz ^[10] discussed the impact of credit default risk on option prices and called this option with credit risk a vulnerable option. In 2022, Xie and Deng ^[26] studied the pricing of European vulnerable options under the conditions of Heston stochastic volatility and a stochastic interest rate model. In 2021, Liang and Wang ^[21] proposed a closed-form hybrid credit risk model to price vulnerable options with stochastic volatility. In 2019, Zhou and Li ^[30] proposed a method to estimate the price of vulnerable options when the volatility of the underlying assets is within a small interval.

For Cox-Ingersoll-Ross(CIR) interest rate models, most of the related research is carried out in the field of randomization. In 2022, Zheng ^[31] priced European export-oriented barrier options by using a CIR model. In 2020, Lei ^[20] studied the asset liability management problem with a CIR interest rate by using a Heston model. In 2019, Sun et al. ^[23] studied the Euler grid difference method and convergence analysis of CIR interest rate models under the conditions of a fractional jump diffusion environment. In 2018, Chen and Hsu ^[3] studied barrier option pricing and hedging by using a Markov-modulated double exponential jump diffusion-CIR model. Wu ^[25] discussed the application of a CIR model in the Chinese market under the condition of a stochastic field in 2017. More references can be seen in ^[7,9,24]. Although the CIR interest rate model has many applications in the field of randomness, CIR interest rate models have few applications in the field of uncertainty. In this paper, we get the solution of the CIR interest rate model in terms of distribution. Based on the CIR interest rate model, the pricing formulas of the European vulnerable call option and European vulnerable put option are obtained, and the related risks are analyzed.

This paper gives the pricing formulas of vulnerable options as obtained by implementing the uncertain CIR interest rate model. The rest of the article is arranged as follows. In Section 2, we introduce some definitions and theorems that will be used in this article. In Section 3, the solution in terms of the distribution of an uncertain differential equation is given. Sections 4 and 5 give the pricing formulas of the European vulnerable call option and the European vulnerable put option based on a new uncertain vulnerable option pricing model, respectively. In Section 6, in order to obtain the numerical solution, two numerical algorithms are designed to calculate the prices of European vulnerable call options and European vulnerable put options, and numerical examples are given to verify the effectiveness of the numerical algorithm. Finally, a brief summary is given in Section 7.

2.   Preliminaries

Definition 2.1. ^[13] Let $\Gamma$ be a nonempty set and ${\mathcal{L}}$ be a $\sigma$-algebra on $\Gamma$. The set function ${\mathcal{M}}$ is called an uncertain measure if it satisfies the following axioms:

Axiom 1. (Normality axiom) ${\mathcal{M}}\{\Gamma\} = 1$ for the universal set $\Gamma$.

Axiom 2. (Duality axiom) ${\mathcal{M}}\{\Lambda\}+{\mathcal{M}}\{\Lambda^c\} = 1$ for any $\Lambda \in {\mathcal{L}}$.

Axiom 3. (Subadditivity axiom) For every countable sequence $\Lambda_1, \Lambda_2, \cdots$ in ${\mathcal{L}}$, we have

The triplet $(\Gamma, {\mathcal{L}}, {\mathcal{M}})$ is called an uncertainty space. Moreover, the product uncertainty measure was defined by Liu ^[15] in 2009 as follows.

Axiom 4. (Product axiom) Let $(\Gamma_k, {\mathcal{L}}_k, {\mathcal{M}}_k)$ be uncertainty spaces for $k = 1, 2, \cdots$. The product uncertainty measure ${\mathcal{M}}$ is an uncertainty measure satisfying

where $\Lambda_k$ denotes arbitrarily chosen events from ${\mathcal{L}}_k, k = 1, 2, \cdots$.

Definition 2.2. ^[13] Let $\xi$ be a function from an uncertainty space $(\Gamma, \mathcal{ L}, {\mathcal{M}})$ to the set of real numbers such that ${\xi\in B}$ is an event for any Borel set B of real numbers; then, the function $\xi$ is called an uncertain variable.

Theorem 2.1. ^[16] Let $\xi_1$, $\xi_2$, $\cdots$, $\xi_n$ be independent uncertain variables with regular uncertainty distributions $\Phi_1$, $\Phi_2$, $\cdots$, $\Phi_n$, respectively. If $f(\xi_1, \xi_2, \cdots, \xi_n)$ is a strictly increasing function with respect to $\xi_1$, $\xi_2$, $\cdots$, $\xi_m$ and a strictly decreasing function with respect to $\xi_{m+1}$, $\xi_{m+2}$, $\cdots$, $\xi_n$, then $\xi = f(\xi_1, \xi_2, \cdots, \xi_n)$ has an inverse uncertainty distribution

Definition 2.3. ^[13] The expected value of an uncertain variable $\xi$ is defined by

provided that at least one of the two integrals exists.

Theorem 2.2. ^[13] Let $\xi$ be an uncertain variable with the uncertainty distribution $\Phi$. Then

Theorem 2.3. ^[16] Let $\xi$ be an uncertain variable with the regular uncertainty distribution $\Phi$. Then

where $\Phi^{-1}(\alpha)$ is the inverse uncertain distribution of the uncertain variable $\xi$.

Theorem 2.4. ^[19] Let $\xi_1$, $\xi_2$, $\cdots$, $\xi_n$ be independent uncertain variables with regular uncertainty distributions $\Phi_1$, $\Phi_2$, $\cdots$, $\Phi_n$, respectively. If $f(x_1, x_2, \cdots, x_n)$ is a continuous, strictly increasing function with respect to $x_1$, $x_2$, $\cdots$, $x_m$ and a strictly decreasing function with respect to $x_{m+1}$, $x_{m+2}$, $\cdots$, $x_n$, then the uncertain variable $\xi = f(\xi_1, \xi_2, \cdots, \xi_n)$ has an expected value of

Definition 2.4. ^[14] Let $T$ be a totally ordered set (e.g. time) and let $(\Gamma, \mathcal{ L}, {\mathcal{M}})$ be an uncertainty space. An uncertain process is a function $X_t(\gamma)$ from $T\times(\Gamma, \mathcal{ L}, {\mathcal{M}})$ to the set of real numbers such that $\{X_t\in B\}$ is an event for any Borel set $B$ of real numbers at each time $t$.

Definition 2.5. ^[15] An uncertain process $C_t$ is said to be a Liu process if

(1) $C_0 = 0$ and almost all sample paths are Lipschitz continuous;

(2) $C_t$ has stationary and independent increments;

(3) every increments $C_{t+s}-C_t$ is a normal uncertain variable with an expected value $0$ and variance $t^2$.

It is very clear that a Liu process $C_t\sim \mathcal{N}(0, t^2)$, that is, the uncertainty distribution of $C_t$ is

Definition 2.6. ^[14] Uncertain processes $X_{1t}, X_{2t}, \cdots, X_{nt}$ are said to be independent if for any positive integer $k$ and any times $t_1, t_2, \cdots, t_k$, the uncertain vectors

are independent, i.e., for any Borel sets $B_1, B_2, \cdots, B_n$ of $k$-dimensional real vectors, we have

Definition 2.7. ^[17] The uncertainty distribution $\Phi_{t}(x)$ of an uncertain process $X_t$ is defined by

for any time $t$ and any real number $x$.

Definition 2.8. ^[17] Let $X_t$ be an uncertain process with the regular uncertainty distribution $\Phi_{t}(x)$. Then the inverse function $\Phi_{t}^{-1}(\alpha)$ is called the inverse uncertainty distribution of $X_t$.

Theorem 2.5. ^[27] Let $X_t$ be a sample-continuous independent increment process with the regular uncertainty distribution $\Phi_t(x)$. Then for any time $s > 0$, the time integral

has an inverse uncertainty distribution

Definition 2.9. ^[28] Let $\alpha$ be a number with $0 < \alpha < 1$. An uncertain differential equation

is said to have an $\alpha$-path $X_t^\alpha$ if it solves the corresponding ordinary differential equation

where $\Phi^{-1}(\alpha)$ is the inverse uncertainty distribution of standard normal uncertain variables, i.e.,

Theorem 2.6. ^[28] Let $X_t$ and $X_t^\alpha$ be the solution and $\alpha$-path of the uncertain differential equation

respectively. Then the solution $X_t$ has an inverse uncertain distribution

Theorem 2.7. ^[27] Let $X_t$ and $X_t^\alpha$ be the solution and $\alpha$-path of the uncertain differential equation

respectively. Then for any time $s > 0$ and a strictly increasing function $J(x)$, the time integral $\int_0^{s}J(X_t){{{\rm{d}}}} t$ has an inverse uncertainty distribution $\Psi_s^{-1}(\alpha) = \int_0^{s}J(X_t^\alpha){{{\rm{d}}}} t$.

3.   Solution for the distribution of an uncertain differential equation

In 1985, the well-known interest rate model, the CIR model was proposed for probability theory ^[6]

where $m > 0$, $a\neq0$ and $\sigma$ are constants, and $W_{t}$ is Brownian motion. As its counterpart, Chen and Gao ^[2] proposed an uncertain interest model based on uncertainty theory in 2013. The interest rate $r_t$ follows the next uncertain differential equation driven by the Liu process

where $m > 0$, $a\neq0$ and $\sigma$ are constants, and $C_{1t}$ is the Liu process.

Jiao and Yao ^[11] gave a numerical method of the uncertain interest model and obtained a formula to calculate the price of the zero coupon bond based on it.

Next we will discuss the solution in terms of uncertainty distribution for the expression (3.2).

Theorem 3.1. Let $r_t$ be the solution of the uncertain differential equation (3.2) with the inverse uncertainty distribution $\Omega_t^{-1}(\alpha)$. Then $\Omega_t^{-1}(\alpha)$ can be expressed in three forms with different values of $\Delta$, where $\Delta = [\sigma\Phi^{-1}(\alpha)]^2+4am$.

Case I: $\Delta > 0$.

where $A_1 = \frac{-\sigma \Phi^{-1}(\alpha)+\sqrt {\Delta}}{\sqrt {\Delta}}$, $A_2 = \frac{\sigma \Phi^{-1}(\alpha)+\sqrt {\Delta}}{\sqrt {\Delta}}$, $x_1 = \frac{\sigma \Phi^{-1}(\alpha)-\sqrt {\Delta}}{2a}$ and $x_2 = \frac{\sigma \Phi^{-1}(\alpha)+\sqrt {\Delta}}{2a}$.

Case II: $\Delta = 0$.

Case III: $\Delta < 0$.

where $p = \frac{\Delta}{-4a^2}$ and $u = \sqrt{\Omega_t^{-1}(\alpha)}-\frac{\sigma \Phi^{-1}(\alpha)}{2a}.$

Proof. From Definition 2.9, the uncertain differential equation

has the $\alpha$-path

In order to obtain the solution of the differential equation (3.3), we divide it into three cases.

Case I: $\Delta = [\sigma\Phi^{-1}(\alpha)]^2+4am > 0$. For the convenience of presentation, let

By solving Eq (3.3), we can get

where $c$ is an arbitrary constant. Substituting the initial conditions $r_0^\alpha = r_0$ into the above equation, we get

Finally

By Theorem 2.6, Case I is true.

Case II: $\Delta = [\sigma\Phi^{-1}(\alpha)]^2+4am = 0$. For the convenience of presentation, let $A_1 = 1$, $A_2 = x_1 = x_2 = \frac{\sigma \Phi^{-1}(\alpha)}{a}$.

The general solution of Eq (3.3) is

where $c$ is an arbitrary constant. From the initial value $r_0^\alpha = r_0$

Finally we get the special solution of Eq (3.3) as

By Theorem 2.6, the result of Case II be proved.

Case III: $\Delta = [\sigma\Phi^{-1}(\alpha)]^2+4am < 0$. For the convenience of presentation, let $p = \frac{\Delta}{-4a^2}$, $u = \sqrt{r_t^\alpha}-\frac{\sigma \Phi^{-1}(\alpha)}{2a}.$

In this case, the general solution of Eq (3.3) is

where $c$ is an arbitrary constant. By applying the initial value $r_0^\alpha = r_0$ we get the special solution of Eq (3.3) as

From Theorem 2.6, the result of Case III is true.

We have completed the proof of this theorem.

4.   European vulnerable call option pricing formula

As is well known, the European call option is a contract which gives the holder the right rather than the obligation to buy stocks at an expiration date $T$ for a strike price $K$. The European vulnerable call option supposes that the value of a company is $Z_t$ at the time $t$. Then the option seller promises to give $(Y_T-K)^+$ to the option holder at the expiration date $T$. If the option seller cannot give $(Y_T-K)^+$ to the holder at the expiration date $T$, the option holder will immediately take over the company. In other words, the final payoff of the option holder at time $T$ is $\min\left(\left(Y_T-K\right)^+, Z_T\right)$. We assume that the price of this European vulnerable call option is $f_c$. According to the fair price principle, we can get the price of the European vulnerable call option

In order to obtain the price of options, Liu ^[15] first modeled the change in financial asset price by using uncertain differential equations and proposed the Liu model, which is the counterpart of the famous B-S model ^[1]. From then on, based on the uncertainty theory, some scholars have put forward other uncertain financial derivatives models that are more suitable for market practice, such as the mean reversion stock model ^[22] and uncertain exponential Ornstein-Uhlenbeck model ^[8]. The above models always assume that the risk interest rate is a constant. However, in the real financial market, interest rates are often uncertain, so interest rates should follow an uncertain differential equation.

In this paper, let $r_t$, $Y_t$ and $Z_t$ be the interest rate, stock price and the company value at time $t$ of a European vulnerable option, respectively, and they follow the uncertain differential equations

where $m > 0$, $a\neq0, e_1, e_2, \sigma, \sigma_1$ and $\sigma_2,$ are all constants and $C_{1t}$, $C_{2t}$ and $C_{3t}$ are three independent Liu processes.

Theorem 4.1. Assume that a European vulnerable call option satisfies the model (4.1) with a strike price $K$ and an expiration date $T$; then, the price of the European vulnerable call option is

where $\Phi_{1T}^{-1}(\alpha) = \exp \left(-\int_0^T \Omega_t^{-1}(1-\alpha){{{\rm{d}}}} t\right),$ $\Upsilon_{1T}^{-1}(\alpha) = \left(Y_0\left(e_1T+\frac{\sqrt{3}\sigma_1 T}{\pi}\ln \frac{\alpha}{1-\alpha}\right)-K\right)^+$ and $\Psi_T^{-1}(\alpha) = Z_0\left(e_2T+\frac{\sqrt{3}\sigma_2 T}{\pi}\ln \frac{\alpha}{1-\alpha}\right)$.

Proof. The inverse uncertainty distribution $\Omega_t^{-1}(\alpha)$ of $r_t$ has been obtained by Theorem 3.1.

From Theorem 2.5, we can get the inverse uncertainty distribution $\Phi_T^{-1}(\alpha) = \int_0^T \Omega_t^{-1}(\alpha) {{{\rm{d}}}} t$ of $\int_0^T r_t {{{\rm{d}}}} t.$ Since $y = \exp(-x)$ is a decreasing function of $x$, from Theorem 2.1,

has an inverse uncertainty distribution

Let $Y_t^\alpha$ be an $\alpha$-path of the uncertain differential equation

By solving the ordinary differential equation

we can get

It follows from Theorem 2.6 that $Y_T$ has an inverse uncertainty distribution

Due to $(Y_T-K)^+$ being an increasing function with respect to $Y_T$, by Theorem 2.1, $(Y_T-K)^+$ has an inverse uncertainty distribution

Similarly, we can get

Thus from Theorem 2.6, $Z_T$ has an inverse uncertainty distribution

Following Theorem 2.1, the expression

has an inverse uncertainty distribution

Thus according to Theorem 2.1 and Theorem 2.3, the price of the European vulnerable call option is shown as follows.

We have completed the proof of this theorem.

5.   European vulnerable put option pricing formula

In this section, we will give the pricing formulas of the European vulnerable put option. Note that $r_t$, $Y_t$ and $Z_t$ are the same as in Theorem 4.1.

The European put option is a contract which gives the holder the right rather than the obligation to sell stocks at an expiration date $T$ for a strike price $K$.

For the European vulnerable put option, the option seller promises to give $\left(K-Y_T\right)^+$ to the option holder at the expiration date $T$. If the option seller cannot give $\left(K-Y_T\right)^+$ to the holder at the expiration date $T$, the option holder will immediately take over the company. In other words, the final payoff of the option holder at time $T$ is $\min\left(\left(K-Y_T\right)^+, Z_T\right)$. We assume that the price of this European vulnerable put option is $f_p$.

According to the fair price principle, we can get the price of the European vulnerable put option

Theorem 5.1. Assume that a European vulnerable put option satisfies the uncertain stock model (4.1) with a strick $K$ and an expiration date $T$; then, the price of the European vulnerable put option is

where $\Phi_{1T}^{-1}(\alpha) = \exp \left(-\int_0^T \Omega_t^{-1}(1-\alpha){{{\rm{d}}}} t\right),$ $\Upsilon_{2T}^{-1}(\alpha) = \left(K-Y_0\left(e_1T+\frac{\sqrt{3}\sigma_1 T}{\pi}\ln \frac{1-\alpha}{\alpha}\right)\right)^+$ and $\Psi_T^{-1}(\alpha) = Z_0\left(e_2T+\frac{\sqrt{3}\sigma_2 T}{\pi}\ln \frac{\alpha}{1-\alpha}\right)$.

Proof. Similar to the proof of Eqs (4.3)–(4.5) in Theorem 4.1, the inverse uncertainty distributions of $\exp \left(-\int_0^T r_t {{{\rm{d}}}} t\right)$, $Y_T$ and $Z_T$ are $\exp \left(-\Phi_T^{-1}(1-\alpha)\right)\triangleq \Phi_{1T}^{-1}(\alpha),$ $Y_T^\alpha\triangleq \Upsilon_T^{-1}(\alpha)$ and $Z_T^\alpha\triangleq \Psi_T^{-1}(\alpha)$, respectively. Due to $(K-Y_T)^+$ being a decreasing function with respect to $Y_T$, by Theorem 2.1, $(K-Y_T)^+$ has an inverse uncertainty distribution

Following Theorem 2.1, the expression

has an inverse uncertainty distribution

Thus according to Theorem 2.1 and Theorem 2.3, the price of the European vulnerable put option is shown as follows.

We have completed the proof of this theorem.

6.   Numerical results

In this section, we design numerical algorithms to calculate the numerical solutions of the European vulnerable call option $f_c$ and European vulnerable put option $f_p$, respectively.

6.1.   European vulnerable call option

Step 0: Set the values of the corresponding parameters $a, m, \sigma, Y_0, e_1, \sigma_1, Z_0, e_2, \sigma_2, T$ and $K.$

Step 1: Choose two appropriate $N$ and $M$ values according to the required accuracy; set $\alpha_i = i/N$ and $t_j = jT/M$, $i = 1, 2, \cdots N-1$, $j = 1, 2, \cdots, M.$

Step 2: Set $i = 0$.

Step 3: Set $i = i+1$.

Step 4: Set $j = 0$.

Step 5: Set $j = j+1$.

Step 6: For each $\alpha_i$, determine the value of $\Delta = \left(\frac{\sqrt{3}\sigma}{\pi}\ln\frac{\alpha_i}{1-\alpha_i}\right)^2+4am.$

If $\Delta > 0$, solve the following ordinary differential equation

where

$A_1 = \frac{-\sigma \Phi^{-1}(1-\alpha_i)+\sqrt {\left[\sigma \Phi^{-1}(1-\alpha_i)\right]^2+4am}}{\sqrt {\left[\sigma \Phi^{-1}(1-\alpha_i)\right]^2+4am}}$, $A_2 = \frac{\sigma \Phi^{-1}(1-\alpha_i)+\sqrt {\left[\sigma \Phi^{-1}(1-\alpha_i)\right]^2+4am}}{\sqrt {\left[\sigma \Phi^{-1}(1-\alpha_i)\right]^2+4am}}$, $x_1 = \frac{\sigma \Phi^{-1}(1-\alpha_i)-\sqrt{\left[\sigma \Phi^{-1}(1-\alpha_i)\right]^2+4am}}{2a}$, $x_2 = \frac{\sigma \Phi^{-1}(1-\alpha_i)+\sqrt {\left[\sigma \Phi^{-1}(1-\alpha_i)\right]^2+4am}}{2a}$.

Else if $\Delta = 0$, solve the following ordinary differential equation

Else if $\Delta < 0$, solve the following ordinary differential equation

where $p = \frac{{\left[\sigma \Phi^{-1}(1-\alpha_i)\right]^2+4am}}{-4a^2}$ and $u = \sqrt{\Omega_{t_j}^{-1}(1-\alpha_i)}-\frac{\sigma \Phi^{-1}(1-\alpha_i)}{2a}.$

If $j < M$, return to Step 5.

Step 7: Calculate the discount rate

and

Step 8: It is obvious that

Step 9: Calculate

if $i < N-1$, return Step 3.

Step 10: $f_c \rightarrow \frac{1}{N-1} \sum_{i = 1}^{N-1}\exp\left(-\int_0^T \Omega_{s}^{-1}(1-\alpha_i){{{\rm{d}}}} s \right)\min\left(\Upsilon_{1T}^{-1}(\alpha_i), \Psi_T^{-1}(\alpha_i)\right).$

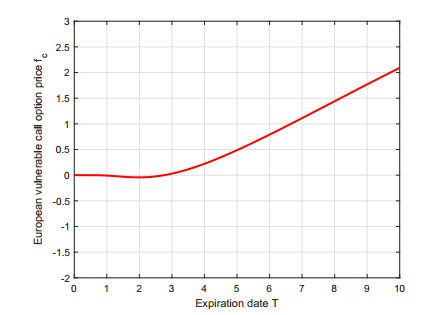
Example 6.1. For the European vulnerable call option pricing formula (6), we assume the $M = 100, N = 100, a = 0.001, m = 0.002, \sigma = 5*10^{-5}, Y_0 = 5, e_1 = 0.1, \sigma_1 = \frac{\pi}{10\sqrt{3}}, Z_0 = 10, e_2 = 0.2, \sigma_2 = \frac{\pi}{8\sqrt{3}}, T = 5$ and $K = 3.6.$ Thus the European vulnerable call option price is $f_c = 0.49944278.$ When the parameters aside from the parameter expiration date $T$ remain unchanged, the relationship between the price of the European vulnerable call option $f_c$ and the expiration date $T$ is as shown in Figure 1. When all parameters except for the parameter volatility $\sigma_1$ remain unchanged, the relationship between the price of the European vulnerable call option $f_c$ and volatility $\sigma_1$ is as shown in Figure 2. When all parameters except for the parameter log-drift $e_1$ remain unchanged, the relationship between the price of the European vulnerable call option $f_c$ and the log-drift $e_1$ is as shown in Figure 3.

It can be seen in Figure 1 that with the increase of the expiration date $T$, the price of European vulnerable call options shows an overall upward trend. When the expiration date $T$ is in the range of [0, 3], the price changes are not obvious, and the price shows a slow growth trend in the range of [3, 10]. Although the direction of time is deterministic, the trend of expiration $T$ is still a focus of attention. As can be seen in Figure 2, with the increase of volatility $\sigma_1$, the price of European vulnerable call options shows an overall upward trend. When the volatility is in the range of [0, 0.04], the option price is negative, indicating that the power of the sellers is far greater than that of the buyers. At this time, the investor should carefully consider the future prospect of this option according to their own risk preference. In the later period, with the increase of volatility $\sigma_1$, the option price shows an upward trend. The slope of the figure represents the vega of the option price, which is the ratio of the change in the corresponding option price to the change in the volatility of the underlying asset. It can be seen in the figure that the vega presents a trend of first increasing and then decreasing under the conditions of this uncertain model. This indicates that the sensitivity of the European vulnerable call option price to volatility changes increases first and then decreases. At this time, it is best to frist buy and then sell the corresponding stock in the form of dynamic hedging, so as to ensure risk neutrality. It can be seen in Figure 3 that with the increase of log-drift $e_1$, the price of European vulnerable call options shows an overall upward trend. When investing, investors should combine log-drift $e_1$ and other indicators to reasonably choose the time to buy and sell.

6.2.   European vulnerable put option

The first six steps of the numerical algorithm for European vulnerable put options are the same as those for the European vulnerable call option.

Step 7: Calculate the discount rate

and

Step 8: It is obvious that

Step 9: Calculate

if $i < N-1$, return Step 3.

Step 10: $f_p \rightarrow \frac{1}{N-1} \sum_{i = 1}^{N-1}\exp\left(-\int_0^T \Omega_{s}^{-1}(1-\alpha_i){{{\rm{d}}}} s \right)\min\left(\Upsilon_{2T}^{-1}(\alpha_i), \Psi_T^{-1}(\alpha_i)\right).$

Example 6.2. For the European vulnerable put option pricing formula (7), we assume that $M = 100, N = 100, a = 0.001, m = 0.002, \sigma = 5*10^{-5}, Y_0 = 5, e_1 = 0.1, \sigma_1 = \frac{\pi}{10\sqrt{3}}, Z_0 = 10, e_2 = 0.2, \sigma_2 = \frac{\pi}{8\sqrt{3}}, T = 5$ and $K = 3.6.$ Thus the European vulnerable put option price is $f_p = 1.3576985.$ When all parameters except for the parameter expiration date $T$ remain unchanged, the relationship between the price of the European vulnerable put option $f_p$ and the expiration date $T$ is as shown in Figure 4. When all parameters except for the parameter volatility $\sigma_1$ remain unchanged, the relationship between the price of the European vulnerable put option $f_p$ and volatility $\sigma_1$ is as shown in Figure 5. When all parameters except for the parameter log-drift $e_1$ remain unchanged, the relationship between the price of the European vulnerable put option $f_p$ and the log-drift $e_1$ is as shown in Figure 6.

It can be seen in Figure 4 that with the increase of the expiration date $T$, the price of the European vulnerable put option generally increases first and then decreases. When the expiration date $T$ is in the range of [0, 1.6], the price gradually increases, and in the range of [1.6, 10], the price gradually decreases. As can be seen in Figure 5, with the increase of volatility $\sigma_1$, the price of European vulnerable put options shows an overall upward trend. When the volatility is in the range of [0, 0.04], option prices are negative. In the range of [0.04, 0.45], with the increase of volatility $\sigma_1$, the option prices show an upward trend. At this time, the vega is not very sensitive to changes in the current underlying asset, so there is no need to make significant adjustments. It can be seen in Figure 6 that with the increase of log-drift $e_1$, the price of the European vulnerable put option shows a downward trend. When investing, investors should combine log-drift $e_1$ and other indicators to reasonably choose the time to buy and sell.

7.   Conclusions

In this paper, first, we obtained the solution in terms of the distribution of the uncertain CIR interest rate model. Second, we obtained the pricing formulas of the European vulnerable call option and European vulnerable put option in the model. Finally, according to the the above pricing formulas, the corresponding numerical algorithms and numerical examples were given to verify them.

Acknowledgments

This work was supported by the Colleges and Universities in Hebei Province Science and Technology Research Project (ZD2019047) and the National Natural Science Foundation (61806133).

Conflict of interest

The authors declare that they have no conflicts of interest.