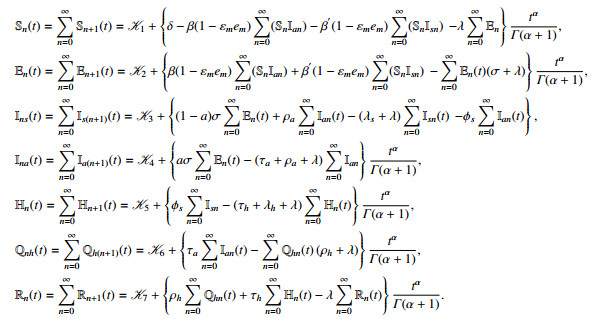A review on portfolio optimization models for Islamic finance

1.   Introduction

The outbreak of the coronavirus started in December 2019 in China ^[1]. It has been categorized as a pandemic by the World Health Organization. This new virus causes a severe acute respiratory illness, which can lead to death, that has been spread worldwide. This badly affects the general health system and the economic growth of the developing and underdeveloped countries. Because of the beginning of the first outbreaks, it is assessed that the worldwide disease burden due to COVID-19 amounts to over 91.2 million people infected globally and 1.9 million deaths worldwide ^[1,2]. From the coronavirus across 215 countries has brought the whole word the series threat ^[3]. It has been confirmed that large number of huge reported COVID-19 cases tend to be observed as mild to moderate respiratory disorders with symptoms, like coughing, fever, and breathing difficulty. This virus transmits mostly through beads from the nose or mouth when an infected individual sneezes or coughs. When the uninfected one breathes the droplets from the air, they will be presented with the risk of getting the infection. As a result, the best technique to control the spread of the coronavirus is to keep it away from people. Thus, there have been research works to interpret the mechanism to prevent the spread of the coronavirus and examine the impacts of different drugs and non-drug mediation. Mathematical modeling is an importing technique for investigating the underlying dynamics of a virus disperse and developing a control technique when enough data about the infection is scant. Models have also been utilized to predict the infection elements and estimate the efficiency of the intervention strategies disease spreading ^[4,5,6,7]. In this way different models have been developed that focus on minimizing the spread of coronavirus ^[8,9,10], such as the isolation of victims, maintaining social distancing, face maskes, washing hands with soap, all official and unofficial gatherings like sports club, games matches, schools, colleges and universities. Mumbu et al. ^[10] and Verma et al. ^[11] proposed a model with seven compartments, which include the susceptible population, exposed population, infected population, asymptotic population and recovered population. This model shows the coronavirus infection India and South Korea countries.

Fractional order epidemic models are more helpful and realistic as a tool to evaluate the dynamics of a contagious disease than classical integer order models ^[12,13]. Because classical mathematical models do not provide a high degree of accuracy for modeling these diseases, fractional differential equations were developed to handle such problems, which have many applications in applied fields related to optimization problems, production problems, artificial intelligence, robotics, cosmology, medical diagnoses, and many more ^[14,15]. The fractional differential equation has been employed in the mathematical modelling of biological phenomena for many decades. Because mathematical models are effective tools for studying infectious diseases, recently, a lot of scientists have been investing mathematical models of the COVID-19 pandemic with fractional order derivatives; they have produced excellent results ^[16,17].

Recently, Srivastav et al. ^[18] developed another compartmental model of the COVID-19 pandemic, particularly for the effects of face masks, hospitalization, and quarantine as follows:

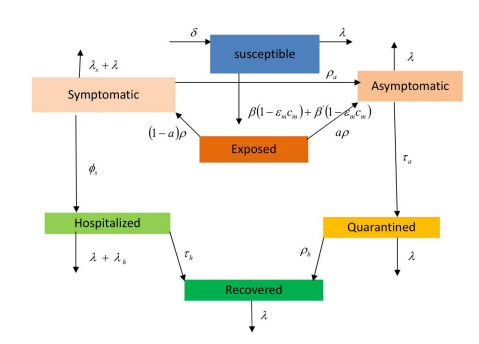
The transmission dynamics of Model (1.1) are represented in the Figure 1 flowchart.

In this model, they have divided the whole population $\mathbb{N}(t)$ into seven epidemiological groups: $\mathbb{S}(t)$ (susceptible population), $\mathbb{E}(t)$ (exposed population), $\mathbb{I}_{s}(t)$ (symptomatic population), $\mathbb{I}_{a}(t)$ (asymptomatic population), $\mathbb{H}(t)$ (hospitalized population), $\mathbb{Q}_{h}(t)$ (quarantined population) and $\mathbb{R}(t)$ (recovered population). They categorized the infectious peoples into two subgroups $\mathbb{I}_{a}$ and $\mathbb{I}_{s}$. They assumed that as quickly as symptoms appear, an $\mathbb{I}_{a}$ individual would join the $\mathbb{I}_{s}$ class. The biological interpretations of parameters are given in Table 1.

Their model focused on the effects of face masks, hospitalization of the $\mathbb{I}_{a}$ population and quarantine of $\mathbb{I}_{s}$ individuals on the spread of the coronavirus. Recently many researchers have proposed models of the COVID-19 pandemic based on the Caputo fractional derivative; they obtained some good results; for details see ^[19,20]. Consequently, inspired by the previously mentioned work, here we study Model (1.1) under the conditions of using fractional-order derivatives. For $\alpha\in(0, 1],$

We apply the following initial conditions:

We believe that a good mathematical model will assist health authorities in taking preventative steps against the spread of the new coronavirus disease. Therefore, we first introduce a Caputo fractional-order model and then derive the existence and non-negativity of the Caputo fractional order model solutions by applying the fractional Gronwall-Bellman inequality using the Laplace transform method(LTM). The uniqueness of the solutions of the model is founded on the use of fixed-point theory. Then, we expand the Laplace Adomian decomposition method (LADM) for numerical simulations. The coupling of the Adomian decomposition method and LTM leads to a powerful technique known as Laplace Adomian decomposition. With the application of LTM, we transform a CFDE into algebraic equations. The nonlinear terms in the first two equations are decomposed in terms of Adonmain polynomials. We see that this iterative method works efficiently for a stochastic system as well as deterministic differential equation. More explicitly, we can also use it for a system of linear and nonlinear ordinary differential equations and partial differential equations of an integer and fractional order. In the above process, no perturbation is required. It is to be proved that the LADM is a better technique than the standard ADM method ^{[21,22,23,24]}.

The rest of the paper is organized as follows: Section 1 is the introduction. Section 2 includes the basic definitions. The existence and non-negativity of the solution are discussed in Section 3. Section 4 is devoted to the uniqueness of the solution. The LAD method is applied to the soolution of the model in Section 5, and the numerical discussion is considered in Section 6. The last section is the conclusion of our work.

2.   Preliminaries

Definition 2.1. ^[25] The CFD of order $\gamma\in(\mathscr{K}-1, \mathscr{K}]$ of $\mathscr{U}(t)$ is defined as

where $\mathscr{K} = [\gamma]+1$ and $[\gamma]$ represents the integral parts of $\gamma$.

Definition 2.2. Magin ^[26] The Riemann-Liouville fractional integration of order $0 < \gamma\leq1$ of the continuous function $\mathscr{U}$ is defined as

Definition 2.3. ^[27] The Laplace transform of $\mathbb{G}(t)$, as denoted by $\mathbb{G}(\mathit{S})$ is defined as

Definition 2.4. Mittag-Leffler function (MLF) is defined as

and

where $\alpha$ and $\beta$ are greater than zero and the convergence of the MLF is described in ^[28,29].

Lemma 2.1. ^[30] The Laplace transform of the Caputo FDO is

where $\mathscr{K}-1 < \gamma < \mathscr{K}$, $\mathscr{K} = [\gamma]+1$ and $[\gamma]$ shows theinteger part of $\gamma.$

Lemma 2.2. ^[31] The following result holds for Caputo FDO

for any $\gamma > 0, \mathscr{K}\in \mathit{N},$ where $\mathscr{K} = [\gamma]+1$ and $[\gamma]$shows the integer part of $\gamma.$

3.   Main work

This section is dedicated to proving the positivity and boundedness of the solution of System (1.2). The size of each class of the population varies over time, and the whole population $\mathbb{N}(t)$ is given by

Applying Caputo fractional order derivatives and using the linearity property of the Caputo operator, we get

Applying the LTM to solve the FGB inequality given by Eq (3.1) with initial conditions $\mathbb{N}(t_{0})\geq0$, we obtain

Splitting Eq (3.2) into partial fractions, we get

By using binomial series expansion, we get

Therefore, Eq (3.3) becomes

Applying the inverse Laplace transform to Eq (3.4) gives

Now, we apply the definition of MLF

where Eq (3.5), $E_{\alpha, 1}\left(-\lambda t^{\alpha}\right)$ and $\mathscr{E}_{\alpha, \mathscr{K}+1}\left(-\lambda t^{\alpha}\right)$ represent the series of entire function. Hence the solutions of Model (1.2) are bounded.

Thus,

4.   Existence and uniqueness

Using the fixed point theory, we will discuss the uniqueness of the solutions of the Caputo fractional-order Model (1.2). For this need, we will follow the following procedure.

Applying the initial conditions and the fractional integral to System (1.2), we obtain

It is assumed that

We define the functions under the integral signs in Eq (4.1) as

Substituting Eq (4.4) into Eq (4.1), we get

So, System (4.5) becomes

Consider a Banach space $\Theta = \mathcal{C}[0, \mathcal{T}]x\mathcal{C}[0, \mathcal{T}]$, with a norm

Let $\varPsi:\Theta\rightarrow \Theta$ be a mapping defined as

Theorem 4.1. System (4.4) has at least one solution if there existconstants $\mathscr{M}_{\mathscr{C}} > 0,$ and $\mathscr{N}_{\mathscr{C}} > 0$, such that

Proof. To show that the operator $\varPsi$ is bounded on $\Omega:\left\{ \mathscr{U}\in\Omega\left|\Lambda\geq\left\Vert \mathscr{U}\right\Vert \right.\right\},$ where

is a closed and convex subset of $\Theta.$ Now, take

It means that $\mathscr{U}\in\varTheta\Rightarrow \varPsi(\varOmega)\subseteq\Omega$, which shows that d is bounded. Next, to show that $\varPsi$ is completely continuous, let $t_{1} < t_{2}\in[0, \mathscr{T}]$ and take

This shows that $\left\Vert \Psi\left(\mathscr{U}\right)(t_{2})-\Psi\left(\mathscr{U}\right)(t_{1})\right\Vert \rightarrow0,$as $t_{2}\rightarrow t_{1}$. Hence, the operator $\Psi$ is completely continuous according to the Arzelá-Ascoli theorem. Therefore, the given system, System (4.4) has at least one solution according to Schauder's fixed-point theorem.

Next, the fixed-point theorem of Banach was used to demonstrate that System (4.4) has a unique solution.

Theorem 4.2. System (4.4) has a unique solution if there exists a constant$\mathcal{C}_{\mathscr{C}} > 0,$ such that for each $\mathscr{U}_{1}(t), \mathscr{U}_{2}(t)\in\Theta,$such that

Proof. Let $\mathscr{U}_{1}(t), \mathscr{U}_{2}(t)\in\Theta.$ Take

Hence, $\Psi$ is the contraction. System (4.4) has a unique solution based on the Banach contraction theorem.

5.   The Laplace Adomian decomposition method

Here, we discuss the use of the Laplace Adomian algorithm for the nonlinear and linear fractional differential equations. The nonlinear terms in this model are $\mathbb{S}\mathbb{I}_{s}$ and $\mathbb{S}\mathbb{I}_{a}$. Further, $\delta, \; \beta, \; \beta^{'}, \; \varepsilon_{m}, \; e_{m}, \; \sigma, \; a, \; \rho_{a}, \; \phi_{s}, \; \tau_{a}, \; \tau_{h}, \; \rho_{h}, \; \lambda, \; \lambda_{s},$ and $\lambda_{h}$ are known constants.

Applying the Laplace transform to Model (1.2), we get

Using the differentiation property of the LT and given initial conditions given in Eq (5.1), we get

Now, applying the inverse Laplace transform to System (5.2) and the initial conditions, we get

Now, we assume that the solution of $\mathbb{S}(t), \mathbb{E}(t), \mathbb{I}_{s}(t), \mathbb{I}_{a}(t), \mathbb{H}(t), \mathbb{Q}_{h}(t)$ and $\mathbb{R}(t)$ in the form of infinite series is defined as

The nonlinear terms of the fractional order model are $\mathbb{S}\mathbb{I}_{s}$ and $\mathbb{S}\mathbb{I}_{a}$. The nonlinear terms are decomposed by using an Adomian polynomial, as follow:

where $\mathbb{C}_{\mathscr{P}}$ and $\mathbb{B}_{\mathscr{P}}$ are called Adomian polynomials, and they depend upon $\mathbb{S}_{0}\mathbb{I}_{s0}, \mathbb{S}_{1}\mathbb{I}_{s1}, ...\mathbb{S}_{m}\mathbb{I}_{sm}$ and $\mathbb{S}_{0}\mathbb{I}_{a0}, \mathbb{S}_{1}\mathbb{I}_{a1}, ...\mathbb{S}_{m}\mathbb{I}_{am},$ respectively. We can calculate the polynomials by using the following formula:

Substituting Eqs (5.4) and (5.5) into Eq (5.3), we get

The subsequent terms are

By applying the initial conditions, we obtained $\mathbb{C}_{0} = \mathbb{S}_{0}\mathbb{I}_{s0} = \mathscr{K}_{1}\mathscr{K}_{3},$ $\mathbb{B}_{0} = \mathbb{S}_{0}\mathbb{I}_{ao} = \mathscr{K}_{1}\mathscr{K}_{4}.$

Then, applying the inverse Laplace transform to Eq (5.8), we obtain the values for Eq (5.8) recursively.

Similarly, we get the following series

We noted that the result obtained via LADM is the same as the ADM ^[32,33].

6.   Numerical simulation

Now, we considered a graphical representation of the obtained approximate solutions given by Eq (5.10). Here, we calculated only three terms for the required approximate solutions of System (1.2). The values of the parameters have either been taken from suitable sources or were assumed. The importance of these parameters is given in Table 2.

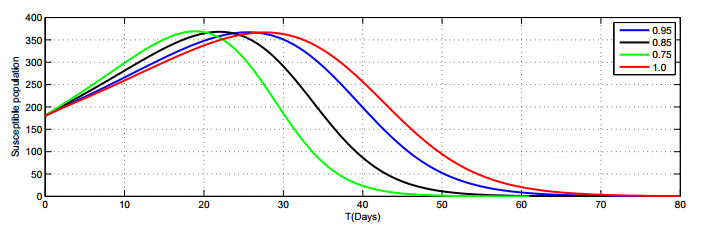
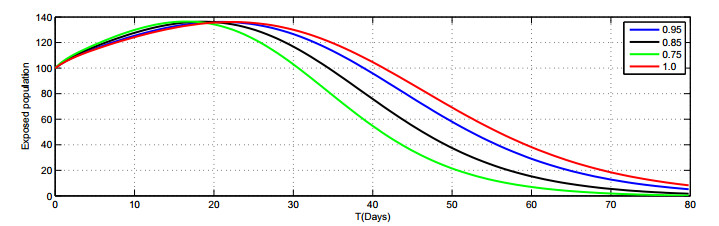
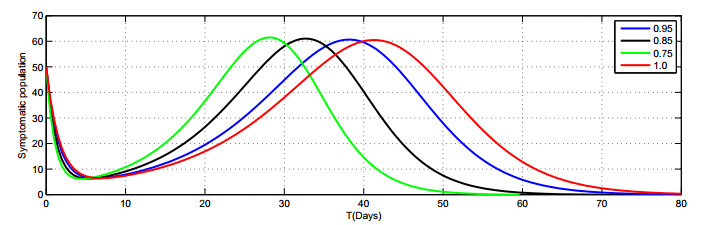
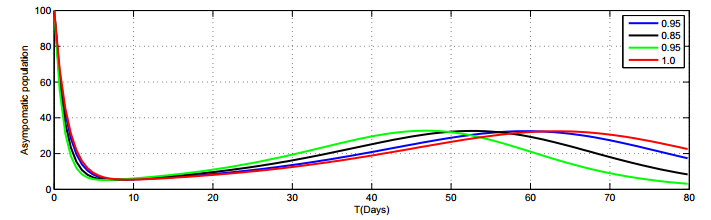
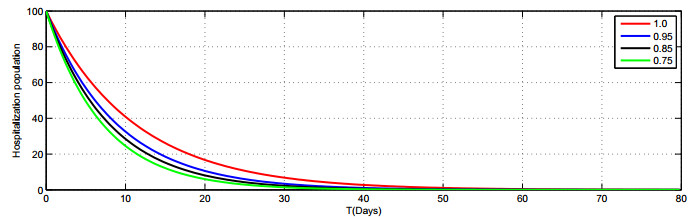
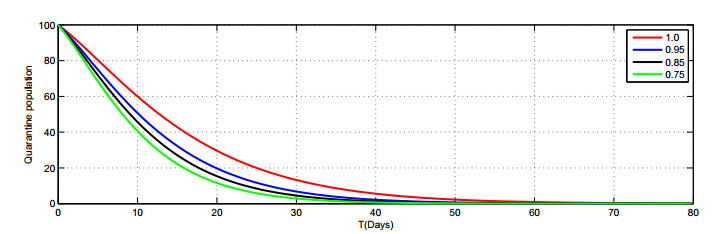
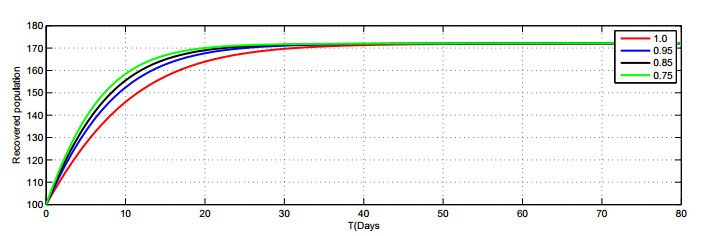
In Figures 2–8, we present the approximate solutions of the Caputo fractional-order model given by Model (1.2) by using the LADM corresponding to different fractional-order values of $\alpha\in(0, 1]$. Figure 2 demonstrates that the susceptible population rapidly decreases when the value of $\alpha$ decreases. The graph in Figure 3 shows the exposed class when the value of $\alpha$ goes down, the rate of increase slowly reduces. The graph in Figure 5 shows that the number of asymptomatic populations decreases for different values of $\alpha$. Therefore, it can be seen in Figure 8 that the people are recover very quickly with different fractional values of $\alpha.$ We also notice that the combined effects of face masks and the hospitalization of asymptomatic individuals on the asymptomatic populations which consequently decreases very rapidly Figure (5). The plot shows that the asymptomatic population disappears completely in a shorter time if the face masks are used together with the hospitalization of confirmed infected people.

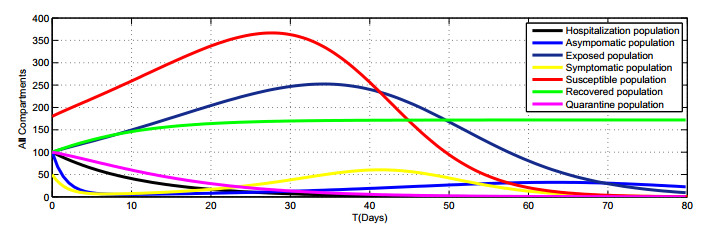
Figure 9 shows all the seven compartments of Model (1.2) when the integer order $\alpha = 1$, and considering the data from Table 2. As compered to traditional derivatives of integer order, fractional order derivatives give more accuracy.

7.   Conclusions

This study investigated the caputo fractional-order model of the COVID-19 pandemic, wherein we modeled the effects of quarantine, hospitalization, and face mask use on the COVID-19 pandemic. The existence and non-negativity of the solutions of Model (1.2) have been demonstrated by solving the FGB inequality using the LTM. We proved the uniqueness of the solution of the Caputo fractional order model. We found that the LADM is a powerful technique capable of heading linear and nonlinear Caputo fractional differential equations. This method produces the same solution as the ADM with the correct choice of initial approximation. From these examples, we can see that this method is considered effective for solving many Caputo fractional-order models. Finally, we derived the graphical results of the obtained approximate solutions presented in Eq (5.10) with different values of the fractional-order $\alpha\in(0, 1].$

Acknowledgments

The authors received financial support from Taif University Researchers Supporting Project (TURSP-2020/031)at Taif University, Taif, Saudi Arabia.

Conflict of interest

The authors declare that they have no competing interests.