Some results on multivariate measures of elliptical and skew-elliptical distributions: higher-order moments, skewness and kurtosis

1.   Introduction and motivation

Fractional calculus has garnered significant attention across various fields of study because of its ability to capture non-local and long-range dependencies in data analysis and modeling. Fractional calculus provides a more flexible framework for capturing intricate dynamics in real-world systems. By incorporating non-integer orders, it becomes possible to model processes that exhibit fractal or self-similar behavior, which are prevalent in many natural and man-made systems ^[2,18]. This flexibility allows for a more accurate representation of complex phenomena, leading to improved understanding and enhanced predictive capabilities. Moreover, the application of fractional calculus can unveil hidden patterns and long-range dependencies that may go unnoticed when using integer-order operators ^[3,4,12,13]. In physics, fractional derivatives have been used to model anomalous diffusion ^[41], viscoelastic materials ^[17], and complex transport phenomena ^[20,43].

A wide range of real-world processes exhibit memory effects or non-local interactions, where the behavior of the system is significantly influenced by distant events or past observations ^[18]. For a detailed discussion, we refer to the monographs by Kilbas et al. ^[27], Lakshmikanthem et al. ^[28], Miller and Ross ^[29], Podlubny ^[31], Almeida et al. ^[11], and the references therein. Kilbas et al. ^[27] provided generalized Riemann-Liouville fractional operators to define the derivative with respect to a function. Several fractional derivatives concerning a function have been introduced, and their properties have been studied ^{[5,8,9,14,24,34,37,38,39]}. Katugampola expands upon the established framework of Erd'elyi-Kober operators, which are commonly used in the field of fractional derivatives. However, Katugampola introduced a specific modification and variation to these operators, which is referred to as the Hilfer-Katugampola fractional derivative ^[26]. These properties provide insights into the behavior of such fractional derivatives and their interactions with other mathematical operations.

Terminal value problems have applications in various fields where the ability to specify a desired final state is crucial to the problem at hand. For instance, in optimal control, terminal value problems are employed to determine the optimal control that minimizes a cost function over a given time frame. The terminal value serves as a constraint, allowing the specification of a particular final position or velocity for the system. Researchers have extensively investigated the existence and uniqueness of solutions to the terminal value problem, exploring the conditions under which a unique value can be determined for the system. For example, Benchohra et al. ^[16] investigated the existence and uniqueness of solutions for the terminal value problem in the Hilfer-Katugampola operator by using different types of classical fixed point theory. Almalahi et al. ^[6,7], developed sufficient conditions for the existence and uniqueness of solutions as well as stability results for the new terminal problems with respect to another function. Shah et al. ^[35] introduced some important notes on terminal value problems for fractional differential equations (FDEs) on infinite intervals. Abdo et al. ^[1] investigated the novel properties for the solution of a coupled system for terminal value problems involving a generalized Hilfer fractional operator. On the other hand, the symmetric solutions offer valuable insights into the behavior, stability, and simplification of mathematical and physical systems. They play a crucial role in simplifying analysis, facilitating physical interpretation, aiding in stability analysis, enhancing numerical computations, and contributing to the development of mathematical theories ^[42,44].

All of the aforementioned studies solely examined the properties of solutions within a single Banach space. However, our study seeks to expand upon this by investigating how the behavior of solutions is influenced by different weighted Banach spaces. Also, we aim to explore the impact of altering the function $w$ on the solutions, while also examining multiple symmetric cases to observe the resulting variations in their behavior.

In this study, we investigate the existence and uniqueness of solutions for a system of terminal FDEs with $w$-Hilfer fractional derivatives and study their Ulam-Hyers (UH) stability ^[19,33,40]. Specifically, we study the fractional system

where

● $w\in \mathcal{C}^{1}([a, b], \mathbb{R})$ is an increasing function such that $w^{\prime }(\iota)\neq 0,$ for all $\iota \in (a, b).$

● $\mathbb{D}_{a^{+}, w(\iota)}^{p_{i}, \alpha }$ denotes the $w$ -Hilfer fractional derivatives of order $p_{i}, (0 < p_{i} < 1)$ and type $\alpha, (0\leq \alpha \leq 1),$ for each $i = 1, 2, ...., n.$

● The functions $\mathbb{F}_{i}:\mathbb{J}\times \mathbb{R} ^{n}\rightarrow \mathbb{R}, i = 1, 2, ...., n,$ are continuous and satisfy some conditions that will be described later.

One of the primary motivations for studying terminal value problems with fractional derivatives is to analyze the stability properties of the corresponding dynamical systems. The $w$-Hilfer fractional derivative can capture complex behaviors such as subdiffusion or superdiffusion, which are not possible with classical integer-order derivatives. By formulating the problem in a weighted space, stability analysis can be performed in a manner that accounts for the importance or significance of different components or variables within the system. The innovative aspects of this work compared to the existing literature can be summarized as follows:

● We extend the analysis from single Banach spaces to different weighted Banach spaces, exploring how the change of weights affects solution properties. This allows us to capture additional structural information and understand the impact of weight functions on solutions.

● We investigate the sensitivity of solutions to changes in the weight function, providing insights into the relationship between the weighted functions and solution behavior by considering multiple symmetric cases to observe variations in solution behavior under different symmetry conditions.

● Furthermore, our study examines the system's properties in various Banach weighted spaces. We establish the existence, uniqueness, and stability of solutions for the system of $w$-Hilfer FDEs with minimal hypotheses, contributing to the theoretical understanding and providing a foundation for further analysis and applications.

● To the best of our knowledge, this is the first study to establish the existence, uniqueness, and stability of solutions for a system of $w$-Hilfer FDEs in different Banach-weighted spaces. Our approach expands the understanding of the system's behavior and broadens the range of potential applications.

● Additionally, the study addresses various parallel problems by considering specific function instances $w$. System (1.1) encompasses a fractional derivative that integrates several traditional fractional derivatives. This broadens the scope of the analysis and allows for a comprehensive investigation of the system's properties.

Notations: To enhance the readability, we fix the above notations and the following ones, we use these without any further mention.

$(1)$ For $0 < a < b$, let $\mathbb{J}: = (a, b]\subset \mathbb{R}.$

$(2) \; \Gamma (p)$ is the standard Gamma function given in ^[15].

$(3) \; \mathcal{C}(\bar{\mathbb{J}}, \mathbb{R})$ is the Banach space for all real-valued continuous functions defined on $\bar{\mathbb{J}},$ equipped with the norm $\left\Vert \varsigma \right\Vert = \underset{\iota \in \mathbb{ J}}{\max }\left\vert \varsigma (\iota)\right\vert,$ where $\bar{\mathbb{J}} = [a, b]$. The space $\prod_{i = 1}^{n}\mathcal{C}(\bar{\mathbb{J}}, \mathbb{R})$ is the product space of $n$ copies of $\mathcal{C}(\bar{\mathbb{J}}, \mathbb{R })$.

$(4)$ For each $i = 1, 2, ..., n,$ let $\gamma _{i} = p_{i}+\alpha (1-p_{i}),$ such that $p_{i}\in \left(0, 1\right)$ and $\alpha \in \left[ 0, 1\right]$. Then, we define the following spaces:

and

The spaces $\mathcal{C}_{1-\gamma _{i}, w}(\mathbb{J}, \mathbb{R})$ are called weighted spaces. Clearly, these are Banach spaces equipped with the norm

$(5) \; \mathcal{B} = \prod_{i = 1}^{n}\mathcal{C}_{1-\gamma _{i}, w}(\mathbb{J}, \mathbb{R})$ is the product space of $\mathcal{C}_{1-\gamma _{i}, w}(\mathbb{J }, \mathbb{R}), i = 1, 2, ...., n.$ The product spaces $\mathcal{B}$ are Banach spaces equipped with the norm

Hypotheses: To obtain our results, the following hypotheses must be satisfied:

$(Hy_{1})$ For each $\left(\iota, \varsigma _{1}, \varsigma _{2}, ...., \varsigma _{n}\right), \left(\iota, \varsigma _{1}^{\ast }, \varsigma _{2}^{\ast }, ...., \varsigma _{n}^{\ast }\right) \in \mathbb{J} \times \mathbb{R}^{n},$ there exist constants $\kappa _{\mathbb{F} _{i}}^{j} > 0, i, j = \; 1, 2, ...., n$ such that

$(Hy_{2})$ For each $\left(\iota, \varsigma _{1}, \varsigma _{2}, ....\varsigma _{n}\right) \in \mathbb{J}\times \mathbb{R}^{n},$ there exist $\varphi _{\mathbb{F}_{i}}^{j} > 0$ with

This paper is organized as follows. In Section 2, we state the needed fundamental notions of fractional derivatives, lemmas, and theorems that will be used in the conversion of the system into a fixed-point problem. In Section 3, we study the existence and uniqueness results of system (1.1), and discuss some properties of the symmetric cases of system (1.1). In Section 4, we investigate the UH stability of the solutions of system (1.1) and its symmetric cases. To illustrate our findings, Section 5 exhibits numerical examples with four cases and provides graphs of the solutions for all cases. We end the paper with concluding remarks.

2.   Basic definitions and essential interpretations

In this section, the background definitions, lemmas, and theorems are given ^[8,27,30,37].

Definition 2.1. Let $0 < p < 1$, $\varsigma$ be a continuous function on $[a, b]$, and $w$ be an increasing function on $(a, b)$ such that $w^{\prime }(\iota)\neq 0$ for all $\iota \in (a, b)$. Then

(1) The $w$-Riemann-Liouville fractional integral for $\varsigma$ of order $p$ is given as

(2) The Riemann-Liouville fractional derivative for $\varsigma$ of order $p$ with respect to $w$ is given as

Definition 2.2. Let $0 < p < 1$, $0\leq \alpha \leq 1$, $\iota > a,$ and $w$ be an increasing function on $(a, b)$ such that $w^{\prime }(\iota)\neq 0$ for all $\iota \in (a, b).$ Then, the $w-$Hilfer fractional derivative of $\varsigma$ of order $p$ and type $\alpha$ is defined by

Clearly,

where $\gamma = p+\alpha (1-p).$

Lemma 2.3. For $p, \eta, \; \delta > 0,$ we have

(1) $\mathbb{I}_{a^{+}, w(\iota)}^{p}\mathbb{\ I}_{a^{+}, w(\iota)}^{\eta }\varsigma (\iota) = \mathbb{I}_{a^{+}, w(\iota)}^{p+\eta }\varsigma (\iota).$

(2) $\mathbb{I}_{a^{+}, w(\iota)}^{p}(w(\iota)-w(a))^{\delta -1} = \frac{ \Gamma (\delta)}{\Gamma (p+\delta)}(w(\iota)-w(a))^{p+\delta -1}.$

Note that $\mathbb{D}_{a^{+}, w(\iota)}^{\gamma }(w(\iota)-w(a))^{\gamma -1} = 0,$ where $\gamma = p+\alpha (1-p).$

Lemma 2.4. Let $\varsigma \in \mathcal{C}(\mathbb{J}, \mathbb{R})$, $p\in (0, 1)$ and $\alpha \in \lbrack 0, 1]$. For $\gamma = p+\alpha (1-p),$ we have

Lemma 2.5. For each $0 < p < 1, 0\leq \alpha \leq 1, \gamma = p+\alpha (1-p)$, and $\varsigma \in \mathcal{C}_{1-\gamma; w(\iota)}^{\gamma }(\mathbb{J}, \mathbb{R})$, we have

and

Definition 2.6. (Contraction mapping) Let $\left(X, d\right)$ be a metric space, and $\mathbb{Q}:X\rightarrow X$ be a mapping. Then, $\mathbb{Q }$ is a contraction mapping if there exists a constant $0\leq L < 1$ such that for all $\varsigma, y\in X,$ the following inequality holds:

The constant $L$ is referred to as the contraction constant. If $L = 0$, the mapping is called a strict contraction.

Theorem 2.7. (Banach fixed point theorem) Let $\left(X, d\right)$ be a complete metric space, and $\mathbb{Q}:X\rightarrow X$ be a contraction mapping. Then, the mapping $\mathbb{Q}$ has a unique fixed point in $X.$

Definition 2.8. Let $a < b$ be real numbers, and $X$ be the space of all continuous function $h$ on $[a, b]$. The set $\Omega \subset X$ is said to be

(1) a uniformly bounded set if there exists $M > 0$ with $\left\Vert h\right\Vert = \sup_{\iota \in \lbrack a, b]}\left\vert h(\iota)\right\vert < M,$ for every $h\in \Omega.$

(2) an equicontinuous set if for every $\varepsilon > 0$ there exists $\delta > 0$ such that

for all $h\in \Omega$ and for any $\iota, \iota ^{\ast }\in \left[ a, b \right].$

Theorem 2.9. (Arzelá-Ascoli's theorem) Let $a < b$ be real numbers, and $X$ be the space of all continuous function on $[a, b]$. The set $\Omega \subset X$ is relatively compact if it is a uniformly bounded and equicontinuous set.

Theorem 2.10. (Schauder's fixed-point theorem) Let $X$ be a Banach space and $\Omega \subset X$ be a non-empty, compact, convex subset. If $\mathbb{Q} :\Omega \rightarrow \Omega$ is a continuous mapping, and $\mathbb{Q}(\Omega)$ is a relatively compact subset of $X$, then $\mathbb{Q}$ has at least one fixed point in $\Omega$.

3.   Main results

In this section, we establish and develop sufficient conditions for the existence and uniqueness as well as UH stability results for the system (1.1). We begin by stating an equivalent integrals for the considered system.

3.1.   Equivalent integral equation

In the following theorem, we convert system (1.1) into equivalent integral equations.

Theorem 3.1. Let $0 < p_{i} < 1$, $0\leq \alpha \leq 1$, and $\gamma _{i} = p_{i}+\alpha (1-p_{i}), i = 1, 2, ...., n.$ If $\mathbb{F}_{i}(\cdot, \varsigma _{1}(\cdot), \varsigma _{2}(\cdot), ......, \varsigma _{n}(\cdot))\in \mathcal{C}_{1-\gamma, w}(\mathbb{J}, \mathbb{R}),$ and $\varsigma _{i}\in \mathcal{C}_{1-\gamma _{i}, w}^{\gamma _{i}}(\mathbb{J}, \mathbb{R}),$ then $\varsigma _{i}$ satisfies system (1.1) if and only if $\varsigma _{i}$ is given by:

where

and

Proof. Let $\varsigma _{i}\in \mathcal{C}_{1-\gamma _{i}, w}^{\gamma _{i}}(\mathbb{J}, \mathbb{R})$ be a solution of system (1.1). We prove that $\varsigma _{i}$ is also a solution of Eq (3.1). From the definition of $\mathcal{ C}_{1-\gamma _{i}, w}^{\gamma _{i}}(\mathbb{J}, \mathbb{R})$, and using the definition 2.2, we have

By the definition of the space $\mathcal{C}_{1-\gamma _{i}, w}^{n}(\mathbb{J}, \mathbb{R}),$ it follows that

Using Lemma 2.4$,$ with $p = \gamma _{i}$, we obtain

By hypothesis $\left(\varsigma _{i}\in \mathcal{C}_{1-\gamma _{i}, w}^{\gamma _{i}}(\mathbb{J}, \mathbb{R})\right)$ and Lemma 2.5, we have

Since $\mathbb{D}_{a^{+}, w(\iota)}^{p_{i}, \alpha }\varsigma _{i}(\iota) = \mathbb{F}_{i}(\iota, \varsigma _{1}(\iota), \varsigma _{2}(\iota), ......, \varsigma _{n}(\iota))$, we have

Comparing Eqs (3.3) and (3.4), we see that

Replacing $\iota$ with $b$ in Eq (3.5), we get

Using the terminal condition $\varsigma _{i}(b) = \upsilon _{i}$, we get

Thus,

Putting Eq (3.6) into Eq (3.5), we get

Hence, $\varsigma _{i}(\iota)$ satisfies Eq (3.1).

Conversely, let $\varsigma _{i}\in \mathcal{C}_{1-\gamma _{i}, w}^{\gamma _{i}}(\mathbb{J}, \mathbb{R})$ be functions satisfying (3.1). We prove that $\varsigma _{i}$ is also a solution of the system (1.1). Applying the operator $\mathbb{D} _{a^{+}, w(\iota)}^{\gamma _{i}}$ on both sides of Eq (3.1), we get

By Lemma 2.3, we have $\mathbb{D}_{a^{+}, w(\iota)}^{\gamma _{i}}(w(\iota)-w(a))^{\gamma _{i}-1} = 0,$ and hence Eq (3.7) becomes

Then, from Lemma 2.5, the right side of Eq (3.8) becomes

Thus, Eq (3.8) becomes

From Eq (3.2), we have $\mathbb{D}_{a^{+}, w(\iota)}^{\gamma _{i}}\varsigma _{i}(\iota)\in \mathcal{C}_{1-\gamma _{i}, w}(\mathbb{J}, \mathbb{R}),$ and hence, Eq (3.8) implies

As $\mathbb{F}_{i}(\cdot, \varsigma _{1}(\cdot), \varsigma _{2}(\cdot), ......, \varsigma _{n}(\cdot))\in \mathcal{C}_{1-\gamma _{i}, w}(\mathbb{J}, \mathbb{R})$, it follows that

From Eqs (3.9) and (3.10) and the definition of the space $\mathcal{ C}_{1-\gamma _{i}, w}^{n}(\mathbb{J}, \mathbb{R}),$ we get

Now, by applying the operator $\mathbb{I}_{a^{+}, w(\iota)}^{\alpha (1-p_{i})}$ on both sides of Eq (3.9) and using Lemma 2.4, we have

From Eq (2.1), Eq (3.11) reduces to

Thus, Eq (1.1) holds. □

Let $\mathbb{Q}:\mathcal{B\rightarrow B}$ be an operator defined by $\mathbb{ Q} = (\mathbb{Q}_{1}, \mathbb{Q}_{2}, ....., \mathbb{Q}_{n})$, where

3.2.   Existence result

Theorem 3.2. Assume both $(Hy_{1})$ and $(Hy_{2})$ hold. For $r = 1, 2, ....., n,$ let

and

If $\zeta = \underset{r}{\max }\left\{ \zeta _{r}\right\} < 1$ and $\mathcal{P} = \underset{r}{\max }\left\{ \mathcal{P}_{r}\right\} < 1,$ then system (1.1) has at least one solution.

Proof. Let $\beta \geq \frac{1}{1-\mathcal{P}}\sum_{i = 1}^{n}\frac{\left\vert \upsilon _{i}\right\vert }{(w(b)-w(a))^{\gamma _{i}-1}}$, and define a closed ball $\mathcal{S}_{\beta }$ as

To apply Schauder's fixed point theorem, we divide the proof into the following steps.

Step 1: $\mathbb{Q}\left(\mathcal{S}_{\beta }\right) \subset \mathcal{S}_{\beta }.$ For any $\left(\varsigma _{1}, \varsigma _{2}, ....\varsigma _{n}\right) \in \mathcal{S}_{\beta }$, we have

From ($Hy_{2}$), we get

Taking into consideration that $\left(\varsigma _{1}, \varsigma _{2}, ....\varsigma _{n}\right) \in \mathcal{B},$ we have

From (3.13) and (3.14), it follows that

Since $\gamma _{i} < 1,$ then $1-\gamma _{i} > 0$, and hence $(w(\iota)-w(a))^{1-\gamma _{i}} < (w(b)-w(a))^{1-\gamma _{i}}.$ Then, we get

Thus,

Hence, $\mathbb{Q}\left(\mathcal{S}_{\beta }\right) \subset \mathcal{S} _{\beta }.$

Step 2: $\mathbb{Q}$ is continuous. Let $(\varsigma _{1k}, \varsigma _{2k}, ...., \varsigma _{nk})$ be a sequence in $\mathcal{S} _{\beta }$ such that $(\varsigma _{1k}, \varsigma _{2k}, ...., \varsigma _{nk})\rightarrow (\varsigma _{1}, \varsigma _{2}, ...., \varsigma _{n})$ in $\mathcal{S}_{\beta }$ as $k\rightarrow \infty.$ Then, we have

This implies that $\left\Vert \mathbb{Q}(\varsigma _{1k}, \varsigma _{2k}, ...., \varsigma _{nk})-\mathbb{Q}(\varsigma _{1}, \varsigma _{2}, ...., \varsigma _{n})\right\Vert _{\mathcal{B}}\rightarrow 0$ as $k\rightarrow \infty.$ So, $\mathbb{Q}$ is continuous.

Step 3: $\mathbb{Q}$$\left(\mathcal{S}_{\beta }\right)$is equicontinuous.

For $\iota _{1}, \iota _{2}\in \mathbb{J}$ with $\iota _{1} < \iota _{2}$, and for any $(\varsigma _{1}, \varsigma _{2}, ...., \varsigma _{n})\in \mathcal{S} _{\beta }$, we have

Since $\mathbb{F}_{i}(\cdot, \varsigma _{1}(\cdot), ...., \varsigma _{n}(\cdot))$ are continuous on $\mathbb{J}$, there exist $\xi _{\mathbb{F} _{i}}\in \mathbb{R}$ such that

Hence,

Thus, we get

Since $w(\iota)$ is an increasing function, then

This implies that $\mathbb{Q}$$\left(\mathcal{S}_{\beta }\right)$ is equicontinuous. Since $\mathbb{Q}$$\left(\mathcal{S}_{\beta }\right)$ is also uniformly bounded, then by Arzelá-Ascoli's theorem, it is relatively compact. By Theorem 3.1, $\mathbb{Q}$ has a fixed point. Consequently, system (1.1) possesses at least one solution. □

3.3.   Uniqueness result

Theorem 3.3. Suppose that hypothesis $(Hy_{1})$ holds. For $r = 1, 2, ..., n,$ let

If $\zeta = \underset{r}{\max }\left\{ \zeta _{r}\right\} < 1$, then system (1.1) has a unique solution.

Proof. To show that system (1.1) has a unique solution, we show that the operator $\mathbb{Q}$ is a contraction, where $\Phi$ as defined in Theorem 3.1.

For all $\iota \in \mathbb{J}$ and $(\varsigma _{1}, \varsigma _{2}, ...., \varsigma _{n}), (\varsigma _{1}^{\ast }, \varsigma _{2}^{\ast }, ...., \varsigma _{n}^{\ast })\in \mathcal{B},$ we have

Since $\zeta < 1$, the operator $\mathbb{Q}$ is a contraction map. Thus, by Theorem 2.7, system (1.1) has a unique solution. □

3.4.   Symmetric cases of system (1.1)

In this subsection, we consider some symmetric cases of system (1.1):

Case1: $w(\iota) = \iota$. In this case, system (1.1) reduces to a system of Hilfer fractional equations in the following form

where $\mathbb{D}_{a^{+}, \iota }^{p_{i}, \alpha }$ represents the Hilfer fractional derivative of order $p_{i}$ ^[23]. Let $\mathcal{B} _{1} = \prod_{i = 1}^{n}C_{1-\gamma _{i}, \iota }\left(\mathbb{J}, \mathbb{R} \right),$ where $\mathcal{C}_{1-\gamma _{i}, \iota }$ is the weighted space defined as in the notation part and equipped with the norm

Theorems 3.2 and 3.3 imply the following corollary.

Corollary 3.4. Assume that both $($Hy$_{1})$ and $($Hy$_{2})$ hold. For $1\leq r\leq n,$ let

and

If $\mathcal{P}^{\star } = \underset{r}{\max }\left\{ \mathcal{P}_{r}^{\star }\right\} < 1,$ and $\zeta ^{\star } = \underset{r}{\max }\{\zeta _{r}^{\star }\} < 1$, then system (3.16) has at least one solution $(\varsigma _{1}, \varsigma _{2}, ...., \varsigma _{n})\in \mathcal{B}_{1}$, where $\varsigma _{i}$ is given by

where

and

Case 2: $w(\iota) = \log \iota$. In this case, system (1.1) has the form

where, $\mathbb{D}_{1^{+}, \log \iota }^{p_{i}, \alpha }$ is the Hilfer-Hadamard fractional derivative of order $p_{i}$ ^[22,32]. Let $\mathcal{B}_{2} = \prod_{i = 1}^{n}C_{1-\gamma _{i}, \log \iota }\left(\mathbb{J}, \mathbb{R}\right),$ where $\mathcal{C}_{1-\gamma _{i}, \log \iota }$ is equipped with the norm

Theorems 3.2 and 3.3 then imply the following corollary.

Corollary 3.5. Assume that both $(Hy_{1})$ and $(Hy_{2})$ hold. For $1\leq r\leq n,$ let

and

If $\mathcal{P}^{\ast \ast } = \underset{r}{\max }\left\{ \mathcal{P} _{r}^{\ast \ast }\right\} < 1,$ and $\zeta ^{\ast \ast } = \underset{r}{\max } \{\zeta _{r}^{\ast \ast }\} < 1,$ then, system (3.20) has at least one solution $(\varsigma _{1}, \varsigma _{2}, ...., \varsigma _{n})\in \mathcal{B} _{2},$ where $\varsigma _{i}$ is given by

where

and

Case 3: $w(\iota) = \iota ^{q},$ where $q > 0$. In this case, system (1.1) becomes a system of Hilfer-Katugampola in the following form.

where $\mathbb{D}_{a^{+}, \iota ^{p}}^{p_{i}, \alpha }$ is the Hilfer-Katugampola fractional derivative of order $p_{i}$ ^[26,30]. Let $\mathcal{B}_{3} = \prod_{i = 1}^{n}C_{1-\gamma _{i}, \iota ^{q}}\left(\mathbb{J}, \mathbb{R}\right),$ where $\mathcal{C}_{1-\gamma _{i}, \iota ^{q}}$ is the weighted space equipped with the norm

Theorems 3.2 and 3.3 imply the following corollary.

Corollary 3.6. Assume that $(Hy_{1})$ and $(Hy_{2})$ hold. For $1\leq r\leq n,$ let

and

If $\mathcal{P}^{\ast \ast \ast } = \underset{r}{\max }\left\{ \mathcal{P} _{r}^{\ast \ast \ast }\right\} < 1,$ and $\zeta ^{\ast \ast \ast } = \underset{r }{\max }\{\zeta _{r}^{\ast \ast \ast }\} < 1,$ then system (3.20) has at least one solution $(\varsigma _{1}, \varsigma _{2}, ...., \varsigma _{n})\in \mathcal{B}_{3},$ where $\varsigma _{i}$ is given by

where

and

Remark 3.7. There are many symmetric cases of the function $w$ and parameter $\alpha$ that result in symmetric systems, some of which have already been discussed in the literature. For example.

$1)$ For $w(\iota) = \iota$ and $\alpha = 0$, system (1.1) is equivalent to the Riemann-Liouville system ^[27].

$2)$ For $w(\iota) = \iota$ and $\alpha = 1$, system (1.1) is equivalent to the Caputo system ^[27].

$3)$ For $w(\iota) = \iota ^{q}$ and $\alpha = 1$, system (1.1) is equivalent to the Caputo-Katugampola system ^[10].

$4)$ For $w(\iota) = \iota ^{q}$ and $\alpha = 0,$ system (1.1) is equivalent to the Katugampola system ^[26].

$5)$ For $w(\iota) = \iota$ and $\alpha \in (0, 1)$, system (1.1) is equivalent to the Hilfer system ^[23].

$6)$ For $w(\iota) = \iota ^{q}, q > 0$ and $\alpha \in (0, 1)$ system (1.1) is equivalent to the Hilfer-Katugampola system ^[30].

$7)$ For $w(\iota) = \log \iota$ and $\alpha \in (0, 1)$, system (1.1) is equivalent to the Hilfer-Hadamard system ^[32].

$8)$ For $w(\iota) = \log \iota$ and $\alpha = 0),$ system (1.1) is equivalent to the Hadamard system ^[22].

$9)$ For $w(\iota) = \log \iota$ and $\alpha = 1,$ system (1.1) is equivalent to the Caputo-Hadamard system ^[25].

4.   Ulam-Hyers stability analysis

The UH stability of system (1.1) is discussed in this section. Following the notation of this paper, we state the following definition for UH for system (1.1) ^[19,33,40].

Definition 4.1. System (1.1) is UH stable if there exists a positive constant $\Upsilon = \max \{\Upsilon _{1}, \Upsilon _{2}, ..., \Upsilon _{n}\}$ such that for some $\varepsilon = \max \{\varepsilon _{1}, \varepsilon _{2}, ..., \varepsilon _{n}\} > 0$ and for each solution $(z_{1}, z_{2}, ...., z_{n})$ of system (1.1) satisfying the following inequality

there exists a unique solution $(\varsigma _{1}, \varsigma _{2}, ...., \varsigma _{n})$ for system (1.1) such that

Remark 4.2. The functions $(z_{1}, z_{2}, ...., z_{n})$ are a solution of inequality (4.1) if and only if there exist functions $\sigma _{i}(\iota)\in \mathcal{C}_{1-\gamma _{i}, w}, i = 1, 2, ...., n$ (which depends on solution $z_{i}$) such that

● $\left\vert \sigma _{i}(\iota)\right\vert \leq \varepsilon _{i}$.

● $\mathbb{D}_{a^{+}, w(\iota)}^{p_{i}, \alpha }z_{i}(\iota) = \mathbb{F} _{i}(\iota, z_{1}(\iota), z_{2}(\iota), ......, z_{n}(\iota))+\sigma _{i}(\iota).$

Theorem 4.3. Under hypothesis $(Hy_{1})$, system (1.1) is UH stable, provided that

for all $1\leq i\leq n.$

Proof. Let $\varepsilon = \max \left\{ \varepsilon _{1}, \varepsilon _{2}, ...., \varepsilon _{n}\right\} > 0$ and let $(z_{1}, z_{2}, ...., z_{n})\in \mathcal{B}$ be a solution of system (1.1) satisfying inequality (4.1), and let $(\varsigma _{1}, \varsigma _{2}, ...., \varsigma _{n}) \; \in \mathcal{B}$ be the unique solution of system (1.1). By virtue of Theorem 3.1, we obtain

where

since, we have assumed that $(z_{1}, z_{2}, ...., z_{n})\in \mathcal{B}$ is a solution of system (1.1) satisfying the inequality (4.1). Then, by Remark 4.2, we conclude that $(z_{1}, z_{2}, ...., z_{n})$ satisfies the following system

By Theorem 3.1, the solution $z_{i}(\iota)$ of system (4.5) is given as

where

Hence, we have

By (4.4) and (4.6), we have $\mathcal{A}_{z_{i}} = \mathcal{A} _{\varsigma _{i}}.$ Since the function $w$ is increasing for each $\iota \in \mathbb{J}$ and $\gamma _{i} < 1$ for $i = 1, 2, ...n,$ we get

Hence, Eq (4.7) becomes

By the first part of Remark 4.2 and $(Hy_{1}),$ we get

Thus, for $i = 1,$ we have

Since $\left\Vert \varsigma _{i}\right\Vert _{1-\gamma _{i}, w} = \max_{\iota \in \mathbb{J}}\left\vert (w(\iota)-w(a))^{1-\gamma _{i}}\varsigma _{i}(\iota)\right\vert,$ and $w$ is increasing function, then

Hence, we have

Note that the positive values of the Gamma function on $(0, 1]$ are necessary to obtain the last inequality.

Let $c_{1} = 1-2\frac{\kappa _{\mathbb{F}_{1}}^{1}\Gamma \left(\gamma _{1}\right) }{\Gamma (p_{1}+\gamma _{1})}(w(b)-w(a))^{p_{1}}$, and

If $2\frac{\kappa _{\mathbb{F}_{1}}^{1}\Gamma \left(\gamma _{1}\right) }{ \Gamma (p_{1}+\gamma _{1})}(w(b)-w(a))^{p_{1}} < 1$, then $c_{1} > 0$. Then, we obtain

Similarly, for each $i = 2, 3, .., n$, provided that $2\frac{\kappa _{\mathbb{F} _{i}}^{i}\Gamma \left(\gamma _{i}\right) }{\Gamma (p_{i}+\gamma _{i})} (w(b)-w(a))^{p_{i}} < 1,$ we have

where $c_{i} = 1-2\frac{\kappa _{\mathbb{F}_{i}}^{i}\Gamma \left(\gamma _{i}\right) }{\Gamma (p_{i}+\gamma _{i})}(w(b)-w(a))^{p_{i}}$, and

Therefore, if $2\frac{\kappa _{\mathbb{F}_{i}}^{i}\Gamma \left(\gamma _{i}\right) }{\Gamma (p_{i}+\gamma _{i})}(w(b)-w(a))^{p_{i}} < 1, i = 1, 2, ..n,$ then

where $\varepsilon = \underset{i}{\max }\{\varepsilon _{i}\}$ and $\Upsilon = \sum_{i = 1}^{n}\frac{\Upsilon _{i}}{c_{i}}.$ By Definition 4.1, the solution of system (1.1) is UH stable. □

4.1.   Ulam-Hyers stability of symmetric cases

According to Theorem 4.3, we can easily prove the UH stability of symmetric systems as follows.

$(1)$ Under hypothesis $(Hy_{1})$, system (3.16) is UH stable, provided that

for all $1\leq i\leq n.$

$(2)$ Under hypothesis $(Hy_{1})$, system (3.20) is UH stable, provided that

for all $1\leq i\leq n.$

$(3)$ Under the hypothesis $(Hy_{1})$, the system (3.24) is UH stable, provided that

for all $1\leq i\leq n.$

5.   An example

In this section, we consider an example of a system of $w$-Hilfer FDEs with different functions $w$.

Example 5.1. We study the system

for the cases $w(\iota) = e^{\iota }, w(\iota) = \iota, w(\iota) = \log \iota$, and $w(\iota) = \iota ^{q}.$

Here, $p_{i} = \frac{1}{2}, \; \alpha _{i} = \frac{1}{2}, \; \gamma _{i} = \frac{3}{4}, \; a = 0, \; b = 1, \; \upsilon _{i} = \frac{3i}{2},$ and

Clearly, $\mathbb{F}_{i}(\iota, \varsigma _{1}(\iota), \varsigma _{2}(\iota), ......, \varsigma _{n}(\iota))$ are continuous functions on $\left[ 0, 1\right] \times \mathbb{R}^{n}$ and satisfy

and

for all $\left(\varsigma _{1}, \varsigma _{2}, ....\varsigma _{n}\right), \left(z_{1}, z_{2}, ....z_{n}\right),$ i.e., $\varphi _{\mathbb{F} _{i}}^{j} = \kappa _{\mathbb{F}_{i}}^{j} = \frac{1}{18}.$

We fix the number of equations to be $n = 5$, and investigate the following cases:

Case 1: $w(\iota) = e^{\iota }.$ In this case, we have $\mathcal{ P} = \max \{\mathcal{P}_{1}, ..., \mathcal{P}_{5}\}\simeq 0.75 < 1,$ and $\zeta = \max \left\{ \zeta _{1}, ..., \zeta _{5}\right\} = 0.75 < 1,$ where $\mathcal{P} _{r}$ and $\zeta _{r}$ are given in Theorems 3.2 and 3.3, respectively.

Hence, all conditions in Theorem 3.2 and Theorem 3.3 are satisfied. Thus, the system has a unique solution $\left(\varsigma _{1}, \varsigma _{2}, ..., \varsigma _{5}\right).$ This solution has the form

On the other hand, let $\iota \in \left(0, 1\right]$ and $\varepsilon _{i} > 0, i = 1, 2, ..., n$ satisfying the following inequality

Then, system (1.1) is UH stable with

where

and

Symmetric cases:

Case 2: $w(\iota) = \iota$. In this case, we have $\mathcal{ P^{\ast }} = \max \{\mathcal{P}_{1}^{\ast }, ..., \mathcal{P}_{5}^{\ast }\}\simeq 0.37 < 1,$ and $\zeta ^{\ast } = \max_{\iota \in \mathbb{J}}\left\{ \zeta _{1}^{\ast }, ..., \zeta _{5}^{\ast }\right\} = 0.37 < 1$, where $\mathcal{P }_{r}^{\mathcal{\ast }}$ and $\zeta _{r}^{\ast }$ are given in (3.18) and (3.19), respectively.

Hence, all conditions in Theorem 3.2 and Theorem 3.3 are satisfied. Thus, the system has at least one solution $\left(\varsigma _{1}, \varsigma _{2}, ..., \varsigma _{5}\right)$ given by

On the other hand, let $\iota \in \left(0, 1\right]$ and $\varepsilon _{i} > 0, i = 1, 2, ..., n$, satisfying the following inequality,

Then, system (3.16) is UH stable with

where

and

Case 3: $w(\iota) = \log \iota.$ For this case, we need to change the interval $\mathbb{J}$, as the function $w$ is not defined on $(0, 1]$. So, in this case, only $a$ and $b$ will be changed to be $a = 1, b = 2$, $\mathcal{P}^{\ast \ast } = \max \{\mathcal{P}_{1}^{\ast \ast }, ..., \mathcal{P}_{5}^{\ast \ast }\}\simeq 0.75 < 1,$ and $\zeta ^{\ast \ast } = \max \left\{ \zeta _{1}^{\ast \ast }, ..., \zeta _{5}^{\ast \ast }\right\} = 0.76 < 1$, where $\mathcal{P}_{r}^{\ast \ast }$ and $\zeta _{r}^{\ast \ast }$ are defined in (3.22) and (3.23), respectively. Hence, all conditions in Theorem 3.2 and Theorem 3.3 are satisfied. Thus, the system has at least one solution $\left(\varsigma _{1}, \varsigma _{2}, ..., \varsigma _{5}\right)$ given by

On the other hand, let $\iota \in \left(1, 2\right]$ and $\varepsilon _{i} > 0, i = 1, 2, ..., n$, satisfying the following inequality.

Then, system (3.20) is UH stable with

where

and

Case 4: $w(\iota) = \iota ^{q}, q > 0.$ We also consider this case on $(1, 2]$, even though we can consider the system on $[0, 1]$, where it will be generalizing case 2. In this case, we have $\mathcal{P} = \max \{\mathcal{P} _{1}^{\ast \ast \ast }, .., \mathcal{P}_{5}^{\ast \ast \ast }\}\simeq 0.75 < 1,$ and $\zeta = \max \left\{ \zeta _{1}^{\ast \ast \ast }, .., \zeta _{5}^{\ast \ast \ast }\right\} = 0.75 < 1$, where $\mathcal{P}_{r}^{\ast \ast \ast }$ and $\zeta _{r}^{\ast \ast \ast }$ are defined in (3.26) and (3.27), respectively. Hence, all conditions in Theorem 3.2 are satisfied. Thus, the system has at least one solution $\left(\varsigma _{1}, \varsigma _{2}, ..., \varsigma _{n}\right)$ given by

Let $q = 2$ and $\varepsilon _{i} > 0, i = 1, 2, ..., n$, satisfying the following inequality.

Then, system (3.24) is UH stable with

where

and

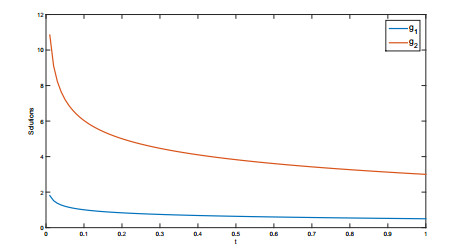
We fix $i = 2$ and present the graphical presentations of solutions for the above four cases in Figures 1, 2, 3, and 4 respectively as follows:

In Figure 1, we have presented the graphical presentation of Case I using $i = 2$ to investigate the properties of the system under the Banach weighted spaces and provide insights into the system's response by using the weighted measurable function $w(\iota) = e^{\iota }$ over the interval $[0, 1].$ From Figure 1, the UH stability is obvious and the symmetry in the approximation solution also arises. Moreover, the uniqueness of the solutions here clearly corresponds to the coupled system of two equations. Remember, we use for graphical presentation (1.1) using $i = 2$.

In Figure 2, we have presented the approximate solution for the system using $i = 2$ to investigate the properties of the system under the Banach weighted spaces and provide insights into the system's response by using the weighted measurable function $w(\iota) = \iota$ over the interval $[0, 1].$ The graphical illustration for the approximate solution demonstrates the symmetry in both solutions for the given weighted measurable function. Here, we have also used (5.2) to illustrate graphs for the approximate solution using $i = 2$.

In Figure 3, the approximate solutions using the weighted measurable function $w(\iota) = \log \iota$ in Banach weighted spaces are displayed by selecting the interval $[1, 2]$. We considered again (5.3) using $i = 2$ and demonstrated the approximate solutions to elaborate the behaviors of both graphs. From the graphs, we see that, as $\log \iota$ is considered, we have displayed the approximate solutions over the interval $[1, 2]$. The UH stability can be observed in the graphs and the symmetry also is understandable. There is a little bit of difference in both graphs' behaviors is due to the reason that we do not know the exact solution as the problem is very highly nonlinear.

In Figure 4, we have displayed the approximate solution of (5.4) using $i = 2$ by utilizing the weighted measurable function $w(\iota) = \iota {^{q}}$ in Banach weighted spaces. The solutions for the coupled system have been plotted over $[1, 2]$. From the graphs, we see the symmetric behaviors and UH stability. From these discussions, we conclude that symmetry concepts are significant when it comes to natural laws. Further, it is highly interesting that symmetry is the key to nature, but symmetry-breaking processes are mostly responsible for the texture of the universe. There are many different ways that nature's symmetry can be obscured or disturbed. All these discussions about the symmetry in solutions of type as mentioned above integrals will be helpful for those researchers working in physical sciences including quantum physics, mechanics, etc.

6.   Conclusions

In our study, we focused on exploring the existence and uniqueness of symmetric solutions for a system of terminal FDEs in the context of weighted spaces. The specific operator we utilized was the $w$-Hilfer FD, which is known for its importance in fractional calculus. To examine the existence and uniqueness of symmetric solutions, we employed two fixed-point theorems, the Schauder and Banach fixed-point theorems. These theorems provide the mathematical tools for establishing the existence and uniqueness of solutions in various settings. By applying Schauder and Banach fixed-point theorems to our system, we were able to obtain two key theoretical findings and four symmetry cases. These findings clarify the behavior and properties of symmetric solutions in the considered Banach weighted spaces. By mathematical analysis, we discussed two types of stability in the Ulam sense. The investigation of terminal FDEs using the $w$-Hilfer FD operator in Banach weighted spaces represents a recent and cutting-edge research direction. We believe this study contributes to the advancement of knowledge in this particular area. Overall, our study not only addresses the challenge of examining the existence and uniqueness of symmetric solutions, but also provides valuable insights into the dynamics and applications of such solutions in fractal mediums. By offering a comprehensive explanation of these processes, our research contributes to the existing literature and expands the understanding of the real-world application of fractional calculus. In future work, we will extend these results with a piecewise fractional operator with the concept of Atangana-Baleanu.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia (grant no. 6057). This study is supported via funding from Prince Sattam bin Abdulaziz University, project number (PSAU/2024/R/1445). The researchers wish to extend their sincere gratitude to the Deanship of Scientific Research at the Islamic University of Madinah for the support provided to the Post-Publishing Program.

Conflict of interest

The author declares that the research was conducted in the absence of any conflict of interest.