Herein the research objects, a hyperbolic quasi-linear system of governing equations was solved by an asymptotic method (far-field technique) with explaining a 1-D unsteady planar and cylindrically symmetric flows in magnetogasdynamics. The evolution equation was obtained by generalized Burger's equation. A relatively accurate systematic result of the evolution equation was gotten by us through the analytic homotopy analysis method (HAM). We are allowed by the method to determine the various effects of nonlinearity and geometrical spreading. One of the fundamental problems of conservation laws are represented by the non-linear waves from preliminary data.
Citation: Anoop Kumar, Aziz Khan, Rajan Arora, Thabet Abdeljawad, K. Karthikeyan, Mohamed Houas. Analysis of the far-field behavior of waves in magnetogasdynamic[J]. AIMS Mathematics, 2023, 8(3): 7329-7345. doi: 10.3934/math.2023369
| [1] | Jingye Zhao, Zonghua Wei, Jiahui Liu, Yongqiang Fan . Vanishing magnetic field limits of solutions to the non-isentropic Chaplygin gas magnetogasdynamics equations. AIMS Mathematics, 2025, 10(1): 1675-1703. doi: 10.3934/math.2025077 |
| [2] | Mubashir Qayyum, Efaza Ahmad, Hijaz Ahmad, Bandar Almohsen . New solutions of time-space fractional coupled Schrödinger systems. AIMS Mathematics, 2023, 8(11): 27033-27051. doi: 10.3934/math.20231383 |
| [3] | Azhar Iqbal, Abdullah M. Alsharif, Sahar Albosaily . Numerical study of non-linear waves for one-dimensional planar, cylindrical and spherical flow using B-spline finite element method. AIMS Mathematics, 2022, 7(8): 15417-15435. doi: 10.3934/math.2022844 |
| [4] | Y. Massoun, C. Cesarano, A. K Alomari, A. Said . Numerical study of fractional phi-4 equation. AIMS Mathematics, 2024, 9(4): 8630-8640. doi: 10.3934/math.2024418 |
| [5] | Yousef Jawarneh, Humaira Yasmin, M. Mossa Al-Sawalha, Rasool Shah, Asfandyar Khan . Fractional comparative analysis of Camassa-Holm and Degasperis-Procesi equations. AIMS Mathematics, 2023, 8(11): 25845-25862. doi: 10.3934/math.20231318 |
| [6] | Samia Bushnaq, Sajjad Ali, Kamal Shah, Muhammad Arif . Approximate solutions to nonlinear fractional order partial differential equations arising in ion-acoustic waves. AIMS Mathematics, 2019, 4(3): 721-739. doi: 10.3934/math.2019.3.721 |
| [7] | Ahmed A. Gaber, Abdul-Majid Wazwaz . Dynamic wave solutions for (2+1)-dimensional DJKM equation in plasma physics. AIMS Mathematics, 2024, 9(3): 6060-6072. doi: 10.3934/math.2024296 |
| [8] | Mobeen Munir, Muhammad Athar, Sakhi Sarwar, Wasfi Shatanawi . Lie symmetries of Generalized Equal Width wave equations. AIMS Mathematics, 2021, 6(11): 12148-12165. doi: 10.3934/math.2021705 |
| [9] | Waleed Hamali, Abdulah A. Alghamdi . Exact solutions to the fractional nonlinear phenomena in fluid dynamics via the Riccati-Bernoulli sub-ODE method. AIMS Mathematics, 2024, 9(11): 31142-31162. doi: 10.3934/math.20241501 |
| [10] | Khalid Khan, Amir Ali, Manuel De la Sen, Muhammad Irfan . Localized modes in time-fractional modified coupled Korteweg-de Vries equation with singular and non-singular kernels. AIMS Mathematics, 2022, 7(2): 1580-1602. doi: 10.3934/math.2022092 |
Herein the research objects, a hyperbolic quasi-linear system of governing equations was solved by an asymptotic method (far-field technique) with explaining a 1-D unsteady planar and cylindrically symmetric flows in magnetogasdynamics. The evolution equation was obtained by generalized Burger's equation. A relatively accurate systematic result of the evolution equation was gotten by us through the analytic homotopy analysis method (HAM). We are allowed by the method to determine the various effects of nonlinearity and geometrical spreading. One of the fundamental problems of conservation laws are represented by the non-linear waves from preliminary data.
During the precedent decenniums, the propagation of non-linear waves in diverse pastures for instance plasma physics, astrophysics, geophysics and nuclear science etc, established an importance to researchers. The asymptotic investigation of non-linear waves has been the focus of large awareness as of equally mathematical and physical point of sights. Seeing that a precise investigative result of the system of non-linear partial differential equations (PDEs) is not achievable generally, an argument of estimate result is of significant concern. The work of Becker [1], Blythe [2], Sichel and Yin [3], Wegener and Benjamin [4], Clarke and McChesney [5], Ockenden and Spence [6], Parker [7,8], Scott and Johannesen [9] is worth mentioning in this context. There has been prevalent significance in non-linear wave phenomena primarily throughout the alleged asymptotic equation received on or after a great system of equations of non-linear PDEs, corresponding to a significant feature of the close relative system (see Hunter and Keller [10], Sharma et al. [11,12] and Radha and Sharma [13]).
Nonlinearity in waves exhibits itself in many ways, in case of waves governed by a hyperbolic system of equations it gives rise in the direction of non-linear distortion of the initial wave profile, discontinuities in the flow-field and the formation of shocks from smooth initial data.
In gas dynamics the convergence of shock waves has been a study of vast interest in the recent years. Here, we will deliberate on the hyperbolic systems of primary order quasi-linear partial differential equations governing flow-field in gas dynamics. Shock is a discontinuous solution to this system of non-linear PDEs, stated in preservation outline, which gratifies Rankine-Hugoniot (R-H) conditions and entropy condition.
Converging shock waves happen to be a field of ongoing study in excess of the years for high temperature plasmas, generating high pressure in addition to appreciate the fundamental fluid dynamics engaged in the procedure. We will learn the motion of shock waves (its position, its velocity and how it converges or diverges in the medium) in gas dynamics.
Depending on what medium is chosen, different names have been given to the subject. For example, the astrophysicists, who first observed the natural phenomena, labeled their study cosmically electrodynamics. Experiments with magnets and mercury yielded the name mercury dynamics. Physicists and electrical engineers have called it plasma physics or plasma dynamics; however, their descriptions do not necessarily imply the presence of an externally applied magnetic field. The word, magneto aerodynamics, which implies experiments with air, has been used by aerodynamicists, while mechanical engineers have employed various descriptive terms depending on what turn their research took; for instance, the word magneto hydrodynamics describes the use of a magnetic field coupled with water or other liquids moving at a high rate of speed, while magnetogasdynamics would imply that an electrically conducting gas or plasma is involved. Of course the subject finds application also in the case of very dense media or solids, and may be called magneto-elasticity. Probably the most general name would be magneto-fluid mechanics, and this has been suggested by Theodore von Karman. In this present article, we shall emphasize the shock waves in magnetogasdynamics by using the far-field technique.
Herein, we develop an evolution equation which illustrates the far-field behavior of the quasi-linear hyperbolic system of leading equations of magnetogasdynamics, with taking into consideration the leisurely fluctuating answers of the magnetogasdynamics system during a prescribed spreading out the method in stipulations of the stretched out coordinates. Acquired asymptotic equation is also called the generalized Burgers' equation which facilitates us to learn the solution of the original system.
In topology the indispensable idea of the homotopy to put forward a common investigative scheme for non-linear PDEs was given by Liao [14] in 1992, which is known as the HAM (homotopy analysis method) [15,16,17]. Supported on the homotopy of topology, in considered equation, the legality of the HAM is autonomous of whether or not nearby stay alive diminutive constraints. Hence, the HAM can overcome limitations of perturbation techniques [18,19]. The HAM gives a valuable numerical solution with minimum calculation, accurate result and more over let alone the discretization of realm and unrealistic assumptions. I have included the some applications of HAM to solve the non-linear partial differential equations (PDEs) from applied sciences are [20,21,22,23,24].
In addition, the HAM for all time gives a group of way out appearances in the assisting constraint-h, the rate of convergence of every solution and convergence region may be found easily by the assisting constraint-h. On behalf of the determination of solution of the evolution equation, HAM has been used by numerous researchers. We assumed the situation along which just solitary constituent wave is agitated, and afterward learn the consequences of non-planar and planar geometry on the wave proposition so as to develops lastly.
This article has been planned as trails: in Sec-Ⅱ, we explain the derivation of the evolution equation for non-linear equations of magnetogasdynamics. In Sec-Ⅲ, the fundamental perception of the HAM is provided. In Sec-Ⅳ, we relate the HAM to obtain the estimated solution of the asymptotic equation. The outline of the results and discussion are accessible at the closing stages.
The fundamental equations of unsteady 1-D motion in magnetogasdynamics for (α=1) planar and for (α=2) cylindrically symmetric can be represented as [25]:
| ρt+ρur+uρr+(α−1)ρur=0, |
| ut+uur+1ρ(pr+hr)=0, | (1) |
| pt+upr−a2(ρt+uρr)=0, |
| ht+uhr+2hur+2h(α−1)ur=0, |
where we have assumed that in direction of magnetic field the trajectories of the gas are orthogonal and the electrical conductivity to be infinite. Here gas velocity, density and pressure are denoted by u,ρ,p, respectively, γ is defined by the specific heats ratio, time variable is defined by t, space variable is represented by r, and the sound speed is a2=γp/ρ, respectively. The magnetic pressure is h denoted by h=H2μ2, where μ and H are the magnetic permeability and transverse magnetic field, correspondingly. The system of Eq (1) is complemented with equation of state ρRT=p, where R and T represent translational temperature and ideal gas constant, respectively.
Let us think about a solution in which the interruption is propagating and U the speed of the interruption remains constant in quiescent gas. Here, we want to obtain the solution of the system (1) in wave form, which depend on ξ=r−Ut variable and the time t. With the help of coordinate system (ξ,t), the Eq (1) turns into
| ρt+(u−U)ρξ+ρuξ+(α−1)ρuξ+Ut=0, |
| ut+(u−U)uξ+1ρ(pξ+hξ)=0, |
| pt+(u−U)pξ−γpρ(ρt+(u−U)ρξ)=0, | (2) |
| ht+(u−U)hξ+2huξ+2h(α−1)uξ+Ut=0. |
Now, we formulate a leisurely unreliable solution of Eq (2) in the course of a proper spreading out method in the form of new coordinate system (ζ,η), where ζandη are defined by ζ=εξ,η=ε2t with ε as minute parameter having the ratio of attenuation length of the medium in the direction of its attribute length. The Eq (2) is articulated in form of new-fangled variables ζ and η like
| ερη+(u−U)ρζ+ρuζ+(α−1)ρuε(ζε+Uη)=0, | (3) |
| εuη+(u−U)uζ+1ρ(pζ+hζ)=0, | (4) |
| εpη+(u−U)pζ−γpρ(ρηε+(u−U)ρζ)=0, | (5) |
| εhη+(u−U)hζ+2huζ+2h(α−1)uε(ζε+Uη)=0. | (6) |
We assume the asymptotic solutions of the system (3)–(6) in the following forms:
| ρ(ζ,η)=ρ0+ερ(1)(ζ,η)+ε2ρ(2)(ζ,η)+..., | (7) |
| u(ζ,η)=εu(1)(ζ,η)+ε2u(2)(ζ,η)+..., | (8) |
| p(ζ,η)=p0+εp(1)(ζ,η)+ε2p(2)(ζ,η)+..., | (9) |
| h(ζ,η)=h0+εh(1)(ζ,η)+ε2h(2)(ζ,η)+..., | (10) |
where ρ,p and h, are the values of ρ0,p0 and h0, respectively, in uninterrupted area. Introducing the Eqs (7)–(10) into Eqs (3)–(6) and using the uniform state u=0,ρ=ρ0,p=p0 and h=h0, and after that the coefficients of similar powers of ε putting equal to zero, consequently, we find the system of equations for first and second order variables:
| O(ε):−Uρ(1)ζ+ρ0u(1)ζ=0,−Uu(1)ζ+1ρ0(p(1)ζ+h(1)ζ)=0, | (11) |
| −Up(1)ζ+γp0ρ0Uρ(1)ζ=0,−Uh(1)ζ+2h0u(1)ζ=0, | (12) |
| O(ε2):ρ(1)η+u(1)ρ(1)ζ−Uρ(2)ζ+ρ(1)u(1)ζ+ρ0u(2)ζ+(α−1)ρ0u(1)Uη=0, | (13) |
| u(1)η+u(1)u(1)ζ−Uu(2)ζ−ρ(1)ρ(2)0(p(1)ζ+h(1)ζ)+1ρ0(p(2)ζ+h(2)ζ)=0, | (14) |
| p(1)η+u(1)p(1)ζ−Up(2)ζ−γp0ρ0ρ(1)η−γp0ρ0u(1)ρ(1)ζ+γp(1)ρ0Up(1)ζ+γp0ρ0Up(2)ζ−γp0ρ0ρ(1)ρ0Up(1)ζ=0, | (15) |
| h(1)η+u(1)h(1)ζ−Uh(2)ζ+2h(1)u(1)ζ+2h0u(2)ζ+2h0(α−1)u(1)Uη=0. | (16) |
Equations (11) and (12) admit a nontrivial solution offered
| U=a0√[2h0γp0+1],wherea0=√γp0ρ0. | (17) |
Equations (11) and (12), give the following associations satisfied by first order variables:
| ρ(1)=p(1)a20, |
| u(1)=Up(1)(ρ0U2−2h0), | (18) |
| h(1)=2h0p(1)γp0. |
We obtain values of ρζ(2),pζ(2) and hζ(2) from Eqs (13), (15) and (16), substitute these values in Eq (14) and use the Eq (18). In this way, the transport equation, we attain for p(1):
| p(1)η{Uγp0+1ρ0U+2h0ρ0Uγp0}+p(1)p(1)ζ{(Uγp0)2+1ρ0p0+4h0ρ0(γp0)2}+p(1){(α−1)ρ0Uη+2h0(α−1)ρ0Uηγp0}=0. | (19) |
On simplifying the Eq (19), we obtain:
| p(1)η+(α−1)2ηp(1)+{(6h0+(γ+1)γp0)2γp0√ρ0(2h0+γp0)}p(1)p(1)ζ=0. | (20) |
The generalized Burger's equation or an evolution Eq (20) allows us to learn the unusual results of nonlinearity that appears in propagation of α=2 cylindrical and α=1 planar waves in magnetogasdynamics.
To non-dimensionalize, we initiate the parameters of non-dimensional as follows:
| η∗=ηa0x0,ζ∗=ζx0,P=p(1)ρ0a20. | (21) |
Therefore, we can represent the Eq (20):
| ∂P∂η+μPPζ+(α−1)2ηP=0, | (22) |
where μ={(6h0+(γ+1)γp0)2√γp0(2h0+γp0)}.
It may be observed that for α≠1, the Eq (22) does not have an exact solution. At this time, we applied HAM for learning the various effects of nonlinearity on the flow.
We think about the standard non-linear equation as follows:
| N[u(x,t)]=0, | (23) |
where the unknown function is u(x,t), t and x refer to the time and space variables, correspondingly, and non-linear operator is defined by N. Liao [14] formulated the equation of zero-order deformation:
| qℏHN[ϕ(x,t;q)]=(1−q)L[ϕ(x,t;q)−u0(x,t)], | (24) |
where non-zero supporting parameter is refer by ℏ≠0, q is the embedding parameter belongs to [0,1], u0(x,t) is a preliminary estimate of u(x,t), supporting linear operator is L, H is a auxiliary non-zero function and the unknown function is ϕ(x,t;q). It is significant to communication that we have luxury to prefer the auxiliary items in HAM. Clearly, when q=1 and q=0, it embraces that
| u(x,t)=ϕ(x,t;1),u0(x,t)=ϕ(x,t;0). | (25) |
The solution ϕ(x,t;q) differs as of the starting estimate u0(x,t) to solution u(x,t) as q enhances from 0 to 1. Taylors' series spreading out of ϕ(x,t;q) about q=0 is specified by
| ϕ(x,t;q)=u0(x,t)+∞∑Δ=1uΔ(x,t)qΔ, | (26) |
where
| uΔ(x,t)=1Δ!∂Δϕ(x,t;q)∂qΔ|q=0. | (27) |
If we properly choose ℏ non-zero supporting parameter, preliminary estimate u0(x,t), non-zero auxiliary function H and the supporting linear operator L, at q=1, the series (26) converges and after that we obtain:
| ϕ(x,t;1)=u0(x,t)+∞∑Δ=1uΔ(x,t), | (28) |
which is the series solutions of Eq (24). For briefness, we identify the vector:
| un(x,t)={u0(x,t),u1(x,t),u2(x,t),...,un(x,t),}. | (29) |
The Δ-time's derivative of Eq (24) w.r. to q, finally, throughout dividing by Δ! and putting q=0, we find the deformation equation of Δ-th order:
| L[uΔ(x,t)−χΔuΔ−1(x,t)]=ℏHRΔ(uΔ−1,x,t), | (30) |
where
| RΔ(uΔ−1,x,t)=1(Δ−1)!∂Δ−1N[φ(x,t;q)]∂qΔ−1|q=0 and χΔ={0,Δ≤1,1,Δ>1 | (31) |
Here, we will use the HAM to recognize the solution of Eq (22) in two parts:
We consider the Eq (22) together with the initial condition used by Manickam et al. [26] as P(ζ,η=1)=sinζ. Taking η−1=η′ in Eq (22) and then dropping the prime sign in the ensuing equation, we achieve the initial value problem
| ∂P∂η+μPPζ+(α−1)2(η+1)P=0, | (32) |
with the initial condition P(ζ,η=0)=sinζ. We define linear operator
| L[ϕ(ζ,η;q)]=∂ϕ(ζ,η;q)∂η, | (33) |
the operator 'L' of a constant term 'c' is zero (L(c)=0). We apply the non-linear operator in Eq (32) as
| N[ϕ(ζ,η;q)]=∂ϕ(ζ,η;q)∂η+μϕ(ζ,η;q)∂ϕ(ζ,η;q)∂ζ+(α−1)ϕ(ζ,η;q)2(η+1). | (34) |
Applying above mentioned definition, we formulate the deformation equation of zero-order
| (1−q)L[ϕ(ζ,η;q)−P0(ζ,η)]=qℏHN[ϕ(ζ,η;q)]. | (35) |
Clearly, when q=0 and q=1,
| ϕ(ζ,η;0)=P0(ζ,η),ϕ(ζ,η;1)=P(ζ,η). | (36) |
Differentiating Δ-time's the Eq (35) w. r. to q, lastly, throughout dividing by Δ! and substituting q=0, we find the deformation equation of order Δ.
| L[PΔ(ζ,η)−χΔPΔ−1(ζ,η)]=ℏHRΔ(PΔ−1), | (37) |
through preliminary form PΔ(ζ,0)=0, where
| RΔ(PΔ−1)=∂PΔ−1(ζ,η)∂η+μΔ−1∑j=0Pj∂PΔ−j−1(ζ,η)∂ζ+(α−1)PΔ−1(ζ,η)2(η+1). | (38) |
On behalf of straightforwardness, we prefer ℏ=h and H=1.
Clearly, the deformation Eq (37) of Δ-th order has the solution in following form for Δ⩾1:
| PΔ(ζ,η)=χΔPΔ−1(ζ,η)+hL−1[RΔ(PΔ−1)]. | (39) |
We assume the primary approximation as
| P0(ζ,η)=−(η1+η)cosζ+sinζ1+η. | (40) |
We, therefore, successively obtain
| P0(ζ,η)+P1(ζ,η)=−(η1+η)cosζ+3hηcosζ2(1+η)+hαηcosζ2(1+η)+hημcos2ζ2(1+η)+hcosζlog(1+η)2(1+η)−hαcosζlog(1+η)2(1+η)+hcosζlog(1+η)2(1+η)−hαηcosζlog(1+η)2(1+η)−hμcos2ζlog(1+η)(1+η)−hημcos2ζlog(1+η)(1+η)+sinζ(1+η)−3hηsinζ2(1+η)+hαηsinζ2(1+η)−hημcosζsinζ(1+η)−hη2μcosζsinζ(1+η)+2hμcosζlog(1+η)sinζ(1+η)+2hημcosζlog(1+η)sinζ(1+η), | (41) |
and so on.
Therefore, the seven-terms approximation solution is given by
| P(ζ,η)=6∑i=0Pi(ζ,η). | (42) |
Seeing as the many other computed terms for Pi(ζ,η),i>1 occupies extremely huge expressions, therefore, we have not written the equations involving these terms here. However, we have computed the seven-terms approximation solution in this case.
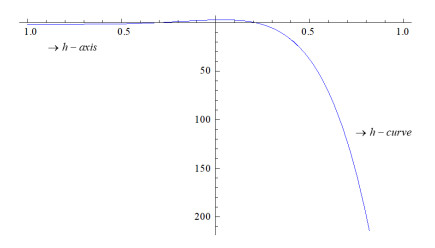
The Eq (42) gives the series solution of the function P(ζ,η). For the HAM the rate of convergence of this series depend upon the value of h, which is well-known as the parameter of convergence control. To control the convergence of the approximation series, we choose a proper value of h from the h-curve. The range of acceptable values of h is given by the h-curves of Pηη(1,0) which is attained by the seven-terms estimation solution of the HAM that are presented in Figure 1. From this figure, we observed that the line fragmental most similar to the sleeping (horizontal) line represents the suitable areas of h. We can achieve the truthful approximation solution by using only a small number of terms if we choose good primary presumption as well as the auxiliary linear operator. However, one can still acquire convergent consequences by appropriately selecting h the auxiliary parameter still if the preliminary estimate and linear operator are not good quality although sensible.
In Figure 1, we can take the convergence area of the h-axis where the h-curve is approximately similar or almost matching to the h-axis. So, the most perfect selected value of his -0.75 for this problem. We have selected h=−0.75 as this is the most suitable value of h for Eq (32). For α≠1, there is no accurate solution of Eq (32), therefore, we found the approximate solution of the Eq (32). The computed approximate solutions by the HAM are given in the Tables 1 and 2. The computed values of the approximation solutions of the evolution Eq (32) are given in Table 1 for planar case and in Table 2 for cylindrically symmetric case.
| ζ | η | ||||||
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | |
| 0.2 | 0.140756 | 0.108877 | 0.087685 | 0.059442 | -0.028350 | -0.286601 | -0.859809 |
| 0.4 | 0.279515 | 0.217031 | 0.177139 | 0.150895 | 0.129664 | 0.063022 | -0.220862 |
| 0.6 | 0.414191 | 0.323878 | 0.264933 | 0.215813 | 0.160263 | 0.106874 | 0.098196 |
| 0.8 | 0.542543 | 0.428264 | 0.359674 | 0.333968 | 0.323823 | 0.251927 | 0.011992 |
| 1.0 | 0.662086 | 0.527460 | 0.434395 | 0428821 | 0.623460 | 1.122934 | 1.927806 |
| 1.2 | 0.769930 | 0.623449 | 0.471533 | 0.276959 | 0.154606 | 0.446511 | 1.682932 |
| 1.4 | 0.862445 | 0.723334 | 0.559456 | 0.132508 | -0.879053 | -2.636836 | -4.922342 |
| 1.6 | 0.935055 | 0.820678 | 0.783193 | 0.643563 | -0.249660 | -2.962633 | -8.749512 |
| 1.8 | 0.982520 | 0.886745 | 0.988207 | 1.621657 | 2.751749 | 3.619788 | 2.540358 |
| ζ | η | ||||||
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | |
| 0.2 | 0.135149 | 0.101482 | 0.079061 | 0.041971 | -0.095138 | -0.526588 | -1.549660 |
| 0.4 | 0.268337 | 0.202233 | 0.161242 | 0.137527 | 0.125627 | 0.062164 | -0.290879 |
| 0.6 | 0.397523 | 0.301735 | 0.239078 | 0.179495 | 0.104897 | 0.043803 | 0.086486 |
| 0.8 | 0.520508 | 0.399199 | 0.330099 | 0.295206 | 0.227083 | -0.009127 | -0.566375 |
| 1.0 | 0.634860 | 0.491060 | 0.406810 | 0.445138 | 0.713459 | 1.248982 | 1.905814 |
| 1.2 | 0.737786 | 0.577809 | 0.429100 | 0.314891 | 0.154606 | 1.322817 | 3.486958 |
| 1.4 | 0.825795 | 0.667733 | 0.475131 | 0.035098 | -0.825656 | -1.978815 | -2.804509 |
| 1.6 | 0.894433 | 0.759209 | 0.660638 | 0.323081 | -0.938645 | -4.058777 | -9.919616 |
| 1.8 | 0.938500 | 0.826352 | 0.888267 | 1.266203 | 1.618688 | 0.859084 | -2.923729 |
We again consider the Eq (22). Taking T=δη and X=βζ in Eq (22), we obtain
| δ∂P∂T+μβP∂P∂X+(α−1)δ2TP=0. | (43) |
Choosing δ and β such that δ=μ2 and β=μ, we obtain
| ∂P∂T+P∂P∂X+(α−1)2TP=0. | (44) |
The Eq (44) is the concentrated form of Eq (22).
Equation (44) is the generalized Burgers' equation and it does not have an exact solution for α≠1. However, for α=1, the Eq (44) is described as the inviscid Burgers' equation and then it becomes:
| ∂P∂T+P∂P∂X=0. | (45) |
Now, we will think about the Eq (45) through primary form
| P(X,0)=X. | (46) |
The accurate solution for Eq (44) obtained by Arora et al. [27] subject to the primary condition (46) is offered by
| P(X,T)=X(1+T). | (47) |
We again apply the HAM to find out the solution of Eq (45). We will measure up to the solutions achieved by the HAM with the faithful solution provided in Eq (47) on the way to express the helpfulness of the method. We denote the linear operator
| L[ϕ(X,T;q)]=∂ϕ(X,T;q)∂T, | (48) |
where operator 'L' of a constant term 'c' is zero (L(c)=0).
Now, we apply 'N' the non-linear operator in Eq (32) as
| N[ϕ(X,T;q)]=∂ϕ(X,T;q)∂T+ϕ(X,T;q)∂ϕ(X,T;q)∂X. |
Applying the above mentioned definition, we formulate the deformation equation of order zero as:
| (1−q)L[ϕ(X,T;q)−P0(X,T)]=qℏHN[ϕ(X,T;q)]. | (49) |
Clearly, when q=1 and q=0,
| ϕ(X,T;1)=P(X,T),ϕ(X,T;0)=P0(X,T). | (50) |
Differentiating Δ-time's the Eq (49) w. r. to q, replacing q=0 and at last dividing by Δ! both sides; we find the deformation equation of order Δ
| L[PΔ(X,T)−χΔPΔ−1(X,T)]=ℏHRΔ(PΔ−1), | (51) |
subject to primary form PΔ(X,0)=0, where
| RΔ(PΔ−1)=∂PΔ−1(X,T)∂T+Δ−1∑j=0Pj∂PΔ−j−1(X,T)∂X. | (52) |
on behalf of straightforwardness, we desire ℏ=h and H=1.
We obtain the required result of deformation Eq (51) of order Δ for Δ⩾1 as
| PΔ(X,T)=χΔPΔ−1(X,T)+hL−1[RΔ(PΔ−1)]. | (53) |
We take value of original approximation from Eq (45) as
| P0(X,T)=X. | (54) |
We, therefore, successively obtain
| P0(X,T)+P1(X,T)=X+hTX, |
| P0(X,T)+P1(X,T)+P2(X,T)=X+2hTX+h2TX+h2T2X, |
| P0(X,T)+...+P3(X,T)=X+3hTX+3h2TX+h3TX+3h2T2X+2h3T2X+h3T3X, |
| P0(X,T)+...+P3(X,T)+P4(X,T)=X+4hTX+6h2TX+4h3TX+h4TX+6h2T2X+8h3T2X+3h4T2X+4h3T3X+3h4T3X+h4T4X, |
| P0(X,T)+...+P4(X,T)+P5(X,T)=X+5hTX+10h2TX+10h3TX+5h4TX+h5TX+10h2T2X+20h3T2X+15h4T2X+4h5T2X+10h3T3X+15h4T3X+6h5T3X+5h4T4X+4h5T4X+h5T5X, |
| P0(X,T)+...+P5(X,T)+P6(X,T)=X+6hTX+15h2TX+20h3TX+15h4TX+6h5TX+h6TX+15h2T2X+40h3T2X+45h4T2X+24h5T2X+5h6T2X+20h3T3X+45h4T3X+36h5T3X+10h6T3X+15h4T4X+24h5T4X+10h6T4X+6h5T5X+5h6T5X+h6T6X, |
and proceeding likewise.
On simplifying the above system of equations, we get Pj(X,T) for j=1,2,3,...6. On the other hand, we have calculated the approximation solution up to seven-terms and it is written as:
| P(X,T)=6∑j=0Pj(X,T). | (55) |
The Eq (55) gives solution in series form of the function P(X,T). For the HAM, the rate of convergence of this Eq (55) depends winning the value of the supporting parameter h, which is identified as the control parameter of convergence. To control the convergence of the approximation series, we choose an appropriate value of h from the h-curve. The range of acceptable values of h is given by the h-curves of PTT(1,0) which is found by the seven-terms estimation solution of the HAM that are presented in Figure 2. From this figure, we observed that the line segment almost similar to the sleeping (horizontal) line represents the applicable regions of h. We can obtain the precise approximation solution by only a few terms if we prefer excellent primary estimate as well as linear operator. However, one can at rest obtain convergent results through appropriately desiring supporting parameter h even if the linear operator and initial guess are not good but reasonable.
In Figure 2, we can take the convergence area of the h-axis, where h-curve is approximately equivalent to the h-axis. So, a good number selected h=−1 as the suitable worth of h for Eq (45). We compared the achieved approximate result of (45) through the faithful result (47) in Table 3.
| T | X | HAM | Exact | Absolute error |
| 0.01 | 0 | 0.00000000 | 0.00000000 | 0.00000000 |
| 1 | 0.99009901 | 0.99009901 | 0.00000000 | |
| 2 | 1.98019802 | 1.98019802 | 0.00000000 | |
| 3 | 2.97029703 | 2.97029703 | 0.00000000 | |
| 4 | 3.96039604 | 3.96039604 | 0.00000000 | |
| 5 | 4.95049505 | 4.95049505 | 0.00000000 | |
| 0.03 | 0 | 0.00000000 | 0.00000000 | 0.00000000 |
| 1 | 0.97087379 | 0.97087379 | 0.00000000 | |
| 2 | 1.94174757 | 1.94174757 | 0.00000000 | |
| 3 | 2.91262136 | 2.91262136 | 0.00000000 | |
| 4 | 3.88349515 | 3.88349515 | 0.00000000 | |
| 5 | 4.85436893 | 4.85436893 | 0.00000000 | |
| 0.05 | 0 | 0.00000000 | 0.00000000 | 0.00000000 |
| 1 | 0.95238095 | 0.95238095 | 0.00000001 | |
| 2 | 1.90476190 | 1.90476191 | 0.00000000 | |
| 3 | 2.85714286 | 2.85714286 | 0.00000000 | |
| 4 | 3.80952381 | 3.80952381 | 0.00000001 | |
| 5 | 4.76190477 | 4.76190476 | 0.00000000 | |
| 0.07 | 0 | 0.00000000 | 0.00000000 | 0.00000000 |
| 1 | 0.93457945 | 0.93457944 | 0.00000001 | |
| 2 | 1.86915889 | 1.86915888 | 0.00000001 | |
| 3 | 2.80373834 | 2.80373832 | 0.00000002 | |
| 4 | 3.73831779 | 3.73831776 | 0.00000003 | |
| 5 | 4.67289723 | 4.67289720 | 0.00000003 | |
| 0.09 | 0 | 0.00000000 | 0.00000000 | 0.00000000 |
| 1 | 0.91743124 | 0.91743119 | 0.00000005 | |
| 2 | 1.83486247 | 1.83486239 | 0.00000008 | |
| 3 | 2.75229371 | 2.75229358 | 0.00000013 | |
| 4 | 3.66972495 | 3.66972477 | 0.00000018 | |
| 5 | 4.58715618 | 4.58715596 | 0.00000022 |
Pursuing an asymptotic loom, single of the most important objectives of this article is to learn the multifarious wave proposition (motion) on behalf of one-dimensional hyperbolic system of equations from side to side results of greatly effort less although nontrivial Burgers' equation to demonstrates the distinguishing aspects of the close relative system and explains how the waves converge in far-field behavior of main system of equations. In this article, we applied an asymptotic method (far-field technique) to attain an evolution equation of non-linear system of PDEs with explaining a planar and cylindrically symmetric unsteady flow in magnetogasdynamics; the HAM is applied to find a homogeneously legitimate result to this asymptotic equation. With the help of this method, we find fairly accurate result of this asymptotic equation. Here, we have taken initial condition used by Manickam [26] to attain fairly accurate result of this evolution equation. We have achieved the fairly accurate solutions in favor of the planar flow in Table 1 and for the cylindrically symmetric flow in Table 2. We have shown these approximate solutions in Figures 3 and 4. Figure 3 explains the outlines of approximate solution for planar case and Figure 4 shows the outlines of approximate solution for the cylindrically symmetric flow. Thus, in both cases the value of flow variable P(ζ,η) enhances when we increase the value of variable ζ, but after some point the value of the flow variable P(ζ,η) shrinks through increase in the value of ζ. In Case Ⅱ, we have first reduced the evolution equation into the inviscid Burgers' equation. As a result of using the HAM, we have obtained the seven-terms approximation solution of the inviscid Burgers' equation. In Table 3, we have compared the values of seven-terms approximation solution with the exact analytical solution; they are in high-quality conformity with each other. Thus, the HAM is very good technique for obtaining the approximate solution.
In this paper we used an asymptotic method (far-field technique) to derive an evolution equation of the governing hyperbolic system of the equations describing planar and cylindrically symmetric flows in magnetogasdynamics. We studied the behavior of propagation of waves in the far-field of the original system with the help of the so-obtained asymptotic equation, i.e., Burgers' equation. This asymptotic equation explains the features of its parent system. We have achieved the approximate solutions in favor of the planar flow in Table 1 and for the cylindrically symmetric flow in Table 2. We have shown these approximate solutions in Figures 3 and 4. Figure 3 clarifies the outlines of approximate solution for planar case and Figure 4 demonstrates the outlines of approximate solution for the cylindrically symmetric flow. In Case Ⅱ, we have first reduced the evolution equation into the inviscid Burgers' equation. Using the HAM, we have obtained the seven-terms approximation solution of the inviscid Burgers' equation. In Table 3, we have contrasted the values of seven-terms approximation solution with the exact solution; they are in super agreement with each other. Thus, the HAM is extremely high-quality method for achieving the fairly accurate solution.
The first author Anoop Kumar feels like to thankfulness for financial support grant by the DST-FIST, New Delhi, India. The authors Aziz Khan and Thabet Abdeljawad would like to thanks Prince Sultan University for paying the APC and the support through TAS research lab.
The author's declares that there is no conflict of interests regarding the publication of this paper. All data generated or analyzed during this study are included in this published article (and its supplementary files).
| [1] |
E. Becker, Chemically reacting flows, Ann. Rev. Fluid Mech., 4 (1972), 155–194. https://doi.org/10.1146/annurev.fl.04.010172.001103 doi: 10.1146/annurev.fl.04.010172.001103

|
| [2] |
P. Blythe, Nonlinear wave propagation in a relaxing gas, J. Fluid Mech., 37 (1969), 31–50. https://doi.org/10.1017/S0022112069000401 doi: 10.1017/S0022112069000401

|
| [3] |
M. Sichel, Y. Yin, Viscous transonic flow in relaxing gases, ZAMM, 56 (1976), 315–329. https://doi.org/10.1002/zamm.19760560706 doi: 10.1002/zamm.19760560706

|
| [4] |
P. Wegener, B. Wu, Gasdynamics and homogeneous nucleation, Adv. ColloidInterfac., 7 (1977), 325–417. https://doi.org/10.1016/0001-8686(77)85008-2 doi: 10.1016/0001-8686(77)85008-2

|
| [5] | J. Clarke, M. Mc Chesney, Dynamics of relaxing gases, London: Butterworths, 1976. |
| [6] |
H. Ockenden, D. Spence, Nonlinear wave propagation in a relaxing gas, J. Fluid Mech., 39 (1969), 329–345. https://doi.org/10.1017/S0022112069002205 doi: 10.1017/S0022112069002205

|
| [7] |
D. Parker, Nonlinearity, relaxation and diffusion in acoustic and ultrasonics, J. Fluid Mech., 39 (1969), 793–815. https://doi.org/10.1017/S0022112069002473 doi: 10.1017/S0022112069002473

|
| [8] |
D. Parker, Propagation of rapid pulses through a relaxing gas, The Physics of Fluids, 15 (1972), 256. https://doi.org/10.1063/1.1693902 doi: 10.1063/1.1693902

|
| [9] |
W. Scott, N. Johannesen, Spherical nonlinear wave propagation in a vibrationally relaxing gas, Proc. R. Soc. Lond. A, 382 (1982), 103–134. https://doi.org/10.1098/rspa.1982.0092 doi: 10.1098/rspa.1982.0092

|
| [10] |
J. Hunter, J. Keller, Weakly nonlinear high frequency waves, Commun. Pur. Appl. Math., 36 (1983), 547–569. https://doi.org/10.1002/cpa.3160360502 doi: 10.1002/cpa.3160360502

|
| [11] |
V. Sharma, L. Singh, R. Ram, The progressive wave approach analyzing the decay of a saw tooth profile in magnetogasdynamics, The Physics of Fluids, 30 (1987), 1572. https://doi.org/10.1063/1.866222 doi: 10.1063/1.866222

|
| [12] |
V. Sharma, R. Sharma, B. Pandey, N. Gupta, Nonlinear analysis of a traffic flow, Z. Angew. Math. Phys., 40 (1989), 828–837. https://doi.org/10.1007/BF00945805 doi: 10.1007/BF00945805

|
| [13] |
Ch. Radha, V. Sharma, Propagation and interaction of waves in a relaxing gas, Philosophical Transactions of the Royal Society of London Series A: Physical and Engineering Sciences, 352 (1995), 169–195. https://doi.org/10.1098/rsta.1995.0062 doi: 10.1098/rsta.1995.0062

|
| [14] | S. Liao, The proposed homotopy analysis technique for the solution of nonlinear problems, Ph. D Thesis, Shanghai Jiao Tong University, 1992. |
| [15] | S. Liao, Beyond perturbation: introduction to the homotopy analysis method, Boca Raton: Chapman and Hall/CRC Press, 2003. |
| [16] |
S. Liao, Comparison between the homotopy analysis method and homotopy perturbation method, Appl. Math. Comput., 169 (2005), 1186–1194. https://doi.org/10.1016/j.amc.2004.10.058 doi: 10.1016/j.amc.2004.10.058

|
| [17] |
C. Liu, Y. Liu, Comparison of the general series method and the homotopy analysis method, Mod. Phys. Lett. B, 24 (2010), 1699–1706. https://doi.org/10.1142/S0217984910024079 doi: 10.1142/S0217984910024079

|
| [18] |
F. Allan, K. Al-Khaled, An approximation of the analytic solution of the shock wave equation, J. Comput. Appl. Math., 192 (2006), 301–309. https://doi.org/10.1016/j.cam.2005.05.009 doi: 10.1016/j.cam.2005.05.009

|
| [19] |
F. Allan, Derivation of the Adomian decomposition method using the homotopy analysis method, Appl. Math. Comput., 190 (2007), 6–14. https://doi.org/10.1016/j.amc.2006.12.074 doi: 10.1016/j.amc.2006.12.074

|
| [20] |
K. Hosseinia, M. Ilie, M. Mirzazadeh, A. Yusuf, T. Sulaiman, D. Baleanue, et al., An effective computational method to deal with a time-fractional nonlinear water wave equation in the Caputo sense, Math. Comput. Simulat., 187 (2021), 248–260. https://doi.org/10.1016/j.matcom.2021.02.021 doi: 10.1016/j.matcom.2021.02.021

|
| [21] |
K. Hosseini, M. Ilie, M. Mirzazadeh, D. Baleanu, An analytic study on the approximate solution of a nonlinear time-fractional Cauchy reaction-diffusion equation with the Mittag-Leffler law, Math. Method. Appl. Sci., 44 (2021), 6247–6258. https://doi.org/10.1002/mma.7059 doi: 10.1002/mma.7059

|
| [22] | K. Hosseini, K. Sadri, M. Mirzazadeh, A. Ahmadian, Y.Chu, S. Salahshour, Reliable methods to look for analytical and numerical solutions of a nonlinear differential equation arising in heat transfer with the conformable derivative, Math. Method. Appl. Sci., in press. https://doi.org/10.1002/mma.7582 |
| [23] |
A. Loyinmi, T. Akinfe, An algorithm for solving the Burgers-Huxley equation using the Elzaki transform, SN Appl. Sci., 2 (2020), 7. https://doi.org/10.1007/s42452-019-1653-3 doi: 10.1007/s42452-019-1653-3

|
| [24] | B. Sangani, K. Engolikar, R. Jana, M. Kumar, Homotopy analysis method for Burgers' equation: application of gradient descent approach, Authorea Preprints, in press. https://doi.org/10.22541/au.165942007.79344292/v1 |
| [25] | L. Singh, A. Husain, M. Singh, An analytical study of strong non planar shock waves in magnetogasdynamics, Adv. Theor. Appl. Mech., 3 (2010), 291–297. |
| [26] |
S. Manickam, Ch. Radha, V. Sharma, Far field behaviour of waves in a vibrationally relaxing gas, Appl. Numer. Math., 45 (2003), 293–307. https://doi.org/10.1016/S0168-9274(02)00214-3 doi: 10.1016/S0168-9274(02)00214-3

|
| [27] |
R. Arora, M. Siddiqui, V. Singh, Solutions of inviscid Burgers' and Equal width wave equations by RDTM, IJAPM, 2 (2012), 212–214. https://doi.org/10.7763/IJAPM.2012.V2.92 doi: 10.7763/IJAPM.2012.V2.92

|
| 1. | Adebowale Martins Obalalu, Adil Darvesh, Lateefat Aselebe, Sulyman Olakunle Salawu, Kazeem Issa, Heat transfer analysis of thermal radiative over a stretching curved surface using molybdenum disulfide and silicon dioxide composite material under the influence of solar radiation, 2024, 20, 1573-6105, 707, 10.1108/MMMS-01-2024-0038 | |
| 2. | Rekha Satish, B. T. Raju, P. Durga Prasad, S. V. Siva Rama Raju, C. S. K. Raju, M. Dinesh Kumar, Dynamics of comparative analysis of Reynold’s and Vogel’s models (variable viscosity) in a wire coating process filled with magnetized porous, 2024, 38, 0217-9792, 10.1142/S0217979224504174 | |
| 3. | M. Sivakumar, M. Mallikarjuna, R. Senthamarai, A kinetic non-steady state analysis of immobilized enzyme systems with external mass transfer resistance, 2024, 9, 2473-6988, 18083, 10.3934/math.2024882 |
| ζ | η | ||||||
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | |
| 0.2 | 0.140756 | 0.108877 | 0.087685 | 0.059442 | -0.028350 | -0.286601 | -0.859809 |
| 0.4 | 0.279515 | 0.217031 | 0.177139 | 0.150895 | 0.129664 | 0.063022 | -0.220862 |
| 0.6 | 0.414191 | 0.323878 | 0.264933 | 0.215813 | 0.160263 | 0.106874 | 0.098196 |
| 0.8 | 0.542543 | 0.428264 | 0.359674 | 0.333968 | 0.323823 | 0.251927 | 0.011992 |
| 1.0 | 0.662086 | 0.527460 | 0.434395 | 0428821 | 0.623460 | 1.122934 | 1.927806 |
| 1.2 | 0.769930 | 0.623449 | 0.471533 | 0.276959 | 0.154606 | 0.446511 | 1.682932 |
| 1.4 | 0.862445 | 0.723334 | 0.559456 | 0.132508 | -0.879053 | -2.636836 | -4.922342 |
| 1.6 | 0.935055 | 0.820678 | 0.783193 | 0.643563 | -0.249660 | -2.962633 | -8.749512 |
| 1.8 | 0.982520 | 0.886745 | 0.988207 | 1.621657 | 2.751749 | 3.619788 | 2.540358 |
| ζ | η | ||||||
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | |
| 0.2 | 0.135149 | 0.101482 | 0.079061 | 0.041971 | -0.095138 | -0.526588 | -1.549660 |
| 0.4 | 0.268337 | 0.202233 | 0.161242 | 0.137527 | 0.125627 | 0.062164 | -0.290879 |
| 0.6 | 0.397523 | 0.301735 | 0.239078 | 0.179495 | 0.104897 | 0.043803 | 0.086486 |
| 0.8 | 0.520508 | 0.399199 | 0.330099 | 0.295206 | 0.227083 | -0.009127 | -0.566375 |
| 1.0 | 0.634860 | 0.491060 | 0.406810 | 0.445138 | 0.713459 | 1.248982 | 1.905814 |
| 1.2 | 0.737786 | 0.577809 | 0.429100 | 0.314891 | 0.154606 | 1.322817 | 3.486958 |
| 1.4 | 0.825795 | 0.667733 | 0.475131 | 0.035098 | -0.825656 | -1.978815 | -2.804509 |
| 1.6 | 0.894433 | 0.759209 | 0.660638 | 0.323081 | -0.938645 | -4.058777 | -9.919616 |
| 1.8 | 0.938500 | 0.826352 | 0.888267 | 1.266203 | 1.618688 | 0.859084 | -2.923729 |
| T | X | HAM | Exact | Absolute error |
| 0.01 | 0 | 0.00000000 | 0.00000000 | 0.00000000 |
| 1 | 0.99009901 | 0.99009901 | 0.00000000 | |
| 2 | 1.98019802 | 1.98019802 | 0.00000000 | |
| 3 | 2.97029703 | 2.97029703 | 0.00000000 | |
| 4 | 3.96039604 | 3.96039604 | 0.00000000 | |
| 5 | 4.95049505 | 4.95049505 | 0.00000000 | |
| 0.03 | 0 | 0.00000000 | 0.00000000 | 0.00000000 |
| 1 | 0.97087379 | 0.97087379 | 0.00000000 | |
| 2 | 1.94174757 | 1.94174757 | 0.00000000 | |
| 3 | 2.91262136 | 2.91262136 | 0.00000000 | |
| 4 | 3.88349515 | 3.88349515 | 0.00000000 | |
| 5 | 4.85436893 | 4.85436893 | 0.00000000 | |
| 0.05 | 0 | 0.00000000 | 0.00000000 | 0.00000000 |
| 1 | 0.95238095 | 0.95238095 | 0.00000001 | |
| 2 | 1.90476190 | 1.90476191 | 0.00000000 | |
| 3 | 2.85714286 | 2.85714286 | 0.00000000 | |
| 4 | 3.80952381 | 3.80952381 | 0.00000001 | |
| 5 | 4.76190477 | 4.76190476 | 0.00000000 | |
| 0.07 | 0 | 0.00000000 | 0.00000000 | 0.00000000 |
| 1 | 0.93457945 | 0.93457944 | 0.00000001 | |
| 2 | 1.86915889 | 1.86915888 | 0.00000001 | |
| 3 | 2.80373834 | 2.80373832 | 0.00000002 | |
| 4 | 3.73831779 | 3.73831776 | 0.00000003 | |
| 5 | 4.67289723 | 4.67289720 | 0.00000003 | |
| 0.09 | 0 | 0.00000000 | 0.00000000 | 0.00000000 |
| 1 | 0.91743124 | 0.91743119 | 0.00000005 | |
| 2 | 1.83486247 | 1.83486239 | 0.00000008 | |
| 3 | 2.75229371 | 2.75229358 | 0.00000013 | |
| 4 | 3.66972495 | 3.66972477 | 0.00000018 | |
| 5 | 4.58715618 | 4.58715596 | 0.00000022 |
| ζ | η | ||||||
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | |
| 0.2 | 0.140756 | 0.108877 | 0.087685 | 0.059442 | -0.028350 | -0.286601 | -0.859809 |
| 0.4 | 0.279515 | 0.217031 | 0.177139 | 0.150895 | 0.129664 | 0.063022 | -0.220862 |
| 0.6 | 0.414191 | 0.323878 | 0.264933 | 0.215813 | 0.160263 | 0.106874 | 0.098196 |
| 0.8 | 0.542543 | 0.428264 | 0.359674 | 0.333968 | 0.323823 | 0.251927 | 0.011992 |
| 1.0 | 0.662086 | 0.527460 | 0.434395 | 0428821 | 0.623460 | 1.122934 | 1.927806 |
| 1.2 | 0.769930 | 0.623449 | 0.471533 | 0.276959 | 0.154606 | 0.446511 | 1.682932 |
| 1.4 | 0.862445 | 0.723334 | 0.559456 | 0.132508 | -0.879053 | -2.636836 | -4.922342 |
| 1.6 | 0.935055 | 0.820678 | 0.783193 | 0.643563 | -0.249660 | -2.962633 | -8.749512 |
| 1.8 | 0.982520 | 0.886745 | 0.988207 | 1.621657 | 2.751749 | 3.619788 | 2.540358 |
| ζ | η | ||||||
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | |
| 0.2 | 0.135149 | 0.101482 | 0.079061 | 0.041971 | -0.095138 | -0.526588 | -1.549660 |
| 0.4 | 0.268337 | 0.202233 | 0.161242 | 0.137527 | 0.125627 | 0.062164 | -0.290879 |
| 0.6 | 0.397523 | 0.301735 | 0.239078 | 0.179495 | 0.104897 | 0.043803 | 0.086486 |
| 0.8 | 0.520508 | 0.399199 | 0.330099 | 0.295206 | 0.227083 | -0.009127 | -0.566375 |
| 1.0 | 0.634860 | 0.491060 | 0.406810 | 0.445138 | 0.713459 | 1.248982 | 1.905814 |
| 1.2 | 0.737786 | 0.577809 | 0.429100 | 0.314891 | 0.154606 | 1.322817 | 3.486958 |
| 1.4 | 0.825795 | 0.667733 | 0.475131 | 0.035098 | -0.825656 | -1.978815 | -2.804509 |
| 1.6 | 0.894433 | 0.759209 | 0.660638 | 0.323081 | -0.938645 | -4.058777 | -9.919616 |
| 1.8 | 0.938500 | 0.826352 | 0.888267 | 1.266203 | 1.618688 | 0.859084 | -2.923729 |
| T | X | HAM | Exact | Absolute error |
| 0.01 | 0 | 0.00000000 | 0.00000000 | 0.00000000 |
| 1 | 0.99009901 | 0.99009901 | 0.00000000 | |
| 2 | 1.98019802 | 1.98019802 | 0.00000000 | |
| 3 | 2.97029703 | 2.97029703 | 0.00000000 | |
| 4 | 3.96039604 | 3.96039604 | 0.00000000 | |
| 5 | 4.95049505 | 4.95049505 | 0.00000000 | |
| 0.03 | 0 | 0.00000000 | 0.00000000 | 0.00000000 |
| 1 | 0.97087379 | 0.97087379 | 0.00000000 | |
| 2 | 1.94174757 | 1.94174757 | 0.00000000 | |
| 3 | 2.91262136 | 2.91262136 | 0.00000000 | |
| 4 | 3.88349515 | 3.88349515 | 0.00000000 | |
| 5 | 4.85436893 | 4.85436893 | 0.00000000 | |
| 0.05 | 0 | 0.00000000 | 0.00000000 | 0.00000000 |
| 1 | 0.95238095 | 0.95238095 | 0.00000001 | |
| 2 | 1.90476190 | 1.90476191 | 0.00000000 | |
| 3 | 2.85714286 | 2.85714286 | 0.00000000 | |
| 4 | 3.80952381 | 3.80952381 | 0.00000001 | |
| 5 | 4.76190477 | 4.76190476 | 0.00000000 | |
| 0.07 | 0 | 0.00000000 | 0.00000000 | 0.00000000 |
| 1 | 0.93457945 | 0.93457944 | 0.00000001 | |
| 2 | 1.86915889 | 1.86915888 | 0.00000001 | |
| 3 | 2.80373834 | 2.80373832 | 0.00000002 | |
| 4 | 3.73831779 | 3.73831776 | 0.00000003 | |
| 5 | 4.67289723 | 4.67289720 | 0.00000003 | |
| 0.09 | 0 | 0.00000000 | 0.00000000 | 0.00000000 |
| 1 | 0.91743124 | 0.91743119 | 0.00000005 | |
| 2 | 1.83486247 | 1.83486239 | 0.00000008 | |
| 3 | 2.75229371 | 2.75229358 | 0.00000013 | |
| 4 | 3.66972495 | 3.66972477 | 0.00000018 | |
| 5 | 4.58715618 | 4.58715596 | 0.00000022 |