A novel Muth generalized family of distributions: Properties and applications to quality control

1.   Introduction

In this paper, we focus on numerical methods to solve FIDEs involving weakly singular kernels, i.e., equations of the form

where $0 < \alpha, \beta < 1$, $u_0$ is any real number, $g(x)$ and $p(x)$ are continuous and bounded functions on $I_T: = [0, T]$, $q(x, t)$ is nonzero continuous function of $x$ and $t$ defined on

The symbol $_0^CD_x^{\alpha}$ denotes a Caputo-type fractional derivative defined by ^[3]

Correspondingly,

During the last few decades, fractional-order derivatives has been widely used to model physical phenomena in many different contexts (see ^[1,2,3,4,5]). It is usually very hard to find exact solutions of fractional order differential equations and much attention has been devoted to develop efficient approaches to approximately solve these problems. Khader et al. ^[6] developed a Chebyshev pseudo-spectral method based on a new formula of Caputo derivative to solve FIDEs systems numerically. In ^[7], Zhao et al. transformed FIDEs to Volterra integral equations with weakly singular kernels and presented a piecewise polynomials collocation method to solve the problem. Wang ^[8] presented an one-step spectral collocation method for nonlinear fractional boundary value problems. Dehestani et al. ^[9] investigated fractional Genocchi functions (FGFs) and their Pseudo-operational matrix, and construct the collocation method based on FGFs to find the numerical solution of the fractional partial integro-differential equations with variable-order. Sadri et al. ^[10] explored the two-variable Vieta-Fibonacci polynomials and their operational matrices to derive a collocation method for time-fractional telegraph equations.

Relevant results may be found in ^{[11,12,13,14,15,16,17,18]}. Most of of the approaches correspond to $p$-version methods, which are usually inefficient to deal with local weak singularities and always result in lower order of accuracy nearby the singular points.

Recently, Wang have obtained results using multi-step or $hp$-version spectral methods for Volterra integral equations (see ^{[19,20,21,22]}). Guo and Wang ^[23,24] investigated multi-step spectral collocation methods based on classical shifted Jacobi polynomials for single order and multi-order fractional differential equations. Yao et al. ^[25] developed a hybrid spectral element method to solve VIEs with vanishing delays, using different kinds of meshes and different orthogonal functions as basis to obtain higher accuracy. Based on these results we further explore $hp$-version spectral collocation approaches for FIDEs (1.1) and (1.2). Our main results may be summarized as follows:

(ⅰ) The original problems (1.1) and (1.2) are recasted as a VIE with two different singular kernels, and an $hp$-version Legendre spectral collocation method is proposed. The time step $h$ and polynomial degree $M$ in the scheme may be chosen arbitrarily, according to the requirements of accuracy or storage. The explicit form and the iteration method make the new scheme highly convenient.

(ⅱ) The priori error estimate for the new method is derived rigorously for $\frac{1}{2} < \alpha < 1$. The convergence characteristic of our method is verified numerically on the basis of several typical examples, which fits the theoretical results well. The numerical comparison illustrates that our $hp$-version spectral collocation approaches also suits well to the case $\frac{1}{2} < \alpha < 1$, and allows one to achieve higher accuracy than other piecewise polynomial collocation methods.

The article is structured as follows: Section 2 is for preliminaries. In Section 3, the FIDEs is transformed into Volterra integral equation and its piece-wised form. Then, a multi-step spectral collocation scheme based on the reformulated problem is constructed. In Section 4, the $hp$-version convergence of the proposed method is analyzed in the $L^2$ function space. In Section 5, we present the results of some numerical experiments to illustrated the suitability of this method. Finally, some concluding remarks were presented at the end of the paper.

2.   Preliminaries

To make a preparation for the later work, some basic definitions and properties of the shifted Legendre polynomials shall be introduced at first. We make an arbitrary partition on the given interval $I = [0, 1]$, which can be denoted by

We set $I_n = \big(x_{n-1}, x_{n}\big]$, $h_n = x_{n}-x_{n-1}$.

$L_k(t),$ $t\in (-1, 1)$ denotes the standard Legendre polynomial of the degree $k$. The shifted form of Legendre polynomial with degree $k$ over $I_n$ is defined by ^[22]

We denote the set of polynomials of degree not greater than $M_n$ on the sub-interval $I_n$ by $\mathcal{P}_{M_n}(I_n)$. Let $\{t_{n, j}, \omega_{n, j}\}_{j = 0}^{M_n}$ be the nodes and the corresponding quadrature weights for the standard Legendre-Gauss interpolation over $(-1, 1),$ and $x_{n, j}$ be the nodes for the shifted form of Legendre-Gauss quadrature on the sub-interval $I_n,$

It has been known that ^[22]

where $\delta_{k, j}$ is the Kronecker function. Furthermore, it can be verified that ^[21]

and

Let $\mathcal{I}_{x, M_n}:C(I_n)\to \mathcal{P}_{M_n}(I_n)$ denote the shifted Legendre-Gauss interpolation operator implemented on the $n$-th sub-interval $I_n$, such that

For later uses, we transfer the integral interval $\big(x_{n-1}, x\big]$ to $I_n$ via the following transformation:

Then, we introduce another interpolation operator

defined by

where $\xi_{n, i}$ are the shifted Legendre-Gauss points on the interval $(x_{n-1}, x).$ Obviously,

Due to the presence of the weak singularity, we naturally introduce the interpolatory quadrature formula with weight depending on the weakly singular kernel $(x-t)^{\delta}$, which was mentioned in ^[26] and defined as follows: For any $\phi(t)\in \mathcal{P}_{M_k}(I_k)$, one has

where

and $\{h_{k, q}(t)\}_{q = 0}^{M_k}$ are Lagrange interpolation basis function corresponding to the quadrature points $\{x_{k, q}\}_{q = 0}^{M_k}$.

3.   The multi-step Legendre-Gauss spectral collocation method

In this part, we first convert the original problem to VIE and its piecewise form equivalently. Then we shall present the multi-step Legendre-Gauss spectral collocation approach to solve numerically the reformulated problem (3.7).

3.1.   Reformulation of the original problem

To obtain the reformulation of the discussed problem, we recall the equation of the classical form

The equivalence between (3.1) and the second kind VIEs is given by the following statements:

Lemma 1. Assume that $\alpha > 0$, $n-1 \leq \alpha < n$, $n \in N$, $f$ is a continuous function, then the Eq (3.1) is equvalent to the following Volterra Integral equation of the second kind:

Applying the above Lemma into the problems (1.1) and (1.2), we can deduce that

This is an equivalent VIE to the original problem. By exchanging the integration order of the last part, (3.3) can be expressed as follows:

By introducing variable substitution $t = s+\tau(x-s)$, the above formula can be transformed into

where

Since $q(x, t)$ is bounded and continuous in ${\triangle}_T$, assuming that $q_{max}$ is the maximum of $q$ for $(x, t)\in {\triangle}_T$, and $q_{min}$ is the minimum, correspondingly, then

where $B(\cdot, \cdot)$ is Beta function defined by

Thus $K(x, t)$ is a bounded and continuous founction of $x$ and $t$ in ${\triangle}_T$.

As a result, Eqs (1.1) and (1.2) can be reformulated as the following equivalent form:

According to the basic results of VIEs (Theorem 6.1.2 in ^[26]), the above equation possesses a unique solution $u\in C(I)$. Equation (3.7) is different from the reformation in ^[7]. We have two different singular kernels which can be treated respectively. That means we can choose suitable collocation methods for each kernel for the sake of solving the problem more conveniently and efficiently.

3.2.   The multi-step Legendre-Gauss collocation scheme

Now, we aim to construct an efficient multi-step spectral collocation scheme for (1.1) and (1.2). We set $T = 1$ for the sake of convenience and simplicity. Denote by $u_{n}(x)$ the exact solution to (1.1) and (1.2) on the $n$-th sub-interval, that is,

where $I_n$ is defined in Section 2. From (1.1) we know that for any $x\in I_n$

Using the transformation in (2.5), the Eq (3.8) becomes

The multi-step spectral collocation method to solve (3.7) based on Legendre-Gauss points is to seek $U_n(x)\in \mathcal{P}_{M_n}(I_n)$, such that

where $U_k(x)$ is the approximate solution of $u_k(x)$ on the element $I_k$. To describe the numerical implementations in details for scheme (3.10), we set

Then by applying (2.4), (2.6) and (3.11), one has

Using similar techniques, we can obtain

and

Using (2.2)–(2.4) and (3.11), we have

and

In addition

One can easily verify that

Next, using (3.10)–(3.17), we deduce that

Comparing the expansion coefficients on the two sides of (3.19), yields

The system (3.20) is obviously implicit, which always couldn't be easily solved by a direct method. Actually, we can employ an iterative method to solve out the expansion coefficients $Z_p^n$. Here, we prefer to using the successive substitution method for its simplicity and convenience. In short, we compute the successive coefficients $\{Z_p^n\}_{p = 0}^{M_n}$ based on the previously obtained quantities $\{Z_p^k\}_{p = 0}^{M_k}, k = 1, \cdots, n-1.$

4.   Convergence analysis

4.1.   Some useful results

In this part, some useful results are introduced, which are fundamental for the convergence analysis.

For any given interval $\Lambda$, we denote by $L^2(\Lambda)$ the space of measurable functions whose square is Lebesgue integrable on $\Lambda$. Let $H^m(\Lambda)$ be the standard Sobolev space with the integer order $m$.

Lemma 1. (^[22]) Assume that $v\in H^m(I_n)$ is any given function with $1\leq m \leq M_n+1,$ there holds

Lemma 2. (^[22]) Let the assumption in Lemma 1 holds. Then we have

In order to discuss the convergence of singular solutions, we next consider the error estimates for Legendre-Gauss interpolation of $x^\nu$-type functions which have singularity at the endpoint $x = 0$.

Lemma 3. (^[21]) Let $M_n = M\geq 0$ and $h_n \approx h$. Suppose that $u(x) = x^{\nu}$ with a non-integer $\nu$ satisfying $\nu > 0$. Then for $\alpha > -1$, $M > \nu-1$,

In addition, since $x^\nu$ only has a singular point at the left end of the first interval, we have

Lemma 4. (^[19]) Given that $\{r_k\}$, $\{q_k\}$ and $\{\rho_k\}\; (k\geq 0)$ are non-negative sequences. $\{e_n\}$ is the sequence satisfying $e_0\leq\rho_0$ and

Then there holds that

4.2.   Error analysis under $L^2$-norm

In this part, we shall analyze the error bounds in the $L^2(I)$ function space for smooth solutions. Thus, the term $\|U_n-\mathcal{I}_{x, M_n}u_n(x)\|_{L^2(I_n)}$ would be estimated first. According to (3.8), one has

Subtracting (3.10) from (4.1) and using the inverse of transformation (2.5), we can obtain that

where

We estimate $\{B_j\}^5_{j = 1}$ one by one. For simplicity, we make the assumption $\mathcal{(A)}$ as follows:

● $q(x, t)$ is continuous, for any given $x \in I$, $q(x, t)|_{t\in I_k}\in H^{m_k}(I_k)$ with the integer $1\leq m_k\leq M_k+1$.

● $g, p, u$ is continuous on $I$, $g|_{t\in I_k}$, $p|_{t\in I_k}$, $u_k\in H^{m_k}(I_k)$ with the integer $1\leq m_k\leq M_k+1$.

It can be found that the first item of $\mathcal{(A)}$ implies the same result for $K(x, t)$.

Lemma 5. Under the assumption $\mathcal{(A)}$. If $\alpha \in \big(\frac{1}{2}, 1\big)$, then for any $1\leq n \leq N,$ we have

Proof. For the sake of convenience and simplification, we make the notation as follows:

Applying this formula and (2.2) to the first formula of (4.3), we have

Using Cauchy-Schwarz inequality, we can easily get

Since $\alpha \in \big(\frac{1}{2}, 1\big)$ and $\sum_{i = 0}^{M_n}\omega_{n, i} = 2$, we can deduce that

where

Next, we shall estimate $B_1$ by evaluating $B_{11}$ and $B_{12}$ one by one. Using (2.2) again, one has

Clearly, by triangle inequality, the above becomes

By Lemma 1, we get

Combining (4.7), (4.10) with (4.11), the desired estimate follows. □

Lemma 6. Under the assumption $\mathcal{(A)}$. If $\alpha \in \big(\frac{1}{2}, 1\big)$, then there holds that

Proof. Using the Triangle Inequality to the second formula of (4.3), one has

where

Since $\alpha \in \big(\frac{1}{2}, 1\big)$, according to Cauchy-Schwarz inequality and (2.2), we obtain that

From Lemma 2, we deduce that

Furthermore, applying the Cauchy-Schwarz inequality, we get

Thus, by (4.15) and 4.16), the desired result is obtained. □

Lemma 7. Under the assumption $\mathcal{(A)}$, suppose that $\alpha \in \big(\frac{1}{2}, 1\big)$, $0 < \beta < 1$, then we have

Proof. We define

Thus

Since $\alpha \in \big(\frac{1}{2}, 1\big)$ and $0 < \beta < 1$, we easily deduce that $-1 < 2(\alpha-\beta) < 2$. Using Cauchy-Schwarz Inequality, we get

where

Using (2.2) and triangle inequality again, we get

By Lemma 1, we get

Plugging (4.21) and (4.22) into (4.19), we complete the proof. □

Lemma 8. Under the assumption $\mathcal{(A)}$, suppose that $\alpha \in \big(\frac{1}{2}, 1\big)$, $0 < \beta < 1$, then we have

Proof. Since $-1 < 2\alpha-2\beta < 2$, using Cauchy-Schwarz inequality and (2.2), we obtain

where

By computing directly, we obtain

Furthermore, applying the Cauchy-Schwarz inequality, we get

Thus, by (4.24), (4.26) and (4.27), the desired result is obtained. □

Using the same skills as above, we deduce the following estimates:

Lemma 9. Under the assumption $\mathcal{(A)}$, suppose that $\alpha \in \big(\frac{1}{2}, 1\big)$, $0 < \beta < 1$, there holds

Combining the above estimates for $\{B_j\}^5_{j = 1}$, we obtain local convergence as follows:

Theorem 1. Under the assumption $\mathcal{(A)}$, suppose that $\alpha \in \big(\frac{1}{2}, 1\big)$, $0 < \beta < 1$, then for any $1\leq n \leq N$, we have

Proof. Obviously, it follows from the triangle inequality that

According to Lemma 1, one has

The above formula along with (4.2), Lemmas 5–9 lead to

Assume that $\alpha \in \big(\frac{1}{2}, 1\big)$, $0 < \beta < 1$ and $h_n$ is small enough, such that

Then we can obtain from (4.32) that

Using the Lemma 4, we can obtain that

This is the desired result. □

Summing (4.29) from $n = 1$ to $N$, we get the following $L^2$-norm error estimate on the entire interval $I$.

Theorem 2. Under the assumption $\mathcal{(A)}$, if $\alpha \in \big(\frac{1}{2}, 1\big)$, $0 < \beta < 1$, then we have

Remark 1. Theorem 2 established the $hp$-version error bounds for sufficiently smooth solutions. However, for $0 < \alpha < 1$ in the Volterra integral Eq (3.7), smooth functions $p, q, g$ result in the weakly singular solution $u(x)$ which typically has the form of $u(x) = O(x^{\alpha})$ near $x = 0$ (see ^[26]). Thus, applying the Lemma 3 and executing the same procedure as above, we can obtain the following results:

on the uniform meshes ($h_n = h$) and uniform approximation degree ($M_n = M$).

Remark 2. For the sake of getting higher order methods to solve the problems with weakly singular kernels, some special partitions (such as graded meshes or geometric meshes) are always considered. Here we implemented the proposed method on the graded meshes of the form $x_n = \big(\frac{i}{N}\big)^rT$. Thus $M$ order convergence for $h$ can be obtained under the condition $r = (M+1)/\alpha$, where $M$ is the degree of interpolation polynomials on $I_n$ and $M+1$ is the number of collocation points.

5.   Numerical experiments

To demonstrate the effectiveness of the proposed method and the validity of the theoretical results derived in the previous sections, here we present some numerical experiments.

5.1.   Problems with smooth solutions

Example 1. We first consider the following FIDE with sufficiently smooth solution:

where

The solution of this problem can be written as $u(x) = x^{19/3}$, which is sufficiently smooth on the interval $[0, 1].$ We can transform this problem into the equivalent form:

where

In Figure 1, we show the discrete $L^2$-errors for decreasing $h$ and fixed polynomial degree $M = 1, 2, 3, 4.$ These approximately diagonal lines indicate that the $h$-version convergence is algebraic in $h$. In Table 1, the discrete $L^2$-norm errors in $h$-version and the order of convergence are summarized. Results are agreement with the theoretical results of Theorem 2.

In Figure 2, we show the discrete $L^2$-errors of the $p$-version with increasing polynomial degree $M$ at fixed time step, $h = 1, 1/2, 1/4, 1/8,$ respectively. We see that exponential convergence of $p$-version is achieved, which confirms the results of Theorem 2.

5.2.   Problems with weakly singular solutions

Example 2. We use the proposed method to solve the following problem with weakly singular solution:

where

The above equation has the exact solution $u(x) = x^{\frac{2}{3}},$ which has a weak singularity at the left endpoint $x = 0.$

In Figure 3, we present the discrete $L^2$-errors for various $h$ and fixed polynomial degree $M = 1, 2, 3, 4$, respectively. They indicates that the $h$-version convergence of the proposed method is algebraic for decreasing $h$. In Table 2, we list the discrete $L^2$-errors of the $h$-version and the convergence order. The convergence order is about $1.17$, which corresponds to the theoretical results about $h$-version predicted in Remark 1 (the $h$-version convergence rate is $\mathcal{O}(h^{\alpha+\frac{1}{2}}$) for singular solutions).

In Figure 4, the discrete $L^2$-errors in the $p$-version for Example 2 are shown. The mode $M$ is increasing for each fixed time step $h = 1, 1/2, 1/4, 1/8$. This means that the $p$-version convergence for different $h$ is algebraic and the convergence orders are similar since the solution is weakly singular.

In Table 3, $p$-version error bounds and convergence order are presented in details. The convergence order for the $L^2$-errors is about 2.3, which coincides with the $p$-version results predicted in Remark 1 ($p$-version convergence rate is $\mathcal{O}(M^{-2\alpha-1})$) and is twice as fast as the $h$-version results.

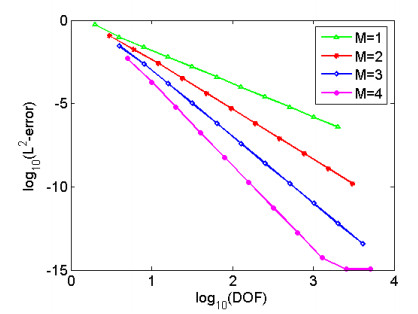
To obtain higher convergence order and improve the effectiveness of our method, we make use of graded meshes $x_i = (i/N)^r$ for $i = 0, 1, \cdots, N$ with $r = (M+1)/\alpha$, where the spectral collocation method uses shifted Legendre polynomials of degree $M$. The value $M = 1, 2, 3$ are examined in our experiments. In Figure 5, we plot the discrete $L^2$-errors against the degrees of freedom. In Table 4, the discrete $L^2$-errors in $h$-version and the corresponding convergence order are listed in details, for increasing grid points number $N$ for each fixed mode $M = 1, 2, 3, 4$, respectively. Clearly, $M+1$-order convergence is achieved, as predicted in Remark 2.

5.3.   Numerical comparison

Example 3. We apply the proposed method to solve the following problem with weakly singular solution in ^[7]:

where

The exact solution is $u(x) = x^3+x^{\frac{4}{3}},$ which has weak singularity at the left endpoint $x = 0.$

Figures 6 and 7 show that the discrete $L^2$-error in both $h$ and $p$-version converges algebraically as they behaved in Example 2, when the problem is solved on the uniform meshes. In Figure 8, one can find that the discrete $L^2$-errors on graded meshes converge approximately exponentially. We compare the maximum errors on uniform meshes of our method and the $h$-version collocation method (45) in ^[7]. Table 5 indicates that the accuracy of our method are higher than those of the method (45) in ^[7]. Moreover, the time step $h$ and polynomial degree $M$ in our $hp$-version spectral collocation method may be chosen arbitrarily, according to the demands of users. Thus $hp$-version spectral collocation method is much more convenient and flexible to be implemented.

6.   Conclusions

In this paper, we have addressesed an $hp$-version spectral collocation method for FIDEs (1.1) and (1.2) with singular kernels. We have converted the problem into a piece-wised Volterra integral equations and then presented a multi-step Legendre-Gauss spectral collocation scheme for the problem. The $L^2$-norm error bounds have been established for $\alpha \in \big(\frac{1}{2}, 1\big)$. Numerical experiments has demonstrated the effectiveness of the suggested approach and the validity of the theoretical results. As a matter of fact, theoretical and numerical results expected to hold for $\alpha \in \big(0, 1).$ In the further research, we will analyze the convergence for $\alpha \in \big(0, 1\big)$ and the design of corresponding numerical methods for efficiently solve nonlinear FIDEs.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research was funded by the National Natural Science Foundation of China (Grant No. 11901509) and the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (Grant No. 19KJB110023). The authors are thankful to the referees for their constructive suggestions which helped to improve the presentation of this paper.

Conflict of interest

The authors declare no conflicts of interest.