Sequential fractional order Neutral functional Integro differential equations on time scales with Caputo fractional operator over Banach spaces

1.   Introduction

${MS}$-algebras were considered by T. S. Blyth and J. C. Varlet^[15] as a common properties of de Morgan algebras and Stone algebras. T. S. Blyth and J. C. Varlet^[16] described the lattice $\Lambda{({MS})}$ of all subclasses of the class ${MS}$ of all $MS$-algebras by identities.

A. Badawy, D. Guffov$\acute{a}$ and M. Haviar^[10] introduced and characterized the class of principal $MS$-algebras and the class of decomposable $MS$-algebras by means of principal $MS$-triples and decomposable $MS$-triples, respectively. They obtained a one-to-one correspondence between principal $MS$-algebras (decomposable $MS$-algebras) and principal $MS$-triples (decomposable $MS$-triples). Moreover, they proved that the class of principal $MS$-algebras is a subclass of the class of decomposable $MS$-algebras.

A. Badawy^[6] established the relationship between de Morgan filters and congruences of a decomposable $MS$-algebra. A. Badawy^[3] introduced the notion of $d_{L}$-filters of a principal $MS$-algebra and characterized certain congruences in terms of $d_{L}$-filters. Recently, A. Badawy, M. Haviar and M. Plo$\check{s}\check{c}$ica^[11] introduced and described the notions of congruence pairs and perfect extensions of principal $MS$-algebras. They characterized the lattice of congruences of a principal $MS$-algebra in terms of congruence pairs. In 2021, S. El-Assar and A. Badawy^[19] characterized permutability of congruences and strong extensions of decomposable $MS$-algebras by means of congruence pairs.

We review in Section 2 many basic concepts and results that we are using throughout this article. We give an example (Example 2.1) to determine the principsl $MS$-triple $(L^{\circ\circ}, D(L), \varphi_{L})$ assosiated with a certain principal $MS$-algebra $L$. In Section $3$, we give equivalent conditions for a pair of congruence $(\theta_{1}, \theta_{2})\in Con(L^{\circ\circ})\times Con_{lat}(D(L))$ to become an $MS$-congruence pair of a principal $MS$-algebra $L$, where $\theta_{1}$ is a congruence on a de Morgan algebra $L^{\circ\circ}$ and $\theta_{2}$ is a lattice congruence on the lattice $D(L)$. Also, we characterize the lattice of all $MS$- congruence pairs which are induced by the Boolean elements of a principal $MS$-algebra. In Section $4$, we discuss many properties of the congruence relation $\Psi$ which defined on a principal $MS$-algebra $L$ by

We prove that $\Psi$ permutes with each congruence relation $\theta$ on $L$. Also, we characterize $2$-permutability of congruences (briefly permutability) by means of $MS$-congruence pairs. We illustrate Examples 3.1 and 4.1 to clarify Theorems 3.1 and 4.4, respectively. Also, Example 4.2 introduces certain principal $MS$-algebra $L$, which has not $2$-permutable congruences as well as $D(L)$ has not also $2$-permutable congruences. In Section $5$, A characterization of $n$-permutability of congruences of a principal $MS$-algebra is given, which is a generalization of the characterization of $2$-permutability of congruences of such algebras.

2.   Preliminaries

In this section, we recall some specific definitions and remarkable results which are discussed in previous articles ^{[10,14,15,16,17,19]}.

Definition 2.1. ^[16] A de Morgan algebra is an algebra $(L; \vee, \wedge, ^{-}, 0, 1)$ of type (2, 2, 1, 0, 0), where $(L; \vee, \wedge, 0, 1)$ is a bounded distributive lattice and the unary operation $^{-}$ satisfying:

Definition 2.2. ^[15] A Stone algebra is an algebra $(L; \vee, \wedge, ^{*}, 0, 1)$ of type $(2, 2, 1, 0, 0)$, where $(L; \vee, \wedge, 0, 1)$ is a bounded distributive lattice and the unary operation $^{*}$ satisfying:

Definition 2.3. ^[15] An $MS$-algebra is an algebra $(L; \vee, \wedge, ^{\circ}, 0, 1)$ of type (2, 2, 1, 0, 0), where $(L; \vee, \wedge, 0, 1)$ is a bounded distributive lattice and a unary operation $^{\circ}$ satisfying:

The class $MS$ of all $MS$-algebras is equational. A de Morgan algebra is an $MS$-algebra satisfying the identity, $a = a^{\circ\circ}$. The class $S$ of a Stone algebra is a subclass of $MS$ satisfying $a\wedge a^{\circ} = 0$.

The basic properties of $MS$-algebras which were shown in^[15] are given in the following theorem.

Theorem 2.1. Let $a, b$ be any two elements of an $MS$-algebra $\; L$. Then

(1) $0^{\circ\circ} = 0$ and $1^{\circ\circ} = 1$,

(2) $a\leq b\Rightarrow b^{\circ}\leq a^{\circ}$,

(3) $a^{\circ\circ\circ} = a^{\circ}$,

(4) $a^{\circ\circ\circ\circ} = a^{\circ\circ}$,

(5) $(a\vee b)^{\circ} = a^{\circ}\wedge b^{\circ}$,

(6) $(a\vee b)^{\circ\circ} = a^{\circ\circ}\vee b^{\circ\circ}$,

(7) $(a\wedge b)^{\circ\circ} = a^{\circ\circ}\wedge b^{\circ\circ}$.

An element $a$ of an $MS$-algebra $L$ is called a closed element of $L$ if $a = a^{\circ\circ}$ and an element $d\in L$ is called a dense element of $L$ if ${d}^{\circ} = 0$.

Theorem 2.2. Let $L$ be an $MS$-algebra. Then

(1) the set $L^{\circ\circ} = \{a\in L:a = a^{\circ\circ}\}$ of all closed elements of $L$ is a de Morgan subalgebra of $L$, see ^[17],

(2) the set $D(L) = \{a\in L:a^{\circ} = 0\}$ of all dense elements of $L$ is a principal filter of $L$, see ^[10].

Definition 2.4. ^[10] An $MS$-algebra $(L; \vee, \wedge, ^\circ, 0, 1)$ is called a principal $MS$-algebra if it satisfies the following conditions:

(1) the filter $D(L)$ is principal, that is, there exists an element $d_{L}\in L$ such that $D(L) = [d_{L})$,

(2) $a = a^{\circ\circ} \wedge (a\vee d_{L})$, for all $a\in L$.

A principal $MS$-algebra $L$ is a principal Stone algebra if $x^{\circ}\vee x^{\circ\circ} = 1$, for all $x\in L$.

Definition 2.5. ^[8] A principal $MS$-triple is $(M, D, \varphi)$, where

(1) $\; M$ is a de Morgan algebra,

(2) $\; D$ is a bounded distributive lattice,

(3) $\; \varphi$ is a $(0, 1)$-lattice homomorphism from $M$ into $D$.

Lemma 2.1. ^[10] Let $L$ be a principal $MS$-algebra. Define a map $\varphi_{L}:L^{\circ\circ}\rightarrow [d_{L})$ by the following rule

Then $\varphi_{L}$ is a $(0, 1)$-lattice homomorphism.

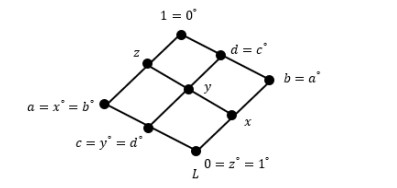
Example 2.1. Consider the $MS$-algebra $L$ in Figure 1.

It is clear that $L$ is a principal $MS$-algebra with the smallest dense element $z$. Then the principal triple $(L^{\circ\circ}, D(L) = [z), \varphi_{L})$ which associated with $L$ is given in Figure 2.

Definition 2.6. ^[22] An equivalence relation $\theta$ on a lattice $L$ is called a lattice congruence if $(a, b)\in \theta$ and $(c, d)\in \theta$ imply $(a\vee c, b\vee d)\in \theta$ and $(a\wedge c, b\wedge d)\in \theta$.

Definition 2.7. An equivalence relation $\theta$ on an $MS$-algebra $L$ is called a congruence on $L$ if

(1) ${\theta}$ is a lattice congruence,

(2) $(a, b)\in \theta$ implies $(a^{\circ}, b^{\circ})\in \theta$.

We use $Con_{lat}(L)$ for the lattice of all lattice congruences of a lattice $(L; \vee, \wedge)$ and $Con(L)$ for the lattice of all congruences of an $MS$-algebra $(L; \vee, \wedge, ^{\circ}, 0, 1)$.

Definition 2.8. Let $L$ be a lattice and $\theta\in Con_{lat}(L)$. Then we define the principal congruence generated by $(a, b)$ which denoted by $\theta(a, b)$ as follows:

If $L$ is an $MS$-algebra and $\theta\in Con(L)$, then

Let $L$ be an $MS$-algebra. Then $(\theta_{L^{\circ\circ}}, \theta_{D(L)})\in Con(L^{\circ\circ})\times Con_{lat}(D(L))$, where $\theta_{L^{\circ\circ}}$ and $\theta_{D(L)}$ are the restrictions of $\theta \in Con(L)$ to $L^{\circ\circ}$ and $D(L)$, respectively. It is clear that $\theta_{L^{\circ\circ}}$ is a congruence relation on a de Morgan algebra $L^{\circ\circ}$ and $\theta_{D(L)}$ is a lattice congruence on a lattice $D(L)$.

The symbols $\bigtriangledown_{L}$ and $\bigtriangleup_{L}$ will be used for the universal congruence $L\times L$ and the equality congruence on $L$, respectively.

The concept of $MS$-congruence pairs is given as follows:

Definition 2.9. ^[11] Let $L$ be a principal $MS$-algebra with a smallest dense element $d_{L}$. A pair of congruences $(\theta_{1}, \theta_{2})\in Con(L^{\circ\circ})\times Con_{lat}(D(L))$ will be called an $MS$-congruence pairs if

A characterization of congruences on a principal $MS$-algebra via $MS$-congruence pairs is given in the following theorem.

Theorem 2.3. ^[11] Let $L$ be a principal $MS$-algebra with the smallest dense element $d_{L}$. For every congruence $\theta$ on $L$, the restrictions of $\theta$ to $L^{\circ\circ}$ and $D(L)$ determine the $MS$-congruence pair $(\theta_{L^{\circ\circ}}, \theta_{D(L)})$.

Conversely, every $MS$-congruence pair $(\theta_{1}, \theta_{2})$ uniquely determines a congruence $\theta$ on $L$ satisfying $\theta_{L^{\circ\circ}} = \theta_{1}$ and $\theta_{D(L)} = \theta_{2}$. Such congruence can be defined by the rule

Throughout this paper, $d_{L}$ denotes to the smallest dense element of a principal $MS$-algebra $L$.

For extra information of $MS$-algebras, principal $MS$-algebras and decomposable $MS$-algebras, we refer the reader to^{[1,2,3,4,5,6,7,8,9,12,13,14,15,16,17,18,20,21,22,23,24]}.

3.   Characterization of $MS$-congruence pairs

In this section, we characterize $MS$-congruence pairs of a principal $MS$-algebra and a principal Stone algebra. Also, we describe the lattice of all $MS$-congruence pairs which induced by the Boolean elements of a principal $MS$-algebra, in fact such lattice forms a Boolean algebra on it is own.

Lemma 3.1. Let $L$ be a principal $MS$-algebra and $(\theta_{1}, \theta_{2})$ be an $MS$-congruence pair. Then

Proof. Let $(a, b)\in \theta_{1}$ and $(x, y)\in \theta_{2}.$ Then $(a\vee d_{L}, b\vee d_{L})\in \theta_{2}$ (by Definition 2.9) and $(x, y)\in \theta_{2}$ imply that $(a\vee x\vee d_{L}, b\vee y\vee d_{L})\in \theta_{2}.$ Therefore $(a\vee x, b\vee y)\in \theta_{2}$ as $x, y\geq d_{L}$. □

Now, we give an important characterization of $MS$-congruence pairs of a principal $MS$-algebra.

Theorem 3.1. Let $L$ be a principal $MS$-algebra with the smallest dense element $d_{L}.$ Then the following statements are equivalent:

(1) $\; (\theta_{1}, \theta_{2})$ is an $MS$-congruence pair of $L$,

(2) $Con_{\varphi_{L}}(L)\subseteq \theta_{2},$ where

Proof. $(1\Rightarrow2)$ Let $(\theta_{1}, \theta_{2})$ be an $MS$-congruence pair of $L$ and $(x, y)\in Con_{\varphi_{L}}(\theta_{1}).$ Then $(x, y) = (\varphi_{L}(a), \varphi_{L}(b)) = (a\vee d_{L}, b\vee d_{L}),$ where $(a, b)\in \theta_{1}.$ Since $(a, b)\in \theta_{1},$ then $(a\vee d_{L}, b\vee d_{L})\in \theta_{2},$ by $(1).$ Thus $(x, y)\in \theta_{2}$. So $Con_{\varphi_{L}}(\theta_{1})\subseteq \theta_{2}$.

$(2\Rightarrow 1)$ Let $Con(\theta_{1})\subseteq \theta_{2}.$ We prove that $(\theta_{1}, \theta_{2})$ is an $MS$-congruence pair of $L$. Let $(a, b)\in \theta_{1}.$ Then by (2), $(a\vee d_{L}, b\vee d_{L}) = (\varphi_{L}(a), \varphi_{L}(b))\in \theta_{2}$. □

A characterization of congruence pairs of a principal Stone algebra is given in the following.

Theorem 3.2. Let $L$ be a principal Stone algebra. Let $(\theta_{1}, \theta_{2})\in Con(L^{\circ\circ})\times Con_{lat}(D(L)).$ Then the following statements are equivalent:

(1) $(\theta_{1}, \theta_{2})$ is an $MS$-congruence pair of $L$,

(2) $Con_{\varphi_{L}}(\theta_{1})\subseteq \theta_{2}$,

(3) $(a, 1)\in \theta_{1}$ and $u\geq a, u\in D(L)$ imply $(u, 1)\in \theta_{2}$.

Proof. In Theorem 3.1, we proved that $(1)$ and $(2)$ are equivalent.

$(2\Rightarrow 3)$ Let $Con_{\varphi_{L}}(\theta_{1})\subseteq \theta_{2}$. Let $(a, 1)\in \theta_{1}$ and $u\geq a, u\in D(L)$. Then $(\varphi_{L}(a), \varphi_{L}(1))\in \theta_{2}$ by (2). Thus $(a\vee d_{L}, 1)\in \theta_{2}$.

Now $(a\vee d_{L}, 1)\in \theta_{2}$ and $(u, u)\in \theta_{2}, u\geq a, u\in D(L)$ imply $(a\vee u\vee d_{L}, 1\vee u)\in \theta_{2}$. Thus $(u, 1)\in \theta_{2}$ as $u\geq a, d_{L}$.

$(3\Rightarrow 1)$ Since $L$ is a Stone algebra then $L^{\circ\circ}$ is a Boolean subalgebra of $L$ and hence $a\vee a^{\circ} = 1$ for each $a\in L^{\circ\circ}$. Suppose $(3)$ holds and $(a, b)\in \theta_{1}.$ Then $(b^{\circ}, b^{\circ})\in \theta_{1}$ implies $(a\vee b^{\circ}, b\vee b^{\circ}) = (a\vee b^{\circ}, 1)\in \theta_{1}$ and $(a\vee a^{\circ}, b\vee a^{\circ}) = (b\vee a^{\circ}, 1)\in \theta_{1}$. Therefore $(\beta, 1)\in \theta_{1}$, where $\beta = (a\vee b^{\circ})\wedge (a^{\circ}\vee b)$. It is clear that $\beta\in L^{\circ\circ}$ and $\beta\wedge a = \beta\wedge b = a\wedge b$. Since $\beta\leq \beta\vee d_{L}\in D(L)$ and $(\beta, 1)\in \theta_{1}$ then $(\beta\vee d_{L}, 1)\in\theta_{2}$ by (3). Thus $(a\vee d_{L}, a\vee d_{L})\wedge (1, \beta\vee d_{L})\in \theta_{2}$ implies $(a\vee d_{L}, (a\wedge \beta)\vee d_{L}) = (a\vee d_{L}, (a\wedge b)\vee d_{L})\in \theta_{2}$. Similarly, we can get $(b\vee d_{L}, (b\wedge \beta)\vee d_{L}) = (b\vee d_{L}, (a\wedge b)\vee d_{L})\in \theta_{2}$. Then $(b\vee d_{L}, b\vee d_{L})\in \theta_{2}$. □

Example 3.1. Consider the principal $MS$-algebra $L$ in Example 2.1 (Figure 1). The lattices $Con(L)$ and $A(L)$ of all congruences of $L$ and all $MS$-congruence pairs of $L$ are given in Figure 3, respectively.

Where,

And

It is clear that $Con(L)$ isomorphic to $A(L)$ under the isomorphism $\theta \longmapsto (\theta_{L^{\circ\circ}}, \theta_{D(L)})$.

A subset $I$ of a lattice $L$ with $0$ is called an ideal of $L$ if

A principal ideal of $L$ generated by $a \in L$ is defined by

A subset $F$ of a lattice $L$ with $1$ is called a filter of $L$ if

A principal filter of $L$ generated by $a \in L$ is defined by

Definition 3.1. Let $\theta$ be a lattice congruence on a bounded lattice $L$. Then we have the following important subsets

(i) The Kernel of $\theta$ ($Ker \theta)$ is the set $\{x\in L:(x, 0)\in \theta\}$, which is an ideal of L,

(ii) The Cokernel of $\theta$ ($Coker \theta)$ is the set $\{x\in L:(x, 1)\in \theta\}$, which is a filter of L.

Definition 3.2. ^[7] An element $c$ of an $MS$-algebra $L$ is called a Boolean element of $L$ if $c\vee {c}^{\circ} = 1$.

It is ready seen that the set $B(L) = \{c:c\vee c^{\circ} = 1\}$ of all Boolean elements of $L$ forms a Boolean subalgebra of $L^{\circ\circ}$.

Lemma 3.2. Let $c$ be a Boolean element of a principal $MS$-algebra $L.$ Then

(1) $\theta(0, c)$ is a principal congruence relation on $L^{\circ\circ}$ with $Ker\; {\theta(0, c)} = (c]$, where

(2) $\theta(\varphi_{L}{(c)}, 1)$ is a principal congruence relation on $D(L)$ with $Coker\; {\theta(\varphi_{L}(c), 1)} = [\varphi_{L}(c))$, where

Proof.

(1) It is easy to check that $\theta(0, c)$ is a principal congruence relation on $L^{\circ\circ}$ with $Ker\; {\theta(0, c)} = (c]$.

(2) It is easy to show that $\theta(\varphi_{L}(c), 1)$ is an equivalence relation on $D(L)$. Let $(x, y), (m, n)\in \theta(\varphi_{L}(c), 1).$ Thus $x\wedge (c\vee d_{L}) = y\wedge (c\vee d_{L})$ and $m\wedge (c\vee d_{L}) = n\wedge(c\vee d_{L}).$ Then, we get $(x\wedge m, y\wedge n)\in \theta(\varphi_{L}(c), 1)$ and $(x\vee m, y\vee n)\in \theta(\varphi_{L}(c), 1).$ Therefore $\theta(\varphi_{L}(c), 1)$ is a principal congruence on the lattice $D(L)$. Also, we have

□

Now, we observe that every Boolean element $c$ of a principal $MS$-algebra $L$ associated with the $MS$-congruence pair of the form $(\theta(0, c), \theta(\varphi_{L}(c^{\circ}), 1))$.

Theorem 3.3. Let $L$ be a principal $MS$-algebra and $c\in L^{\circ\circ}.$ Then $c$ is a Boolean element of $L$ if and only if $(\theta(0, c), \theta(\varphi_{L}(c^{\circ}), 1))$ is an $MS$-congruence pair of $L$.

Proof. Let $c$ be a Boolean element of $L.$ We proved that $\theta(0, c)$ and $\theta(\varphi_{L}(c^{\circ}), 1)$ are $MS$-congruence on $L^{\circ\circ}$ and lattice congruence on $D(L)$, respectively (Lemma 3.2). To show that $(\theta(0, c), \theta(\varphi_{L}(c^{\circ}), 1))$ is an $MS$-congruence pair, let $(x, y)\in \theta(0, c).$ Then

Conversely, let $(\theta(0, c), \theta(\varphi_{L}(c^{\circ}), 1))$ be an $MS$-congruence pair. Since $(0, c)\in \theta(0, c)$ then $c\wedge c^{\circ}$ = $0\wedge c^{\circ} = 0.$ Now, $c\vee c^{\circ} = (c^{\circ}\wedge c)^{\circ} = 1$. Therefore $c$ is a Boolean element. □

The basic properties of principal congruence relations $\theta(0, a)$ and $\theta(\varphi_{L}(a), 1), \forall a\in B(L)$ are given in the following:

Lemma 3.3. Let $a, b$ be Boolean elements of a principal $MS$-algebra $L$. Then

(1) $a\leq b$ if and only if $\theta(0, a)\subseteq \theta(0, b)$,

(2) $a = b$ if and only if $\theta(0, a) = \theta(0, b)$,

(3) $\theta(0, 0) = \triangle_{L^{\circ\circ}}$ and $\theta(0, 1) = \triangledown_{L^{\circ\circ}}$,

(4) $\theta(0, a)\vee \theta(0, b) = \theta (0, a\vee b)$,

(5) $\theta(0, a)\cap \theta(0, b) = \theta (0, a\wedge b)$.

Lemma 3.4. Let $L$ be a principal $MS$-algebra. Then for every $a, b\in B(L)$, we have

(1) $a\leq b$ implies $\theta(\varphi_{L}(a^{\circ}), 1)\subseteq \theta (\varphi_{L}(b^{\circ}), 1)$,

(2) $\theta(\varphi_{L}(a^{\circ}), 1)\vee \theta(\varphi_{L}(b^{\circ}), 1) = \theta(\varphi_{L}(a\vee b)^{\circ}, 1)$,

(3) $\theta(\varphi_{L}(a^{\circ}), 1)\wedge \theta(\varphi_{L}(b^{\circ}), 1) = \theta(\varphi_{L}(a\wedge b)^{\circ}, 1)$,

(4) $\theta(\varphi_{L}(0), 1) = \triangledown_{D(L)}$ and $\theta(\varphi_{L}(1), 1) = \triangle_{D(L)}$.

Proof.

(1) Let $a\leq b$. Then $a^{\circ}\geq b^{\circ}$. Let $(x, y)\in \theta(\varphi_{L}(a^{\circ}), 1)$ then $x\wedge (a^{\circ}\vee d_{L}) = y\wedge (a^{\circ}\vee d_{L})$. Now

Then $(x, y)\in \theta(\varphi_{L}(b^{\circ}), 1)$. Therefore $\theta(\varphi_{L}(a^{\circ}), 1)\subseteq \theta(\varphi_{L}(b^{\circ}), 1)$.

(2) Since $a, b\leq a\vee b$ then by $(1)$, we have

Then $\theta(\varphi_{L}(a\vee b)^{\circ}, 1)$ is an upper bound of $\theta(\varphi_{L}(a^{\circ}), 1)$ and $\theta(\varphi_{L}(b^{\circ}), 1)$. Let $\theta(\varphi_{L}(c^{\circ}), 1)$ be an upper bound of $\theta(\varphi_{L}(a^{\circ}), 1)$ and $\theta(\varphi_{L}(b^{\circ}), 1)$.

Then $\theta(\varphi_{L}(a^{\circ}), 1), \theta(\varphi_{L}(b^{\circ}), 1)\subseteq \theta(\varphi_{L}(c^{\circ}), 1)$ implies $\varphi_{L}(c^{\circ})\leq \varphi_{L}(a^{\circ})$, $\varphi_{L}(b^{\circ}).$ Thus $\varphi_{L}(c^{\circ})\leq \varphi_{L}(a^{\circ}\wedge b^{\circ}) = \varphi_{L}(a\vee b)^{\circ}$ and hence $\theta(\varphi_{L}(a\vee b)^{\circ}, 1)\subseteq\theta(\varphi_{L}(c^{\circ}), 1).$ Therefore $\theta(\varphi_{L}(a\vee b)^{\circ}, 1)$ is the least upper bound of $\theta(\varphi_{L}(a^{\circ}), 1)$ and $\theta(\varphi_{L}(b^{\circ}), 1)$.

(3) Since $a\wedge b\leq a, \; b$ then by (1) $\theta(\varphi_{L}(a\wedge b)^{\circ}, 1)\subseteq \theta(\varphi_{L}(a^{\circ}), 1), \theta(\varphi_{L}(b^{\circ}), 1)$. Then $\theta(\varphi_{L}(a\wedge b)^{\circ}, 1)$ is a lower bound of $\theta(\varphi_{L}(a^{\circ}), 1)$ and $\theta(\varphi_{L}(b^{\circ}), 1)$. Let $\theta(\varphi_{L}(c^{\circ}), 1)$ be a lower bound of $\theta(\varphi_{L}(a^{\circ}), 1)$ and $\theta(\varphi_{L}(b^{\circ}), 1)$. Then $\theta(\varphi_{L}(c^{\circ}), 1)\subseteq\theta(\varphi_{L}(a^{\circ}), 1), \theta(\varphi_{L}(b^{\circ}), 1)$ implies $\varphi_{L}(a^{\circ}), \varphi_{L}(b^{\circ})\leq\varphi_{L}(c^{\circ}).$ Thus $\varphi_{L}(a\wedge b)^{\circ} = \varphi_{L}(a^{\circ})\vee \varphi_{L}(b^{\circ})\leq \varphi_{L}(c^{\circ})$ and hence $\theta(\varphi_{L}(c^{\circ}), 1)\subseteq \theta(\varphi(a\wedge b)^{\circ}, 1).$ Therefore $\theta(\varphi_{L}(a\wedge b)^{\circ}, 1)$ is the greatest lower bound of $\theta(\varphi_{L}(a^{\circ}), 1)$ and $\theta(\varphi_{L}(b^{\circ}), 1)$.

(4) Since $d_{L}, 1\in\theta (d_{L}, 1)$, then $\theta (d_{L}, 1) = D(L)\times D(L) = \triangledown_{D(L)}$. Also, let $(x, y)\in \theta (\varphi_{L}(1), 1)$ then $x\wedge(1\vee d_{L}) = y\wedge(1\vee d_{L})$. It follows, $x = y$ and hence $\theta (\varphi_{L}(1), 1) = \triangle_{D(L)}$. □

Theorem 3.4. Let $L$ be a principal $MS$-algebra. Consider the subsets $H$ and $G$ of $Con(L^{\circ\circ})$ and $Con(D(L))$, respectively as follows:

Then we have

(1) $(H; \vee, \wedge, \; ^{\prime}\;, \triangle_{L^{\circ\circ}}, \triangledown_{L^{\circ\circ}})$ is a Boolean algebra, where $(\theta(0, a))^{\prime} = \theta(a^{\circ}, 0)$,

(2) $(G; \vee, \wedge, \; ^{\prime}\;, \triangle_{D_(L)}, \triangledown_{D_{L}})$ is a Boolean algebra, where $(\theta(\varphi_{L}(a), 1))^{\prime} = \theta(\varphi_{L}(a^{\circ}), 1)$.

Proof.

(1) Since $\theta(0, 0) = \triangle_{L^{\circ\circ}}$ and $\theta(0, 1) = \triangledown_{L^{\circ\circ}}$. Then $\triangledown_{L^{\circ\circ}}, \; \triangle_{L^{\circ\circ}} \in H$. Let $\theta(0, a), \theta(0, b)\in H$. Then we get

and

Therefore $H$ is a bounded lattice. Since $B(L)$ is a Boolean algebra, then $a^{\circ}\in B(L)$ for all $a\in B(L)$. Thus $\theta(0, a^{\circ})\in H$. Then we have

and

Therefore $(H; \vee, \wedge, ^{\prime}, \triangle_{L^{\circ\circ}}, \triangledown_{L^{\circ\circ}})$ is a Boolean algebra.

(2) We have $\triangle_{D(L)} = \theta(\varphi_{L}(1), 1)\in G$ and $\triangledown_{D(L)} = \theta(\varphi_{L}(0), 1) = \triangledown_{D(L)}\in G$. Let $\theta(\varphi_{L}(a), 1), \theta(\varphi_{L}(b), 1)\in G$. Then we get

and

Therefore $G$ is a bounded lattice. Since $B(L)$ is a Boolean algebra, then $a^{\circ}\in B(L)$ for all $a\in B(L)$. Thus $\theta(\varphi_{L}(a^{\circ}), 1)\in G$. Then we have

and

Therefore $(G; \vee, \wedge, ^{\prime}, \triangle_{D_{L}}, \triangledown_{D_{L}})$ is a Boolean algebra. □

Let $L$ be a principal $MS$-algebra. Let $A(L)$ be the lattice of all $MS$-congruence pairs of $L$. We consider a subset ${A}^{\prime}(L)$ of $A(L)$ as follows:

From the above results, we observe that the set ${A}^{\prime}(L)$ of all $MS$-congruence pairs induced by the Boolean elements of a principal $MS$-algebra forms bounded sublattice of the lattice $A(L)$. Moreover ${A}^{\prime}(L)$ is a Boolean algebra on its own.

Theorem 3.5. Let $L$ be a principal $MS$-algebra. Then $({A}^{\prime}(L); \vee, \wedge, \; ^{'}\;, 0_{A^{\prime}(L)}, 1_{A^{\prime}(L)})$ is a Boolean algebra, where

Example 3.2. Consider the principal $MS$-algebra $L$ in Example 2.1. The lattices $B(L)$ and ${A}^{\prime}(L)$ of all Boolean elements of $L$ and all $MS$-congruence pairs of $L$ of the form $(\theta(0, a), \theta(\varphi_{L}(a^{\circ}), 1)), \; a\in B(L)$ are given in the following Figure 4, respectively. It is clear that $B(L)$ and $A(L)$ are isomorphic Boolean algebras under the isomorphism $a\longmapsto (\theta(0, a), \theta(a^{\circ}\vee z, 1))$. Also, ${A}^{\prime}(L)$ is a bounded sublattice of $A(L)$.

4.   $2$-permutability of principal $MS$-algebras

In this section, we characterize the notion of $2$-permutability of congruences of a principal $MS$-algebra by means of $MS$-congruence pairs.

Let $L$ be an algebra. We say the congruences $\theta, \Phi \in Con(L)$ are 2-permutable if $\theta \circ \Phi = \Phi \circ \theta$, that is, $(x, a)\in\theta$ and $(a, y)\in\Phi$, $\; x, y, a \in L$ imply $(x, b) \in \Phi$ and $(b, y)\in \theta$ for some $\; b\in L$. We call the algebra $L$ has $2$-permutable congruences (briefly permutable) if every pair of congruences of $L$ permute.

Lemma 4.1. A principal $MS$-algebra $L$ has $2$-permutable congruences if and only if every pair of principle congruences of $L$ permute.

Proof. Assume that every pair of principal congruences on $L$ permute. Let $\theta$ and $\Phi$ be arbitrary congruences on $L$ and $(a, b)\in (\theta\circ \Phi), \; a, b\in L$. Then $(a, t)\in \theta$ and $(t, b)\in \Phi$ for some $t\in L$. Then $(a, t)\in \theta(a, t)$ and $(t, b)\in \theta(t, b)$ imply that $(a, b)\in \theta(a, t)\circ \theta(t, b)$. Thus $(a, b)\in \theta(t, b)\circ \theta(a, t).$ Since $\theta(a, t)\subseteq \theta$ and $\theta(t, b)\subseteq \Phi$, then $(a, b)\in (\Phi\circ \theta).$ Therefore $\theta$ and $\Phi$ permute. The second implication is obvious. □

Define a relation $\Psi$ on a principal $MS$-algebra $L$ as follows:

Theorem 4.1. Let $L$ be a principal $MS$-algebra with the smallest dense element $d_{L}$. Then

(1) $\Psi$ is a congruence relation on $L$ with $Ker \; \Psi = \{0\}$ and $Coker\; \Psi = D(L),$

(2) $\Psi$ is closed congruence on $L$, that is, $(x, x^{\circ\circ})\in {\Psi}, \forall x\in L$,

(3) max $[x]_{\Psi} = x^{\circ\circ}, x\in L$, where $[x]_{\Psi} = \{y\in L:y^{\circ\circ} = x^{\circ\circ}\}$ is the congruence class of $x$ modulo $\Psi$.

Proof.

(1) One can check that $\Psi$ is a congruence relation on $L$. Now, we have

and

(2) Since $x^{\circ\circ\circ\circ} = x^{\circ\circ}$ then $x^{\circ\circ}\in [x]_{\Psi}$. Thus $(x^{\circ\circ}, x)\in \Psi$.

(3) Let $y\in [x]_{\Psi}.$ Then $y\leq y^{\circ\circ} = x^{\circ\circ}$ and $x^{\circ\circ}\in [x]_{\Psi}.$ Thus $x^{\circ\circ}$ is the greatest member of the congruence class $[x]_{\Psi}$. □

Theorem 4.2. Let $L$ be a principal $MS$-algebra. Then

(1) $L/{\Psi}$ is a de Morgan algebra,

(2) $L/{\Psi}$ and $L^{\circ\circ}$ are isomorphic de Morgan algebras.

Proof.

(1) It is ready seen that $(L/\Psi; \vee, \wedge, \{0\}, D(L))$ is a bounded distributive lattice, where $L/\Psi = \{[a]_{\Psi}:a\in L\}$ is the set of all congruence classes module $\Psi$ and

Define $^\square$ on $L/\Psi$ by $([a]_{\Psi})^{\square} = [a^{\circ}]_{\Psi}, \forall a\in L.$ We have

Then $L/\Psi$ is a de Morgan algebra.

(2) Define $g:L^{\circ\circ}\rightarrow L/{\Psi}$ by

Let $a, b \in L^{\circ\circ}$ and $a = b.$ Then $a^{\circ\circ} = b^{\circ\circ}$ implies $[a]_{\Psi} = [b]_{\Psi}$. It follows that $g$ is well defined map of $L^{\circ\circ}$ into $L/\Psi$. Let $a, b\in L^{\circ\circ}$, we get

and

Let $[a]_{\Psi} = [b]_{\Psi}.$ Then ${a}^{\circ\circ} = b^{\circ\circ}$ implies $a = b$. Therefore $g$ is an injective map. Let $[a]_{\Psi}\in L/{\Psi}$. Then $[x]_{\Psi} = [x^{\circ\circ}]_{\Psi} = g(x)$. Then $g$ is a surjective map. This deduce that $g$ is an isomorphism of de Morgan algebras. □

Now, we observe that ${\Psi}$ satisfies the following property,

Theorem 4.3. Let $L$ be a principal $MS$-algebra. Then $\Psi$ permutes with each congruence of $L$.

Proof. We prove that $\Psi\circ \theta = \theta\circ \Psi$ for all $\theta \in Con(L)$. Let $(a, b)\in \Psi\circ \theta.$ Then $(a, z)\in \Psi$ and $(z, b)\in \theta$ for some $z\in L$. It follows that $a^{\circ\circ} = z^{\circ\circ}$ and $(z, b)\in \theta$. Now

Since $[b^{\circ\circ}\wedge (a\vee d_{L})]^{\circ\circ} = b^{\circ\circ},$ then $(b^{\circ\circ}\wedge (a\vee d_{L}), b)\in \Psi.$ Therefore $(a, b^{\circ\circ}\wedge (a\vee d_{L}))\in \theta$ and $(b^{\circ\circ}\wedge (a\vee d_{L}), b)\in \Psi.$ imply $(a, b)\in \theta\circ \Psi$. Then $\Psi\circ \theta = \theta\circ\Psi, \; \forall \theta\in Con(L)$. □

Lemma 4.2. Let $L$ be a principal $MS$-algebra. Then

(1) $\triangle_{L}$ permutes with every congruence on $L$,

(2) $\triangledown_{L}$ permutes with every congruence on $L$.

Proof.

(1) Let $(a, b)\in \theta\circ \triangle_{L}$. Then $(a, t)\in \theta$ and $(t, b)\in \triangle_{L}$ for some $t\in L.$ Thus $(a, t)\in \theta$ and $t = b$. Then $(a, a)\in \triangle_{L}$ and $(a, b)\in \theta$ imply $(a, b)\in\triangle_{L}\circ \theta.$ Therefore $\theta \circ \triangle_{L} = \triangle_{L}\circ \theta$.

(2) It is obvious. □

In the following theorem, we characterize $2$-permutability of congruences of a principal $MS$-algebra $L$ using $MS$-congruence pairs.

Theorem 4.4. Let $L$ be a principal $MS$-algebra$.$ Then the following conditions are equivalent:

(1) $L$ has $2$-permutable congruences.

(2) $L^{\circ\circ}$ and $D(L)$ have $2$-permutable congruences.

Proof. To prove the conditions (1) and (2) are equivalent, we show that the two congruences $\theta\;, \Phi\; \in Con(L)$ are $2$-permutable if and only if their restrictions $\theta_{L^{\circ\circ}}, \; \Phi_{L^{\circ\circ}}$ and $\theta_{D(L)}, \; \Phi_{D(L)}$ have $2$-permutable congruences on $L^{\circ\circ}$ and $D(L)$, respectively. Firstly, suppose that $\theta\;, \Phi$ have $2$-permutable congruences on $L$. Let $(x, z)\in \theta_{L^{\circ\circ}}\circ {\Phi_{L^{\circ\circ}}}$. Then there exist $y\in {L^{\circ\circ}}$ such that $(x, y)\in \theta_{L^{\circ\circ}}$ and $(y, z)\in\Phi_{L^{\circ\circ}}$. Then we have $(x, y)\in\theta$ and $(y, z)\in \Phi$. Since $\theta, \Phi$ are $2$-permutable, then there exists $a\in L$ such that $(x, a)\in \Phi$ and $(a, y)\in\theta.$ We get $(x, a^{\circ\circ}) = (x^{\circ\circ}, a^{\circ\circ})\in \Phi_{L^{\circ\circ}}$ and $(a^{\circ\circ}, z^{\circ\circ})\in \theta_{L^{\circ\circ}}$. Therefore $\theta_{L^{\circ\circ}}, \; \Phi_{L^{\circ\circ}}$ are $2$-permutable. Also, to prove that $\theta_{D(L)}, \; \Phi_{D(L)}$ are $2$-permutable, let $(x, z) \in \theta_{D(L)}\circ {\Phi_{D(L)}}$. Then there exist $y\in D(L)$ such that $(x, y)\in \; \theta_{D(L)}$ and $(y, z)\in\Phi_{D(L)}$. Then we have $(x, y)\in\theta$ and $(y, z)\in \Phi$. Since $\theta, \Phi$ are $2$-permutable, there exists $a\in L$ such that

Thus $\theta_{D(L)}, \; \Phi_{D(L)}$ have $2$-permutable congruences on $D(L).$

Conversely, let $\theta\;, \Phi\; \in Con(L)$. Assume that $\theta_{L^{\circ\circ}}, \; \Phi_{L^{\circ\circ}}$ and $\theta_{D(L)}, \; \Phi_{D(L)},$ have $2$-permutable congruences on $L^{\circ\circ}$ and $D(L)$, respectively. Let $(x, z)\in\theta \circ \Phi$. Suppose that $x, \; y, \; z\in L$ with $(x, y)\in\theta$ and $(y, z)\in\Phi$. Then, by using Theorem 2.3, we get the following statements.

Since $\theta_{L^{\circ\circ}}, \; \Phi_{L^{\circ\circ}}$ have $2$-permutable congruences on $L^{\circ\circ}$, there exists an element $a\in L^{\circ\circ}$ such that

Since $\theta_{D(L)}, \Phi_{D(L)}$ have $2$-permutable congruences on $D(L)$, there exists $e\in D(L)$ such that $(x\vee d_{L}, e)\in \Phi_{D_{L}}$ and $(e, z\vee d_{L})\in \theta_{D_{L}})$. It follows that $(x^{\circ\circ}, a)\in \Phi, (a, z^{\circ\circ})\in\theta$ and $(x\vee d_{L}, e)\in \Phi, (e, z\vee d_{L})\in \theta$. Since $L$ is a principal $MS$-algebra we have

Since $\theta, \Phi$ are compatible with the $\wedge$ operation, then $(x^{\circ\circ}, a)\in \Phi$ and $(x\vee d_{L}, e)\in \Phi$ imply $(x, a\wedge e) = (x^{\circ\circ} \wedge (x\vee d_{L}), a\wedge e)\in \Phi$. Also $(a, z^{\circ\circ})\in\theta$ and $(e, z\vee d_{L})\in \theta$ imply $(a\wedge e, z) = (a\wedge e, z^{\circ\circ} \wedge (z\vee d_{L}))\in \theta$. Consequently, we deduce that $(x, a\wedge e)\in \Phi$ and $(a\wedge e, z)\in \theta\;, a\wedge e\in L$. Then $(x, z)\in \Phi\circ \theta$, and hence $\theta, \; \Phi$ are $2$-permutable. □

Now, we construct two examples to clarify the above theorem.

Example 4.1. Consider the principal $MS$-algebra $L$ in Example 2.1 (Figure 1). From Table 1, we show that $L$ has $2$-permutable congruences. Also, Tables 2 and 3 show that $L^{\circ\circ}\text{and}\; D(L)$ have $2$-permutable congruences, respectively. Where $\alpha_{L^{\circ\circ}} = \beta_{L^{\circ\circ}}$ and $\delta_{L^{\circ\circ}} = \triangle_{{L}^{\circ\circ}}$.

In the following example, we give a principal $MS$-algebra $L$ which has not $2$-permutable congruences as well as $D(L)$ has not also $2$-permutable congruences.

Example 4.2. Consider the principal $MS$-algebra $L$ in Figure 5.

It is clear that $D(L) = \{z, z_{1}, 1\}$ and $L^{\circ\circ} = \{0, c, a, b, d, 1\}$. Consider $\theta, \Phi\in Con(L)$ as follows:

We observe that $\theta\circ \Phi \neq \Phi\circ \theta$ as $(z, 1)\in \Phi\circ\theta$ but $(z,1)\notin \theta\circ \Phi$.

Then $L$ has not $2$-permutable congruences and $D(L)$ has not $2$-permutable congruences as $\theta_{D(L)}\circ \Phi_{D(L)}\neq \Phi_{D(L)}\circ \theta_{D(L)}$.

5.   $n$-permutability of principal $MS$-algebras

We generalize the concept of $2$-permutability to the concept of n-permutability of congruences of principal $MS$-algebras.

Definition 5.1. A principal $MS$-algebra $L$ is said to have n-permutable congrunces if every two congruences $\theta, \Phi$ of $L$ are n-permutable, that is,

At first, we need the following two lemmas.

Lemma 5.1. Let $L$ be a principal $MS$- algebra with the smallest dense element $d_{L}$. Let $\theta, \Phi$ be two congruences on $L.$ Then we have

(i) $(\theta \circ \Phi \circ \theta \circ...)_{L^{\circ\circ}} = \theta _{L^{\circ\circ}}\circ \Phi_{L^{\circ\circ}}\circ...$(n times),

(ii) $(\theta \circ \Phi \circ \theta \circ...)_{D(L)} = \theta _{D(L)}\circ \Phi_{D(L)}\circ...$(n times).

Proof.

(i) Recall that $\theta_{L^{\circ\circ}}, \Phi_{L^{\circ\circ}}$ are the restrictions of $\theta, \Phi$ on $L^{\circ\circ}$, respectively. Let $a, b \in L^{\circ\circ}$ and $(a, b)\in (\theta _{L^{\circ\circ}}\circ \Phi_{L^{\circ\circ}}\circ...).$ Then there exist $c_{1}, c_{2}, ..., c_{n-1}\in L^{\circ\circ}$ such that

Then

Then $(a, b)\in (\theta \circ \Phi \circ \theta \circ...)$ and hence $(a, b)\in (\theta \circ \Phi \circ \theta \circ...)_{L^{\circ\circ}}$. Therefore

Conversely, let $a, b\in L^{\circ\circ}$ such that $(a, b)\in (\theta \circ \Phi \circ \theta \circ...)_{L^{\circ\circ}}$. Then $(a, b)\in (\theta\circ \Phi\circ \theta\circ...$). Then there exist $c_{1}, c_{2}, ..., c_{n-1}\in L$ such that

Then we get

Since ${c_{1}}^{\circ\circ}, {c_{2}}^{\circ\circ}, ..., {c_{n-1}}^{\circ\circ}\in L^{\circ\circ}$, we have

Therefore

and hence

Then we get

(ii) Take $x, y\in D(L)$, let $(x, y)\in(\theta_{D(L)}\circ \Phi_{D(L)}\circ \Phi_{D(L)}\circ\theta_{D(L)}\circ...)$. Then $(x, y)\in(\theta\circ\Phi\circ\theta\circ...)$ and hence $(a, b)\in (\theta\circ\Phi\circ\theta\circ...)_{D(L)}$. Then $(\theta\circ\Phi\circ\theta\circ...)\subseteq (\theta\circ\Phi\circ\theta\circ...)_{D(L)}$.

Conversely, let $(x, y)\in (\theta \circ \Phi \circ \theta \circ...)_{D(L)}$, then $(x, y)\in (\theta\circ \Phi\circ...)$. There exist $d_{1}, d_{2}, ...d_{n-1}\in L$, such that

Since $x, y \geq d_{L}$, we get,

Hence $(x, y)\in(\theta _{D(L)}\circ \Phi_{D(L)}\circ \theta_{D(L)}\circ...)$. Then the required equality is proved. □

Lemma 5.2. Let $\theta$ and $\Phi$ be congruences on a principal $MS$-algebra $L$. Let $\psi$ denoted to the relation $\theta \circ \Phi \circ \theta \circ...$(n times). Then $(a, b)\in \psi$ and $(c, d)\in \psi$ imply $(a\wedge c, b\wedge d)\in \psi$.

Proof. Let $(a, b)\in \psi$ and $(c, d)\in \psi$. Then there exist $a_{1}, a_{2}, ..., a_{n-1}, c_{1}, c_{2}, ..., c_{n-1}\in L$ such that

And

Since $\theta, \Phi$ are congruence on $L$ then we get,

Thus $(a\wedge c, b\wedge d)\in \psi$. □

Now, a characterization of $n$-permutability of principal $MS$-algebras is given.

Theorem 5.1. Two congruences $\theta, \Phi$ on a principal $MS$-algebra $L$ are n-permutable if and only if their restrictions $\theta_{L^{\circ\circ}}, \Phi_{L^{\circ\circ}}$ and $\theta_{D(L)}, \Phi_{D(L)}$ with respect to $L^{\circ\circ}$ and $D(L)$ respectively are n-permutable.

Proof. Let $L$ has n-permutable congruences. Let $\theta, \Phi$ be any two congruences on $L$. Then by $(i)$ and $(ii)$ of Lemma 5.1, respectively, we have

and

Therefore $L^{\circ\circ}$ and $D(L)$ have n-permutable congruences.

Conversely, let $L^{\circ\circ}$ and $D(L)$ have n-permutable congruences. If $(a, b)\in (\theta\circ\Phi\circ\theta\circ...)$, using Theorem 2.3, we get

and

By lemma 5.1, we get

and

Since $\theta_{L^{\circ\circ}}, \Phi_{L^{\circ\circ}}$ and $\theta_{D(L)}, \Phi_{D(L)}$ are n-permutable on $L^{\circ\circ}, D(L),$ respectively, we have

and

It follows that, $(a^{\circ\circ}, b^{\circ\circ})\in(\Phi\circ\theta\circ\Phi\circ...)$ and $(a\vee d_{L}, b\vee d_{L})\in(\Phi\circ\theta\circ\Phi\circ...)$. Since $L$ is a principal $MS$-algebra, then $a = a^{\circ\circ}\wedge (a\vee d_{L})$ and $b = b^{\circ\circ}\wedge (b\vee d_{L})$. By Lemma 5.2, we get

Thus $(\theta\circ\Phi\circ\theta\circ...)\subseteq(\Phi\circ\theta\circ\Phi\circ...)$. Similarly we can show that $(\Phi\circ\theta\circ\Phi\circ...)\subseteq (\theta\circ\Phi\circ\theta\circ...)$. Then $L$ has n-permutable congruences. □

6.   Conclusions

With the aid of the technique of $MS$-congruence pairs, many properties were investigated for principal $MS$-algebras, deal with a characterization of congruence pairs of a principal $MS$-algebra (a Stone algebra), a description of the lattice $A(L)$ of all $MS$-congruence pairs of $L$ via Boolean elements of $L$, characterizations of $2$-permutability and $n$-permutability of congruences of a principal $MS$-algebra. This work leads us in the future to study many aspects of principal $MS$-algebras and related structures, for instance, it can be applied to triple construction of principal $MS$-algebra, affine and locally complete of principal $MS$-algebras.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare no conflict of interest.