1.
Introduction
The family of probability distributions based on the Weibull distribution has been extensively used in numerous research papers. The Weibull distribution (WD) is a continuous probability distribution that was first studied by Fréchet [1] to describe the distribution of particle volume. Recently, it was noticed that the inverse Weibull distribution (IWD) is a very important distribution used in reliability analysis, such as, the depreciation of mechanical components, e.g., pistons and engines, see Balakrishnan[2].
Assume X is a random variable that follows the inverse Weibull distribution with two parameters, then the cumulative distribution function (CDF) and the probability density function (pdf) for x≥0 defined as
and
respectively, where α and β are the scale and shape parameters.
Corderio and Lemonte [3] proposed the parameter estimates for the inverse Weibull distribution using the maximum likelihood and least squares methods.
When we decrease the original distribution's domain to a smaller one, we get truncated distributions, which are conditional distributions. When it is impossible to determine what is happening above or below the phenomenon being examined, truncation is used. So, by setting the appropriate truncated value to the upper whisker limit, we employ a technique to exceed the outliers in the data. Behdani et al. [4] acknowledged that the Pareto distribution is a well-known long-tailed distribution and proposed a truncated variant to circumvent its long tail. Zaninetti [5] proposed a right and left truncated gamma distribution that serves as the distribution's upper and lower boundaries. The distribution's properties and features were studied. El-Din et al. [6] derived the probability density function of the mid-truncated Lindley distribution as a particular case. The failure of the components and units that make up an operating system's main structure was researched by statisticians in the fields of industrial and mechanical engineering. They employed statistical inference techniques to collect the data for their study, which also included examining the lifetime of the operational units until failure and predicting the reliability and risk functions for the entire system using data. The number of experimental units and the length of the lifetime experiment of some units must be limited because they are expensive and extremely valuable. Due to the time and cost constraints of the experiment, it is frequently necessary to remove items before they fail. In such cases, it is not possible for an experimenter to collect all of the sample data in a short amount of time during a lifetime test. This brings us to the subject of censoring, where some operating units are eliminated from the experiment due to a particular censoring scheme, see Aggarwala and Balakrishnan [7]. The progressive type-Ⅱ technique supports the demands of observing good estimators with no lifetime experimental lack. As the examiner assigns independent and identical units on the test, the progressive type-Ⅱ scheme can be observed and summarized as follows: Assume that n independent items are placed through a test with X1,X2,…,Xn failure times that are continuous and identically distributed. Assume that a censoring scheme (R1,R2,…,Rm) is predetermined so that immediately after the first failure X1,R1 surviving items are removed from the experiment at random, and immediately after the second failure X2,R2 surviving items are removed from the experiment at random. When the mth observed failure occurs, the remaining Rm surviving items are removed from the test, or Xm. The order statistics of size m that have been gradually type Ⅱ right-censored from a sample of size n using a progressive censoring scheme (R1,R2,…,Rm) are the m ordered observed failure times represented by X(R1,R2,…,Rm)1:m:n,X(R1,R2,…,Rm)2:m:n,…,X(R1,R2,…,Rm)m:m:n. There is no doubt that n=m+R1+R2+…+Rm. The particular situation of traditional type Ⅱ right-censored sampling occurs when R1=R2=…=Rm−1=0 and R=n−m. The progressive censoring scheme has been studied by many researchers, such as [8].
Many studies, like Meeker et al. [9], Mann et al. [10], Lawless [11], and Buzaridah et al. [12] have explored progressive type-Ⅱ censoring with varied failure time breakdowns. Balakrishnan [2] investigated the characteristics of progressively censored samples and reported that a collection of several advances in the inferential procedures depend on types-Ⅰ and -Ⅱ censored samples. A generalization of the progressive type-Ⅱ censoring was obtained, and it has more realistic applications, for example, Montanari et al. [13], as well as by Bairamov and Eryilmaz [14]. Additionally, Mahmoud et al. [15] presented a lifetime parameter estimation for a new extension of the exponential distribution with a mechanical application. Ramadan et al. [16] introduced the Bayesian estimation of some distributions under progressive type-Ⅱ censoring. Haj Ahmad et al. [17,18] used different models under a progressive type-Ⅱ censoring scheme and modeled water reservoir capacity, and the strength of aircraft's windows respectively. Shrahili et al. [19] derived some recurrence relations for the moments. Luo et al. [20] introduce modeling and estimation of a reliability system with a dynamic functioning area and some lifetime constraints. More work was achieved by many authors, for example, Buzaridah et al. [21] among others. This study's objective is to compare the two methods of inference with a new right-truncated Fréchet-inverted Weibull (RTFIW) distribution based on the progressive type-Ⅱ censoring scheme with an application.
The basic objective of creating these models is to truncate the original distribution's domain to a smaller one. Additionally, based on complete data, the asymptotic confidence intervals for the maximum likelihood estimator (MLE) of the unknown parameters were examined. In addition, the Markov chain Monte Carlo (MCMC) technique was derived for the Bayesian estimator. The purpose of this study is to present both traditional and Bayesian estimating methods for the unknown parameters of the RTFIW distribution under the progressive type-Ⅱ censoring scheme, where Bayesian methods are based on two different types of loss functions. In addition, a simulation study is conducted to evaluate the accuracy of the results and the quality of the loss function choice.
The contents of this paper are organized as follows: The structural characteristics of the RTFIW distribution are introduced in Section 2. In Section 3, we introduce order statistics, extreme values, the quantile function, the moments, and the moment-generating function. In Section 4, asymptotic confidence intervals based on the MLE are computed along with the point estimation of the parameters, the hazard rate, and reliability functions. In Section 5, methods are detailed to estimate the unknown parameters using Bayes estimation under the square error and the linear exponential (LINEX) loss function estimators. A simulation study is undertaken in Section 6, to evaluate the effectiveness of the different estimation methods developed in this study. In Section 7, two real data are examined. Finally, concluding remarks are summarized in Section 8.
2.
Right truncated Fréchet-inverted Weibull distribution
The right truncated Fréchet-inverted Weibull (RTFIW) distribution has a CDF F(x) that can be obtained by
If the cumulative distribution function of a random variable X is given by Eq (2.1), it can be given as
where α and β are the scale and shape parameters respectively. The value of b is a constant that represents the truncated part.
The probability density function pdf for RTFIW is given by
The survival function S(x) and the hazard rate function h(t) for the RTFIW distribution are given by
and,
respectively.
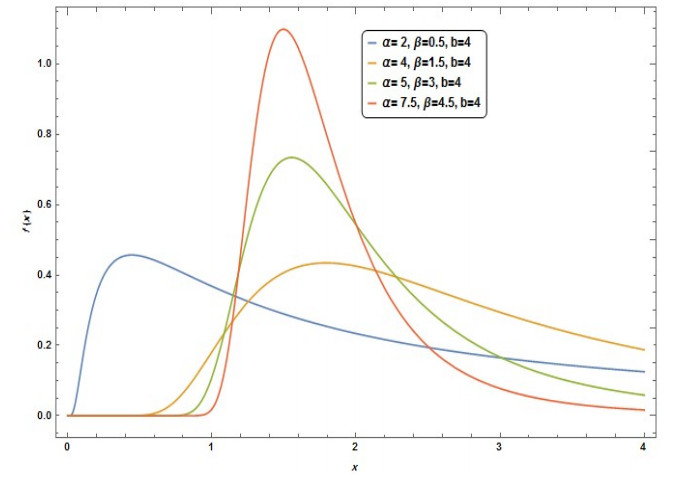
Figures 1–4 depict the RTFIW distribution's density function, the cumulative distribution function, hazard rate, and survival function for various parameter choices. Figure 1 shows the behavior of the pdf when changing the parameters α,β where b=4. Figure 2 shows how the CDF behaves, affected by the change in parameters α,β where b=4. The behavior of CDF is increasing depending on the values of the parameters. Figure 3 demonstrates the behavior of S(x) when the parameters α,β are changed, where b=4, and how it decreases based on the parameter values. Figure 4 depicts how changing the settings affects the behavior of h(x). The behavior of h(x) may exhibit unimodality. Depending on the values of the parameters, it is either increasing or decreasing.
3.
Statistical properties
Now, we will propose several statistical characteristics of the RTFIW distribution.
3.1. Median and the quantile function
The Quantile function has a variety of significant applications, including calculating the median, skewness, and kurtosis, as well as generating random variables, see Moors [22]. The quantile function of X is given by
where z∼uniform(0,1), it is simple to obtain random numbers using
By inputting z=0.5, the median of the RTEIW distribution from Eq (3.2) is defined as
3.2. Mode
By differentiating the probability density function of the RTEIW distribution at x>0 and making it equal to zero. The mode is defined as:
and
3.3. Moments
The moments of distributions are used to characterize several of the most essential model properties, such as dispersion, skewness, and kurtosis. As a result, the rth moment of the RTFIW distribution is given by
Let −αx−β=t, we get
where γ(r−β−1β−1,αb−β) is the lower incomplete gamma function. Then,
3.4. Moment generating function
The moment generating function (MGF) of the RTFIW distribution is the following:
As a result, using Taylor series to extend MX(t) produces
Hence the MGF of the RTFIWD is
3.5. Order statistics
The fields of reliability and testing provide several applications for order statistics. Numerous areas of statistical reasoning include the use of order statistics. Let X1, X2,....Xn represent a random sample of size n from the RTFIW with cumulative distribution function F(x) and probability density function f(x). Following that, order statistics are represented by the notations X (1)≤X(2)≤....X(n), X(1)=min(X1,X2,....Xn), and X(n)=max(X1,X2,....Xn). The pdf of the RTFIW's kth-order statistics is
The pdf of f(1:n)(x)-order statistics when k=1 is
The pdf of f(n:n)(x)-order statistics when k=n is
Distribution of maximum, minimum, and median
Assume that X1,X2,...,Xn are samples selected at random from a continuous distribution with PDF and CDF. Now we will compute the PDF for X(1), the smallest value of the sample. In order statistics, it is usually easier to begin by considering the CDF. Then, the pdf for the minimum value from distribution is given by
Then, the pdf for the maximum and median from the RTFIW distribution is given by
and
4.
Maximum-likelihood estimators
According to a progressive type-Ⅱ censored sample, see [23], with the RTFIW failures times X1:m:n,X2:m:n,....,Xm:m:n,1≤m≤n and the removal units are R1,R2,...,Rm, m<n, the likelihood function is expressed by
where C=n(n−R1−1)....(n−m−1∑i=1(Ri−1)), is a constant.
The likelihood function follows as
The log-likelihood function is obtained as
Notice that b is a constant. By computing the partial derivatives of ℓ with respect to α and β and equating each one to zero, we get,
and
The estimates for Eqs (4.4) and (4.5) without a closed-form solution are obtained using the Newton-Raphson iteration method. Additionally, by substituting α and β with ˆα and ˆβ as shown, the MLEs of S(t) and h(t) can be determined using the invariance property of MLEs. The entries of the Fisher information matrix Iij= E{−[∂2ℓ(Ψ)/∂ψi∂ψj]}, where i,j=1,2 and Ψ=(ψ1,ψ2)=(α,β), represent the asymptotic variances and covariances of the MLEs, ˆα and ˆβ. Consequently, it is challenging to find the precise closed forms for the aforementioned demands. The observed Fisher information matrix ˆIij= {−[∂2ℓ(Ψ)/∂ψi∂ψj]}Ψ=ˆΨ, which is produced by eliminating the expectation operator E, which will be used to generate confidence intervals (CIs) for the parameters. This is represented by
where
and
The observed information matrix ˆI(α,β) is inverted in order to derive the approximate asymptotic variance-covariance matrix [ˆV] for the MLEs, therefore, it is defined as
A multivariate normal distribution with a mean (α,β) and covariance matrix I−1(α,β) is believed to be similar to the Normal distribution under certain regularity conditions, see Lawless [11]. The two-sided 100(1−γ)% confidence interval of α and β and can be obtained by
and
where Zγ2 represents the right-tail probability γ2 of the standard normal distribution.
It is also important to determine their variances in order to calculate the asymptotic CI of S(t) and h(t), which are functions in the parameters α and β. The approximation of estimation of the variance of ˆS(t) and ˆh(t) are computed using the delta approach, see Greene [24]. The variance of ˆS(t) and ˆh(t) can be estimated using this method, respectively, by
where the gradient of ˆS(t)and ˆh(t) with respect to αand β are denoted by ∇ˆS(t)and ∇ˆh(t), respectively. Then, the (1−γ)100% two-sided confidence intervals of S(t) and h(t) can be provided by
5.
Bayes inference
The Bayesian estimation of the RTFIW distribution based on progressive type-Ⅱ censoring is obtained. According to Zellner et al., [25], the following gamma prior distributions are applied when α and β are independent parameters.
where, the hyper-parameters ai and bi, i=1,2 are non negative and known. Combining the likelihood function from Eq (4.3) and the priors from Eq (5.1) to get the posterior distribution of the parameters α and β, which is represented by π∗(α,β∣x)
The square error loss function (SEL) is a symmetry-identical loss function that is frequently used. It is defined as the squared difference between the actual parameter ϕ and an estimator ˆϕ.
As a result, under the SEL function the Bayes estimator of any function of α and β, say g(α,β), can be calculated as follows
Hence,
For a parameter ϕ, the LINEX loss function (L(△)) is denoted by
LINEX loss is used to discuss Bayesian estimation and prediction. As a result, under the LINEX loss function, the Bayes estimate of a function g(α,β) is
where
where the calculations in Eqs (5.5) and (5.8) cannot be evaluated analytically. Thus, in Eq (5.2), the Markov chain Monte Carlo MCMC technique is employed to produce samples from the joint posterior density function. The Metropolis-Hasting (M-H) and Gibbs sampling methods are two popular MCMC approaches in statistics. From Eq (5.2), the joint posterior distribution is
The posterior conditionals for α and β are
and
However, the conditional posteriors of α and β in Eqs (5.10) and (5.11) do not have standard forms. Consequently, it is difficult to sample directly by standard methods; however, the plots presented in Figures 5 and 6 display that they have curves that are symmetric and hence, similar to the normal distribution.
As a result, Gibbs sampling is not an obvious choice, meaning the Metropolis-Hastings sampler is necessary for the MCMC approach implementations. Within Gibbs sampling, the Metropolis-Hastings method is as follows:
(1) Begin by including an accurate assumption (α(0),β(0)).
(2) Let k=1.
(3) Create α(k) and β(k) by using the M-H technique from π∗1(α(k−1)∣β(k),x_) and π∗2(β(k−1)∣α(k),x_) with standard proposed distributions N(α(k−1),var(α)) and N(β(k−1),var(β)), where var(α) and var(β) are the variance of parameters α and β respectively.
(4) Create a proposed α∗ from N(α(k−1),var(α)) and β∗ from N(β(k−1),var(α)).
(i) Compute the possibilities of acceptance.
(ii) Produce a Z1 and Z2 from a uniform distribution.
(iii) If Z1<ωα, accept the suggestion and put α(k)=α∗, else put α(k)=α(k−1).
(iv) If Z2<ωβ, accept the suggestion and put β(k)=β∗, else put β(k)=β(k−1).
(5) Evaluate h(k)(t) and S(k)(t).
(6) k=k+1.
(7) We can get α(l),β(l),S(l)(t) and h(l)(t),l=1,2,...N by repeating steps 3 to 6, N times.
(8) The 100(1−γ)% CRIs of ψj are (ψj(Nγ/2),ψj(N(1−γ/2))), that computes the CRs of α, β, S(t) and h(t) ψ(l)j,j=1,2,3,4,(ψ1,ψ2,ψ3,ψ4)=(α,β,S(t),h(t)) as ψ(1)j<ψ(2)j...<ψ(N)j.
The chosen samples are ψ(i)j,k=M+1,...N, for sufficiently large N. The Bayesian estimations of ψj based on the SEL function are given by
The Bayesian estimations ofψk from Eq (5.8) under the LINEX loss function are
6.
Simulation study
For each simulation, 1000 progressive type-Ⅱ censored samples are used to evaluate parameter estimators, some lifetime parameters, and the RTFIW distribution's hazard and reliability functions. To create a sample size of progressive type-Ⅱ censored from the RTFIW distribution with initial values of α∘ = 0.5 and β∘ = 0.05. The mean square error (MSE) of the estimators of the results α,β,S(t) and h(t), at t=0.4, has been estimated based on a comparison of the various methods. The various approaches are used to estimate the 95% confidence intervals CIs derived from asymptotic distributions of the MLEs and CRIs. The coverage probability (CP) and the average confidence interval lengths (ACLs) are developed to assess the performance of estimation methods under study. The percentage of times the interval contains the interest-generating beginning value is known as a coverage probability (CP). In this study, the following progressive schemes are introduced:
● Scheme Ⅰ: R1=n−m,Rj=0for j≠1.
● Scheme Ⅱ: Rm2=Rm2+1=n−m2,Rj=0 for j≠m2 and j≠m2+1.
● Scheme Ⅲ: Rm=n−m,Rj=0for j≠m.
The results of the estimated parameters and their MSE are presented in Tables 1–4. Tables 5 and 6 present the results of the ACL and CP of the 95% CIs.
The following conclusions can be made based on the results:
(1) According to Tables 1–4, MSEs decrease as sample size increases, and Bayes estimates get the smallest MSEs for α, β,S(t)and h(t). As a result, in every case that has been studied, Bayes estimates outperform MLE approaches.
(2) With c=2, the Bayes estimator under LINEX provides superior results in terms of smaller MSEs.
(3) Scheme Ⅱ is better than schemes Ⅰ and Ⅲ in terms of decreased MSEs for a specified sample n and m effective size values.
(4) It is evident from Tables 5 and 6 that, for various sample sizes, observed failures, and schemes, CRIs provide more accurate results than ACIs.
7.
Application of real-life data
In the following subsections, two real data selected from the medical field are examined. The purpose of this study is to test the suitability of the proposed RTFIW distribution with these data sets.
7.1. Analgesic pain relief times
The first data set of failure numbers for 20 patients' analgesic relief times (in minutes) is used for the suggested estimation methods. This lifetime data set was introduced by Gross and Clark [26] and is associated with relief times (in minutes) of patients taking an analgesic. These data are provided in Table 7. By comparing the new model RTFIW with the modified Fréchet-exponential distribution (MFED) and exponentiated exponential (EE) under the data set where the value of b is the maximum value of the data. Table 8 shows the MLEs for the distributions. To assess the fitted models, the following measures were used: Bayesian information criterion (BIC), consistent Akaike information criterion (CAIC), Akaike information criterion (AIC), Hannan-Quinn information criterion (HQIC), Kolmogorov-Smirnov (K-S) and the negative log-likelihood (-Log), to seek out the model with the lowest information criterion and good fit parameters. The numerical results in Table 9 show that the RTFIW model fits the data better than other models. The considered data is fitted as shown in Figure 7.
The empirical failure data distribution's Kolmogorov-Smirnov (K-S) distance from the RTFIW distribution's CDF is 0.100217, with a P-value of 0.955062. As a result, the RTFIW distribution fits the provided data. From n=20 failure data, a progressive type-Ⅱ censored a sample of size m=10 with R=(6,4,0,0,0,0,0,0,0,0) based on the information that these generated. The MLE are computed to be ˆα,ˆβ,ˆS(t) and ˆh(t) such that t=0.4 depend on the progressive type-Ⅱ data reported in Table 7 are shown in Table 10. The Bayes estimator in relation to SEL and LINEX functions are calculated and are also shown in Table 10. From Table 11, the 95% ACIs and CRIs are computed for parameters. Additionally, the 95% ACIs and CRIs for S(t) and h(t) are derived using the delta approach, with the results displayed in Table 11.
Substituting the MLEs of the unknown parameters α and β for the data set into the inverse of the observed information matrix, we get an estimation of the variance-covariance matrix as follows:
I−1=(3.562041.097231.097230.607173).
The two sided 95% confidence interval ranges are [1.9207,13.7014] and [2.5453,4.92549], for the parameters α and β respectively.
7.2. Leukemia patients' recovery
The second data set given by Abouammoh et al. [27] represents 40 patients suffering from leukemia in one of the Ministry of Health Hospitals in Saudi Arabia. The survival times of those patients are recorded as follows:
We aim to compare the new model RTFIW distribution with exponentiated generalized inverse Weibull (EGIW) distribution and generalized inverse Weibull (GIW) distribution under the data set where the value of b is the maximum value of the data.
Table 12 shows the MLEs for the distributions. To assess the fitted models, the following measures were used: Bayesian information criterion (BIC), Consistent Akaike information criterion (CAIC), Akaike information criterion (AIC), Hannan-Quinn information criterion (HQIC), Kolmogorov-Smirnov (K-S) and the negative log-likelihood (-Log), to seek out the model with the lowest information criterion and good fit parameters. The numerical results in Table 13 show that the RTFIW model fits the data better than other models. The considered data is fitted as shown in Figure 8.
From n=40 failure data, a progressive type-Ⅱ censored a sample of size m= 20 with R=(10,5,5,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0) based on the information that these generated. The MLEs computed for ˆα,ˆβ,ˆS(t) and ˆh(t) such that t=0.4 and b=1815 based on the progressive type-Ⅱ data are shown in Table 14. The Bayes estimates of SEL and LINEX functions are calculated and are also shown in Table 14.
From Table 15, the 95% ACIs and CRIs are computed for parameters. Furthermore, the delta method is employed to derive the 95% ACIs and CRIs for S(t) and h(t), hence, the results are shown in Table 15.
8.
Conclusions
This study introduces a new truncated distribution called the RTFIW distribution. The new distribution's statistical properties are derived. Using progressive type-Ⅱ censoring, this study aims to provide a number of methods for generating confidence intervals for RTFIW distribution parameters and derivations. The time-relief periods of patients receiving analgesic treatment were studied in addition to Leukemia patient recovery numbers by using various estimation techniques proposed in this study. Different confidence intervals are provided when the MLEs of the unknown parameters are calculated. On the other hand, a simulation study was carried out to assess the accuracy of the suggested estimations. As a result, it is demonstrated that Bayesian approaches perform well in all cases. Due to the pattern of RTFIW's good fit to the applied data, Scheme Ⅱ also performs better than Schemes Ⅰ and Ⅲ in terms of smaller MSEs. In future works, estimation of the RTFIW distribution's parameters using adaptive progressive type-Ⅱ censored data can be obtained, and also can be compared with other types of censored algorithms.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia [GRANT No. 5023].
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad:










