Approximate numerical algorithms and artificial neural networks for analyzing a fractal-fractional mathematical model

1.   Introduction

In the past, humans knew of different types of deadly epidemics, among which we can mention influenza, malaria and cholera. In fact, the main reason for the spread of such diseases in the first stage was the insufficient development of medicine. At that time, the researchers noted that the acquired immunity may disappear after a certain period of time, depending on the nature of the epidemic, which puts community members at potential risk (see ^[1,2]), and it was also noted in some cases that patients who recovered from the disease can mix with other uninfected individuals, believing that they have acquired antibodies that prevent them from transmitting infection. This has led to the recording of many injuries and a large number of deaths as a result of these diseases. But, with the passage of time, humans became able to overcome them thanks to scientific development, especially in the medical field.

As we all know, a new virus called the coronavirus recently appeared, which has caused a wide range of infections, among which the symptoms are colds, fever, fatigue, etc. This epidemic has also led to a very large death toll. This caused the researchers to compete with time and try to make new medical discoveries that reduce the severity and danger of the virus. On February 12, 2020, the disease due to this virus was officially named COVID-19 by the World Health Organization. This epidemic also has a simple mechanism of disease spread, i.e., through the sneezing or coughing of the infected person, which result in transmission to people close to it, as droplets quickly enter their bodies through the nose and mouth; then, the virus in their lungs begins to damage their respiratory system.

Some studies have concluded that infected surfaces are also a means of transmission of the virus, which has different lifespans depending on the nature of these different surfaces. The World Health Organization has also provided many tips and instructions, especially regarding the methods of spreading this virus and how to prevent it.

With the great development of fractional calculus, many researchers have applied it in most of their new studies, especially with the recent emergence of viruses and infectious diseases; this has become an interesting topic for researchers. What follows is a set of articles that feature diverse mathematical models, covering a wide range of topics, such as the spread and control of diseases like COVID-19 ^[3,4], hepatitis C ^[5] and chaotic circuits ^[6], as well as models for the environmental persistence of infections ^[7], Langevin systems ^[8], computer viruses ^[9], thermostat control models ^[10,11], stochastic models ^[12], resource-consumer dynamics ^[13], Navier systems ^[14], quantum systems ^[15], etc.

It should be noted that there are still many studies that have been purposed to make predictions for this epidemic, and they involve the use of several mathematical models, such as differential equations with integer and fractional orders with various definitions (see ^{[16,17,18,19,20,21,22,23,24,25,26]} and the references cited therein).

The primary focus of this work is on developing a model that utilizes the fractal-fractional structure under the conditions of two fractional order and fractal dimensions. In epidemic models, the incidence rates, which reflect the rate of new infections per unit of time, play a critical role in determining the extent of disease spread. Therefore, we employ $\beta SI$ and its extension $\beta SI/(1+\alpha I)$ to account for this important factor.

The references discussed in this collection encompass a wide spectrum of mathematical models and epidemiological studies aimed at comprehending and effectively managing various infectious diseases. In ^[27], the authors introduce a nonlinear fractional mathematical model to address a smoke epidemic affecting multiple age groups; they employed the Atangana-Baleanu-Caputo fractional derivative. Another previous article ^[28] focuses on the transmission dynamics of $Q$ fever in livestock, with an emphasis on the role of ticks in disease spread and the proposal of management strategies. In ^[29], a fractional-order mathematical model is developed to evaluate the impact of lockdown measures on the spread of a virus; this was achieved by utilizing a system of nonlinear fractional-order differential equations. Addai et al. ^[30] investigated the transmission dynamics of the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) through the use of a Caputo-Fabrizio fractional-order epidemiological model; they explored its potential connection with Alzheimer's disease. In ^[31], the co-infection of Ebola virus and malaria in impoverished areas is the primary focus, particularly in regions burdened by high malaria prevalence and sporadic Ebola virus epidemics. Finally, Ngungu et al. ^[32] presented a mathematical model to examine the transmission of monkeypox virus under non-pharmaceutical interventions; their study included detailed exploration of key mathematical properties, like the positivity, invariance and boundedness of solutions, using real-time data. Together, these studies significantly contribute to our comprehension of infectious disease dynamics and provide valuable insights into strategies for their management and prevention.

In this work, we utilize fractal-fractional analysis to characterize the crowding effects of COVID-19 through the use of a mathematical model, which is taken as a classical SIR model described by the following system with a recruitment rate $\mu N$ for susceptible persons, along with the nonlinear incidence rate $\beta SI/(1 + \alpha I).$ The model being examined is separated into three distinct categories: The susceptible class is denoted as $S$, the infected class is denoted as $I$ and the recovered class is denoted as $R$:

The force of infection of the disease and the crowding effect are represented by $\beta I$ and $\frac{1}{1+\alpha I}$, respectively. Additionally, the parameters $\mu$, $\gamma$ and $\beta$ are used to denote the death rate, recovery rate and infection rate, respectively. The total constant population is expressed by $N$ such that

with

and

In view of the standard model (1.1), we will turn to the following fractal-fractional-order mathematical model for the spread of COVID-19

endowed with the initial conditions

The fractal-fractional derivative, denoted as ${}^{\mathcal{FFP}}\mathcal{D}_{0, t}^{\varrho, \nu}$, utilizes a power-law type kernel and is characterized by both a fractional order $\varrho \in (0, 1]$ and a fractal dimension $\nu \in (0, 1]$, which is recalled in the sequel. It is worth noting that the model (1.4) employs only non-negative parameters, and the state functions of the model are defined by

where $N(t)$ represents the total population at time $t\in \mathbb{O}: = [0, T]$ and $T > 0$.

After the development of some theorems on the existence and stability of solutions, two approaches, i.e., the (classic) Adams-Bashforth approach and (new) artificial neural network approach, have been proposed for the numerical approximation of the fractal-fractional SIR problem's solutions. We will analyze the numerical and graphical results obtained via each of these two methods. The main novelty of this paper is that we have tried to use a new tool to approximate the solutions of the given system. This method is based on the artificial neural network, which is applied in a fractal-fractional model for the first time. Our results proved that these findings are more accurate than the ones obtained via the standard Adams-Bashforth method. In general, we wanted to apply this method to a well-known mathematical model of diseases, i.e., COVID-19, since it still receives the attention of many researchers.

Artificial neural networks serve as a robust tool for approximating solutions to a variety of mathematical problems, including partial differential equations, differential equations, and ordinary differential equations. By leveraging insights from density results for the specific function spaces, we construct a function, as described by (4.1), within this research paper. Next, we will fine-tune the network's weights through an optimization process, optimizing its parameters to achieve a more precise fit for our problem. For more information, and to find new applications, we refer the reader to some newly published papers, namely, ^{[33,34,35,36,37,38,39]}.

The rest of the paper is divided into several sections. In the next section of the paper, we provide the problem's definition, along with a discussion on the existence and uniqueness of the solution and its stability. Following this section, we concentrate on the application of the classical Adams-Bashforth method to approximate the solutions of the problem (1.4). Section 4 was constructed to use the artificial neural network architecture to approximate the same solution of the fractal-fractional SIR problem (1.4) from a new perspective. To realize, we begin this section by giving a historical background that describes these artificial neural networks, along with the corresponding algorithms of the method. Next, we apply the method to the given SIR problem and establish a graphical illustration of the approximate solutions. Finally, this paper is concluded with a paragraph containing the main results with some perspectives.

2.   Mathematical study of the SIR problem

2.1.   Fractal-fractional operators and fixed-point theorems

To start our work, we first introduce some essential details about the fractal-fractional operators ^[40,41] and fixed-point theorems, which will be employed in the subsequent analysis.

Definition 2.1. ^[40,41] Assume that $\mathcal{Z}$ is a continuously differentiable function with the fractal dimension on an open interval $(a, b)$ with a fixed order $\nu$. Then, the fractal-fractional derivative of $\mathcal{Z}$ with order $\varrho$, via the power-law type kernel, can be defined by using the Riemann-Liouville structure as follows:

where the fractal derivative is

When $\nu = 1$, the fractal-fractional derivative denoted as ${}^{\mathcal{FFP}}\mathcal{D}_{a, t}^{\varrho, \nu}$ reduces to the standard fractional Riemann-Liouville derivative of order $\varrho$, which is denoted as ${}^{\mathcal{RL}}\mathcal{D}_{a, t}^{\varrho}$.

Definition 2.2. ^[40,41] If $\mathcal{Z}$ is a continuous function defined on $(a, b)$, the fractal-fractional integral of $\mathcal{Z}$ with the fractional order $\varrho$ and the fractal order $\nu$, via the power-law type kernel, is defined as follows:

Take $\varPsi$ as a subclass of the functions $\Bbbk: [0, \infty) \to [0, \infty)$ that are non-decreasing so that, for each $t > 0$,

Definition 2.3. ^[42] Assume that the normed space is denoted by $\mathcal{X}$, and that $\mathcal{Z}: \mathcal{X}\to \mathcal{X}$ is a self-map and $\sigma: \mathcal{X}^2 \to \mathbb{R}^{+}$. Then, we have the following:

(i) $\mathcal{Z}$ is $\sigma$-$\Bbbk$-contraction, if for $v_1, v_2\in \mathcal{X}$,

(ii) $\mathcal{Z}$ is $\sigma$-admissible if $\sigma (v_1, v_2) \geq 1$ yields $\sigma (\mathcal{Z}v_1, \mathcal{Z}v_2) \geq 1$.

Theorem 2.4. ^[42] Suppose that $(\mathcal{X}, d)$ is a metric space which is complete, $\sigma: \mathcal{X} \times \mathcal{X} \to \mathbb{R}$, $\Bbbk \in \varPsi$ and $\mathcal{Z}:\mathcal{X} \to \mathcal{X}$ is a $\sigma$-$\Bbbk$-contraction. Let the following be true:

(i) $\mathcal{Z}$ is $\sigma$-admissible on $\mathcal{X}$;

(ii) $\sigma(v_0, \mathcal{Z}v_0) \geq 1$ for some $v_0 \in \mathcal{X}$;

(iii) If $\{v_n\} \subseteq \mathcal{X}$ is an arbitrary sequence with $v_n \to v$ and $\sigma(v_n, v_{n+1}) \geq 1, \, \forall\, n \geq 1$, then $\sigma(v_n, v) \geq1, \, \forall\, n \geq1$.

Then, there is a fixed point for $\mathcal{Z}$.

Theorem 2.5. ^[43] Given a Banach space $\mathcal{X}$, a bounded convex closed subset $\mathbb{E}$ of $\mathcal{X}$ and an open set $\mathbb{O}$ containing $0$ and that is also contained in $\mathbb{E}$, if $\mathcal{G}:\bar{\mathbb{O}}\to\mathbb{E}$ is a continuous and compact mapping, then either

(i) $\mathcal{G}$ admits a fixed point belonging to $\bar{\mathbb{O}}$, or

(ii) $\exists v \in \partial \mathbb{O}$ and $\mu \in (0, 1)$ so that $v = \mu \mathcal{G} (v)$.

2.2.   Reformulation of the model using integral equations

For the study of a biological model, one tends to question whether such a dynamic problem really exists. To answer this question, we use the theory of the fixed point. So, here, we apply this theory to our fractal-fractional problem (1.4). For a qualitative study, we consider the Banach space $(\mathcal{X}, \Vert.\Vert_{\mathcal{X}})$ such that $\mathcal{X} = \mathbb{K} \times \mathbb{K} \times \mathbb{K},$ with $\mathbb{K} = C(\mathbb{O}, \mathbb{R})$ and

Now, we write the other sides of the equations in the system (1.4) as follows:

Thanks to the differentiability of the integral, we can reformulate the given problem (1.4) as follows:

By exploiting (2.3) and for each $t\in \mathbb{O}$, the initial value problem given by

can be written instead of the extended main system (1.4) so that

and

Now, by applying the fractal-fractional integral defined by (2.1) to both side of the differential equation (2.4), it becomes

Consequently, the non-compact form of the integral equation (2.7) is given by

For the continuation of our study, we define the operator $\mathcal{G}: \mathcal{X} \to \mathcal{X}$ by

2.3.   Existence of solutions

Now, based on the information reported in the previous sections, we can begin to state the first existence result.

Theorem 2.6. Let there be a continuous function $\Xi:\mathbb{R}^2\to \mathbb{R}$, a non-decreasing function $\Bbbk\in \varPsi$ and a continuous function $\mathcal{Z}: \mathbb{O} \times \mathcal{X}\to \mathcal{X}$ satisfying the following three hypotheses:

$(\mathfrak{Cond}_1)$ For each $\phi_1, \phi_2 \in \mathcal{X}$ and $t\in \mathbb{O}$,

such that $\delta = \frac{\Gamma(\nu+\varrho)}{\nu T^{\nu+\varrho-1}\Gamma(\nu)}$ and $\Xi\big(\phi_1(t), \phi_2(t)\big)\geq0.$

$(\mathfrak{Cond}_2)$ There exists $\phi_0 \in \mathcal{X}$ that satisfies the following for any $t\in \mathbb{O}:$

also, for any $\phi_1, \phi_2 \in \mathcal{X}$ and $t\in \mathbb{O}$, we have

$(\mathfrak{Cond}_3)$ For each sequence $\{\phi_n\}_{n\geq1}$ in $\mathcal{X}$ which converges to $\phi$ and

$\forall\, t\in \mathbb{O},$ the inequality

holds.

Then, the given fractal-fractional model (1.4) admits at least one solution.

Proof. Let $\phi_1$, $\phi_2\in \mathcal{X}$, where $\Xi\big(\phi_1(t), \phi_2(t)\big)\geq0$ for any $t\in \mathbb{O}.$ Then, as a result of exploiting the definition of the beta function, the following estimates hold:

Hence,

Now, for any $\phi_1, \phi_2 \in \mathcal{X},$ we consider the function $\sigma:\mathcal{X}\times\mathcal{X}\to [0, +\infty)$, defined as follows:

Then, for any $\phi_1, \phi_2 \in \mathcal{X},$ we will get

Consequently, $\mathcal{G}$ is a $\sigma$-$\Bbbk$-contraction. To show that $\mathcal{G}$ is $\sigma$-admissible, let $\phi_1, \phi_2\in \mathcal{X}$ be arbitrary with $\sigma(\phi_1, \phi_2)\geq1.$ In view of the definition of the function $\sigma,$ we can write

Therefore, from the hypothesis $(\mathfrak{Cond}_2),$ we have

Again, by definition of the function $\sigma$, we deduce that $\sigma\big(\mathcal{G}\big(\phi_1\big), \mathcal{G}\big(\phi_2\big)\big)\geq1.$ This means that $\mathcal{G}$ is $\sigma$-admissible.

In addition, $(\mathfrak{Cond}_2)$ guarantees that there is a $\phi_0 \in \mathcal{X}$ that satisfies that $\Xi\big(\phi_0(t), \mathcal{G}\big(\phi_0(t)\big)\big)\geq0, \, \forall\, t\in \mathbb{O}$. Obviously, $\sigma\big(\phi_0, \mathcal{G}\big(\phi_0\big)\big)\geq1$.

Now, assume that $\{\phi_n\}_{n\geq1} \subseteq \mathcal{X}$ converges to $\phi$ and satisfies, for all $n\geq1,$ $\sigma\big(\phi_n, \phi_{n+1}\big)\geq1.$ From the definition of the function $\sigma$, we get

So, the hypothesis $(\mathfrak{Cond}_3)$ leads to

This implies that $\sigma\big(\phi_n, \phi\big)\geq1$ for any $n\geq1.$ As a result, Theorem 2.4 satisfies condition $(iii)$. Consequently, Theorem 2.4 holds under the given assumptions. Therefore, $\mathcal{G}$ has a fixed point $\phi^* \in \mathcal{X}$ that gives the result that $\phi^* = \big(S^*, I^*, R^*\big)^T$ is a solution of the model (1.4); and this ends the proof. □

Now, we apply the Leray-Schauder nonlinear alternative to demonstrate that, under some assumptions, there is a solution of the considered fractal-fractional model of (1.4) for $\mathbb{O}.$

Theorem 2.7. Let $\mathcal{Z}\in C(\mathbb{O}\times\mathcal{X}, \mathcal{X})$ and

$(\mathcal{HY}_1)$ there exist $\varphi\in L^1(\mathbb{O}, [0, +\infty))$ and an increasing map $\mathbb{B}\in C([0, +\infty), (0, +\infty))$ with

$(\mathcal{HY}_2)$ $\exists\, \alpha > 0$ such that

with $\varphi_{0}^{*} = \sup_{t\in \mathbb{O}}|\varphi(t)|.$

Then the fractal-fractional problem (2.4) has a solution. Consequently, the given fractal-fractional model of (1.4) possesses a solution on $\mathbb{O}.$

Proof. To initiate the proof, it is necessary to introduce the operator $\mathcal{G}$, as defined in (2.9), and the closed ball.

First, the continuity of $\mathcal{Z}$ comes from that of $\mathcal{G}.$ Now, from the condition $(\mathcal{HY}_1)$, we have the following, for $\phi\in \Gamma_{\varepsilon}$:

Therefore, we obtain

Therefore, the operator $\mathcal{G}$ is bounded in the uniform sense on $\mathcal{X}.$ To prove the equicontinuity of $\mathcal{G},$ we select two points $t, \tau\in [0, T]$ such that $t < \tau$, and we take an arbitrary $\phi\in \Gamma_{\varepsilon}.$ By considering

we have

As $\tau$ approaches $t$, the expression on the right-hand side of (2.12) tends to $0$ regardless of the choice of $\phi$, i.e.,

as $\tau\to t.$ This guarantees that $\mathcal{G}$ is equicontinuous. After applying the Arzelà-Ascoli theorem, it is confirmed that $\mathcal{G}$ is compact on $\Gamma_{\varepsilon}.$ Therefore, all assumptions of Theorem 2.5 are met for $\mathcal{G},$ implying that either $(i)$ or $(ii)$ is held. Additionally, we are aware that there is some $\alpha > 0$ because of $(\mathcal{HY}_2)$, with

Next, we define

We will now suppose that there exist $\phi\in \partial\mathbb{U}$ and $\mu\in (0, 1)$ subject to $\phi = \mu \mathcal{G}(\phi).$ For such a selection of $\phi$ and $\mu,$ one can prove, by (2.13), that

and this is not possible. As a result, we have shown that the consequence $(ii)$ is impossible, and that, by Theorem 2.5, there exists a fixed point of $\mathcal{G}$ in $\overline{\mathbb{U}}$, which corresponds to a solution of the fractal-fractional model (1.4). Thus, this ends the proof. □

2.4.   Uniqueness result

To show the uniqueness property in relation to the solution of the fractal-fractional model (1.4), we utilize the fact that the functions $\mathcal{Z}_{i} (i = 1, 2, 3)$, defined in (2.2), satisfy the Lipschitz condition.

Lemma 2.8. Suppose that $S, I, R, S^{*}, I^{*}, R^{*}\in \varPi = C(\mathbb{O}, \mathbb{R})$, and assume the following:

$(\mathcal{PR}_1)$ $\|S\|\leq \gamma_1, \|I\|\leq \gamma_2$ and $\|R\|\leq \gamma_3$ for some constants $\gamma_1, \gamma_2, \gamma_3 > 0.$

Then, $\mathcal{Z}_{1}, \mathcal{Z}_{2}, \mathcal{Z}_{3}$ given by (2.2) satisfy the Lipschitz condition if

Proof. We start with $\mathcal{Z}_1$. For any $S, S^{*}\in \varPi = C(\mathbb{O}, \mathbb{R})$, we get

Hence, $\mathcal{Z}_1$ is Lipschitz with respect to the function $S$ with the constant $\ell_1.$ Regarding the function $\mathcal{Z}_2$, for each $I, I^{*}\in\varPi = C(\mathbb{O}, \mathbb{R}),$

This implies that $\mathcal{Z}_2$ is Lipschitz with respect to $I$ with the constant $\ell_2.$ For every $R, R^{*}\in\varPi = C(\mathbb{O}, \mathbb{R}),$ we have

Then, $\mathcal{Z}_3$ is Lipschitz with respect to the function $R$ with the constant $\ell_3$. The above results confirm that the three functions $\mathcal{Z}_1, \mathcal{Z}_2, \mathcal{Z}_3$ satisfy the Lipscitz condition with the constants $\ell_1, \ell_2, \ell_3$, respectively. □

Here, we utilize the results obtained in Lemma 2.8 to establish a criterion for the uniqueness of solutions to the given fractal-fractional system (1.4).

Theorem 2.9. If the condition $(\mathcal{PR}_1)$ is satisfied, then (1.4) has a unique solution if

Proof. Let us suppose that the conclusion is not true; that is, there is another solution to the fractal-fractional system (1.4). Let $\big(S^{*}, I^{*}, R^{*} \big)$ be a solution with the initial condition $\big(S_0, I_0, R_0 \big)$ such that, by (2.8), we have

and

We are now able to provide the following estimation:

This gives

Consequently, by using (2.15), we can deduce that $\big\Vert S -S^{*}\big\Vert = 0,$ which implies that $S = S^{*}.$ Similarly, we get

This leads to the conclusion that $\big\Vert I -I^{*}\big\Vert$ equals zero; hence, $I = I^{*}.$ Using analogous reasoning, we arrive at

Therefore, $\big\|R -R^{*}\big\| = 0$ and, consequently, $R = R^{*}.$ Then,

Therefore, we have established the uniqueness of the solution to the fractal-fractional model (1.4); thus, the proof is concluded. □

2.5.   Stability results

The focus of this section is to investigate various types of stability, including the Ulam-Hyers, generalized Ulam-Hyers, Ulam-Hyers-Rassias and generalized Ulam-Hyers-Rassias stability, for solutions of the fractal-fractional model (1.4).

Definition 2.10. ^[53,54] If there is $M_{\mathcal{Z}_{i}} > 0,$ $i\in{1, 2, 3}$ such that, for all $\epsilon_i > 0$ and each $\big(S^{*}, I^{*}, R^{*}\big)\in \mathcal{X}$ satisfying the following conditions:

there is $\big(S, I, R\big)\in \mathcal{X}$ as a solution for (1.4) with

then, the fractal-fractional system (1.4), is Ulam-Hyers-stable.

Definition 2.11. ^[53,54] The fractal-fractional model (1.4) is said to have generalized Ulam-Hyers stability if there exist continuous functions $M_{\mathcal{Z}{i}}:\mathbb{R}^{+}\rightarrow \mathbb{R}^{+}$ $(i\in{1, 2, 3})$ with $M_{\mathcal{Z}{i}}(0) = 0$ such that, for all $\epsilon_{i} > 0$ and each $\big(S^{*}, I^{*}, R^{*}\big)\in \mathcal{X}$ satisfying (2.16), $\exists\, \big(S, I, R\big)\in \mathcal{X}$ as a solution of (1.4), with

Remark 2.12. The triplet $\big(S^{}, I^{}, R^{}\big)\in \mathcal{X}$ is a solution of (2.10) if and only if $\exists\, \zeta_1, \zeta_2, \zeta_3 \in C(\mathbb{O}, \mathbb{R})$, dependent on $S^{*}, I^{*}, R^{*}$, respectively such that for all $t\in \mathbb{O},$ we have the following:

$(i)$ $\big|\zeta_{i}(t)\big| < \epsilon_{i}$ $(i\in\{1, 2, 3\}),$

$(ii)$

Definition 2.13. ^[53,54] The fractal-fractional system of the COVID-1 model (1.4) is said to be Ulam-Hyers-Rassias-stable with respect to $\Phi_{i}$ $(i\in\{1, 2, 3\})$ if there exist positive real constants $M_{(\mathcal{Z}_{i}, \Phi_{i})}$ so that, for all $\epsilon_{i} > 0$ and all $\big(S^{*}, I^{*}, R^{*} \big)\in \mathcal{X}$ satisfying the following:

there is $\big(S, I, R \big)\in \mathcal{X}$ as a solution of (1.4), with

Definition 2.14. ^[53,54] The fractal-fractional system of COVID-19 model (1.4) is generalized Ulam-Hyers-Rassias-stable with respect to $\Phi_{i}$ $(i\in\{1, 2, 3\})$ if there exist positive real constants $M_{(\mathcal{Z}_{i}, \Phi_{i})}$ so that, for all $\big(S^{*}, I^{*}, R^{*} \big)\in \mathcal{X}$ satisfying the following:

there is $\big(S, I, R\big)\in \mathcal{X}$ as a solution of (1.4), with

Note that, if we take $\Phi_{i}(t) = 1,$ then Definition 2.13 gives the Ulam-Hyers property for the stability of solutions.

Remark 2.15. It should be noticed that $\big(S^{*}, I^{*}, R^{*} \big)\in \mathcal{X}$ is a solution for (2.11) if and only if there exist $\zeta_1, \zeta_2, \zeta_3 \in C(\mathbb{O}, \mathbb{R})$ (depending respectively on $S^{*}, I^{*}, R^{*}$) such that, for all $t\in \mathbb{O},$ $(i)$ $\big|\zeta_{i}(t)\big| < \epsilon_{i}\Phi_{i}(t)$, $(i\in\{1, 2, 3\})$, and $(ii)$ we have the following:

Here, we examine the Ulam-Hyers stability of the fractal-fractional model described by (1.4).

Theorem 2.16. Suppose that the condition $(\mathcal{PR}_1)$ holds. Then, the fractal-fractional system (1.4) is stable under the Ulam-Hyers criterion on the interval $\mathbb{O} = [0, T]$; thus, it can be considered as generalized Ulam-Hyers-stable if

where $\ell_{i}$ is defined by (2.14).

Proof. Let $\epsilon_{1} > 0$ and $S^{*}\in\varPi$ such that

Then, in view of Remark 2.12, we can find a function $\zeta_{1}(t)$ satisfying

with $|\zeta_{1}(t)|\leq\epsilon_{1}.$ This gives

From Theorem 2.9, consider the unique solution $S\in \varPi$ to the given fractal-fractional system (1.4). Then,

Then,

Therefore,

By setting $M_{\mathcal{Z}_{1}} = \frac{\nu T^{\nu+\varrho-1}\Gamma(\nu)}{\Gamma(\nu+\varrho)-\nu T^{\nu+\varrho-1}\Gamma(\nu)\ell_1}$, it follows that $\big\|S^{*} -S\big\|\leq M_{\mathcal{Z}_{1}}\epsilon_1.$ Similarly, we can obtain

where

Therefore, it follows that the considered fractal-fractional system of COVID-19 model (1.4) is Ulam-Hyers-stable. Next, by putting

with $M_{\mathcal{Z}_{i}}(0) = 0$, our given model satisfies the conditions for the definition of generalized Ulam-Hyers stability. □

The Ulam-Hyers-Rassias stability for the given fractal-fractional system (1.4) will be proved.

Theorem 2.17. Assume that the condition $(\mathcal{PR}_1)$ is satisfied, and that the following is true:

$(\mathcal{PR}_2)$ There is a family of increasing functions $\Phi_{i}\in C(\mathbb{O}, \mathbb{R})$ with corresponding constants $\Omega_{\Phi_i} > 0$ $(i\in {1, 2, 3})$ such that $\forall\, t\in \mathbb{O},$

The Ulam-Hyers-Rassias stability of the fractal-fractional system (1.4) holds, which, in turn, implies the generalized Ulam-Hyers-Rassias stability.

Proof. For any $\epsilon_1 > 0$ and $\forall S^{*} \in\varPi$ such that

we can obtain a function $\zeta_{1}(t)$ satisfying

with $\big|\zeta_{1}(t)\big| < \epsilon_{1}\Phi_{1}(t)$. This gives

By exploiting Theorem 2.9, assume that $S\in \varPi$ is the unique solution of the considered fractal-fractional model (1.4). Then,

Then, from (2.18), we get

Consequently, this gives

If we let

then we find that

Similarly, we have

and

where

Thus, the given fractal-fractional system (1.4) is Ulam-Hyers-Rassias-stable. Additionally, it can be observed that, when $\epsilon_{i} = 1$ for $i\in {1, 2, 3}$, the given fractal-fractional system of the COVID-19 model (1.4) satisfies the conditions for the definition of the generalized Ulam-Hyers-Rassias stability. □

3.   Approximation of solutions: Adams-Bashforth method

In this part, we numerically describe the dynamics of the system (1.4). We apply the Adams-Bashforth fractional method, which involves using the two-step Lagrange polynomial technique, to obtain the approximate solutions. To initiate this procedure, we introduce a method for computing the fractal-fractional integral equations of (2.8) by utilizing a different approach for $t_{n+1}$; specifically, we discretized (2.8) with respect to $t = t_ {n+1}$; so, we have the following:

where

By approximating the above integrals, we get the following:

In what follows, we approximate the functions $\lambda_{1}(\vartheta), \lambda_{2}(\vartheta), \lambda_{3}(\vartheta),$ as defined by (3.1) on the interval $[t_{l}, t_{l+1}]$ through the use of the two-step Lagrange interpolation polynomials, by considering the step size ${\bf{h}} = t_{l+1}-t_{l}$, as follows:

Then, we have the following:

By calculating the above integrals, we find the approximate solutions in relation to the fractal-fractional system of the COVID-19 model (1.4) as follows:

thus,

4.   Approximation of solutions: Artificial neural networks

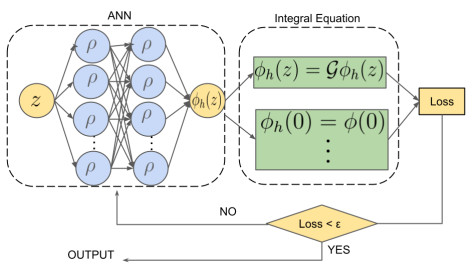
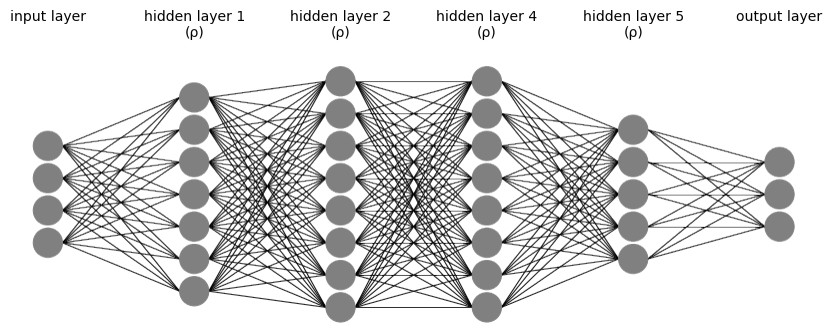
The first experiment in modeling a biological neuron was carried out by McCulloch and Pitts ^[44] in 1943 by using a step function and signal refinement. In 1958, Rosenblatt ^[45] utilized a simple multilayer perceptron to model a network of neurons. The components of this construction are the hidden, input and and output layers, which are specified in Figure 1. Using this structure, such a function can be formed as follows:

so that the following yields $\mathfrak{z}_L$:

where $\mathcal{F}_\ell(\mathfrak{z}) = A_\ell \mathfrak{z} + b_\ell$; $(A_\ell)_{\ell = 1}^L \in \mathbb{R}^{N_\ell\times N_{\ell -1}}$ and $\mathfrak{z}_\ell, b_\ell\in \mathbb{R}^{N_\ell}$ for $N_\ell\in\mathbb{N}, N_0 = p, N_L = q$ and $\ell = 1, \dots, L$; also, $\rho: \mathbb{R}\rightarrow \mathbb{R}$ is an activation function that acts componentwise, i.e.,

$A_\ell$ and $b_\ell$ are named the weights and biases, respectively. The construction of such a neural network is determined by $N_0, \dots, N_L$, along with the activation function $\rho$. All of these functions are represented by the symbol $\mathcal{NN}$.

The density property of these functions in the space of continuous functions is useful in the approximation. The universal approximation theorems of $\mathcal{NN}$ demonstrate that neural networks can represent a wide range of fascinating functions with suitable weights and biases, although they usually do not offer a method for constructing these weights and only assert that such a method exists. Different outcomes of this type of work have been presented. In 1989 ^[46], Cybenko applied the first theorem of density to sigmoid activation functions. Hornik ^[47], in 1991, confirmed that it is not a specific choice of activation function, but, rather, it is the multi-layered forward-propagation architecture itself that gives neural networks the potential to be universal approximators. Leshno et al. ^[48], in 1993, and, later, Pinkus ^[49], in 1999, proved that the universal approximation property is equivalent to using a non-polynomial activation function. It should be noted that the papers mentioned above only considered a single internal layer, which was found to be satisfactory.

Additionally, in the hidden layers, there were no restrictions placed on the number of neurons. Subsequently, several findings have emerged on the appropriate number of neurons in a hidden layer in order to demonstrate the density in numerous function spaces. We refer the readers to ^[50] for more information. Furthermore, there exist several generalizations for other scenarios, such as discontinuous activation functions ^[48], certified networks, non-compact domains ^[51] and other topologies and architectures ^[52]. In this paper, and by applying our conditions, we utilize a new density theorem.

First, define the class of functions $\mathcal{NN}_{p, q, k}^\rho$ as the set of feedforward neural networks that maps $\mathbb{R}^p$ to $\mathbb{R}^q$, with an unspecified number of hidden layers, $k$ neurons in each hidden layer, $p$ neurons in the input layer and $q$ neurons in the output layer, all of which utilize the activation function $\rho$. Furthermore, all neurons in the output layer possess an identity activation function.

Theorem 4.1. ^[51] Let $\rho: \mathbb{R}\rightarrow \mathbb{R}$ be a non-affine continuous mapping and continuously differentiable at a minimum of one point; let it also have a derivative that is not equal to zero at that specific point. Also, assume that $K \subset \mathbb{R}^p$ is compact. Then, $\mathcal{NN}_{p, q, p+q+2}^\rho$ is dense in $\mathcal{C}(K; \mathbb{R}^q)$ under the supremum norm.

The final theorem can be categorized as a form of the universal approximation theorem. By applying the density property to the solution $\phi$ of the operator equation $\mathcal{G}\phi(\mathfrak{z}) = \phi(\mathfrak{z})$, where $\mathcal{G}$ is defined by (2.9), it holds that, for each $\varepsilon > 0$, there exists a function $\phi_h \in \mathcal{NN}_{1, 3, 6}^\rho$ satisfying

so that $h$ depends on the weights and biases.

The proposed algorithm:

● Choose $\varepsilon > 0$. Choose $\phi_h$ in $\mathcal{NN}_{1, 3, 6}^\rho$ with $\rho(\mathfrak{z}) = \dfrac{1}{1+ e^{- \mathfrak{z}}}$.

● Calculate $\mathcal{G}\phi_h$.

● Evaluate $e = \|\mathcal{G}\phi_h - \phi_h\|_{2}$.

● If $e \leq \varepsilon$, stop.

● If not, then the back propagation process can be used to adjust the weights and biases of the function $\phi_h$; see Figure 2.

5.   Numerical simulation

This part, using the obtained numerical solutions and introduced algorithms via the artificial neural network method, presents simulations and discussions about the dynamics of our mathematical model based on different values of the parameters $\mu = 0.15$, $\beta = 0.55$, $\alpha = 0.45$, $\gamma = 0.25$ and $T = 50$, along with the initial values for the state functions:

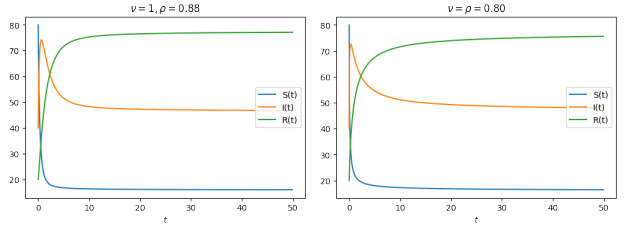
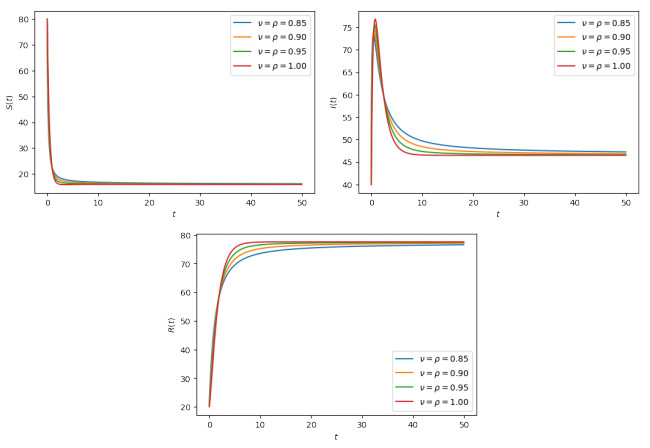
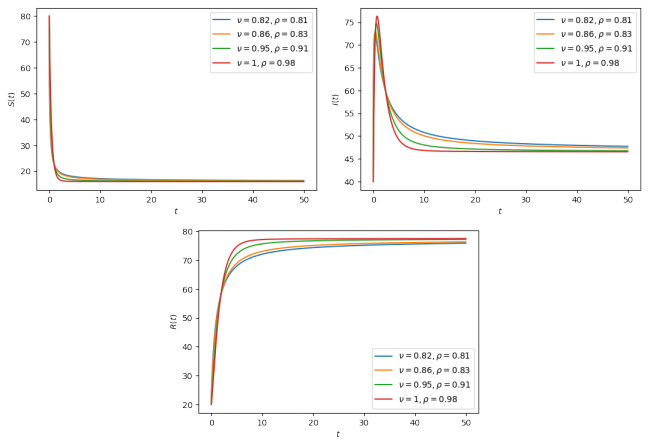
In view of the above data, we plotted various graphs to visualize the dynamics of the three functions $S, I, R$ by considering equal and different values of the fractional and fractal order and dimension; see Figures 1.3–5.

The simulations allowed us to make accurate predictions concerning the spread of COVID-19 and its effects on susceptible and infected groups over a short period of time. Figure 1.3 shows the effects of the fractal dimensions and fractional orders for taking equal and different values; we note that the fractional order controls the dynamics of the disease. Specifically, it decreases, reaching the peak of the epidemic, and reduces the number of infected people. In Figures 4 and 5, we respectively applied equal and different values of the fractal dimensions and fractional orders and illustrate their influence on the spread of the disease. In fact, it is obvious that they reduce the epidemic peak outbreak and the final number of infected people.

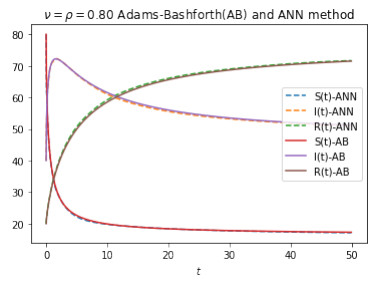
Also, Figure 6 illustrates the graphs of functions $S, I, R$ via Adams-Bashforth method and artificial neural network method for $\varrho = \nu = 0.80$. The solutions plotted via the artificial neural network method are illustrated as dashed lines in Figure 6. These lines overlap closely in both techniques. In view of these graphs, we see that the artificial neural network method gives results that are close to the classical Adam-Bashforth algorithm. Therefore, we can rely on its outcomes in terms of the analysis of many fractal-fractional systems. Note that, because of the lack of data, our new method is validated by using those data that are generated via the appropriate Gauss quadrature method.

Moreover, note that, the execution time of the Python program implementing the Adams-Bashforth method totaled approximately 5 minutes and 46 seconds. This computation was conducted on a machine with the following specifications:

$*$ Processor: Intel$^{\text{(R)}}$ Core$^{\text{(TM)}}$ i5-4440 CPU @ 3.10GHz (3.10 GHz)

$*$ Installed RAM: 4.00 GB

$*$ System type: 64-bit operating system, x64-based processor.

In contrast, when we employed the artificial neural networks, the computational process was notably faster, taking only about 3 minutes and 7 seconds. The inherent intelligence of the artificial neural networks allowed us to harness advanced programming tools and libraries that are readily available within the deep learning domain, including platforms like Colab.

6.   Concluding remarks

In this work, a fractional-order mathematical model for COVID-19 was presented in the context of a three-compartment model. To establish the definition of the initial value problems in the considered system, we have exploited the fractal-fractional operators in the form of a power law-type kernel. In the study of this type of problem, we have generalized some existence and uniqueness results by applying some conditions for special contractions. We were interested in the study of certain types of stability: Ulam-Hyers, generalized Ulam-Hyers, Ulam-Hyers-Rassias and its generalized version, where we showed that our fractal-fractional system is stable with respect to given hypotheses. Regarding the Adams-Bashforth method, we used Lagrange polynomials and numerical solutions derived from numerical algorithms to approximate some of the given fractal-fractional integrals. In the end, we simulated the solutions by choosing various values for the fractional order and fractal dimension to observe their stability and convergence.

The introduction of the use of artificial neural network techniques for infectious disease models is another important contribution of the paper. The technique and algorithm are described and have been applied to the SIR model. Given a set of parameters, the artificial neural network method found the approximate solutions and successfully solved the SIR problem numerically. Both numerical methods, i.e., the Adams-Bashforth and artificial neural network, yielded the same simulated numerical solutions, as shown in Figure 6.

The presented SIR model can be upgraded so that it includes more compartments, such as the exposed, symptomatic, asymptomatic, quarantine and hospitalized compartments, as well as a compartment that represents the pathogen concentration in the environmental reservoir, such as the concentration of droplets in confined areas. Such a model will be considered in future work.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

All authors would like to thank the respected reviewers for their useful and constructive comments to improve the quality of the paper.

This research was funded by the National Science, Research and Innovation Fund (NSRF) and King Mongkut's University of Technology North Bangkok with Contract no. KMUTNB-FF-66-11.

The fourth author would like to thank Azarbaijan Shahid Madani University.

Conflict of interest

The authors declare no conflict of interest.