Differences weighted composition operators in several variables between some spaces of analytic functions

1.   Introduction

The study of graph theory and its applications in various fields has gained a significant amount of attention in recent years. Graph indices, which are numerical measures associated with graphs, have been widely used to capture the structural characteristics of graphs and analyze their properties. Among various types of graph indices, the Zagreb index, harmonic index and Randic index are important measures that provide insights into the structural features of graphs. A lot of literature is being published on topological indices these days; yet, this area has the potential to accommodate new researchers. New topological indices are being defined every day, so research in this field is never-ending. Topological indices were originally developed in the field of chemistry to understand the representations of different chemical structures, but now they are not limited to just chemical graph theory. For example, in ^[1], the lower bounds of the eccentric distance sum index of connected graphs and cacti are presented; in ^[2], the same index is calculated for the bridge graph; in ^[3], the same index is calculated to transform the thorn graph into polynomial form. Studies on the topological indices of tree graphs are also available. In ^[4], a study is conducted on the first Zagreb index of the tree graph and the upper bounds of the first Zagreb index of the tree graph. In ^[5], the eccentric distance sum of a tree is calculated. The eccentric distance sum index and eccentric connectivity index of unicyclic graphs are calculated in ^[6,7]. In ^[8,9,10,11], topological indices of the bipartite graph, composite graph, windmill graph and Sierpinski graphs are presented. Topological indices of some graph operations can also be calculated, and a study was done on this in ^[12]. In recent years, fuzzy graph theory has emerged as a powerful tool to model and analyze uncertain information in graphs. Fuzzy graph theory extends classical graph theory by allowing edges and nodes to have degrees of membership in the range of [0, 1], which reflects the degree of uncertainty or fuzziness in real-world graphs. Fuzzy graph indices, which are extensions of classical graph indices to fuzzy graphs, have been developed to capture the uncertainty in graphs and provide a more comprehensive characterization of their structural properties. The history of algebra goes back to antiquity. The oldest surviving example is an Egyptian papyrus from around 1500 BCE, which describes how to calculate volumes using chords and arc length. The first recorded use of the word algebra dates to around 1000 BC. The term "algebra" comes from the title of the book written by Abu Ja'far Muhammad Ibn Musa al-Khwarizmi, called "Kitab al-jabr wa'l muqabala", which is a Persian version of his Arabic book given a Latin translation in several European languages. It was later translated into other European languages with different titles, such as Liber abaci by Thabit ibn Qurra in 1111, Algebra by Umar Khayyam in 1150 and Algebra by Fibonacci in 1202. Ring theory is a branch of mathematics that deals with the study of rings. The first known published reference to ring theory occurred in 1391, when the Italian mathematician Gerolamo Cardano proposed a method of reducing fractions. Despite this interesting development in mathematics, ring theory as an independent topic had not been given much attention until around 2000 AD. A commutative ring is a type of ring that has an addition defined. The first use of this definition was by Euler in 1766; however, he did not use his definition to define a ring, but, rather, the inverse image and semidirect sum of a ring. The first way to define a commutative ring was given by Freiberger in 1964, who used it as an equivalent to a direct sum. Today, we define a commutative ring as a ring in which multiplication is commutative, or as is an integral domain if it has no zero divisors. In this article, we work on the commutative ring $Z_{\wp}$. We construct the identity graph of $Z_{\wp}$. A graph is the best tool to understand any kind of relationship between the elements of a set. Algebraic graph theory enables us to better visualize the elements of groups or rings. New graphs are being developed by using different algebraic structures, such as in ^[13] with the commuting graph of quaternion and dihedral groups, in ^[14] with some non-commuting graphs and in ^[15] with inverse graphs of some finite groups. In ^[16], some very useful groups and subgroups are presented as graphs with examples and a lot of useful results are presented, especially for the identity graph of groups. in ^[17], studies on conjugate graphs of groups are presented. In ^[18], the subgroup graph of groups is studied. In ^{[19,20,21,22,23,24]}, studies on the non-commuting graph of quasi-dihedral groups, dihedral groups and finite groups in general are conducted. In ^[25,26], the topological indices of the subgroup graphs of the symmetric group and dihedral groups are calculated.

In this research paper, we focus on studying the fuzzy and crisp cases of four well-known graph indices, namely, the first fuzzy Zagreb index, second fuzzy Zagreb index, harmonic index and Randic index for the identity graph of the ring $Z_{\wp}$, where $\wp$ is a prime number. The identity graph of the ring $Z_{\wp}$ is a specific type of graph that has $\wp$ nodes and represents the additive group structure of the integers modulo $\wp$. We aim to investigate the relationships between these fuzzy and crisp indices and the prime number $\wp$ and explore the potential of using machine learning techniques to model these relationships. To achieve these objectives, we first generalize the existing definitions of the first fuzzy Zagreb index, second fuzzy Zagreb index, harmonic index and Randic index to the identity graph of the ring $Z_{\wp}$. We develop new mathematical formulations for these fuzzy and crisp indices based on fuzzy set theory and graph theory concepts. We analyze the properties of these indices and provide insights into their behavior in different scenarios.

Next, we propose a machine learning approach to find the polynomials that show the relationship between these fuzzy and crisp indices and the prime number $\wp$. We collected a large data set of identity graphs of the ring $Z_{\wp}$ for various prime numbers and applied machine learning techniques, such as polynomial regression, to generate $\wp$ polynomials that show the relationship between these fuzzy and crisp indices. To assess the accuracy of these polynomials, we compare the indices computed by using these polynomials with the exact indices that we have generalized.

The results of our study are expected to contribute to the field of fuzzy graph theory by providing a deeper understanding of the behavior of fuzzy and crisp indices in the context of the identity graph of the ring $Z_{\wp}$. Moreover, our machine learning approach can potentially be applied to other graph indices and graph structures, providing a valuable tool for analyzing and predicting the properties of complex graphs in real-world applications.

In the following sections of this research paper, we will present the formal definitions and mathematical formulations of the first Zagreb index, second Zagreb index, harmonic index and Randic index for the identity graph of the ring $Z_{\wp}$. We will also describe our methodology for collecting and preprocessing the data, developing the machine learning model and evaluating its performance. Finally, we will present and discuss the results and provide insights into the implications and potential applications of our findings.

2.   Preliminaries

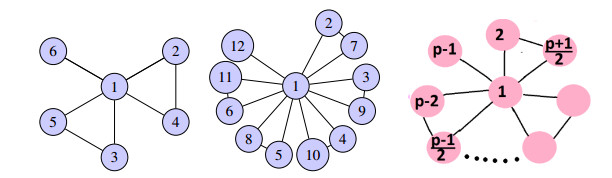
The identity graph of the ring $z_{\wp}$, as defined in ^[27], is denoted by $Id(z_{\wp})$, which is defined as the graph with a vertex set equal to the set of units in $z_{\wp}$; also, two different vertices $\sigma$ and $\varsigma$ are adjacent if $\sigma\varsigma = 1$, and every vertex of $Id(z_{\wp})$ is adjacent to the multiplicative identity of $z_{\wp}$. $Id(z_{7})$, $Id(z_{13})$ and the generalized identity graph of $Z_{\wp}$ are given in Figure 1. The fuzzy graph of the identity graph of $z_{\wp}$, $Id_{fuz}(Z_{\wp})$, is defined as a triplet $(\nu, \varpi, \hbar)$, where $\nu$ is a set of vertices and $\mu$ is a set of edges, furthermore, each edge $(\sigma, \varsigma) \in \mu$ and each vertex $\sigma, \in \nu$ are associated with a membership value $\varpi(\sigma), \hbar(\sigma, \varsigma) \in [0, 1]$, called the vertex weight $\varpi$ and edge weight $\hbar$ fuzzy degree of a vertex. The fuzzy degree of a vertex $\sigma$ in $Id_{fuz}(Z_{\wp})$ is the sum of the membership values of all edges incident to that vertex. It measures the degree of connectedness of a vertex in the graph and is given by the formula $\aleph(\sigma) = \sum_{\sigma \in \nu, (\sigma, \varsigma) \in \mu} \hbar(\sigma, \varsigma)$. The crisp degree of a vertex in a simple graph is simply the number of edges connected to that vertex. Here, we will represent the crisp degree of vertex $\sigma$ as $\xi(\sigma)$. A topological index is a numerical value that characterizes the topological structure of a graph. It can be used to study the chemical or physical properties of molecules represented by graphs. The formulae for crisp and fuzzy topological indices are given in Table 1.

3.   Generalization of topological indices into $\wp$-dependent polynomials and formulae

In this section, we will present the generalized formulae and $\wp$-dependent polynomials to calculate the topological indices of $Id_{crisp}(Z_{\wp})$ for higher values of $\wp$. Using these formulae and polynomials, the process of calculating and computing topological indices becomes significantly easier and faster.

3.1.   Generalization of crisp topological indices

For the sake of simplicity, we have relabeled $Id(z_{\wp})$ in Figure 1 as the graph given below in Figure 2.

Theorem 3.1. The crisp first Zagreb index $M_1(Id_{crisp}(Z_{\wp})) = \wp^2-7$, where $\wp\geq5$.

Proof. In $Id_{crisp}(Z_{\wp}), \quad \xi(\wp-1) = 1 \:, \xi(1) = \wp-2$ and $\xi(\sigma) = 2\; \forall\; \sigma \in V \wedge \sigma \ne1, \wp-1$. Because the total number of vertices in $Id_{crisp}(Z_{\wp}) = \wp-1$, the number of vertices with degree 2 is $\wp-3$.

□

Theorem 3.2. The crisp second Zagreb index $M_2(Id_{crisp}(Z_{\wp})) = 2\wp^2-7\wp+4$, where $\wp\geq5$.

Proof.

□

Theorem 3.3. The crisp Randic index $R[Id_{crisp}(Z_{\wp})] = \frac{1}{\sqrt{(p-2)}}+\frac{\wp-3}{\sqrt{2(\wp-2)}}+\frac{\wp-3}{4}$, where $\wp\geq5$.

Proof.

□

Theorem 3.4. The crisp harmonic index $H[Id_{crisp}(Z_{\wp})] = \frac{2}{\wp}(\wp-3)+\frac{\wp-3}{4}+\frac{2}{\wp-1}$, where $\wp\geq5$.

Proof. As $H[Id_{crisp}(Z_{\wp})] = \sum_{\sigma\varsigma\in E}\frac{2}{\xi(\sigma)+\xi(\varsigma)}$. In the $Id_{crisp}(Z_{\wp})$ vertex, one has an edge with $\wp-2$ vertices. Among those vertices, only the vertex $(\wp-1)$ has degree 1; all other vertices have degree 2, so vertex one is connected to $\wp-3$ vertices with degree 2 and one vertex with degree 1. vertex one has degree $\wp-2$. There are $\frac{\wp-3}{2}$ edges in which the degree of both vertices is 2. Hence,

□

3.2.   Comparative analysis of generalized crisp topological indices

In this subsection, we delve into a comparative examination of the generalized topological indices. These indices have been methodically calculated in line with four distinct theorems, notably, Theorems 3.1–3.4. To explain the nuanced variations and different applications of these generalized indices, Figure 3 and Table 2 are provided in this subsection. This visual depiction will aid in illustrating the relative strengths and unique qualities of these indices in diverse analytical scenarios.

3.3.   Generalization of fuzzy topological indices

For the sake of simplicity, we relabel $Id(z_{\wp})$ in Figure 1 as the graph given below in Figure 4 for a generalized fuzzy $Id(z_{\wp})$.

Theorem 3.5. The fuzzy first Zagreb index

where $\wp\geq5$.

Proof.

□

Theorem 3.6. The second fuzzy Zagreb index

where $\wp\geq5$.

Proof.

□

Theorem 3.7. The fuzzy harmonic index

where $\wp\geq5$.

Proof.

□

Theorem 3.8. The second fuzzy Randic index

where $\wp\geq5$.

Proof.

To calculate $\sum_{\sigma\varsigma\not\in E}\ \varpi(\sigma)\aleph(\sigma)\varpi(\varsigma)\aleph(\varsigma)$, we can see that the non-adjacent pairs of vertices are $(2, 4), (2, 5), (2, 6)....(2, \wp-3), (2, \wp-2), (2, \wp-1), (3, 4), (3, 5), (3, 6)....(3, \wp-3), (3, \wp-2), (3, \wp-1), (4, 6), (4, 7), (4, 8)....(4, \wp-3), (4, \wp-2), (4, \wp-1).....(\wp-4, \wp-3), (\wp-4, \wp-2), (\wp-4, \wp-1).$

□

3.4.   Comparative analysis of generalized fuzzy topological indices

In this subsection, we dig into a comparative evaluation of the generalized topological fuzzy indices. These indices have been meticulously determined in conformity with four distinct theorems, i.e Theorems 3.5–3.8. To clarify the nuanced variations and diverse applications of these generalized indices, Figure 5 and Table 4 are provided below this paragraph. This graphic depiction will aid in presenting the relative strengths and unique properties of various indices in diverse analytical contexts.

4.   Use of machine learning to find relationships between fuzzy and crisp topological indices

We generated topological indices using mathematical formulas and polynomials, yielding numerical descriptions of the identity graph of $Z_{\wp}$. These indices give insight on the mathematical characteristics of the ring $Z_{\wp}$. Our investigation extended to employing machine learning, specifically, polynomial regression, to build a polynomial equation that can explain the link between fuzzy and crisp topological indices. This technique describes this relationship as an $n$th-degree polynomial function.

4.1.   Relationship between fuzzy first Zagreb index and crisp first Zagreb index

Equation (4.1) shows the relationship between the fuzzy first Zagreb index and crisp first Zagreb index. In this equation, $x$ is the fuzzy first Zagreb index and $y$ is the crisp first Zagreb index.

The error analysis given in Figure 6 shows the absolute error between the exact crisp first Zagreb index and the approximated crisp first Zagreb index, as obtained by putting the values of the fuzzy first Zagreb index in equation (4.1).

4.2.   Relationship between fuzzy second Zagreb index and crisp second Zagreb index

Equation (4.2) shows the relationship between the fuzzy second Zagreb index and crisp second Zagreb index. In this equation, $x$ is the fuzzy second Zagreb index and $y$ is the crisp 2nd Zagreb index.

The error analysis given in Figure 7 shows the absolute error between the exact crisp second Zagreb index and the approximated second Zagreb index, as obtained by putting the values of the fuzzy second Zagreb index in equation (4.2).

4.3.   Relationship between fuzzy Randic index and crisp Randic index

Equation (4.3) shows the relationship between the fuzzy Randic index and crisp Randic index. In this equation, $y$ is the fuzzy Randic index and $x$ is the crisp Randic index.

The error analysis given in Figure 8 shows the absolute error between the exact crisp Randic index and the approximated crisp Randic index by putting the values of fuzzy Randic index, as obtained in equation (4.3).

4.4.   Relationship between fuzzy harmonic index and crisp Harmonic index

The equation (4.4) shows the relationship the between fuzzy harmonic index and crisp harmonic index. In this equation, $y$ is the fuzzy harmonic index and $x$ is the crisp harmonic index.

The error analysis given in Figure 9 shows the absolute error between the exact crisp harmonic index and the approximated crisp harmonic index, as obtained by putting the values of the fuzzy harmonic index in equation(4.4).

5.   Entropy analysis of fuzzy and crisp harmonic indices

A histogram was created based on the values in Table 5 to visualize the distribution of values of the crisp and fuzzy harmonic indices, where each value haws a frequency of 1. The histogram was normalized by calculating the probability $\mathfrak{p}_{\wp}$ for each value of $\wp$, which is obtained by dividing 1 by the total number of data points (22 unique values). Using the entropy formula $\mathfrak{H} = -\sum(\mathfrak{p}_{\wp} \times log2(\mathfrak{p}_{\wp}))$, we can calculate the entropy for one value and multiply it by the total number of unique values,

The calculated entropy for the crisp and fuzzy harmonic index data sets was approximately 4.4594 bits, indicating a high level of diversity or variability in the data sets. Since, in both sets of fuzzy and crisp harmonic index data we had 22 unique values, we obtained similar entropy for both cases.

6.   Conclusions and opportunity for future work

In conclusion, this research paper introduces a set of generalized formulae that are dependent on $\wp$ for both fuzzy and crisp versions of several graph indices. The formulae have been applied to the identity graph of the commutative ring $Z_{\wp}$, and the resulting indices were computed by using MATLAB software for 20 prime numbers. The data obtained from these calculations were then utilized for machine learning purposes by using Python and Jupyter notebook to explore the correlation between fuzzy and crisp indices. The paper also establishes the connection between fuzzy and crisp indices through the representation of six-degree polynomials, and it provides an error analysis. The findings of this study significantly contribute to the comprehension of the relationship between fuzzy and crisp graph indices. This knowledge holds potential applications in various fields, particularly in the realms of computer science and engineering. By establishing generalized formulae and analyzing the relationship between fuzzy and crisp indices, researchers and practitioners can gain deeper insights into the behavior of graph indices in different contexts. This understanding can enhance the development of more efficient algorithms and decision-making processes in various domains.

Additionally, it was observed that the accuracy of the results is influenced by the proximity of the input data set. Specifically, when the input data set is closer, the accuracy of the computed indices improves. This finding underscores the importance of selecting appropriate data sets and emphasizes the need for careful consideration when applying these generalized formulae in practical applications. By taking into account the proximity of the input data set, researchers and practitioners can enhance the accuracy of their calculations and ensure more reliable results. This further strengthens the significance of this research, as it provides valuable insights into the factors that impact the relationship between fuzzy and crisp graph indices. Overall, this research not only contributes to the understanding of the relationship between fuzzy and crisp graph indices, it also highlights the importance of data quality and proximity in achieving accurate results. These findings have implications for a wide range of fields, offering opportunities for improved decision-making processes and algorithmic advancements in the fields of computer science and engineering.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence(AI) tools in the creation of this article.

Acknowledgment

The authors extend their appreciation to the Deputyship for Research and Innovation, Ministry of Education in Saudi Arabia, for funding this research through the project number IFP-IMSIU-2023042. The authors also appreciate the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) for supporting and supervising this project.

Conflict of interest

The authors declare no conflicts of interest.