Extremal unicyclic and bicyclic graphs of the Euler Sombor index

1.   Introduction

As an important class of molecular descriptors, topological indices play a crucial role in mathematical chemistry as well as in graph theory. They have been applied to the physico-chemical properties, biological activity, and many other aspects of compounds ^[1,2]. Among these topological indices, the vertex-degree-based (VDB) indices are undoubtedly the most widely investigated, and have new chemical and pharmacological applications, see ^[3,4,5]. In recent years, some new VDB indices with geometric interpretations have been discovered.

In 2021, the Sombor index was introduced by Gutman ^[5], defined as

This is the first topological index with geometric significance, which has attracted a lot of attention. Many results have been gained in recent papers, such as the extremal values of the Sombor index for trees and any connected graph $G$ ^[5], the extremal value of this index among all molecular trees ^[6], the correlation between this index and Zagreb index ^[7], and the upper and lower bounds of this index for unicyclic graphs as well as the extremal value of chemical unicyclic graphs with given girth ^[8]. Furthermore, a few new indices with geometric significance, such as the elliptic Sombor index ^[9], KG-Sombor index ^[10], etc. have been introduced. For more results on these indices, readers are referred to the review papers ^[11,12,13].

Recently, Gutman ^[14] and Tang et al. ^[15] proposed another index with geometric significance, defined as

Due to its origin from an approximate expression of the perimeter of the ellipse, which was given by Euler in 1773, it is named the Euler Sombor index.

As the latest VDB index with geometric significance, the Euler Sombor index has irreplaceable importance. Formally an approximate expression of the perimeter for the ellipse, Gutman ^[14] determined some actual relations between the Euler Sombor index and Sombor index, and it can be used to estimate the Sombor index.

In ^[15], Tang, Li, and Deng fitted the boiling point (bp) and concentricity factor (AcenFac) with the Euler Sombor index of octane isomers, and showed that it has strong discriminability for compounds and is very effective in predicting physical and chemical properties. They also determined the extremal values for the Euler Sombor index among all (molecular) trees and characterized the corresponding extremal graphs.

Unicyclic graphs and bicyclic graphs are two important classic graphs in the study of topological indices, which are composed of various chemical structures. Cruz and Rada ^[16] attained the minimal values of (chemical) unicyclic and bicyclic graphs for the Sombor index and obtained an upper bound on the Sombor index of unicyclic and bicyclic graphs, but did not characterize the extremal graphs. In the same paper, they mentioned that the maximal graphs over the set of unicyclic and bicyclic graphs with respect to Sombor index is an interesting open problem. Very recently, Das completely solved these open problems in ^[17].

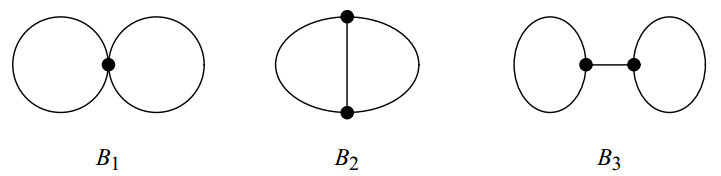
Inspired by these, we mainly study maximal and minimal values for the Euler Sombor index over all unicyclic and bicyclic graphs, and characterize corresponding extremum graphs. In Section 2, we present that $C_n$ and $B_i(n, 1)(i = 2, 3)$, see Figure 1, are the only unicyclic and bicyclic graphs with the minimal value of $EP(G)$, respectively. Moreover, we obtain that $S_n'$ is the unique unicyclic graph with the maximal value of $EP(G)$ in Section 3, and also determine that $C_{n, 4}'$ is the only bicyclic graph with maximal value of $EP(G)$ in Section 4, where $n\geq 28$.

All graphs considered are simple and connected. Let $G = (V(G), E(G))$ be a graph with its vertex set $V(G)$ and edge set $E(G)$. The degree of a vertex $v_i$ is denoted by $d_G(v_i)$ or $d(v_i)$. In particular, the maximal degree and the second maximal degree will be denoted by $\Delta$ and $\Delta_2$, respectively. A vertex $v_i$ is said to be pendant if $d(v_i) = 1$. Similarly, an edge $\{v_iv_j\}$ is called pendant if $d(v_i) = 1$ or $d(v_j) = 1$. The neighbors of vertex $v_i$, denoted by $N_G(v_i)$ or $N(v_i)$, are the set of vertices adjacent to $v_i$. For notations and terminology not mentioned, see ^[18].

Recall that a $k$-cyclic graph $G$ with $|V(G)| = n$ vertices is a connected graph with $|E(G)| = n+k-1$ edges. We denote by $\mathcal{G}_{n, k}$ the set of $k$-cyclic graphs $G$ with $n$ vertices. In particular, $\mathcal{G}_{n, 1}$ is the set of unicyclic graphs, while $\mathcal{G}_{n, 2}$ is the set of bicyclic graphs. Let $C_{n, 4}'$ be the graph obtained by attaching $(n-4)$ pendant edges to a vertex of degree three in $K_4-e$, and $S_n'$ the graph obtained from the star $S_n$ by adding an edge. For convenience, an edge $\{v_iv_j\}$ in $G$ with $(d(v_i), d(v_j)) = (x, y)$ (joining a vertex of degree $x$ with a vertex of degree $y$) is called $(x, y)$-type, and $m_{x, y} = m_{x, y}(G)$ is the number of edges with $(x, y)$-type in $G$.

2.   The minimal Euler Sombor index of unicyclic and bicyclic graphs

Let $\mathbb{P}_n = \{(x, y)\in \mathbb{N}\times \mathbb{N}:1\leq x\leq y\leq n-1\}-\{(1, 1), (2, 2), (2, 3), (3, 2), (3, 3)\}$ and $\mathbb{P}_{n, k} = \{(x, y)\in \mathbb{P}_n: x+y\leq n+k\}$.

Lemma 2.1. Let

Then $g(2, 2) < 0$, $g(2, 3) = g(3, 2) = g(3, 3) = 0$, and $g(x, y) > 0$ for $(x, y)\in \mathbb{P}_n$.

Proof. We can easily to check $g(2, 2) < 0$, and $g(2, 3) = g(3, 2) = g(3, 3) = 0$. Note that

For $5\leq x\leq y$, immediately, $g(x, y) > g_1(5, 5) = \sqrt{75}+4\sqrt{19}-15\sqrt{3} > 0.11 > 0$. For $1\leq x\leq 4$ and $y\geq 8$, we have $g(x, y) > g(1, 8) > g_1(5, 5) > 0$. Eventually, for $1\leq x\leq 4$ and $2\leq y\leq 7$, one can easily check that $g(x, y) > 0$ by tedious algebraic calculations. □

Lemma 2.2. Let $G\in \mathcal{G}_{n, k}$ and $k\in\{1, 2\}$. Then

where $g(x, y)$ is defined as in Lemma 2.1.

Proof. For $G\in \mathcal{G}_{n, k}$, it was proved in ^[16] that

Substituting the above equations into $EP(G)$, it yields

This completes the proof. □

Theorem 2.3. Let $G\in \mathcal{G}_{n, 1}$. Then,

with equality if and only if $G\cong C_n$.

Proof. First, by Lemma 2.2 and $k = 1$, we have

Using Lemma 2.1, one can easily obtain that $g(x, y) > 0$ for all $(x, y)\in \mathbb{P}_{n, 1}$, and $5\sqrt{3}-2\sqrt{19} = g(2, 2) < -0.05 < 0$. Moreover, $m_{2, 2}\leq n$ by $G\in \mathcal{G}_{n, 1}$, and

with equality if and only if $\mathbb{P}_{n, 1} = \emptyset$ and $m_{2, 2} = n$, i.e., $G\cong C_n$. □

The three bicyclic graphs $B_1$, $B_2$, and $B_3$ with $n$ vertices are depicted in Figure 1, where two vertices of degree 3 in $B_2$ and $B_3$ are adjacent. One can easily obtain that

Theorem 2.4. Let $G\in \mathcal{G}_{n, 2}$. Then,

with equality if and only if $G\cong B_2$ or $G\cong B_3$.

Proof. Since $G\in \mathcal{G}_{n, 2}$, we have $m_{2, 2}\leq n-3$, and the only graph with $m_{2, 2} = n-3$ is the graph $B_1(n)$. Furthermore, one can check that $EP(B_1) > EP(B_2) = EP(B_3)$, and hence, we consider only the graphs with $m_{2, 2}\leq n-4$.

By Lemma 2.2 and $k = 2$, we have

On the other hand, Lemma 2.1 implies that $g(2, 2) = 5\sqrt{3}-2\sqrt{19} < -0.05 < 0$, and $g(x, y) > 0$ for $(x, y)\in \mathbb{P}_{n, 2}$. With $m_{2, 2}\leq n-4$, we obtain

with equality if and only if $\mathbb{P}_{n, 2} = \emptyset$ and $m_{2, 2} = n-4$, i.e., $G\cong B_2$ or $G\cong B_3$. □

3.   The maximal Euler Sombor index of unicyclic graphs

In the remainder of this paper, we assume $f(x, y) = \sqrt{x^2+y^2+xy}$ with $x, y\geq 1$. Let $v_i, v_j\in V(G)$. Then

In this section, we use $\mathbb{U}_{n, k}$ to represent the set of unicyclic graphs with order $n$ and girth $k$.

Lemma 3.1. Let $f(x, y) = \sqrt{x^2+y^2+xy}$ with $x, y\geq 1$, and $x\geq y$. Then, $f(x, y)\leq (2-\sqrt{3})x+(\sqrt{3}-1)(x+y)$.

Proof. It can be concluded that

So, $f(x, y)\leq x+(\sqrt{3}-1)y = (2-\sqrt{3})x+(\sqrt{3}-1)(x+y)$. □

Lemma 3.2. Let $G\in \mathbb{U}_{n, k}$, $k\geq 3$, $G\not\cong C_n$, and $v_i\neq v_j\in V(G)$.

(1) If $G\in \mathbb{U}_{n, 3}$, then $\Delta(G)\leq n-1$ and $d(v_i)+d(v_j)\leq n+1$.

(2) If $G\in \mathbb{U}_{n, 4}$, then $\Delta(G)\leq n-2$ and $d(v_i)+d(v_j)\leq n$.

(3) If $G\in \mathbb{U}_{n, k} \; (k\geq 5)$, then $\Delta(G)\leq n-3$ and $d(v_i)+d(v_j)\leq n-1$.

Proof. $G\in \mathbb{U}_{n, k}$ implies that $|V(G)| = |E(G)| = n$. There are at least $(k-2)$ edges not incident with the vertex of degree $\Delta$. Hence, $\Delta(G)\leq n-k+2$. By the condition $C_n\not\cong G\in \mathbb{U}_{n, k}$, $E(G) = E(C_k)\cup \{e_1, e_2, \cdots, e_{n-k}\}$, where $e_1, e_2, \cdots, e_{n-k}$ are edges not on the cycle $C_k$. If all $e_1, e_2, \cdots, e_{n-k}$ are incident with at most two vertices on $C_k$, then we obtain that $d(v_i)+d(v_j) = n-k+4$. Otherwise, $d(v_i)+d(v_j)\leq n-k+3$. Therefore, (1)–(3) of this lemma hold. □

Lemma 3.3. Let $G\in \mathbb{U}_{n, 3}$ and $G\not\cong C_n$. Then $EP(G)\leq EP(S_n')$ with equality if and only if $G\cong S_n'$.

Proof. From Lemma 3.2(1), we have $\Delta(G)\leq n-1$ and $d(v_i)+d(v_j)\leq n+1$ for any $v_i\neq v_j\in V(G)$.

If $\Delta = n-1$, then $G\cong S_n'$ and

If $\Delta = n-2$, then $G\cong F_{1, 1}$ or $G\cong F_2$ (see Figure 2) since $G$ contains a cycle $C_3$, and we can easily obtain

If $\Delta\leq n-3$, we assume that there is a graph $G\in \mathbb{U}_{n, 3}$ with $EP(G)\geq EP(S_n')$. Then the following claims will hold.

Claim 1. $\Delta\geq n-8$ and there exists $v_i\neq v_j\in V(G)$ with $d(v_i)+d(v_j) = n+1$ for $n-8\leq \Delta\leq n-6$.

Proof. Otherwise, $\Delta\leq n-9$. From Lemma 3.1, we have

Using this result, we can deduce that

a contradiction to $EP(G)\geq EP(S_n')$. So, $\Delta\geq n-8$.

Next, we will prove the rest of the claim. Otherwise, let $n-8\leq \Delta\leq n-6$ and $d(v_i)+d(v_j)\leq n$ for all $v_i\neq v_j\in V(G)$. Then,

and

a contradiction to $EP(G)\geq EP(S_n')$. Claim 1 is proved. □

Claim 2. If $n-5\leq \Delta\leq n-3$, then there exist two vertices $v_i\neq v_j\in V(G)$ such that $d(v_i)+d(v_j) = n+1$ or $n$. In particular, if there are two vertices $v_i\neq v_j\in V(G)$ such that $d(v_i)+d(v_j) = n$, then $G$ has no $(1, 2)$-type or $(2, 2)$-type edge.

Proof. Otherwise, $d(v_i)+d(v_j)\leq n-1$ for any $v_i\neq v_j\in V(G)$. We have

and

a contradiction to $EP(G)\geq EP(S_n')$.

In the following, we will show that $G$ has no $(1, 2)$-type or $(2, 2)$-type edge if there are two vertices $v_i\neq v_j\in V(G)$ such that $d(v_i)+d(v_j) = n$. Otherwise, there is an edge $v_kv_l\in E(G)$ such that $f(d(v_k), d(v_l))\leq \sqrt{12}$. By Lemma 3.1,

Consequently, we obtain

a contradiction to $EP(G)\geq EP(S_n')$. □

Based on Claims 1 and 2, we have the following in two cases.

Case 1. $n-8\leq \Delta\leq n-3$. Then, there exists two vertices $v_i\neq v_j\in V(G)$ such that $d(v_i)+d(v_j) = n+1$.

If $\Delta = n-3$, then $G\cong F_{1, 2}$, where $n\geq 7$. Similarly, it can be concluded that $G\cong F_{1, 1+k}$ if $\Delta = n-(3+k)$, where $1\leq k\leq 5$ and $n\geq 7+2k$. Consequently, $G\cong F_{1, i}$ (shown in Figure 2), where $2\leq i\leq 7$. We deduce that

Case 2. $n-5\leq \Delta\leq n-3$. Then, there exist two vertices $v_i\neq v_j\in V(G)$ such that $d(v_i)+d(v_j) = n$, and there is no edge with $(1, 2)$-type or $(2, 2)$-type.

If $\Delta = n-3$, then $G\cong F_3$, where $n\geq 6$. Similarly, if $\Delta = n-4$ or $\Delta = n-5$, then $G\cong F_{4}$ or $G\cong F_{5}$, where $n\geq 8$ and $n\geq 10$, see Figure 3. We obtain

Therefore, together with Cases 1 and 2, Lemma 3.3 is done. □

Lemma 3.4. Let $G\in \mathbb{U}_{n, 4}$ and $G\not\cong C_n$. Then $EP(G) < EP(S_n')$.

Proof. By Lemma 3.2(2), $\Delta\leq n-2$, and $d(v_i)+d(v_j)\leq n$ for $v_i\neq v_j\in V(G)$. We will prove the lemma by contradiction, and assume there exists a graph $G\in \mathbb{U}_{n, 4}$ such that $EP(G)\geq EP(S_n')$. We give the following claims at first.

Claim 1. There is no edge with $(1, 2)$-type and $(2, 2)$-type.

Proof. Otherwise, there exists an edge $e = v_kv_l$ such that $f(d(v_k), d(v_l))\leq f(2, 2) = \sqrt{12}$. By Lemma 3.1, we have

And

So, Claim 1 is done. □

Claim 2. $n-5\leq \Delta\leq n-2$ and there exists two vertices $v_i$ and $v_j$ in $G$ with $d(v_i)+d(v_j) = n$.

Proof. Otherwise, $\Delta\leq n-6$. From Lemma 3.1, we have

and

a contradiction. Consequently, $n-5\leq \Delta\leq n-2$.

Next, we will prove there exists two vertices $v_i\neq v_j\in V(G)$ such that $d(v_i)+d(v_j) = n$.

If $\Delta = n-2$, then $G\cong H_{1, 0}$, as shown in Figure 4, and there exists two vertices $v_i$ and $v_j$ such that $d(v_i)+d(v_j) = n$.

If $n-5\leq \Delta\leq n-3$, and $d(v_i)+d(v_j)\leq n-1$ for any vertices $v_i\neq v_j\in V(G)$, then we have

and

a contradiction. Claim 2 is proved. □

Now, we consider the following cases according to Claims 1 and 2.

If $\Delta = n-2$, then $G\cong H_{1, 0}$, and this graph contains edges of $(2, 2)$-type, which contradicts with Claim 1.

If $\Delta = n-3$, there exists $v_i\neq v_j\in V(G)$ with $d(v_i)+d(v_j) = n$, and there is no edge with $(2, 2)$-type. Then $G\cong H_{1, 1}$, see Figure 4.

If $\Delta = n-4$ or $\Delta = n-5$, then we have only $G\cong H_{1, 2}$ or $G\cong H_{1, 3}$, as shown in Figure 4.

Therefore, we deduce that

So, the assumption is not true, and this completes the proof. □

Theorem 3.5. Let $G\in \mathcal{G}_{n, 1}$, $n\geq 4$. Then,

with equality if and only if $G\cong S_n'$.

Proof. If $G\cong C_n$, then

and the theorem holds.

Next, let $G\in \mathbb{U}_{n, k}$ and $G\not\cong C_n$.

Using Lemmas 3.3 and 3.4, the theorem holds for $G\in \mathbb{U}_{n, 3}$ and $G\in \mathbb{U}_{n, 4}$, especially, with equality if $G\cong S_n'$. Otherwise, $G\in \mathbb{U}_{n, k}$ and $k\geq 5$. Lemma 3.2 implies that $\Delta\leq n-3$, and $d(v_i)+d(v_j)\leq n-1$ for $v_i, v_j\in G$. With Lemma 3.1, we deduce that

and

□

4.   The maximal Euler Sombor index of bicyclic graphs

In this section, we establish the upper bound of $EP(G)$ for bicyclic graphs, as well as characterize the extremal graph, where $n\geq 28$.

Theorem 4.1. Let $G\in \mathcal{G}_{n, 2}$, $n\geq 28$. Then,

with equality if and only if $G\cong C_{n, 4}'$.

Proof. Let $v_i\neq v_j\in V(G)$. We divide into the following three cases.

Case 1. $3\leq \Delta\leq n-13$.

For $3\leq \Delta\leq 14$, we have

With $n\geq 28$, we deduce that

For $15\leq \Delta\leq n-13$, we assume that $d(v_i)\geq d(v_j)$. Because $G$ is a bicyclic graph, $d(v_i)+d(v_j)\leq n+2$. Let $g(x) = x^2-(n+2)x+(n+2)^2$. Then, $g(x)$ is monotonically decreasing for $x\in [15, \frac{n+2}{2}]$, and monotonically increasing for $x\in [\frac{n+2}{2}, n-13]$. Therefore,

If $n\geq 32$, then $\sqrt{n^2-11n+199} < \sqrt{n^2-5n+\frac{25}{4}} = (n-\frac{5}{2})$, and

If $28\leq n\leq 31$, then we can also conclude that $EP(G) < EP(C_{n, 4}')$ by (4.1), and the detailed results see Table 1.

Case 2. $n-12\leq \Delta\leq n-3$.

Recall that $\Delta_2$ is the second maximal degree in $G$. Since $G\in \mathcal{G}_{n, 2}$, $\Delta+\Delta_2\leq n+2$. Next, we will consider two subcases.

Subcase 2.1. $\Delta_2 = n+2-\Delta$.

In this case, $G\cong G_{1, n-1-\Delta}$, as shown in Figure 5. Consequently,

For $n-12\leq \Delta\leq n-3$, we have the following relations:

Together with (4.2), we have

Subcase 2.2. $\Delta_2\leq n+1-\Delta$.

For any $v_i\neq v_j\in V(G)$, $d(v_i)+d(v_j)\leq n+1$. If $n-12\leq \Delta\leq n-9$, then

In this case, we obtain

If $n-8\leq \Delta\leq n-3$, then we deduce that

Furthermore, we have the relations

and

Thus, the Eq (4.3) yields that

Case 3. $n-2\leq \Delta\leq n-1$.

Subcase 3.1. $\Delta = n-2$.

One can easily check that $\Delta_2\leq 4$. If $\Delta_2 = 4$, then we deduce that $G\cong G_{1, 1}$, shown in Figure 5. Recall that $n\geq 28$. We obtain

Next, we assume $\Delta_2 = 3$. In this case, $G\cong G_3$ or $G\cong G_4$ (see Figure 6). Since $n\geq 28$, we have an immediate consequence by calculation:

Otherwise, $\Delta_2\leq 2$, we deduce that

Subcase 3.2. $\Delta = n-1$.

If $G\cong C_{n, 4}'$, then

Otherwise, $G\cong G_2$, where $G_2$ is shown in Figure 5. Noting that $\sqrt{n^2-n+1}+\sqrt{n^2+n+7}\geq 2\sqrt{n^2+3}$, we have

and the theorem is proved. □

5.   Conclusions

Topological indices are commonly molecular structure descriptors that can be used to simulate and predict the physical, chemical, and biological properties of compounds, and they promoted the development of applied disciplines such as chemistry and pharmacology. Recently, the Euler Sombor index derived from geometry, has been shown to have excellent discriminability for compounds and has therefore received much attention.

In this paper, we present $C_n$, and $B_i(n, 1)(i = 2, 3)$ are the only graphs with the minimum Euler Sombor index among all unicyclic and bicyclic graphs, respectively. Moreover, we completely obtain that $S_n'$ is the unique unicyclic graph with the maximum value of $EP(G)$, and also determine that $C_{n, 4}'$ is the only bicyclic graph with maximal value of $EP(G)$, where $n\geq 28$. The extremal values of the Euler Sombor index among multi-cyclic graphs, as well as its chemical applications in compounds, may be the research interests of mathematics and chemistry in the future.

Author contributions

Zhenhua Su: Writing-original draft preparation, Writing-review and editing; Zikai Tang: Formal analysis, Methodology. All authors have read and agreed to the published version of the manuscript.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors would like to thank the anonymous reviewers for their helpful comments.

This work was supported by Hunan Province Natural Science Foundation (2025JJ70485).

Conflict of interest

The authors declare no conflict of interest.