Multiplicity of positive periodic solutions for a discrete impulsive blood cell production model

1.   Introduction

Hematopoiesis is a continuous physiological process of blood cell formation that occurs primarily in the bone marrow ^[1]. In this procedure, as a common origin, hematopoietic stem cells are responsible for the lifetime generation of the three major cell lines: erythrocytes (red blood cells), leukocytes (white blood cells), and platelets. These stem cells have the extraordinary ability to renew, self-replicate, and differentiate into other functional cells. Blood cell numbers in the hematopoietic system maintain a dynamic balance through complex regulatory mechanisms ^[2]. The concentration of blood cells can be measured in venous blood samples ^[3]. Under normal physiological conditions, cell concentrations are maintained within the determinable normal range. However, blood cell counts appear to have wide abnormal fluctuations under pathological conditions, leading to a variety of blood diseases ^[4,5]. For instance, an increased red blood cell count indicates polycythemia vera, cardiovascular disease and stress. A decreased red blood cell count is an indicator of anemia, chronic renal failure and acute hemorrhaging. Therefore, exploring the dynamic changes in blood cell counts is of crucial importance for human life and health.

Conceptually simple differential equations are believed to be fundamental for modeling a large number of different physiological processes ^[6]. Delay is typically incorporated into such models to provide a more accurate description for the dynamical systems ^[7,8]. Delay differential equations are used to describe the development systems that depend on not only the current state but also the historical state and have been widely applied into many fields such as biology, engineering and epidemiology ^[9,10]. To understand the dynamics of blood cell production, the behaviors of blood cell number have been widely employed by delay differential models. In 1977, first-order nonlinear autonomous differential equations, called by Mackey-Glass equations, with time delay were proposed in ^[11]. Blood cells change over time with the increase or decrease in number. Hence, different feedback control mechanisms, responsive to the body's demand for cells, are operated in these models. They showed the dynamic behaviors including limit cycle, oscillations and chaotic solutions of models. Lasota ^[12] studied a delay feedback model in which the nonlinear feedback has an exponential term. By using the approach of ergodic theory, chaotic behaviour of this biological model was obtained.

Considering the important effects of environmentally driven cyclical factors on organisms, Berezansky et al. ^[13] studied a continuous hematopoiesis model with periodic coefficient and time delay. The feedback control mechanism was implemented by a monotonically decreasing function. In their other work ^[14], a unimodal feedback control mechanism was taken into account to show the different behaviors of blood cell number. More comprehensive hematopoiesis models were presented by considering the different maturation times required for different blood cells in hematopoietic system. Continuous hematopoiesis models with multiple feedback loops dominated by different time delays (maturation times) were used in Liu et al. ^[15] and Wu et al. ^[16]. On the other hand, Yao ^[17] and the present author ^[18] explored such models from a discrete perspective, wherein the discrete models are more effective than continuous ones. All these results suggest the existence or global attractivity of positive periodic solutions for hematopoiesis models under some suitable conditions. The research of positive periodic solutions is of great significance both in theoretical interest and real applications ^{[19,20,21,22]}.

Impulses maybe generated in evolutionary system due to transient changes in state experienced at certain moments. In the hematopoietic process, these instantaneous and abrupt changes are caused by external interference such as received radiation, medication or other forms of blood cell pressure ^[23,24]. The blood cell model driven by impulse effects allows discrete rapid changes in cell number and is more accurate and effective in capturing external disturbances ^[25]. For relevant literatures about impulse in other research areas, we refer to ^{[26,27,28,29,30,31,32,33,34]}.

The mechanism by which blood cells increase and decrease have gradually elucidated by clinical studies. On the other hand, it is also important to identify the essence of hematopoietic phenomena by studying relatively simple mathematical models based on various facts. From that point of view, models of blood cells production have been investigated by various studies. Existing studies on continuous models of blood cell dynamics conducted with impulsive effects can be referred to ^{[23,35,36,37,38]}. By contrast, relatively few studies on discrete dynamical models have considered the impulse terms. Therefore, in this paper, we formulate a new discrete blood cell production model considering the key impacts of impulse to study the dynamics of blood cell numbers in hematopoietic system.

The present paper is organized as follows: In Section 2, we investigate the multiplicity of positive periodic solutions of discrete impulsive blood cell production model. Section 3 constructs a solution transformation and a solution representation for the positive periodic solution of the model. Section 4 discusses the multiple positive periodic solutions, which are found by using the Krasnosel'skii fixed point theorem. Section 5 provides a numerical example and its simulations to illustrate our main result.

2.   Blood cell production model

In this paper, we focus on the positive periodic solutions of a hematopoietic system with impulse effects. We begin with the Lasota equation ^[12], which describes the dynamics of the formation of blood cells based on experimental results

In this model, $x$ denotes the number of blood cells in blood circulation. The first term on the right-hand side represents the destruction of blood cells and $\alpha$ is the death rate of blood cells. The second term on the right-hand side represents the influx of blood cells into blood circulation, in which $\beta$ and $n$ are positive constants. The production process of blood cells is inherently nonlinear in nature, and the parameter $n$ is intended to capture this nonlinearity that has nonmonotonic character. The delay $\tau$ is the time required for blood cells to attain maturity from immature cells made in bone marrow to mature ones.

Cyclical fluctuations in the environment have an important effect on many living systems and they give the organisms inherent periodicity. However, constant coefficients and constant time delay could not reflect such periodic environmental influence on blood cells. Hence, it is reasonable and realistic to consider the environmental cyclicity by assuming that mortality, productivity, and maturation during hematopoietic processes change periodically.

Incorporating periodicity and impulsive effects into the hematopoietic system, we discuss the following blood cell production model:

Here, $\Delta$ is the forward difference operator defined by $\Delta x(k) = x(k+1) - x(k)$ for $k\in\mathbb{Z}$; $m\ge 1$ is a natural number and $n > 1$ is a real constant; $\alpha\!: \mathbb{Z}\! \to (0, 1)$, $\beta_i\!: \mathbb{Z}\! \to (0, \infty)$, and $\tau_{i}\!: \mathbb{Z}\! \to \mathbb{Z}^+ \; (1 \le i \le m)$ are $\omega$-periodic; sequence of real numbers $\{\gamma_j\}_{j\in\mathbb{N}} \; (\gamma_j > -1)$ and increasing sequence of natural numbers $\{k_j\}_{j\in\mathbb{N}}$ are $\omega$-periodic, i.e., there exists a $q\in\mathbb{N}$ such that $k_{j+q} = k_j+\omega$ and $\gamma_{j+q} = \gamma_j$. For this model, we assume that

(H) $\prod\limits_{0 \le k_{j} < \omega}(1+\gamma_{j})\prod\limits_{r \neq k_{j}, \, 0 \le r < \omega}(1-\alpha(r)) < 1$.

The initial condition of system (2.1) is

where $\overline{\tau} = \max_{1 \le i \le m}\bigg\{\max_{0 \le k < \omega}\tau_i(k)\bigg\} \in \mathbb{Z}^+\!$ and $\mathbb{Z}[-\, \overline{\tau}, 0] = \{-\, \overline{\tau}, -\, \overline{\tau}+1, \dots, 0\}$. We note that $0 < \alpha(k) < 1$ for $k \in \mathbb{Z}$ and $\gamma_j > -1$ for $j \in \mathbb{N}$. The solution of (2.1) denoted by $x(\cdot; \phi)$ is obviously positive. The purpose of this study is to present a sufficient condition that ensures that system (2.1) has at least two positive $\omega$-periodic solutions. The main result is the following:

Theorem 2.1. Assume that (H) holds. Let $\underline{\beta}_i = \!\min\limits_{k \neq k_j, 0 \le k < \omega}\beta_i(k)$ for each $i = 1, 2, \dots, m$ and $\gamma^{-}_j \! = \min\{\gamma_j, 0\}$ for $j\in\mathbb{N}.$ If

holds, then (2.1) has at least two positive $\omega$-periodic solutions, where

3.   Krasnosel'skii fixed point theorem and solution transformation

In this section, we start with the well-known Krasnosel'skii fixed point theorem ^[39] which is an efficient method for searching periodic solutions of nonlinear differential or difference equations.

Lemma 3.1. (Krasnosel'skii fixed point theorem) Let $(X, ||\cdot||)$ be a Banach space, and let $P \subset X$ be a cone in $X.$ Suppose that $\Omega_1$ and $\Omega_2$ are open bounded subsets of $X$ with $\theta \in \Omega_1 \subset \overline\Omega_1 \subset \Omega_2$. Let $\Phi\!: P \to P$ be a completely continuous operator on $P$ such that, either

(i) $||\Phi x|| \le ||x||$ for $x \in P\cap\partial\Omega_1$ and $||\Phi x|| \ge ||x||$ for $x \in P\cap\partial\Omega_2,$ or

(ii) $||\Phi x|| \ge ||x||$ for $x \in P\cap\partial\Omega_1$ and $||\Phi x|| \le ||x||$ for $x \in P\cap\partial\Omega_2.$

Then, $\Phi$ has a fixed point in $P\cap\, \left(\, \overline{\Omega}_2\!\!\setminus\!\Omega_1\right)$.

For $i = 1, 2, \dots, m$, let

Under the initial condition $y(s) = \phi(s) > 0$ for $s \in \mathbb{Z}[-\, \overline{\tau}, 0]$, we consider the following nonimpulsive difference equation with time-delays:

and we perform the transformation between the solutions of (2.1) and (3.1).

Lemma 3.2. $(i)$ If $y(k)$ is a solution of (3.1), then $x(k) = y(k)\prod_{0 \le k_{j} < k}(1+\gamma_{j})$ is a solution of (2.1); $(ii)$ If $x(k)$ is a solution of (2.1), then $y(k) = x(k)\prod_{0 \le k_{j} < k}(1+\gamma_{j})^{-1}$ is a solution of (3.1).

Proof. We first prove part (i). For any $k \neq k_j$ and $j \in \mathbb{N}$, we obtain

It follows from (3.1) that $y(k_j+1) = y(k_j)$. Then,

Thus, $x(k) = y(k)\prod_{0 \le k_{j} < k}(1+\gamma_{j})$ is a solution of (2.1).

Now, we prove part (ii). For any $k \neq k_j$ and $j \in \mathbb{N}$, one has

Moreover, from (2.1), we have

Hence, it follows the definition of $y$ that

for $j\in \mathbb{N}$. That is, $y(k)$ satisfies (3.1). Therefore, $y(k) = x(k)\prod_{0 \le k_{j} < k}(1+\gamma_{j})^{-1}$ is a solution of (3.1). The proof is complete. □

We define $X = \big\{x\!: x(k) = x(k+\omega) \in \mathbb{R} \; \; \text{for}\; \, k \in \mathbb{Z}\big\}$. Then, $X$ is a finite dimensional Banach space with the norm $||x|| = \max_{0 \le k < \omega}|x(k)|$. Let $x$ be an element of $X$ satisfying $x(k) > 0$ for $k \in \mathbb{Z}$ and then we set $\hat{x}(k) = x(k)$ for $k \in \mathbb{Z}[-\, \overline{\tau}, \infty) \overset{\mathrm{def}}{ = }[-\, \overline{\tau}, \infty)\cap\mathbb{Z}$ and $\hat{\phi}(k) = x(k)$ for $k \in \mathbb{Z}[-\, \overline{\tau}, 0]$. Denote

Then, the following representation of a positive $\omega$-periodic solution of (2.1) can be obtained.

Lemma 3.3. Assume that (H) holds. Then a positive $\omega$-periodic sequence $\hat{x}$ is the solution $x(\cdot; \hat{\phi})$ of (2.1) if and only if the original sequence $x \in X$ satisfies

Proof. (Necessity) Suppose that the positive $\omega$-periodic sequence $\hat{x}$ is the solution $x(\cdot; \hat{\phi})$ of (2.1). Then it is obvious that $x(k) > 0$ for $k \in \mathbb{Z}$. We rewrite (3.1) as

Due to Lemma 3.2, we multiply both sides of the above equality by $\prod_{0 \le r < k+1} 1/(1-\tilde{\alpha}(r))$ to obtain

Summing up both sides from $k$ to $k+\omega-1$ results in

which leads to

Using the periodicity of $\tilde{\alpha}$ and $\gamma_j$, we have

for $k \in \mathbb{Z}$. Thus, $x$ satisfies (3.2).

(Sufficiency) Direct computation shows that

Hence, $H$ is $\omega$-periodic with respect to both variables $k$ and $s$. Then, we can prove that an element $x$ of $X$ having the expression (3.2) is $\omega$-periodic. In fact,

Now, we construct $\hat{x}$ and $\hat{\phi}$ from the element $x$ of $X$ given by (3.2). To prove that $\hat{x}$ is the positive $\omega$-periodic solution $x(\cdot; \hat{\phi})$ of (2.1), it suffices to show that $x$ satisfies (2.1). For $k \neq k_j$, since $\tilde{\beta}_i = \beta_i \; (i = 1, 2, \dots, m)$ for $k \in \mathbb{Z}$, we have

Moreover,

Then, we obtain

For $k = k_j$, one has

and

Because of the periodicity of $\gamma_j$, we see that $x(k_j+1) = (1 + \gamma_j)x(k_j).$ Hence, $x$ satisfies system (2.1). The proof is complete. □

We define a cone in Banach space $X$ by $P = \big\{x \in X\!: x(k) \ge \rho||x||\; \; \text{for}\; \, k \in \mathbb{Z}\big\}.$ Let

Then, it is easy to obtain the following property of the operator $\Phi$.

Lemma 3.4. Assume that (H) holds. Then the operator $\Phi\!: P \to P$ is completely continuous.

Proof. In view of the proof of sufficiency of Lemma 3.3, it follows from (3.3) that $\Phi x(k+\omega) = \Phi x(k)$. Hence, $\Phi x \in X$. Since $0 < \tilde{\alpha} < 1$ for $k \in \mathbb{Z}$, we can estimate that

Moreover,

The above two inequalities lead to

Hence,

Therefore,

Thus, $\Phi x \in P$. The straightforward calculations can show that $\Phi$ is a completely continuous operator. The proof is complete. □

4.   Multiplicity of positive $\omega$-periodic solutions

In this section, we investigate the multiplicity of positive $\omega$-periodic solutions. The main result Theorem 2.1 is proved by the Krasnosel'skii fixed point theorem below.

Proof. From the solution representation (3.2) in Lemma 3.3, we observe that the positive $\omega$-periodic solution of (2.1) is a fixed point of the completely continuous operator $\Phi$ defined by (3.3). It suffices to establish the existence of two fixed points of $\Phi$. Let $\overline{\beta}_i = \max_{k \neq k_j, 0 \le k < \omega}\beta_i(k)$ for each $i = 1, 2, \dots, m$ and $\gamma^{+}_j = \max\{\gamma_j, 0\}$ for $j = 1, 2, \dots$. It follows that

Choose a constant $\varepsilon_0$ satisfying

where $d = 1/(1-\prod_{0 \le k_{j} < \omega}(1+\gamma_{j})\prod_{r\neq k_{j}, \, 0\le r < \omega}(1-\alpha(r)))$. Then one can find an $u_0$ with $0 < u_0 < n$ and an $U$ with $n < U$ such that

Let $u_1 = U/\rho > U.$ The condition (2.3) implies that there exists a sufficiently small $\sigma_* \in (0, u_1-n)$ such that

Then we define four open bounded subsets $\Omega_i (1\le i \le 4)$ of $X$ by

with $\theta \in \Omega_1 \subset \overline{\Omega}_1 \subset \Omega_2 \subset \overline{\Omega}_2\subset \Omega_3 \subset \overline{\Omega}_3 \subset \Omega_4 \subset \overline{\Omega}_4$.

According to the characteristics of the open bounded sets $\Omega_i\; (1 \le i \le 4)$, the discussion is divided into four cases.

Case 1. Suppose that $x$ is an element of $P\cap\partial\Omega_1 \subset X$. For $k \in \mathbb{Z}$, we see that $0 \le x(k) < u_0$ and $x$ is $\omega$-periodic. By (3.4) and (4.1), one has

for $k \in \mathbb{Z}$. Hence, $||\Phi x|| < u_0 = ||x||$ for $x \in P\cap\partial\Omega_1$.

Case 2. Suppose that $x$ is an element of $P\cap\partial\Omega_2 \subset X$. For $k \in \mathbb{Z}$, we see that $n\rho \! = \! \rho \|x\| \le x(k) \! < \! n$ and $x$ is $\omega$-periodic. The unimodal property of $u^n/e^u$ shows that $\min_{n\rho \le u \le n}\!u^n/e^u = n^n\rho^n/e^{n\rho}.$ Hence, from (2.3) and (3.4), it leads to

for $k \in \mathbb{Z}$. Whence $||\Phi x|| > n = ||x||$ for $x \in P\cap\partial\Omega_2$.

Case 3. Suppose that $x$ is an element of $P\cap\partial\Omega_3 \subset X$. For $k \in \mathbb{Z}$, we see that $\rho(n + \sigma_*) = \rho \|x\| \le x(k) \le n + \sigma_*$ and $x$ is $\omega$-periodic. Note that $\sigma_*$ is a sufficiently small positive constant, then

It follows from (3.4) and (4.2) that, for $k \in \mathbb{Z}$,

Hence, $||\Phi x|| > n + \sigma_* = ||x||$ for $x \in P\cap\partial\Omega_3$.

Case 4. Suppose that $x$ is an element of $P\cap\partial\Omega_4 \subset X$. For $k \in \mathbb{Z}$, we see that $\rho u_1 \le x(k) \le u_1$ and $x$ is $\omega$-periodic. By (3.4) and (4.1), one has

for $k \in \mathbb{Z}$, which implies that $||\Phi x|| < u_1 = ||x||$ for $x \in P\cap\partial\Omega_4$.

Now we are in the position to conclude that the conditions of the Krasnosel'skii fixed point theorem are satisfied by $\Omega_1$, $\Omega_2$ and by $\Omega_3$, $\Omega_4$, respectively. Therefore, the operator given by (3.3) has two fixed points. Among them, one is $x_1\in P\cap\left(\, \overline{\Omega}_2\!\!\setminus\!\Omega_1\right)$ which satisfies $x_1(k) \ge \rho||x_1||$ for $k \in \mathbb{Z}$ and $0 < u_0 \le ||x|| \le n$, and the other is $x_2\in P\cap\left(\, \overline{\Omega}_4\!\setminus\!\Omega_3\right)$ which satisfies $x_2(k) \ge \gamma||x_2||$ for $k \in \mathbb{Z}$ and $0 < n + \sigma_* \le ||x_2|| \le u_1$. Let $\hat{x}_1(k) = x_1(k)$ for $k \in \mathbb{Z}[-\, \overline{\tau}, \infty)$ and $\hat{\phi}_1(k) = x_1(k)$ for $k \in \mathbb{Z}[-\, \overline{\tau}, 0]$. Moreover, let $\hat{x}_2(k) = x_2(k)$ for $k \in \mathbb{Z}[-\, \overline{\tau}, \infty)$ and $\hat{\phi}_2(k) = x_2(k)$ for $k \in \mathbb{Z}[-\, \overline{\tau}, 0]$. Then, Lemma 3.3 implies that $\hat{x}_1$ is a positive $\omega$-periodic solution of (2.1) with the initial function $\hat{\phi}_1$ and $\hat{x}_2$ is another positive $\omega$-periodic solution of (2.1) with the initial function $\hat{\phi}_2$. Thus, (2.1) has two different positive $\omega$-periodic solutions $\hat{x}_1$ and $\hat{x}_2$ satisfying $\|\hat{x}_1\| \le n < n + \sigma_* \le \|\hat{x}_2\|$. The proof is complete. □

5.   Numerical example

Let us consider the difference equation

Here, all coefficients are positive 4-periodic discrete functions defined as follows:

The impulse values are $\gamma_1 = -0.5$ for $k_1 = 1$ and $\gamma_2 = 1.5$ for $k_2 = 3$. We can verify that there are at least two positive $4$-periodic solutions of (5.1).

It is obvious that $\sum_{i = 1}^{2}\underline{\beta}_i = 35+8 = 43$. Since $\gamma^{-}_1 \! = \min\{-0.5, 0\} = -0.5$, $\gamma^{-}_2 \! = \min\{1.5, 0\} = 0$, it follows that

In view of values of $\alpha$, we have

Hence,

Note that $n = 2$. It can be checked easily that

Therefore, condition (2.3) is satisfied. Thus, from Theorem 2.1, we see that (5.1) has at least two positive $4$-periodic solutions.

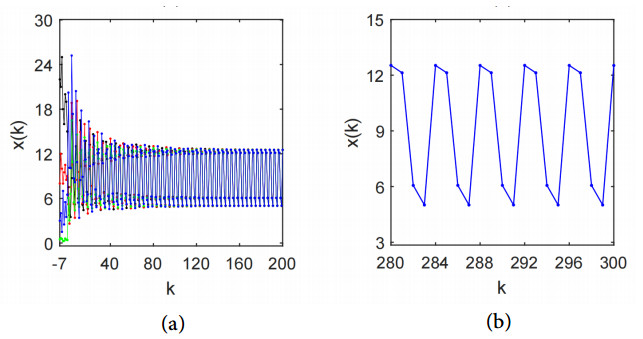
Figure 1a shows that as k gradually increases, the four solutions separately determined by arbitrarily given four initial functions display the same periodic changes. In other words, there exists a positive $4$-periodic solution of (5.1). The details of this positive $4$-periodic solution are revealed in Figure 1b.

Theorem 2.1 ensures the existence of two positive $4$-periodic solutions. In addition to the locally asymptotically stable positive $4$-periodic solution described above, system (5.1) has another positive $4$-periodic solution. In general, this solution is considered unstable and very difficult to find.

6.   Conclusions

A discrete blood cell production model subjected to impulse effects is studied in this paper. This model considers sudden changes in the number of blood cells at certain times that cannot be ignored. The sufficient condition that guarantees the multiplicity of positive periodic solutions is established by Krasnoseli-skii fixed point theorem. To be precise, there exist at least two positive periodic solutions of the model under this condition. By using coefficients and impulse values, this sufficient condition can be easily verified.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The paper was supported by Fundamental Research Funds for the Central Universities (Grant No. 41422003).

Conflict of interest

The author declares no conflict of interest regarding the publication of this paper.