Persistence, extinction and practical exponential stability of impulsive stochastic competition models with varying delays

1.   Introduction

The stochastic model of a predator and prey has been widely investigated for many years^[1,2,3,4]. It is well known that two species models are difficult to describe ecological changes, and the critical behaviors can only be expressed by population models of more species. Because of its theoretical and practical significance, it is also one of the most important problems in theoretical ecology to study the dynamic characteristics of the one predator and two competitive prey population model, such as permanent existence, extinction, stability and periodicity ^[5,6,7,8,9]. Ma et al. ^[5] proposed the one predator and two competitive preys model for the first time. Ahmad considered a competitive trio of species satisfying two inequalities involving the growth rate and the average interaction coefficient, which implies persistence ^[7]. By constructing auxiliary equations and Lipschitz conditions, Qiu ^[9] proved that the three-dimensional Lotka-Volterra system has a stationary distribution. Freedman's analysis of equilibrium points for three-level models, stability criteria, and minimum carrying capacity for population persistence and extends the work on the Lotka-Volterra model. It is shown that the recent research models are closer to reality and increase in dimensionality ^[8].

In addition, time delays can not be ignored in biological model. Time delay is a common problem in many practical systems, which will lead to system instability or oscillation. Therefore, the stability of time-delay systems has been one of the hot topics in recent twenty years ^{[10,11,12,13,14,15,16,17,18,19]}. Xu ^[12] used some differential inequalities and random analysis techniques to study a class of switched systems with delays. Nevertheless, the impulse is a discrete moment in a very short time interval to a supercritical state ^[20,21,22]. Pulse perturbation has been extensively studied in the fields of ecology and epidemiology. The population dynamic system is studied extensively by impulse differential equation ^{[11,12,19,23,24,25,26,27]}. Lu ^[25] obtained the threshold between weak persistence and extinction by using Itô's formula theorem and mathematical analysis.

Bio-mathematic stability refers to the ability of a biological system to maintain its stable state when various factors or parameters change. Biological systems are usually affected by internal and external environments, including changes in temperature, nutrition, water, oxygen, light and other factors, as well as interactions between organisms. Exponential stability means that the index remains relatively stable within a certain period of time. Hutson ^[6] pointed out that asymptotic stability and global asymptotic stability are intuitive concepts that neither of the two most widely used conditions can reflect persistence in a satisfactory way. Practical exponential stability of differential equations is a kind of asymptotic stability with good properties and a kind of Lyapunov stability. That is, the system state is kept stable by allowing the system to oscillate in a small neighborhood ^{[28,29,30,31,32]}. Yao investigated the practical exponential stability of mild solutions with delays using direct and indirect methods ^[29]. As far as we know, there are few studies on stochastic impulsive high-dimensional models with time-varying delays. The study of the delay independent and Markovian effects of the practical exponential stability of the following impulsive stochastic model with time varying delay for one predator and two competitive preys model has not been done:

where $x_i(\theta) = \phi_i(\theta), -\tau_0 \le \theta \le 0, t \ge 0$. $x_i(t)$, $i = 1, 2, 3$ stands for population size of the two independent prey and one predator population at $t$, respectively. $a_{ij} > 0$($i, j = 1, 2, 3$). $\tau_{min} \le \tau_i(t) \le \tau_{max}$ represent the time-varying delay, where $\tau_{min}$ and $\tau_{max}$ are given bounds. ${\boldsymbol{\phi}}(\theta) = (\phi_1(\theta), \phi_2(\theta), \phi_3(\theta))^\top \in U$, $U = C([-\tau_0, 0], \mathbb{R}_+^3)$ represent the space of all the continue function. The Brownian motions $B_i(t)(i = 1, 2, 3)$ defined on a complete probability space $(\Omega, \mathscr{F}_t, (\mathscr{F}_t)_{t\geq0}, \mathbb{P})$ with a filtration $(\mathscr{F}_t)_{t\geq0}$ are independent to each other. $0 < t_1 < t_2 < \cdots < t_k < \cdots$ and ${\lim_{k \to +\infty} t_k} = +\infty$. In view of biological significance in reality, we just consider $1+\alpha_{ik} > 0 (i = 1, 2, 3)$, which is a natural constraint. Pulse parameter $\alpha_{ik}$ refer to specific properties of the pulse, such as pulse width, frequency, peak voltage and repetition rate. In biological research, pulse parameters can affect the response and reaction mode of organisms. The biological interpretations of these parameters are described in Table 1.

This paper studies the well-posedness and asymptotic behavior of the model (1.1). The main contributions of this paper lie in that this paper reveals the following facts: (ⅰ) The practical exponential stability under the condition of bounded pulse intensity is not affected by the impulsive perturbation. (ⅱ) Razumikhin inequality can be used to transform the solution of the stability of non-Markovian processes to the solution of the stability of Markovian ones. (ⅲ) In some cases, a non-Markovian process can produce Markovian effects. Moreover, examples obtained the theoretical results for the existence of practical exponential stability through the relationship between parameters, pulse intensity and noise intensity. The work in literature ^[11] is generalized.

2.   Prilimary

For convenience, we use the following notations. If $f(t)$ is a continuous bounded function on $\mathbb{R}_{+}$, define $f^{ \rm{u}} = \sup_{t \in \mathbb{R}^+}f(t)$, $f^{ \rm{l}} = \inf_{t \in \mathbb{R}^+}f(t)$. $\overline{f(t)} = t^{-1} \int_{0}^{t}f(s)ds$, $f^* = \limsup_{t \to +\infty }f(t)$, $f_* = \lim \rm{inf}_{t \to +\infty }f(t)$. Define the norm $|{{\boldsymbol{y}}}| = \sum_{i = 1}^{n}$.

Next, we consider the stochastic equations

where ${\boldsymbol{\phi}} \in C ([-\tau_0, 0], \mathbb{R}^n)$, ${{\boldsymbol{x}}}\in \mathbb{R}^n$, $x_t \in L_{F_t}^p([-\tau_0, 0], \mathbb{R}^n)$, ${{\boldsymbol{f}}}: L_{F_t}^p(\mathbb{R}_+\times ([-\tau_0, 0], \mathbb{R}^n))\rightarrow \mathbb{R}^n$, ${{\boldsymbol{g}}}: L_{F_t}^p(\mathbb{R}_+\times ([-\tau_0, 0], \mathbb{R}^n))\rightarrow \mathbb{R}^{n\times m}$.

The Lyapunov operator is defined as:

Definition 1. Let ${{\boldsymbol{x}}}(t) = (x_1(t), x_2(t), x_3(t))^\top$ be the solution of model (1.1).

1) $p$ is a positive integer, and if $\lim_{t\to +\infty}E|x(t)|^p >0$, then the species is $p$th moment persistent, and $\lim_{t\to +\infty}E|x(t)|^p = 0$, the species is $p$th moment extinct ^[30].

2) If $\lim_{t\to +\infty}x_i(t) = 0$, and species $x_i(t)$ is extinction, $\lim_{t\to +\infty}\overline{x_i(t)} = 0$, then species $x_i(t)$ is considered to be non-persistent in the mean.

3) If $\overline{x_i}^*>0$, and species $x_i(t)$ is weakly persistent in the mean, $x_i^*>0$, then species $x_i(t)$ is considered to be weakly persistent.

4) Moment stabilization, also known as $p$th moment stabilization, requires convergence to zero moments of order $p$.

5) For $p>0$, system (1.1) is said to be $p$th moment practical exponential stability^[28]. If there exist positive constants $Z_1>0$, $Z_2 \ge 0$ and $\ell>0$, then

Lemma 1. (^[4]) The solution $x(t)$ of the predator-prey model (1.1) obeys

3.   Global positive solutions

Under the condition of bounded pulse intensity, an equivalent equation is established to obtain a pure differential equation of the same type as (2.4) in ^[34], and the existence of a global solution is obtained. Building an equivalence system:

where $y_i(\theta) = \phi_i(\theta)$, $-\tau_{0} \le \theta \le 0, t\ge0$, $x_{i}(t) = A_i(t)y_i(t)$ and $A_i(t) = (\prod_{j = 1}^{k}(1+\alpha_{ij}))^{-t}\prod_{t_k < t}(1+\alpha_{ik})$.

Let ${{\boldsymbol{y}}}(t) = (y_1(t), y_2(t), y_3(t))^\top$,

$d{{\boldsymbol{B}}}(t) = (dB_1(t), dB_2(t), dB_3(t))^\top$, ${\boldsymbol{\phi}}(\theta) = (\phi_1(\theta), \phi_2(\theta), \phi_3(\theta))^\top$, then (3.1) can be rewritten as

For model (1.1), we always assume

$(T_1)$ In terms of biological significance, we consider $1+\alpha_{ij} > 0$, $j \in N$, $i = 1, 2, 3$.

$(T_2)$ $\exists$ $C_1 > 0$, $C_2 > 0$, $C_{1}\leq \prod_{j = 1}^{k}(1+\alpha_{ij})\le C_{2}$, $C_{1}\leq\sum_{j = 1}^{k}(1+\alpha_{ij})\le C_{2}$, $i = 1, 2, 3$.

Theorem 1. Assume $(T_1)$ and $(T_2)$ hold, there exists a unique solution ${{\boldsymbol{y}}}(t)$ on $t \in \mathbb{R}^+ = [0, \infty)$, and the solution remain in $\mathbb{R}_+^3$ with probability 1 in (3.2).

Proof. Because $r_i+\sum_{j = 1}^{k} \ln(1+\alpha_{ij})(i = 1, 2)$, $-r_3+\sum_{j = 1}^{k} \ln(1+\alpha_{3j})$ and $A_i(t), i = 1, 2, 3$ are bounded, we can prove that the model (3.2) has a unique global solution ${{\boldsymbol{y}}}(t)$ remain in $\mathbb{R}_+^3$ with probability 1 under the condition of $(T_1)$ and $(T_2)$ by the same method as lemma 2.2 in ^[34]. In fact, Eq (2.4) in ^[34] is pure differential equation, while the Eq (3.2) in this paper is a simultaneous differential equation of the same type. It's proof is similar, so we omit. □

Theorem 2. By the equivalence system and ${{\boldsymbol{x}}}_{i}(t) = A_i(t){{\boldsymbol{y}}}_i(t)$, ${{\boldsymbol{x}}}_{i}(t)$ is a solution of the original system (1.1).

Proof. The proof of the theorem is along the same lines as in ^[15]. □

Remark 1. Theorem 2 shows that under conditions $(T_1)$ and $(T_2)$, the solutions to the original system and the auxiliary system has the same asymptotic behavior. In order to facilitate the study, we convert the four-dimensional equation into the three-dimensional equivalent equation, which provides convenience for the following studies on the extinction, non-persistence and practical exponential stability of the system.

4.   Persistence and extinction

Theorem 3. (Ⅰ) If $h_i^*<0(i = 1, 2)$, then the prey $x_i(i = 1, 2)$ will be extinct, where $h_i(t) = \sum_{j = 1, 0<t_k<t}^k\ln(1+\alpha_{ij})+r_i-0.5\sigma_i^2+\frac{1}{t} \ln A_i(t)$, $(i = 1, 2)$.

(Ⅱ) If $h_i^* = 0 (i = 1, 2)$, then the prey $x_i(i = 1, 2)$ is non-persistent in the mean.

(Ⅲ) If $h_i^*>0 (i = 1, 2)$, $\limsup_{t\rightarrow +\infty } \frac{\sum_{j = 1, 0<t_k<t}^k\ln(1+\alpha_{ij})}{\ln t}<\infty (i = 1, 2)$ and $h_3^*<0$, then the prey $x_i(i = 1, 2)$ is weakly persistent in the mean, where }$h_3(t) = \sum_{j = 1, 0<t_k<t}^k\ln(1+\alpha_{3j})-r_3-0.5\sigma_3^2+\frac{1}{t} \ln A_3(t)$.

Proof. Applying Itô's formula to the model (3.1) yields

and

where ${{\boldsymbol{x}}}(0) = \phi_0$, $\Lambda_i(t) = \int_{0}^{t}\sigma_i dB_i(s)$(i = 1, 2, 3), local martingale quadratic variation satisfies $\langle \Lambda_i, \Lambda_i\rangle (t) = \int_{0}^{t}\sigma_{i}^{2} dB_i(s) \le \sigma_{i}^2t$ (i = 1, 2, 3). Using strong law of large numbers ^[27], we obtain

Case (Ⅰ). Taking the limit in (4.1), (4.2) and using (4.4),

So, $\lim_{t\rightarrow +\infty} x_i(t) = 0$(i = 1, 2) a.s. hold.

Case (Ⅱ). By (4.4), for $\forall\varepsilon > 0$, $\exists$ $T > 0$, then$\frac{\ln x_i(0)}{t} < \frac{\varepsilon}{3}$, $h_i(t) < h_i^*+\frac{\varepsilon}{3}$ and $\frac{\Lambda _i}{t} < \frac{\varepsilon}{3}(i = 1, 2)$. Add (4.1) and (4.2) to the equation above, we have

So,

Using Lemma 3.2 in ^[25], then

For $\forall\varepsilon$, we have $\lim_{t\rightarrow +\infty} \overline {x_i(t)} = 0$.

Case (Ⅲ). By Lemma 1 and the condition $\limsup_{t\rightarrow +\infty } \frac{ \sum_{j = 1, 0 < t_k < t}^k \ln(1+\alpha_{ij})}{\ln t} < \infty$$(i = 1, 2)$, we can easily get $[t^{-1}\ln x_i(t)]^* \le 0 (i = 1, 2)$ a.s. The following formula can be obtained by taking limit in (4.1) and (4.2)

Therefore, $\overline {x_i}^* > 0$ (i = 1, 2) a.s. For $\forall\omega \in \{\overline{x_i(t, \omega)} = 0, i = 1, 2 \}$, $\overline{x_3(t-\tau_3(t), \omega)}^* > 0$. Yet, for (4.3) take the superior limit and use $\overline{x_i}^* = 0(i = 1, 2)$ a.s. yields

In other words, $\lim_{t\rightarrow \infty}x_3(t, \omega) = 0$, which the contradiction arises. Therefore, $\overline{x_i}^* > 0(i = 1, 2)$ a.s. □

Corollary 1. (Ⅰ) If, in addition to $(T_2)$, the model (1.1) satisfies the condition $r_i < 0.5 \sigma_{i}^{2}$, $1\leq i \leq 2$, the prey $x_i, 1\leq i \leq 2$, will be extinct.

(Ⅱ) If, in addition to $(T_2)$, the model (1.1) satisfies the condition $r_i = 0.5 \sigma_{i}^{2}$, $1\leq i \leq 2$, the prey $x_i, 1\leq i \leq 2$, will be non-persistent in the mean.

(Ⅲ) If, in addition to $(T_2)$, the model (1.1) satisfies the condition $r_i > 0.5 \sigma_{i}^{2}$, $1\leq i \leq 2$ and $-r_3 < 0.5 \sigma_{3}^{2}$, the prey $x_i, 1\leq i \leq 2$, will be weakly persistent in the mean.

Proof. The impulsive perturbations are bounded by $(T_2)$.

So,

From ($T_2$), we have

Similarly,

Based on Theorem 3, we can get Corollary 1.

Theorem 4. (Ⅰ) If ${a_{11}}{a_{22}}h_3^*+a_{31}a_{22} h_1^*+a_{32}a_{11} h_2^* < 0$ and $h_3^* < 0$, then the predator $x_3$ will be extinct.

(Ⅱ) If ${a_{11}}{a_{22}}h_3^*+a_{31}a_{22} h_1^*+a_{32}a_{11} h_2^* = 0$, $h_3^* < 0$ and $\limsup\limits_{t\rightarrow +\infty } \frac{\sum_{j = 1, 0 < t_k < t}^k\ln(1+\alpha_{ij})}{\ln t} < \infty(i = 1, 2, 3)$, then the predator $x_3$ is non-persistent in the mean.

(Ⅲ) If $h_3^* > 0$, $a_{31}a_{22}h_1^*+a_{11}a_{32}h_2^*+a_{11}a_{22}h_3^* > a_{32}a_{11}a_{21}\overline{x_1}^*+a_{31}a_{22}a_{12}\overline{x_2}^*$

and $\limsup\limits_{t\rightarrow +\infty } \frac{\sum_{j = 1, 0 < t_k < t}^k\ln(1+\alpha_{ij})}{\ln t} < \infty$$(i = 1, 2, 3)$, then predator $x_3$ is weakly persistent in the mean.

Proof. Case (Ⅰ). If $h_i^* \le 0$$(i = 1, 2)$ $a.s.$, $\overline{x_i}^* = 0(i = 1, 2)$ a.s. can be obtained by Theorem 3. Since superior limit $h_3^* < 0$, for $\forall\varepsilon > 0$, $\exists T > 0$ such that $h_3(t) < h_3^*+\varepsilon$, for all $t > T$. From (4.3), we get

In order to seek the type on the limit, we have

Thus, $\lim\limits_{t\rightarrow +\infty}x_3(t) = 0, a.s.$ If $h_i^* > 0(i = 1, 2)$, from (4.1), (4.2) and (4.4), we can obtain

Using Lemma 3.2 in ^[25], we have

From (4.3) and (4.7), we see

So, $\lim\limits_{t\rightarrow +\infty}x_3(t) = 0, a.s.$ If $h_1^* > 0, h_2^* = 0$ or $h_1^* = 0, h_2^* > 0$, we can also obtain the same result. Here we omit the proof.

Case (Ⅱ). It has been proved from case (Ⅰ) that if $h_i^* \le 0(i = 1, 2)$, we can get $\lim_{t\rightarrow \infty}x_3(t) = 0$, a.s. That is, $\overline{x_3(t)}^* = 0$, a.s. Now suppose $h_i^* > 0(i = 1, 2)$. If $\overline{x_3(t)}^* > 0$, a.s., $[t^{-1}\ln x_3(t)]^* = 0.$ a.s. is obtained from Lemma 1 and from assumption $\limsup_{t\rightarrow \infty} \frac{\sum_{j = 1, 0 < t_k < t}^{k} \ln(1+\alpha_{3k})}{\ln t} < \infty$. By (4.3), we have

On the flip hand, for $\forall\varepsilon > 0$, $\exists$ $T > 0$, then

From (4.3), we get

Using Lemma 3.2 in ^[25], we have

which indicates that

Substituting (4.7) into the above inequality yields

Then conflict arises. Thus, $\overline{x_3}^* = 0$ a.s.

Case (Ⅲ). Multiplying (4.1)–(4.3) by $a_{31}a_{22}$, $a_{32}a_{11}$ and $a_{11}a_{22}$, respectively, we find

Local martingale, the strong law was applied to get $\lim_{t\rightarrow \infty} \frac{\int_0^t a_{31}a_{22}\sigma_1dB_1}{t} = 0$, $\lim_{t\rightarrow \infty} \frac{\int_0^t a_{32}a_{11}\sigma_2dB_2}{t} = 0$, $\lim_{t\rightarrow \infty} \frac{\int_0^t a_{11}a_{22}\sigma_3dB_3}{t} = 0, a.s$. To find the superior limit of (4.8) and noting that $(t^{-1}\ln x_i(t))^*\le 0, 1 \leq i\leq 3\; a.s.$, we have

That is

So $\overline{x_3}^* > 0$ a.s., i.e., the predator $x_3$ is weakly persistent in the mean.

The proof is therefore completed. □

Corollary 2. (Ⅰ) If, in addition to ($T_2$), the model (1.1) satisfies the condition $a_{31}a_{22}(r_1-0.5\sigma_1^2)+a_{32}a_{11}(r_2-0.5\sigma_2^2)\leq a_{11}a_{12}(r_3+0.5\sigma_3^2)$, the predator $x_3$ will be extinct.

(Ⅱ) If, in addition to ($T_2$), the model (1.1) satisfies the condition $a_{31}a_{22}(r_1-0.5\sigma_1^2)+a_{32}a_{11}(r_2-0.5\sigma_2^2) = a_{11}a_{12}(r_3+0.5\sigma_3^2)$, the predator $x_3$ is non-persistent in the mean.

Proof. From ($T_2$), we know that $\sum_{j = 1, 0 < t_k < t}^{k}\ln(1+\alpha_{ij}) = \ln\prod_{j = 1, 0 < t_k < t}^{k}(1+\alpha_{ij})$, $1\leq i\leq 3$, is bounded variable. So, $\limsup_{t\rightarrow \infty} \frac{\sum_{j = 1, 0 < t_k < t}^{k}\ln(1+\alpha_{ij})}{\ln t} = \limsup_{t\rightarrow \infty} \frac{\ln\prod_{j = 1, 0 < t_k < t}^{k}(1+\alpha_{ij})}{\ln t} = 0, \; 1\leq i\leq 3$.

Based on $h_i^* = r_i-0.5\sigma_i^2, \; (1 \leq i\leq 2), \; t > 0,$ and $h_3^* = -r_3-0.5\sigma_3^2, \; t > 0$, we have the following conclusions.

1) If $a_{31}a_{22}(r_1-0.5\sigma_1^2)+a_{32}a_{11}(r_2-0.5\sigma_2^2) < a_{11}a_{22}(r_3+0.5\sigma_3^2)$, then $a_{31}a_{22}h_3^*+a_{31}a_{22}h_1^*+a_{32}a_{11}h_2^* < 0$ and $h_3^* < 0$ hold. From Theorem 4, the predator $x_3$ will be extinct.

2) If $a_{31}a_{22}(r_1-0.5\sigma_1^2)+a_{32}a_{11}(r_2-0.5\sigma_2^2) = a_{11}a_{22}(r_3+0.5\sigma_3^2)$, then $a_{31}a_{22}h_3^*+a_{31}a_{22}h_1^*+a_{32}a_{11}h_2^* = 0$ and $h_3^* < 0$ hold. From Theorem 4, the predator $x_3$ is non-persistent in the mean. □

Remark 2. When $a_{13} = a_{23} = a_{31} = a_{32} = a_{33} = 0$, $r_3 = 0$, $\tau_{ij(}t) = 0$, $\sigma_3 = 0$, the model (1.1) degenerates into the model studied in Wu et al. ^[23]. Theorems 3 and 4 include some results of Wu et al. ^[23] as a special case.

Practical exponential stability is a kind of asymptotic stability with good properties and a kind of Lyapunov stability. According to Lemmas 2 and 3 in ^[15], we obtain the first moment practical exponential stability of the system. The system (2.1) is also considered to be $p$th moment exponential stability ^[30]. Indeed, ignoring the impulse in Theorem 3.1 in ^[30], the theorem reduces to Lemma 2 in ^[15]. Practical exponential stability means to some extent the permanence of the population. The system (2.1) is considered to be $p$th moment exponential stability^[30].

Proof. The proof is similar to ^[30], here we omit it. □

Theorem 5. Let $R_i = r_i+\sum_{j = 1}^k\ln(1+\alpha_{ij})(i = 1, 2)$, $R_3 = -r_3+\sum_{j = 1}^k\ln(1+\alpha_{3j})$, and $2a_{11}a_{22}a_{33}A_3-a_{22}a_{31}^2A_1-a_{11}a_{32}^2A_2 \neq 0$.

$I = \frac{a_{11}a_{22}(R_3-a_{33}A_3)^2}{4a_{11}a_{22}a_{33}A_3-2a_{22}a_{31}^2A_1-2a_{11}a_{32}^2A_2} +$ $A_1(2a_{11})^{-1}(\frac{R_1}{A_1}-a_{11}-a_{21}+a_{31})^2 +A_2(2a_{22})^{-1}(\frac{R_2}{A_2}-a_{12}-a_{22}+a_{32})^2 +(R_1+R_2+R_3)+\frac {\sigma_1^2 +\sigma_2^2 +\sigma_3^2}{2}$. Assume that $A_{ij}(t-\tau_{ij}(t))<A_{ij}(t)$, $(T_1)$, $(T_2)$ and the Razumikhin conditions hold

where $t\ge 0, i, j = 1, 2, 3$. If $I > 0$, then model (3.1) is $1$th moment practical exponential stability, that is model (1.1) is $1$th moment persistence. On the contrary, when $I < 0$, then model (3.1) is 1st moment exponential stability, that is model (1.1) is 1st moment extinction.

Proof. Let $V_i(y) = y_i+\ln (y_i+1)$, $V(y) = V_1+V_2+V_3$.

Then

From (4.9) and (4.11), we get

The constructed $V$ function, and inequality (4.18)–(4.20) satisfies the Lemma 2 in ^[15], then

Similarly, we have

So

If $I > 0$, the system (1.1) is 1st moment practical exponential stability. $I < 0$, the system (3.1) is 1st moment exponential stability. Practical exponential stability means to some extent the permanence of the population, exponential stability implies a degree of extinction. □

Corollary 3. (Ⅰ) In addition to ($T_2$) and (4.18), if the model (1.1) meets the following conditions

then

(Ⅰ)

the system (1.1) is 1st moment persistence.

(Ⅱ)

the system (1.1) is 1st moment extinction.

Proof. If the condition (4.17)–(4.19) hold, from (4.16), we have

From Theorem 5, the Corollary 3 is true.

In fact, when $\alpha_{ij} = 0, 1\leq i \leq 3$, $j = 1, 2, \cdots$, then $A_i = 1, 1\leq i\leq3$ and $R_i = r_i+\sum_{j = 1}^k\ln (1+\alpha_{ij}) = r_i, 1\leq i\leq3$. From (4.17)–(4.19), we have $r_i = R_i = a_{1i}+a_{2i}-a_{3i}, 1\leq i\leq 2$, $r_3 = R_3 = a_{33}$. The following conditions can be obtained by using Corollary {3}. □

Remark 3. Since the model (1.1) contains time delay, it is a non-Markov process. In solving the stability of non-Markovian processes, it is transformed into solving the stability of Markovian processes by applying Razumikhin's inequality. In some cases, a non-Markovian process can produce Markovian effects.

5.   Results

In this section, the numerical simulation results prove the correctness of Theorem 5. We will give some reasonable parameters to get the corresponding time series diagram and corresponding histogram, which can more intuitively reflect the persistence and extinction of the population. In addition, we discussed how impulse and white noise affect the persistence and extinction in model.

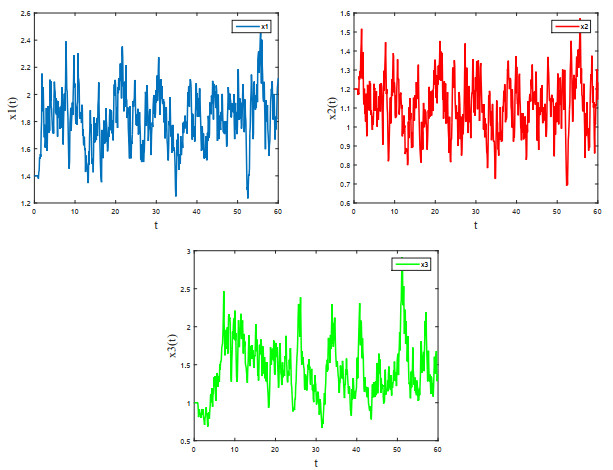
Case 1. Set up the system of the initial value (1.1) is $(x_{10}, x_{20}, x_{30})^\top = (1, 1.2, 1.4)^\top$. We have chosen the parameters values as $r_1 = 0.2$, $r_2 = 0.2$, $r_3 = 0.9$, $a_{11} = 0.3$, $a_{12} = 0.3$, $a_{13} = 0.2$, $a_{21} = 0.2$, $a_{22} = 0.4$, $a_{23} = 0.1$, $a_{31} = 0.6$, $a_{32} = 0.4$, $a_{33} = 0.6$, $\sigma_1 = 1$, $\sigma_2 = 1$, $\sigma_3 = 1$, $\alpha_{1k} = 0$, $\alpha_{2k} = 0$, $\alpha_{3k} = e^{\frac{1}{k^2}}-1$, $\tau_{ij}(t) = 0.3+0.1 \sin t$. By calculating $I > 0$, the theorem condition is satisfied. See Figure 1 for details. In bio-mathematics, practical exponential stability usually refers to the stable property of a dynamic system, which describes the exponential rate at which the state of the system tends to a stable state when the system experiences some perturbation.

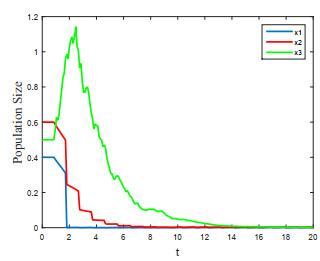
Case 2. Set up the system of the initial value (1.1) for $(0.4, 0.6, 0.5)^\top$. We have chosen the parameters values as $r_1 = 0.2$, $r_2 = 0.07$, $r_3 = 0.9$, $a_{11} = 0.3$, $a_{12} = 0.23$, $a_{13} = 0.6$, $a_{21} = 0.1$, $a_{22} = 0.3$, $a_{23} = 0.16$, $a_{31} = 1.2$, $a_{32} = 1.1$, $a_{33} = 0.1$, $\sigma_1 = 0.001$, $\sigma_2 = 0.001$, $\sigma_3 = 0.5$, $\alpha_{1k} = e^\frac{1}{k^2}-2$, $\alpha_{1k} = e^\frac{1}{k^2}-1.5$, $\alpha_{3k} = e^{\frac{1}{k^2}}-1$, $\tau_{ij}(t) = 0.1+0.1\sin t$. According to Theorem 5, all the species are 1st moment extinction. See Figure 2 for details. The significance of exponential stability in bio-mathematics is that it can help us predict the population dynamics of individual species in an ecosystem and assess the effects of different disturbance factors on ecosystem stability. This will help us better protect and manage ecosystems and maintain ecological balance and biodiversity.

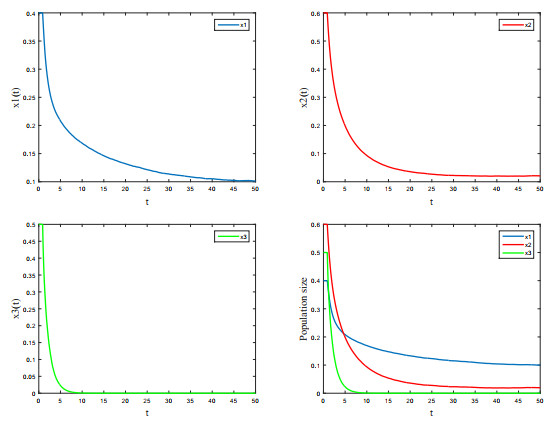
Case 3. Set up the system of the initial value (1.1) for $(0.4, 0.6, 0.5)^\top$. We have chosen the parameters values as $r_1 = 0.01$, $r_2 = 0.01$, $r_3 = 1.6$, $a_{11} = 0.24$, $a_{12} = 0.15$, $a_{13} = 0.7$, $a_{21} = 0.4$, $a_{22} = 0.6$, $a_{23} = 0.15$, $a_{31} = 0.8$, $a_{32} = 1.3$, $a_{33} = 1.8$, $\sigma_1 = 0.0001$, $\sigma_2 = 0.0001$, $\sigma_3 = 0.0001$, $\alpha_{1k} = 0$, $\alpha_{2k} = 0$, $\alpha_{3k} = e^{\frac{1}{k^2}}-1$. Extinction means that all populations in the system have disappeared, that is, completely extinct. In ecology, extinction usually refers to the disappearance or extinction of a species. A species is considered extinct if it can no longer reproduce or survive in its natural environment.

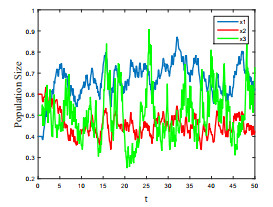
Case 4. All parameters are the same as case 3. We modify the intensity of white noise $\sigma_1 = 0.2$, $\sigma_2 = 0.1$, $\sigma_3 = 1$. The mean-square weak persistence parameter is used to describe the magnitude of change in the number of individuals in a system. It represents the change trend of the population number in the system from the perspective of time series. The larger the mean square weak persistence parameter, the more drastic the population fluctuation and the worse the stability of the system.

Remark 4. As shown in Figures 3 and 4, the model is unstable under the condition of normal pulse and weak white noise. By increasing the intensity of white noise appropriately, the model can be changed from weak persistent to persistent.

Remark 5. When the intensity of the white noise is high or the intensity of the pulse is high, it will cause the extinction of the population. Under the condition of bounded pulse intensity, the impulsive perturbation does not affect the practical exponential stability of species in time average. We get the same conclusion as Lu et al. ^[11]. When the delay of our model is 0, the three-dimensional model becomes a two-dimensional model, and we generalize the partial work of Lu et al. ^[11].

Remark 6. Under the Razumikhin condition, the future population development will be better than the past population development, and since this process is a Markov process, plus Lipschitz condition, the solution of the model is globally unique.

Remark 7. In the study of the extinction, non-persistence in mean square and mean square weak persistence of preys are only described by the relationship between pulse parameters and noise intensity parameters. However, the sufficient condition to obtain the practical exponential stability of the population is the characterization of the relationship between noise, pulse intensity and equation coefficient. Practical exponential stability uses more comprehensive parameters. At the same time, delay has no effect on the persistence, extinction and practical exponential stability of the stochastic system.

6.   Conclusions

This paper has studied the persistence, extinction and practical exponential stability of impulsive stochastic competition models with time-varying delays. The paper has obtained the following facts: The impulsive perturbation does not affect the practical exponential stability under the condition of bounded pulse intensity. In solving the stability of non-Markovian processes, it can be transformed into solving the stability of Markovian processes by applying Razumikhin inequality. In some cases, a non-Markovian process can produce Markovian effects. Finally, numerical simulations obtained the importance and validity of the theoretical results for the existence of practical exponential stability through the relationship between parameters, pulse intensity and noise intensity.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported in part by the National Natural Science Foundation of China under Grant (61972235), and in part by the Scientific Research Startup Fund for Shenzhen High-Caliber Personnel of SZPT (6021310027K).

Conflict of interest

No conflicts.