Depth and Stanley depth of the edge ideals of multi triangular snake and multi triangular ouroboros snake graphs

1.   Introduction

Let $S : = K[x_{1}, \ldots, x_{r}]$ be a polynomial algebra over a filed $K$. Let $X$ be a finitely generated $\mathbb{Z}^{r}$-graded $S$-module. A Stanley decomposition of $X$ is a presentation of $K$-vector space $X$ as a finite direct sum

where $z_{f}\in X$ is a homogeneous element and $W_{f}\subset \{x_{1}, \ldots, x_{r}\}$ and $z_{f}K[W_{f}]$ is the $K$-subspace of $X$ generated by all elements $z_fb$, where $b$ is a monomial in $K[W_{f}]$. The $\mathbb{Z}^{r}$-graded $K$-subspace $z_{f}K[W_{f}]\subset X$ is called a Stanley space of dimension $|W_{f}|$, if $z_{f}K[W_{f}]$ is a free $K[W_{f}]$-module. Define

The number ${{\rm{sdepth}}}(\mathcal{T})$ is called the Stanley depth of decomposition $\mathcal{T}$ and ${{\rm{sdepth}}}(X)$ is called the Stanley depth of $X$. Let $R$ be a local noetherian ring with a unique maximal ideal ${\bf{m}}$ and $X$ be a finitely generated $R$-module. The common length of all maximal $X$-sequences in ${\bf{m}}$ is called the depth of $X$. Stanley conjectured in ^[27] that for a ${\mathbb{Z}}^{r}$-graded module $X$, ${{\rm{sdepth}}}(X)\geq {\rm{depth}}(X)$. Afterwards, a number of articles have been published in which this conjecture has been discussed for different cases. This conjecture was disproved by Duval et al. in ^[8]. Stanley depth gained attention when Herzog et al. gave an algorithm in ^[10] for computing ${{\rm{sdepth}}}(X)$ for module of the type $X = Q_2/Q_1$, where $Q_1\subset Q_2\subset S$ are monomial ideals. Though the algorithm is useful for studying Stanley depth in some special cases, but computing Stanley depth by using this algorithm is a hard combinatorial problem, in general. In ^[24], Rinaldo gave a computer implementation for this algorithm, in the computer algebra system CoCoA. This algorithm is useful only when the ring has small number of variables. Therefore, it's worth giving values and bounds for Stanley depth of some classes of modules. For some literature related to depth and Stanley depth the readers are referred to ^{[7,12,14,15,16,20,22,23]}. Herzog conjectured in ^[11]:

Conjecture 1.1. (Herzog) Let $Q\subset S$ be a monomial ideal. Then ${{\rm{sdepth}}}(Q)\geq {{\rm{sdepth}}}(S/Q).$

The above conjecture has been proved in some special cases; see for instance ^{[13,17,21,23]}. In this paper we study depth and Stanley depth of the edge ideals and their residue class rings for some classes of graphs which we call multi triangular snake graphs and multi triangular ouroboros snake graphs. We find the exact values of depth and Stanley depth of the cyclic module associated to the triangular and multi triangular snake graphs, when $n\equiv 1\, (\mod\, 2)$ and give tight bounds when $n\equiv 0\, (\mod \, 2)$. We also find the exact values of depth and Stanley depth of cyclic modules associated to the triangular and multi triangular ouraboros snake graphs. In the last section of this paper we give a lower bound for Stanley depth of edge ideal of triangular and multi triangular snake and ouraboros snake graphs and we prove the the Conjecture 2.11 for the edge ideal of all classes of graphs we considered. The use of the computer algebra system CoCoA ^[28] is gratefully acknowledged.

2.   Definitions and notation

Let $G = (V(G), \, E(G))$ be a graph with vertex set $V(G)$ and edge set $E(G)$. A graph is called simple if it has no loops and no multiple edges. In this paper we consider only simple graphs. If $V(G) = \{x_1, x_2, \dots, x_r\}$ and $S = K[x_1, x_2, \dots\, , x_r]$, then the edge ideal $I(G)$ of the graph $G$ is the ideal of $S$ generated by all monomials of the form $x_ix_j$ such that $\{x_i, x_j\}\subset E(G).$ Note that by abuse of notation, $x_i$ will denote both a vertex of a graph $G$ and the corresponding variable of the given polynomial ring. For a given graph $G$, $K[V(G)]$ will denote the polynomial ring whose variables are the vertices of the graph $G$. If $G$ is a graph on $\{x_1, x_2, \dots, x_r\}$ vertices, then $G$ is called a ${\textbf{path}}$ if $E(G) = \{\{x_i, x_{i+1}\}:i = 1, 2, \dots, \, r-1\}$. A path on $r$ vertices is usually denoted by $P_r$. The number of edges in the path $P_r$ is called the length of $P_r$. Let $G$ be a connected graph. If $x_i, x_j\in V(G)$ then the distance between $x_i$ and $x_j$ is the length of the shortest path between $x_i$ and $x_j$, denoted by $d(x_i, x_j)$. The maximum distance between any two vertices of a graph $G$ is called the ${\textbf{diameter}}$ of $G$ and is denoted by ${\rm{diam}}(G)$. A vertex in a connected graph is a ${\textbf{cut}}\; {\textbf{vertex}}$ if removing it (and edges through it) disconnects the graph.

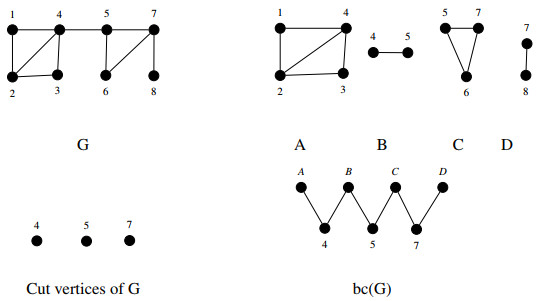
Definition 2.1. A ${\textbf{block}}$ of a graph $G$ is a maximal connected subgraph of $G$ that has no cut vertex. If $G$ itself is connected and has no cut vertex, then $G$ is a block.

Definition 2.2. (^[6]) The ${\textbf{block}}\; {\textbf{cut}}\; {\textbf{vertex}}$ graph of a connected graph $G$, denoted ${\rm{bc}}(G)$, is a graph whose vertices are the blocks and cut vertices of $G$. The edges of ${\rm{bc}}(G)$ join cut vertices with those blocks to which they belong.

An example of the block cut vertex graph ${\rm{bc}}(G)$, associated to a graph $G$, is given in Figure 1.

Definition 2.3. (^[25]) A ${\textbf{triangular}}\; {\textbf{snake}}$ is a connected graph in which all blocks are triangles and the block cut point (or block cut vertex) graph is a path. If we have $n$ blocks in a triangular snake graph then this graph is denoted by $\Delta_n$.

Definition 2.4. (^[26]) Let $n\geq1$ and $m\geq 2$, then $\Delta_{n, m}$ is a triangular snake with $n$ blocks and every block has $m$ number of triangles with one common edge.

Let $m, n\geq 1$. We call $\Delta_{n, m}$ an $m$-triangular snake. In particular, if $m = 1$, then $\Delta_{n, 1} = \Delta_n$ is a triangular snake, and if $m\geq2$, then we call $\Delta_{n, m}$ a multi triangular snake. For $i\in \{1, 2, \dots, n\}$, the vertices in the $i$-th block that are connected by the common edge of the $m$ triangles in $\Delta_{n, m}$ are labeled as $y_i$ and $y_{i+1}$, while the remaining vertices in the $i$-th block of $\Delta_{n, m}$ are labeled by $\{u_{i1}, u_{i2}, \dots, u_{im}\}$, see Figure 2 for examples and labeling of $\Delta_{n, m}$. Let $S_{n, m}: = K[V(\Delta_{n, m})]$ be the ring of polynomials whose variables are the vertices of $\Delta_{n, m}.$ Clearly, $|V(\Delta_{n, m})| = nm+n+1$ and $|E(\Delta_{n, m})| = 2nm+n$. For some more types of snake graphs, we refer readers to ^[18,19].

Let us consider a super graph $\Delta^{*}_{n, m}$ of the graph $\Delta_{n, m}$. For $m\geq 2$, the vertex and edge sets of $\Delta^{*}_{n, m}$ are $V(\Delta^{*}_{n, m}) = V(\Delta_{n, m}) \bigcup \{ u_{(n+1)1}, u_{(n+1)2}, \dots, u_{(n+1)m}\}$ and $E(\Delta^{*}_{n, m}) = E(\Delta_{n, m})\bigcup \{ y_{n+1}u_{(n+1)1}, y_{n+1}u_{(n+1)2}, \dots, y_{n+1}u_{(n+1)m}, \}$. See Figure 2 for example of $\Delta^{*} _{n, m}$.

Definition 2.5. The vertices $x_1$ and $x_2$ in a graph $G$ are said to be ${\textbf{fused}}\; {\rm{or}}\; {\textbf{merged}} \; {\rm{or}}\; {\textbf{identified}}$, if $x_1$ and $x_2$ are replaced by a single new vertex $x$, such that, every edge that was adjacent to either $x_1$ or $x_2$ or both, is adjacent to $x$.

If we fuse vertices $y_1$ and $y_{n+1}$ in the $\Delta_{n, m}$ graph, we get a new graph denoted $\Omega_{n, m}$, we call $\Omega_{n, m}$ an $m -{\textbf{triangular}}\; {\textbf{ouraboros}}\; {\textbf{snake}}$. In particular, if $m = 1$, then we call $\Omega_{n, 1}$ a triangular ouroboros snake, and if $m\geq2$, then we call $\Omega_{n, m}$ a multi triangular ouroboros snake. For $i\in \{1, 2, \dots, n\}$, the vertices of degree two in the $i$-th block of $\Omega_{n, m}$ are labeled as $\{u_{i1}, u_{i2}, \dots, u_{im}\}$, while the remaining vertices in the $i$-th block for $i\in \{2, \dots, n-1\}$ are labeled by $y_i$ and $y_{i+1}$. The fused vertex $v$ in $\Omega_{n, m}$ is labeled as $y_1$. Clearly, $|V(\Omega_{n, m})| = nm+n$ and $|E(\Omega_{n, m})| = 2nm+n$. Let us consider a super graph $\Delta^{**}_{n, m}$ of the graph $\Delta^{*}_{n, m}$. The vertex and edge sets of $\Delta^{**}_{n, m}$ are $V(\Delta^{**}_{n, m}) = V(\Delta^{*}_{n, m}) \bigcup \{q_{1}, q_{2}, \dots, q_{m}\}$ and $E(\Delta^{**}_{n, m}) = E(\Delta^{*}_{n, m})\bigcup \{y_{1}q_{1}, y_{1}q_{2}, \dots, y_{1}q_{m}\}$. See Figure 3 for examples of $\Delta^{**} _{n, m}$ and $\Omega_{m, n}.$

Definition 2.6. Let $k\geq 2$. A $k$-star denoted $\mathcal{S}_k$ is a graph on $k$ vertices, in which one vertex has degree $k-1$ and all other vertices have degree 1.

The following theorem give the values of depth and Stanley depth for the cyclic module associated to a $k$-star.

Theorem 2.7. ([1,Theorem 2.6]) Let $\mathcal{S}_k$ be a {$k$-{star}}. If $Q = I(\mathcal{S}_k)$, then ${\rm{depth}}({K[V(\mathcal{S}_k)]}/Q) = {{\rm{sdepth}}}({K[V(\mathcal{S}_k)]}/Q) = 1.$

Now we recall two lemmas that play a key role in proofs of our main theorems.

Lemma 2.8. ([23,Lemma 2.2])For a short exact sequence $0\rightarrow U_1\rightarrow U_2\rightarrow U_3\rightarrow 0$ of ${\mathbb{Z}}^{n}$-graded $S$-modules, we have

Lemma 2.9. (Depth Lemma) If $0\rightarrow U_1 \rightarrow U_2 \rightarrow U_3 \rightarrow 0$ is a short exact sequence of modules over alocal ring $S$, or a Noetherian graded ring with $S_0$ local, then

(1) ${\rm{depth}} (U_2) \geq \min\{{\rm{depth}}(U_1), {\rm{depth}}(U_3)\}$.

(2) ${\rm{depth}} (U_1) \geq \min\{{\rm{depth}}(U_2), {\rm{depth}}(U_3) + 1\}$.

(3) ${\rm{depth}} (U_3) \geq \min\{{\rm{depth}}(U_1)- 1, {\rm{depth}}(U_2)\}$.

We have the following intresting result of Biro et. al. for the graded maximal ideal of $S$.

Theorem 2.10. ([2,Theorem 2.2])Let ${\textbf{m}} = (x_1, x_2, \dots, x_r)$ be the graded maximal ideal of $S$. Then ${{\rm{sdepth}}}({\textbf{m}}) = \lceil\frac{r}{2}\rceil$, where $\lceil t\rceil$, with $t\in {\mathbb{Q}}$, denotes the smallest integer which is not less than $t$.

The following corollaries and lemmas are frequently used in this paper.

Corollary 2.11. ([3,Corollary 1.3])Let $Q$ be a monomial ideal of $S$. Then ${{\rm{sdepth}}}(S/Q)\leq {{\rm{sdepth}}}(S/(Q:q))$ for all monomials $q\notin Q$.

Corollary 2.12. ([23,Corollary 1.3]) Let $Q$ be a monomial ideal of $S$. Then ${\rm{depth}}(S/Q)\leq {\rm{depth}}(S/(Q:q))$ for all monomials $q\notin Q$.

Lemma 2.13. ([10,Lemma 3.6])Let $Q_1\subset Q_2$ be a monomial ideals of $S$ and $S^{'} = S[x_{r+1}]$ be the polynomial ring in variable $x_{r+1}$ over $S$. Then ${\rm{depth}}(Q_2S^{'}/Q_1S^{'}) = {\rm{depth}}(Q_2/Q_1) + 1$ and ${{\rm{sdepth}}}(Q_1S^{'}/Q_1S^{'}) = {{\rm{sdepth}}}(Q_2/Q_1) +1.$

Lemma 2.14. ([13,Lemma 4.1])Let $A_1$ and $A_2$ be two non-empty subsets of $\{x_1, x_2, \dots, x_r\}$ and $A_1\cap A_2 = \emptyset$. If $Q_1 \subset K[A_1]\, \, \mathit{{\rm{and}}} \, \, Q_2 \subset K[A_2]$ are squarefree monomial ideals such that ${{\rm{sdepth}}}_{K[A_1]}(Q_1) > {{\rm{sdepth}}}(K[A_1]/Q_1).$ Then

Fouli et al. gave the following lower bound for depth and Stanley depth of $S/I(G)$.

Theorem 2.15. ([9,Theorems 3.1 and 4.18])Let $G$ be a connected graph. If $Q = I(G)\subset S$ and $\delta = {\rm{diam}}(G)$, then ${\rm{depth}}(S/Q), {{\rm{sdepth}}}(S/Q)\geq \Big\lceil\frac{\delta+1}{3}\Big\rceil.$

We end this section with the following elementary lemma for the Stanley depth of $I(\mathcal{S}_k)$.

Lemma 2.16. Let $k\geq2$. If $Q = I(\mathcal{S}_k)$, then ${{\rm{sdepth}}}_{K[V(\mathcal{S}_k)]}(Q) = 1+\lceil\frac{k-1}{2}\rceil.$

Proof. Since $Q = I(\mathcal{S}_k) = (xy_1, xy_2, \dots, x y_{k-1})$, then $Q = xQ^{'}$ and $Q^{'} = (I:x) = (y_1, y_2, \dots, y_{k-1})$. By Lemma 2.13 and Theorem 2.10, we have ${{\rm{sdepth}}}_{K[V(\mathcal{S}_k)]}(Q) = {{\rm{sdepth}}}_{K[V(\mathcal{S}_k)]}(Q^{'}) = {{\rm{sdepth}}}_T(Q^{'})+1$, where $T = K[y_1, y_2, \dots, y_{k-1}]$. Now using [4,Theorem 1.1], we get ${{\rm{sdepth}}}_{K[V(\mathcal{S}_k)]}(Q) = \lceil\frac{k-1}{2}\rceil+1.$

3.   Depth and Stanley depth of cyclic modules associated to the triangular snake and multi triangular snake graphs

In this section we find the value of depth and Stanley depth of the cyclic module $S_{n, m}/I(\Delta_{n, m})$ when $n\equiv 1\, (\mod\, 2)$, and give tight bounds when $n\equiv 0\, (\mod\, 2)$. For this purpose, we first find depth and Stanley depth of the cyclic module $S^{*}_{n, m}/I(\Delta^{*}_{n, m})$. We will use these results in our main proofs.

Lemma 3.1. Let $n, m\geq1$. Then ${\rm{depth}}(S^{*}_{n, m}/I(\Delta^{*}_{n, m})) = {{\rm{sdepth}}}(S^{*}_{n, m}/I(\Delta^{*}_{n, m})) = \lceil\frac{n+1}{2}\rceil$.

Proof. Let us consider two sets, $A_{n, m}: = \{y_{n}, u_{n1}, u_{n2}, \dots, u_{nm}, u_{(n+1)1}, u_{(n+1)2}, \dots, u_{(n+1)m}\}$ and $A^{'}_{n, m}: = \{u_{(n+1)1}, u_{(n+1)2}, \dots, u_{(n+1)m}\}$. We have the following short exact sequence:

If $n = 1$, then $(I(\Delta^{*}_{1, m}):y_{2}) = (A_{1, m})$ and $S^{*}_{1, m}/(I(\Delta^{*}_{1, m}):y_{2})\cong K[y_2]$, so ${\rm{depth}}(S^{*}_{1, m}/(I(\Delta^{*}_{1, m}):y_{2})) = 1.$ Since $(I(\Delta^{*}_{1, m}), y_{2}) = (I(\mathcal{S}_{m+1}), y_2)$ and $S^{*}_{1, m}/(I(\Delta^{*}_{1, m}), y_{2})\cong K[V(\mathcal{S}_{m+1})]/I(\mathcal{S}_{m+1})[A^{'}_{1, m}]$, thus by Theorem 2.7 and Lemma 2.13, we get ${\rm{depth}}(S^{*}_{1, m}/(I(\Delta^{*}_{1, m}), y_{2})) = 1+m.$ Hence by Depth Lemma ${\rm{depth}}(S^{*}_{1, m}/I(\Delta^{*}_{1, m})) = 1$, as required. If $n = 2$, then $(I(\Delta^{*}_{2, m}):y_{3}) = (I(\mathcal{S}_{m+1}), A_{2, m})$ and $S^{*}_{2, m}/(I(\Delta^{*}_{2, m}):y_{3})\cong K[V(\mathcal{S}_{m+1})]/I(\mathcal{S}_{m+1})[y_3],$ again by Lemma 2.13 and Theorem 2.7 ${\rm{depth}}(S^{*}_{2, m}/(I(\Delta^{*}_{2, m}):y_{3})) = 1+1 = 2.$ Also we have, $(I(\Delta^{*}_{2, m}), y_{3}) = (I(\Delta^{*}_{1, m}), y_{3})$ and $S^{*}_{2, m}/(I(\Delta^{*}_{2, m}), y_{3}) \cong S^{*}_{1, m}/I(\Delta^{*}_{1, m})[A^{'}_{2, m}]$, thus by case $n = 1$ and Lemma 2.13, ${\rm{depth}}(S^{*}_{2, m}/(I(\Delta^{*}_{2, m}), y_{3})) = 1+m.$ Hence by Depth Lemma, ${\rm{depth}}(S^{*}_{2, m}/I(\Delta^{*}_{2, m})) = 2$, this proves the result for $n = 2$. Let $n\geq 3$. We have $(I(\Delta^{*}_{n, m}):y_{n+1}) = (I(\Delta^{*}_{n-2, m}), A_{n, m})$ and $(I(\Delta^{*}_{n, m}), y_{n+1}) = (I(\Delta^{*}_{n-1, m}), y_{n+1})$, thus $S^{*}_{n, m}/(I(\Delta^{*}_{n, m}):y_{n+1})\cong S^{*}_{n-2, m}/I(\Delta^{*}_{n-2, m})[y_{n+1}]$ and $S^{*}_{n, m}/(I(\Delta^{*}_{n, m}), y_{n+1}) \cong S^{*}_{n-1, m}/I(\Delta^{*}_{n-1, m}) [A^{'}_{n, m}].$ Now by induction on $n$ and Lemma 2.13 we get ${\rm{depth}}(S^{*}_{n, m}/(I(\Delta^{*}_{n, m}):y_{n+1})) = \lceil\frac{n-1}{2}\rceil+1 = \lceil\frac{n+1}{2}\rceil$ and ${\rm{depth}}(S^{*}_{n, m}/(I(\Delta^{*}_{n, m}), y_{n+1})) = \lceil\frac{n}{2}\rceil+m = \lceil\frac{n+2m}{2}\rceil.$ Hence by Depth Lemma ${\rm{depth}}(S^{*}_{n, m}/I(\Delta^{*}_{n, m})) = \lceil\frac{n+1}{2}\rceil.$

Applying Lemma 2.8 instead of Depth Lemma on the above short exact sequence and proceeding on the same lines we get, ${{\rm{sdepth}}}(S^{*}_{n, m}/(I(\Delta^{*}_{n, m}))) \geq \lceil\frac{n+1}{2}\rceil.$ Now we prove that this lower bound is an upper bound as well. Since $y_{n+1}\notin I(\Delta^{*}_{n, m})$, by Corollary 2.11, we get ${{\rm{sdepth}}}(S^{*}_{n, m}/I(\Delta^{*}_{n, m})) \leq {{\rm{sdepth}}}(S^{*}_{n, m}/(I(\Delta^{*}_{n, m}):y_{n+1}))$. Using the same arguments as we used in the case of depth, ${{\rm{sdepth}}}(S^{*}_{1, m}/(I(\Delta^{*}_{1, m}):y_{2})) = 1$ and ${{\rm{sdepth}}}(S^{*}_{2, m}/(I(\Delta^{*}_{2, m}):y_{3})) = 2$. This implies that ${{\rm{sdepth}}}(S^{*}_{n, m}/I(\Delta^{*}_{n, m}))\leq \lceil\frac{n+1}{2}\rceil$, for $n = 1, 2$. Let $n\geq 3$. Then ${{\rm{sdepth}}}(S^{*}_{n, m}/I(\Delta^{*}_{n, m})) \leq {{\rm{sdepth}}}(S^{*}_{n, m}/(I(\Delta^{*}_{n, m}):y_{n+1})) = {{\rm{sdepth}}} (S^{*}_{n-2, m}/I(\Delta^{*}_{n-2, m})[y_{n+1}])$. The proof follows by applying induction on $n$.

Theorem 3.2. Let $n, m\geq1$. Then $\lceil\frac{n}{2}\rceil\leq{\rm{depth}}(S_{n, m}/I(\Delta_{n, m})), {{\rm{sdepth}}}(S_{n, m}/I(\Delta_{n, m}))\leq \lceil\frac{n+1}{2}\rceil.$

Proof. Let $B_{n, m}: = \{y_n, u_{n1}, u_{n2}, \dots, u_{nm}\}$ be a set of variables. Consider the following short exact sequence:

If $n = 1$, then $(I(\Delta_{1, m}):y_{2}) = (B_{1, m})$ and $S_{1, m}/(I(\Delta_{1, m}):y_{2})\cong K[y_2]$, so ${\rm{depth}}(S_{1, m}/(I(\Delta_{1, m}):y_{2})) = 1$. Also $(I(\Delta_{1, m}), y_{2}) = (I(\mathcal{S}_{m+1}), y_2)$, that is, $S_{1, m}/(I(\Delta_{1, m}), y_{2}) \cong K[V(\mathcal{S}_{m+1})]/I(\mathcal{S}_{m+1})$, so by Theorem 2.7 ${\rm{depth}}(S_{1, m}/(I(\Delta_{1, m}), y_{2})) = 1.$ Hence by Depth Lemma ${\rm{depth}}(S_{1, m}/I(\Delta_{1, m})) = 1$. If $n = 2$, then $(I(\Delta_{2, m}):y_{3}) = (I(\mathcal{S}_{m+1}), B_{2, m}),$ and $S_{2, m}/(I(\Delta_{2, m}):y_{3})\cong K[V(\mathcal{S}_{m+1})]/I(\mathcal{S}_{m+1})[y_3].$ By Lemma 2.13 and Theorem 2.7 ${\rm{depth}}(S_{2, m}/(I(\Delta_{2, m}):y_{3})) = 2.$ We have $(I(\Delta_{2, m}), y_{3}) = (I(\Delta^{*}_{1, m}), y_{3})$ and $S_{2, m}/(I(\Delta_{2, m}), y_3) \cong S^{*}_{1, m}/I(\Delta^{*}_{1, m}),$ thus by case $n = 1$, ${\rm{depth}}(S_{2, m}/(I(\Delta_{2, m}), y_{3})) = 1.$ Applying Depth Lemma, we get ${\rm{depth}}(S_{2, m}/I(\Delta_{2, m}))\geq 1$. Since $y_3\notin I(\Delta_{2, m})$, by Corollary 2.12, we get ${\rm{depth}}(S_{2, m}/I(\Delta_{2, m})) \leq {\rm{depth}}(S_{2, m}/(I(\Delta_{2, m}):y_{3})).$ This shows that ${\rm{depth}}(S_{2, m}/I(\Delta_{2, m}))\leq 2,$ which proves the result for $n = 2$. Let $n\geq3$. We have $(I(\Delta_{n, m}):y_{n+1}) = (I(\Delta^{*}_{n-2, m}), B_{n, m}),$ that is, $S_{n, m}/(I(\Delta_{n, m}):y_{n+1})\cong (S^{*}_{n-2, m}/(I(\Delta^{*}_{n-2, m})))[y_{n+1}]$. Also we have that $(I(\Delta_{n, m}), y_{n+1}) = (I(\Delta^{*}_{n-1, m}), y_{n+1})$ and $S_{n, m}/I(\Delta_{n, m}), y_{n+1}) \cong S^{*}_{n-1, m}/(I(\Delta^{*}_{n-1, m})$. By Lemmas 3.1 and 2.13 we have ${\rm{depth}}(S_{n, m}/(I(\Delta_{n, m}):y_{n+1})) = \lceil\frac{n+1}{2}\rceil$, ${\rm{depth}}(S_{n, m}/(I(\Delta_{n, m}), y_{n+1})) = \lceil\frac{n}{2}\rceil$ and by Depth Lemma, ${\rm{depth}}(S_{n, m}/I(\Delta_{n, m}))\geq \lceil\frac{n}{2}\rceil$. For the upper bound since $y_{n+1}\notin I(\Delta_{n, m})$ by Corollary 2.12, we get ${\rm{depth}}(S_{n, m}/I(\Delta_{n, m}))\leq {\rm{depth}}(S_{n, m}/(I(\Delta_{n, m}):y_{n+1})) = \lceil\frac{n+1}{2}\rceil$.

Proof for Stanley depth is similar we use Lemma 2.8 instead of Depth Lemma and Corollary 2.11 instead of Corollary 2.12.

Corollary 3.3. If $n\equiv 1\, (\mod 2)$, then ${\rm{depth}}(S_{n, m}/I(\Delta_{n, m})) = {{\rm{sdepth}}}(S_{n, m}/I(\Delta_{n, m})) = \lceil\frac{n+1}{2}\rceil.$

Remark 3.4. If $n\geq2$ and $m\geq 1$, then our Theorem 3.2 says that ${\rm{depth}}(S_{n, m}/I(\Delta_{n, m})), {{\rm{sdepth}}}(S_{n, m}/I(\Delta_{n, m}))\in \big\{ \lceil\frac{n}{2}\rceil, \lceil\frac{n+1}{2}\rceil$\big\}. Whereas, one of the existing known bound for theses modules is given in Theorem 2.15, that is, ${\rm{depth}}(S_{n, m}/I(\Delta_{n, m})), {{\rm{sdepth}}}(S_{n, m}/I(\Delta_{n, m}))\geq\lceil\frac{{\rm{diam}}(\Delta_{n, m})+1}{3}\rceil = \lceil\frac{n+1}{3}\rceil$. This means that this bound is far away form the actual value for large values of $n$.

4.   Depth and Stanley depth of cyclic modules associated to the triangular ouroboros snake and multi triangular ouroboros snake graphs

In this section we find out the exact value of depth and Stanley depth of the cyclic module $T_{n, m}/I(\Omega_{n, m})$. For this purpose we first find depth and Stanley depth of the cyclic module $S^{**}_{n, m}/I(\Delta^{**}_{n, m})$ associated to the super graph $\Delta^{**}_{n, m}$ of $\Delta^{*}_{n, m}$. These results will be used in our main proofs.

Lemma 4.1. Let $n, m\geq1$. Then

Proof. Let $A_{n, m}$ and $A^{'}_{n, m}$ the sets as defined in Theorem 3.1. Consider the following short exact sequence:

If $n = 1$, then $(I(\Delta^{**}_{1, m}):y_{2}) = (A_{1, m})$ and $(I(\Delta^{**}_{1, m}), y_{2}) = (I(\mathcal{S}_{2m+1}), y_2)$. We have $S^{**}_{1, m}/(I(\Delta^{**}_{1, m}):y_{2})\cong K[y_2, q_1, q_2, \dots, q_m]$, and ${\rm{depth}}(S^{**}_{1, m}/(I(\Delta^{**}_{1, m}):y_{2})) = m+1$. Also we have $S^{**}_{1, m}/(I(\Delta^{**}_{1, m}), y_{2})\cong K[V(\mathcal{S}_{2m+1})]/I(\mathcal{S}_{2m+1})[A^{'}_{1, m}],$ so by using Theorem 2.7 and Lemma 2.13 we get ${\rm{depth}}(S^{**}_{1, m}/(I(\Delta^{**}_{1, m}), y_{2})) = 1+m.$ Hence by Depth Lemma ${\rm{depth}}(S^{**}_{1, m}/I(\Delta^{**}_{1, m})) = 1+m.$ If $n = 2$, then $(I(\Delta^{**}_{2, m}):y_{3}) = (I(\mathcal{S}_{2m+1}), A_{2, m})$ and $(I(\Delta^{**}_{2, m}), y_{3}) = (I(\Delta^{**}_{1, m}), y_{3})$, we have that $S^{**}_{2, m}/(I(\Delta^{**}_{2, m}):y_{3})\cong K[V(\mathcal{S}_{2m+1})]/I(\mathcal{S}_{2m+1})[y_3],$ and $S^{**}_{2, m}/(I(\Delta^{**}_{2, m}), y_{3})\cong S^{**}_{1, m}/I(\Delta^{**}_{1, m})[A^{'}_{2, m}]$. Thus by Lemma 2.13 and Theorem 2.7, ${\rm{depth}} (S^{**}_{2, m}/(I(\Delta^{**}_{2, m}):y_{3})) = 1+1 = 2.$ By Lemma 2.13 and case $n = 1$, we have ${\rm{depth}}(S^{**}_{2, m}/(I(\Delta^{**}_{2, m}), y_{3})) = m+1+m = 2m+1.$ Hence by Depth Lemma ${\rm{depth}}(S^{**}_{2, m}/I(\Delta^{**}_{2, m})) = 2$. Let $n\geq 3$. We have $(I(\Delta^{**}_{n, m}):y_{n+1}) = (I(\Delta^{**}_{n-2, m}), A_{n, m})$ and $(I(\Delta^{**}_{n, m}), y_{n+1}) = (I(\Delta^{**}_{n-1, m}), y_{n+1})$ it is easy to see that $S^{**}_{n, m}/(I(\Delta^{**}_{n, m}):y_{n+1})\cong (S^{**}_{n-2, m}/(I(\Delta^{**}_{n-2, m})))[y_{n+1}]$ and $S^{**}_{n, m}/(I(\Delta^{**}_{n, m}), y_{n+1})\cong S^{**}_{n-1, m}/I(\Delta^{**}_{n-1, m})[A^{'}_{n, m}]$. Thus by Lemma 2.13 we have

and

Case 1. If $n\equiv 0\, (\mod 2)$. Since $n-2\equiv 0\, (\mod 2)$ and $n-1\equiv 1\, (\mod 2)$ thus by induction on $n$, ${\rm{depth}}(S^{**}_{n, m}/(I(\Delta^{**}_{n, m}):y_{n+1})) = \big\lceil\frac{n-2+2}{2}\big\rceil+1 = \big\lceil\frac{n+2}{2}\big\rceil,$ and ${\rm{depth}}(S^{**}_{n, m}/(I(\Delta^{**}_{n, m}), y_{n+1})) = \big\lceil\frac{n+1}{2}\big\rceil+m.$ Applying Depth Lemma we get ${\rm{depth}}(S^{**}_{n, m}/I(\Delta^{**}_{n, m})) = \big\lceil\frac{n+2}{2}\big\rceil.$

Case 2. If $n\equiv 1\, (\mod 2)$. Since $n-2\equiv 1\, (\mod 2)$ and $n-1\equiv 0\, (\mod 2)$ thus by induction on $n$, ${\rm{depth}}(S^{**}_{n, m}/(I(\Delta^{**}_{n, m}):y_{n+1})) = \big\lceil\frac{n-1}{2}\big\rceil+1+m = \big\lceil\frac{n+1}{2}\big\rceil+m$ and ${\rm{depth}}(S^{**}_{n, m}/(I(\Delta^{**}_{n, m}), y_{n+1})) = \big\lceil\frac{n+1}{2}\big\rceil+m.$ Again by Depth Lemma ${\rm{depth}}(S^{**}_{n, m}/I(\Delta^{**}_{n, m})) = \big\lceil\frac{n+1}{2}\big\rceil+m$.

If $n = 1$, then proof for Stanley depth is similar to the proof for depth. If $n = 2$, then we use Lemma 2.8 on the short exact sequence and get ${{\rm{sdepth}}} (S^{**}_{2, m}/(I(\Delta^{**}_{2, m})))\geq 2$. Now by using Corollary 2.11 we have ${{\rm{sdepth}}} (S^{**}_{2, m}/(I(\Delta^{**}_{2, m})))\leq {{\rm{sdepth}}} (S^{**}_{2, m}/(I(\Delta^{**}_{2, m}):y_{3}))$. Using Lemma 2.13 and Theorem 2.7, we have ${{\rm{sdepth}}}(S^{**}_{n, m}/(I(\Delta^{**}_{n, m}):y_{3})) = {{\rm{sdepth}}}(K[V(\mathcal{S}_{2m+1})]/I(\mathcal{S}_{2m+1})[y_3]) = 1+1 = 2$, this completes the proof for case $n = 2$. Let $n\geq 3$.

and

Case 1. If $n\equiv 0\, (\mod 2)$. Since $n-2\equiv 0\, (\mod 2)$ and $n-1\equiv 1\, (\mod 2)$ thus by induction on $n$, ${{\rm{sdepth}}}(S^{**}_{n, m}/(I(\Delta^{**}_{n, m}):y_{n+1})) = \big\lceil\frac{n-2+2}{2}\big\rceil+1 = \big\lceil\frac{n+2}{2}\big\rceil,$ and ${{\rm{sdepth}}}(S^{**}_{n, m}/(I(\Delta^{**}_{n, m}), y_{n+1})) = \big\lceil\frac{n+1}{2}\big\rceil+m.$ By Lemma 2.8 we get ${{\rm{sdepth}}}(S^{**}_{n, m}/I(\Delta^{**}_{n, m}))\geq \big\lceil\frac{n+2}{2}\big\rceil$ and by Corollary 2.11 we have ${{\rm{sdepth}}}(S^{**}_{n, m}/I(\Delta^{**}_{n, m}))\leq\big\lceil\frac{n+2}{2}\big\rceil$.

Case 2. If $n\equiv 1\, (\mod 2)$. Since $n-2\equiv 1\, (\mod 2)$ and $n-1\equiv 0\, (\mod 2)$ thus by induction on $n$, ${{\rm{sdepth}}}(S^{**}_{n, m}/(I(\Delta^{**}_{n, m}):y_{n+1})) = \big\lceil\frac{n-1}{2}\big\rceil+1+m = \big\lceil\frac{n+1}{2}\big\rceil+m$ and ${{\rm{sdepth}}}(S^{**}_{n, m}/(I(\Delta^{**}_{n, m}), y_{n+1})) = \big\lceil\frac{n+1}{2}\big\rceil+m.$ By Lemma 2.8 we have ${{\rm{sdepth}}}(S^{**}_{n, m}/I(\Delta^{**}_{n, m}))\geq \big\lceil\frac{n+1}{2}\big\rceil+m$ and by Corollary 2.11 we have ${{\rm{sdepth}}}(S^{**}_{n, m}/I(\Delta^{**}_{n, m}))\leq\big\lceil\frac{n+1}{2}\big\rceil+m$.

Theorem 4.2. Let $n\geq3$ and $m\geq1$. Then

Proof. Consider the short exact sequence

Let $n = 3$. Clearly, $T_{3, m}/(I(\Omega_{3, m}):y_1)\cong K[y_1, u_{21}, u_{22}, \dots, u_{2m}]$, and $T_{3, m}/(I(\Omega_{3, m}), y_1) \cong S^{**}_{1, m}/I(\Delta^{**}_{1, m})$. We have ${\rm{depth}}(T_{3, m}/(I(\Omega_{3, m}):y_1)) = m+1$ and by Lemma 4.1, ${\rm{depth}}(T_{3, m}/(I(\Omega_{3, m}), y_1)) = m+1.$ Hence by Depth Lemma ${\rm{depth}}(T_{3, m}/I(\Omega_{3, m})) = m+1 = m+\lceil\frac{3-1}{2}\rceil$. If $n = 4$, then $T_{4, m}/(I(\Omega_{4, m}):y_1)\cong \big(K[V(\mathcal{S}_{2m+1})]/I(\mathcal{S}_{2m+1})\big)[y_1]$ and $T_{4, m}/(I(\Omega_{4, m}), y_1) \cong S^{**}_{2, m}/I(\Delta^{**}_{2, m}),$ by Lemmas 2.13, 4.1 and Theorem 2.7 ${\rm{depth}}(T_{4, m}/(I(\Omega_{4, m}):y_1)) = 1+1 = 2$ and ${\rm{depth}}(T_{4, m}/(I(\Omega_{4, m}), y_1)) = 2$. By Depth Lemma ${\rm{depth}}(T_{4, m}/I(\Omega_{4, m})) = 2 = \lceil\frac{4}{2}\rceil$. If $n\geq 5$, then $T_{n, m}/(I(\Omega_{n, m}):y_1)\cong (S^{**}_{n-4, m}/I(\Delta^{**}_{n-4, m}))[y_1]$ and $T_{n, m}/(I(\Omega_{n, m}), y_1) \cong S^{**}_{n-2, m}/I(\Delta^{**}_{n-2, m})$ By Lemma 2.13, ${\rm{depth}}(T_{n, m}/(I(\Omega_{n, m}):y_1)) = {\rm{depth}}(S^{**}_{n-4, m}/(I(\Delta^{**}_{n-4, m})))+1$ and similarly ${\rm{depth}}(T_{n, m}/(I(\Omega_{n, m}), y_1)) = {\rm{depth}}(S^{**}_{n-2, m}/I(\Delta^{**}_{n-2, m})).$

Case 1. If $n\equiv 0\, (\mod 2)$. Since $n-4\equiv 0\, (\mod 2)$ and $n-2\equiv 0\, (\mod 2)$ thus by Lemma 4.1, ${\rm{depth}}(T_{n, m}/I(\Omega_{n, m}):y_1) = \lceil\frac{n-2}{2}\rceil+1 = \lceil\frac{n}{2}\rceil$ and ${\rm{depth}}(T_{n, m}/I(\Omega_{n, m}), y_1) = \lceil\frac{n}{2}\rceil$. Using Depth Lemma we get ${\rm{depth}}(T_{n, m}/I(\Omega_{n, m})) = \lceil\frac{n}{2}\rceil$.

Case 2. If $n\equiv 1\, (\mod 2)$. Since $n-4\equiv 1\, (\mod 2)$ and $n-2\equiv 1\, (\mod 2)$ thus by Lemma 4.1, ${\rm{depth}}(T_{n, m}/I(\Omega_{n, m}):y_1) = \lceil\frac{n-1}{2}\rceil+m$ and ${\rm{depth}}(T_{n, m}/I(\Omega_{n, m}), y_1) = \lceil\frac{n-1}{2}\rceil+m$. Again by Depth Lemma we get ${\rm{depth}}(T_{n, m}/I(\Omega_{n, m})) = \lceil\frac{n-1}{2}\rceil+m$.

When $n = 3$, applying Lemma 2.8 instead of Depth Lemma and Lemma 4.1 and conclude that ${{\rm{sdepth}}}(T_{3, m}/(I(\Omega_{3, m})))\geq m+1.$ For the upper bound since $y_1\notin I(\Omega_{3, m})$ by Corollary 2.11, we get ${{\rm{sdepth}}}(T_{3, m}/I(\Omega_{3, m}))\leq {{\rm{sdepth}}}(T_{3, m}/(I(\Omega_{3, m}):y_1)).$ This implies that ${{\rm{sdepth}}}(T_{3, m}/I(\Omega_{3, m}))\leq m+1$ and the result follows. When $n = 4$, using Lemma 2.8, Corollary 2.11, Theorem 2.7, Lemmas 2.13 and 4.1 and proceeding with the same manner, we conclude that ${{\rm{sdepth}}}(T_{4, m}/I(\Omega_{4, m})) = 2 = \lceil\frac{4}{2}\rceil.$ If $n\geq5$, then

and

Proof for Stanley depth is similar we use Corollary 2.11 and Lemma 2.8 instead of Depth Lemma.

Remark 4.3. In Theorem 4.2 we have exact values for depth and Stanley depth of $T_{n, m}/I(\Omega_{n, m})$. By Theorem 2.15, we have ${\rm{depth}}(T_{n, m}/I(\Omega_{n, m})), {{\rm{sdepth}}}(T_{n, m}/I(\Omega_{n, m}))\geq \lceil\frac{{\rm{diam}}(\Omega_{n, m})}{3}\rceil.$ Since ${\rm{diam}}(\Omega_{n, m}) = \lceil\frac{n}{2}\rceil$ so we have ${\rm{depth}}(T_{n, m}/I(\Omega_{n, m})), {{\rm{sdepth}}}(T_{n, m}/I(\Omega_{n, m}))\geq \lceil\frac{n+2}{6}\rceil$. This shows that the bound given in Theorem 2.15 is too weak in this case.

5.   Stanley depth of edge ideals associated to the triangular and multi triangular snake and triangular and multi triangular ouroboros snake graphs

In this section, we find sharp lower bounds for the edge ideal of triangular and multi triangular snake and ouroboros snake graphs. These lower bounds are good enough to show that the Conjecture 2.11 holds in all cases.

Lemma 5.1. Let $n, m\geq 1$. Then ${{\rm{sdepth}}} (I(\Delta^{*}_{n, m})) \geq {{\rm{sdepth}}}(S^{*}_{n, m}/I(\Delta^{*}_{n, m}))+1+m = \lceil\frac{n+1}{2}\rceil+1+m$.

Proof. Let us define a set, $A_{n, m} = \{y_{n}, u_{n1}, u_{n2}, \dots, u_{nm}, u_{(n+1)1}, u_{(n+2)2}, \dots, u_{(n+1)m}\}$. As $y_{n+1}\not\in I(\Delta^{*}_{n, m})$, we have

Let $n = 1$. We have $I(\Delta^{*}_{1, m})\cap {\overline{S}_{1, m}} = (I(\mathcal{S}_{m+1})){\overline{S}_{1, m}} {\rm{ and }} (I(\Delta^{*}_{1, m}):y_{2})S^{*}_{1, m} = (A_{1, m})S^{*}_{1, m}.$ Therefore

By using Lemma 2.13 and Theorem 2.10, ${{\rm{sdepth}}} ((A_{1, m})S^{*}_{1, m}) = \lceil\frac{2m+1}{2}\rceil+1 = m+2.$ Also by Lemmas 2.16 and 2.13, we get

Thus ${{\rm{sdepth}}} (I(\Delta^{*}_{1, m}))\geq m+2 = \Big\lceil\frac{1+1}{2}\Big\rceil+1+m.$ Let $n = 2$. We get $I(\overline{S}_{2, m} (\Delta^{*}_{1, m})){\overline{S}_{2, m}}$ and $(I(\Delta^{*}_{2, m}):y_{3})S^{*}_{2, m} = (I(\mathcal{S}_{m+1}), A_{2, m}){\overline{S}_{2, m}}[y_3].$ This implies ${{\rm{sdepth}}} (I(\Delta^{*}_{2, m}))\geq \min\{{{\rm{sdepth}}}(I(\Delta^{*}_{1, m})){\overline{S}_{2, m}}, {{\rm{sdepth}}}(I(\mathcal{S}_{m+1}), A_{2, m}){\overline{S}_{2, m}}[y_3]\}.$ Now Lemma 2.13 and by [3,Theorem 1.3],

Now using Lemma 2.16, Theorems 2.10 and 2.7, we have

Also by the case $n = 1$ and Lemma 2.13, we get

Thus

Let $n\geq3.$ We have $I(\Delta^{*}_{n, m})\cap{\overline{S}_{n, m}} = (I(\Delta^{*}_{n-1, m})){\overline{S}_{n, m}}, \, \, {\rm{ and }}\, \, (I(\Delta^{*}_{n, m}):y_{n+1})S^{*}_{n, m} = ((I(\Delta^{*}_{n-2, m}), A_{n, m}){\overline{S}_{n, m}}[y_{n+1}]{).} \, \, {\rm{Thus}}$ by induction on $n$, Lemmas 2.14 and 2.13, we have ${{\rm{sdepth}}}((I(\Delta^{*}_{n-2, m}), A_{n, m}){\overline{S}_{n, m}}[y_{n+1}]) \geq {{\rm{sdepth}}}((S^{*}_{n-2, m}/I(\Delta^{*}_{n-2, m}))S^{*}_{n-2, m})+{{\rm{sdepth}}}((A_{n, m})K[A_{n, m}])+1.$ Now by Theorem 2.10, and Proposition 3.1, we have ${{\rm{sdepth}}} ((I(\Delta^{*}_{n-2, m}), A_{n, m}){\overline{S}_{n, m}}[y_{n+1}])\geq \lceil\frac{n-1}{2}\rceil+\lceil\frac{2m+1}{2}\rceil+1 = \lceil\frac{n+1}{2}\rceil+\lceil\frac{2m+1}{2}\rceil = \lceil\frac{n+1}{2}\rceil+m+1.$ Moreover, by induction on $n$ and Lemma 2.13, we get

Thus

Theorem 5.2. If $n = 1$ and $m\geq 1$, then ${{\rm{sdepth}}} (I(\Delta_{1, m}))\geq {{\rm{sdepth}}}(S_{1, m}/I(\Delta_{1, m}))+\lceil\frac{m}{2}\rceil = 1+\lceil\frac{m}{2}\rceil.$ And if $n\geq 2$ and $m\geq 1$, then ${{\rm{sdepth}}} (I(\Delta_{n, m}))\geq \lceil\frac{n+1}{2}\rceil+\lceil\frac{m+1}{2}\rceil\geq {{\rm{sdepth}}}(S_{n, m}/I(\Delta_{n, m}))+\lceil\frac{m+1}{2}\rceil.$

Proof. Let $B_{n, m} = \{y_n, u_{n1}, u_{n2}, \dots, u_{nm}\}$. As $y_{n+1}\not\in I(\Delta_{n, m}),$ thus we have

Case 1. Let $n = 1$. We have $I(\Delta_{1, m})\cap S^{'}_{1, m} = I(\mathcal{S}_{m+1})S^{'}_{1, m} {\rm{ and }} (I(\Delta_{1, m}):y_{2})S_{1, m} = ((B_{1, m})S_{1, m}).$ Thus ${{\rm{sdepth}}}(I(\Delta_{1, m}))\geq \min\{{{\rm{sdepth}}}(I(\mathcal{S}_{m+1}))S^{'}_{1, m}, {{\rm{sdepth}}}((B_{1, m})S_{1, m})\}.$ By Lemma 2.13, we have ${{\rm{sdepth}}}((B_{1, m})S_{1, m}) = \Big\lceil\frac{m+1}{2}\Big\rceil+1 = \Big\lceil\frac{m+3}{2}\Big\rceil$. Now by Lemma 2.16, we have ${{\rm{sdepth}}}((I(\Delta^{*}_{1, m}))S_{1, m}) = {{\rm{sdepth}}}((I(\mathcal{S}_{m+1})K[V(\mathcal{S}_{m+1})])) = 1+\Big\lceil\frac{m}{2}\Big\rceil.$ ${\rm{Hence}}, \, \, {{\rm{sdepth}}}(I(\Delta_{1, m}))\geq 1+ \Big\lceil\frac{m}{2}\Big\rceil.$

Case 2. Let $n = 2$. We get $I(\Delta_{2, m})\cap S^{'}_{2, m} = (I(\Delta^{*}_{1, m}))S^{'}_{2, m}$ and $(I(\Delta_{2, m}):y_{3})S_{2, m} = ((I(\mathcal{S}_{m+1}), B_{2, m})S^{'}_{2, m}[y_3]).$ Thus

By Lemma 2.13 and [3,Theorem 1.3],

Now by Theorems 2.10 and 2.7, we get

Now by Lemma 5.1, we have ${{\rm{sdepth}}}((I(\Delta^{*}_{1, m}))S^{'}_{2, m}) = {{\rm{sdepth}}}((I(\Delta^{*}_{1, m}))S^{*}_{1, m})\geq m+2.$ Hence

Finally, consider $n\geq3.$ We have $I(\Delta_{n, m})\cap S^{'}_{n, m} = (I(\Delta^{*}_{n-1, m}))S^{'}_{n, m} \, \, \, {\rm{ and }} \, \, \, (I(\Delta_{n, m}):y_{n+1})S_{n, m} = ((I(\Delta^{*}_{n-2, m}), B_{n, m})S^{'}_{n, m}[y_{n+1}]).$ By Lemma 5.1, Lemmas 2.14 and 2.13, we have

Now by Theorem 2.10 and Lemma 3.1, we obtain

Also by Lemma 5.1, we get

To sum up

Lemma 5.3. Let $n = 1$ and $m\geq1$, then ${{\rm{sdepth}}}(I(\Delta^{**}_{1, m}))\geq 2m+1.$ Let $n\geq2$ and $m\geq1$. If $n\equiv 0\, (\mod 2)$, then ${{\rm{sdepth}}}(I(\Delta^{**}_{n, m}))\geq {{\rm{sdepth}}}(S^{**}_{n, m}/I(\Delta^{**}_{n, m}))+1+m = \lceil\frac{n+2}{2}\rceil+1+m.$ And if $n\equiv 1\, (\mod 2)$, then ${{\rm{sdepth}}}(I(\Delta^{**}_{n, m}))\geq {{\rm{sdepth}}}(S^{**}_{n, m}/I(\Delta^{**}_{n, m}))+2m = \lceil\frac{n+1}{2}\rceil+1+2m.$

Proof. Let $A_{n, m} = \{y_{n}, u_{n1}, u_{n2}, \dots, u_{nm}, u_{(n+1)1}, u_{(n+1)2}, \dots, u_{(n+1)m}\}$. As $y_{n+1}\not\in I(\Delta^{**}_{n, m})$, therefore we have

Case 1. Let $n = 1$. We have $I(\Delta^{**}_{1, m})\cap S^{''}_{1, m} = I(\mathcal{S}_{2m+1})S^{''}_{1, m}$ and $\big(I(\Delta^{**}_{1, m}):y_{2}\big)S^{**}_{1, m} = (A_{1, m})S^{**}_{1, m}.$ Therefore, ${{\rm{sdepth}}}(I(\Delta^{**}_{1, m}))\geq \min\{{{\rm{sdepth}}}(I(\mathcal{S}_{2m+1})S^{''}_{1, m}), {{\rm{sdepth}}}((A_{1, m})S^{**}_{1, m})\}.$ By Lemma 2.13 and Theorem 2.10 we have

Now by Lemmas 2.16 and 2.13, we get

As a result ${{\rm{sdepth}}}(I(\Delta^{**}_{1, m}))\geq 2m+1.$

Case 2. Now we will prove this result by induction on $n$. Let $n = 2$. $I(\Delta^{**}_{2, m})\cap S^{''}_{2, m} = (I(\Delta^{**}_{1, m}))S^{''}_{2, m}\, \, {\rm{ and }} (I(\Delta^{**}_{2, m}):y_{3})S^{**}_{2, m} = (I(\mathcal{S}_{2m+1}, A_{2, m})S^{''}_{2, m}[y_3]).$ Consequently

By Lemma 2.13 and [3,Theorem 1.3],

Now by Lemma 2.16, Theorems 2.10 and 2.7, we have

Now by the Case 1 and Lemma 2.13, we get ${{\rm{sdepth}}}((I(\Delta^{**}_{1, m}))S^{''}_{2, m}) = {{\rm{sdepth}}}((I(\Delta^{**}_{1, m}))S^{**}_{1, m})+m\geq 3m+1.$ ${\rm{To sum up}}, \, \, \, {{\rm{sdepth}}}(I(\Delta^{**}_{2, m}))\geq m+3.$ In general, for $n\geq3.$ We have

By induction on $n$, Lemmas 2.14 and 2.13,

Case 2(a). If $n\equiv 0\, (\mod 2)$, then $n-1\equiv 1\, (\mod 2)$ and $n-2\equiv 0\, (\mod 2)$. By Theorem 2.10 and Lemma 4.1, we have ${{\rm{sdepth}}} ((I(\Delta^{**}_{n-2, m}), A_{n, m})S^{''}_{n, m}[y_{n+1}])\geq \lceil\frac{n}{2}\rceil+m+1+1 = \lceil\frac{n+2}{2}\rceil+m+1.$ Also by induction on $n$ and Lemma 2.13, we get

Thus ${{\rm{sdepth}}}(I(\Delta^{**}_{n, m}))\geq \Big\lceil\frac{n+2}{2}\Big\rceil+1+m.$

Case 2(b). If $n\equiv 1\, (\mod 2)$, then $n-1\equiv 0\, (\mod 2)$ and $n-2\equiv 1\, (\mod 2)$. By Theorem 2.10 and Lemma 4.1, we have ${{\rm{sdepth}}} ((I(\Delta^{**}_{n-2, m}), A_{n, m})S^{''}_{n, m}[y_{n+1}])\geq \lceil\frac{n-1}{2}\rceil+m+m+1+1 = \lceil\frac{n+1}{2}\rceil+2m+1.$ Also by induction on $n$ and Lemma 2.13, we get

Thus ${{\rm{sdepth}}}(I(\Delta^{**}_{n, m})) = \lceil\frac{n+1}{2}\rceil+1+2m.$

Theorem 5.4. Let $n = 3$ and $m\geq1.$ Then ${{\rm{sdepth}}}(I(\Omega_{3, m}))\geq {{\rm{sdepth}}}(T_{3, m}/I(\Omega_{3, m}))+m = 2m+1.$ Let $n\geq4$ and $m\geq1$.

Proof. Let $C_{n, m} = \{y_{2}, y_{n}, u_{11}, u_{12}, \dots, u_{m}, u_{n1}, u_{n2}, \dots, u_{nm}\}$. Since $y_1\not\in I(\Omega_{n, m})$, so we have

Let $n = 3$. It can be seen that $I(\Omega_{3, m})\cap T^{'}_{3, m} \cong(I(\Delta^{**}_{1, m}))T^{'}_{3, m}$ and $I(\Omega_{3, m}):y_1)T_{3, m}\cong (C_{3, m})T_{3, m}.$ Hence

By Lemma 2.13 and by Theorem 2.10, ${{\rm{sdepth}}} ((C_{3, m})T_{3, m}) = {{\rm{sdepth}}} ((C_{3, m}) K[C_{3, m}])+m+1 = 2m+1.$ ${\rm{Also by Lemma 5.3}}, \, \, {{\rm{sdepth}}}((I(\Delta^{**}_{1, m}))T^{'}_{3, m}) = {{\rm{sdepth}}}((I(\Delta^{**}_{1, m}))S^{**}_{1, m})\geq 2m+1.$ ${\rm{Thus}}\, \, \, {{\rm{sdepth}}} (I(\Omega_{3, m}))\geq 2m+1.$ Let $n = 4$. we get $I(\Omega_{4, m})\cap T^{'}_{4, m} = (I(\Delta^{**}_{2, m}))T^{'}_{4, m}\, \, \, {\rm{ and }}\, \, \, (I(\Omega_{4, m}):y_1)T_{4, m} = ((I(\mathcal{S}_{2m+1}), C_{4, m})T^{'}_{4, m}[y_1]).$ Thus

By Lemma 2.13 and [3,Theorem 1.3],

And by Lemma 2.16, Theorems 2.10 and 2.7, we have

Now by Lemma 5.3, we get ${{\rm{sdepth}}}((I(\Delta^{**}_{2, m}))T^{'}_{4, m})\cong {{\rm{sdepth}}}((I(\Delta^{**}_{2, m}))S^{**}_{2, m})\geq m+3.$ Thus ${{\rm{sdepth}}} (I(\Omega_{4, m}))\geq m+3.$ In general, for $n\geq5.$ It is clear that

By Lemmas 5.3, 2.14 and 2.13, we have

Case 1. if $n\equiv 0\, (\mod 2)$, then $n-2\equiv 0\, (\mod 2)$ and $n-4\equiv 0\, (\mod 2).$ By Theorem 2.10 and Lemma 4.1 ${{\rm{sdepth}}} ((I(\Delta^{**}_{n-4, m}), C_{n, m})T^{'}_{n, m}[y_1])\geq \Big\lceil\frac{n-2}{2}\Big\rceil+m+1+1 = \Big\lceil\frac{n}{2}\Big\rceil+m+1.$ Also by Lemma 5.3, ${{\rm{sdepth}}}((I(\Delta^{**}_{n-2, m}))T^{'}_{n, m})\cong {{\rm{sdepth}}}((I(\Delta^{**}_{n-2, m}))S^{**}_{n-2, m})\geq \Big\lceil\frac{n}{2}\Big\rceil+1+m.$ Thus ${{\rm{sdepth}}}(I(\Omega_{n, m}))\geq\lceil\frac{n}{2}\rceil+1+m.$

Case 2. If $n\equiv 1\, (\mod 2)$, then $n-2\equiv 1\, (\mod 2)$ and $n-4\equiv 1\, (\mod 2).$ By Theorem 2.10 and Lemma 4.1 ${{\rm{sdepth}}} ((I(\Delta^{**}_{n-4, m}), C_{n, m})T^{'}_{n, m}[y_1])\geq \lceil\frac{n-3}{2}\rceil+m+m+1+1 = \lceil\frac{n+1}{2}\rceil+2m.$ Also by Lemma 5.3, ${{\rm{sdepth}}}((I(\Delta^{**}_{n-2, m}))T^{'}_{n, m})\cong {{\rm{sdepth}}}((I(\Delta^{**}_{n-2, m}))T^{*}_{n-2, m})\geq \Big\lceil\frac{n-1}{2}\Big\rceil+1+2m = \Big\lceil\frac{n+1}{2}\Big\rceil+2m.$ Thus ${{\rm{sdepth}}}(I(\Omega_{n, m}))\geq \lceil\frac{n+1}{2}\rceil+2m.$

6.   Conclusions

In this paper we consider the residue class rings of the edge ideals associated to the triangular and multi triangular snake and ouroboros snake graphs. In most of the cases, we give precise values for depth and Stanley depth of these residue class rings. We also prove that Stanley depth of the edge ideal of any graph considered in this paper is an upper bounds for the Stanley depth of its residue class ring.

Conflict of interest

The authors declare that there is no conflict of interest in this paper.