A new very simply explicitly invertible approximation for the standard normal cumulative distribution function

1.   Introduction

The normal probability density function (PDF) is given by

where $\mu$ is the mean of the distribution and $\sigma$ is the standard deviation. The normal distribution plays an important role in research for the natural and social sciences, providing models for phenomena occurring in biology, quantum mechanics, finance, optics, and stochastic modelling. Examples of models that utilize the normal distribution include human blood pressure ^[1], electron velocity distributions ^[2], and risk assessment in finance ^[3].

The standard normal PDF occurs for $\mu = 0$ and $\sigma = 1$. Henceforth, we refer to the "standard normal PDF" $\phi_{0, 1}(x)$ as the "normal distribution" for simplicity. The cumulative distribution function (CDF) of the normal distribution is given by

No method is known to evaluate the normal CDF using only elementary functions. Fortunately, many software libraries exist that can produce high-quality numerical approximations to $\Phi_{0, 1}(z)$, e.g., the $\texttt{cdf}$ command in MATLAB ^[4]. However, it may be desirable to have explicit functions (especially very simply explicitly invertible ones ^[5]) to efficiently approximate $\Phi_{0, 1}(z)$. Several of these approximations have been published and offer varying degrees of accuracy. These approximations are typically not very simply explicitly invertible; i.e., having only one appearance of the argument $z$ and the existence of inverse that consists only of elementary functions. In general, explicitly invertible quantile functions (i.e., the inverse of the CDF) facilitate Monte Carlo simulations and the generation of random numbers following desired distributions. Specifically, the CDF of the standard normal distribution plays a crucial role in the theory of transformations of random variables and in stochastic modelling methods aiming to preserve any desired marginal distribution and correlation structure ^[6]. In such cases, explicit expressions of the CDF can facilitate numerical computations.

We propose a new approximate function for the normal CDF as given by

where $\bf{c} = (c_1, c_2, \ldots, c_{ 5})$ is a vector of design parameters to be chosen such that $F(z; \bf{c})$ is a good approximation to $\Phi_{0, 1}(z)$. The starting point to construct this equation was the logistic distribution,

which was then progressively generalized to include more parameters to offer more flexibility. This approximate function is very simply explicitly invertible and can be constructed to possess errors that are superior to the most accurate simply and very simply explicitly invertible normal CDF approximations published. The parameters, $\bf{c}$, were determined via global optimization, which was performed using both MATLAB's Global Optimization Toolbox ^[4] and BARON ^[7].

This paper is organized as follows. Section 2 contains an extensive (but non-exhaustive) summary of published normal CDF approximations. Section 3 provides a brief description of the procedure used to solve for the design parameters, $\bf{c}$. Section 4 discusses the results from various fits of the function, including the determined parameters and the resulting errors in the fits and their inverses. Section 5 provides a practical example of where such an approximation may be useful and compares the run-time with that of MATLAB's built-in normal $\texttt{cdf}$. Section 6 concludes the paper by summarizing the main findings.

2.   Summary of published approximations

Table 1 presents a summary of published approximations to the normal CDF. The table is not exhaustive; however, the samples included provide a broad representation of functions used to approximate the normal CDF for $z \ge 0$, with the identity $\Phi_{0, 1}(-z) \equiv 1 - \Phi_{0, 1}(z)$ used for values $z < 0$. Explicitly invertible approximations are denoted with an asterisk (*).

Table 1.  A sampling of published normal CDF approximations. Explicitly invertible functions denoted with asterisks (*).

Author, Year [Citation]	Proposed Approximation	Maximum Absolute Error
Pólya, $1949$* [8]	$\Phi^*(z)=\frac{1}{2}\left[1+\left(1-\exp\left(-\frac{2z^2}{\pi}\right)\right)^\frac{1}{2}\right]$	3.00e-03*
Cadwell, $1951$ [9]	$\Phi(z)=\frac{1}{2}\left[1-\exp\left(-\frac{2z^2}{\pi}-\frac{2\left(\pi-3\right)}{3\pi^2}z^4\right)\right]^\frac{1}{2}$	7.00e-04
Hart, $1957$ [10]	$\Phi(z)= 1-\frac{1}{\sqrt{2\pi}}\frac{\exp\left(-\frac{z^2}{\pi}\right)}{z+0.8\exp\left(-0.4z\right)}$	4.30e-03
Tocher, $1963$* [11]	$\Phi^*(z)= \frac{\exp\left(\sqrt{\frac{8}{\pi}z}\right)}{1+\exp\left(\sqrt{\frac{8}{\pi}z}\right)}$	1.77e-02*
Abramowitz and Stegun, 1964 [12]	$\Phi(z)=1-\left[a_{1}\frac{1}{1+pz}-a_{2}\left(\frac{1}{1+pz}\right)^{2}+a_{3}\left(\frac{1}{1+pz}\right)^{3}\right]\frac{\exp\left(-\frac{z^2}{2}\right)}{\sqrt{2\pi}}$	1.00e-05
Page, $1977$ [13]	$\Phi(z)=0.5\left[1+\tanh\left(\sqrt{\frac{2}{\pi}z\left(1+0.044715z^2\right)}\right)\right]$	1.79e-04
Derenzo, $1977$* [14]	$\Phi(z) = 1 -0.5 \left(\exp\left(-\frac{\left(83z+351\right)z+562}{\frac{703}{z}+165}\right)\right)$	7.17e-05$^*$
Hamaker, $1978$ [15]	$\Phi(z)=1-0.5\sqrt{1-\exp\left(-0.806z\left(1-0.018z\right)^2\right)}$	6.23e-04
Hawkes, $1982$ [16]	$\Phi(z) = 0.5-0.5\left[1-\exp\left(-\frac{2\left(z-7.5166e-03z^3+3.1737e-04z^5-2.9657e-06z^7\right)^2}{\pi}\right)\right]^\frac{1}{2}$	1.70e-05
Lin, $1989$ [17]	$\Phi(z)=1-\frac{1}{2}\exp\left(-0.717z-0.416z^2\right)$	6.20e-03
Vedder, $1993$* [18]	$\Phi(z) = \left(1+\exp\left(-\left(\frac{8}{\pi}\right)^{1/2}x-\frac{\left(\frac{2}{\pi}\right)^{1/2}\left(4-\pi\right)}{3\pi}x^3\right)\right)^{-1}$	3.13e-04*
Bagby, $1995$ [19]	$\Phi(z) = \frac{1}{2}\left[1-\frac{1}{30}\left(7\exp\left(-\frac{z^2}{2}\right)+16\exp\left(-z^2\left(2-\sqrt{2}\right)\right)+\left(7+\frac{\pi}{4}z^{2}\right)\exp\left(-z^2\right)\right)\right]^\frac{1}{2}$	3.00e-04
Waissi and Rossin, $1996$ [20]	$\Phi(z)= \frac{1}{1+\exp\left(-\sqrt{\pi}\left(0.9z+0.0418198z^3-0. 0004406z^5\right)\right)}$	4.31e-05
Bryc, $2002a$ [21]	$\Phi(z)= \frac{\left(4-\pi\right)z+\sqrt{2\pi}\left(\pi-2\right)}{\left(4-\pi\right)z^2\sqrt{2\pi}+2\pi z+2\sqrt{2\pi}\left(\pi-2\right)} \exp\left(-\frac{z^{2}}{2}\right)$	7.10e-04
Bryc, $2002b$ [21]	$\Phi(z)= \frac{z^2+5.575192695z+12.77436324}{\sqrt{2\pi}z^3+14.38718147z^2+31.53531977z+25.54872648} \exp\left(-\frac{z^{2}}{2}\right)$	1.90e-05
Shore, $2005$ [22]	$\Phi(z) = 0.5\left[1+g(-z)-g(z)\right]$; see footnotea for $g(z)$	6.00e-07
Kundu et al., $2006$* [23]	$\Phi^*(z) = \left(1-\exp\left[-\exp\left(0.3820198z+1.07925\right)\right]\right)^{12.8}$	3.00e-04*
Aludaat and Alodat, $2008$* [24]	$\Phi^* (z)=0.5 + 0.5\sqrt{1-\exp\left(-\sqrt{\frac{\pi}{8}}z^2\right)}$	1.97e-03 *
Bowling et al., $2009a$* [25]	$\Phi^*(z)= \frac{1}{1+\exp\left(-1.702z\right)}$	9.50e-03*
Bowling et al., $2009b$ [25]	$\Phi(z)= \frac{1}{1+\exp\left(-0.07056z^3-1.5976z\right)}$	1.40e-04
Vazquez et al., $2012$ [26]	$\Phi(z)= \frac{1}{1+\exp\left(-\frac{358} {23}z+111\arctan\left(\frac{37z}{294}\right) \right)}$	9.00e-05
Soranzo and Epure, $2014$* [5]	$\Phi^*(z)=2^{-22^{1-41^{\frac{z}{10}}}}$	1.3e-04*
Abderrahmane and Boukhetala, $2016$ [27]	$\Phi(z)=1-0.39894\left[\frac{\exp\left(-0.5078z^2\right)}{z+0.79758\exp\left(-0.4446z\right)}\right]$	2.72e-04
Abderrahmane and Boukhetala, $2016$* [27]	$\Phi^*(z)=0.5 + 0.5\sqrt{1-\exp\left(-0.62306179z^2\right)}$	1.62e-03*
Eidous and Al-Saman, $2016$* [28]	$\Phi^*(z) = 0.5+0.5\sqrt{1-\exp\left(-\frac{5}{8}z^2\right)}$	1.81e-03*
Matic et al., $2018$ [29]	$\Phi(z) = \frac{1}{2}+\frac{{\rm{sgn}}(z)}{2}\sqrt{1-\exp\left(-\frac{2z^2}{\pi}\left(1+a_1z^2+a_2z^4+a_3z^6+a_4z^8+a_5z^{10}\right)\right)}$	5.79e-06
Eidous and Abu-Shareefa, $2019$ [30]	$\Phi(z) = 1 - \frac{1}{\sqrt{2\pi}}\frac{\exp\left(-\frac{z^2}{2}\right)}{z+\sqrt{\frac{2}{\pi}}\exp\left(-y\left(z\right)z\right)}$; see footnoteb for $y(z)$	4.23e-08
Shchigolev, $2019$ [31]	$\Phi(z) = \frac{1}{2}+\frac{1}{\sqrt{\pi}}\left[7-\left(7+3\sqrt{2}z+\frac{5}{4}z^2+\frac{\sqrt{2}}{4}z^3+\frac{1}{8}z^4\right)\exp\left(-\frac{z^2}{\sqrt{2}}\right)\right]$	4.50e-04
a$g(z) = \exp\left[-\log(2)\exp\left(\frac{\alpha}{\frac{\lambda}{S_1}}\left(\left(1+S_1z\right)^{\frac{\lambda}{S_1}}-1\right)+S_2z\right)\right]$   b$y(z) =0.455428-0.0329012z-0.00681111z^2+0.00300713z^3-0.00039299z^4-0.00004552z^5+0.00002614z^6+0.00000412z^7+0.00000025z^8$

---

 | Show Table

DownLoad: CSV

There is generally a tradeoff between the accuracy and the explicit invertibility of a function designed to approximate the normal CDF. Highly accurate approximations of the normal CDF tend to rely on complicated expressions or multi-term polynomials to achieve their level of accuracy (e.g., ^[16], ^[20], ^[21], ^[22], ^[29], ^[30]). In fact, many normal CDF approximations proposed in recent years are simply previously published approximations whose accuracy has been improved through the addition of more terms in a polynomial expansion. For example, ^[30] is an improvement of ^[10], achieving a significantly smaller maximum absolute error through the addition of a multi-term polynomial. The improvement reported in ^[29] over ^[8] was achieved similarly. Although high accuracy may be desirable when approximating the normal CDF, complicated approximate functions generally cannot be inverted explicitly and thus cannot be conveniently used to approximate the inverse normal CDF. Such is the case of ^[29]: the function proposed has a better maximum absolute error than that proposed in ^[8], but it is no longer explicitly invertible.

Explicitly invertible approximations of the normal CDF are often relatively simpler expressions with fewer degrees of freedom for the purposes of fitting (e.g., ^[5], ^[8], ^[11], ^[23], ^[25], ^[27], ^[28]). Consequently, explicitly invertible approximations tend to possess larger maximum absolute errors. To the best of the authors' knowledge, the best explicitly invertible approximation to the normal CDF is from ^[14] with a maximum absolute error of 7.17e–5. Similarly, the most accurate published very simply explicitly invertible approximation of the normal CDF is the particularly elegant one given by Soranzo and Epure ^[5] (see Table 1) with a maximum absolute error of 1.3e–04. Section 4 of this paper shows that all maximum absolute errors of the proposed function Equation (1.1) reported here are superior to both of these approximations, with the best maximum absolute errors having a value of 2.7 3e–05, almost five times smaller than that of ^[5] and twice as small as that of ^[14].

3.   Optimization problem and solution procedure

3.1.   Definition of the optimization problem

The function $F(z; \bf{c})$ is constructed by solving an optimization problem to minimize the ordinary (unweighted) least-squares residual

where $N$ denotes the total number of sample points $z_n$ to be fit, $\bf{c}$ denotes a vector of unknown parameters to be optimized, $\Phi_{0, 1}{(z)}$ denotes the normal CDF as approximated by MATLAB's built-in $\texttt{cdf}$ function, and $F(z; \bf{c})$ denotes the newly proposed approximate function given by Equation (1.1).

We minimize the residual because it is a computable and smooth function of $\bf{c}$. However, we assess the quality of the approximate function $F(z; \bf{c})$ by estimating the maximum absolute error (MAE). The MAE is defined as

where $\Phi_{0, 1}(z)$ is given by MATLAB's built-in normal $\texttt{cdf}$. In practice, Equation (3.2) cannot be evaluated exactly. Hence, the MAE in this study is estimated by uniformly sampling the absolute error on the fitting domain with $5N$ sample points (i.e., five times as many points used for fitting).

To adequately cover the value of $z$ most likely to be used in practice, the $z_n$ was chosen to be $N = 141$ uniformly spaced points on a fitting domain $0 \le z \le 7$. Values of $\Phi_{0, 1}(z)$ for $z > 7$ can be taken to be 0 to high accuracy. Because $\Phi_{0, 1}(z)$ has an odd symmetry about the point $(0, 1/2)$, i.e., it satisfies the property

it is reasonable to fit an approximate function to $\Phi_{0, 1}(z)$ for $z \geq 0$ then obtain all values for $z < 0$ from Equation (3.3). Fits at points over the domain $-7 \leq z \leq 7$ with a uniform sample spacing and $N = 141$ were attempted, but they yielded MAEs no better than the one given in ^[5].

An important property of the normal CDF is $\Phi_{0, 1}(0) = 0.5$. As can be seen in Section 4, an unconstrained minimization of eq. (3.1) will not satisfy this property. To rectify this shortcoming, the constraint $F(0; \bf{c}) = 0.5$ was explicitly introduced into fits for eq. (1.1). Of the three results presented in Section 4, two were fit subject to this constraint.

3.2.   Optimization algorithms and solution procedure

A potential global minimum of Equation (3.1) was determined using both the GlobalSearch algorithm from MATLAB's Global Optimization Toolbox and BARON (via the MATLAB-BARON interface).

The GlobalSearch algorithm ^[32] is a heuristic algorithm based on the assumption that all basins of attraction of a minimum are spherical. It locates a potential global minimum by generating random start points and then using those start points to locally optimize within multiple basins of attraction. Each set of start points is assigned a score based on a scoring algorithm. If the score does not meet a specified set of standards, the points are deemed unlikely to improve the solution and are discarded without running the local optimization. Thus, GlobalSearch does not run a local optimization from all generated start points; rather, it only runs local optimization on start points it deems likely to improve the solution. The solutions from each local optimization are stored in an array, and the best solution is returned at the end of the search.

BARON ^[33] is a "Branch and Reduce" algorithm. Instead of utilizing randomly generated start points to run local solvers across the search domain, BARON subdivides the problem by branching on selected variables and defining subdomains of the search space within nodes. For each node, BARON relaxes the given objective function, providing a lower bound for a minimum solution that exists within the given subdomain of the search space. BARON then selects upper bounds for the node. If a lower bound for a node is larger than any given upper bound for a different node, BARON discards the node. Further reduction of the search space is performed during the pre- and post-processing of each node. Branching, bounding, and reducing continues until BARON locates a potential global minimum.

It is generally impossible to guarantee that the solution returned by a numerical routine such as GlobalSearch or BARON is the true global minimum of a given objective function. In order to increase the likelihood of obtaining the global minimum of Equation (3.1), both algorithms were run multiple times. The smallest residual found within those runs is reported as the best solution. GlobalSearch was run 10 000 times from 10 000 randomly generated starting points, whereas BARON was run 1 000 times from 1 000 randomly generated starting points. To ensure the results are reproducible, each run is assigned a unique seed.

Different bounds for each element of $\bf{c}$ were selected for the different algorithms. For the fits utilizing GlobalSearch, the choice $\bf{c} \in [-10^4, 10^4]$ was made. In order to enhance the performance of BARON, tighter bounds were selected for each parameter based on the parameter's sensitivity (i.e., how much variance each parameter causes in the objective function, Equation (3.1)). In order to identify sensitive parameters in the approximate function Equation (1.1), sensitivity analysis was performed on Equation (3.1) using the Variogram Analysis of Response Surfaces (VARS) software toolbox ^[34]. The analysis showed parameters $c_3$ and $c_{ 5}$ to contribute to $97.4\%$ of overall variance in Equation (3.1), and therefore, tighter bounds were selected for $c_3$ and $c_{ 5}$ relative to the rest of the parameters (except for $c_1$, for which previous runs of the optimization problem indicated that there was no need to increase bounds outside of $0$ and $1$). The lower and upper bounds for Equation (1.1) are shown in Table 2. Final bound selection is based on results of previous optimizations of the problem using GlobalSearch.

Table 2.  BARON parameter bounds for Equation (1.1).

Bound	$c_1$	$c_2$	$c_3$	$c_4$	$c_5$
Lower	0	0	-5	0	0
Upper	1	60	5	30	1

---

 | Show Table

DownLoad: CSV

The above procedure was applied to the unconstrained and constrained cases for Equation (1.1); the resulting parameter vectors of best fit are presented in Section 4. To ensure a fair comparison, the MAE given for the best explicitly invertible CDF approximations in ^[14] and ^[5] were recalculated using the definition given above. The MAEs calculated by this method were 7.17e–5 and 1.27e–04, respectively, with the latter respecting the bound 1.3e–04 reported in ^[5]. We offer no theoretical guarantee of global optimality; however, the results reported are superior to those that have been published to date in terms of estimated MAE.

4.   Results

The function defined by eq. (1.1) was fit to MATLAB's built-in normal $\texttt{cdf}$ function using either GlobalSearch or BARON, as per the procedure described in Section 3. Table 3 contains the best-fit parameter vectors from three separate fits for 1.1. Each vector of best-fit parameters is reported with its corresponding residual, MAE, and location of the MAE. The table also specifies the solver used for each fit: either GlobalSearch (GS) or BARON (BA). Fits that were subject to the constraint $F(0; \bf{c}) = 0.5$ are denoted with superscript ($^{\dagger}$). Section 4.1 provides further discussion on the unconstrained fit; Section 4.2 provides further discussion on the two fits subject to the constraint $F(0; \bf{c}) = 0.5$.

Table 3.  Results from fitting (1.1) to MATLAB's built-in normal $\texttt{cdf}$.

Solver	$c_1$	$c_2$	$c_3$	$c_4$	$c_5$	Residual	MAE	MAE Location
GS	0.00165264063	3.41198528753	3.27828832050	7.36525492695	0.82347307439	1.33e-04	3.39e-05	0.00
GS$^{\dagger}$	0.00141349455	3.143479998875	3.12017824876	13.4751284391	0.80551656318	2.73e-04	5.08e-05	3.02
BA$^{\dagger}$	0.00161826615	3.38692114553	3.26862849061	7.80500878654	0.82116764005	1.42e-04	2.73e-05	0.17

---

 | Show Table

DownLoad: CSV

4.1.   Unconstrained fit

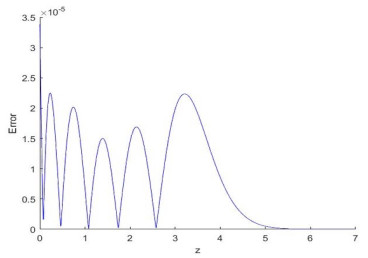
The first fit of Equation (1.1) was performed without any additional constraints. As can be seen in Table 3, the smallest residual found by the procedure outlined in Section 3 is 1.33e–04. The corresponding MAE is 3.39e–05. This MAE is superior to the best MAE for published very simply explicitly invertible CDF approximations, given by ^[5], by about a factor of four.

The results for the unconstrained fit given in Table 3 are from the GlobalSearch procedure. BARON returned a similar solution to GlobalSearch, and thus, the result was omitted. A plot of the absolute errors for the unconstrained fit are given in Figure 1. The plot clearly shows the MAE occurring at the origin. We refer to Table 3 for the corresponding parameters of best fit.

Figure 1.  Absolute error for the unconstrained GlobalSearch procedure.

DownLoad: Full-Size Img PowerPoint

4.2.   Constrained fits

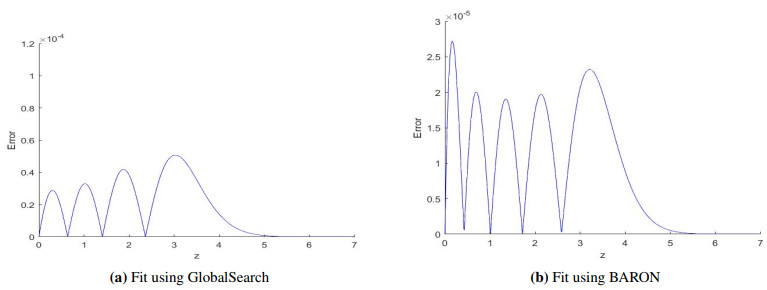
For fitting Equation (1.1) subject to the constraint $F(0) = 0.5$, BARON and GlobalSearch returned differing results, thus are both included in Table 3. The smallest residual found using the GlobalSearch procedure is 2.73e–04, with a corresponding MAE of 5.08e–05, located at the point $z = 3.02$. The smallest residual found by the BARON procedure is 1.42e–04, with a corresponding MAE of 2.73e–05, located at the point $z = 0.17$.

All MAEs mentioned above are superior to the best MAE given by published explicitly invertible normal CDF approximations. Each of these fits returned a larger residual than those found in Section 4.1; however, each of these fits satisfies the condition $F(0; \bf{c}) = 0.5$ within an error much less than the MAE. Furthermore, the results from the constrained BARON procedures offer the lowest MAE ever reported for an analytically invertible normal CDF approximation.

Although the results from the constrained GlobalSearch run do not provide the smallest MAE or smallest residual, they are still worthwhile to consider. The purpose of the normal CDF is to calculate the probability that a random variable is less than or equal to $z$. Therefore, the further from the origin the MAE occurs, the more likely the MAE will lie outside of values of $z$ to be relevant for many practical applications. The constrained GlobalSearch results offers and approximation with a reasonable MAE that potentially occurs outside of the range of interest of $z$ for many practical applications.

Plots of the absolute errors for the constrained BARON and GlobalSearch procedures are given in Figure 2. We note the differing locations of the MAE for each result and refer to Table 3 for corresponding parameters.

Figure 2.  Absolute errors for the constrained procedures.

DownLoad: Full-Size Img PowerPoint

4.3.   Sensitivity analysis

To recall, a sensitivity analysis using the VARS software toolbox applied to Equation (1.1) yielded that only two parameters ($c_3$ and $c_{ 5}$) accounted for almost all the variance in Equation (3.1). A sensitivity analysis is also applied to the model of Soranzo and Epure ^[5]; see Table 1. The values $22$, $41$, and $10$ in the function are treated as being the result of a fitting procedure; i.e.,

where $\bf{c} = (c_1, c_2, c_3) = (22, 41, 10)$. The sensitivity analysis yields that the three parameters in Equation (4.1) contribute approximately equal amounts to the overall variance in Equation (3.1). Accordingly, the model can be made no less simple through a reduction in the number of parameters while still maintaining its effectiveness in terms of goodness of fit. The model Equation (1.1) appears more parsimonious from this perspective, with only two important degrees of freedom in its parameter set.

4.4.   Accuracy of the inverse

Finally, we assess the accuracy of the inverses produced by the leading explicitly invertible functions. Specifically, we consider the explicitly invertible function from ^[14], the very simply explicitly invertible function from ^[5], and the very simply explicitly invertible function eq. (1.1) with parameter values of the unconstrained fit given in the first row of Table 3. The magnitudes of the errors are shown in Table 4 for the three commonly used probabilities $p = 0.9, 0.95$, and $0.99$. We see that the error obtained from the simply explicitly invertible function eq. (1.1) is generally superior to the simply explicitly invertible function of Soranzo and Epure ^[5]. Otherwise, the explicitly invertible function of Dorenzo ^[14] appears to have the best error performance.

Table 4.  Magnitude of the errors in the inverse from ^[14], ^[5], and (1.1).

Probability	[14]	[5]	(1.1)
$0.90$	2.23e-4	4.63e-5	7.41e-5
$0.95$	1.09e-4	5.49e-4	5.76e-5
$0.99$	6.09e-5	3.14e-3	4.94e-4

---

 | Show Table

DownLoad: CSV

5.   Application example

To demonstrate the use of the approximate function and compare the runtime of the approximate function to that of MATLAB's built-in normal $\texttt{cdf}$, we choose to compute an example of a double integral involving the CDF of the standard normal distribution, which plays a crucial role in stochastic modelling and generation of time series and random spatiotemporal fields with desired characteristics ^[6,35]. Specifically, it is well known that any nonlinear transformation $g$ applied to a bivariate normal variable $(Z(t), Z(\tau))$ correlated by $\rho _{Z}(\tau)$ leads to a random variable $(g(Z(t)), g(Z(\tau)))$ with correlation $\rho _{g(Z)}(\tau)$ that is always smaller than $\rho_ {Z}(\tau)$ by the maximal property of the bivariate normal distribution ^[36]. A popular modelling strategy in time series generation involves generating Gaussian time series and transforming them into ones with a desired distribution; this is achieved by applying the transformation $Q_{\chi}(\Phi(Z(t)))$, where $Q_{\chi}$ is the quantile of the desired marginal. Because this transformation is nonlinear, to generate time series with non-Gaussian marginal distributions and desired correlations, one has to estimate the decrease of this correlation (for details, see ^[6]). The correlation coefficient of the process having a non-Gaussian marginal is given by $\rho_{X(\tau)} = \frac{E(X(t)X(\tau))-\mu_{x}^{2}}{\sigma_{x}^{2}}$, and to estimate the correlation decrease due to the $Q_{\chi}(\Phi(Z(t)))$ transformation, one has to estimate the double integral

where $Q_{\chi}$ is the inverse of the marginal distribution of random variable $\chi(t)$, $\Phi$ is the standard normal CDF, $Z(t)$ is a standard Gaussian process following the standard normal distribution, $\varphi_{Z(t)Z(\tau)}$ is the bivariate probability density function of $Z(t)$ and $Z(\tau)$, and $\rho_{Z}$ is the correlation coefficient between $Z(t)$ and $Z(\tau) = Z(t-\tau)$.

For the purposes of this example, $Q_{\chi}$ was chosen to be the inverse of the marginal of the gamma distribution function, and $\rho_{Z}$ was chosen to be $0.8$. The autocovariance defined in Equation (5.1) was evaluated $100\, 000$ times using Equation (1.1) and $100\, 000$ times using MATLAB's built-in normal $\texttt{cdf}$; the time it took to perform the $100\, 000$ evaluations was recorded for both functions. This process was repeated ten times, and the minimum evaluation time for each function was selected for comparison. The minimum time to perform $100\, 000$ evaluations for the approximate function was 2 053 seconds. The minimum time for MATLAB's built-in $\texttt{cdf}$ to perform $100\, 000$ evaluations was 2 138 seconds. Thus, using Equation (1.1) is approximately 5% faster than using MATLAB's built-in normal $\texttt{cdf}$ for this problem. The solution to Equation (5.1) computed by MATLAB's built-in normal $\texttt{cdf}$ was $0.00623672$ and the solution to Equation (5.1) computed by the approximate function was $0.00622242$. The relative percentage difference between the solutions is $0.23\%$, showing that using Equation (1.1) does not result in an appreciable loss of accuracy for this example.

6.   Conclusions

Many published explicitly invertible approximate functions for the normal CDF currently exist in the literature. The most accurate of these functions that we found that is also very simply explicitly invertible is given by Soranzo and Epure ^[5], possessing an MAE of 1.27e–04. This paper proposes a new very simply explicitly invertible approximation to the normal CDF, eq. (1.1), which was fit to MATLAB's built-in $\texttt{cdf}$ function using both MATLAB's Global Optimization Toolbox and BARON.

Results from three separate fits of Equation (1.1) are presented in this paper: an unconstrained fit and two fits subject to the constraint $F(0) = 0.5$. Each of the results possesses characteristics that make them noteworthy. As expected, the result from the unconstrained fit provides the smallest residual. The result for the constrained fit using the BARON procedure provides the smallest MAE. The result for the constrained fit using the GlobalSearch procedure provides an MAE occurring furthest from the origin. Regardless of these properties, all three fits resulted in MAEs superior to the best MAE for published very simply explicitly invertible normal CDF approximations by factors of about four or five. Furthermore, the best approximation has an MAE that is about a factor of two smaller than the best explicitly invertible normal CDF approximation. The approximate function is also shown to run approximately $5\%$ faster than MATLAB's built-in normal $\texttt{cdf}$.

By presenting more than a single result with the best MAE, we provide researchers with a set of very simply explicitly invertible normal CDF approximations that possess differing characteristics. Thus, researchers may evaluate the options presented in this paper and may choose an approximation best suited to their needs.

Acknowledgments

The authors gratefully acknowledge financial support received from the Global Institute for Water Security under its Global Water Futures program and Canada's National Science and Engineering Research Council (NSERC).

Conflict of Interest

The authors declare that there is no conflict of interests in this paper.