Shifted-Legendre orthonormal method for high-dimensional heat conduction equations

1.   Introduction

Let $\Omega\subset \mathbb{R}^n$ ($n\ge2$, possibly $n = 1971$) be a bounded smooth domain and consider the problem

where $c \in \mathbb{R}$ is a constant and $\nu$ denotes the outward unit normal to $\partial \Omega$. Imposing both Dirichlet and Neumann conditions on $\partial\Omega$ makes the problem overdetermined so that, in general, (1.1) has no solution. In a celebrated paper published in 1971, Serrin ^[15] proved that if (1.1) admits a smooth solution, then $\Omega$ must necessarily be a ball. This paper has raised a great interest and, nowadays (half a century later), it has reached almost 600 citations in the Mathscinet. Serrin's original proof combines analytic arguments, such as the Maximum Principle and a refinement of Hopf's boundary Lemma, with geometric techniques such as the moving plane method inspired to the Alexandrov characterization of spheres ^[1,2]. Starting from ^[18], several different approaches have been devised as an alternative to Serrin's original proof, see ^[14] and the references therein for a fairly complete survey.

The moving plane method has been fruitfully used in symmetry results for semilinear elliptic equations, see ^[4,10] for second order equations and ^[3] for higher order problems. Let ${\bf B}\subset \mathbb{R}^n$ be the unit ball and consider the semilinear polyharmonic problem under Dirichlet boundary conditions:

Here $r = |x|$ denotes the radial variable and, hence, the outward normal direction to $\partial {\bf B}$. The following result, valid for second order equations with $m = 1$, is a restatement of [10,Theorem 1], combined with deep remarks by Spruck [10,Remark 1].

Theorem 1.1. (^[4,10]) Let $n\ge2$ and $m = 1$. Assume that

Then, every positive strong solution $u\in W_{\rm loc}^{2, n}({\bf B}) \cap \mathcal{C}(\overline{ {\bf B}})$ ($u > 0$ in ${\bf B}$) of $(1.2)$ is radially symmetric ($u = u(r)$) and $u'(r) < 0$ for all $r \in (0, 1)$. Moreover, if

then every nonnegative and non-trivial strong solution $u\in W_{\rm loc}^{2, n}({\bf B}) \cap \mathcal{C}(\overline{ {\bf B}})$ ($u\ge0$, $u\not\equiv0$ in ${\bf B}$) of $(1.2)$ is radially symmetric ($u = u(r)$) and $u'(r) < 0$ for all $r \in (0, 1)$.

This result was extended in [3,Theorem 1] to the case $m\ge2$, in the following form:

Theorem 1.2. (^[3]) Let $n\ge2$ and $m\ge1$. Assume that

Then, every nonnegative and non-trivial strong solution $u\in H_0^m({\bf B}) \cap L^\infty({\bf B})$ ($u\ge0$, $u\not\equiv0$ in ${\bf B}$) of $(1.2)$ is radially symmetric ($u = u(r)$) and $u'(r) < 0$ for all $r \in (0, 1)$.

In its original version, Theorem 1.2 was stated by requiring that the solution $u$ was strictly positive, $u > 0$ in ${\bf B}$. But this is not necessary since [9,Theorem 5.1] ensures that if $u\ge0$ is nontrivial, then $u > 0$ (recall that $f(u)\ge0$ in view of (1.5)). Assumption (1.5) is stronger than (1.3) and one may wonder whether Theorem 1.2 also holds under weaker assumptions. A nice example by Sweers ^[16] shows that, for a smooth and decreasing $f$, positive radial solutions may not be radially decreasing. Therefore, (1.3) is not enough to obtain the full statement of Theorem 1.1 (radial symmetry and monotonicity) in the higher order case $m\ge2$. This discrepancy of assumptions between the cases $m = 1$ and $m\ge2$ is due to the lack of a maximum principle for polyharmonic operators; see [9,Section 1.2].

To find conditions, different from (1.5), ensuring both radial symmetry and radial monotonicity for (1.2) in the case $m\ge2$ is a challenging problem. The first purpose of this paper is precisely to discuss some conditions on the source $f$ which ensure the radial symmetry of the solutions of (1.2) and their radial monotonicity. In Section 2, particular attention is devoted to the regularity and monotonicity of $f$: for the biharmonic equation in ${\bf B}\subset\mathbb{R}^{n}$, in Theorem 2.3 we exhibit a Hölder-continuous function $f$ for which the radial symmetry of solutions fails, while Proposition 2.4 displays a strictly decreasing and sign-changing $f$ that still ensures the existence of a radially symmetric and strictly decreasing solution.

Contrary to the case of Navier boundary conditions, considered in ^[17], (1.2) cannot be reduced to a second order system when $m\ge2$. This is why the moving plane procedure used in the proof of Theorem 1.2 was carried on by using fine estimates of the Green function $G$ associated to the polyharmonic operator $(-\Delta)^m$, see [3,Section 2]. The second purpose of the present paper is to obtain new properties of the Green function in the so-called conformal dimensions $n = 2m$. In Section 3 we prove that some estimates become explicit identities in conformal dimensions, see formula (3.6). Combined with the inversion in the sphere and the Kelvin transform, this enables us to obtain an elegant symmetry property of the Green function, see Theorem 3.2 and the sketchy representation in Figures 3 and 4. In turn, this result is used in Corollary 3.5 where we present an alternative formula for the computation of the partial derivatives of solutions of (1.2): since the sign of these partial derivatives is the fundamental feature to implement the moving plane procedure, this formula can become useful under suitable assumption on the source $f$. Indeed, based on this formula, Proposition 3.7 suggests that the radial symmetry and monotonicity of the solutions of (1.2) is ensured if $\|f'\|_{L^{\infty}(\mathbb{R}_+)}$ is small.

Finally, as an application of Proposition 3.7, in Section 4 we revisit the counterexample by Sweers ^[16] where radial monotonicity of the solution fails: by appropriately modifying the source $f$ (enforcing the conditions given in Proposition 3.7) we numerically obtain radially symmetric and strictly decreasing solutions of the biharmonic equation in the unit ball of $\mathbb{R}^{4}$ for a decreasing function $f$ with sufficiently small derivative. Throughout this work, some open problems and questions are posed.

2.   Assumptions ensuring radial symmetry and monotonicity

In this section we discuss radial properties (symmetry and monotonicity) of solutions of (1.2). Let us recall the weak formulation of (1.2) within the Sobolev space $H_0^m({\bf B})$, which is a Hilbert space if endowed with the scalar product

We denote the induced norm by $\|\cdot\|_m$; in particular, $\|\cdot\|_0$ is the $L^2({\bf B})$-norm. A function $u\in H_0^m({\bf B})$ is called a weak solution of (1.2) if $f(u) \in H^{-m}({\bf B})$ (the dual space of $H_0^m({\bf B})$) and (1.2) is satisfied in a weak sense, that is

where $\langle \cdot, \cdot \rangle$ stands for the duality product between $H^{-m}({\bf B})$ and $H_0^m({\bf B})$. In the present article, however, we will mostly deal with slightly more regular solutions: when $f$ is continuous and $u\in H_0^m({\bf B}) \cap L^{\infty}({\bf B})$, we say that $u$ is a strong solution of (1.2) if

the integral exists since $u\in L^{\infty}({\bf B})$ and $f$ is continuous. By elliptic regularity, any such strong solution $u$ belongs to $\mathcal{C}^{2m-1, \alpha}(\overline {\bf B})$, for some $\alpha \in (0, 1)$, and all partial derivatives of order less than $m$ vanish on $\partial {\bf B}$. Moreover, if $f$ is Hölder continuous, then $u \in \mathcal{C}^{2m, \alpha}(\overline {\bf B})$ is a classical solution, see ^[9]. In the sequel, we always take (at least) $f\in \mathcal{C}(\mathbb{R}; \mathbb{R})$.

Our first (elementary) result is a restatement of [3,Remark (iv)] and gives a different condition for radial symmetry (but not for radial monotonicity).

Theorem 2.1. Let $n\ge2$ and $m\ge1$. Let $\lambda_1$ be the first Dirichlet eigenvalue for $(-\Delta)^m$ in ${\bf B}$. If

then there exists at most one strong solution $u\in H_0^m({\bf B}) \cap L^\infty({\bf B})$ of problem (1.2) which is, moreover, radially symmetric.

Proof. By contradiction, assume that (1.2) admits two strong solutions $u_1, u_2 \in H_0^m({\bf B}) \cap L^\infty({\bf B})$. Then by (2.1) we have both that

Set $w \doteq u_1-u_2$, subtract these two equations and choose $v = w$ as a test function to obtain

By (2.2) we know that

with strict inequality in a set of positive measure since $w\not\equiv0$ (recall $u_2\not\equiv u_1$). Therefore, (2.3) yields

which contradicts the Poincaré inequality and proves uniqueness.

Once uniqueness is established, it suffices to remark that if $u$ is a nonradial solution of (1.2), then for any given nontrivial rotation $A \in SO(n)$, also the function $u_A \doteq u\circ A$ is a (different) strong solution of (1.2), which contradicts the just proved uniqueness statement.

We have so shown that, if (2.2) holds, then there exists at most a unique solution of (1.2) which is necessarily radially symmetric. This proves the theorem.

Theorem 2.1 states that one cannot expect radial monotonicity under the sole assumption (2.2). Note also that Theorem 2.1 does not require the positivity of the solution and its elementary proof is based on the invariance properties of polyharmonic operators under rotations, a fact that ensures uniqueness. Let us recall that symmetry is also ensured if $f'(s) < \lambda_2$, for all $s \in \mathbb{R}$ (with $\lambda_2$ being the second Dirichlet eigenvalue for $(-\Delta)^m$ in ${\bf B}$, see ^[6]), and uniqueness is guaranteed if $f \in \mathcal{C}(\mathbb{R}_{+}; \mathbb{R})$ is sublinear at $0$ and $+\infty$ (see ^[7]). All this raises a natural question:

Problem 2.2. Is radial symmetry related to uniqueness? Are there examples of multiple radial positive solutions? Except, of course, when $f(u) = \lambda_1u$!

Some attention also deserves the regularity of $f$, as this feature is related to the existence of non-radial solutions. The counterexample in [10,Remark 1] shows that Theorem 1.1 ($m = 1$) does not hold if the Lipschitz continuity assumption on $f$ is relaxed to Hölder continuity. We extend this example to the biharmonic equation ($m = 2$), showing that the monotonicity requirement in (1.5) cannot be dropped even in an arbitrarily small interval. We only deal with the biharmonic operator since the amount of computations grows very quickly as $m$ increases.

Theorem 2.3. Let $n \geq 2$. For every ${\varepsilon} > 0$ there exists a Hölder-continuous function $g_{\varepsilon}: \mathbb{R}_+ \longrightarrow \mathbb{R}$ such that

and such that the problem

admits both

$-$ a radial solution ($u = u(r)$) in $\mathcal{C}^4({\bf B})$, nonnegative (but not strictly positive) and radially decreasing (but not strictly radially decreasing): namely, $u(r_{0}) = 0$ and $u'(r_{0}) = 0$ for some $r_{0} \in (0, 1)$;

$-$ infinitely many nonnegative nontrivial solutions in $\mathcal{C}^4({\bf B})$ which are not radially symmetric.

Proof. For any $p > 4$ define the function $g : \mathbb{R}_+ \longrightarrow \mathbb{R}$ by

Then $g \in \mathcal{C}^{0, 1-\frac{4}{p}}([0, \infty); \mathbb{R}) \cap \mathcal{C}^{\infty}((0, \infty); \mathbb{R})$ and

The quantities between brackets in both the expressions of $g(w)$ and $g'(w)$ can be seen as second order polynomials in the variable $w^{1/p}$. In particular, there must exist finite numbers $M = M(n, p) > 0$, $\Gamma_1 = \Gamma_1(n, p) > 0$, $\Gamma_2 = \Gamma_2(n, p)\in(0, \Gamma_1)$ such that

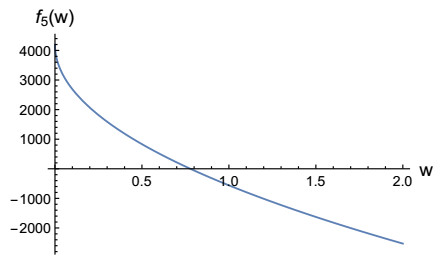
Two plots of $g$, for given values of $p > 4$ and $n \geq 2$, are displayed in Figure 1.

Since $m = 2$, the Eq (1.2) in radial coordinates becomes

where the conditions $u'(0) = u'''(0) = 0$ are needed to ensure the smoothness of $u$ in ${\bf B}$, see ^[8]. By putting $u(r) \doteq (1-r^2)^p$, for $r \in [0, 1]$, one sees that such $u$ satisfies $u(1) = u'(1) = 0$ (fulfilling the Dirichlet boundary conditions) and also the equation in (2.6), where $g\big(u(r)\big)$ is as in (2.4). Hence,

is a $\mathcal{C}^{4}(\overline{ {\bf B}})$-positive, radial and strictly radially decreasing solution ($u'(r) < 0$ in $(0, 1)$) of the problem

In order to obtain the statement, we need some rescaling. First we extend $u$ to all $\mathbb{R}^n$ by setting

so that $u\in\mathcal{C}^{4}(\mathbb{R}^{n})$ is nonnegative and nontrivial (but not strictly positive), radial and radially decreasing (but not strictly decreasing). We now argue as in [10,p. 220]: take any point $x_{0} \in \mathbb{R}^{n}$ such that $| x_{0} | = 3$ and consider the function $\hat{u} \in \mathcal{C}^{4}(\mathbb{R}^{n})$ defined as

which is a nonnegative solution of the problem

where ${\bf B}_5\subset \mathbb{R}^{n}$ is the (open) ball of radius 5 centered at the origin of $\mathbb{R}^{n}$, and $g$ is given by (2.4). Nevertheless, $\hat{u}$ is not radially symmetric!

Then we rescale the problem as follows. For $u = u(r)$ as in (2.7) and for some $\gamma > 0$, define $v(r) \doteq u(5r)/\gamma$ for $r \in [0, 1]$, so that

and $v$ solves

Finally, fix ${\varepsilon} > 0$ and let us construct the function $g_{\varepsilon}$ in the statement. Choose $\gamma_{0} > 0$ such that

Then $g_{\varepsilon} \doteq g^{\gamma_{0}}$ satisfies all the assumptions of the statement and the function $v$ is a radial solution, nonnegative but not strictly positive (since it vanishes in ${\bf B}\setminus {\bf B}_{1/5}$), and radially decreasing but not strictly radially decreasing (since it is constant in ${\bf B}\setminus {\bf B}_{1/5}$). Moreover, after rescaling the function $\hat{u}$ in (2.8), we obtain infinitely many nonnegative nontrivial solutions which are not radially symmetric, one for each $x_0$ and, possibly with multiple bumps.

The next result shows that the monotonicity assumption in (1.5) is not necessary to obtain the statement of Theorem 1.2. For $n \geq 2$, consider the function

which is strictly decreasing and sign-changing, see Figure 2 below.

However, we can prove

Proposition 2.4. Let $f_n$ be as in $(2.9)$. The unique strong solution of the problem

is given by

and, hence, it is positive, radially symmetric and strictly decreasing in the radial variable.

Proof. The function $f_{n}$ defined in (2.9) satisfies the assumption (2.2) so that, by arguing as in the proof of Theorem 2.1, we infer that (2.10) admits at most one strong solution, which is necessarily radially symmetric.

In radial coordinates, when $m = 2$, the Eq (1.2) becomes (2.6). The fact that $u(r) = (1-r^4)^2$, for $r \in [0, 1]$, is a (radial) solution follows by noticing that $u(1) = u'(1) = 0$ (fulfilling the Dirichlet boundary conditions), and then, by inserting the expressions of $u(r)$ and $f_{n}\big(u(r)\big)$ into (2.6).

3.   A reflection property in conformal dimensions

We introduce here the Green function of the polyharmonic operator $(-\Delta)^m$ under Dirichlet boundary conditions in ${\bf B}\subset \mathbb{R}^n$ and we determine some of its properties. Let us firstly define

Then for $x, y \in {\bf B}$, with $x \not = y$, Boggio [5,p.126] (see also [9,Section 2.6]) gave the following explicit representation of the Green function:

where $k_n^m$ is a positive constant defined by

see [9,Lemma 2.27], and $H:(0, \infty)\times[0, \infty)\rightarrow \mathbb{R}$ is defined as

The following statement is a direct consequence of Boggio's work ^[5], elliptic regularity (see [9,Section 2.5]) and the estimates in ^[12].

Proposition 3.1. Let $h \in L^{\infty}({\bf B})$, and let $u \in H_0^m({\bf B})$ be a weak solution of $(-\Delta)^m u = h$ in ${\bf B}$ under Dirichlet boundary conditions, that is

Then $u \in \mathcal{C}^{2m-1, \alpha}(\overline\Omega)$ and it satisfies

where $D^k$ stands for any partial derivative of order $|k| < 2m$. In particular, $u$ is a strong solution and $D^k u \equiv 0$ on $\partial {\bf B}$ for $|k|\le m -1$.

In conformal dimensions $n = 2m$, the Green function admits a simpler representation. Indeed, the change of variables $\xi = \frac{1}{z+1}$ yields

Therefore, by setting $\kappa_{m} \doteq k_{2m}^{m}$, for every $x, y \in {\bf B}$ we have

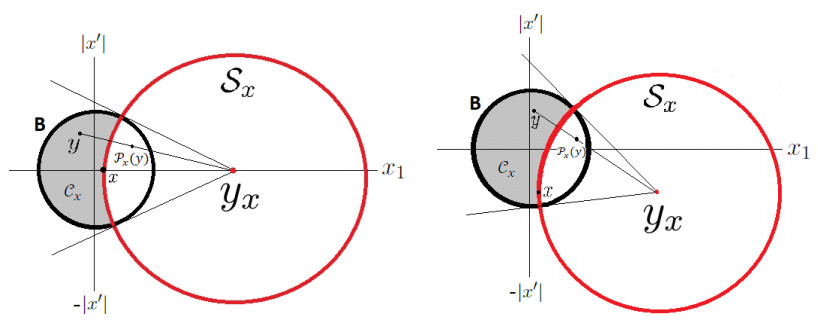
The main result of this section (Theorem 3.2) shows that, in conformal dimensions, the Green function satisfies an elegant reflection property. For this, given the point $x = (x_{1}, x')\in {\bf B}$ with $x_{1} > 0$, we define

and the set

which is a sphere with center at $y_x$ and radius $R_x$ (see the proof of Theorem 3.2 below and also Figure 4). We then denote by $\mathcal{P}_{x} : \mathbb{R}^{n} \setminus \{y_{x}\} \longrightarrow \mathbb{R}^{n}$ the inversion in $\mathcal{S}_{x}$, given by the expression

Finally, the Kelvin transform of a function $h : \mathcal C_{x} \longrightarrow \mathbb{R}$ with respect to $\mathcal{S}_{x}$ is defined as

Then we prove

Theorem 3.2. For any $x = (x_{1}, x')\in {\bf B}\subset\mathbb{R}^{2m}$ with $x_1 > 0$ and any $u \in H^{2m}({\bf B}) \cap H_0^m({\bf B})$ we have

Proof. The following identities hold for the function $H$ defined in (3.3): for all $s, t > 0$ we have

see also ^[3]. Moreover, for every $x, y \in {\bf B}$ we have

We then prove the announced symmetry property, namely that the zero level sets of $\partial_{x_{1}} G(x, \cdot)$ are spherical caps. Let us denote the zero level set by

By (3.10) and by (3.11) we have

Therefore, $\partial_{x_{1}} G(x, y)$ vanishes if and only if $y\in {\bf B}$ belongs to the set $\mathcal{S}_{x}$ defined in (3.8). Then we notice that $y\in {\bf B}\cap\mathcal{S}_{x}$ if and only if

Hence, $\mathcal{S}_{x}$ is a sphere with center at $y_x$ and radius $R_x$ and the set of negativity of $\partial_{x_{1}} G(x, y)$ is the cap $\mathcal C_{x}$ defined in (3.7).

Next, we notice that, by definition of $y_{x}$ and $R_x$, we have

Then we compute

This computation has two main consequences. First, that the unit sphere $\partial {\bf B}$ is invariant under the inversion in $\mathcal{S}_{x}$, that is,

Second, that

We next claim that if $\mathcal C_{x}$ is the cap defined in (3.7), then ${\bf B} = \mathcal C_{x} \cup \mathcal{P}_{x}(\mathcal C_{x}) \cup \mathcal{L}_{x}$. To this end, it suffices to show that

Indeed, let $y \in \mathcal C_{x}$, so that $\mathcal{P}_{x}(y) \in \mathcal{P}_{x}(\mathcal C_{x})$ and $\vert y - y_{x} \vert > R_x$. By definition of $\mathcal{P}_{x}$ we have

thus proving that $\mathcal{P}_{x}(\mathcal C_{x}) \subset \left\{y\in {\bf B}\; ; \, \vert y - y_{x} \vert < R_x\right\}$. On the other hand, let $y \in {\bf B}$ be such that $\vert y - y_{x} \vert < R_x$. Since the function $\mathcal{P}_{x}$ is bijective, there exists a point $y_{0} \in \mathbb{R}^{n}$ such that $\mathcal{P}_{x}(y_{0}) = y$. By definition, we then have

implying $y_{0} \in \mathcal C_{x}$, and subsequently, that $y \in \mathcal{P}_{x}(\mathcal C_{x})$ and $\left\{y\in {\bf B}\; ; \, \vert y-y_{x} \vert < R_x \right\} \subset \mathcal{P}_{x}(\mathcal C_{x})$.

Since ${\bf B} = \mathcal C_{x} \cup \mathcal{P}_{x}(\mathcal C_{x}) \cup \mathcal{L}_{x}$, by Proposition 3.1, we have

where we used that the Jacobian matrix $\mathcal{P}'_{x}$ satisfies

In view of (3.12) and (3.13) we can write

so that

where

To compute $I_{2}(x)$, we first notice that

whereas, for every $y \in {\bf B}$ we have

After plugging (3.14), (3.17) and (3.18) into $I_{2}(x)$ we get

and, after recalling (3.16), we deduce

A direct computation (see [13,Proposition 7.3]) shows that

which concludes the proof after changing the sign.

Problem 3.3. It is not clear how to derive an expression similar to $(3.9)$ in non-conformal dimensions $n \geq 2$, $n \neq 2m$. This can be seen after computing

so that the determination of the level sets of $\partial_{x_{1}} G(x, \cdot)$ as in $(3.12)$ becomes a delicate task. Is it possible to obtain a representation formula similar to $(3.9)$ in any dimension $n \geq 2$?

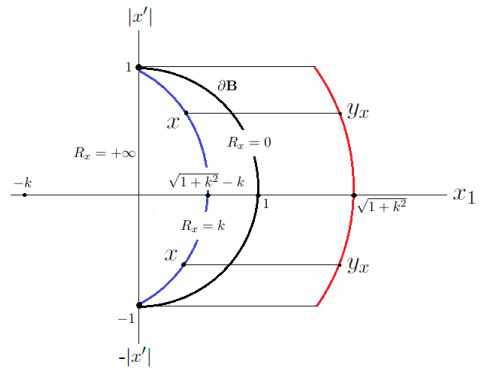
Clearly, a representation formula similar to (3.9) holds for any other directional derivative of $u$. Note that (3.7) may be rewritten as $y_x = x+(R_x, 0)$, which implies that $y_x$ is an "horizontal translation" of $x \in {\bf B}$. Moreover, $R_x\to0$ if $x\to\partial {\bf B}$ while $R_x\to+\infty$ if $x_1\to0$: the limit of the map $x\mapsto R_x$ does not exist when $x$ approaches the equator $\partial {\bf B}\cap \{x_1 = 0\}$. The level surfaces of $x\mapsto R_x$ are spheres:

The center of the level-surface sphere is then $(x_1, x') = (-k, 0)$ and its radius is $\sqrt{1+k^2}$. For a fixed $k > 0$, when $x$ runs over the level surface $R_x = k$, the corresponding $y_x$, defined by (3.7), runs over a portion of the sphere centered in the origin with the same radius $\sqrt{1+k^2}$, see Figure 3.

Note also that $\mathcal C_{x}$, the domain of negativity of $\partial_{x_{1}} G(x, y)$, is the intersection between two balls. In Figure 4 we sketch the mutual position of the sphere $\mathcal{S}_x$ and the ball ${\bf B}$. In particular, we emphasize that

which, again, tells us that $y_x$ is exterior to ${\bf B}$ and it approaches $\partial {\bf B}$ as $x$ approaches $\partial {\bf B}$, while it goes to infinity if $x$ approaches the plane $x_1 = 0$.

Theorem 3.2 has several relevant consequences. Firstly, we deduce

Corollary 3.4. Let $m \geq 1$. For every $x \in {\bf B} \subset \mathbb{R}^{2m}$ such that $x_{1} > 0$, the following identities hold

Proof. We start by noticing that

where $n = 2m$. By induction we then obtain

Consider the polyharmonic version of the original problem (1.1) proposed by Serrin:

A direct application of the binomial expansion yields

that is

Since $U_{m}$ satisfies the Dirichlet boundary conditions in (3.22)$_{2}$, it is a strong $\mathcal{C}^{\infty}(\overline{ {\bf B}})$-solution of (3.22). Applying identity (3.9) to the function $U_{m}$ and recalling (3.2) (with $n = 2m$), we derive equality (3.20). The identity (3.21) is a straightforward consequence of (3.20), after replacing $\theta(x, y)$.

It is remarkable that the right hand side of (3.21) does not depend on $x\in {\bf B}$. As a further consequence of Theorem 3.2, we give an alternative formula to compute the partial derivatives of the solutions of (1.2), which should be compared with Proposition 3.1.

Corollary 3.5. Let ${\bf B}\subset \mathbb{R}^{2m}$ be the unit ball. Suppose that $f \in \mathcal{C}(\mathbb{R}; \mathbb{R})$ and that $u\in H_0^m({\bf B}) \cap L^{\infty}({\bf B})$ is a strong solution of (1.2). Then, for every $x \in {\bf B}$ such that $x_{1} > 0$, the following formula holds:

Formula (3.24) follows directly from (3.9)–(3.19) and suggests the problem:

Problem 3.6. Since the moving plane procedure developed in [3,Section 3] requires that

is it possible to use $(3.24)$ to prove this inequality and to relax assumption $(1.5)$, but still ensuring the statement of Theorem 1.2?

In connection with Problem 3.6 we notice that, by looking at (3.24), it is clear that the overall sign of the integral over $\mathcal{C}_{x}$ is determined by the behavior of the quantity

Fixing $x \in {\bf B}$ such that $x_{1} > 0$ and $u\in H_0^m({\bf B})$, notice that $\Phi_{x}(y) = 0$ for all $y \in \partial \mathcal{C}_{x} \cap {\bf B}$, while for $y \in \partial \mathcal{C}_{x} \cap \partial {\bf B}$ (so that $\mathcal{P}_{x}(y) \in \partial {\bf B}$) we have that $\Phi_{x}(y) = 0$ if $f(0) = 0$, and $\Phi_{x}(y) > 0$ if $f(0) > 0$.

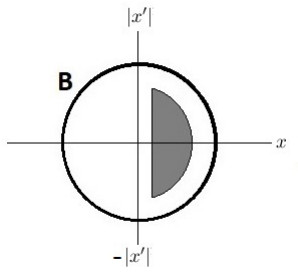
Under suitable assumptions on the source $f$, in the next result we give an upper bound for the partial derivative of $u$ (recall that $|x| < 1$!), which shows that $\partial_{x_{1}}u(x) < 0$ for all $x \in {\bf B}$ located far away from $\partial {\bf B}$, with $x_1\geq\varepsilon$ for some $\varepsilon > 0$, see Figure 5 for a schematic representation. Therefore, in order to solve Problem 3.6, one should mainly focus the attention on the complement of this region.

To this end, we define

and we state:

Proposition 3.7. Assume that $f \in W^{1, \infty}(\mathbb{R}_+; \mathbb{R}_+)$ satisfies

and let $u\in H_0^m({\bf B}) \cap L^{\infty}({\bf B})$ be a strong solution of (1.2). For any point $x = (x_{1}, x')\in {\bf B}$ with $x_1 > 0$ we have

where $\mathbb{K}_m > 0$ is defined in (3.21).

Proof. In view of Corollary 3.4, by the Maximum Principle and assumption (3.25), any strong solution $u\in H_0^m({\bf B}) \cap L^{\infty}({\bf B})$ of (1.2) satisfies

By embedding theorems and elliptic regularity we also have that

Then, by the Mean Value Theorem, we obtain the inequality

From this we deduce that

thus yielding

and, by using (3.25), we finally obtain

By inserting this bound within (3.24), we get

where

From Corollary 3.4 we infer that

In order to bound $I_2(x)$, we notice that

Hence,

From (3.15) and Proposition 3.1, and by proceeding as in the proof of Corollary 3.4, we obtain

After plugging this into (3.28) we deduce that

The conclusion is reached after inserting (3.27) and (3.29) into (3.26).

Proposition 3.7 suggests that the radial symmetry and monotonicity of the solutions of (1.2) can be ensured if $\|f'\|_{L^{\infty}(\mathbb{R}_+)}$ is small. This assumption is not needed if $m = 1$ (see Theorem 1.1), while for $m \geq 2$, the required condition is that $f'$ be nonnegative (see Theorem 1.2). Therefore, one is led to analyze the cases where the negative part of $f'$ is small, that is, $\|(f')_{-}\|_{L^{\infty}(\mathbb{R}_+)}$ small. This issue is tackled numerically in the next section, for the biharmonic equation in ${\bf B}\subset\mathbb{R}^{4}$.

4.   On a counterexample by Guido Sweers

As a direct consequence of the Hopf-type lemma by Grunau-Sweers [11,Theorem 3.2] we obtain

Proposition 4.1. Assume that $f \in W^{1, \infty}(\mathbb{R}_+; \mathbb{R}_+)$ satisfies $(3.25)$, and let $u\in H_0^m({\bf B}) \cap L^{\infty}({\bf B})$ be a strong solution of $(1.2)$. Then, there exists $\gamma_{f} > 0$ such that

Guido Sweers ^[16] provided an explicit example of a non-decreasing radial solution of a linear biharmonic problem in ${\bf B}\subset\mathbb{R}^{2}$ (equation (1.2) with $m = 2$). In this section we take advantage of his example and give numerical evidence to claim that Proposition 4.1 might be complemented with the statement that $\gamma_{f}$ can be made arbitrarily small (possibly zero) provided that $\|(f')_{-}\|_{L^{\infty}(\mathbb{R}_+)}$ is sufficiently small.

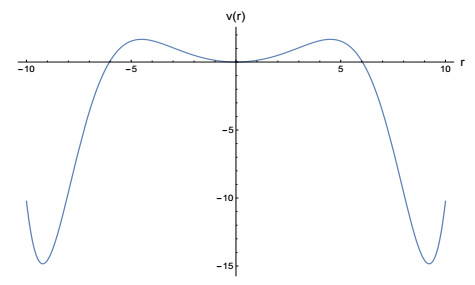
Consider the following radial function defined in $\mathbb{R}^{4}$ (the conformal dimension for the biharmonic operator):

whose plot in the interval $[-10, 10]$ is displayed in Figure 6 below.

Since $m = 2$ and $n = 4$, the biharmonic operator in radial coordinates becomes

After noticing that

one readily sees that

Let $r_0\approx 9.2218$ be the first nonzero local minimum of $v$; numerically, we find that $v(r_0)\approx-14.8388$. Then define the function

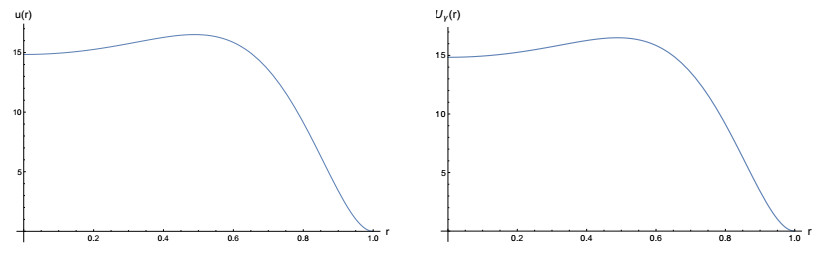
which is radially symmetric and strictly positive in $[0, 1)$, but not decreasing, in the interval $[0, 1]$; see the left picture in Figure 7 below.

By defining

we observe that $f'(w)\equiv-r_{0}^{4} < 0$, so that $f$ is decreasing and (2.2) is satisfied. By Theorem 2.1 we then know that there exists at most one strong solution of the following problem:

The solution is radially symmetric and a simple computation shows that it coincides with $u$ defined in (4.1). Note that $u(0) = |v(r_{0})|$ and $u(0.5) > 16.5 > |v(r_{0})|$, so that $f(u)$ is sign-changing in $[0, 1]$.

We now modify $f$ in order to reduce $\|(f')_{-}\|_{L^{\infty}(\mathbb{R}_+)}$. We take

being $\gamma > 0$ a variable parameter. Then we consider the problem

and prove the following result:

Proposition 4.2. For every $\gamma > 0$, the unique strong solution $U_{\gamma} \in H^{2}_{0}({\bf B}) \cap L^\infty({\bf B})$ of (4.2) (which is radially symmetric) is analytic and can be written as

for some coefficients $\{ A_{k}(\gamma) \}_{k \in \mathbb{N}} \subset \mathbb{R}$ that satisfy the following properties:

Moreover, there exists $\gamma_{0} > 0$ such that, for every $\gamma \in (0, \gamma_{0})$, the function $U_{\gamma}$ is positive in $[0, 1)$ and strictly decreasing in the radial variable.

Proof. For every $\gamma > 0$ we notice that the condition (2.2) is satisfied. Then, Theorem 2.1 guarantees the existence of at most one strong solution $U_{\gamma} \in H^{2}_{0}({\bf B}) \cap L^\infty({\bf B})$ to problem (4.2) which is, moreover, radially symmetric and analytic in $\overline{ {\bf B}}$. Problem (4.2) in radial coordinates reads:

Upon substitution of (4.3) into (4.4)$_1$ we obtain

which yields the identities

Moreover, the boundary conditions in (4.4)$_2$ imply that

In connection with (3.23) we define

By Corollary (3.4) and by continuous dependence, we have that

in fact, the convergence holds in a stronger norm. Notice that

Thus, by uniform convergence of $U_\gamma''$ and $U_\gamma'''$, there exist $\delta_{0} \in (0, 1)$ and $\gamma_{0} > 0$ such that:

Since $U'_{\gamma}(0) = U'_{\gamma}(1) = 0$ for every $\gamma > 0$, this implies that

Moreover, by uniform convergence of $U'_{\gamma}$, there exists $\gamma_{1} > 0$ such that $U'_{\gamma}(r) < 0$ if $r \in [\delta_{0}, 1-\delta_{0}]$, for every $\gamma \in (0, \gamma_{1})$. Therefore $U'_{\gamma} < 0$ in $(0, 1)$ whenever $\gamma < \min \{ \gamma_{0} \, , \gamma_{1} \}$, which also implies that $U_{\gamma}$ is strictly positive in $[0, 1)$, since $U_{\gamma}(1) = 0$.

In fact, the function $U_{\gamma}$ is also unique within the class of weak solutions. Proposition 4.2 does not come unexpected, since the solution of (4.4) is closely related to a Bessel function, see ^[16]. Therefore, the number of critical points of $U_{\gamma}$ is increasing with respect to $\gamma$ and becomes arbitrarily large as $\gamma \to \infty$, whereas there are no critical points for any sufficiently small $\gamma$. By taking $\gamma = 1$, we numerically obtain the solution displayed in the right picture of Figure 7, which represents the function $u$ in (4.1). Several numerical simulations were performed in order to yield a radially decreasing solution of problem (4.2). The obtained results may be summarized as follows:

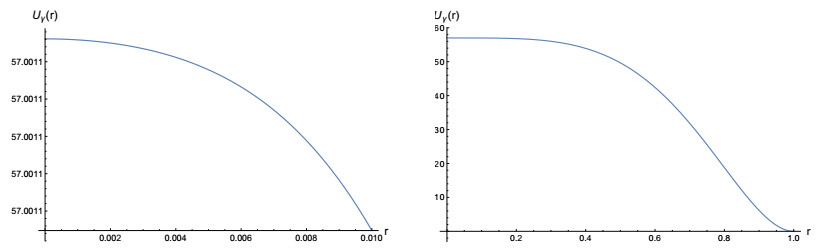
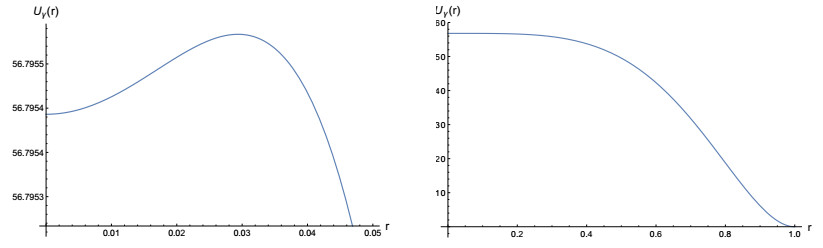
● if $\gamma \leq 0.317$, then the associated solution $U_{\gamma}$ of (4.2) is radially symmetric and strictly decreasing in the radial variable in the interval $[0, 1]$ (and therefore, positive), see Figure 8;

● if $\gamma \geq 0.318$, then the associated solution $U_{\gamma}$ of (4.2) is radially symmetric but not strictly decreasing in the interval $[0, 1]$, see Figure 9.

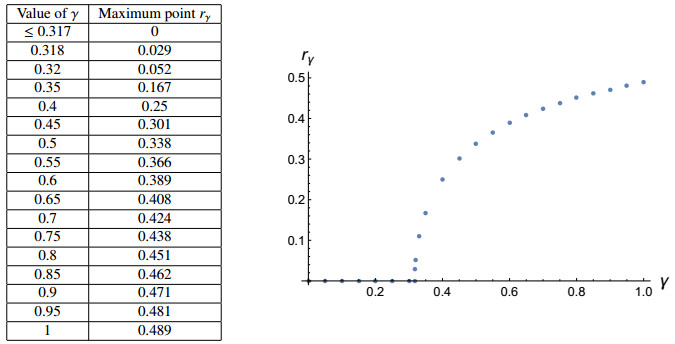
We numerically determined the position of the maximum point $r_{\gamma} \in [0, 1]$ of $U_{\gamma}$ as a function of $\gamma \in [0, 1]$, see the Table and Figure below. From these data we deduce that the map $\gamma \in [0, 1] \mapsto r_{\gamma}$ is increasing (but not continuous!), giving thus consistency to the discussion following Proposition 4.1. Finally, in connection with the condition (3.25) given in Propositions 3.7 and 4.1, we observe that, for the unique radial solution $U_{\gamma} \in H^{2}_{0}({\bf B})$ of problem (4.2), the following inequality holds:

From the Table and Figure displayed below we further deduce that

recall that $U_{\gamma}$ is nonnegative in $[0, 1]$ for every $\gamma \in [0, 0.317]$. Numerical experiments yield the value of $\gamma = 0.057$ as a threshold for ensuring the positivity of the right-hand side of (4.6), in the sense that

Acknowledgments

The first Author is supported by the PRIN project Direct and inverse problems for partial differential equations: theoretical aspects and applications and by INdAM. The second Author is supported by the Research Programme PRIMUS/19/SCI/01, by the program GJ19-11707Y of the Czech National Grant Agency GA\v{C}R, and by the University Centre UNCE/SCI/023 of the Charles University in Prague.

Conflict of interest

The authors declare no conflict of interest.