Figure 1.
3D plot of the exact solution u1, 1(x, t) and its projection at t = 1.
Citation: M. A. Habib, H. M. Shahadat Ali, M. Mamun Miah, M. Ali Akbar. The generalized Kudryashov method for new closed form traveling wave solutions to some NLEEs[J]. AIMS Mathematics, 2019, 4(3): 896-909. doi: 10.3934/math.2019.3.896
| [1] | Mohammed Aly Abdou, Loubna Ouahid, Saud Owyed, A. M. Abdel-Baset, Mustafa Inc, Mehmet Ali Akinlar, Yu-Ming Chu . Explicit solutions to the Sharma-Tasso-Olver equation. AIMS Mathematics, 2020, 5(6): 7272-7284. doi: 10.3934/math.2020465 |
| [2] | M. TarikulIslam, M. AliAkbar, M. Abul Kalam Azad . Traveling wave solutions in closed form for some nonlinear fractional evolution equations related to conformable fractional derivative. AIMS Mathematics, 2018, 3(4): 625-646. doi: 10.3934/Math.2018.4.625 |
| [3] | M. Ali Akbar, Norhashidah Hj. Mohd. Ali, M. Tarikul Islam . Multiple closed form solutions to some fractional order nonlinear evolution equations in physics and plasma physics. AIMS Mathematics, 2019, 4(3): 397-411. doi: 10.3934/math.2019.3.397 |
| [4] | Yanxia Hu, Qian Liu . On traveling wave solutions of a class of KdV-Burgers-Kuramoto type equations. AIMS Mathematics, 2019, 4(5): 1450-1465. doi: 10.3934/math.2019.5.1450 |
| [5] | Gaukhar Shaikhova, Bayan Kutum, Ratbay Myrzakulov . Periodic traveling wave, bright and dark soliton solutions of the (2+1)-dimensional complex modified Korteweg-de Vries system of equations by using three different methods. AIMS Mathematics, 2022, 7(10): 18948-18970. doi: 10.3934/math.20221043 |
| [6] | Baojian Hong, Jinghan Wang, Chen Li . Analytical solutions to a class of fractional coupled nonlinear Schrödinger equations via Laplace-HPM technique. AIMS Mathematics, 2023, 8(7): 15670-15688. doi: 10.3934/math.2023800 |
| [7] | Xiaoli Wang, Lizhen Wang . Traveling wave solutions of conformable time fractional Burgers type equations. AIMS Mathematics, 2021, 6(7): 7266-7284. doi: 10.3934/math.2021426 |
| [8] | Hammad Alotaibi . Solitary waves of the generalized Zakharov equations via integration algorithms. AIMS Mathematics, 2024, 9(5): 12650-12677. doi: 10.3934/math.2024619 |
| [9] | F. A. Mohammed, Mohammed K. Elboree . Soliton solutions and periodic solutions for two models arises in mathematical physics. AIMS Mathematics, 2022, 7(3): 4439-4458. doi: 10.3934/math.2022247 |
| [10] | Jamilu Sabi'u, Sekson Sirisubtawee, Surattana Sungnul, Mustafa Inc . Wave dynamics for the new generalized (3+1)-D Painlevé-type nonlinear evolution equation using efficient techniques. AIMS Mathematics, 2024, 9(11): 32366-32398. doi: 10.3934/math.20241552 |
Nonlinear evolution equations (NLEEs) attracted much attention in a wide variety of scientific analysis in various fields of applied science and engineering. The nonlinear complex physical phenomena are related to NLEEs which play a significant role in many attributions: especially in nonlinear optics, electric control theory, solid-state physics, nuclear physics, high energy physics, mathematical biology, biochemistry, chemically reactive materials, biophysics, optical fibers, fluid mechanics, plasma physics etc. Since the modeling of real world problems are essentially nonlinear, it is necessary to extract their exact, approximate or numerical solutions. Due to the availability of high performance computer facilities and symbolic computation software like Mathematica, the task of handling computational methods to acquire exact solutions of NLEEs is very fascinating for many scholars. For this reason, in the last decades, a number of potential methods have been formulated and implemented to search exact solution, such as the homogeneous balance method [1], the modified simple equation method [2], the F-expansion method [3,4], the sine-Gordon equation expansion method [5,6,7], the (G'/G)-expansion method [8], the modified exponential function method [9], the tanh method [10], the sine-cosine method [11,12], the (G'/G, 1/G)-expansion method [13,14,15], the new extension of (G'/G)-expansion method [16], the tanh-coth method [17], the generalized bilinear operator method [18,19,20], the Exp-function method [21], the modified tanh-function method [22], the extended tanh method [23], the Hirota's bilinear method [24,25,26,27], the exponential rational function method [28], Jacobi elliptic function method [29], the improved (G'/G)-expansion method [30], the Bernoulli sub-equation function method [31], the improved Bernoulli sub-equation function method [32], the generalized Riccati equation method [33], the finite difference method [34,35,36], the modified Kudryashov method [37,38,39,40,41,42] and others are developed to extract wave solutions of NLEEs.
Recently, the generalized Kudryashov method [43,44,45,46,47,48] was introduced to examine the NLEEs modeled the physical problems. The main objective of this article is: we introduce and implement the originative method, named the generalized Kudryashov method to establish new closed form traveling wave solutions to some NLEEs, viz. the Burgers-Huxley, the mKdV and the first extended fifth order nonlinear equations. To the best of our comprehension no one studied the aforesaid equations through the generalized Kudryashov method.
The Burgers-Huxley equation is of the form [49]:
| ut=uxx+uux+u(k−u)(u−1),k≠0. | (1) |
The mKdV equation is of the form [50]:
| ut−u2ux+δuxxx=0,δ>0. | (2) |
The first extended fifth order nonlinear equation is of the form [51]:
| uttt−utxxxx−utxx−4(uxut)xx−4(uxuxt)x=0. | (3) |
The Burgers-Huxley equation can be considered as a model to relate the interaction between reaction mechanisms, convection effects and diffusion transports [52]. Many physical applications of mKdV equation, first extended fifth order nonlinear equation and is used as a model for nonlinear dispersive waves.
The remainder of this article contains the following portions: In section 2, recapitulation of the generalized Kudryashov method is briefly described. In section 3, applications of the method to some NLEEs, as for example, the Burgers-Huxley equation, the mKdV equation and the first extended fifth order nonlinear equation are provided. Physical assertion and graphical illustration is presented in section 4. Finally, in section 5, conclusions are provided.
We assume the NLEEs for a function u(x, t) of two variables x and t as follows:
| P(u,ut,ux,utt,uxx,uxt,…...)=0, | (4) |
where P being a polynomial of u and its partial derivatives in which the nonlinear terms and the highest order derivatives are engaged. The procedures of the generalized Kudryashov method [43,44,45,46,47,48] are given in briefly as follows:
First Step
First, we consider the following wave variable for reducing the NLEE (4) to an ordinary differential equation (ODE)
| u(x,t)=U(η),η=kx−v t, | (5) |
where k is the wave number and v indicates the wave velocity. Therefore, the Eq. (4) moves to the subsequent ODE,
| Q(U,U′,U′′,……)=0, | (6) |
wherein prime " ' " indicates the ordinary derivative in terms of η.
Second Step
As per the gKM, the exact solution of Eq. (6) can be presented as [38,39,40]
| U(η)=∑Ni=0aiRi(η)∑Mj=0bjRj(η), | (7) |
where ai, bj are arbitrary constants with aN≠0, bM≠0 to be calculated later and R(η) is the solution of the auxiliary equation
| dRdη=R(R−1). | (8) |
The solution of Eq. (8) has the following form
| R=11+Aexp(η) , | (9) |
where A is the constant of integration.
Third Step
The homogeneous balance principle provides the values of positive integers M and N from Eq. (6) by using the highest order derivative and nonlinear term.
Fourth Step
In order for calculating the constants ai and bj, insert Eq. (7) into Eq. (6) and by means of Eq. (8) yields a polynomials of R(η). Equalizing these coefficients to zero offers a system of algebraic equations. Mathematica software package program is used for solving this system of equations to find out the constants as we desired. Finally, these constants provided the new closed form traveling wave solutions to the NLEE (4).
In this section, the generalized Kudryashov method has been conducted to study the new closed form traveling wave solutions to the mentioned equations.
Within this subsection, we implement the gKM to establish the closed form traveling wave solution to the Burgers-Huxley equation (1). The following transformation is considered
| u(x,t)=U(η),η=x−c t, | (10) |
where c is a wave velocity. Substituting the transformation (10), Eq. (1) turns out to be
| cU′+U′′+UU′+U(k−U)(U−1)=0, | (11) |
wherein " ' " stands for ddη. By the homogeneous balance principle from Eq. (11), we attain
| N=M+1. | (12) |
M is free parameter, therefore, if we set M = 1, it yields N = 2.Thus, solution (7) moves to
| U(η)=a0+a1R+a2R2b0+b1R, | (13) |
where a0, a1, a2, b0, b1 are constants and R(η) obtain from (8). By the gKM the following system of equations are produces,
| R0(η):−a30+a20b0+a20kb0−a0kb20=0, |
| R1(η):−3a20a1+a0a1b0+2ka0a1b0+a1b20−ca1b20−ka1b20+2a20b1++ka20b1−a0b0b1+ca0b0b1−2ka0b0b1=0, |
| R2(η):−3a0a21−3a20a2+a0a1b0+ka21b0+2ka0a2b0−3a1b20+ca1b20+4a2b20−2ca2b20−ka2b20−a20b1+3a0a1b1+2ka0a1b1+3a0b0b1−ca0b0b1−a1b0b1−ca1b0b1−2ka1b0b1+a0b21+ca0b21−ka0b21=0, |
| R3(η):−a31−6a0a1a2+a21b0+2a0a2b0−a1a2b0+2ka1a2b0+2a1b20−10a2b20+2ca2b20−a0a1b1+a21b1+ka21b1+2a0a2b1+2ka0a2b1−2a0b0b1+a1b0b1+ca1b0b1+3a2b0b1−3ca2b0b1−2ka2b0b1−a0b21−ca0b21−ka1b21=0, |
| R4(η):−3a21a2−3a0a22+3a1a2b0−a22b0+ka22b0+6a2b20+a1a2b1+2ka1a2b1−9a2b0b1+3ca2b0b1+a2b21−ca2b21−ka2b21=0, |
| R5(η):−3a1a22+2a22b0+a1a2b1+ka22b1+6a2b0b1−3a2b21+ca2b21=0, |
| R6(η):−a32+a22b1+2a2b21=0, |
Solving above set of equations by using Mathematica, we obtain two sets of values of the constants and by means of these values the required solutions can be found.
Set 1:
| a0=b0,a1=−b0+b1,a2=−b1 and c=k−1. | (14) |
Inserting the above values into solution (13), the exact solution of Eq. (1) takes the shape
| u1,1(x,t)=A(cosh(x−(k−1)t2)+sinh(x−(k−1)t2))(1+A)cosh(x−(k−1)t2)−(1−A)sinh(x−(k−1)t2). | (15) |
Since A is the integral constant, one might randomly choose its values, thus if we choose A = 1, the above solution transforms to the subsequent simplest form
| u1,1(x,t)=12(1+tanh(x−(k−1)t2)). | (16) |
Again, if we choose A = -1, the solution takes the form
| u1,1(x,t)=12(1+coth(x−(k−1)t2)). | (17) |
The other choice of the value of A produces many further general form solutions to the Burgers-Huxley equation, but for conciseness the rest of the solutions are not documented.
Set 2:
| a0=0,a1=b1,a2=−b1,b0=0, and c=k−1. | (18) |
For set 2, the exact solution of Eq. (1) becomes
| u1,2(x,t)=A(cosh(12(x−(k−1)t))+sinh(12(x−(k−1)t))(A+1)cosh(12(x−(k−1)t)+(A−1)sinh(12(x−(k−1)t)). | (19) |
If we set A = 1, the above solutionis simplified as
| u1,2(x,t)=12(1+tanh(12(x−(k−1)t))). | (20) |
Again, if we set A = -1, the solution converts to
| u1,2(x,t)=12(1+coth(12(x−(k−1)t))). | (21) |
The other selection of the estimation of A produces various extensive wave solution to the Burgers-Huxley equation, yet for succinctness whatever remains of the arrangements are not reported.
In this subsection, we will derive the exact solutions to the mKdV equation by the eminent method and for this application we consider the same traveling wave transformation as given in Eq. (10). Plugging in this transformation and integrating once with zero constant, Eq. (2) turns out to be
| δU′′−13U3−cU=0, | (22) |
where δ > 0 and by homogeneous balance principle between highest order derivative and nonlinear term in the above equation, as before we consider the Eq. (13) is the solution of Eq. (22).
In order to find out the constants a0, a1, a2, b0, b1, appearing in (13), we use the generalized Kudryashov method and by using package program Mathematica for solving the system of equations gives different sets of values and by means of these values the desired closed form traveling wave solutions of Eq. (2) can be derived.
Set 1:
| a0=0,a1=−2√6√δb0,a2=2√6√δb0,b1=−2b0,c=δ | (23) |
Inserting these values in solution (13), the exact solution of Eq. (2) becomes
| u2,1(x,t)=2√6√δ×A(1−A2)cosh(x−δt)−(1+A2)sinh(x−δt). | (24) |
For as much as A is constant of integration, one might choose its values arbitrarily. In particular, when A = ±1, the above solution converts into following form
| u2,1(x,t)=±√6√δ csch(x−δt). | (25) |
Set 2:
| a0=0,a1=−√32√δb1,a2=√6√6b1,b0=0,c=−δ2 | (26) |
By means of these values from solution (13), the exact solution of Eq. (2) is obtained as
| u2,2(x,t)=√32√δ×(1−A)cosh(x+δ2t2)−(1+A)sinh(x+δ2t2)(1+A)cosh(x+δ2t2)−(1−A)sinh(x+δ2t2). | (27) |
In as much as A is arbitrary constant, one may pick its values subjectively. Specifically, when A = 1, the above arrangement changes over into the following structure
| u2,2(x,t)=−√32√δtanh(12(x+12δ t)). | (28) |
Again, when A = -1, the solution becomes
| u2,2(x,t)=−√32√δcoth(12(x+12δ t)). | (29) |
Set 3:
| a0=√6√δb0,a1=−2√6√δb0,a2=2√6√δb0,b1=−2b0,c=−2δ | (30) |
For the above values of the constants the exact solution of Eq. (2) turns out to be
| u2,3(x,t)=√6δ×(A2+1)cosh(x+2δt)+(A2−1)sinh(x+2δt)(A2−1)cosh(x+2δt)+(A2+1)sinh(x+2δt). | (31) |
In particular, if we choose A = ± 1, we obtain the solution
| u2,3(x,t)=√6√δ coth(x+2δt). | (32) |
Again, we select A = -1, the same solution will be attained and hence has not been written down.
In this subsection, we extract the wave solutions to the first extended fifth order nonlinear Eq. (3) by the introduced eminent method and to this end we consider the subsequent wave transformation
| u(x,t)=U(η),η=kx−v t, | (33) |
By means of the above transformation the Eq. (3) is converted into
| −v3U′′′+v k4U′′′′′+v k2U′′′+4v k3(U′U′)′′+4v k3(U′U′′)′=0. | (34) |
Integrating twice with respect to η and taking the integrating constant zero, Eq. (33) moves to the following form
| (k2−v2)U′+6k3(U′)2+k4U′′′=0. | (35) |
The homogeneous balancing principle between highest order derivative and nonlinear term in the above equation as before, Eq. (13) is the solution of Eq. (35).Using the gKM and computer package program Mathematica the desired solutions of the associated algebraic equations are,
Set 1:
| a1=−2a0,a2=2kb0,b1=−2b0,v=−k√1+4k2. | (36) |
where a0 and b0 are an free parameters.
By using the above values into (13), the exact solution of Eq. (3) turns out to be
| u3,1(x,t)=(A2+2k−1)cosh(kx−vt)+(A2−2k+1)sinh(kx−vt)(A2−1)cosh(kx−ωt)+(A2+1)sinh(kx−vt), | (37) |
where, v=−k√1+4k2.
If we set A = ±1, the solution becomes
| u3,1(x,t)=1−k(1−coth(kx+(k√1+4k2)t)). | (38) |
Set 2:
| a1=−kb20+a0b1b0,a2=−kb1,v=−k√1+k2 | (39) |
where a0, b0 and b1 are free parameters.
By using the values arranged in (39) into solution (13), the exact solution of Eq. (3) becomes
| u3,2(x,t)=(A−k+1)cosh(kx−vt2)+(A+k−1)sinh(kx−vt2)(A+1)cosh(kx−vt2)+(A−1)sinh(kx−vt2), | (40) |
where, v=−k√1+k2.
In particular, if we pick A = 1, the above solution shrink to
| u3,2(x,t)=1−k2(1−tanh(kx+(k√1+k2)t2)). | (41) |
On the other hand, if we pick A = -1, the solution is minimized as
| u3,2(x,t)=1−k2(1−coth(kx+(k√1+k2)t2)). | (42) |
Set 3:
| a0=0,a2=−kb1,b0=0,v=−k√1+k2 | (43) |
wherein a1 and b1 are free parameters.
In this case, the exact solution of Eq. (3) becomes
| u3,3(x,t)=(1+A−k)cosh(12(kx−v t))−(1−A−k)sinh(12(kx−v t))(1+A)cosh(12(kx−v t))−(1−A)sinh(12(kx−v t)), | (44) |
where, v=−k√1+k2.
If we sort A = 1, the solution takes the form
| u3,3(x,t)=k2(tanh(12(kx+(k√1+k2)t))−1+2k). | (45) |
Furthermore, if we sort A = -1,
| u3,3(x,t)=k2(coth(12(kx+(k√1+k2)t))−1+2k). | (46) |
Now, we will study physical significance and graphical representation of the established solutions of the Burgers-Huxley equation, the mKdV equation and the first extended fifth order nonlinear equation. We obtain the solitary waves from the traveling wave solutions through assigning specific quantities to its indefinite parameters. By altering these parameters, one can get an internal localize mode. The solutions for the above referred equations that we have obtained include different types of soliton. Appropriate selection of parameters enables us to develop the soliton, kink, periodic, singular, discontinuous periodic, and the soliton-like solutions. Kink solitons have significant application prospects in optical fiber communication. Singular solitons are another sort of solitary waves that show up with a singularity, typically infinite discontinuity. Singular solitons can be associated with solitary waves when the midpoint position of the singular wave is nonexistent. Along these lines it isn't superfluous to address the issue of singular solitons. This solution has spike and in this manner can likely give a clarification to the development of Rogue waves.
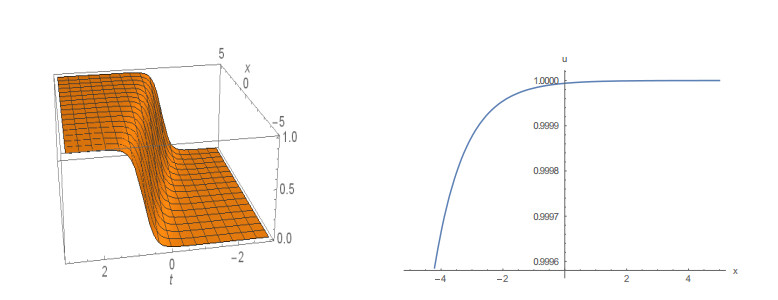
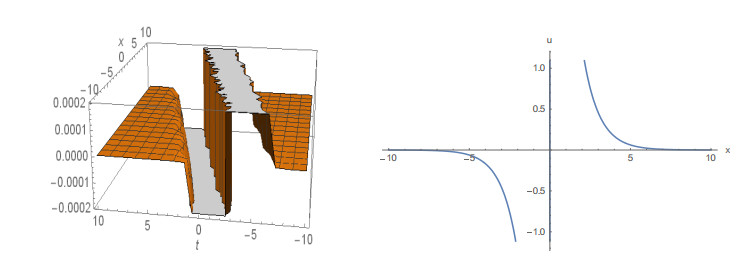
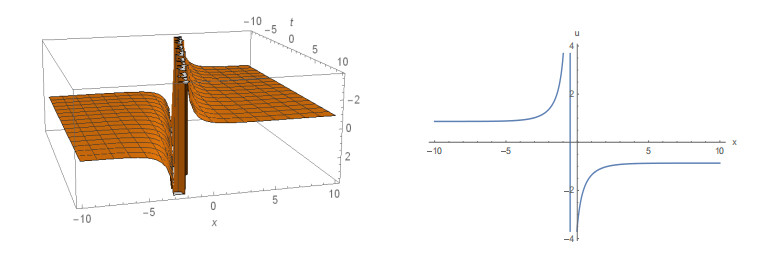
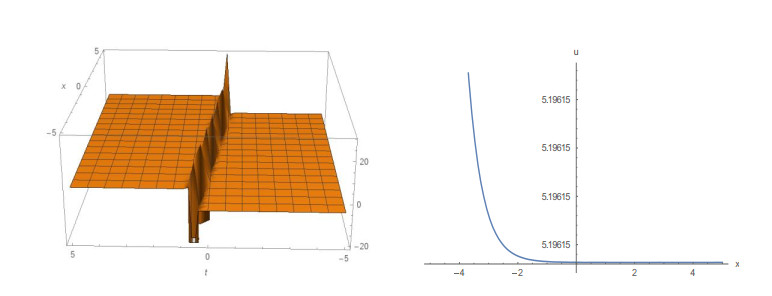
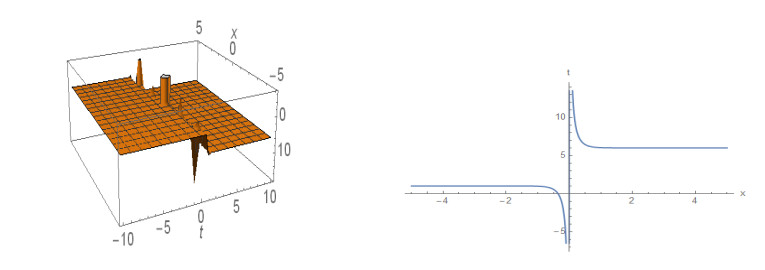
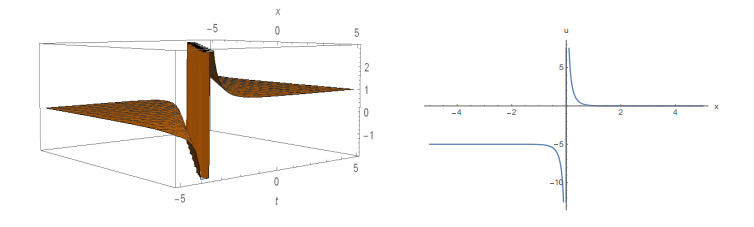
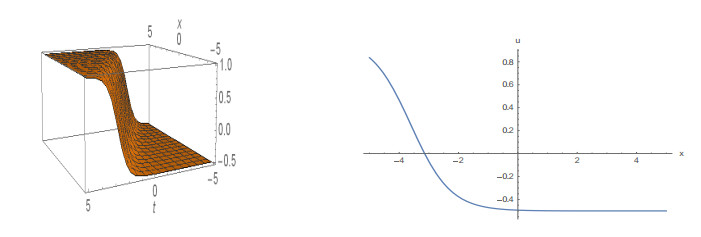
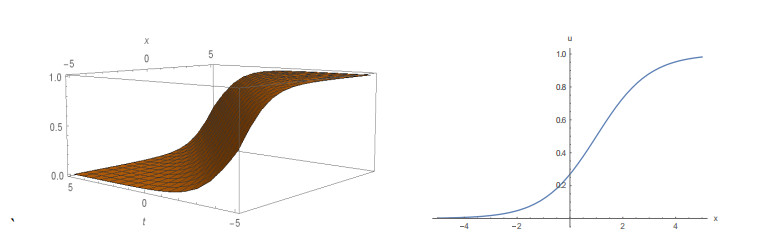
The graphical illustrations of 3D plot and 2D plot of some obtained solutions are given in Figures 1 to 8. Figure 1, depicts the 3D plot and the corresponding 2D plot of solution (15) that behaves like the kink solution for k = 2 and A = 1 within the interval -5≤x, t≤5. Figure 2, also represents the kink shape soliton depicted from the solution (19) for k = -5, A = 1 within the interval -5≤x≤5 and -3≤t≤3. The solution (24) is represented in Figure 3, for A = -1 and δ = 3.5 within the interval -10≤x, t≤10. Figure 4, shows the 3D and the corresponding 2D plot of solution (27) represents the singular soliton for A = -1 and δ = 0.5 within the interval -10≤x, t≤10. Figure 5, depicts the profile of solution (31) that is soliton solution in 3D and the corresponding 2D for A = ±1 and δ = 4.5 within the interval -5≤x, t≤5. Figure 6, represents the singular soliton solution of solution (37) for a0 = 1, b0 = 1, K = -2.5 and A = ±1 within the interval -5≤x≤5 and -10≤t≤10. Figure 7, shows the profile of solution (39) which represents the shape of a singular kink soliton for a0 = 1, b0 = 1, b1 = 5, k = 1 and A = -1 within the interval -5≤x≤5 and -5≤t≤5. Also, Figure 8 represents the kink soliton of solution (44) in 3D and the corresponding 2D with a1 = 1, b1 = 1, k = 1.5 and A = 1 within the same interval.
In this study, we constitute the exact solutions for a large category of nonlinear evolution equations by making use of the generalized Kudryashov method. The method has been effectively appointed to attain the exact solutions to the Burgers-Huxley, the mKdV and the first extended fifth order nonlinear equations. The obtained solutions are ascertained by setting them back into the said physical model and are observed to be very convenient over various existing methods. For the precision of the result, the solutions are graphically illustrated in 3D and 2D. The key advantage of this method against other methods is that the method provides more general and a large number of exact solutions in an identical way. The execution of this method is fruitful, effective, simple and reliable. Also, we emphasize that this method is very effectual and exigent from the theoretical and practical point of view. Moreover, it is also quite capable and can be implemented for attaining exact solutions of other nonlinear evolution equations in applied nonlinear science.
The authors declare no conflict of interests.
| [1] |
M. Wang, Y. Zhou, Z. Li, Application of homogeneous balance method to exact solutions of non-linear equations in mathematical physics, Phys. Lett. A, 216 (1996), 67-75. doi: 10.1016/0375-9601(96)00283-6
|
| [2] | M. Younis, A. Zafar, The modified simple equation method for solving the non-linear Phi-four equation, Int. J. Innov. Appl. Stud., 2 (2013), 661-664. |
| [3] | W. W. Li, Y. Tian, Z. Zhang, F-expansion method and its application for finding new exact solutions to the Sine-Gordon and Sinh-Gordon equations, Appl. Math. Comput., 219 (2012), 1135-1143. |
| [4] |
S. Zhang, T. Xia, An improved generalized F-expansion method and its application to the (2+1) dimensional KdV equations, Commun. Nonlinear Sci., 13 (2008), 1294-1301. doi: 10.1016/j.cnsns.2006.12.008
|
| [5] |
H. M. Baskonus, New acoustic wave behaviors to the Davey-Stewartson equation with power-law nonlinearity arising in fluid dynamics, Nonlinear Dynam., 86 (2016), 177-183. doi: 10.1007/s11071-016-2880-4
|
| [6] | C. Cattani, T. A. Sulaiman, H. M. Baskonus, et al. Solitons in an inhomogeneous Murnaghan's rod, Eur. Phys. J. Plus, 133 (2018), 228. |
| [7] | C. Cattani, T. A. Sulaiman, H. M. Baskonus, et al. On the soliton solutions to the Nizhnik-Novikov-Veselov and the Drinfel's-Sokolov systems, Opt. Quant. Electron., 50 (2018), 138. |
| [8] |
O. A. Ilhan, A. Esen, H. Bulut, et al. Singular solitons in the pseudo-parabolic model arising in nonlinear surface waves, Results Phys., 12 (2019), 1712-1715. doi: 10.1016/j.rinp.2019.01.059
|
| [9] | A. M. Wazwaz, Multiple soliton solutions for the Boussinesq equation, Appl. Math. Comput., 192 (2007), 479-486. |
| [10] | A. M. Wazwaz, The tanh method for traveling wave solutions of non-linear equations, Appl. Math. Comput., 154 (2004), 713-723. |
| [11] |
A. Bekir, New exact traveling wave solutions of some complex nonlinear equations, Commun. Nonlinear Sci., 14 (2009), 1069-1077. doi: 10.1016/j.cnsns.2008.05.007
|
| [12] |
M. Mirzazadeh, M. E. Slami, E. Zerrad, et al. Optical solitons in nonlinear directional couplers by sine-cosine function method and Bernoulli's equation approach, Nonlinear Dynam., 81 (2015), 1933-1949. doi: 10.1007/s11071-015-2117-y
|
| [13] | M. Kaplan, A. Bekir, M. N. Ozer, Solving non-linear evolution equation system using two different methods, Open Phys., 13 (2015), 383-388. |
| [14] | M. M. Miah, H. M. S. Ali, M. A. Ali, et al. Some applications of the (G′/G, 1/G)-expansion method to find new exact solutions of NLEEs, Eur. Phys. J. Plus, 132 (2017), 252. |
| [15] | M. M. Miah, H. M. S. Ali, M. A. Ali, An investigation of abundant traveling wave solutions of complex nonlinear evolution equations: The perturbed nonlinear Schrodinger equation and the cubic-quintic Ginzburg-Landau equation, Cog. Math., 3 (2016), 1277506. |
| [16] |
A. Neirameh, New analytical solutions for the coupled nonlinear Maccari's system, Alex. Eng. J., 55 (2016), 2839-2847. doi: 10.1016/j.aej.2016.07.007
|
| [17] |
A. J. M. Jawad, M. J. Abu-Alshaeer, A. Biswas, et al. Hamiltonian perturbation of optical solitons with parabolic law non-linearity using three integration methodologies, Optik, 160 (2018), 248-254. doi: 10.1016/j.ijleo.2018.01.104
|
| [18] |
X. Lu, S. T. Chen, W. X. Ma, Constructing lump solutions to a generalized Kadomtsev-Petviashvili-Boussinesq equation, Nonlinear Dynam., 86 (2016), 523-534. doi: 10.1007/s11071-016-2905-z
|
| [19] |
X. Lu, W. X. Ma, Y. Zhou, et al. Rational solutions to an extended Kadomtsev-Petviashvili-like equation with symbolic computation, Comput. Math. Appl., 71 (2016), 1560-1567. doi: 10.1016/j.camwa.2016.02.017
|
| [20] |
X. Lu, W. X. Ma, S. T. Chen, et al. A note on rational solutions to a Hirota-Satsuma-like equation, Appl. Math. Lett., 58 (2016), 13-18. doi: 10.1016/j.aml.2015.12.019
|
| [21] |
J. H. He, M. A. Abdou, New periodic solutions for nonlinear evolution equations using Exp-function method, Chaos Soliton. Fract., 34 (2007), 1421-1429. doi: 10.1016/j.chaos.2006.05.072
|
| [22] |
Y. Y. Wang, Y. P. Zhang, C. Q. Dai, RE-study on localized structures based on variable separation solutions from the modified tanh-function method, Nonlinear Dynam., 83 (2016), 1331-1339. doi: 10.1007/s11071-015-2406-5
|
| [23] |
E. Fan, Extended Tanh-Function method and its applications to nonlinear equations, Phys. Lett. A, 277 (2000), 212-218. doi: 10.1016/S0375-9601(00)00725-8
|
| [24] |
J. Manafian, M. F. Aghdaei, M. Khalilian, et al. Application of the generalized (G′/G) expansion method for non-linear PDEs to obtaining soliton wave solution, Optik, 135 (2017), 395-406. doi: 10.1016/j.ijleo.2017.01.078
|
| [25] |
L. N. Gao, X. Y. Zhao, Y. Y. Zi, et al. Resonant behavior of multiple wave solutions to a Hirota bilinear equation, Comput. Math. Appl., 72 (2016), 1225-1229. doi: 10.1016/j.camwa.2016.06.008
|
| [26] |
L. N. Gao, Y. Y. Zi, Y. H. Yin, et al. Backlund transformation, multiple wave solutions and lump solutions to a (3+1)-dimensional nonlinear evolution equation, Nonlinear Dynam., 89 (2017), 2233-2240. doi: 10.1007/s11071-017-3581-3
|
| [27] |
Y. H. Yin, W. X. Ma, J. G. Liu, et al. Diversity of exact solutions to a (3+1)-dimensional nonlinear evolution equation and its reduction, Comput. Math. Appl., 76 (2018), 1275-1283. doi: 10.1016/j.camwa.2018.06.020
|
| [28] |
M. Kaplan, K. Hosseini, Investigation of exact solutions for the Tzitzéica type equations in nonlinear optics, Optik, 154 (2018), 393-397. doi: 10.1016/j.ijleo.2017.08.116
|
| [29] |
A. R. Adem, B. Muatjetjeja, Conservation laws and exact solutions for a 2D Zakharov-Kuznetsov equation, Appl. Math. Lett., 48 (2015), 109-117. doi: 10.1016/j.aml.2015.03.019
|
| [30] | H. Naher, F. A. Abdullah, M. A. Akbar, Generalized and improved (G′/G)-expansion method for (3+1) dimensional modified KdV-Zakharov-Kuznetsev equation, PLOS One, 8 (2013), 64618. |
| [31] | H. M. Baskonus, Complex Soliton Solutions to the Gilson-Pickering Model, Axioms, 8 (2019), 18. |
| [32] | H. M. Baskonus, New complex and hyperbolic function solutions to the generalized double combined Sinh-Cosh-Gordon equation, AIP Conference Proceedings, 1798 (2017), 020018. |
| [33] | H. Naher, F. A. Abdullah, New traveling wave solutions by the extended generalized Riccati equation mapping method of the (2+1)-dimensional evolution equation, J. Appl. Math., 2012 (2012), 486458. |
| [34] | A. Yokus, Comparison of Caputo and conformable derivatives for time-fractional Korteweg-de Vries equation via the finite difference method, Int. J. Mod. Phys. B, 32 (2018), 1850365. |
| [35] |
A. Yokus, Numerical solution for space and time fractional order Burger type equation, Alex. Eng. J., 57 (2018), 2085-2091. doi: 10.1016/j.aej.2017.05.028
|
| [36] | A. Yokus, H. Bulut, On the numerical investigations to the Cahn-Allen equation by using finite difference method, An International Journal of Optimization and Control: Theories & Applications (IJOCTA), 9 (2018), 18-23. |
| [37] |
K. Hosseini, D. Kumar, M. Kaplan, et al. New exact traveling wave solutions of the unstable nonlinear Schrodinger equations, Commun. Theor. Phys., 68 (2017), 761-767. doi: 10.1088/0253-6102/68/6/761
|
| [38] | S. M. Ege, E. Misirli, The modified Kudryashov method for solving some Fractional-order nonlinear equations, Adv. Differ. Equ-Ny, 2014 (2014), 135. |
| [39] |
K. Hosseini, P. Mayeli, D. Kumar, New exact solutions of the coupled Sine-Gordon equations in nonlinear optics using the modified Kudryashov method, J. Mod. Optic., 65 (2018), 361-364. doi: 10.1080/09500340.2017.1380857
|
| [40] |
K. Hosseini, P. Mayeli, R. Ansari, Modified Kudryashov method for solving the conformable Time-Fractional Klein-Gordon equations with Quadratic and cubic nonlinearities, Optik, 130 (2017), 737-742. doi: 10.1016/j.ijleo.2016.10.136
|
| [41] | A. Korkmaz, K. Hosseini, Exact solutions of a nonlinear conformable Time-Fractional parabolic equation with Exponential nonlinearity using reliable methods, Opt. Quant. Electron., 49 (2017), 278. |
| [42] | K. Hosseini, E. Y. Bejarbaneh, A. Bekir, et al. New exact solutions of some nonlinear evolution equations of pseudo parabolic type, Opt. Quant. Electron., 49 (2017), 241. |
| [43] |
F. Mahmud, M. Samsuzzoha, M. A. Akbar, The generalized kudryashov method to obtain exact traveling wave solutions of the PHI-four equation and the Fisher equation, Results Phys., 7 (2017), 4296-4302. doi: 10.1016/j.rinp.2017.10.049
|
| [44] |
S. Bibi, N. Ahmed, U. Khan, et al. Some new exact solitary wave solutions of the van der Walls model arising in nature, Results Phys., 9 (2018), 648-655. doi: 10.1016/j.rinp.2018.03.026
|
| [45] |
M. Kaplan, A. Bekir, A. Akbulut, A generalized kudryashov method to some nonlinear evolution equations in mathematical physics, Nonlinear Dynam., 85 (2016), 2843-2850. doi: 10.1007/s11071-016-2867-1
|
| [46] | S. T. Demiray, Y. Pandir, H. Bulut, Generalized Kudryashov method for Time-fractional differential equations, Abstr. Appl. Anal., 2014 (2014), 901540. |
| [47] |
K. A. Gepreel, T. A. Nofal, A. A. Alasmari, Exact solutions for nonlinear integro-partial differential equations using the generalized Kudryashov method, Journal of the Egyptian Mathematical Society, 25 (2017), 438-444. doi: 10.1016/j.joems.2017.09.001
|
| [48] | M. Koparan, M. Kaplan, A. Bekir, et al. A novel generalized Kudryashov method for exact solutions of nonlinear evolution equations, AIP Conference Proceedings, 1798 (2017), 020082. |
| [49] |
H. Kheiri, M. R. Moghaddam, V. Vafaei, Application of the (G'/G)-expansion method for the Burgers, Burgers-Huxley and modified Burgers-KdV equations, Pramana, 76 (2011), 831-842. doi: 10.1007/s12043-011-0070-y
|
| [50] |
M. L. Wang, X. Li, J. Wang, The (G'/G)-expansion method and traveling wave solutions of nonlinear evolutions in mathematical physics, Phys. Lett. A, 372 (2008), 417-423. doi: 10.1016/j.physleta.2007.07.051
|
| [51] | A. K. M. Kazi Sazzad Hossain, M. A. Akbar, Closed-form solutions of two nonlinear equations via the enhanced (G'/G)-expansion method, Cog. Math., 4 (2017), 1355958. |
| [52] | A. M. Wazwaz, Analytic study on Burgers, Fisher, Huxley equations and combined forms of these equations, Appl. Math. Comput., 195 (2008), 754-761. |
| 1. | Sekson Sirisubtawee, Sanoe Koonprasert, Surattana Sungnul, New Exact Solutions of the Conformable Space-Time Sharma–Tasso–Olver Equation Using Two Reliable Methods, 2020, 12, 2073-8994, 644, 10.3390/sym12040644 | |
| 2. | Gulnur Yel, New wave patterns to the doubly dispersive equation in nonlinear dynamic elasticity, 2020, 94, 0304-4289, 10.1007/s12043-020-1941-x | |
| 3. | Mustafa Inc, Mamun Miah, Chawdhury Akher, Shahadat Ali, Hadi Rezazadeh, Mehmet Ali Akinlar, Yu-Ming Chu, New exact solutions for the Kaup-Kupershmidt equation, 2020, 5, 2473-6988, 6726, 10.3934/math.2020432 | |
| 4. | M. Akher Chowdhury, M. Mamun Miah, H.M. Shahadat Ali, Yu-Ming Chu, M.S. Osman, An investigation to the nonlinear (2 + 1)-dimensional soliton equation for discovering explicit and periodic wave solutions, 2021, 23, 22113797, 104013, 10.1016/j.rinp.2021.104013 | |
| 5. | Mohammed O Al-Amr, Hadi Rezazadeh, Khalid K Ali, Alper Korkmazki, N1-soliton solution for Schrödinger equation with competing weakly nonlocal and parabolic law nonlinearities, 2020, 72, 0253-6102, 065503, 10.1088/1572-9494/ab8a12 | |
| 6. | Şeyma TÜLÜCE DEMİRAY, Serife DUMAN, The Modified Trial Equation Method To The (2+1)-Dimensional Broer-Kaup-Kupershmidt Equation and Kolmogorov-Petrovskii-Piskunov Equation, 2021, 1301-7985, 10.25092/baunfbed.853756 | |
| 7. | Md Ashik Iqbal, Ye Wang, Md Mamun Miah, Mohamed S. Osman, Study on Date–Jimbo–Kashiwara–Miwa Equation with Conformable Derivative Dependent on Time Parameter to Find the Exact Dynamic Wave Solutions, 2021, 6, 2504-3110, 4, 10.3390/fractalfract6010004 | |
| 8. | Abd-Allah Hyder, The influence of the differential conformable operators through modern exact solutions of the double Schrödinger-Boussinesq system, 2021, 96, 0031-8949, 115211, 10.1088/1402-4896/ac169f | |
| 9. | Ambreen Sarwar, Muhammad Arshad, Muhammad Farman, Ali Akgül, Iftikhar Ahmed, Mustafa Bayram, Shahram Rezapour, Manuel De la Sen, Construction of Novel Bright-Dark Solitons and Breather Waves of Unstable Nonlinear Schrödinger Equations with Applications, 2022, 15, 2073-8994, 99, 10.3390/sym15010099 | |
| 10. | Hamood Ur Rehman, Aziz Ullah Awan, ElSayed M. Tag-ElDin, Sharifah E. Alhazmi, Mansour F. Yassen, Rizwan Haider, Extended hyperbolic function method for the (2 +1)-dimensional nonlinear soliton equation, 2022, 40, 22113797, 105802, 10.1016/j.rinp.2022.105802 | |
| 11. | Md Nur Hossain, M. Mamun Miah, Abdul Hamid Ganie, M. S. Osman, Wen-Xiu Ma, Discovering new abundant optical solutions for the resonant nonlinear Schrödinger equation using an analytical technique, 2024, 56, 1572-817X, 10.1007/s11082-024-06351-5 | |
| 12. | Md Nur Hossain, K. El-Rashidy, Faisal Alsharif, Mohammad Kanan, Wen-Xiu Ma, M. Mamun Miah, New optical soliton solutions to the Biswas–Milovic equations with power law and parabolic law nonlinearity using the Sardar-subequation method, 2024, 56, 1572-817X, 10.1007/s11082-024-07073-4 | |
| 13. | Md Nur Hossain, M. Mamun Miah, Moataz Alosaimi, Faisal Alsharif, Mohammad Kanan, Exploring Novel Soliton Solutions to the Time-Fractional Coupled Drinfel’d–Sokolov–Wilson Equation in Industrial Engineering Using Two Efficient Techniques, 2024, 8, 2504-3110, 352, 10.3390/fractalfract8060352 | |
| 14. | Rajib Mia, M. Mamun Miah, M.S. Osman, A new implementation of a novel analytical method for finding the analytical solutions of the (2+1)-dimensional KP-BBM equation, 2023, 9, 24058440, e15690, 10.1016/j.heliyon.2023.e15690 | |
| 15. | Nirmoy Kumar Das, Dhanashri Barman, Ashoke Das, Towhid E Aman, 2024, Chapter 36, 978-3-031-66873-9, 457, 10.1007/978-3-031-66874-6_36 | |
| 16. | Muhammad Zain Yousaf, Muhammad Abbas, Farah Aini Abdullah, Tahir Nazir, Ahmed SM. Alzaidi, Homan Emadifar, Construction of travelling wave solutions of coupled Higgs equation and the Maccari system via two analytical approaches, 2024, 56, 1572-817X, 10.1007/s11082-024-06708-w | |
| 17. | Mst. Munny Khatun, M. Ali Akbar, Dynamical behavior of dark and bright solitons of the space–time fractional Fokas–Lenells equation, 2023, 55, 0306-8919, 10.1007/s11082-023-04867-w | |
| 18. | Md Nur Hossain, M Mamun Miah, Faisal Z Duraihem, Sadique Rehman, Wen-Xiu Ma, Chaotic behavior, bifurcations, sensitivity analysis, and novel optical soliton solutions to the Hamiltonian amplitude equation in optical physics, 2024, 99, 0031-8949, 075231, 10.1088/1402-4896/ad52fd | |
| 19. | Mashael M. ALBaidani, Umair Ali, Abdul Hamid Ganie, The closed-form solution by the exponential rational function method for the nonlinear variable-order fractional differential equations, 2024, 12, 2296-424X, 10.3389/fphy.2024.1347636 | |
| 20. | M Mamun Miah, M Ashik Iqbal, M S Osman, A study on stochastic longitudinal wave equation in a magneto-electro-elastic annular bar to find the analytical solutions, 2023, 75, 0253-6102, 085008, 10.1088/1572-9494/ace155 | |
| 21. | Md Nur Hossain, M. Mamun Miah, Faisal Z. Duraihem, Sadique Rehman, Stability, modulation instability, and analytical study of the confirmable time fractional Westervelt equation and the Wazwaz Kaur Boussinesq equation, 2024, 56, 1572-817X, 10.1007/s11082-024-06776-y | |
| 22. | Muath Awadalla, Arzu Akbulut, Jihan Alahmadi, Simulation of a Combined (2+1)-Dimensional Potential Kadomtsev–Petviashvili Equation via Two Different Methods, 2024, 12, 2227-7390, 427, 10.3390/math12030427 | |
| 23. | A. Hussain, Younes Chahlaoui, F.D. Zaman, T. Parveen, Ahmed M. Hassan, The Jacobi elliptic function method and its application for the stochastic NNV system, 2023, 81, 11100168, 347, 10.1016/j.aej.2023.09.017 | |
| 24. | M. Akher Chowdhury, M. Mamun Miah, Md Mamunur Rasid, Sadique Rehman, J.R.M. Borhan, Abdul-Majid Wazwaz, Mohammad Kanan, Further quality analytical investigation on soliton solutions of some nonlinear PDEs with analyses: Bifurcation, sensitivity, and chaotic phenomena, 2024, 103, 11100168, 74, 10.1016/j.aej.2024.05.096 | |
| 25. | Md Nur Hossain, Faisal Alsharif, M. Mamun Miah, Mohammad Kanan, Abundant New Optical Soliton Solutions to the Biswas–Milovic Equation with Sensitivity Analysis for Optimization, 2024, 12, 2227-7390, 1585, 10.3390/math12101585 | |
| 26. | Md Nur Hossain, Md Mamunur Rasid, I. Abouelfarag, K. El-Rashidy, M. Mamun Miah, Mohammad Kanan, A new investigation of the extended Sakovich equation for abundant soliton solution in industrial engineering via two efficient techniques, 2024, 22, 2391-5471, 10.1515/phys-2024-0096 |
Figures(8)
M. A. Habib, H. M. Shahadat Ali, M. Mamun Miah, M. Ali Akbar. The generalized Kudryashov method for new closed form traveling wave solutions to some NLEEs[J]. AIMS Mathematics, 2019, 4(3): 896-909. doi: 10.3934/math.2019.3.896
DownLoad:
