Rough sets in graphs using similarity relations

1.   Introduction

Rough set theory (RST), introduced by Pawlak ^[22], provides elegant and powerful techniques to extract information from data associated with various structures. It also provides terminology to minimize the number of significant attributes in data tables, also called information systems. It is always interesting and insightful to know about the objects having similar characteristics to simplify the study of objects under consideration. The objects which are indistinguishable from each other are called information granules. Zadeh introduced and studied information granularity in ^[36]. Information granules are objects placed together due to similarity of features of interest and are dealt together yielding partition of objects based upon features. Many applications of granular computing appear in connection with fuzzy set theory ^[13,26], information science ^[17,35], data mining ^[12,16,34], formal concept analysis ^[15,33], database theory ^[11,27] and rough set theory ^{[2,9,23,24,25,30]} etc. in fields, such as medicine, economy, finance, business, document clustering, environment, electrical and computer engineering. Granular computing and rough sets have been studied in the context of graphs ^[5,6], digraph ^[19] and hyper graphs ^[3]. In ^[14], Hu et al. investigated novel approach to attribute reduction based on weighted neighborhood rough sets and gave an algorithm to evaluate reduct of a decision information table. The reader is referred to the following ^[4,28,29,31] for further reading in this area of study. Chiaselotti et al. ^[5,6,8] have studied well-known families of graphs using the notion of neighbourhood of vertices as a clustering criterion. They have remarked two vertices $x, \, y$ as indiscernible with respect to a vertex subset $\mathcal{A}$ when these vertices have same neighbours with respect to $\mathcal{A}$. Symbolically, $x\equiv_{\mathcal{A}}y\Leftrightarrow N(x)\cap \mathcal{A} = N(y)\cap \mathcal{A}$. In ^[8], they have remarked $\mathcal{A}$ as symmetry axis and two vertices are indiscernible with respect to $\mathcal{A}$ if they are in a 'symmetrical' position with respect to all vertices of $\mathcal{A}$. Equivalence classes induced by indiscernibility relation of $\mathcal{A}$ are the granules and yield partition of the vertex set of the graph, denoted by $\gamma_{\mathcal{A}}(\mathcal{G})$. Rough set theory can be thought of as a particular type of granular computing. Chiaselotti et al. ^[8] referred the triplet $(\mathcal{G}, \mathcal{A}, \gamma_{\mathcal{A}}(\mathcal{G}))$ as $\mathcal{A}$-granular reference system. Intersection of granular computing and rough set theory provides tools to analyze graphs, digraphs and hypergraphs. In ^[18], Liu et al. discussed the approach of using covering-based neighborhood with various similarity measures. In ^[9], Chiaselotti et al. explained how objects can be classified into the same granule using the approach of their similarity measures which is a refinement of the indiscernibility relation. The information about granules will simplify studies associated to graphs and can give important insights about graphs, enriching their applications in various fields and introduce new perspectives to obtain knowledgeable patterns using different data-mining techniques ^{[1,7,9,10,18,20,21,32]}.

By associating rough set and graphs, properties of rough sets can be understood with the help of graphs and those of graphs can be explained by using RST. Graphs have been studied using rough set ^[4,6,19] and rough sets may yield graphs ^[29]. A strategy developed in one domain can give insights in another domain. It is worth noting that the partition in the granular reference system may be induced using different paradigms and it will give useful insights in various directions. Making comparisons, identifying similarities and studying differences are canonical approaches of study. In this paper, we study graphs using the idea of orbit of vertices as clustering criterion and we remark two vertices $u, v$ are indiscernible when orbits intersect with $\mathcal{A}$ in the same set or equivalently two vertices $u, v$ are indiscernible if they belong to same orbits of elements of $\mathcal{A}$. Chiaselotti et al. ^[5] remarked two vertices as indiscernible if their open neighbourhoods intersect with a given set $\mathcal{A}$ in the same set. We consider a different approach than that of Chiaselotti et al. ^[5] and consider similarity relation yielded by graph automorphisms to fill the entries of information table. We will study indiscernibility relations introduced with the help of orbits and prove several results including parallel to those of Chiaselotti et al. ^[5,6,8] using the concept of orbits of vertices.

2.   Notations and background

A graph $\mathcal{G}$ is an ordered pair consisting of two finite sets, $\mathcal{V}(\mathcal{G})$ and $\mathcal{E}(\mathcal{G})$, called the vertex set and the edge set respectively. In this paper, all considered graphs are simple and non-trivial, represented by $\mathcal{G} = (\mathcal{V}(\mathcal{G}), \mathcal{E}(\mathcal{G}))$. When there is no ambiguity, we simply write $\mathcal{G} = (\mathcal{V}, \mathcal{E})$. Two vertices are called adjacent or neighbours of each other if there is an edge between them. The cardinality of the vertex set $\mathcal{V}$ and the edge set $\mathcal{E}$ of $\mathcal{G}$ are termed as $order$ and $size$ of $\mathcal{G}$, respectively. For $x, y\in\mathcal{V}$, $x\sim y$ means $x$ and $y$ are adjacent to each other and $x \nsim y$ means $x$ and $y$ are non-adjacent. Open neighbourhood of $x\in\mathcal{V}$ is defined as $\mathcal{N}_{\mathcal{G}}(x) = \{y\in\mathcal{V}: x\sim y\}$. Similarly, closed neighbourhood of $x$ is defined as $\mathcal{N}_{\mathcal{G}}[x] = \mathcal{N}_{\mathcal{G}}(x)\cup \{x\}$.

A $permutation$ of a set is a bijection from the set to itself. A graph $automorphism$ is a permutation of the vertex set that preserves adjacency and non-adjacency of the vertices. Alternatively, $\pi:\mathcal{V}(\mathcal{G})\rightarrow \mathcal{V}(\mathcal{G})$ is an automorphism of a graph $\mathcal{G}$ if for all $x, y\in\mathcal{V}(\mathcal{G}), \pi(x)\sim \pi(y)$ if and only if $x\sim y$. The collection of all automorphisms of graph $\mathcal{G}$ forms a group, named as the automorphism group of the graph $\mathcal{G}$. We use $\Gamma(\mathcal{G})$ or $\Gamma$ if $\mathcal{G}$ is clear from context, to represent the group of automorphisms of graph $\mathcal{G}$. For $y\in\mathcal{V}$, the $orbit$ of $y$, denoted by $\mathcal{O}(y)$, is defined as $\mathcal{O}(y) = \{\pi(y):\pi\in\Gamma\}$ and for any set $\mathcal{A}$, the orbit of $\mathcal{A}$ is represented by $\mathcal{O}(\mathcal{A})$ and is defined as $\mathcal{O}(\mathcal{A}) = \cup\mathcal{O}(x_i)\forall x_i\in\mathcal{A}$. Two vertices in the same orbit are called $similar$ vertices.

A partition $\gamma$ on a finite set $\mathcal{V}$ is a family of non-empty subsets $B_1, B_2, \dots, B_n$ of $\mathcal{V}$ such that $B_i\cap B_j = \emptyset$ for all $i\neq j$ and $\cup_{i = 1}^nB_i = \mathcal{V}$. The subsets $B_1, B_2, \dots, B_n$ are termed as blocks of $\gamma$, we write $\gamma: = B_1|B_2|\dots|B_n$ to represent that $\gamma$ is a partition of sets with blocks $B_1, B_2, \dots, B_n$. If $x \in \mathcal{V}$, we denote $\gamma (x)$ as the block of $\gamma$ containing the element $x$. An information table, denoted by $\mathcal{I} = \langle \mathcal{U}, \mathbb{A}, \mathcal{V}al, \mathcal{F} \rangle$ is a quadruple, where $\mathcal{U}$ represents the universal set of objects, $\mathbb{A}$ represents the attribute set, $\mathcal{V}al$ is a set of outcomes and $\mathcal{F}:\mathcal{U}\times \mathbb{A}\rightarrow \mathcal{V}al$ represents an information map. The information table is called Boolean if $\mathcal{V}al = \{0, 1\}$. For the purpose of our paper, both universal set $\mathcal{U}$ and attribute set $\mathbb{A}$ are the vertex set $\mathcal{V}$ of the graph $\mathcal{G}$ and the $indescernibility$ relation $\equiv_{\mathcal{A}}$ between the two vertices of the graphs is an equivalence relation which depends upon a set of attributes $\mathcal{A}\subseteq \mathcal{V}$ defined as: $x\equiv_{\mathcal{A}} y$ if and only if for all $z\in \mathcal{A}$, if $z\in\mathcal{O}(x)$ then $z\in\mathcal{O}(y)$. If there exists $z\in \mathcal{A}$ such that $z$ does not belong to $\mathcal{O}(x)$ and $\mathcal{O}(y)$ simultaneously, then we say $x$ and $y$ do not belong the same equivalence class and write it as $\urcorner(x\equiv_{\mathcal{A}}y)$. Equivalence classes also called $\mathcal{A}$-granules of object $x$ under consideration of $\equiv_{\mathcal{A}}$ are represented by $\mathcal{O}_{\mathcal{A}}(x)$ and the indiscernibility partition of $\mathcal{I}$ with respect to $\mathcal{A}$ is the family of all equivalence classes, $i.e.,$ $\gamma_{\mathcal{A}}(\mathcal{G}): = \{\mathcal{O}_{\mathcal{A}}(x):x\in \mathcal{V}\}$. Given an attribute subset $\mathcal{A}$ and object subset $\mathcal{Q}$, lower and upper approximations of $\mathcal{Q}$ by considering the information presented by $\mathcal{A}$ are defined as:

In general, $\mathbb{L}_{\mathcal{A}}(\mathcal{Q})$ is subset of $\mathcal{Q}$ while $\mathbb{U}_{\mathcal{A}}(\mathcal{Q})$ is a superset of $\mathcal{Q}$. A subset $\mathcal{Q}$ is termed as $\mathcal{A}-exact$ if and only if $\mathbb{L}_{\mathcal{A}}(\mathcal{Q}) = \mathbb{U}_{\mathcal{A}}(\mathcal{Q})$, $\mathcal{A}-rough$ otherwise. Let $\mathcal{A}, \mathcal{Q}\subseteq\mathcal{V}$ then rough membership function is defined by:

For $\mathcal{A}, \mathcal{D}\subseteq\mathcal{V}$, the positive region is defined as $POS_{\mathcal{A}}(\mathcal{D}) = \{x\in\mathcal{V}:\mathcal{O}_{\mathcal{A}}(x) \subseteq\mathcal{O}_{\mathcal{D}}(x)\}$ and the number $deg_{\mathcal{A}}({\mathcal{D}}) = \frac{|POS_{\mathcal{A}}({\mathcal{D}})|}{|\mathcal{V}|}$ is called $\mathcal{A}$-degree dependency of $\mathcal{D}$.

Important terms associated with rough set theory include the indiscernibility relations, lower and upper approximations, reducts, essential sets and the discernibility matrix. The reduct ^[22] of an information table consists of the set of attributes which provide same information and characterization as does the set of all attributes. Essential sets and the core ^[22] of an information table usually consists of the set of attributes which are considered most important in characterization of an information table. The discernibility matrix ^[28] is a square matrix with $ij^{th}$ entry consisting of attributes for which the attribute value is different for objects $x_i$ and $x_j$.

This paper is organized as follows: In section 3, we introduce and study the indiscernibility partitions and we also discuss the action of automorphisms in connection with indiscernibility relations. In section 4, we study lower and upper approximations of graphs in terms of orbits. We also examine the rough membership function and dependency measures for graphs. In section 5, we discuss essential sets, discernibility matrix and their relationships. Conclusions are given as last section of the paper.

3.   Indiscernibility partitions of graphs

An undirected simple graph $\mathcal{G}$ is described by an information table represented by $\mathcal{I}(\mathcal{G})$. Suppose that the vertex set $\mathcal{V}(\mathcal{G}) = \{x_1, x_2, \dots, x_n\}$ and both universal and attribute sets of information table $\mathcal{I}(\mathcal{G})$ are equal to $\mathcal{V}$ and characterize the information map as follows: For $x_i \in \mathcal{A}$, $\mathcal{F}(x_i, x_j) = 1$ if $x_j\in \mathcal{O}(x_i)$ and $\mathcal{F}(x_i, x_j) = 0$ if $x_j\notin \mathcal{O}(x_i)$.

In Theorem 3.1, we show how indiscernibility relation $\equiv_{\mathcal{A}}$ and the concept of orbit are related.

Theorem 3.1. For an attribute subset $\mathcal{A}\subseteq \mathcal{V}$, any two vertices $x, y\in \mathcal{V}$ are indiscernible if and only if $\mathcal{O}(x)\cap \mathcal{A} = \mathcal{O}(y)\cap \mathcal{A}$.

Proof. If $z\in\mathcal{O}(x)\cap\mathcal{A}$ then $\mathcal{F}(x, z) = 1 = \mathcal{F}(y, z)$ by definition it implies that $z\in\mathcal{O}(y)\cap\mathcal{A}$. Hence $\mathcal{O}(x)\cap \mathcal{A}\subseteq\mathcal{O}(y)\cap \mathcal{A}$. Using similar argument, $\mathcal{O}(y)\cap \mathcal{A}\subseteq\mathcal{O}(x)\cap \mathcal{A}$. Hence $\mathcal{O}(x)\cap \mathcal{A} = \mathcal{O}(y)\cap \mathcal{A}$. Now suppose $\mathcal{O}(x)\cap \mathcal{A} = \mathcal{O}(y)\cap \mathcal{A}$, then $z\in\mathcal{O}(x)\cap \mathcal{A}$ implies that $\mathcal{F}(x, z) = 1$ which implies that $\mathcal{F}(y, z) = 1$. Hence $\mathcal{F}(x, z) = \mathcal{F}(y, z)$, which implies that $x\equiv_{\mathcal{A}}y$.

Theorem 3.1, serves as criterion to decide indiscernibility of vertices. Before we provide a sketch of indiscernibility partitions of a graph $\mathcal{G}$ in the form of orbits, please note the relationship of similarity of vertices of graph with indiscernibility of vertices. If $\mathcal{O}(x) = \mathcal{O}(y)$ in $\mathcal{G}$, then $x\equiv_\mathcal{A} y$ for any attribute subset $\mathcal{A}$. Moreover, converse is not true in general. Consider a path graph, $P_5$ with the vertex set $\{x_1, x_2, x_3, x_4, x_5\}$ and $x_i$ is adjacent to $x_{i+1}$ for $i = 1, 2, 3, 4$. The orbits of $P_5$ are $\{x_1, x_5\}$, $\{x_2, x_4\}$ and $\{x_3\}$. For $\mathcal{A} = \{x_1\}$ be an attribute set, the $\mathcal{A}$-equivalence classes are $\{x_1, x_5\}$, $\{x_2, x_3, x_4\}$. Check that $x_2\equiv_\mathcal{A} x_3$ but $x_2$ is not similar to $x_3$ in $P_5$, hence converse is not true in general.

For a subset $\mathcal{A}$ of $\mathcal{V}$, set $\mathcal{O}(\mathcal{A}) = \cup_{x\in \mathcal{A}}\mathcal{O}(x)$. In the following proposition, we give a complete sketch for the indiscernibility partitions of graph $\mathcal{G}$ in the form of orbits.

Proposition 3.2. Let $\mathcal{G}$ be a graph and $\mathcal{A}\subseteq \mathcal{V}$ be a given attribute subset. If $\mathcal{B}_\mathcal{A}(\mathcal{G}) = (\mathcal{O}(\mathcal{A}))^c$ and $\mathcal{A} = \{x_1, x_2, \ldots, x_k\}$ such that $\mathcal{O}(x_i)\cap \mathcal{O}(x_j) = \emptyset$ for each $i\neq j$ and $\mathcal{O}(\mathcal{A}) = \cup^{k}_{i = 1}\mathcal{O}(x_i)$, then $\gamma_{\mathcal{A}}(\mathcal{G}) = \mathcal{B}_\mathcal{A}(\mathcal{G})| \mathcal{O}(x_1)|\mathcal{O}(x_2)| \ldots|\mathcal{O}(x_k)$.

Proof. Let $x, y\in \mathcal{V}$ such that $x\equiv_\mathcal{A} y$ then $\mathcal{O}(x)\cap \mathcal{A} = \mathcal{O}(y)\cap \mathcal{A}$ and we have the following two cases.

Case 1. Suppose $\mathcal{O}(x)\cap \mathcal{A} = \mathcal{O}(y)\cap \mathcal{A} = \emptyset$, clearly $x, y\in \mathcal{B}_\mathcal{A}(\mathcal{G})$ which gives that $\mathcal{B}_\mathcal{A}(\mathcal{G})$ is an $\mathcal{A}$-equivalence class in $\mathcal{V}$.

Case 2. Suppose $\mathcal{O}(x)\cap \mathcal{A} = \mathcal{O}(y)\cap \mathcal{A}\neq\emptyset$ which implies that $x, y\in \mathcal{O}(\mathcal{A}) = \cup^{k}_{i = 1}\mathcal{O}(x_i)$ and $\mathcal{O}(x_i)\cap \mathcal{O}(x_j) = \emptyset$. This gives that $x, y\in \mathcal{O}(x_i)$ for some $1\leq i\leq k$ because if $x\in \mathcal{O}(x_i)$ and $y\in \mathcal{O}(x_j)$ for $i\neq j$ then $\mathcal{O}(x)\cap \mathcal{A}\neq\mathcal{O}(y)\cap \mathcal{A}$. Note that $\mathcal{O}(x) = \mathcal{O}(y)$ implies $x\equiv_\mathcal{A} y$, hence $\mathcal{O}_\mathcal{A}(x) = \mathcal{O}_\mathcal{A}(y) = \mathcal{O}_\mathcal{A}(x_i) = \mathcal{O}(x_i)$ and $\mathcal{O}_\mathcal{A}(x_i) = \mathcal{O}(x_i)$ for each $i$.

Concluding above two cases and using the fact that $\mathcal{B}_\mathcal{A}(\mathcal{G})$, $\mathcal{O}(x_1)$, $\mathcal{O}(x_2), \ldots, \mathcal{O}(x_k)$ give a partition of $\mathcal{V}$, we have $\gamma_{\mathcal{A}}(\mathcal{G}) = \mathcal{B}_\mathcal{A}(\mathcal{G})|\mathcal{O}(x_1)| \mathcal{O}(x_2)|\ldots|\mathcal{O}(x_k)$.

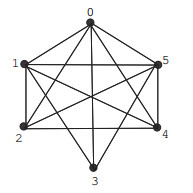
Example 3.1. Consider a graph $\mathcal{G}$ as in Figure 1.

In Figure 1, subscripts of the vertices are used as labels. We have $\mathcal{O}(0) = \{0, 5, 1\} = \mathcal{O}(5) = \mathcal{O}(1), \mathcal{O}(4) = \{2, 4\} = \mathcal{O}(2), \mathcal{O}(3) = \{3\}$. Fix a vertex subset $\mathcal{A} = \{1, 5\}$, then we have $0\equiv_{\mathcal{A}} 1 \equiv_{\mathcal{A}} 5$, and similarly $2\equiv_{\mathcal{A}} 3 \equiv_{\mathcal{A}} 4$ so $\gamma_{\mathcal{A}}(\mathcal{G}) = 015|234$.

Proposition 3.2 clearly suggests that indiscernibility partition of $\mathcal{G}$ depends upon the choice of $\mathcal{A}$. However, it remains an interesting question to identify conditions under which for given two attribute sets $\mathcal{A}_1$ and $\mathcal{A}_2$, $\gamma_{\mathcal{A}_1}(\mathcal{G}) = \gamma_{\mathcal{A}_2}(\mathcal{G})$. We now provide a necessary and sufficient condition under which the indiscernibility partitions associated to two different attribute sets are same.

Proposition 3.3. For an attribute subset $\mathcal{A}\subseteq\mathbb{A}$, define $\mathcal{B}_{\mathcal{A}}(\mathcal{G}) = (\mathcal{O}(\mathcal{A}))^c$. Let $\mathcal{A}_1, \mathcal{A}_2$ be two attribute subsets, then $\gamma_{\mathcal{A}_1}(\mathcal{G}) = \gamma_{\mathcal{A}_2}(\mathcal{G})$ if and only if one of the following hold:

(1) $\mathcal{B}_{\mathcal{A}_1}(\mathcal{G}) = \mathcal{B}_{\mathcal{A}_2}(\mathcal{G})$;

(2) $\mathcal{B}_{\mathcal{A}_1}(\mathcal{G}), \mathcal{B}_{\mathcal{A}_2}(\mathcal{G})$ are either empty or consists of only one orbit.

Proof. (1) Suppose that $\mathcal{B}_{\mathcal{A}_1}(\mathcal{G}) = \mathcal{B}_{\mathcal{A}_2}(\mathcal{G})$ then $\mathcal{O}(\mathcal{A}_1) = \mathcal{O}(\mathcal{A}_2)$. Hence by Proposition 3.2, $\gamma_{\mathcal{A}_1}(\mathcal{G}) = \gamma_{\mathcal{A}_2}(\mathcal{G})$.

(2) Suppose that $\mathcal{B}_{\mathcal{A}_1}(\mathcal{G}) = \emptyset$ and $\mathcal{B}_{\mathcal{A}_2}(\mathcal{G})$ consists of only one orbit. Then the orbit of $\mathcal{B}_{\mathcal{A}_2}(\mathcal{G})$ must coincide with at least one orbit of $\gamma_{\mathcal{A}_1}(\mathcal{G})$. Hence by Proposition 3.2, $\gamma_{\mathcal{A}_1}(\mathcal{G}) = \gamma_{\mathcal{A}_2}(\mathcal{G})$. Similarly, if $\mathcal{B}_{\mathcal{A}_2}(\mathcal{G}) = \emptyset$ and $\mathcal{B}_{\mathcal{A}_1}(\mathcal{G})$ consists of only one orbit, then $\gamma_{\mathcal{A}_1}(\mathcal{G}) = \gamma_{\mathcal{A}_2}(\mathcal{G})$.

Now, suppose contrary that $\mathcal{B}_{\mathcal{A}_1}(\mathcal{G})\neq\mathcal{B}_{\mathcal{A}_2}(\mathcal{G})$ and neither $\mathcal{B}_{\mathcal{A}_1}(\mathcal{G})$ nor $\mathcal{B}_{\mathcal{A}_2}(\mathcal{G})$ is empty or consists of only one orbit. By Proposition 3.2, this implies that $\gamma_{\mathcal{A}_1}(\mathcal{G})\neq\gamma_{\mathcal{A}_2}(\mathcal{G})$ but $\gamma_{\mathcal{A}_1}(\mathcal{G}) = \gamma_{\mathcal{A}_2}(\mathcal{G})$, a contradiction.

From Proposition $3.3$, it can be noted that different attribute sets can yield same indiscernibility partitions. Further, in the next proposition, we prove that for a graph $\mathcal{G}$ having $n$ orbits and two attribute sets having elements from $n$ or $n-1$ orbits, yield the same partition.

Proposition 3.4. If a graph $\mathcal{G}$ has $n$ orbits and attribute subsets $\mathcal{A}_1$ and $\mathcal{A}_2$ contain elements of $n$ or $n-1$ orbits then $\gamma_{\mathcal{A}_1}(\mathcal{G}) = \gamma_{\mathcal{A}_2}(\mathcal{G})$.

Proof. Since graph $\mathcal{G}$ has $n$ orbits. If $\mathcal{O}(\mathcal{A}_1) = \mathcal{O}(\mathcal{A}_2)$, then $\mathcal{B}_{\mathcal{A}_1}(\mathcal{G}) = \mathcal{B}_{\mathcal{A}_2}(\mathcal{G})$ hence by Proposition 3.3, $\gamma_{\mathcal{A}_1}(\mathcal{G}) = \gamma_{\mathcal{A}_2}(\mathcal{G})$. Now suppose that $\mathcal{A}_1$ contains elements of $n$ orbits and $\mathcal{A}_2$ contains elements of $n-1$ orbits, then by second part of Proposition 3.3, $\gamma_{\mathcal{A}_1}(\mathcal{G}) = \gamma_{\mathcal{A}_2}(\mathcal{G})$.

Proposition $3.4$ yields that for a graph $\mathcal{G}$ with $n$ orbits, the indiscernibility partitions remain same under different attributes from $n$ or $n-1$ orbits. For two attribute sets having elements from $n-2$ orbits, we have the following proposition.

Proposition 3.5. If $\mathcal{A}_1$ and $\mathcal{A}_2$ are two subsets of attributes with elements from at most $n-2$ orbits then $\gamma_{\mathcal{A}_1}(\mathcal{G}) = \gamma_{\mathcal{A}_2}(\mathcal{G})$ if and only if $\mathcal{O}(\mathcal{A}_1) = \mathcal{O}(\mathcal{A}_2)$.

Proof. As $\mathcal{O}(\mathcal{A}_1) = \mathcal{O}(\mathcal{A}_2)$, by Proposition 3.3, $\gamma_{\mathcal{A}_1}(\mathcal{G}) = \gamma_{\mathcal{A}_2}(\mathcal{G})$. Suppose contrary that $\mathcal{O}(\mathcal{A}_1)\neq\mathcal{O}(\mathcal{A}_2)$ but $\gamma_{\mathcal{A}_1}(\mathcal{G}) = \gamma_{\mathcal{A}_2}(\mathcal{G})$. Since $\mathcal{A}_1$ and $\mathcal{A}_2$ contain elements of at most $n-2$ orbits. Hence their complement will consist of the elements of at least two different orbits which implies that $\mathcal{B}_{\mathcal{A}_1}(\mathcal{G})\neq\mathcal{B}_{\mathcal{A}_2}(\mathcal{G})$, yielding $\gamma_{\mathcal{A}_1}(\mathcal{G})\neq\gamma_{\mathcal{A}_2}(\mathcal{G})$, a contradiction.

Proposition $3.5$ implies that indiscernibility partitions remain same if their orbits under different attributes remain same with elements from $n-2$ orbits. In the next proposition, we show that the automorphisms of $\mathcal{G}$ preserve the structure of blocks in indiscernibility partition.

Proposition 3.6. For a graph $\mathcal{G}$, let $\mathcal{A}\subseteq\mathcal{V}(\mathcal{G})$ be any attribute subset. If $\eta\in \Gamma(\mathcal{G})$ then $\gamma_{\mathcal{A}}(\mathcal{G}) = \gamma_{\eta(\mathcal{A})}(\mathcal{G})$.

Proof. Suppose $\gamma_{\mathcal{A}}(\mathcal{G}) = \mathcal{B}_1|\mathcal{B}_2|\dots|\mathcal{B}_m$ and $\gamma_{\eta(\mathcal{A})}(\mathcal{G}) = \mathcal{K}_1|\mathcal{K}_2|\dots|\mathcal{K}_n$. Let $\mathcal{B}_i = \mathcal{O}_{\mathcal{A}}(x_i) = \{x_j:\mathcal{O}(x_j)\cap \mathcal{A} = \mathcal{O}(x_i)\cap \mathcal{A}\}$ and $\mathcal{K}_i = \mathcal{O}_{\eta({\mathcal{A}})}(x_i) = \{x_j:\mathcal{O}(x_j)\cap \eta(\mathcal{A}) = \mathcal{O}(x_i)\cap \eta(\mathcal{A})\}$.

It is easy to see that for $\eta \in \Gamma(\mathcal{G})$, $\mathcal{O}(x_i)\cap \mathcal{A}\neq \emptyset$ if and only if $\mathcal{O}(x_i)\cap \eta(\mathcal{A}) \neq \emptyset$ for $1\leq i \leq k$ because $x_k \in \mathcal{O}(x_i)\cap \mathcal{A}$ if and only if $\eta(x_k) \in \mathcal{O}(x_i)\cap \eta(\mathcal{A})$. By 3.2, $\mathcal{B}_i = \mathcal{K}_i = \mathcal{O}(x_i)$ or $\mathcal{B}_i = \mathcal{K}_i = (\mathcal{O}(\mathcal{A}))^c$ which implies that $\gamma_{\mathcal{A}}(\mathcal{G}) = \gamma_{\eta(\mathcal{A})}(\mathcal{G})$.

For a set of attributes $\mathcal{A}\subseteq \mathcal{V}$, $IND_{\mathcal{A}}(\mathcal{V}) = \{(x, y)\in \mathcal{V}^2|\mathcal{O}(x)\cap \mathcal{A} = \mathcal{O}(y)\cap \mathcal{A}\}.$ An attribute $x \in\mathcal{A}$ is called dispensable in $\mathcal{A}$ if $IND_{\mathcal{A}}(\mathcal{V}) = IND_{\mathcal{A}\setminus\{x\}}(\mathcal{V})$, otherwise $x$ is called indispensable with respect to $\mathcal{A}$. A minimal subset $\mathcal{R}$ of an attribute set $\mathcal{A}$ that yields the same partition as provided by the set of all attributes is called $reduct$.

Proposition 3.7. For a graph $\mathcal{G}$ with a reduct $\mathcal{R}$ and orbits $\mathcal{O}_1, \mathcal{O}_2, \ldots, \mathcal{O}_k$, $|\mathcal{R} \cap \mathcal{O}_i| = 1$ for all $i = 1, 2, \ldots, k$ except one $i$.

Proof. Suppose there exists two orbits for which $\mathcal{R}\cap \mathcal{O}_{i}$ and $\mathcal{R}\cap \mathcal{O}_{j}$ is empty then $\mathcal{O}_{i}\cup \mathcal{O}_{j}$ forms one class. Hence, $\mathcal{R}$ must have empty intersection with at most one orbit. Now, suppose that there exists an orbit $\mathcal{O}_{k}$ such that $|\mathcal{R}\cap \mathcal{O}_{k}| > 1$. Let $x_{1}, \, x_{2}\in \mathcal{R}\cap \mathcal{O}_{k}$ then $\gamma_{\mathcal{R}}(\mathcal{I}) = \gamma_{\mathcal{R}\setminus \{x_{2}\}}(\mathcal{I})$. This implies $\mathcal{R}$ is not minimal (a contradiction). Hence, $|\mathcal{R} \cap \mathcal{O}_i| = 1$ for all $i = 1, 2, \ldots, k$ except one $i$.

Proposition $3.7$ gives the method to identify reducts for any given graph $\mathcal{G}$ with $k$ orbits. Also, it is obvious that any attribute subset $\mathcal{A}$ may have more than one reducts, the set of all reducts of an attribute subset is denoted by $\mathcal{RED}_{\mathcal{A}}(\mathcal{G})$. Let $\mathcal{K}\in\mathcal{RED}_{\mathcal{A}}(\mathcal{G})$ then $\gamma_{\mathcal{A}}(\mathcal{G}) = \gamma_{\mathcal{K}}(\mathcal{G}) = \mathcal{B}_1| \mathcal{B}_2|\dots|\mathcal{B}_n$. By Proposition 3.6, $\gamma_{\eta(\mathcal{A})}(\mathcal{G}) = \gamma_{(\mathcal{\eta(K)})}(\mathcal{G}) = \mathcal{B}_1|\mathcal{B}_2|\dots|\mathcal{B}_n$. We note that the automorphism of $\mathcal{G}$ preserves the structure of reducts. Hence we have the following proposition:

Proposition 3.8. For a graph $\mathcal{G}$, let $\mathcal{A}\subseteq\mathcal{V}$. If $\eta\in\Gamma(\mathcal{G})$, then $\mathcal{K}\in\mathcal{RED}_{\mathcal{A}}(\mathcal{G})$ if and only if $\eta(\mathcal{K})\in\mathcal{RED}_{\eta(\mathcal{A})}(\mathcal{G})$.

According to Proposition 3.8, for a graph $\mathcal{G}$, attribute set $\mathcal{A}$ and $\eta\in\Gamma(\mathcal{G})$, $\mathcal{K}\in\mathcal{RED}_{\mathcal{A}}(\mathcal{G})$ implies that $\eta(\mathcal{K})\in\mathcal{RED}_{\eta(\mathcal{A})}((\mathcal{G}))$. If $\mathcal{K}$ is a reduct for attribute set $\mathcal{A}$, then $\eta(\mathcal{K})$ does not necessarily belong to $\mathcal{RED}_{\mathcal{A}}(\mathcal{G})$.

Consider a graph $\mathcal{G}$ in Figure 2. Note that $\mathcal{O}(1) = \mathcal{O}(4) = \{1, 4\}$, $\mathcal{O}(2) = \mathcal{O}(3) = \{2, 3\}$ and $\mathcal{O}(5) = \mathcal{O}(6) = \mathcal{O}(7) = \mathcal{O}(8) = \{5, 6, 7, 8\}$. Let $\mathcal{A} = \{1, 2, 5, 6\}$ and take $\eta = (14)(23)(57)(68)$, then $\mathcal{K} = \{1, 2\}$ is a reduct of $\mathcal{A}$ and $\eta(\mathcal{K}) = \{3, 4\}$ is a reduct of $\eta(\mathcal{A})$ but not that of $\mathcal{A}$.

Let $\texttt{P}(\mathcal{V})$ denotes the set of all partitions of $\mathcal{V}$. For two partitions $\gamma_1$ and $\gamma_2$ of $\mathcal{V}$, $\gamma_1$ is called finer than $\gamma_2$ if all blocks of $\gamma_1$ are subset of the blocks of $\gamma_2$, denoted by $\gamma_1\preceq \gamma_2$. It is straightforward to see that for two attribute sets, $\mathcal{A}_1$ and $\mathcal{A}_2$ of graph $\mathcal{G}$ with $\mathcal{A}_1\subseteq\mathcal{A}_2$, then $\gamma_{\mathcal{A}_2}(\mathcal{G}) \preceq \gamma_{\mathcal{A}_1}(\mathcal{G})$. For a graph $\mathcal{G}$ with orbits $\mathcal{O}_1, \mathcal{O}_2, \ldots, \mathcal{O}_k$ and attribute sets $\mathcal{A}_1\subseteq \mathcal{A}_2$, $\gamma_{\mathcal{A}_2}(\mathcal{G}) = \gamma_{\mathcal{A}_1}(\mathcal{G})$, if $\mathcal{A}_1$ and $\mathcal{A}_2$ have non-empty intersection with same orbits $\mathcal{O}_i$ for $1\leq i\leq k$. If $\mathcal{A}_1\subseteq \mathcal{A}_2$ and there exists some $\mathcal{O}_{i}$ $(1\leq i\leq k)$ such that $\mathcal{A}_1\cap \mathcal{O}_{i} = \emptyset$ and $\mathcal{A}_2\cap \mathcal{O}_{i}\neq \emptyset$ then $\gamma_{\mathcal{A}_2}(\mathcal{G})\prec \gamma_{\mathcal{A}_1}(\mathcal{G})$. From this discussion, we conclude that a partition consisting of orbits of the graphs is the finest partition of the vertex set in $\texttt{P}(\mathcal{V})$.

Now, we introduce three sets, namely $\mathcal{A}$-interior set, $\mathcal{A}$-exterior set and $\mathcal{A}$-delimiting set as follows.

Definition 3.1. For an attribute subset $\mathcal{A}\subseteq\mathbb{A}$, let $x\in\mathcal{V}$. Then

● $x$ is called $\mathcal{A}$-interior, if $\mathcal{O}(x)\subseteq\mathcal{A}$.

● $x$ is called $\mathcal{A}$-exterior, if $\mathcal{O}(x)\subseteq\mathcal{V}\backslash\mathcal{A}$.

● $x$ is called $\mathcal{A}$-delimiting, if $\mathcal{O}_{\mathcal{A}}(x)\neq\emptyset$ and $\mathcal{O}_{\mathcal{V}\backslash\mathcal{A}}(x)\neq\emptyset$.

Represent by $Int(\mathcal{A})$, $Ext(\mathcal{A})$ and $Del(\mathcal{A})$ respectively, the subset of all $\mathcal{A}$-interior, $\mathcal{A}$-exterior and $\mathcal{A}$-delimiting vertices of graph $\mathcal{G}$.

Note that the family of all subsets of Definition 3.1 is a set partition of $\mathcal{V}(\mathcal{G})$ and for an attribute subset $\mathcal{A}\subseteq\mathcal{V}(\mathcal{G})$, and $\mathcal{A}^c = \mathcal{V}\backslash\mathcal{A}$ then $Int(\mathcal{A}) = Ext(\mathcal{A}^c)$ and $Del(\mathcal{A}) = Del(\mathcal{A}^c)$. For an attribute subset $\mathcal{A}\subseteq\mathcal{V}(K_n)$, following is straightforward.

$(i)$ If $|\mathcal{A}| < n$ then $Int(\mathcal{A}) = Ext(\mathcal{A}) = \emptyset$ and $Del(\mathcal{A}) = \mathcal{V}(K_n)$.

$(ii)$ If $|\mathcal{A}| = n$ then $Del(\mathcal{A}) = Ext(\mathcal{A}) = \emptyset$ and $Int(\mathcal{A}) = \mathcal{V}(K_n)$.

$(iii)$ If $\mathcal{A} = \emptyset$ then $Int(\mathcal{A}) = Del(\mathcal{A}) = \emptyset$ and $Ext(\mathcal{A}) = \mathcal{V}(K_n)$.

Proposition 3.9. For an attribute subset $\mathcal{A}\subseteq\mathbb{A}$, a non-empty $Ext(\mathcal{A})$ is a block of $\mathcal{A}$-indiscernible partition $\gamma_{\mathcal{A}}(\mathcal{G})$.

Proof. Let $x, x\prime\in Ext(\mathcal{A})$ then for all $y\in\mathcal{A}$, we have $\mathcal{F}(x, y) = \mathcal{F}(x\prime, y) = 0$, so $x\equiv_{\mathcal{A}}x\prime$. If $z\in \mathcal{V}(\mathcal{G})$ such that for some $z\prime \in Ext(\mathcal{A})$, $z\equiv_{\mathcal{A}}z\prime$ then $\mathcal{O}_{\mathcal{A}}(z) = \emptyset$ implying that $z \in Ext(\mathcal{A})$. Because if there exists a vertex $y\in\mathcal{O}_{\mathcal{A}}(z)$ then $1 = \mathcal{F}(y, z)\neq\mathcal{F}(y, z\prime) = 0$, which is contradiction to the assumption that $z\equiv_{\mathcal{A}}z\prime$. Therefore, $\mathcal{O}_{\mathcal{A}}(z) = \emptyset$ and $z\in Ext(\mathcal{A})$.

Remark 1. It is straightforward to observe that the $Int(\mathcal{A})$ and $Del(\mathcal{A})$ need not be a block of $\gamma_{\mathcal{A}}(\mathcal{G})$. Further, $Int(\mathcal{A})$ and $Del(\mathcal{A})$ are blocks of $\gamma_{\mathcal{A}}(\mathcal{G})$ if and only if it consists of only one orbit.

Proposition 3.10. For an attribute subset $\mathcal{A}$, if $x, y\in Int(\mathcal{A})\cup Del(\mathcal{A})$, then $x\equiv_{\mathcal{A}}y$ if and only if $\mathcal{O}(x) = \mathcal{O}(y)$.

Proof. Suppose that $x, y\in Int(\mathcal{A})\cup Del(\mathcal{A})$ and $\mathcal{O}(x) = \mathcal{O}(y)$, then by definition of indiscernibility, $x\equiv_{\mathcal{A}}y$. Conversely, suppose that $x\equiv_{\mathcal{A}}y$ and $\mathcal{O}(x)\neq \mathcal{O}(y)$. Then there exists $z \in \mathcal{A}$ which will belong to at most one of $\mathcal{O}(x)$ or $\mathcal{O}(y)$ because if no such $z \in \mathcal{A}$ belongs to $\mathcal{O}(x)$ or $\mathcal{O}(y)$ then $x, y\in Ext(\mathcal{A})$. Therefore, $\urcorner(x\equiv_{\mathcal{A}}y)$, contradiction. Hence $\mathcal{O}(x) = \mathcal{O}(y)$.

4.   Upper and lower approximations in graphs

In this section, lower and upper approximations of various subsets of vertices are studied using similarity relations.

Theorem 3.1, provides information about the behavior of objects in the indiscernibility relation $\equiv_{\mathcal{A}}$. Indiscernibility relations can be considered as a type of symmetry relations as for the attribute subset $\mathcal{A}$. Using the fact that for any two distinct vertices $x, y\in \mathcal V (\mathcal{G})$ either $\mathcal{O}(x) = \mathcal{O}(y)$ or $\mathcal{O}(x) \cap \mathcal{O}(y) = \emptyset$, it is straightforward to note that every proper subset $X$ of $\mathcal{V(\mathcal{G})}$ is rough if $\mathcal{O}(x) = \mathcal{V(\mathcal{G})}$. Also note that for $x, y \in \mathcal{V(\mathcal{G})}$ with $O(x)\neq O(y)$ and $O(x)\cup O(y) = \mathcal{V(\mathcal{G})}$, a subset X of $\mathcal{V(\mathcal{G})}$ is rough if and only if $X \neq \mathcal{O}(x), \, X \neq \mathcal{O}(y)$ and $X \neq \mathcal{V(\mathcal{G})}$.

Note that the indiscernibility partition of complete graph on $n$ vertices consists of only one orbit yielding one block. If $\mathcal{V}(K_n) = \{x_1, \dots, x_n\},$ then $\gamma_{\mathcal{A}}(K_n) = x_1, \dots, x_n$ for any attribute subset $\mathcal{A}\subseteq K_n$ and every proper subset $\mathcal{Q}$ of $\mathcal{V}(K_n)$ is $\mathcal{A}$-rough because $\mathbb{L}_\mathcal{A}(\mathcal{Q}) = \emptyset$ and $\mathbb{U}_\mathcal{A}(\mathcal{Q}) = \mathcal{V}(K_n)$. A subset $\mathcal{Q}$ of $\mathcal{V}(K_n)$ is $\mathcal{A}$-exact if and only if $\mathcal{Q} = \mathcal{V}(K_n)$.

A given graph $\mathcal{G}$ in which $\mathcal{V} = \mathcal{V}_1\cup \mathcal{V}_2$, $\mathcal{V}_1\cap \mathcal{V}_2 = \emptyset$, $x\sim y$ for each $x\in \mathcal{V}_1$, $y\in \mathcal{V}_2$ and $x\nsim y$ if and only if $x, y\in \mathcal{V}_1$ or $x, y\in \mathcal{V}_2$, is called a complete bipartite graph. For a complete bipartite graph $\mathcal{K}_{m, n} = (\mathcal{V}_1|\mathcal{V}_2)$ where $\mathcal{V}_1 = \{x_1, x_2, \dots, x_m\}$ and $\mathcal{V}_2 = \{y_1, y_2, \dots, y_n\}$, $\gamma_{\mathcal{A}}(\mathcal{K}_{m, n}) = x_1, x_2, \dots, x_m|y_1, y_2, \dots, y_n$, for any non-empty attribute subset $\mathcal{A}$.

In the following proposition, we study rough sets in complete bipartite graphs.

Proposition 4.1. If $\mathcal{G}$ is a complete bipartite graph then a subset $\mathcal{Q}$ of $\mathcal{V}$ is rough with respect to attributes $\mathcal{A}$ if and only if $\mathcal{Q}\neq \mathcal{V}_1$, $\mathcal{Q}\neq \mathcal{V}_2$ and $\mathcal{Q}\neq \mathcal{V}$, where $\mathcal{V}_1, \mathcal{V}_2$ are partites of $\mathcal{G}$.

Proof. Let $\mathcal{Q}$ be a rough set in $\mathcal{G}$. If $\mathcal{Q} = \mathcal{V}$ then clearly $\mathcal{Q}$ is exact, hence $\mathcal{Q}\neq \mathcal{V}$. Now if $\mathcal{Q} = \mathcal{V}_1$ then for each $x\in \mathcal{V}_2$, $\mathcal{O}(x)\cap \mathcal{Q} = \emptyset$ which gives that $\mathcal{Q}$ is exact. Similar arguments holds for $\mathcal{Q} = \mathcal{V}_2$. Hence, $\mathcal{Q}\neq \mathcal{V}_1$, $\mathcal{Q}\neq \mathcal{V}_2$ and $\mathcal{Q}\neq \mathcal{V}$.

Conversely, suppose $\mathcal{Q}\neq \mathcal{V}_1$, $\mathcal{Q}\neq \mathcal{V}_2$ and $\mathcal{Q}\neq \mathcal{V}$, we need to prove that $\mathbb{L}_\mathcal{A}(\mathcal{Q})\neq \mathbb{U}_\mathcal{A}(\mathcal{Q})$. Since $\mathcal{Q}\neq \mathcal{V}_1$ so we have three cases:

(1) Suppose $\mathcal{V}_1\cap \mathcal{Q} = \emptyset$ and $\mathcal{V}_2\cap \mathcal{Q}\neq\emptyset$ then $\mathcal{Q}\neq \mathcal{V}_2$ which implies that $\mathcal{Q}\subset \mathcal{V}_2$. Now for any $x\in \mathcal{V}$, if $x\in \mathcal{V}_1$ then $\mathcal{O}(x)\cap \mathcal{Q} = \emptyset$ because $\mathcal{O}(x) = \mathcal{V}_1$. Moreover, for $x\in \mathcal{V}_2$, $\mathcal{O}(x) = \mathcal{V}_2$ which implies that $\mathbb{L}_\mathcal{A} (\mathcal{Q}) = \emptyset$ and $\mathbb{U}_\mathcal{A} (\mathcal{Q}) = \mathcal{V}_2$. Hence, $\mathcal{Q}$ is a rough set.

(2) For the case $\mathcal{V}_1\cap \mathcal{Q}\neq\emptyset$ and $\mathcal{V}_2\cap \mathcal{Q} = \emptyset$ then $\mathcal{Q}\neq \mathcal{V}_1$ which implies that $\mathcal{Q}\subset \mathcal{V}_1$. Now for any $x\in \mathcal{V}$, if $x\in \mathcal{V}_1$ then $\mathcal{O}(x)\cap \mathcal{Q}\neq\emptyset$ because $\mathcal{O}(x) = \mathcal{V}_1$. Moreover, for $x\in \mathcal{V}_2$, $\mathcal{O}(x) = \mathcal{V}_2$ which implies that $\mathbb{L}_\mathcal{A} (\mathcal{Q}) = \emptyset$ and $\mathbb{U}_\mathcal{A} (\mathcal{Q}) = \mathcal{V}_1$. Hence, $\mathcal{Q}$ is a rough set.

(3) Now suppose $\mathcal{V}_1\cap \mathcal{Q}\neq\emptyset$ and $\mathcal{V}_2\cap \mathcal{Q}\neq\emptyset$ then we have three sub-cases:

ⅰ) Suppose $\mathcal{V}_1\cap \mathcal{Q} = \mathcal{V}_1$ then $\mathbb{L}_\mathcal{A} (\mathcal{Q}) = \mathcal{V}_1$ and $\mathbb{U}_\mathcal{A} (\mathcal{Q}) = \mathcal{V}$ which gives that $\mathcal{Q}$ is rough.

ⅱ) Suppose $\mathcal{V}_2\cap \mathcal{Q} = \mathcal{V}_2$ then for every $x\in \mathcal{V}_2$ we have $x\in \mathbb{L}_\mathcal{A} (\mathcal{Q}) = \mathcal{V}_2$ and $\mathbb{U}_\mathcal{A} (\mathcal{Q}) = \mathcal{V}$ which gives that $\mathcal{Q}$ is rough.

ⅲ) Suppose $\mathcal{V}_1\cap \mathcal{Q}\neq\mathcal{V}_1$ and $\mathcal{V}_2\cap \mathcal{Q}\neq\mathcal{V}_2$. Let $x\in \mathcal{V}$ such that $x\in \mathcal{V}_1$ then $x\in \mathbb{U}_\mathcal{A}(\mathcal{Q})$ because $\mathcal{O}(x) = \mathcal{V}_1$ and $\mathcal{O}(x)\cap \mathcal{Q}\neq \emptyset$ but $\mathcal{O}(x)\nsubseteq \mathcal{Q}$. Similarly, if $x\in \mathcal{V}_2$ then $x\in \mathbb{U}_\mathcal{A}(\mathcal{Q})$. Also, for every $x\in \mathcal{V}$ we have $\mathcal{O}(x)\nsubseteq \mathcal{Q}$ which gives that $\mathbb{L}_\mathcal{A}(\mathcal{Q}) = \emptyset$ so $\mathcal{Q}$ is a rough set in $\mathcal{G}$.

In the following proposition, we discuss lower and upper approximation of a subset $\mathcal{Q}$ of complete bipartite graph $\mathcal{K}_{m, n}$.

Proposition 4.2. Let $\mathcal{K}_{m, n} = (\mathcal{V}_1|\mathcal{V}_2)$ is a complete bipartite graph where $\mathcal{V}_1 = \{x_1, x_2, \dots, x_m\}$ and $\mathcal{V}_2 = \{y_1, y_2, \dots, y_n\}$. Let $\mathcal{Q}$ and $\mathcal{A}$ are two subsets of $\mathcal{V}(\mathcal{K}_{m, n})$ such that $\mathcal{Q}\neq\mathcal{V}$. Then

Proof.

$(1)$ Let $\mathcal{V}_1\subseteq\mathcal{Q}$. If $x\in \mathcal{V}_1$, then it follow by Theorem $3.1$, that $\mathcal{O}_{\mathcal{A}}(x)\subseteq \mathcal{Q}$, thus by definition of the lower approximation, we get $\mathcal{V}_1\subseteq\mathbb{L}_{\mathcal{A}}(\mathcal{Q})$. Moreover, if $x\in\ \mathcal{V}_2\cap\mathbb{L}_{\mathcal{A}}(\mathcal{Q})$, for some $x\in\mathcal{V}$, then, again by Theorem 1.0.1 and definition of the lower approximation, we get $\mathcal{V}_2 = \mathcal{O}_{\mathcal{A}}(x)\subseteq \mathcal{Q}$. Because $\mathcal{V}_1|\mathcal{V}_2$ are set partition for $\mathcal{V}$, so last inclusion implies $\mathcal{Q} = \mathcal{V}$, a contradiction to our assumption. Thus, $\mathcal{V}_1\subseteq\mathbb{L}_{\mathcal{A}}(\mathcal{Q})$ and $\mathcal{V}_2\cap\mathbb{L}_{\mathcal{A}}(\mathcal{Q}) = \emptyset$. Similarly, if $\mathcal{V}_2\subseteq\mathcal{Q}$ then $\mathbb{L}_{\mathcal{A}}(\mathcal{Q}) = \mathcal{V}_2$. Hence let $\mathcal{V}_1\nsubseteq\mathcal{Q}$ and $\mathcal{V}_2\nsubseteq\mathcal{Q}$. but each vertex $x\in\mathcal{V}$ is either in $\mathcal{V}_1$ or $\mathcal{V}_2$. Therefore, by Theorem 1.0.1, we have $\mathcal{O}_{\mathcal{A}}(x) = \mathcal{V}_1\nsubseteq\mathcal{Q}$ and $\mathcal{O}_{\mathcal{A}}(x) = \mathcal{V}_2\nsubseteq\mathcal{Q}$, $i.e.,$ $x\notin\mathbb{L}_{\mathcal{A}}(\mathcal{Q})$. Hence $\mathbb{L}_{\mathcal{A}}(\mathcal{Q}) = \emptyset$.

$(2)$ Let $\mathcal{Q}\subseteq \mathcal{V}_1$. If $x\in \mathcal{V}_1$, then it follow by Theorem $3.1$ that $\mathcal{O}_{\mathcal{A}}(x) = \mathcal{V}_1\cap\mathcal{Q}\neq\emptyset$, because $\mathcal{Q}$ is non-empty subset of $Q_1$. Hence $x\in\mathbb{U}_{\mathcal{A}}(\mathcal{Q})$. Moreover, if $x\in\mathbb{U}_{\mathcal{A}}(\mathcal{Q})$ then by definition of upper approximation we get $\mathcal{O}_{\mathcal{A}}(x)\cap\mathcal{Q}\neq\emptyset$. Let $y\in\mathcal{O}_{\mathcal{A}}(x)\cap\mathcal{Q}$. Since $y\in\mathcal{Q}\subseteq \mathcal{V}_1$, thus by Theorem 1.0.1 we have $\mathcal{V}_1 = \mathcal{O}_{\mathcal{A}}(x) = \mathcal{O}_{\mathcal{A}}(y)$, therefore again by Theorem $3.1$, we deduce that $x\in \mathcal{V}_1$. Hence $\mathbb{U}_{\mathcal{A}}(\mathcal{Q}) = \mathcal{V}_1$. The case of $\mathcal{Q}\subseteq \mathcal{V}_2$ is similar. Finally, $\mathcal{Q}\nsubseteq \mathcal{V}_1$ and $\mathcal{Q}\nsubseteq \mathcal{V}_2$. Since $\mathcal{V}_1|\mathcal{V}_2$ is a partition of $\mathcal{V}$, which implies that $\mathcal{V}_1\cap\mathcal{Q}\neq\emptyset$ and $\mathcal{V}_2\cap\mathcal{Q}\neq\emptyset$. Now select arbitrary a vertex $x\in\mathcal{V}$, then either $x\in \mathcal{V}_1$ or $\mathcal{V}_2$. If $x\in \mathcal{V}_1$, then by Theorem $3.1$, it follows that $\mathcal{O}_{\mathcal{A}}(x)\cap\mathcal{Q} = \mathcal{V}_1\cap\mathcal{Q}\neq\emptyset$. Thus, $x\in\mathbb{U}_{\mathcal{A}}(\mathcal{Q})$. Analogously, if $x\in \mathcal{V}_2$. Then it shows that $\mathcal{V}\subseteq\mathbb{U}_{\mathcal{A}}(\mathcal{Q})$. $i.e.,$ $\mathcal{V} = \mathbb{U}_{\mathcal{A}}(\mathcal{Q})$.

$(3)$ This follow from the definition of exactness and Theorem $3.1$.

In Proposition 4.3, we provide complete description for the lower approximations of graph $\mathcal{G}$.

Proposition 4.3. For a graph $\mathcal{G}$, let $\mathcal{A}, \mathcal{Q}\subseteq\mathcal{V}$. Then

Proof. Let a vertex $x\in\mathcal{A}$ such that $\mathcal{O}_{\mathcal{A}}(x)\setminus \mathcal{Q} = \emptyset$, which give $\mathcal{O}_{\mathcal{A}}(x)\subseteq \mathcal{Q}$, implies that $\mathcal{O}_{\mathcal{A}}(x)\in\mathbb{L}_{\mathcal{A}}(\mathcal{Q})$. Since $x$ is chosen arbitrary, hence $\mathbb{L}_{\mathcal{A}}(\mathcal{Q}) = \mathcal{O}(\mathcal{A})$.

For $\mathcal{O}_{\mathcal{A}}(x)\setminus \mathcal{Q}\neq\emptyset$, $\mathcal{O}_{\mathcal{A}}(x)\nsubseteq \mathcal{Q}$ giving that $\mathcal{O}_{\mathcal{A}}(x)\notin\mathbb{L}_{\mathcal{A}}(\mathcal{Q})$ implies that $\mathbb{L}_{\mathcal{A}}(\mathcal{Q}) = \emptyset$.

In Proposition 4.4, we provide a necessary and sufficient condition for a subset $\mathcal{Q}\subseteq\mathcal{V}$ to be exact.

Proposition 4.4. For a graph $\mathcal{G}$, let $\mathcal{A}, \mathcal{Q}\subseteq\mathcal{V}$. Then $\mathcal{Q}$ is exact with respect to $\mathcal{A}$, if and only if $\mathcal{Q} = \cup_{x\in \mathcal{Q}}\mathcal{O}_{\mathcal{A}}(x)$.

Proof. Suppose $\mathcal{Q}$ is exact then for $x \in \mathcal{Q}$, $\mathcal{O}_{\mathcal{A}}(x)\subseteq \mathcal{Q}$. As $x$ is arbitrary, $\cup_{x\in \mathcal{Q}}\mathcal{O}_{\mathcal{A}}(x)\subseteq\mathcal{Q}$. For each $x\in \mathcal{Q}$, $x \in \mathcal{O}_{\mathcal{A}}(x)$ which yields that $\mathcal{Q} \subseteq \cup_{x\in \mathcal{Q}}\mathcal{O}_{\mathcal{A}}(x)$. Hence $\mathcal{Q} = \cup_{x\in \mathcal{Q}}\mathcal{O}_{\mathcal{A}}(x)$. Conversely, suppose $\mathcal{Q} = \cup_{x\in \mathcal{Q}}\mathcal{O}_{\mathcal{A}}(x)$ which clearly implies $\mathbb{L}_{\mathcal{A}}(\mathcal{Q}) = \mathbb{U}_{\mathcal{A}}(\mathcal{Q})$ giving that $\mathcal{Q}$ is exact.

Proposition 4.4 illustrates the criterion for exactness of any subset $\mathcal{Q}$ of given graph $\mathcal{G}$. Note that for a rigid graph $\mathcal{G}$, in which no two vertices are similar, $\gamma_{\mathcal{A}}(\mathcal{G})$ consists of blocks having singleton elements only, which implies $\mathbb{L}_{\mathcal{A}}(\mathcal{Q}) = \mathbb{U}_{\mathcal{A}}(\mathcal{Q})$. Hence every subset of the vertex set of a rigid graph is exact.

Rough membership function and dependency

Now, we introduce and present results on rough membership function, positive region and degree of dependency of graphs using orbits of the graphs.

Let $\mathcal{G} = (\mathcal{V}, \mathcal{E})$ and $\mathcal{A}, \mathcal{Q}\subseteq\mathcal{V}$. The rough membership function on the vertex set $\mathcal{V}$ is defined by:

For $\mathcal{A}, \mathcal{Q}\subseteq \mathcal{V}$, $POS_{\mathcal{A}}(\mathcal{Q}) = \{x\in \mathcal{V}: (y\in \mathcal{V} \wedge \mathcal{O}(x)\cap \mathcal{A} = \mathcal{O}(y)\cap \mathcal{A})\Rightarrow (\mathcal{O}(x)\cap \mathcal{Q} = \mathcal{O}(y)\cap \mathcal{Q})\}$. The number $deg_{\mathcal{A}}({\mathcal{Q}}) = \frac{|POS_{\mathcal{A}}({\mathcal{Q}})|}{|\mathcal{V}|}$ is referred to as $\mathcal{A}$-degree dependency of $\mathcal{Q}$. It is easy to note that for two different attribute sets $\mathcal{A}$ and $\mathcal{Q}$ which yield the same partition, $deg_{\mathcal{A}}({\mathcal{Q}}) = 1$. Further, if $\mathcal{G}$ has $k$ orbits and $\mathcal{A}$ has non-empty intersection with $k$ or $k-1$ orbits of $\mathcal{G}$, $deg_{\mathcal{A}}({\mathcal{V}}) = 1$.

In Proposition 4.5, we examine the rough membership function of complete bipartite graph $\mathcal{K}_{m, n}$ and compute $\mathcal{A}$-positive region of $\mathcal{Q}$ and the degree of dependency.

Proposition 4.5. For a complete bipartite graph $\mathcal{K}_{m, n}$ with bipartition $(\mathcal{V}_1|\mathcal{V}_2)$, let $\mathcal{A}$ and $\mathcal{Q}$ are two subset of $\mathcal{V}(\mathcal{K}_{m, n})$. Then

Proof. $(i)$ According to Proposition 4.2, we know that $\mathcal{O}_{\mathcal{A}}(x) = \mathcal{V}_i$, if and only if $x\in \mathcal{V}_i$, for $i$ = 1, 2, therefore,

Hence the proof follow directly by definition of rough membership.

$(ii)$. If $\mathcal{A} = \emptyset$ and $\mathcal{Q}\neq\emptyset$ then $\gamma_{\mathcal{A}}(\mathcal{K}_{m, n}) = \mathcal{V}$. As $\gamma_{\mathcal{Q}}(\mathcal{K}_{m, n}) = \mathcal{V}_1|\mathcal{V}_2$. Therefore, $\mathcal{O}_{\mathcal{A}}(x) = \mathcal{V}$ and $\mathcal{O}_{\mathcal{Q}}(x) = \mathcal{V}_i$ for some $i = 1, 2$ which implies that $\mathcal{O}_{\mathcal{A}}(x)\nsubseteq\mathcal{O}_{\mathcal{Q}}(x)$ $\forall x\in\mathcal{V}$, hence $POS_{\mathcal{A}}(\mathcal{Q}) = \emptyset$ if $\mathcal{A} = \mathcal{Q} = \emptyset$ then $\gamma_{\mathcal{A}}(\mathcal{K}_{m, n}) = \gamma_{\mathcal{Q}}(\mathcal{K}_{m, n}) = \mathcal{V}$, therefore $\mathcal{O}_{\mathcal{A}}(x) = \mathcal{V}\subseteq\mathcal{O}_{\mathcal{Q}}(x) = \mathcal{V}$ $\forall$ $x\in\mathcal{V}$. Hence $POS_{\mathcal{A}}(\mathcal{Q}) = \mathcal{V}$. If $\mathcal{A}\neq\emptyset$ and $\mathcal{Q} = \emptyset$ then $\gamma_{\mathcal{A}}(\mathcal{K}_{m, n}) = \mathcal{V}_1|\mathcal{V}_2$ by Proposition 4.2, and $\gamma_{\mathcal{Q}}(\mathcal{K}_{m, n}) = \mathcal{V}$. Which implies that $\mathcal{O}_{\mathcal{A}}(x) = \mathcal{V}_i$ for some $i = 1, 2$ and $\mathcal{O}_{\mathcal{Q}}(x) = \mathcal{V}$ for all $x\in\mathcal{V}$. Hence $POS_{\mathcal{A}}(\mathcal{Q}) = \mathcal{V}$. Finally, if $\mathcal{A}\neq\emptyset$ and also $\mathcal{Q}\neq\emptyset$ then by Proposition 4.2, we have $\gamma_{\mathcal{A}}(\mathcal{K}_{m, n}) = \gamma_{\mathcal{Q}}(\mathcal{K}_{m, n}) = \mathcal{V}_1|\mathcal{V}_2$. This implies that $\mathcal{O}_{\mathcal{A}}(x) = \mathcal{O}_{\mathcal{Q}}(x) = \mathcal{V}_i$ for all $x\in\mathcal{V}$ and for some $i$ = 1, 2. Thus in this case we have $POS_{\mathcal{A}}(\mathcal{Q}) = \mathcal{V}$.

$(iii)$. It is following directly from definition and $(ii)$.

Note that, for complete graphs $K_{n}$ and cycle graphs $C_{n}$, $|POS_{\mathcal{A}}({\mathcal{Q}})| = |\mathcal{V}|$ yields that $deg_{\mathcal{A}}({\mathcal{Q}}) = 1$. It is observed that for $K_{n}$, $C_{n}$, we have $\gamma_{\mathcal{V}} = \mathcal{O}_{1}$ and for complete bipartite graphs $\mathcal{K}_{m, n}$, we have $\gamma_{\mathcal{V}} = \mathcal{O}_{m}|\mathcal{O}_{n}$. Therefore, $deg_{\mathcal{A}}({\mathcal{Q}}) = 1$ when $m = n$ and $deg_{\mathcal{A}}({\mathcal{Q}}) < 1$ when $m\neq n$. For a path graph $P_{n}$, with $k$ orbits and $\mathcal{A}, \mathcal{Q}\subseteq \mathcal{V}$ such that $\mathcal{A}\subseteq \mathcal{Q}$ and $\mathcal{A}\cap \mathcal{O}_{k-i}$ and $\mathcal{Q}\cap \mathcal{O}_{k-1}$ is non-empty $\forall \, i > 1$ then $deg_{\mathcal{A}}(\mathcal{Q}) < 1$ and $deg_{\mathcal{Q}}(\mathcal{A}) = 1$.

It is easy to see that for a graph $\mathcal{G}$ with $\mathcal{A}, \mathcal{Q}\subseteq\mathcal{V}$, $\mu_{\mathcal{Q}}^{\mathcal{A}}(x) = 0$ if $\gamma(x)\cap \mathcal{Q} = \emptyset$, $\mu_{\mathcal{Q}}^{\mathcal{A}}(x) < 1$ if $\gamma(x)\cap \mathcal{Q}\neq \emptyset$ and $\mu_{\mathcal{Q}}^{\mathcal{A}}(x) = 1$ if $\gamma(x)\subset \mathcal{Q}$ where $\gamma(x)$ is the block of partition $\gamma$ containing $x$.

5.   Essential sets and discernibility matrix of graphs

In this section, we will introduce essential sets as well as discernibility matrices of graphs. We will also study the relationship between these two important concepts.

5.1.   Essential sets of graphs

Chiaselotti et al. ^[8] presented classical model of Pawlak's core in a more general way. The core of an information system $\mathcal{I}$ associated to $\mathcal{G}$ is the intersection of all reducts, represented by $\mathcal{CORE}(\mathcal{G})$. Hence removal of any attribute belonging to core of a graph leads to change in the indiscernibility partition. In case, core is empty, this extension becomes important because it provides with a set on minimum number of vertices whose removal yields a partition different from the one yielded by all attributes. Concepts of Definition 5.1 were introduced by Chiaselotti et al. in ^[8].

Definition 5.1. A subset $\mathcal{S}\subseteq \mathcal{A}$, is called $\mathcal{I}$-essential of $\mathcal{G}$, if $\gamma_{\mathcal{A}\setminus\mathcal{S}}(\mathcal{G})\neq\gamma_{\mathcal{A}}(\mathcal{G})$ and $\forall \, \mathcal{Q}\subsetneq\mathcal{S}$ we have $\gamma_{\mathcal{A}\setminus\mathcal{Q}}(\mathcal{G}) = \gamma_{\mathcal{A}}(\mathcal{G}).$

$\mathsf{ESS}(\mathcal{I})$ represents the collection of all $\mathcal{I}$-essential subsets of $\mathcal{G}$. For $l\in\{1, 2, \dots, n\}$, set

and essential numerical sequence of $\mathcal{I}$ is defined by

Finally, essential dimension of $\mathcal{I}$ is defined as the positive integer

Note that, for a graph with at most two orbits, $ESS(\mathcal{I}) = \emptyset$. For complete graphs $K_{n}$, cycles $C_{n}$ and complete bipartite graphs $\mathcal{K}_{m, n}$, $ESS(\mathcal{I}) = \emptyset$. As there exists only one orbit for $K_{n}$ and $C_{n}$, but for $\mathcal{K}_{m, n}$, there exists one orbit when $m = n$ and two orbits when $m\neq n$. Also, it is observed that if $\mathcal{A}\subseteq \mathcal{V}$, then there does not exist any set $\mathcal{S}$ for complete graphs, cycles and complete bipartite graphs such that $\gamma_{\mathcal{A}}(\mathcal{I})\neq \gamma_{\mathcal{A}\backslash\mathcal{S}}(\mathcal{I})$. Therefore, $ens(K_{n}) = (0, 0, 0, ..., 0)$ $\forall \, n$, $ens(C_{n}) = (0, 0, 0, ..., 0)$ $\forall \, n$ and $ens(\mathcal{K}_{m, n}) = (0, 0, 0, ..., 0)$ $\forall \, m, \, n$.

For a path $P_n$ on $n\geq 5$ vertices with vertex set $\mathcal{V} = \{x_1, x_2, \ldots, x_n\}$ and edge set $\mathcal{E} = \{{x_ix_{i+1}}|1\leq i \leq n-1\}$. It is observed that $\{\{x_i, x_{n-i+1}\}|1\leq i \leq \lfloor\frac{n}{2}\rfloor\}$ is the set of orbits of $P_n$. Note that each orbit has at most two elements. It can be easily seen that $ESS_l(\mathcal{I}) = \emptyset$ for $l < 3$. For odd $n$, $\{x_{\frac{n+1}{2}}\}$ forms an orbit on one vertex and $ESS_{3}(\mathcal{I})$ is the union of orbit $\{x_{\frac{n+1}{2}}\}$ with any other orbit of $P_{n}$. Also, $ESS_{4}(\mathcal{I})$ is the union of any two orbits of $P_{n}$. Further, observe that if $n = 2k$ for $k > 2$, then each orbit of path graph $P_n$ will consist of exactly two vertices. Therefore, ${E}dim(P_n) = 4$. Similarly, if $n = 2k+1$ for $k\geq2$, then $P_n$ will contain exactly one orbit of order one and all other orbits of order two. Then ${E}dim(P_n) = 3$. Also note that, for a rigid graph, ${E}dim(\mathcal{G}) = 2$ as the cardinality of each orbit of a rigid graph is one.

Hence, we have the following straightforward proposition for path graphs $P_{n}$.

Proposition 5.1. If $\mathcal{G}$ is a path graph then we have the following:

$(i)$ ${ESS}(P_{n}) = \emptyset$ for $n\leq 4.$

$(ii)$ $|{ESS_{3}}(P_{2k+1})| = k; k\geq 2$ and $|{ESS_{3}}(P_{2k})| = 0; k\geq 2.$

$(iii)$ $|{ESS_{4}}(P_{2k})| = \binom{k}{2}; n\geq 4$

$(iv)$ $ens(P_{2k+1}) = (0, 0, k, \binom{k}{2}, 0, ...)$ if $k\geq 2$ and $ens(P_{2k}) = (0, 0, 0, \binom{k}{2}, 0, ...)$ if $k\geq 3$.

In the next proposition, we prove that essential set $\mathcal{S}$ for any graph $\mathcal{G}$ is exactly union of two orbits which also suggest a criterion to identify essentials for a given graph $\mathcal{G}$.

Proposition 5.2. $\mathcal{I}-essential$ set $\mathcal{S}$ is always union of two orbits of graph $\mathcal{G}$.

Proof. Assume contrary that set $\mathcal{S}\subseteq \mathcal{A}$ is a union of more than two orbits of $\mathcal{G}$ then there exists $\mathcal{Q}\subset \mathcal{S}$ such that $\gamma_{\mathcal{A}\setminus \mathcal{Q}}(\mathcal{G})\neq \gamma_{\mathcal{A}}(\mathcal{G})$, i.e., there exists $x, x\prime \in \mathcal{A}\setminus \mathcal{Q}$ such that $x\equiv_{\mathcal{A}\setminus \mathcal{Q}} x\prime$ and $\urcorner (x\equiv_{\mathcal{A}} x\prime)$ which does not satisfy the minimality condition for $\mathcal{S}$ to be essential. Hence, $\mathcal{S}$ is a union of two orbits of a graph $\mathcal{G}$.

5.2.   Discernibility matrix of graph

In rough set theory, discernibility matrix is a tool to study information system. Here, we concentrate on the structural concept of discernibility matrix in the context of graph theory.

Let $\mathcal{I} = \langle \mathcal{V}, \mathcal{V}, \mathcal{V}al, \mathcal{F}\rangle$ is an information system with $\mathcal{V} = \{x_1, x_2, ,\dots, x_n\}$. The discernibility matrix $\Delta[\mathcal{I}]$ of $\mathcal{I}$ is an $n\times n$ matrix with $ijth$ entry, $\Delta_{\mathcal{G}}(x_i, x_j)$, of the matrix is the attribute subset corresponding to the pair $(x_i, y_j)$ given as:

Note that in context of granular referencing system, $\mathcal{A}$ serves as reference set and helps in identification whether given two vertices are identical. Two elements in an orbit are similar for any choice of $\mathcal{A}$. Therefore, two vertices in different orbits are discernible by any of the vertices in those orbits. We define the entries of the discernibility matrix in the following way.

For a graph $\mathcal{G}$, if $x_i, x_j \in \mathcal{V}$, then

Note that isomorphic graphs have same discernibility matrices. However, for a given discernibility matrix, there may exist more than one non-isomorphic graphs which have the same discernibility matrix. For example, $C_{4}$ and $K_{4}$ have same discernibility matrix but they are not isomorphic.

Please note that rows and columns of discernibility matrix corresponding to similar vertices are equal. Hence instead of considering individual elements, their orbits can be considered. Therefore, we first evaluate the classes of orbits of graphs and then consider the rows and columns of discernibility matrix in terms of the orbits of graphs. We name the discernibility matrix obtained by considering orbits instead of vertices as Quotient Discernibility Matrix (QDM). QDM has order equal to the number of orbits of the graphs. Rows and columns of QDM are labeled by orbits of the graph and entries of QDM are defined as follows: For a graph $\mathcal{G}$, with two arbitrary orbits $\mathcal{O}_i$ and $\mathcal{O}_j$.

Next, we represent by $EQDM(\mathcal{I}(\mathcal{G}))$, the collection of all distinct entries of $\Delta[\mathcal{I}]$.

In Proposition 5.3, we describe a relationship between $EQDM(\mathcal{I}(\mathcal{G}))$ and $ESS(\mathcal{I}(\mathcal{G}))$, the family of $\mathcal{I}$-essential subsets.

Proposition 5.3. Let $\mathcal{G}$ be a graph then $EQDM(\mathcal{I}(\mathcal{G})) = ESS(\mathcal{I}(\mathcal{G}))$.

Proof. Let $S \in ESS(\mathcal{I}(\mathcal{G}))$ then by Proposition 5.2, $S = \mathcal{O}_i \cup \mathcal{O}_j$. Note that $\Delta_{\mathcal{G}}(\mathcal{O}_i, \mathcal{O}_j) = \mathcal{O}_i\cup\mathcal{O}_j$ hence $S \subseteq EQDM(\mathcal{I(G)})$ and $ESS(\mathcal{I}(\mathcal{G}))\subseteq EQDM(\mathcal{I}(\mathcal{G}))$. Conversely, suppose that $S \in EQDM (\mathcal{I(G)})$ then there exist $\mathcal{O}_i$ and $\mathcal{O}_j$ such that $\Delta_{\mathcal{G}}(\mathcal{O}_i, \mathcal{O}_j) = \mathcal{O}_i\cup\mathcal{O}_j$. Note that $\gamma_{\mathcal{V}\setminus \{\mathcal{O}_i \cup \mathcal{O}_j\}}\neq \gamma_{\mathcal{V}}$ which satisfies first condition for $S$ to be an essential set. Let $T\subset \mathcal{O}_i \cup \mathcal{O}_j$ then we have three possibilities. (i). $T \subseteq \mathcal{O}_i$, (ii). $T \subseteq \mathcal{O}_j$, (iii). $T \cap \mathcal{O}_i\neq \emptyset$ and $T \cap \mathcal{O}_j\neq \emptyset$. It is easy to see in all these three cases that $\gamma_{\mathcal{V}\setminus T }(\mathcal{G}) = \gamma_{\mathcal{V}}(\mathcal{G})$ which satisfies the second condition for $S$ to be an essential set. Hence $S \in EES(\mathcal{I(G)})$ and $EQDM(\mathcal{I}(\mathcal{G}))\subseteq ESS(\mathcal{I}(\mathcal{G}))$ which gives required result.

Proposition 5.3 illustrates that the collection of distinct entries of discernibility matrix and collection of all essential subsets of any graph $\mathcal{G}$ under an information system $\mathcal{I}$ remain same.

Example 5.1. Consider the graph $\mathcal{G}$ shown in Figure 1 and its discernibility matrix is given in the following Table 1:

${ESS}(\mathcal{I}(\mathcal{G})) = EQDM(\mathcal{I}(\mathcal{G})) = \{\mathcal{O}(1)\mathcal{O}(2), \mathcal{O}(1)\mathcal{O}(3), \mathcal{O}(2)\mathcal{O}(3) \}$.

We remark the limitations associated with this approach of indiscernibility $\mathcal{O}(u)\cap \mathcal{A} = \mathcal{O}(v)\cap \mathcal{A}$, using orbits. Note that all vertices in one orbit behave alike, which may be thought of as a loss of information about those vertices in the graph $\mathcal{G}$. Also, note that the discernibility matrices with entries as given by $\Delta_{\mathcal{G}}(\mathcal{O}_i, \mathcal{O}_j)$ do not provide information about vertices but about orbits.

Chiaselotti et al. ^[6,7,8] marked two vertices as indiscernible if $\mathcal{N}(u)\cap \mathcal{A} = \mathcal{N}(v)\cap \mathcal{A}$ whereas we defined indiscernibility of the vertices $u$ and $v$ in terms of orbits as $\mathcal{O}(u)\cap \mathcal{A} = \mathcal{O}(v)\cap \mathcal{A}$. It is interesting to note that indiscernibility partitions coincide for both approaches in cases of complete graphs and complete bipartite graphs for any choice of $\mathcal{A}$, whereas indiscernibility partitions are different for families of graphs like cycles and paths etc. Consequently, rough membership function and essential sets remain same for both approaches in complete and complete bipartite graphs but all other parameters are different. Discernibility matrices as defined according to Chiaselotti et al. are of the order $|\mathcal{V}|\times |\mathcal{V}|$ whereas in our case, discernibility matrices are of order $k \times k$ where '$k$' is the number of orbit in the graph.

In the Figure 3, we show the flowchart of the proposed methodology of this paper.

6.   Conclusions

We have used orbits of graphs to construct information systems to study graphs using rough set theory. For a given graph $\mathcal{G}$, we defined indiscernibility relation using concept of orbit of graphs and showed that a partition consisting of orbits of the graphs is the finest partition of the vertex set $\mathcal{V}$. We also gave construction of an indiscernible partition for any given attribute set $\mathcal{A}$. Vertices in classes of a partition are called granules and identification of granules will simplify the graph structures for better insights. We also studied lower and upper approximations of subsets of vertices of graphs, the rough membership function and rough positive region for some well-known families of graphs like cycles, complete and complete bipartite graphs. We also noticed that the automorphism of $\mathcal{G}$ preserves the structure of reducts. If $\mathcal{K}$ is a reduct for any attribute set $\mathcal{A}$ then for $\eta \in Aut(\mathcal{G})$, $\eta(\mathcal{K})$ is not necessarily a reduct. Further, we studied the essential sets and the discernibility matrices of graphs using this indiscernibility relation. We proved that essential sets for cycles, complete, complete bipartite graphs and path graph $P_n$ for $n\leq 4$ are empty sets. For path graph $P_n, \, n > 4$, $ESS_{l}(P_{n}) = \phi$ for $l < 3$. If $n = 2k+1$ for $k\geq2$, then $k$ is the cardinality of $ESS_{l}(P_{n})$ for $l = 3$ and if $n = 2k$ for $k\geq 3$, then $\binom{k}{2}$ is the cardinality of $ESS_{l}(P_{n})$ for $l = 4$. Moreover, we observed that isomorphic graphs have same discernibility matrices whereas, for a given discernibility matrix, there may exist more than one non-isomorphic graphs which have the same discernibility matrix. We believe that the study of concept of granularity for fuzzy environments will yield insights for better applications of those concepts. The terminology emerging from the merger of rough set theory and graph theory will be useful for exploring new problems associated to symmetries of graphs.

Communities in a social network are represented as vertices and connections between communities are represented by edges. Communities with common attributes are represented by similar vertices hence, problems associated with such communities are linked with identification of similarity. Study of similarity and object similarity measures, as discussed in ^[9] are associated with the problems of reducing attributes and for removal of inconsistencies. The idea of using orbits can be used to study similarity measures. The extension of our approach to orbit based similarity measure will yield refined indiscernibility relation like that of the neighbourhood based similarity measure. Our contribution will enrich literature in this direction of study which finds enormous applications in connection with data mining, database theory, different modeling using rough set theory, social networking and document clustering etc.

7.   Acknowledgements

The authors are grateful to the anonymous referees for their suggestions and constructive comments which lead to improvement in this paper.

Conflict of interest

The authors declare that they have no conflicts of interest.