Functional data analysis: Application to daily observation of COVID-19 prevalence in France

1.   Introduction

1.1.   Historical sketch

Daniel Bernoulli described in his 1760' article ^[1] the three dynamical modes of a contagious disease, namely the endemic, epidemic and eradicated behaviors and he took as an example a contagious disease very common at the time, the smallpox. Eradication corresponds to the disappearance of the disease in the human species. This was the case for smallpox, which disappeared permanently 40 years ago, according to the World Health Organization (WHO) which certified the global eradication of the disease in 1980, the last major European outbreak of smallpox having been observed in 1972 in Yugoslavia and the last naturally occurring case having been diagnosed in October 1977 ^[2].

In the past, smallpox had been the subject of measures similar to those implemented today for COVID-19:

1) The inoculation was a vaccination scheme, implemented in the Ottoman Empire during the 16th century. The original idea is probably originated in India, because some ancient Sanskrit medical texts described the process of inoculation ^[3], then the first practice of inoculation is documented in China as the late 10th century, and reached a wide practice by the 16th century, during the Ming dynasty ^[4]. Reports on the Chinese practice of inoculation were received by the Royal Society in London in 1700 and Lady Mary Wortley Montagu, spouse of the British ambassador in Turkey observed smallpox inoculation during her stay in the Ottoman Empire and promoted it in England upon her return in 1718 ^[5].

2) In 1796, Edward Jenner, a doctor in Berkeley (England, ) discovered that an immunity to smallpox was produced by inoculating a person with material from a cowpox lesion in cow (an animal disease similar to small pox). He called the living material used for this new type of inoculation vaccine (from Latin word vacca, the cow).

3) Before the vaccination, many countries adopted quarantine measures during the epidemic waves of variola.

Daniel Bernoulli proposed his famous mathematical model to describe the smallpox epidemic waves, using the first the logistic model as a phenomenological approach to fit data corresponding to the succession of the new daily cases of the disease. He described the endemic state of the disease after a wave, but did not propose a model for describing the endemic dynamic (now considered as a stationary stochastic process with constant average and variance), nor used a precise method to detect the critical boundary times corresponding to ruptures between epidemic and endemic phases. However, we can consider that with his SI (susceptible-infected) model:

with S(0) = S₀, I(0) = I₀ and where S(t) (resp. I(t)) is the size of susceptible (resp. infected) at time t, ß the transmission rate, µ (resp. ν) the natural (resp. viral) death rate, f the fecundity, σ (resp. ρ) the post-infected non immunized (resp. immunized) rate. If f = µ = ν = ρ = σ = 0, the solution of Eq (1) is given by:

with S+I = S_0. If I(0) = 1, then if t₀ = -Log(S₀-1)/ß, S(0) = S₀/(1+e^ßto)≈S₀-1. If S₀ is large, then during the time lapse at which S(t) remains close to S₀, if µS₀ = f, then Eq (1) becomes close to the linear system:

with the solution:

where ßS₀ represents the basic reproduction number of the epidemic disease, usually denoted R₀.

The Bernoulli model has been improved for modelling malaria first by Ross, who added the animal vector ^[6] and after by McKendrick ^[7], who considered a latency period between the moment of the mosquito's contamination and the one when it actually becomes infectious. More recently, models taking into account the spatial diffusion of infected and infectious agents are proposed ^[8,9,10,11] as well as some models including not reported and vaccinated patients ^{[12,13,14,15,16]}.

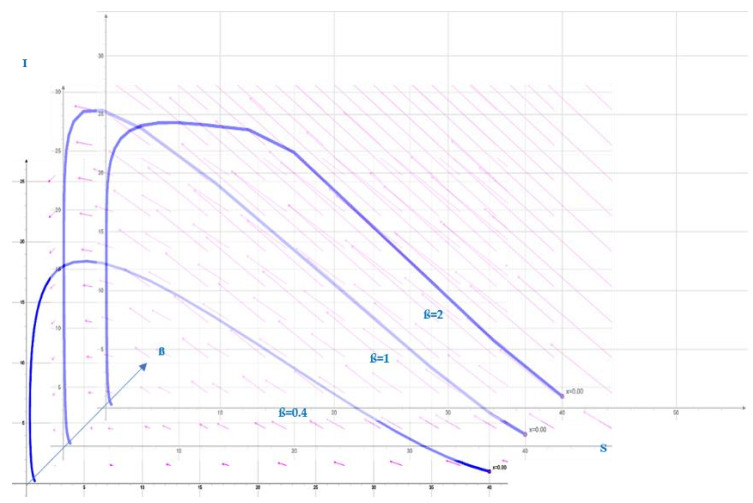
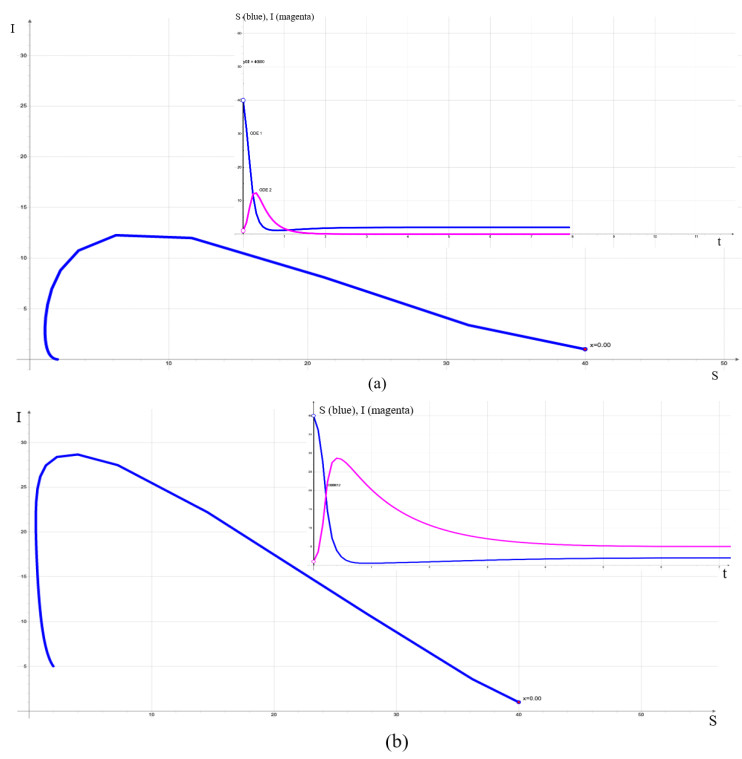
The present models are in general used to simulate an epidemic wave, as an excursion in the phase plane of an ordinary two-dimensional differential system having some excitable ability, i.e., the existence in his phase portrait of large return trajectories after perturbation of its stable stationary state or of its parameters, these trajectories returning to either an endemic or an eradicated final state. The difference between these two asymptotic behaviors is that in endemic case, the final value of the infected, back to the stationary state is non-zero and, in eradicated case, this value is zero. These behaviors are illustrated by simulations of the Bernoulli model in the possible final states corresponding to epidemic (transients in Figure 1), eradication (end state in Figure 1 top) and endemic (low level end in Figure 1 middle and high level in Figure 1 bottom).

If we consider that a parameter of the Bernoulli model like the transmission rate ß is evolving in time due to various influences as geoclimatic factors (temperature, humidity, elevation, etc.), sociodemographic determinant (density and median age of the target population) and economic variables (GDP, Gini's index, inequality index, etc.), the actual curve of the new infected cases observed during the epidemic outbreak is in fact also driven by the slow dynamics of the seasonally varying or linearly growing parameters.

Then, the observed dynamics of new infected cases results from the epidemic dynamics combined with slow evolution of these external factors on variation surfaces mixing both epidemic variables and parameters dynamics. The Figure 2 shows such a surface corresponding to the variations of the transmission rate ß due to climate changes (transition between winter and summer times) or public health policies (quarantine, vaccination, etc.), and the actual (S, I) trajectory lies on the corresponding surface. The influence of these different factors on the variations of the trajectories (S, I) are difficult to take into account in a differential model of the type Eq (1), which is why the article will now emphasize the statistical approach providing a better understanding of the correlations between the exogenous determinants of the epidemic and the level of new cases of infected.

1.2.   Background and literature review

The COVID-19 pandemic is still evolving in France as there has been three waves with possibility of a fourth wave due to a more contagious variant (Delta variant) which may lead to another lockdown following three lockdowns alongside with several non-pharmaceutical measures to mitigate the spread of the diseases. France has a total of 7,275,149 cases as at 14/11/2021,118,137 deaths representing 2% of the 5,280,894 cases which had an outcome (5,162,757 having recovered from the disease), and 1,994,255 currently infected patients with 1,993,206 (99.9%) in mild condition and 1,049 (0.1%) in serious or critical condition (data from ^[17,18,19]). Modeling COVID-19 pandemic across the globe has been approached using different techniques in mathematics and statistics, but the use of functional data analysis (FDA) has been done by few scientists.

Functional data analysis is useful in many fields such as medicine, biology, statistical analysis and econometrics while several books like ^{[20,21,22,23,24,25]} have treated the theoretical aspects and methodology and more recently, researchers have dealt with FDA application to COVID-19 modeling ^[26,27,28], trying to propose forecasting new case counts through a framework facilitating the quantification of the effects of demographic covariates and social mobilities on reproduction number and fatality rate through time-varying regression models. Among these recent works using functional data analysis for the modelling of COVID-19 pandemic, we can notice: ^[26] applies functional data analysis to United States data by using FCPA (Functional Principal Component Analysis) and FCCA (Functional Canonical Correlation Analysis) tools and they finally use functional time series to fit the cumulative confirmed cases in the United States and make forecasts based on the dynamics of FPCA. ^[27] works on the imputation of missing data of COVID-19 hospitalized and intensive care curves in Spain regions. They used function-on-function regression technique to estimate missing values and Canonical Correlation Analysis was performed to interpret the relationship between hospital occupancy rate and illness response variables. The shapes of an epidemic curve using functional data analysis to characterize COVID-19 in Italian regions and their association with mobility, positivity, socio-demographic structure and environmental covariates was worked on by ^[28]. The cited authors have used different methods of functional data analysis like function-on-function regression techniques, clustering methods and smoothing techniques for the functional data considered.

A robust phenomenological approach to France COVID-19 data has been recently investigated by ^[29,30] and a new method to calculate the cumulative cases in France was proposed which illustrates the epidemic and endemic nature of the virus infection in France. Authors in ^[31] used methods like principal component analysis, generalized additive model and hierarchical ascendant classification to study the impacts of population age structure, epidemic spread and transmission mitigation policies on COVID-19 morbidity or mortality heterogeneity in France. Authors in ^[32,33,34] used ARIMA models with different parameters to forecast the spread of COVID-19 across nine countries in Europe, Asia and American continents and the study deduced that the method is useful for the prediction of the pandemic at different stages and in ^[35] they employed statistical methods to analyze the shapes of local COVID-19 incidence rate curves and statistically group them into distinct clusters according to their shapes. The result reveals that pandemic curves often differ substantially across regions of a same country, and the explanation may lie in the existence of a temperature gradient or of differences in other geo-climatic, socio-economic or demographic factors ^{[36,37,38,39,40,41,42,43,44]}.

The main purpose of this article is to revisit the data on COVID-19 from public databases using methods that are still little used, such as functional data analysis (FDA), in which there is a great deal of theoretical work ^{[19,20,21,22,23,2425]}, but practical applications are still rare. In particular, the generalization at the FDA of classical finite-dimensional methods, such as estimation, regression and principal component analysis, shows that it is possible to process epidemic data obtained from a large sample (approximately one million data) concerning the incidence, mortality and exogenous or endogenous factors associated with the COVID-19 epidemic. This sampling concerns about ten variables (sometimes missing, in particular those concerning risk factors) and includes longitudinal (about 600 days all over the world but in our case we considered about 469 days for French departments) and cross-sectional data (about 200 countries, some comprising up to a hundred documented regions while for France which is the main focus of this article there are 101 departments), for the monitoring and prediction of a pandemic whose origin and end are still uncertain, but which, by its magnitude and its dramatic consequences (around 5 million deaths) justifies such a descriptive statistical investment. The descriptive study of many factors associated with the epidemic (namely the socio-economic and geoclimatic ones) makes it possible to understand closely linked mechanisms, those exogenous or endogenous to the viral pathogeny of propagation and endogenous ones of pathogenicity ^{[36,37,38,39,40,41,42,43,44]}. The seminal paper by Bernoulli on the SI model is the origin of all future discussions about epidemic modelling, in particular the first by d'Alembert in his Opuscules mathématiques and Lambert until its last recent refinements. It contains the explicit solution of the SI model given in Eq (4), and permits to consider the empiric S(t) and I(t) curves as functions. We can manipulate (after smoothing) as elements in a functional space. The goal of the article is to apply to these elements the FDA descriptive techniques in order to compare these functions among different departments. This approach is complementary of the works estimating the parameters of the functions S and I (namely R₀ and ß).

1.3.   Time series and curve fitting

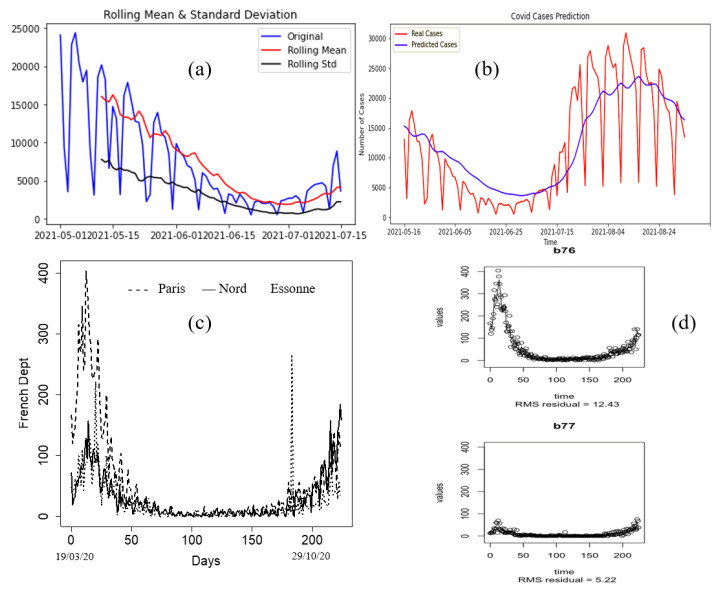
In this section, we present the time series analysis of daily new cases in France, daily hospitalization in three French departments out of 101 in France, and curve fitting for two French departments. The Root Mean Square Error (RMSE) for other curve fittings is shown in Table 1. Figure 3a gives the time series of recent daily cases of COVID-19 in France which shows stationarity with rolling values (window = 12) appearing to be varying slightly. Also, when we used the Augmented Dickey-Fuller Test to test for stationarity of the time series by accepting the alternative hypothesis, we got a p-value less than the 5% (p-value = 0.02) critical value, so we can say with 95 percent certainty that this is a stationary series. Also, in Figure 3c we plotted three French departments (Nord, Paris and Essonne) with more prevalent COVID-19 hospitalization cases and Figure 3d shows the fitted curve of two of the French departments (Paris and Seine-Maritime) while all departments have root mean square error in the interval $0.51\le RMSE\le 17.38$ with Essonne department having the highest Root Mean Square Error (RMSE) and Lozère department having the lowest RMSE. We present other RMSE values in Table 1. We present also (Figure 3b) a deep learning forecasting result using Gated Recurrent Units (GRU) for France data between the beginning of the pandemic in France till September 3 2021 by training 80% of the data and testing 20%. The predicted cases curve values decline over the whole-time. The RMSE was computed using:

where for ${\rm{i}} = 1, {\rm{ }}2, {\rm{ }}\dots, {\rm{ }}{\rm{n}}$, ${{\rm{Y}}}_{{\rm{i}}}{\rm{\text{'}}}{\rm{s}}$ are the observed values, ${\rm{n}}$ is the number of data points and ${{\rm{y}}}_{{\rm{i}}}{\rm{\text{'}}}$s are the predicted values.

The aim of this paper is to model the prevalence of the virus in France by using several functional techniques like FCCA, K-means clustering and FPCA and to finally make some predictions about the evolution of the disease in France. The analysis was done using both Python and R packages. We considered as functional variables numbers of ICU cases, daily deceased, daily return home and hospitalization which are given as ${X}_{1}–{X}_{4}$. Our response variables given as ${Y}_{1}–{Y}_{6}$ are numbers of recovery, deaths, infected, vaccination, vaccination per 1000 population and number of tests. We used data from ^[17,18,19]. The paper is divided as follows: Section 2 describes the various smoothing methods used in the analysis of the shapes of the functional data used, Section 3 presents the functional principal components analysis results and their interpretation to the dynamics of COVID-19 prevalence in French departments, and Section 4 is dedicated to the results of canonical correlation of the variables. Section 5 shows the clustering result using the K-means method and how it appears on a map of France. In Section 6, we made some predictions for some response variables and also performed function-on-function linear regression, and in Section 7, we opened up some perspectives and presented the results of the analysis.

2.   Data smoothing

The first step in analyzing functional data is to smooth the curves. In this section we use different smoothing techniques which we shall illustrate and give some basic explanation of the techniques we deployed for smoothing our functional data. We plotted the mean of the data set and the cross-sectional mean, which corresponds to the karcher-mean under the L2 distance. The karcher-mean has an important role in the warping framework and is used to align the functions in order to improve the matching of features (peaks) across functions for a given set of warping functions ${\partial }_{1}, {\partial }_{2}, \dots, {\partial }_{n}\in \Delta$ as

S is a quotient space, $\Delta$ be the differential geometry, $\partial \in \Delta, {\partial }_{i}$ is the set of warpings functions ^[24]. We used the elastic_mean(fd) and fd.mean tool in Python to do the plotting of Figure A1 (supplementary material).

B-spline technique is one of the tools used in smoothing a functional data and this can be done by changing the number of elements (n = 2, 3, 4, …, p) in the basis functions ^[25]. Sometimes one can use the Fourier basis for the functions to further see the variations in the curves. We give a mathematical expression for the basis representation for the curve of the functional data set of the form:

where ${b}_{j}{\rm{\text{'}}}{\rm{s}}$ are basis coefficients and ${\propto }_{j}\text{'}s$ are the basis functions. For this analysis we choose n = 7 which we discovered best suit for the modelling of our data as our number of elements and the tool in Python named basis.BSpline was used to perform the plotting of the functional data. The result of this smoothing technique can be seen in Figure 4.

In Figure A2 (supplementary material), we present the correlation coefficient between all the departments in France based on the functional data in consideration, in order to see how well our data is well correlated between the departments and it was observed that there is a high correlation between various departments with except in few cases where we observed low correlation as we can see in the contour plots presented in Figure A2a–h (supplementary material).

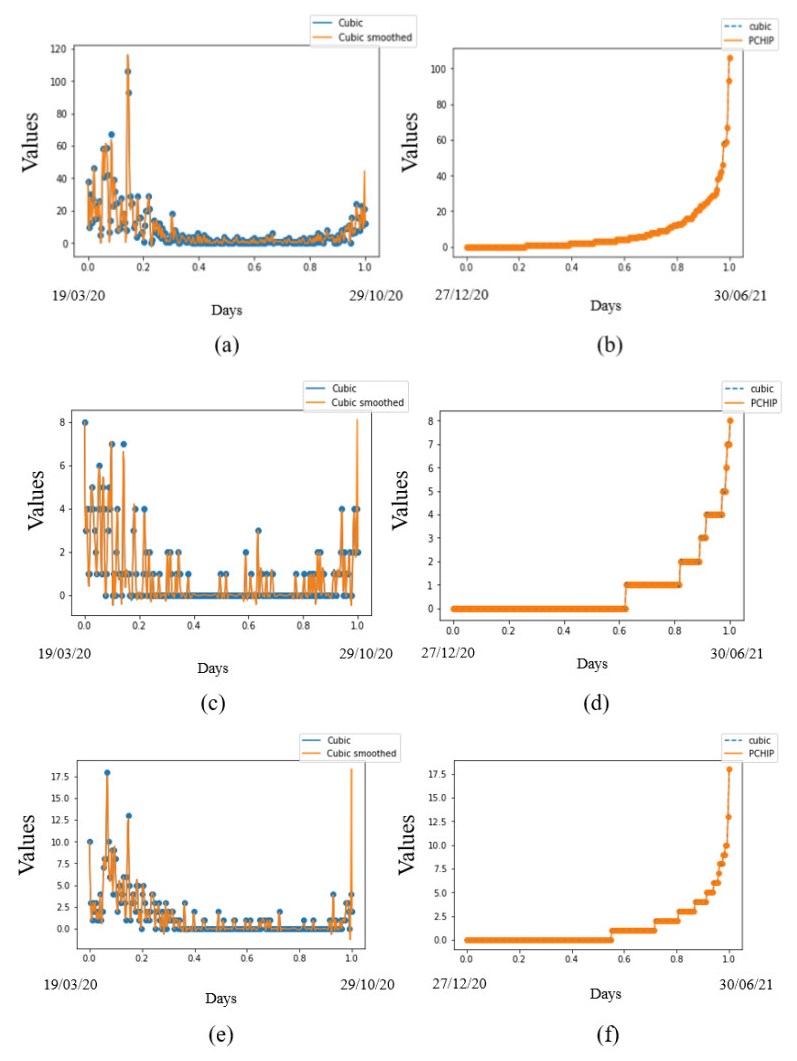
We used spline interpolation of order 3 and then smooth the interpolation using the smoothness parameter equal to 1.5 in the cubic spline smoothing. This technique is implemented using interpolation and smoothness_parameter package in Python. We also use the monotone technique and a piecewise cubic Hermite interpolating polynomial (PCHIP) using a Python package called monotone. We present some of the results on Figure A3 (supplementary material).

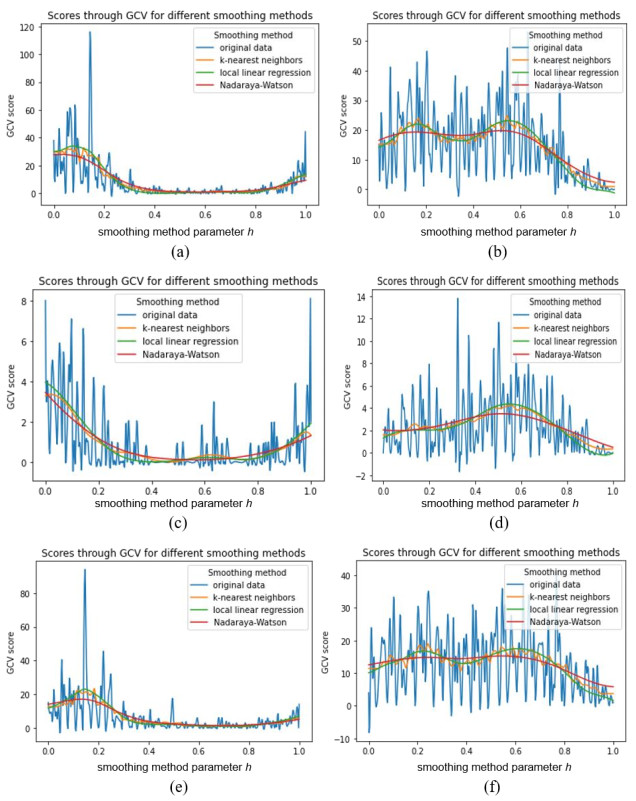
We also performed Kernel smoothing to show how cross validation score varies over a range of different parameters used in smoothing methods. The essence of this section is to estimate the smoothing parameter h that better represents functional data. It has been selected by generalised crossvalidation criteria (GCV). The non-parametric method of smoothing for functional data is based on the smoothing matrix M given:

where K(.) is the Kernel function. We plotted on Figure A4 (supplementary material) the smoothed curves of the functional data set for three different smoothing methods and show the scores through generalised cross-validation for these different methods. The results show a comparable behavior of these scores by varying the smoothing parameter h.

3.   Functional principal component analysis (FPCA)

Principal component analysis is a dimension reduction analysis tool in multivariate statistics while functional principal component analysis (FPCA) is a dimension reduction with high correlation in functional data analysis which completes the statistical tools used in the modelling of biomedical data especially epidemiologic ones ^{[45,46,47,48,49,50,51,52,53,54]}. Let ${\left\{ {{x_i}\left( t \right)} \right\}_{i = 1,m}}$ be a given set of functions, in our case m=101 and let $\alpha$ be a weight, FPCA is computed as follows:

1) It finds the principal component weight function ${\alpha }_{1}\left(t\right)$ for which the principal component score is given by

while maximizing $\sum\nolimits_{i = 1,m} {f_{i1}^2}$ is subjected to

2) Next, the weight function ${\alpha }_{2}\left(t\right)$ is computed and the principal component score maximizes $\sum\nolimits_{i = 1,m} {f_{i2}^2}$, and is subject to the constraint ${‖{\alpha }_{2}‖}^{2} = 1$ and to the additional constraint

3) Then, the process is repeated for as many iterations.

In our analysis, we used a tool called pca.fd for the principal component analysis. We present in this section the 4 PCs values plot throughout the days considered and the principal component scores plot for all the different departments providing functional data being before vaccination started and during vaccination.

3.1.   Functional PCs

3.1.1.   Hospitalization cases

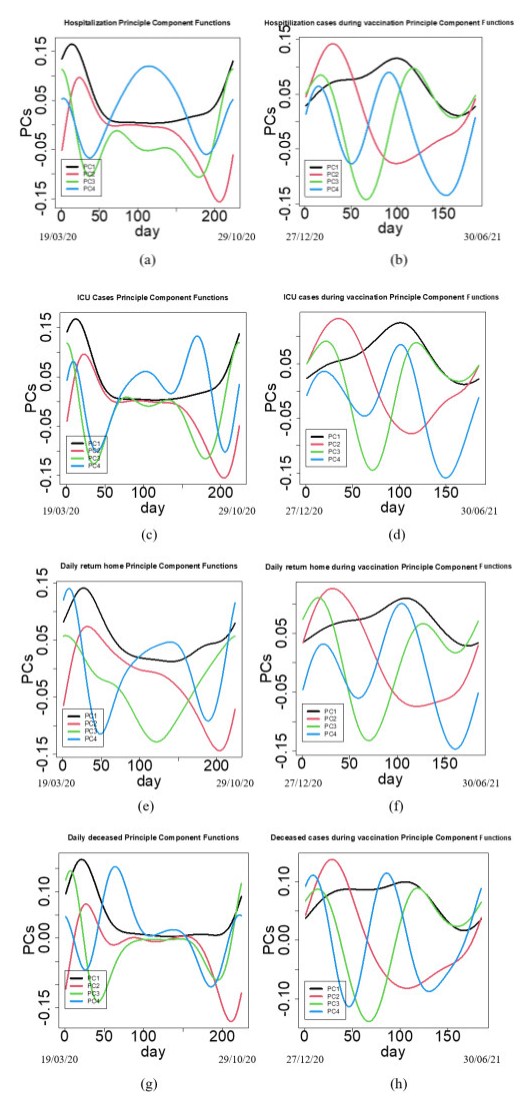
In Figure 5a we observed that PC 1 peaked in the early days of the pandemic between February and March 2020 and then there was a decline after about 50 days becoming stationary till day 150 possibly due to mitigation measures promulgated during this period. The same phenomenon has been observed for PC 2. In Figure 5a, PC 4 shows a sinusoidal shape, peaked at day 100 which is around June 2020 with least values at day 30 and day 180 which are respectively in March and August 2020. Figure 5b shows the same sinusoidal shape for PC 4 and same shape for PC 3 but with a drift in the observation with a difference between the dynamics of hospitalization cases before and after vaccination has started in France. PC 1 in Figure 5b shows a decline across the infective period which may be due to the aggressive vaccination campaign in the country.

3.1.2.   ICU cases

In Figure 5c we observed that from day 50 (around April 2020) till day 150 (around July 2020), the PC 1 value which is the major PC is stable throughout this period of various confinement measures in France and all PCs tend to show increasing behavior after the confinement measures have been relaxed and in Figure 5d, PC 1 has strictly positive values while PCs 2–4 show negative values between February to June 2021.

3.1.3.   Daily return home

In Figure 5e PC 1 peaked with a positive value at the beginning of the pandemic in France which validates the percentage of recovery as presented in the introduction section while PC 1 in Figure 5f shows a positive decline across the days considered, with a disparity between the period of vaccination and without vaccination.

3.1.4.   Daily deceased

On the y-axis of Figure 5g, h, we observe that this is the only result with low values for the PCs because the deaths due to COVID-19 in France remain at a low level, while all PCs show almost the same pattern as that observed in previously for the other variables.

In Table 2, we present the PCs variance proportion and we observe that PC 1 is the most important principal component.

3.2.   Functional principal component scores and clusters

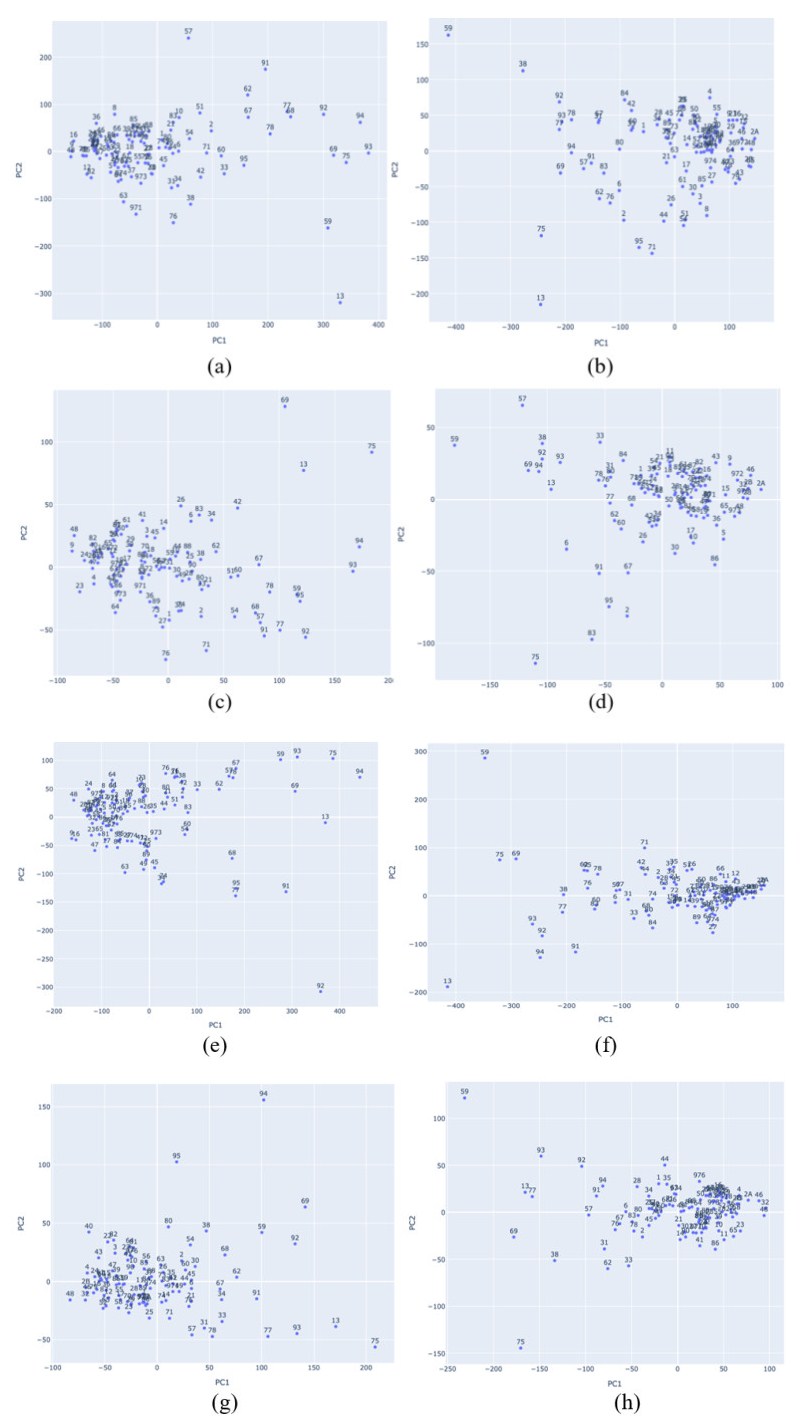
We will now concentrate our efforts on the departments where the pandemic is most prevalent, as well as on PCs 1 and 2, while ignoring the other PCs. We recall that French departments have code numbers, for example, Nord is code number 59, and we will use this number in this section as well as in the visualization of results shown in Figures 6 and 7. We refer readers to ^[55] for a complete list of all French department code numbers. In Figure 6a, the Paris department (code number 75) and Nord department (code number 59) have a positive score in PC 1 and negative score in PC 2 while the Essonne department is positive in both PCs. In Figure 6b, the Paris department and Essonne department (code number 91) are negative in both PCs while the Nord department is positive in PC 2 with the highest score and negative in PC 1. In Figure 6c, Nord and Essonne departments are negative in PC 2 but positive in PC 1 while the Paris department is positive in both PCs. The Paris department and Essonne department are negative in both PCs in Figure 6d while the Nord department is positive in PC 2 and negative in PC 1. In Figure 6e, Paris and Nord departments have positive scores in both PCs while the Essonne department is negative in PC 2 and positive in PC 1. Nord department has the highest positive score in PC 1 for Figure 6f and negative for PC 1, Paris department is positive in PC 2 and negative in PC while Essonne department is negative in both PCs. The Paris department has the highest positive score in PC 1 and negative in PC 2 in Figure 6g, Nord department is positive in both PCs while Essonne department is negative in PC 2 but positive in PC 1. Finally, in Figure 6h while Nord department is positive and highest in PC 2, Paris department is the lowest with negative score in PC 2. Both departments are negative in PC 1. Essonne department is positive in PC 2, but negative in PC 1. The above description shows that there is a difference between the vaccination period in France and the period when measures like lockdown, social distancing etc. were only used to control the spread of the virus despite the fact that it has been proven medically that people can be vaccinated and still be infected.

The diagrams in Figure 6a–h show the same shift toward positive PC 1 values. These shifts demonstrate the effect of various mitigation measures differences in the departments and based on population and migration in this area, particularly the five departments outside France's metropole where the rules in France are not strictly enforced. It also demonstrates that PC 1 is the most important PC, from which the majority of the analysis information can be obtained.

4.   Canonical correlation analysis (CCA)

Canonical correlation is an aspect of multivariate statistical analysis method that is used to simultaneously correlate several metric dependent variables and several metric independent variables measured on or observed with similar experimental units. PCA is often used for dimensionality reduction of a particular data set through linear combinations of the initial variables which maximizes the amount of variance explained by these linear combinations while CCA finds linear combinations within a data set with the goal of maximizing the correlation between these linear combinations ^[23].

Mathematically, it can also be expressed as two groups of n-dimensional variables

and

where

The purpose of canonical correlation analysis is to find coefficient vectors

in order to maximize the correlation $\beta = corr\left(X{\boldsymbol{a}}_{1}, Y{\boldsymbol{b}}_{1}\right),$ while ${U}_{1} = X{\boldsymbol{a}}_{1}$ and ${V}_{1} = Y{\boldsymbol{b}}_{1}$, linear combinations of X and Y components respectively, constitute the first pair of canonical covariates. Then, the second pair of canonical variates can be found in the same way subject to the constraint that they are uncorrelated with the first pair of variables. By repeating this procedure, the $r = min\left\{p, q\right\}$ pairs of the canonical variates can be found and we will finally get the matrix A = $\left[{\boldsymbol{a}}_{1}, {\boldsymbol{a}}_{2}, {\boldsymbol{a}}_{3}, \dots {\boldsymbol{a}}_{\boldsymbol{r}}\right]$ and the matrix B = $\left[{\boldsymbol{b}}_{1}, {\boldsymbol{b}}_{2}, {\boldsymbol{b}}_{3}, \dots {\boldsymbol{b}}_{\boldsymbol{r}}\right]$ to transfer X and Y to canonical variates U and V following the below expression:

If X and Y are both centered, we can concatenate them and calculate the covariance matrix given as:

where ${C}_{xx}$ and ${C}_{yy}$ are within-set covariance matrices, and ${C}_{xy} = {\left[{C}_{yx}\right]}^{T}$ are between-set covariance matrices. The first canonical variates ${\boldsymbol{a}}_{1}$ and ${\boldsymbol{b}}_{1}$ maximize the equation below:

The subsequent pairs of canonical variates ${\boldsymbol{a}}_{\boldsymbol{i}}$ and ${\boldsymbol{b}}_{\boldsymbol{i}}$ (i≥2) maximize:

subject to the constraint:

The analysis was performed using a package CCA. We present the visualization results on Figures 7 and 8 and also present the correlation scores in tabular form (see Table 3). We used the variables as presented in Table 3. X are the variables are listed in the first row of Table 3 i.e., total number of hospitalizations, daily return home, deceased and ICU cases for all departments and Y variables are the response variables described earlier as presented in the first column of Table 3.

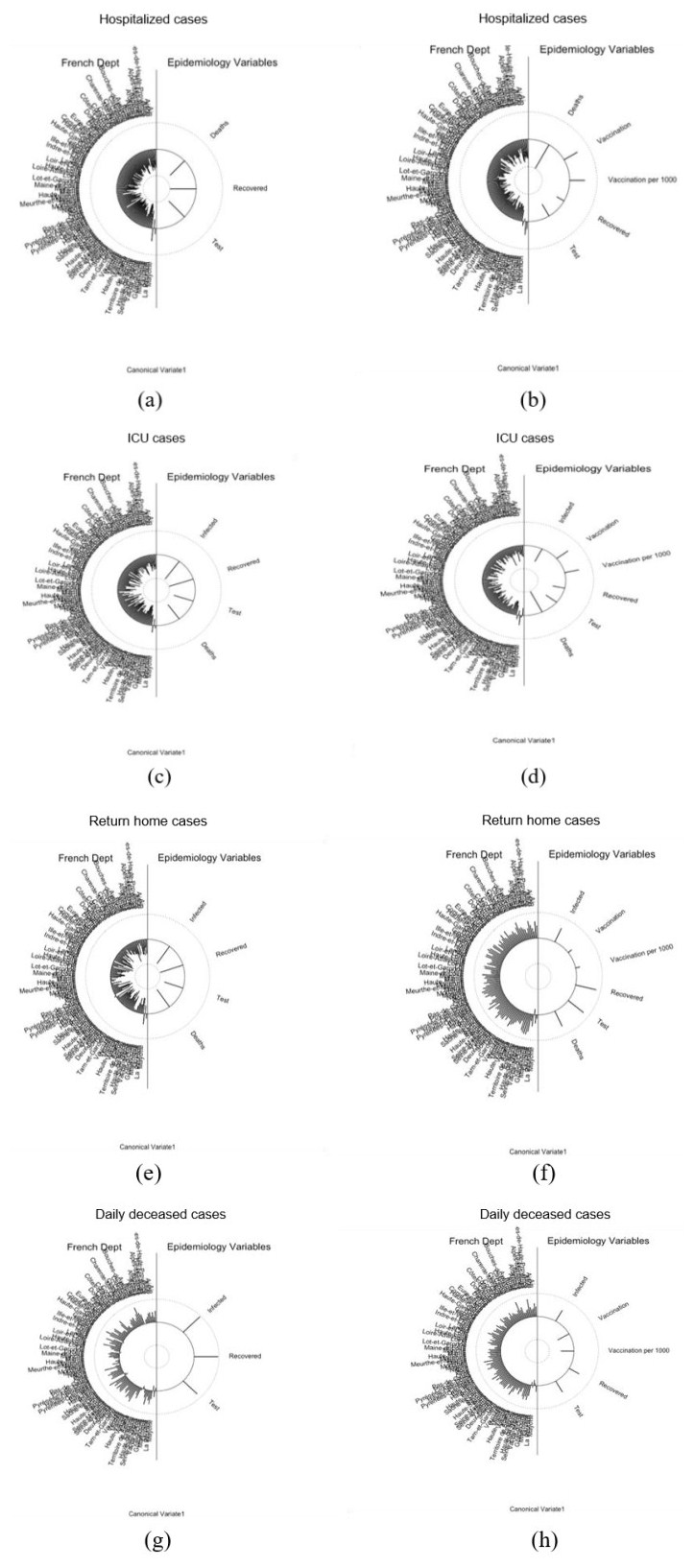
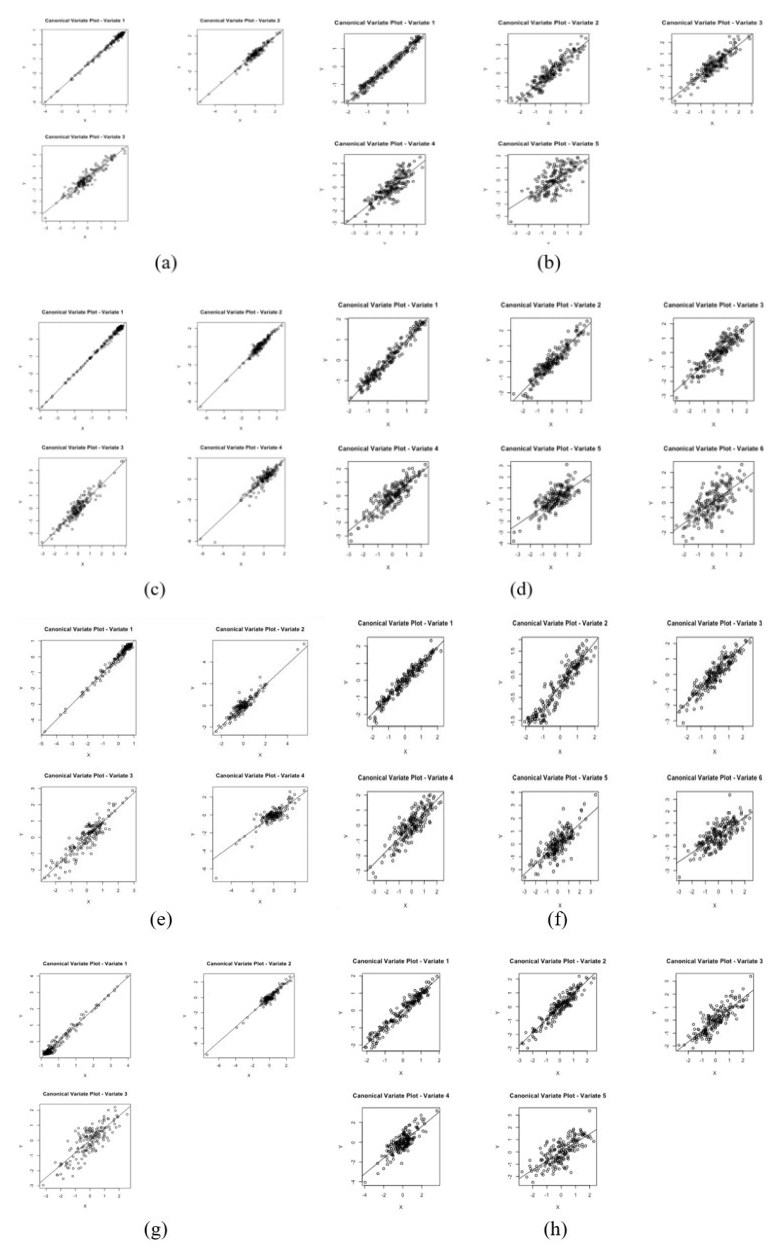
The helio plot in Figure 7 depicts the relationships between the different departments in France, as well as the epidemiology variables and control measures (vaccination). Figure 7a, c, e showed a negative correlation between the epidemiology variables and the hospitalization, ICU, and daily return home cases across departments, whereas Figure 7g showed a positive correlation between the epidemiology variables and the deceased cases across departments. Figure 7b, d, f confirm the effect of vaccination on the number of hospitalizations, ICU, and daily return home during vaccination, demonstrating a positive correlation and the effect of this control measure, whereas Figure 7h shows a negative correlation, indicating a negative relationship between the deceased and the vaccination introduced. The results presented in Figure 8 show the linear relations in the scatter plot as most of the variables show 95% significance level and from Table 3 there is high correlations between the variables considered. The Figure A5 (supplementary material) presents the redundancy between the canonical variates. We tested the canonical correlation, and the null hypothesis is when the canonical correlation is equal to zero. Figure 8a shows hospitalized cases with p-value < 0.05 for all canonical variate, Figure 8b shows hospitalized when vaccination has started with p-value < 0.05 except the last canonical variate with p-value = 0.88, Figure 8c shows ICU cases with p-value < 0.05 for all canonical variate, Figure 8d shows ICU cases when vaccination has started with p-value < 0.05 except the last two Canonical variate with p-value = 0.68 and p-value = 0.87 respectively, Figure 8e shows daily return home with p-value < 0.05 for all canonical variate, Figure 8f shows daily return home when vaccination has started with p-value < 0.05 except the last two canonical variate with p-value = 0.14 and p-value = 0.34 respectively, Figure 8g shows daily deceased with p-value < 0.05 except the last canonical variate with p-value = 0.08 and Figure 8h shows daily deceased when vaccination has started with p-value < 0.05 except the last two canonical variate with p-value = 0.08 and p-value = 0.46 respectively.

5.   Clustering method

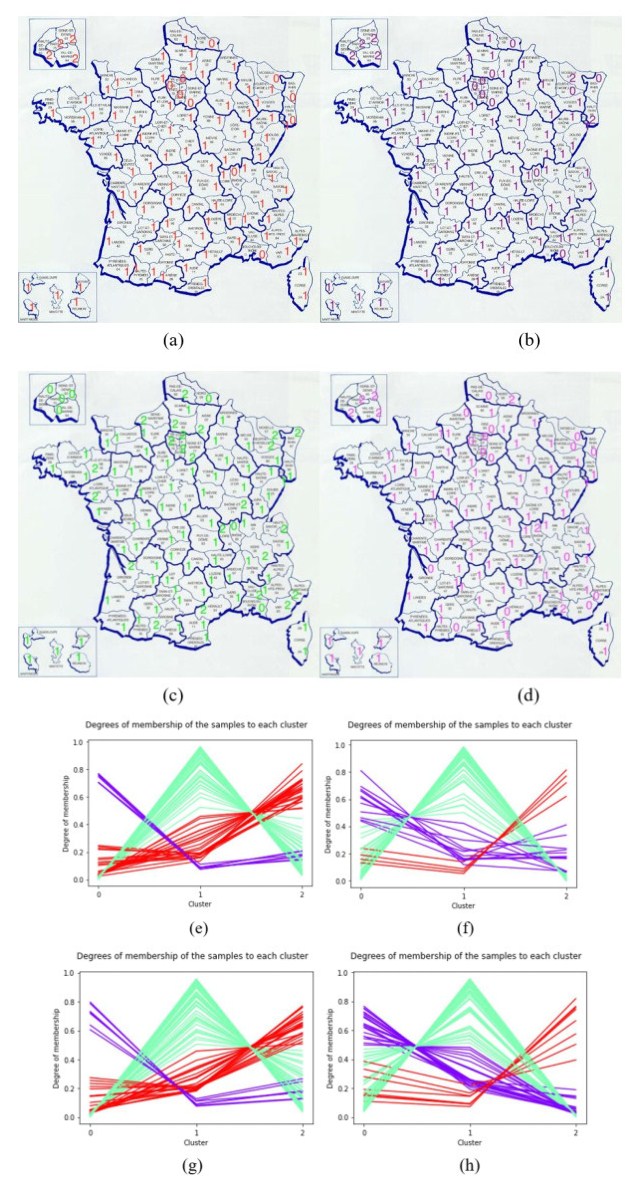
The clustering of functional data is one method that statisticians are always interested in and in this section we used the K-means and fuzzy K-means techniques whose algorithm is already in Python skfd.ml.clustering and FuzzyCMeans. These methods will enable us to visualize how various departments are clustered based on our functional data and to give it the best interpretation based on their geographical location. The basic function used for the K-means clustering is a B-spline and results of our clusters are presented below. We present the result in the cluster form and also on the map of France with indication of the membership to the 3 (i.e., K = 3) clusters (0, 1 or 2) to get a clearer view of the result. Even if we increase the value of K, it won't improve the results as K is optimal. We only presented the result for two cases (daily hospitalized and daily deceased) for the period before vaccination begins in France and two cases (daily return and ICU cases) for the period when vaccination has started in France. In Figure 9a–d we present the clusters (0, 1 or 2) that each French department belongs to. The result clustered French departments outside metropole or the French hexagon to the same clusters which of course are not binded with mitigation measures and rules used in departments within France ^[55]. Also, departments close to Paris are in the same cluster which is the same with departments having the same trend of the pandemic prevalence as presented in Figure 9a–d. In Figure 9e, g we observed same pattern for the data points in the clustering which means that the same way we have more hospitalization cases before vaccination, we also have the more people returning home during vaccination which affirm the fact that the vaccination campaign in France has helped to mitigate the spread of the disease. Figure 9f, h is a bit tricky because of the pattern they followed but it is not surprising that we have more deceased in most departments before vaccination period and less ICU cases during the vaccination period. These patterns of having more cluster points attaining the highest peak in PC 1 is distinct in the results presented.

6.   Prediction

6.1.   Function to scalar linear model

In this section we used functional linear regression model to predict two of our response variables. Let

where $\theta$ is the unknown function of the model, X is a functional covariate belonging to some functional space $\mathbb{H}$ which is endowed with an inner product $< ., \mathbb{ }\mathbb{ }\mathbb{ }\mathbb{ }. >$, Y is the response variable and $ϵ$ is the random error term. Usually, $\mathbb{H}$ is the space ${L}^{2}\left(\left[a, b\right]\right)$ of square integrable functions on some real compact interval $\left[a, b\right]$ and

is the corresponding inner product, where the functions f, g ${\in L}^{2}\left(\left[a, b\right]\right)$. Then, we consider C = $\left[{\rm{0, 1}}\right]$, so the Eq (12) can be written as:

where $\theta$ is a square integrable function which is defined on C and $ϵ$ is a random variable such that $\mathbb{E}\left(ϵ\right) = 0$and $\mathbb{E}\left(X\left(t\right)ϵ\right) = 0$. The Eq (18) can be rewritten as:

where ${\rm{\Psi }}$ represents the integral.

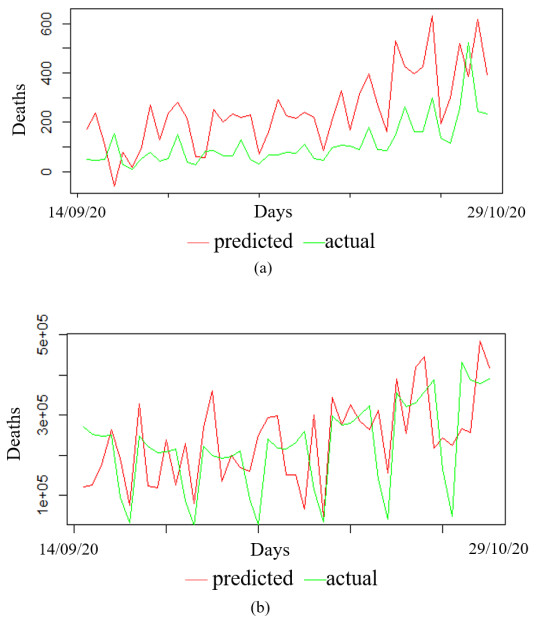
We treated the functional data X (hospitalization) as a curve whose prediction is linked to a scalar Y (number of deaths and tests between 19/03/20–13/09/20 which is the time interval representing $\left[{\rm{1,177}}\right]$) response variable. The time interval for in which the response was predicted is from 14/09/20–29/10/20 which represent $\left[{\rm{178,225}}\right].$ The data considered are data before vaccination started in France and we trained 80% of the data and 20% was tested. The visualization of the results is presented in Figure 10 and the tabular form of the numerical results can be found in Table A1 (supplementary material). The prediction affirms the fact that the relaxation in the mitigation measures during the studied period increases the number of deaths and tests in France, the predicted results of deaths being systematically higher than the observed values as seen in Figure 10a and Table A1.

6.2.   Function-on-function linear model

We consider functional input and output regression model where we treated y(t) as response variable and x(s)'s as predictors at each time t, i.e., $x\left(t\right)\to y\left(t\right).$ The functional linear model with an intercept is of the form:

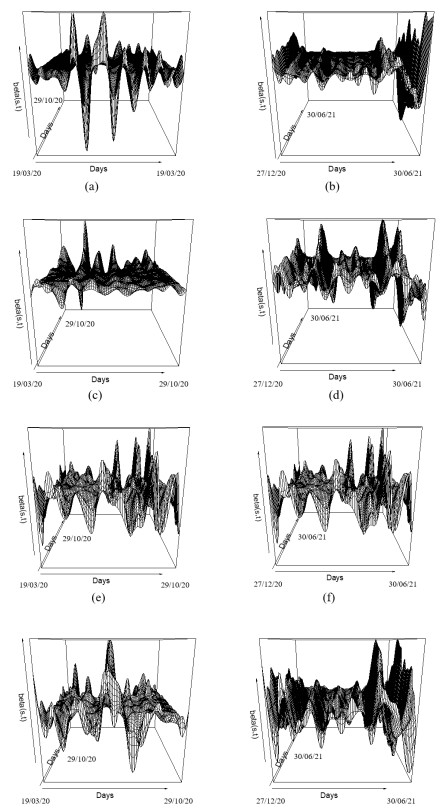
We used this method to perform a function-on-function linear regression on our set of functional data by using the functional data curves of 101 days (predictors) to predict another set of curves of 101 days (response) while also estimating the slope $\beta \left(s, t\right)$, whose results in considered cases are presented in 3D diagrams of Figure 11.

Figure 11a shows hospitalized cases with the slope on the interval $-2.799063\le \beta \left(s, t\right)\le 1.980147$, Figure 11b shows hospitalized when vaccination has started with the slope on the interval $-1.501887\le \beta \left(s, t\right)\le 1.076421$, Figure 11c shows ICU cases with the slope on the interval $-1.0733846\le \beta \left(s, t\right)\le 0.841100$, Figure 11d shows ICU cases when vaccination has started with the slope on the interval $-0.5646148\le \beta \left(s, t\right)\le 0.3661280$, Figure 11e shows daily return home with the slope on the interval $-0.6755000\le \beta \left(s, t\right)\le$0.7030529, Figure 11f shows daily return home when vaccination has started with the slope on the interval $-0.4333295\le \beta \left(s, t\right)\le$0.4300995, Figure 11g shows daily deceased with the slope on the interval $-0.3277864\le \beta \left(s, t\right)\le$0.4002531 and Figure 11h shows daily deceased when vaccination has started with the slope on the interval $-0.3284866\le \beta \left(s, t\right)\le$0.3641679. We observed that in all these Figures in this section, the 3D surfaces yield results whose shapes look roughly similar to the slope curve, functional predictors curve and functional response curve.

7.   Perspectives and conclusions

We studied in this article the best way to summarize temporal information relating to the variations of variables linked to the epidemic dynamics of COVID-19, such as hospitalized cases before and after vaccination has started, medical intensive care unit (MICU) cases before and after vaccination, daily return home cases before and after vaccination, and daily deceased before and after vaccination. Using the functional principal component analysis, it was shown that the first functional principal component well summarized the U or W shape observed for the data related to the first three principal components. This discovery confirms the importance of this first component for the explanation and the qualitative prediction from the observed data. The influence of the vaccination is visible, because the U or W shape is attenuated after vaccination, and does not come close to the shapes observed for seasonal influenza ^[16,44]. The subsequent functional principal components have poor predictive power, but the second component clearly shows the reducing influence of vaccination on all epidemic variables. A further, more in-depth study could undoubtedly show the predictive nature of this second component on the future success of a vaccination policy, by comparing different countries with different vaccination rates and by quantifying the phase of descent of the curves of the second component (for example by its slope at the second inflection and by the value of its minimum). We have given the percentage of variation between actual and predicted values, which quantifies the gain obtained by the mitigation measures during the studied period on the number of deaths in France, systematically higher than the observed values as seen in Figure 8 and Table A1.

Acknowledgments

The authors wish to acknowledge the Petroleum Technology Development Fund (PTDF) Nigeria doctoral fellowship in collaboration with Campus France Africa Unit.

Conflict of interest

Authors declare no conflict of interest.

Supplementary