1.
Introduction
The Takagi-Sugeno (T-S) fuzzy system has a strong ability to approximate the nonlinear systems [1,2,3]. Compared with the T-S fuzzy system based on type-1 theory, the superiority of IT2 T-S is that it can solve the parametric uncertainties existing in the systems. Due to this fact, many significant works based on the IT2 T-S scheme were explored in [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]. Among them, the authors in [4] and [5] investigated reasonable initialization enhanced Karnik-Mendel algorithms and weighted-based non-iterative algorithms for interval type-2 fuzzy logic systems. The authors in [6,7,8,9,10] studied the state feedback control design for the IT2 T-S fuzzy systems. Alternatively, [11,12,13] introduced the output feedback fuzzy control schemes to address this issue. The authors in [14,15,16,17,18] proposed stable fuzzy state feedback controllers for IT2 T-S with the discrete-time form. For IT2 T-S fuzzy interconnected systems, the fuzzy decentralized output feedback controller has been proposed in [19]. However, it is obvious that although the control methods mentioned in the above results can make the T-S systems based on IT2 fuzzy theory reach the asymptotically stable performance, they ignored the finite convergence time problem which is eagerly desired in practical situations.
Note that the control target of the finite time stability is that the trajectory of system state can approximate the periodic orbits or equilibrium values within a finite time. Besides, the systems converge rapidly and have better robustness subject to uncertainties. Hence, the concept of finite-time is introduced in [20,21,22,23] and it has received increasing attention and achieved great progress over past decade [24,25,26,27,28,29,30,31]. Among them, [24,25] respectively studied the H∞ finite-time control design problem subject to the measurable uncertain continuous-time Markovian jump systems and discrete-time Markovian jump systems, respectively. Alternatively, the authors in [26] and [27] studied the output feedback H∞ finite-time control design problems. For IT2 T-S fuzzy systems, the finite-time control design problems subject to time delays and actuator faults are studied in [28] and [29]. Besides, the designed approaches in [30] and [31] have extended the fuzzy decentralized control schemes for IT2 T-S fuzzy interconnected systems while the states of each subsystem is available. However, the aforementioned works are based on the assumption that the system states are measurable, thus they are not suitable for the condition in which the states are immeasurable. Besides, they also ignore the phenomenon of the actuator saturation. In practice, the impact of input saturation will extremely damage the control performance of the systems. Hence, the robust H∞ output feedback finite-time control for IT2 T-S fuzzy systems with input saturation and external disturbances is worthy studying. By far, there are no results on investigating the robust H∞ output feedback finite-time control for IT2 T-S fuzzy systems in presence of external disturbances and input saturation.
This paper develops the robust observer-based H∞ output feedback finite-time controller for the IT2 T-S fuzzy systems in presence of external disturbances and input saturation. In the process of control design, an observer associated with IT2 T-S states is firstly designed, and then a robust fuzzy finite-time controller is developed by using the estimating states. After that, a polyhedron model to represent input saturation is introduced. Based on the Lyapunov function scheme and LMIs theory, the sufficient conditions of finite-time stabilization for system with input saturation and external disturbances are gained. The primary contributions of this paper can be roughly concluded as follows
(i) This paper first studied the fuzzy output feedback finite-time H∞ control design problem for the IT2 T-S fuzzy systems. By developing a state observer, the proposed the fuzzy output feedback finite-time control method can not only guarantee the finite-time stabilization of the closed-loop system, but also solve the state unmeasured problem. Note that although the reference [11,12,13,19] also developed the fuzzy output feedback control methods for a class of IT2 T-S fuzzy systems, they do not consider the finite-time stability, that is, it investigate output feedback asymptotic control, not the output feedback finite-time control like this paper.
(ii) Note that [28,29,30,31] investigated the finite-time control of IT2 T-S fuzzy system, however, the limitation is that the system state must be completely measurable which are not suitable for systems with immeasurable states like this study. Besides, the impact of input saturation is also investigated in this paper.
The rest of this paper is comprised such that: Section 2 gives the descriptions of the IT2 T-S fuzzy systems, state observer design, actuator saturation functions and necessary definitions and lemmas. The robust finite-time H∞ controller design, the finite-time stabilization and the finite-time boundedness conditions of the considered system are derived in Section 3. In order to verify the feasibility of the developed scheme, two practical examples are given in Section 4. Section 5 derives the conclusion.
2.
Preliminaries
In this section, the descriptions of the IT2 T-S fuzzy system and input saturation functions will be shown.
2.1. IT2 T-S fuzzy system
Consider the IT2 T-S fuzzy system with continue-time form as follows.
Plant rule p: If θ1(x(t)) is Fp1 and ⋯ and θi(x(t)) is Fpi, then
where θs(x(t))=[θ1(x(t)),θ2(x(t)),…,θi(x(t))]T represents the premise vector and Fps represents the IT2 fuzzy set. x(t)∈ℜn, sat(u(t))∈ℜm and w(t)∈ℜh are system state vector, saturated control input vector and bounding external disturbances satisfying L2(0,∞], respectively. z(t)∈ℜg is the controlled output and y(t)∈ℜl is the measured output. Ap, Bp, Dp, Ep, Fp and Cp are known constant matrices with appropriate dimensions.
Based on the IT2 fuzzy logic systems theory, the firing strength of the pth fuzzy rule can be defined within the following interval sets
Through utilizing the method of singleton fuzzifier, product fuzzy inference, and weighted average defuzzifier, the IT2 T-S fuzzy system (2.1) is inferred as follows
in which
the above ϑLP(θ(x(t))), ϑUP(θ(x(t))) are the lower and upper grades of memberships, respectively. μ_Fps(x(t)) and ˉμFps(x(t)) are the lower and upper membership functions of IT2 fuzzy sets Fps. υLP(θ(x(t))), υUP(θ(x(t))) are known weighting coefficient nonlinear functions.
2.2. Saturation functions
The aforementioned u(t) is the control signal given by the ideal output feedback fuzzy controller and sat(u(t))=[sat(u1),sat(u2),…,sat(um)]T is the practical control signal, which is used to address saturation problem.
In order to model better saturation effect, the polytopic model introduced in [32,33] will be utilized. Referring from [32,33], we can obtain such that
in which sat(ua)=sign(ua)min{¯ua,|ua|},¯u∈ℜm is the saturation level and u(t)∈ℜm represents the control input, ¯ua and ua are the ath element of the saturation level and the control input, respectively.
Let V be the set of m×m diagonal matrices whose diagonal elements are either 1 or 0. For example, when m=2, then
There are 2m elements in V. Suppose that each that element of V is labeled as Hl,(l=1,2,…,2m), and denote H−l=I−Hl. Clearly, H−l is also an element of V when Hl∈V.
For development, the following lemma associated with input saturation is required.
Lemma 1 [32,33]. Assume |va|≤ˉua, in which va and ua denote the ath element of v∈ℜm and u∈ℜm, respectively. If x(t) is inside r∩j=1{x∈ℜn||hjpx|≤ˉup}, then
in which 0≤δl≤1(l=1,…,2m) are scalars and ∑2ml=1δl=1.
2.3. Observer-based controller design
In this subsection, a state observer will be designed to estimate immeasurable states. Subsequently, the fuzzy controller will be proposed.
The identical membership functions, which rely on estimated states rather than system states, are used to design the fuzzy observer.
Observer Rule q:If θ1(ˆx(t)) is Fq1 and ⋯ and θq(ˆx(t)) is Fqi, then
where ˆx(t)∈ℜn denotes the estimated state vector, ˆz(t)∈ℜl is the estimation output and ˆy(t)∈ℜl is the observer output, Lp is observer gain matrix to be solved.
After that, the final state observer is described such that
Due to that the membership functions of fuzzy observer rely on the estimated state variable rather than x(t), thereby, ˆx(t) is selected as the membership function representations.
For the purpose of improving the flexibly of fuzzy controller design, by utilizing non-PDC design algorithm, the controller possesses its exclusive membership functions which are different from fuzzy system (2.3) and fuzzy observer (2.7). The details are shown such that:
Controller Rule j:If g1(ˆx(t)) is Mj1 and ⋯ and gj(ˆx(t)) is Mjτ, then
where Kj(j=1,2,…,r) are the controller gains to be solved later. Similarly, the jth firing strength can be expressed as
in which
Then, the fuzzy controller based on IT2 fuzzy theory can be obtained
where
the above μ_Mjℏ(gℏ(ˆx(t))), ˉμMjℏ(gℏ(ˆx(t))), ηLj(ˆx(t)), ηUj(ˆx(t)), bLj(ˆx(t)) and bUj(ˆx(t)) respectively denote the lower and upper membership functions, the lower and upper grades of membership, the tradeoff coefficient nonlinear functions.
Then, from Lemma 1, the observer-based controller in presence of input saturation is given as
where Zj is m×n matrix and hjp represents the pth row of Zj.
Define the estimation error ˜x(t)=x(t)−ˆx(t), controlled output error ˜z(t)=z(t)−ˆz(t) and considering equations (2.3), (2.7) and (2.11), one can obtain
where
ξ(t)=[x(t)˜x(t)]T, Apqj=[Ap+δlBpHlKj+δlBpH−lZj−δlBpHlKj−δlBpH−lZjAp−Aq−LqCp−LqCqAq−LqCq], Dpqj=[DpDp], Cpqj=[Ep−EqEq].
Control objective: This study will design a robust H∞ finite-time output feedback controller for the IT2 T-S fuzzy systems (2.3). The developed controller can make the T-S systems based on IT2 fuzzy theory reach the finite-time stable, in which the input saturation and external disturbances are considered.
Remark 1: Note that the authors in [19] studied the output feedback control design problem for IT2 T-S fuzzy system, the developed controller can make the controlled system achieve asymptotic stability. However, the authors in [19] do not consider the finite-time stability problem. Unlike the above work, in this paper, the robust output feedback finite-time control design problem for T-S systems with input saturation based on IT2 theory is studied. Therefore, the control design and stability analysis are more difficult and challenging.
2.4. Main definitions and lemmas
For development, the following definitions and lemmas are needed to achieve the control objective.
Definition 1 [20,21]. If for given constants a2>a1≥0 and a positive matrix R>0 satisfying
Then the system (2.3) can be robust finite-time stable within (a1,a2,R,T).
Definition 2 [34]. System (2.3) is of robust H∞ finite-time boundedness performance if there exist positive constants ˉρ>0 and h>0, and the closed–loop system based on IT2 T-S fuzzy theory satisfies (2.13) and following H∞ performance index
where ‖w(t)‖2<h, and T is a given positive scalar.
Lemma 2 [29]. For full rank matrix rank(C)=l,F∈ℜl×n with l<n, there exist a singular value decomposition (SVD) for C=Cp can be described as C=O[S0]UT, in which V∈ℜl×l, O∈ℜl×n, S∈ℜn×n, U⋅UT=I and O⋅OT=I. Let matrices X>0, X11∈ℜl×l, X22∈ℜ(n−l)×(n−l). Then, there exists ˉX satisfies CX=ˉXC if and only if the following Eigen-value decomposition (EVD) condition holds
3.
Stability analysis
The robust finite-time stability analysis and the robust finite-time H∞ boundedness of the fuzzy system (2.3) will be respectively proved in this section. Based on the Lyapunov function method and LMIs theory, several sufficient conditions will be derived.
Theorem 1: For given positive scalars T>0, a1>0, h>0, β>0, δl>0, ˉρ>0 and a positive symmetric R>0, system (2.3) can achieve robust finite-time stability within (a1,a2,R,T,ˉρ,h), if there exist matrix P=PT>0 satisfying the following matrix inequalities
in which
Proof: Construct the following Lyapunov function
For convenience, one define P=diag{P1,P1} and then calculate the time derivative of (3.6), one has
Define χ(t)=[ξ(t)w(t)]T, and then substituting the definition of Apqj, Cpqj, Dpqj into (3.7), (3.7) can be rewritten as
According to [28], the slack matrix is introduced to avoid conservative results as shown such that
Then, from (3.8) and (3.9), one has
Then, based on Theorem 1, one gets
Multiplying (3.11) by e−βt and integrating both sides of (24) from 0 to t, then since ˜zT(t)˜z(t)>0 and Πpqj<0, one can obtain
Then, multiplying (3.12) by eβt, (3.12) can be represented as
Recalling to V(ξ(t))=ξT(t)Pξ(t), ˜P=R−12PR−12 and ‖w(t)‖2<h, (3.13) leads to
in which λ1=λmax(˜P).
Define λ2=λmin(˜P), since V(ξ(t))=ξT(t)Pξ(t)≥λ2ξT(t)Rξ(t), then form (3.14), one has
Suppose ξT(t)Rξ(t)<eβT(λ1a1+ˉρ2e−βThβ(1−e−βT))λ2,∀t∈[0,T], then from Definition 1, finite-time stability of fuzzy system (2.3) is ensured within (a1,a2,R,T,ˉρ,h).
In what follows, we will give the proof of the robust H∞ output feedback finite-time boundedness performance of the fuzzy system (2.3).
From the inequality (3.7), on can easily find that
Similarly, multiplying (3.16) by e−βt, and then integrating it from 0 to T, one has
Under the condition of V(ξ(0))=0 and V(ξ(T))>0, (3.17) can be rewritten such that
Since e−βT∫T0e−βtwT(t)w(t)dt<∫T0e−βt˜zT(t)˜z(t)dt, ˉρ2e−βT∫T0e−βtwT(t)w(t)dt<ˉρ2e−βT∫T0wT(t)w(t)dt, then from (3.18), one can get
Further, the robust H∞ finite-time boundedness performance index has been obtained. Hence, from Definition 2, the fuzzy system (2.3) is finite-time and can achieve a robust H∞ performance.
The solution of positive controller gains Kj, observer gains Lq and positive definite symmetric matrix P are given in following.
Firstly, define X=P−11, Yj=KjX, Sj=ZjX and Tq=LqˉX, by left and right multiplying diag{X,X,I} on both sides of (3.2) and (3.3), thus one can get the following LMIs
where
with
Subsequently, by solving LMIs (3.19) and (3.20), one can obtain X, Yj, Sj and Tq, the it follows P1, Kj=YjX−1 and Sj=HjX−1. According to Lemma 2, the SVD of the output matrix C∈ℜl×n, for C=Cp with a full rank C=O[S,0]UT, and there exists a matrix ˉX∈ℜn×n satisfying CX=ˉXC, if there exists EVD X=U[X1100X22]UT. Then, one can find that O[S,0]UTU[X1100X22]UT=ˉXO[S,0]UT. By calculation, one gets ˉX=OSX11S−1O−1, thus, ˉX−1=OSX−111S−1O−1. For bilinear terms LqCX=LqˉXC, let Tq=LqˉX, then one can obtain Lq=TqˉX−1=TqOSX−111S−1O−1.
From [28,29], we know that the constraint r∩j=1{x∈ℜn||hjpx|≤ˉup} is equivalent to
By Schur complement, (3.21) is equivalent to the following LMI
The design procedures are organized:
Step1: Choose the fuzzy rules, and then give ˉup(p=1,…,r), T>0, a1>0, h>0, ˉρ>0, β>0 and select 0≤δl≤1(l=1,…,2m) which satisfies ∑2ml=1δl=1, and diagonal matrices Hl, H−l, which satisfies Hl+H−l=In.
Step 2: Solve the LMI (3.19), (3.20) to get X, Kj, Zj and Lq.
Step 3: Substitute the solved gains into (3.1), (3.4) and (3.5) to verify whether they are established.
Step 4: In case of the condition (3.1), (3.4) and (3.5) are not satisfied, increase ˉρ, a2 and ˉup(p=1,…,r) and increase β until the conditions are established. Else, decrease ˉρ, a2 and ˉup(p=1,…,r) and increase β and go to Steps 1-4 until X cannot be obtained.
Step 5: Represent the fuzzy state observer (2.7) and fuzzy controller (2.11).
4.
Simulation results
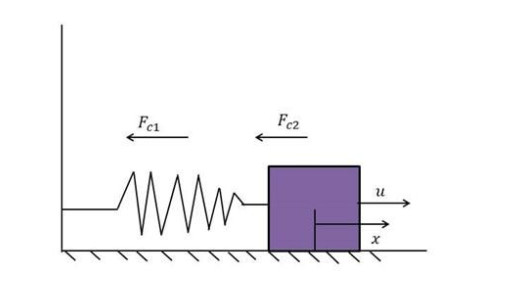
Example 1 (Mass-spring-damping system) A mass-spring-damping system example as shown in Figure 1 is employed to verify the feasibility of the developed scheme in this section. The corresponding dynamical equation is shown as follows
where M is the mass, Fc1 and Fc2=r˙x denote the friction force, Fc2 is the restoring force of the spring, and u(t) denotes the control input. Fc2=r˙x with r>0 and Fc1=d(1+ε2x2)x. Then, (4.1) can be described as
where x is the displacement from a reference point. Define x(t)=[x1(t)x2(t)]T=[x˙x]T and ˜f(t)=(−d−dε2x21(t))/M. The operating domain are x1(t)∈[−2,2] and d∈[5,8]N/M. Let M=1kg, r=2N⋅m/s, and ε=0.3m−1. Then, we can calculate that ˜fmax=−5 in which d=5 and x1(t)=0. ˜fmin=−10.88, d=8 and x21(t)=4.
System (4.2) is approximated by the following two fuzzy models
Rule 1: If θ1(x(t)) is F11, then:
Rule 2: If θ1(x(t)) is F21, then:
where x(t)=[x1(t)x2(t)]T=[x˙x]T, in which x1(t) represents the premise vector.F11 and F21 represent the IT2 fuzzy sets of the known function x1(t).
Finally, the system (4.3) and (4.4) based on IT2 fuzzy theory is represented such that
The fuzzy state observer is designed such that
Then the IT2 T-S fuzzy H∞ output feedback finite-time controller can be obtained as
where H1=1, H−1=0, H2=0, H−2=1, δ1=0.6 and δ2=0.4.
The disturbance input is selected as
The normalized membership functions of fuzzy system, state observer and controller are selected by Table 1, Table 2 and Table 3, respectively.
For given a1=5.8426, a2=12.8613, h=3, β=0.01, ˉρ=0.3, T=10, and then by solving LMIs in Theorem 1 with the saturation levels ˉu=0.18, we are able to get the constants and positive definite matrices as follows:
The results are carried out by choosing the initial conditions x(0)=[0.7−0.6]T, ˆx(0)=[0.6−0.5]T. Then, Figures 2-6 show the responses of closed-loop system. In addition, by Figures 2-3, from which we can see that all the estimations converge to zero asymptotically. Besides, the precise condition ξT(0)Rξ(0)≤a1=5.8426 is verified, and operating domain of the membership functions is established, i.e, x1(t)∈[−2,2]. Figure 4 is the response of the saturated control input u which satisfies the conditions that ˉu≤0.18. From Figure 5, one can find that ξT(t)Rξ(t) stays within the bound of a2=12.8613, which implies that the definition of robust H∞ finite-time stability is satisfied. Figure 6 shows the distance attenuation for the fuzzy system, from which one can know that the robust H∞ finite-time boundedness is satisfied.
Example 2 (Tunnel diode circuit system) A nonlinear tunnel diode circuit system example as shown in Figure 7 is employed to verify the feasibility of the developed scheme in this subsection.
where iL(t) is the inductor current, and iD(t) depicts the nonlinear volt-ampere characteristic of tunnel diode. VC is the voltage of the capacitor C. VD is the voltage of the tunnel diode D, R and L are electrical resistance.
The corresponding dynamical equation is shown as follows
in which τ∈[0.01,0.03] is an uncertain parameter. Let x1(t)=VD(t), x2(t)=iD(t) and g(VD(t))=0.002+τV2D(t) as nonlinear function composed of the terminal voltage across the tunnel diode. Here, state variable is supposed to be x1(t)∈[−3,3]. Then, one can find that gmax=0.0272 with τ=0.03 and x1(t)=3. gmin=0.002 with τ=0.01 and x1(t)=0.
Then, (4.9) can be described as
Then system (4.10) is approximated by the following two fuzzy models
Rule 1: If θ1(x(t)) is F11, then:
Rule 2: If θ1(x(t)) is F21, then:
where x(t)=[x1(t)x2(t)]T, in which x1(t) represents the premise vector.F11 and F21 represent the IT2 fuzzy sets of the known function x1(t).
The normalized membership functions of fuzzy system, state observer and controller are selected by Table 4, Table 5 and Table 6, respectively.
For given δ1=0.7, δ2=0.3, a1=2.9403, a2=10.4953, h=0.3, β=0.2, ˉρ=0.3, T=6, and then by solving LMIs in Theorem 1 with the saturation levels ˉu=0.82, we are able to get the constants and positive definite matrices as follows:
The results are carried out by choosing the initial conditions the same as Example 1. Then, Figures 8-12 show the responses of closed-loop system. In this example, ξT(0)Rξ(0)≤a1=2.9403, saturated control input ˉu≤0.82 and ξT(t)Rξ(t)≤a2=10.4953.
To further verify the feasibility of the proposed fuzzy output feedback finite-time controller, we apply the fuzzy controller in [19], which is designed based on asymptotic stability theory to control system (4.9). Especially pointed out that, the controlled IT2 T-S interconnected system in [19] has been revised as IT2 T-S fuzzy system, thus can be compared further. In the simulation, we utilize the same IT2 T-S fuzzy system and the same initial conditions of x(t) and ˆx(t). The controller and observer gain matrices are as follows:
The simulation results are also depicted by Figs. 8-9. From Figs. 8-9, we clearly know that the variables and their estimations of the controlled system in this study have faster convergent rates than those by [19].
5.
Conclusions
The robust H∞ observer-based finite-time control problem for IT2 T-S fuzzy system in presence actuator saturation has been studied. In order to obtain the finite-time stability and robust H∞ finite-time boundedness for the controlled plant, a fuzzy state observer and a fuzzy robust H∞ finite-time controller with saturation limitation have been proposed. Then, on the basis of the Lyapunov function method and LMIs theory, the finite-time stability sufficient conditions are derived to ensure of IT2 T-S fuzzy systems in presence of input saturation limitation. At last, two practical examples of nonlinear mass-spring-damping and tunnel diode circuit systems is given to verify the feasibility of the developed fuzzy control scheme.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (No. 61903167).
Conflict of interest
The authors declare that there is no conflicts of interest.









 DownLoad:
DownLoad:














